数字信号处理教程课后答案+王世一
- 格式:pdf
- 大小:205.92 KB
- 文档页数:12


第三章1. 解:由DFS 的定义可知{}{}2,0,2,4)k ()(X ~1,...,1,0)(~)(X ~4N 1,0,1,2)()(~10/nk 2=∴-====∑-=-N N n Nj N R k N k e n x k n R n x π,2. 解:题意可知,已知)(~n x 求)(X ~k 的值1,...,1,0k )(~)k (X ~k r )(X ~)(X ~N 1)(~)(X ~N 1)(~n 1,...,1,0r 1,...,1,0)(X ~N 1)(~10n /nk 210n /r -k n 210k 10n /nr 210k /nk 210n /nr 210n /nr 2/nr 2-10k /nk 2-======-=-==∑∑∑∑∑∑∑∑-=--=-=-=--=-=--=--=N e n x r e k e n x e k e e n x N e N n e k n x N Nj N N j N N N j N N j N N j N N j N j N Nj π)(πππππππ代入,得到换元,令到将右式交换求和次序得求和,得到,并在一个周期内对,将等式两边同乘3.解{}{}{}5,4,3,2,16)(R )(~0,0,0,0,1,0)(R )(~6,5,4,3,2,1)(R )(~6N 1,...,1,0)(~)(~1,...,1,0)(~)(~)(~*)(~)(~)(~)(~)(~N 321332101213321,由定义可求得,,且由图可知。
,即一个周期的值,,且只需要计算是在一个周期内进行的注意:周期卷积的运算,则,其周期卷积和的序列若已知两个周期皆为====-=-=-==∑-=n n x n n x n n x N n n x n x N n m n x m x n x n x n x n x n x n x NN N N m 4.1,...,1,0)(X ~N 1)(~10k /nk 2-==∑-=N n e k n x N N j π ,题目给定序列)(~n x 皆为实序列,根据P93页表3-1可知, (a )为了使得)k (X ~为实数,要求 )(~n x 实偶或者虚奇皆可,此处应该是实偶,故现在时间起点时保证序列为偶对称皆可,(a )(b )皆可,[但是(a )图要取在两个采样点的中点。

![《数字信号处理》王世一版北京理工大学出版社部分习题答案【khdaw_lxywyl】[1]](https://uimg.taocdn.com/3617903610661ed9ad51f33f.webp)





————第一章———— 时域离散信号与系统理论分析基础本章1.1节“学习要点”和1.2节“例题”部分的内容对应教材第一、二章内容。
为了便于归纳总结,我们将《数字信号处理(第二版)》教材中第一章和第二章的内容合并在一起叙述,这样使读者对时域离散线性时不变系统的描述与分析方法建立一个完整的概念,以便在分析和解决问题时,能全面考虑各种有效的途径,选择最好的解决方案。
1.1 学 习 要 点1.1.1 时域离散信号——序列时域离散信号(以下简称序列)是时域离散系统处理的对象,研究时域离散系统离不开序列。
例如,在时域离散线性时不变系统的时域描述中,系统的单位脉冲响应()n h 就是系统对单位脉冲响应()n δ的响应输出序列。
掌握()n δ的时域和频域特征,对分析讨论系统的时域特性描述函数()n h 和频域特性描述函数()ωj e H 和()z H 是必不可少的。
1. 序列的概念在数字信号处理中,一般用()n x 表示时域离散信号(序列)。
()n x 可看作对模拟信号()t x a 的采样,即()()nT x n x a =,也可以看作一组有序的数据集合。
要点 在数字信号处理中,序列()n x 是一个离散函数,n 为整数,如图1.1所示。
当≠n 整数时,()n x 无定义,但不能理解为零。
当()()nT x n x a =时,这一点容易理解。
当=n 整数时,()()nT x n x a =,为()t x a 在nT t =时刻的采样值,非整数T 时刻未采样,而并非为零。
在学习连续信号的采样与恢复时会看到,()n x 经过低通滤波器后,相邻的()T n nT 1~+之间的()t x a 的值就得到恢复。
例如,()n x 为一序列,取()()2n x n y =,n 为整数是不正确的,因为当=n 奇数时,()n y 无定义(无确切的值)。
2. 常用序列常用序列有六种:①单位脉冲序列()n δ,②矩形序列()n R N ,③指数序列()n u a n,④正弦序列()n ωcos 、()n ωsin ,⑤复指数序列nj eω,⑥周期序列。

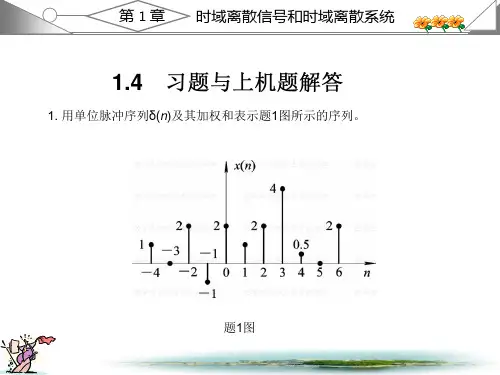
数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n 及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n nn n n n nnn n 2. 给定信号:25,41()6,040,nnx n n其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列;(3)令1()2(2)x n x n ,试画出1()x n 波形;(4)令2()2(2)x n x n ,试画出2()x n 波形;(5)令3()2(2)x n x n ,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n nnnn n n n n n (3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n,A 是常数;(2)1()8()j n x n e 。
解:(1)3214,73w w ,这是有理数,因此是周期序列,周期是T=14;(2)12,168ww,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n;(3)0()()y n x n n ,0n 为整常数;(5)2()()y n x n ;(7)0()()n m y n x m 。
第一章 离散时间信号与系统2.任意序列x(n)与δ(n)线性卷积都等于序列本身x(n),与δ(n-n 0)卷积x(n- n 0),所以(1)结果为h(n) (3)结果h(n-2) (2(4)3 .已知 10,)1()(<<--=-a n u a n h n,通过直接计算卷积和的办法,试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。
4. 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期:)6()( )( )n 313si n()( )()873cos()( )(ππππ-==-=n j e n x c A n x b n A n x a分析:序列为)cos()(0ψω+=n A n x 或)sin()(0ψω+=n A n x 时,不一定是周期序列,nmm m n n y n - - -∞ = - ⋅ = = ≥ ∑ 2 31 2 5 . 0 ) ( 01当 3 4n m nm m n n y n 2 2 5 . 0 ) ( 1⋅ = = - ≤ ∑ -∞ = - 当 aa a n y n a a an y n n h n x n y a n u a n h n u n x m m nnm mn -==->-==-≤=<<--==∑∑--∞=---∞=--1)(11)(1)(*)()(10,)1()()()(:1时当时当解①当=0/2ωπ整数,则周期为0/2ωπ;②;为为互素的整数)则周期、(有理数当 , 2 0Q Q P QP =ωπ ③当=0/2ωπ无理数 ,则)(n x 不是周期序列。
解:(1)0142/3πω=,周期为14 (2)062/13πω=,周期为6 (2)02/12πωπ=,不是周期的 7.(1)[][]12121212()()()()()()[()()]()()()()[()][()]T x n g n x n T ax n bx n g n ax n bx n g n ax n g n bx n aT x n bT x n =+=+=⨯+⨯=+所以是线性的T[x(n-m)]=g(n)x(n-m) y(n-m)=g(n-m)x(n-m) 两者不相等,所以是移变的y(n)=g(n)x(n) y 和x 括号内相等,所以是因果的。
10.讨论一个输入、输出关系由下面线形常系数差分方程联系的因果系统11()(1)()(1)22y n y n x n x n =−++−(a ) 求该系统的单位取样响应(b ) 用(a )中所得结果及卷积和,求对输入()j n x n e ω=的响应 (c ) 求系统的频率响应(d ) 求系统对输入()cos 24x n n ππ⎛=+⎜⎝⎠⎞⎟的响应解:111122)()111122z z a H Z z z −−+==−+−−因为是因果系统,111()[()]()02n h n ZX z n n δ−−==−+≥(1)1)()()()()21212j nn j n nj nj b y n x n h n n eeeeωωωωδ+⎛⎞ =∗=∗−+⎜⎟⎝⎠− =−+−根据1112121212n n n n a a a a a a a a ++−∗= ≠−c)()12()()12()j j j z ej j eH eH z eH ee ωωωωωϕω=+==− =其中(j H e )ω为幅频特性,表示系统对某一频率的幅度响应,()ϕω为相频特性,表示系统对某一频率的相位延迟)sin sin arctan()-arctan()cos 1/2cos 1/2d ωωϕωωω ()=+−题中2πω=,则()1()2arctan 2j H e ωϕω= =所以()cos(2arctan 2)24y n n ππ=++课后答案网 w .k hd aw .c om课后答案网12.试求如下各序列的傅里叶变换 (a )()()3x n n δ=− (b) ()()()11()1122x n n n n δδδ=+++−(c ) ()()0<a<1n x n a u n = (d ) ()(3)(4x n u n u n =+−−)解:334()()1))cos 1))j j nn j j j j j X e x n e a e b c ae e e d e ωωωωωωωω∞−=−∞−−=+1−−1−∑ 13.令表示连续时间线性非时变滤波器的冲激响应,表示离散时间线性非时变滤波器的单位取样相应。
数字信号处理(王世一著)课后答案下载数字信号处理(王世一著)课后答案下载《数字信号处理》这门课介绍的是:将事物的运动变化转变为一串数字,并用计算的方法从中提取有用的信息,以满足我们实际应用的需求。
本定义来自《数字信号处理》杨毅明著,由机械工业出版社发行。
大部分信号的初始形态是事物的运动变化,为了测量它们和处理它们,先要用传感器把它们的特征转换成电信号,等到这些电信号处理完后,再把它们转变为我们能看见、能听见或能利用的形态。
数字信号处理前后需要一些辅助电路,它们和数字信号处理器构成一个系统。
图1是典型的数字信号处理系统,它由7个单元组成。
[2]初始信号代表某种事物的运动变换,它经信号转换单元可变为电信号。
例如声波,它经过麦克风后就变为电信号。
又如压力,它经压力传感器后变为电信号。
电信号可视为许多频率的正弦波的组合。
低通滤波单元滤除信号的部分高频成分,防止模数转换时失去原信号的基本特征。
模数转换单元每隔一段时间测量一次模拟信号,并将测量结果用二进制数表示。
数字信号处理单元实际上是一个计算机,它按照指令对二进制的数字信号进行计算。
例如,将声波信号与一个高频正弦波信号相乘,可实现幅度调制。
实际上,数字信号往往还要变回模拟信号,才能发挥它的作用。
例如,无线电是电磁波通过天线向外发射的,这时的电磁波只能是模拟信号。
数模转换单元将处理后的数字信号变为连续时间信号,这种信号的特点是一段一段的直线相连,如图2所示,有很多地方的变化不平滑。
例如,调制后的数字信号,变成模拟信号后才能送往天线,通过天线就可以向外发射了。
低通滤波单元有平均的作用,不平滑的信号经低通滤波后,可以变得比较平滑。
平滑的信号经信号转换单元后,就变成某种物质的运动变化。
例如扬声器,它可将电波变为声波。
又如天线,它可将电流变为电磁波。
电磁波是一种互相变化的电场和磁场,可以在空间中以波的形式快速移动。
若只考虑电信号的处理过程,数字信号处理系统可看作由五个单元组成,如图3所示。
10.讨论一个输入、输出关系由下面线形常系数差分方程联系的因果系统11()(1)()(1)22y n y n x n x n =−++−(a ) 求该系统的单位取样响应(b ) 用(a )中所得结果及卷积和,求对输入()j n x n e ω=的响应 (c ) 求系统的频率响应(d ) 求系统对输入()cos 24x n n ππ⎛=+⎜⎝⎠⎞⎟的响应解:111122)()111122z z a H Z z z −−+==−+−−因为是因果系统,111()[()]()02n h n ZX z n n δ−−==−+≥(1)1)()()()()21212j nn j n nj nj b y n x n h n n eeeeωωωωδ+⎛⎞ =∗=∗−+⎜⎟⎝⎠− =−+−根据1112121212n n n n a a a a a a a a ++−∗= ≠−c)()12()()12()j j j z ej j eH eH z eH ee ωωωωωϕω=+==− =其中(j H e )ω为幅频特性,表示系统对某一频率的幅度响应,()ϕω为相频特性,表示系统对某一频率的相位延迟)sin sin arctan()-arctan()cos 1/2cos 1/2d ωωϕωωω ()=+−题中2πω=,则()1()2arctan 2j H e ωϕω= =所以()cos(2arctan 2)24y n n ππ=++课后答案网 w .k hd aw .c om课后答案网12.试求如下各序列的傅里叶变换 (a )()()3x n n δ=− (b) ()()()11()1122x n n n n δδδ=+++−(c ) ()()0<a<1n x n a u n = (d ) ()(3)(4x n u n u n =+−−)解:334()()1))cos 1))j j nn j j j j j X e x n e a e b c ae e e d e ωωωωωωωω∞−=−∞−−=+1−−1−∑ 13.令表示连续时间线性非时变滤波器的冲激响应,表示离散时间线性非时变滤波器的单位取样相应。
已知()a h t ()d h n t 0,a>0()0t at a ae h t −⎧ ≥=⎨ <0⎩(a ) 试求模拟滤波器的频率响应,并会出其振幅特性略图(b ) 若,试求数字滤波器的频率响应,并求能使数字滤波器的频率响应在()()d a h n ch nT =0ω=处为1的c 值。
画出(j d )H e ω的幅频特性略图。
解:()001/2221)()1()at j ta j tA A a H j eedt edt a j H j a ∞∞−−Ω−+Ω Ω===+Ω⎛⎞Ω=⎜⎟+Ω⎝⎠∫∫1/220)()()0,0()()11()12cos anT d a j j n anT j n D d aT j n n j D aT aT ce n b h n ch nT n cH e h n e ce e e H e c e e ωωωωωω−∞∞−−−−−=−∞=−−⎧, ≥ ==⎨<⎩ ===−⎛⎞=⎜⎟−+⎝⎠∑∑课后答案网 w ww .k hd aw .c om课后答案网幅度特性1)()1j D aTc H e ce − =+可见要想使0()j D H e为1,则有1aT c e −=+20.下列差分方程表示一线性非时变因果系统()(1)(2)(1y n y n y n x n =−+−+−)(a ) 求这个系统的系统函数()()()X z H z Y z =。
画出()H z 的零、极点分布图,并指出其收敛域。
(b ) 求这个系统的单位取样响应。
(c ) 读者会发现它是一个不稳定系统,求满足上述差分方程的一个稳定(但非因果)系统的单位取样响应。
解:12111212)()()()()()(1a Y z z Y z z Y z z X z Y z z z z X z z z z z )αα−−−−−− =++ ()Η()=== ()−−−− 则零点为,极点为0z=12(1/2)[1 1.62(1/2)[10.62z z αα==+= ==−=−因为是因果系统,所以收敛域为1.62z >,如图所示()12212122)()()()11()[()]()n nzb H z z z z z z z h n Z H z u n ααααααα1−11 =−−⎛⎞=−⎜⎟α−−−⎝⎠==α−α−由于()H z 的收敛域不包括单位圆,所以这是个不稳定系统c)若要使系统稳定,则其收敛域应包括单位圆,则选()H z 的收敛域为0.62 1.62z <<则课后答案网 w ww .k hd aw .c om课后答案网()2121221()1()[()](1)()n nz z H z z z h n Z H z u n u n ααααα1−11⎛⎞=−⎜⎟α−−−⎝⎠==α−−−α−1zz α−对应于一个非因果序列23.见课本58P 上面几行描述,可得(a)----(3), (b)----(1), (c)----(2) 24.考虑一个因果线性非时变系统,它具有下列系统函数()11111a z H z az−−−−=− 式中a 是实数。
(a) 假如0,画出零、极点图,并用斜线画出收敛域。
1a <<(b) 在z 平面内,用通过几何法证明这个系统是一个全通系统。
解:11111)()1a z z a a H z z a az−−−−−− ==−− 零点极点,收敛域为1z a − =z a =z a >)1/1/j b H e a ω === ==见右图,根据余弦定理,有PZ QZ 所以PZ()QZ即频率响应的幅度为常数,所以是一个全通系统第三章 离散傅里叶变换(DFT )2.表示一周期为的周期性序列,而表示它的离散傅立叶级数的系数,也是周期为的周期性序列.试根据确定离散傅立叶级数的系数. %()xn N ()X k N %()xn ()X k 课后答案网 w ww .k hw .c om答案网%%%11110001()01()0()()()()()()()(),N kn Nn N n N kr kn krNN k k n N k n r N n k N k n r Nk X k x n W X k X r X r X k W x n W W x n W N W −=−−−===Ν−1−+=0=−+==⎡⎤ ==⎢⎥⎣⎦= =∑∑∑∑∑∑∑解:据题意,有而的离散傅里叶级数的系数为因为 %%0,()()()n r lNX r N xr lN N x r +=⎧⎨ ⎩=−+=−其他所以N N5.表示一具有周期为的周期性序列, 具有周期为的周期性序列.令表示当看成是具有周期为的周期性序列离散傅立叶级数的系数.而表示当看成是具有周期为的周期性序列离散傅立叶级数的系数.当然为具有周期为的周期性序列, 为具有周期为2的周期性序列.试用确定%()x n N 2N 1()X k %()xn N2()X k %()x n 2N 1()X k N 2()X k N1()X k 2()X k 解:按照题意,有% %%%11021121/2/2220()()()()()()N kn N n N N N kn kn kn N N n n n NX k x n W X k x n W x n W x n W −=−−−======+∑∑∑∑令,则'nn N =− %%% ''11/2'()/2201/201()()()(1)()(1)2N N kn k n N NN n n N jk kn Nn jk X k x n W x n N W e x n W k eX ππ−−+==−−=−=++ =+⎛⎞ =+⎜⎟⎝⎠∑∑∑所以 122,()2k X k X k k ⎧⎛⎞⎪⎜⎟=⎝⎠⎨⎪ ⎩为偶数0,为奇数7. 求下列序列的DFT (a ){ 1,1,-1,-1}(b ){1,j,-1,-j}(c )(n)01x cn n N = ≤≤−课后答案网 w ww .k hd aw .c om课后答案网(d )2(n)sin01nx n NN π= ≤≤− 10()=DFT[()]=()N kn Nn X k x n x n W −=∑ a){}0,2-2j,0,2+2j b) {}0,4,0,0101(1)N-1n=1)()=DFT[()]=()=0,1 (1)(1)()=(1)()=,1,2, (11)(1)(0)2N knN n N k k n N N n kkn NkN N N kN c X k x n cnW W X k cnW k N W X k cW c N W cN cNX k k N W cN N X −=−+= =−−−− =−−− =∑∑∑=− 101(1)(1)01)()=()2j1()2j 2sin12j112sin(0)222cosN n n knN N Nn N k n k nN N n k k NN kk NN d X k W W W W W kW W N k =1,2,.....N -1W W NX Nπππ−−=−−+=− − =−− == , −−=−∑∑ 8.计算下列有限长序列的离散傅里叶变换(假设长度为N )00)()())()())()1n a x n n b x n n n n N c x n a n N δδ = =− 0≤≤ = 0≤≤− 解:1)()=1)()=1)()=0,1, (110)kn N N N n knNk n Na X kb X k W ac X k a W k N aW −=− = =−−∑10. 计算下图两个有限长序列的6点圆周卷积课后答案网 w ww .k hd aw .c om课后答案网x2(-n)的圆周移位x1(n)与x2(n)的6点圆周卷积{5 6 1 2 3 4}11.有限长序列的离散傅里叶变换对应序列在单位圆的z变换的取样。
例如一个10点序列的离散傅里叶变换对应于单位圆上10个等间隔点的()X z的取样。
我们希望找到如下一个取样2100.5()kjNz eX zππ⎡⎛⎞⎛⎞+⎜⎟⎜⎟⎢⎝⎠⎝⎠⎣⎦=⎤⎥,证明如何修改()x n以获得一个序列1()x n致使它的离散傅里叶变换对应于所希望的()X z的取样。
解:[(2/10)/10]9[(2/10)/10]0.59/1010()()[0.5]()0.5j kj kz enn jn knnX z x n ex n e Wπππππ++−==−−===∑∑n可见, 当时, 其离散富立叶变换相当于如图所示的/101()()0.5n jnx n x n eπ−−=()X z的采样.13.列长为8的一个有限长序列具有8点离散傅里叶变换()X k。