2.1整式(2)第二课时

人教版数学七年级上册 2.1整式第二课时教案2.1 整式第二课时1 教学目标1.1 知识与技能：①知道整式、多项式及其概念，能熟练找到多项式的常数项和最高次项，多项式的项数和次数。

②学会正确地用多项式表示实际问题中的数量关系，体会用式子表示数量关系的优越性。

③提高观察、比较、归纳的数学学习能力和语言表达能力。

1.2 过程与方法：①通过具体的情景，发展学生的形象思维。

②通过观察、讨论、自主探究等形式，发展学生的抽象概括能力。

1.3 情感态度与价值观：①通过交流研讨活动，培养学生主动与他人合作的意识。

②在平等的教学氛围中，通过学生之间，师生之间的交流、合作、评价拉近学生之间、师生之间的情感距离。

2 教学重点/难点/易考点2.1 教学重点①多项式的概念及多项式的项、次数的概念。

②整式的概念。

2.2 教学难点①多项式的次数。

②多项式的项。

3 专家建议从学生已掌握的列代数式入手，既复习了所学知识，又巧妙的引入了新知，介绍多项式的项、次数以及常数项的概念后，引导学生循序渐进，一步一步的接近本节课学习的重点、难点。

掌握了所有的概念后由学生自己举一些多项式的例子，这样更能反映出学生掌握知识的程度，同时也体现了学生学习的主体性。

最后列举几个例子，与学生一起完成。

教学中一方面教师要示范严格的书写格式，另一方面也可使学生顺着教师的思路，体验一下老师是如何想的，如何来考虑问题的，然后由学生完成当堂课的练习，也可让一两位同学上黑板完成。

要了解学生是否真正掌握本节课的内容，可由学生自己进行课堂小结，接着布置作业进一步巩固本课所学知识。

4 教学方法知识回顾单项式的概念、系数、次数——多项式的概念——多项式的项、项数、次数——整式的概念——交流讨论——课程小结——巩固练习○1a ○2-y x 231 ○312-x ○422y xy x ++ 多项式有○3○4 练习2 请分别写出下列多项式的项、项数、常数项、多项式是几次几项式。

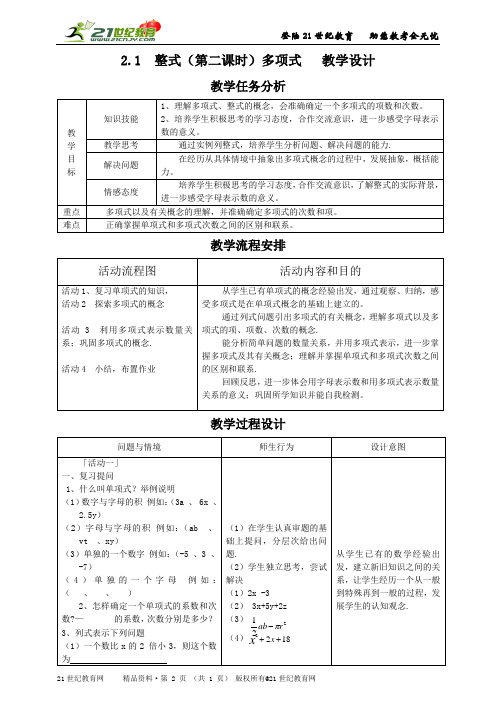
2.1 整式（第二课时）多项式 教学设计教学任务分析教 学 目 标知识技能1、理解多项式、整式的概念，会准确确定一个多项式的项数和次数。

2、培养学生积极思考的学习态度，合作交流意识，进一步感受字母表示数的意义。

教学思考 通过实例列整式，培养学生分析问题、解决问题的能力.解决问题 在经历从具体情境中抽象出多项式概念的过程中，发展抽象，概括能力。

情感态度培养学生积极思考的学习态度，合作交流意识，了解整式的实际背景，进一步感受字母表示数的意义。

重点 多项式以及有关概念的理解，并准确确定多项式的次数和项。

难点正确掌握单项式和多项式次数之间的区别和联系。

教学流程安排活动流程图活动内容和目的活动1、复习单项式的知识， 活动2 探索多项式的概念活动 3 利用多项式表示数量关系；巩固多项式的概念.活动4 小结，布置作业从学生已有单项式的概念经验出发，通过观察、归纳，感受多项式是在单项式概念的基础上建立的。

通过列式问题引出多项式的有关概念，理解多项式以及多项式的项、项数、次数的概念.能分析简单问题的数量关系，并用多项式表示，进一步掌握多项式及其有关概念；理解并掌握单项式和多项式次数之间的区别和联系.回顾反思，进一步体会用字母表示数和用多项式表示数量关系的意义；巩固所学知识并能自我检测。

教学过程设计问题与情境师生行为设计意图「活动一」 一、复习提问 1、什么叫单项式？举例说明 （1）数字与字母的积 例如：（3a 、 6x 、 2.5y ） （2）字母与字母的积 例如：（ab 、 vt 、xy ） （3）单独的一个数字 例如：（-5 、3 、 -7） （4）单独的一个字母 例如：（ 、 、 ） 2、怎样确定一个单项式的系数和次数?— 的系数，次数分别是多少？ 3、列式表示下列问题 （1）一个数比x 的2 倍小3，则这个数为）（1）在学生认真审题的基础上提问，分层次给出问题.（2）学生独立思考，尝试解决 （1）2x -3（2） 3x+5y+2z （3） （4）1822++x x从学生已有的数学经验出发，建立新旧知识之间的关系，让学生经历一个从一般到特殊再到一般的过程，发展学生的认知观念.221r ab π-（2）买一个篮球需要x 元，买一个排球需要y 元买一 个足球需要z 元，买3个篮球、5个排球、2个足球共需要 元。

2.1整式 第二课时测试题一、 选择题1. 如果12221--n b a 是五次单项式，则n 的值为（ ）A. 1B. 2C. 3D. 42. 多项式41232--+y xy x 是（ ）A. 三次三项式B. 二次四项式C. 三次四项式D. 二次三项式3. 多项式23332--xy y x 的次数和项数分别为（ ）A. 5,3B. 5,2C. 2,3D. 3,34. 对于单项式22r π-的系数、次数分别为（ ）A. －2,2B. －2,3C. 2,2π-D. 3,2π-5. 下列说法中正确的是（ ）A. 3223x x x -+-是六次三项式B. 211x x x --是二次三项式 C. 5222+-x x 是五次三项式 D. 125245-+-y x x 是六次三项式6. 下列式子中不是整式的是（ ）A. x 23-B.aba 2- C. y x 512+ D. 0 7. 下列说法中正确的是（ ）A. －5，a 不是单项式B. 2abc-的系数是－2 C. 322y x -的系数是31-，次数是4 D. y x 2的系数为0，次数为28. 下列用语言叙述式子“3--a ”所表示的数量关系，错误的是（ ）A. a -与－3的和B. －a 与3的差C. －a 与3的和的相反数D. －3与a 的差9. 若甲数为x ，甲数是乙数的3倍，则乙数为（ ） A. 3xB. x +3C.13x D. x -310. .小亮从一列火车的第m 节车厢数起，一直数到第n 节车厢（n>m ），他数过的车厢节数是（ ）A. m+nB. n-mC. n-m-1D. n-m+1 二、 填空题11. 下列各式 －41，3xy ，a 2－b 2，53yx -，2x ＞1，－x ，0.5＋x 中，是整式的是 ，是单项式的是 ，是多项式的 。

12. a 3b 2c 的系数是 ，次数是 。

13. 如果222z y x m -的次数与单项式345.3b a 的次数相同，则=m 。

第二课时单项式一、教学目标（一）学习目标1．理解单项式的概念，能正确书写单项式.2．理解单项式的系数和次数的概念.3. 能准确的找出单项式的系数和次数，会用单项式表示实际问题中简单的数量关系. （二）学习重点1.能熟练的运用规X的式子表示实际问题中的数量关系.2.单项式的有关概念.（三）学习难点1.用含字母的式子规X表示实际问题中的数量关系.2.负系数的确定以及准确的确定一个单项式的次数.二、教学设计（一）课前设计（1）表示数或字母的乘积形式的式子叫做单项式．特别地，单独一个数或一个字母也是单项式．（2）单项式中的数字因数叫做这个单项式的系数．（3）一个单项式中，所有字母的指数的和叫做这个单项式的次数．单独一个数字的次数为 0 ．（1）下列各式中单项式的个数是（）3 x ，1x+，52-，4a-，0.72xy，πA．2 B．3 C．4 D．5 【知识点】单项式的定义.【解题过程】解：3x分母含有未知数，不是；1x+不是数或字母的积，不是；剩余四个是单项式，选C.【思路点拨】按单项式的定义进行判断.【答案】C.（2）单项式22x yz -的系数、次数分别是（ ），，，4【知识点】单项式的系数与次数.【解题过程】解：22x yz -的系数是-1，次数是2+1+2=5，选C.【思路点拨】按单项式的系数与次数的定义进行确定.【答案】C. （3）单项式372ab -的系数是，次数是. 【知识点】单项式的系数与次数. 【解题过程】解：372ab -的系数是72-，次数是4. 【思路点拨】按单项式的系数与次数的定义进行确定. 【答案】系数是72-，次数是4. （4）单项式22n x y -与4a b 的次数相同，则n =.【知识点】单项式次数.【解题过程】解：22nx y -的次数是2n +，4a b 的次数是5，所以25n +=，3n =. 【思路点拨】按单项式次数的定义进行确定.【答案】3n =.(二)课堂设计（1）字母表示数的意义.（2）代数式的书写注意的几个问题.（3）列式表示数量关系的方法、步骤.2.问题探究探究一 单项式的有关概念●活动① 回顾列式表示数量关系师问： 用含有字母的式子填空，观察列出的式子有何特点？（1）边长为a 的正方体的表面积为，体积是.（2）铅笔的单价是x 元，圆珠笔的单价是铅笔的单价的2.5倍，圆珠笔的单价是元.（3）一辆汽车的速度是v 千米/时，它小时行驶的路程是千米.（4）数n 的相反数是.学生独立完成，老师课堂巡视，关注中下程度的学生，个别指导.学生举手抢答.【设计意图】通过学生列式，复习书写的规X 和列式解决实际问题的方法和步骤. ●活动② 整合旧知，探究单项式的概念★我们来看引言和例1中的式子：100t ，0.8p ，mn ，2a h ，n -.师问：这些式子中的运算都有哪些共同特点？生答：这些式子都是数与字母、字母与字母之间的乘法运算，它们都是数或字母的乘积. 师问：它们各表示什么意义？生答：100t 表示100·，0.8p ·p ，2a h 表示1·2a ·h ，n -表示-1·n .师问：像这样的式子都是数或字母的乘积运算形式，所以这样的式子叫什么？生答：像这样的式子就叫单项式，还规定单独的一个数或一个字母也是单项式. 师问：单项式定义中应抓住哪些关键特征理解？生答：学生讨论并交流汇报展示总结 ：单项式的特征：1.一种运算----乘法运算；2.三种形式：①数与字母的乘积，②字母与字母的乘积，③单独的数或字母.师问：这些式子哪些是单项式，哪些不是？为什么？(1) 2x y -； (2) 5x - ； (3) 4m ； (4) 5a b + ； (5)-1.生答：（2）、（5）是单项式，（1）（3）（4）不是，因为（2）能写成数或字母的乘积形式，（5）是单独一个数，（1）（3）（4）不能写成数或字母的乘积形式.师问：如何判断一个式子是否是单项式？生答：关键看这个式子能不能写成数或字母的乘积形式.师问：0是单项式吗？π是字母吗？π是单项式吗？生答：0和π都是单项式，π不是字母. 追问：5x -是什么数与字母的乘积？4m为什么不是单项式？他们的区别是什么？ 学生举手抢答.总结：单项式的特征：1.一种运算----乘法运算；2.三种形式：①数与字母的乘积②字母与字母的乘积③单独的数或字母.【设计意图】正确理解单项式的定义以及准确判断一个式子是否是单项式的方法. ●活动③师问：在书写单项式时我们应怎样书写才简洁、美观、规X ？生答：学生小组讨论，再分组回答交流.归纳：老师在学生交流的基础上进行归纳总结强调单项式的书写.① 数与字母、字母与字母相乘一般要省略乘号或者用·表示，如a b ⨯表示ab 或·a b . ②数与字母相乘时，数必须写在字母前面，当这个数为1时可以省略不写，如1ab 表示为ab .当这个数是-1时，只省略1，但“负号”不能省略，如-1ab 表示为 ab -.当这个数是带分数时必须把这个数化为假分数，如235ab -应表示为175ab -. ③式子中出现除法运算时，必须按分数形式来写，如3m ÷应表示为3m . 【设计意图】让学生知道正确规X 的书写单项式使式子更加规X 、简洁.探究二 理解单项式的系数和次数的概念★▲●活动①（探究单项式的系数和次数）师问：什么叫做单项式的系数？生答：单项式中的数字因数叫做单项式的系数，如100t ，0.8p ，mn ，2a h ，n -，2r π的系数分别是100、0.8.1.1.-1.π.师问：我们在指出单项式的系数时应注意哪些？生答：①系数要包含前面的性质符号，②只含字母的单项式的系数为1或-1，③π是数，不能看作字母，常数项没有系数.师问：什么是单项式的次数？生答：单项式中所有字母的指数和.师问：在单项式的次数中我们应该抓哪些关键词理解？生答：学生讨论并交流展示总结：①所有字母的指数和，不要漏掉字母指数为1的情况；②单独一个字母的指数是1；③次数只与字母有关；④单独的一个非零数规定次数为0；⑤单项式根据次数命名的读作几次单项式.【设计意图】通过师生互动加深对单项式的系数和次数的理解.探究三会用单项式表示实际问题中简单的数量关系，并能准确的找出单项式的系数和次数★▲●活动①例1．用单项式填空，指出它们的系数和次数，并正确读出.(1)每包书有12册，n包书有册.(2)底边长为a cm，高为h cm的三角形的面积是2cm.(3)棱长为a的正方体的体积是.(4)一台电视机原价b元，现按原价的9折出售，这台电视机现在售价为元.(5)一个长方形的长为0.9 cm，宽是b cm，这个长方形的面积是cm2.【知识点】单项式表示数量关系，准确判断系数和次数【解题过程】解：（1）12n，系数12，次数1，读作一次单项式；（2）12ah，系数12，次数2次，读作二次单项式；（3）3a b，b，系数0.9，次数1，读作一次单项式.【思路点拨】按照实际问题中数量关系规X写出单项式，再根据单项式的有关概念指出系数和次数.【答案】(1)12n ，系数12，次数1，读作一次单项式；（2）12ah ，系数12，次数2次，读作二次单项式；（3）3a b ，b ，系数0.9，次数1，读作一次单项式. b b 的一个其他的含义吗？总结：用字母表示数后，同一个式子可以表示不同的含义如例3中的（4）和（5）. ，错误的改正过来.（1）单项式2xy -的系数是0，次数是2.（2）单项式722a 的系数是2，次数是9. （3）单项式23n x y -的系数是23-，次数是1n +. 【知识点】单项式的系数和次数.【解题过程】解：（1）错误，系数-1，次数3；（2）错误，系数72，次数2；（3）正确.【思路点拨】按单项式的系数和次数的特征进行判断.【答案】（1）错误，系数-1，次数3，（2）错误，系数72，次数2，（3）正确.【设计意图】进一步熟练准确指出单项式的系数和次数.●活动②例2：若2(72)b a x y +是关于x 、y 的五次单项式，系数为16，求a 和b 的值． 【知识点】单项式的系数和次数.【解题过程】解：因为2(72)b a x y +是关于x 、y 的五次单项式.所以25b +=， 3b =， 又因系数为16， 所以7216a +=， 所以2a =【思路点拨】根据系数和次数的定义分别建立两个方程，从而求解.【答案】2a =， 3b =.练习：如果单项式32nx y -与单项式42a b 的次数相同，则n =. 【知识点】单项式的系数和次数.【解题过程】解：因为两个单项式的次数相同.所以342n +=+， 所以3n =.【思路点拨】根据次数相同建立方程.【答案】3n =.【设计意图】进一步熟练准确指出单项式的系数和次数，培养学生逆向思维.知识梳理（1）单项式的判断需要注意：①数或字母的积；②单独的一个数或一个字母也是单项式；③式子中不含“+、-”，分母中不含未知数.（2）单项式的系数、次数的确定需要注意：①次数是指所有字母指数的和；②系数是指单项式中的数字因数.重难点归纳：（1）单项式的判定方法:数或字母的乘积形式，分母中不含字母（2）单项式的系数:单项式中的数字因数，特别注意包括前面的符号.（3）单项式的次数确定:所有字母的指数和.。

2．1．2整式一、教学目标：1．通过本节课的学习，使学生掌握整式多项式的项及其次数、常数项的概念；2．通过小组讨论、合作交流，让学生经历新知的形成过程，培养比较、分析、归纳的能力；3．由单项式与多项式归纳出整式，这样更有利于学生把握概念的内涵与外延，有利于学生知识的迁移和知识结构体系的更新；体会类比和逆向思维的数学思想．二、教学重点、难点：重点：掌握整式及多项式的有关概念，掌握多项式的定义、多项式的项和次数，以及常数项等概念。

难点：多项式的次数。

三、学法与教学用具：学法：学生通过阅读教材，自主学习、思考、交流、讨论和概括，从而更好地完成本节课的教学目标。

教学用具：投影仪四、教学过程：（一）创设情景，揭示课题列代数式：（1）长方形的长与宽分别为a、b，则长方形的周长是；（2）某班有男生x人，女生21人，则这个班共有学生人；（3）图中阴影部分的面积为_______；（4）鸡兔同笼，鸡a只，兔b只，则共有头个，脚只．2．观察以上所得出的四个代数式与上节课所学单项式有何区别．（1）2（a＋b）；（2）21＋x；（3）a＋b；（4）2a＋4b．列代数式：（二）研探新知1．多项式：上面这些代数式都是由几个单项式相加而成的．像这样，几个单项式的和叫做多项式（polynomial）．在多项式中，每个单项式叫做多项式的项（term）．其中，不含字母的项，叫做常数项（constant term）．例如，多项式有三项，它们是－2x，5．其中5是常数项．一个多项式含有几项，就叫几项式．多项式里，次数最高项的次数，就是这个多项式的次数．例如，多项式是一个二次三项式．注意：（1）多项式的次数不是所有项的次数之和；（2）多项式的每一项都包括它前面的符号．1.例题：例1 判断：①多项式a3－a2ｂ＋aｂ2－ｂ3的项为a3、a2ｂ、aｂ2、ｂ3，次数为12；②多项式3n4－2 n 2＋1的次数为4，常数项为1．例2 指出下列多项式的项和次数：（1）3x－1＋3x2；（2）4x3＋2x－2y2．解：略．例3 指出下列多项式是几次几项式．（1）x 3－x＋1；（2）x 3－2 x 2 y 2＋3 y 2．解：略．整式的定义：单项式与多项式统称整式例4 已知代数式3 x n－（m－1）x＋1是关于x的三次二项式，求m、n的条件．解：略．（三）巩固深化，反馈矫正①填空：－a2b－ab＋1是次项式，其中三次项系数是，二次项为，常数项为，写出所有的项．②已知代数式2x2－mnx2＋y2是关于字母x、y的三次三项式，求m、n的条件．①理解多项式的定义，能说出一个多项式是几次几项式，最高次数是几，分别由哪几项组成，各项的系数分别为多少，常数项为几．（四）归纳小结这堂课学习了多项式，与前一节所学单项式合起来统称为整式，使知识形成了系统．（五）作业布置P59 练习题3,4。

整式的加减2.1整式第二课时教学目标:1.通过本节课的学习,使学生掌握整式、多项式的项及其次数、常数项的概念.2.能运用整式的知识解决问题3.初步体会类比和逆向思维的数学思想.教学重点:掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数以及常数项等概念.教学难点:准确指出多项式的次数.教与学互动设计:(一)设问激趣，导入新课（成功从学习开始）活动一：复习引入1.什么叫单项式？请写出一个单项式，并与同桌交换指出单项式的系数和次数？例：2ab 系数2 次数22.根据题意列出式子：（1）我们班级购买3个篮球、2个排球、1个足球，现一个篮球a元，一个排球b元，一个足球c元，共需 3a+2b+c 元（2）今天綦江气温由21 ℃下降t℃后是 21-t ℃。

（3）永新到綦江距离21千米，一辆汽车速度x千米/小时，走了x小时后还一段距离到达綦江，汽车离綦江的距离多远 21-x2千米（4）一个数等于x2减去负1在加上2a2b，这个数为x2-1+2a2b(二)合作交流,解读探究（成功从相信开始）活动二：思考1.观察3a+2b+c,21-t,21-x2,x2-1+2a2b这些式子是我们所学过的单项式吗？这些式子从加法的角度去看，分别可以看成那些单项式的和？定义：像这样，几个单项式的和叫做多项，在多项式中，每个单项式叫做项，其中不含字母的项，叫做常数项 .活动三：例题精讲1.多项式x2-1+2a2b的项分别是x2，-1，2a2b其中-1是常数项，请指出多项式3a+2b+c,21-t,21-x2中的项，并指出常数项？3a,2b,c没有常数项-t,21常数项为21-x2,21常数项21归纳：多项式的各项应包括它前面的符号活动四思考1.多项式x2-1+2a2b的项分别是x2，-1，2a2b，你能说出每一项的次数？3项中次数最高的项是？x2次数为2称为二次项-1是常数项2a2b次数为3称为三次项2a2b称为这个多项式的最高次项定义：多项式中，次数最高项的次数，叫做这个多项式的次数2.多项式x2-1+2a2b的次数是 3指出下列多项式3a+2b+c,21-t,21-x2的次数？3a+2b+c次数是121-t次数是121-x2次数是23.请同学们自己写一个多项式，让你的同桌指出他的项和多项式的次数？例：2abc+ab+1项有2abc,ab,1次数为3次找多项式的项和次数易错归纳：1.多项式的各项应包括它前面的符号r R2.多项式里， 最高次项 项的次数，叫做这个多项式的 次数3.一个多项式的最高次项可以 不唯一 .4.下列式子100 t,0.8p,mn,a 2h,-n,ν+2.5，12ab −πr 2， x 2+2x +18 那些是单项式，那些是多项式？单项式：100 t,0.8p,mn,a 2h,-n,… 多项式：ν+2.5，12ab −πr 2，x 2+2x +18 …定义：单项式与多项式统称为 整式 .5.多项式与单项式概念的区别与联系？联系：表示数或字母的积的式子叫做单项式；几个单项式的和叫做多项式区别：单项式中所有字母的指数的和叫做这个单项式的次数；多项式里，次数最高项的次数，叫做这个多项式的次数活动五 例题精讲例1：多项式：x 2-1+2a 2b 次数是3，项分别是x 2，-1，2a 2b 多项式：x 2-1+2a 2b 是 三 次 三 项式多项式：3a+2b+c,21-t,21-x 2是几次几项式？一次三项式；一次二项式；二次二项式例2：3x 2−2x +26， x 3+3x 2y +3xy 2+y 3是几次几项式呢二次三项式；三次四项式例3：已知多项式 a n −3a 2+3x −3 的次数是 3，n 的值为 3例4：判断题1.多项式 x 2−3x +1的二次项系数是0。

§2.1整式（第二课时）一、学习目标：1．使学生理解多项式、整式的概念，会准确确定一个多项式的项数和次数．2．通过实例列整式，培养学生分析问题、解决问题的能力．3．培养学生积极思考的学习态度，合作交流意识二、学习重点难点：重点：多项式以及有关概念难点：准确确定多项式的次数和项三、导学流程：（一）、引入新课单项式与多项式定义（二）、尝试指导（1）t-5 (2)x+7x-5x (3)-6ab+ba+8ab（三）．精析问题针对以下问题阅读教材56页—59页内容，并将蓝框和例2中的空直接填到书上①什么叫做多项式？②什么叫做多项式的项？③什么叫做常数项？④什么叫做多项式的次数？⑤什么叫做整式？⑥指出蓝框中多项式的项和次数。

①什么叫做多项式？②什么叫做多项式的项？③什么叫做常数项？④什么叫做多项式的次数？⑤什么叫做整式？⑥指出蓝框中多项式的项和次数。

（四）、变式训练(时间20分钟)1、指出下列代数式中，哪些是多项式？①6x 2-21x-3 ②-4x ③b a 3131+ ④ 3x 2y-21xy 2+x 2-xy-5 ⑤ x 1⑥ 3x+5y+2z ⑦ -21 ⑧-ab2、指出下列多项式的项和次数？①6x 2-21x-3 ②b a 3131+ ③3x 2y-21xy 2+x 2-xy-5 ④ -2.15a 3b +5⑤ 1+2m-3m ⑥3x+5y+2z ⑦3- 3220b a（五）、归纳小结:本节课你学道了什么？（六）、达标检测（时间10分钟）1、判断下列各代数式是否是多项式？如不是，请说明理由；如是，请指出它的系数和次数。

① x+1 ② 2x-x 1-1 ③ 3+2r ④ 2+b-ab-b a 223D. 总结反思(时间2分钟)。

新人教版七年级数学上册导学案：2.1整式(第二课时)—单项式【 学习目标 】1．会说单项式及单项式系数、次数的概念。

2．会准确迅速地确定一个单项式的系数和次数。

【 重点 】单项式及单项式的系数、次数的概念。

【 难点 】区别单项式的系数和次数。

【 使用说明与学法指导 】1.先利用10分钟精读一遍教材P 56――P 57，用红色笔进行勾画重难点；再针对预习案二次阅读教材，解答预习案中的问题；疑惑随时记录在我的疑惑栏内，准备课上讨论质疑。

2.利用25分钟独立完成探究案，找出自己的疑惑和需要讨论的问题，用红笔做好标记。

洁，独立完成，不能讨论。

预 习 案【 预习自学 】(人之所以能，是相信能!)观察：观察式子100t, 0.8p, mn, a 2h, -n 有什么共同特点？归纳：单项式：由_____或_____的乘积组成的式子叫做单项式,单独一个_____或_____也是单项式. 单项式中的_______叫做这个单项式的系数,单项式中____________叫做这个单项式的次数.100t 的系数是_____,100t 是______次单项式;a 2 h 的系数是_____a 2h 是______次单项式; 0.8p 的系数是_____,0.8p 是______次单项式;-n 的系数是_____,-n 是______次单项式;探 究 案【 课堂探究】(只当观众的人永远领不到金牌。

)1、判断下列各代数式哪些是单项式？ (1)21+x ； (2)abc ； (3)b 2； (4)－5ab 2； (5)y+x ； (6)－xy 2； (7)－5。

解：是单项式的有(填序号)： 。

2、单项式系数和次数： 在单项式31a 2h ，2πr ，abc ，－m ，4732y x -，7x 中，请指出它们的系数和次数：检测案 巩固提高1、 判断下列各说法是否正确,将错误的改正过来.（1）单项式-xy 2的系数是0,次数是2. ( )（2）单项式27a 3的系数是2,次数是10 . ( ) （3）单项式 32y x n -的系数是32-,次数是n+1 . ( )【 课堂小结】.知识方面：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。