应用时间序列分析王燕答案

第一章习题答案略第二章习题答案2.1答案：（1）非平稳，有典型线性趋势（2）延迟1-6阶自相关系数如下：（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）1-24阶自相关系数如下（3）自相关图呈现典型的长期趋势与周期并存的特征2.3R命令答案（1）1-24阶自相关系数（2）平稳序列（3）非白噪声序列Box-Pierce testdata: rainX-squared = 0.2709, df = 3, p-value = 0.9654X-squared = 7.7505, df = 6, p-value = 0.257X-squared = 8.4681, df = 9, p-value = 0.4877X-squared = 19.914, df = 12, p-value = 0.06873X-squared = 21.803, df = 15, p-value = 0.1131X-squared = 29.445, df = 18, p-value = 0.04322.4答案：我们自定义函数，计算该序列各阶延迟的Q统计量及相应P值。

由于延迟1-12阶Q统计量的P值均显著大于0.05，所以该序列为纯随机序列。

2.5答案（1）绘制时序图与自相关图（2）序列时序图显示出典型的周期特征，该序列非平稳（3）该序列为非白噪声序列Box-Pierce testdata: xX-squared = 36.592, df = 3, p-value = 5.612e-08X-squared = 84.84, df = 6, p-value = 3.331e-162.6答案（1）如果是进行平稳性图识别，该序列自相关图呈现一定的趋势序列特征，可以视为非平稳非白噪声序列。

如果通过adf检验进行序列平稳性识别，该序列带漂移项的0阶滞后P值小于0.05，可以视为平稳非白噪声序列Box-Pierce testdata: xX-squared = 47.99, df = 3, p-value = 2.14e-10X-squared = 60.084, df = 6, p-value = 4.327e-11（2）差分序列平稳，非白噪声序列Box-Pierce testdata: yX-squared = 22.412, df = 3, p-value = 5.355e-05X-squared = 27.755, df = 6, p-value = 0.00010452.7答案（1）时序图和自相关图显示该序列有趋势特征，所以图识别为非平稳序列。

第七章时间数列分析一、填空题1、时间指标数值2、逐期增长量累计增长量3、增长水平（或增长量）发展速度4、本期水平去年同期水平5、年距发展速度 1（或100%）6、几何平均法方程法7、同季（月）平均法趋势与季节模型法8、平均季节比重法平均季节比率法9、报告期水平基期水平10、序时平均数（或动态平均数）平均数11、和差12、季节变动长期趋势13、逐期增长量环比增长速度14、长明显1-5 A C C A D 6-10 A B A D B三、多选题1、CDE2、ABDE3、ABCE4、ACDE5、BDE6、BD7、ABCD8、ACE9、AE 10、ACE四、简答题1、序时平均数与一般平均数的异同。

答：（1）相同之处。

二者都是将具体数值抽象化，用一个代表性的数指来代表总体的一般水平。

（2）不同之处。

①计算的依据不同。

一般平均数是根据变量数列计算的，而序时平均数则是根据时间数列计算的；②对比的指标不同。

一般平均数是总体标志总量与总体单位总量对比的结果，而序时平均数则是时间数列各期发展水平的总和与时期项数对比的结果；③说明的问题不同。

一般平均数说明现象在同一时间、不同空间上所达到的一般水平，而序时平均数则说明现象在同一空间、不同时间上所达到的一般水平。

2、时期数列与时点数列的区别。

答：①时期数列中的指标值为时期数，时点数列中的指标值为时点数；②时期数列中的指标值具有可加性，而时点数列中的指标值则不具有可加性；③时期数列中指标值的大小与时间间隔的长短有直接关系，而时点数列中指标值的大小与时间间隔的长短则没有直接关系；④时期数列中的指标值是通过连续调查取得的，而时点数列中的指标值则是通过一次性调查取得的。

3、时间数列的编制原则。

答：（1）基本原则：保持数列中的各项指标数值具有可比性。

（2）具体原则：①时间长短统一；②总体范围统一；③指标口径统一；④计算方法统一；⑤计量单位统一。

4、计算和应用平均速度应注意的问题。

month=_n_;cards;0.982 0.943 0.920 0.911 0.925 0.951 0.929 0.940 1.009 1.054 1.100 1.335 ;proc gplot data=example4_7_3; /*画季节指数图*/plot jjzs*month;symbol c=black v=diamond i=join;run;proc gplot data=sasuser.aa; /*画消除季节影响后的序列x1时序图*/plot x1*t;symbol c=black v=circle i=none;run;proc autoreg data=sasuser.aa; /* 对序列x1进行线性拟合*/model x1=t;output predicted=x2 out=results;run;proc gplot data=results; /*画线性趋势拟合图*/plot x1*t=1 x2*t=2/overlay;symbol1c=black v=circle i=none;symbol2c=red v=none i=join;run;proc gplot data=sasuser.bb; /*画残差图*/plot z*t;symbol c=red v=circle i=none;run;proc arima data=sasuser.bb; /*残差序列的检验、建模及预测*/identify var=z nlag=8minic p= (0:5) q= (0:5);run;estimate p=1;run;estimate p=1 noint;run;forecast lead=12id=t out=out;run;proc gplot data=; /*观察值序列x和预测值序列yc联合作图*/plot x*t=1 yc*t=2/overlay;symbol1c=black v=star i=none;symbol2c=red v=none i=join;run;【结果及分析】2、选择拟合模型：根据数据资料，算出该序列的月度季节指数如表从图3-2可以直观地看出每年的第四季度是我国社会消费品零售旺季(该季度的指数值明显大于1)，而前三个季度的季节指数在1附近，销售情况起伏不大，所以该序列有明显的季节效应。

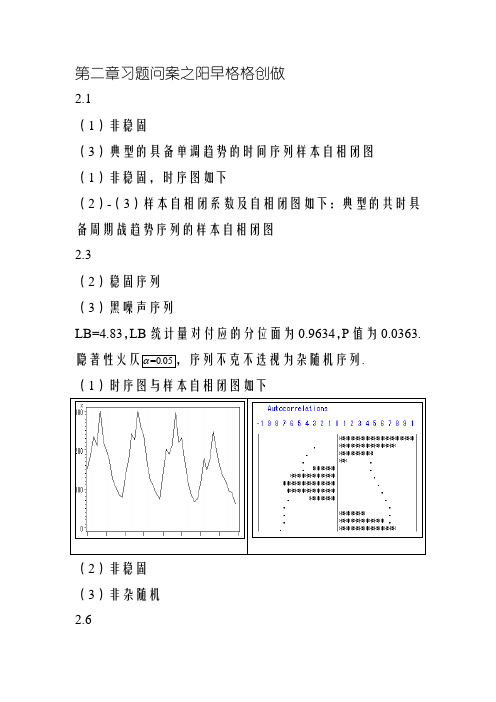
第二章习题问案之阳早格格创做2.1（1）非稳固（3）典型的具备单调趋势的时间序列样本自相闭图（1）非稳固，时序图如下（2）-（3）样本自相闭系数及自相闭图如下：典型的共时具备周期战趋势序列的样本自相闭图2.3（2）稳固序列（3）黑噪声序列LB=4.83，LB统计量对付应的分位面为0.9634，P值为0.0363.隐著性火仄=0.05，序列不克不迭视为杂随机序列.（1）时序图与样本自相闭图如下（2）非稳固（3）非杂随机2.6（1）稳固，非杂随机序列（拟合模型参照：ARMA(1,2)） （2）好分序列稳固，非杂随机 第三章习题问案3.13.2解：对付于AR （2）模型：3.3 解：根据该AR(2)3.4 解：本模型可变形为：型稳固.由此可知c即当－1<c<0时，该AR(2)模型稳固. 3.5说明：已知本模型可变形为：不管c 与何值，皆市有一特性根等于1，果此模型非稳固.3.6 解：（1 （2（3 （4（5）3.7MA(1)3.8解法1解法2展启等号左边的多项式，整治为 合并共类项，本模型等价表黑为3.9解：3.10解法1：（1隐然模型的AR 部分的特性根是1，模型非稳固. （2MA(1)模型，稳固.解法2：（1固序列.（2自相闭系数只与时间隔断少度有闭，与起初时间无闭所以该好分序列为稳固序列.3.11解：（1（2.（3.＋0.2693i（4.（5（6.3.12 解法1解法23.13Green函数3.14的递推公式得：3.15 （1）创造（2）创造（3）创造（4）不可坐3.16 解：（1已知AR(1)模型的Green9.9892＋即[3.8275,16.1509]（210.045＋即[3.9061,16.1839].3.17 （1）稳固非黑噪声序列（2）AR(1)(3) 5年预测截止如下：3.18 （1）稳固非黑噪声序列（2）AR(1)(3) 5年预测截止如下：3.19 （1）稳固非黑噪声序列（2）MA(1)(3) 下一年95%的置疑区间为（80.41,90.96）3.20 （1）稳固非黑噪声序列（2）ARMA(1,3)序列（3）拟合及5年期预测图如下：第四章习题问案4.1 解：4.2 解由代进数据得解得4.3解：（1）（2.其（3）正在移动仄衡法下:正在指数仄滑法中:4.4 解：根据指数仄滑的定义有（1）式创造，（1）式等号二2）式创造（1）-（2）得limtttxt→∞⎛=⎝4.5 该序列为隐著的线性递加序列，利用本章的知识面，不妨使用线性圆程大概者holt二参数指数仄滑法举止趋势拟合战预测，问案不唯一，简直截止略.4.6 该序列为隐著的非线性递加序列，不妨拟合二次型直线、指数型直线大概其余直线，也能使用holt二参数指数仄滑法举止趋势拟合战预测，问案不唯一，简直截止略.4.7 本例正在混同模型结构，季节指数供法，趋势拟合要领等处均有多种可选规划，如下干法仅是可选要领之一，截止仅供参照（1）该序列有隐著趋势战周期效力，时序图如下（2）该序列周期振幅险些不随着趋势递加而变更，所以测（注：如果用乘法模型也不妨）最先供季节指数（不与消趋势，本去不是最透彻的季节指数）序列趋势做用（要领不唯一）（注：该趋势模型截距偶尔思，主假如斜率蓄意思，反映了少久递加速率）残好序列基础无隐著趋势战周期残留.预测1971年奶牛的月度产量序列为得到（3）该序列使用x11要领得到的趋势拟合为趋势拟合图为4.8 那是一个有着直线趋势,然而是有不牢固周期效力的序列,所以不妨正在赶快预测步调中用直线拟合（stepar）大概直线指数仄滑（expo）举止预测（trend=3）.简直预测值略.第五章习题预计下一天5.1 拟合好分稳固序列,的支盘价为2895.2 拟合模型不唯一，问案仅供参照.拟合ARIMA(1,1,0)模型，五年预测值为：5.4 (1)AR(1)，(2)有同圆好性.最后拟合的模型为5.5(1)非稳固（2）与对付数与消圆好非齐，对付数序列一节好分后，拟合疏系数模型AR(1，3)所以拟合模型为（3）预测截止如下：5.6 本序列圆好非齐，好分序列圆好非齐，对付数变更后，好分序列圆好齐性.第六章习题6.1 单位根考验本理略.例2.1 本序列不仄稳，一阶好分后稳固例2.2 本序列不仄稳，一阶与12步好分后稳固例2.3 本序列戴漂移项稳固例2.4 本序列不戴漂移项稳固例2.5固.6.2 （1）二序列均为戴漂移项稳固（2）谷物产量为戴常数均值的杂随机序列，落雨量不妨拟合AR（2）疏系数模型.（3）二者之间具备协整闭系（46.3 （1）掠食者战被掠食者数量皆浮现出隐著的周期特性，二个序列均为非稳固序列.然而是掠食者战被掠食者延缓2阶序列具备协整闭系..模型心径为:已去一周的被掠食者预测序列为：Forecasts for variable xObs Forecast Std Error 95% Confidence Limits 掠食者预测值为：Forecasts for variable yObs Forecast Std Error 95% Confidence Limits 6.4（1）出进心总数序列均不仄稳，然而对付数变更后的一阶好分后序列稳固.所以对付那二个序列与对付数后举止单个序列拟合战协整考验.（2简直心径为：简直心径为：（3（4（5。

第四章5:我国1949年—2008年年末人口总数（单位：万人）序列如表4 — 8所示（行数 据）•选择适当的模型拟合该序列的长期数据，并作 5期预测。

data wangbao4_5; in put x@@; time= 1949 +_n_- 1; cards ;54167 55196 56300 57482 58796 60266 61465 62828 64653 65994 67207 66207 65859 67295 69172 70499 72538 74542 76368 78534 80671 82992 85229 87177 89211 90859 92420 93717 94974 96259 97542 98705100072 101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124761 125786 126743 127627 128453 129227 129988 130756 131448 132129 132802Jproc gplot data =wa ngbao4_5; plot x*time= 1;symbol1 c=black v=star i =joi n; run ;proc autoreg data =wa ngbao4_5;model x=time; output out =out p=wangbao4_5_cup; run ;proc gplot data =out;plot x*time= 1 wangbao4_5_cup*time= 2/ overlay ;symbol2 c=red v=none i =join w=2 l =3; run ;proc forecast data=wa ngbao4_5 method=stepar tre nd= 2 lead= 5 out=out outfulloutest=est; id time; var x;proc gplot data =out;plot x*time=_type_/ href =2008; symbol1 i =none v =star c=black;l =2;symbol2 symbol3 i =joi n i =joi n v =none v =none c=red; c=black symbol4 i =joi n v =none c=blackl =2;run ;分析过程:1、时序图X"血>! TiiTik通过时序图，我可以发现我国1949年一2008年年末人口总数(随时间的变化呈现出线性变化故此时可以用线性模型拟合序列的发展：Xt=a+bt+lt t=1,2,3,…,60E(lt)=0,var(lt)= <r 2其中，It为随机波动；Xt=a+b就是消除随机波动的影响之后该序列的长期趋势。

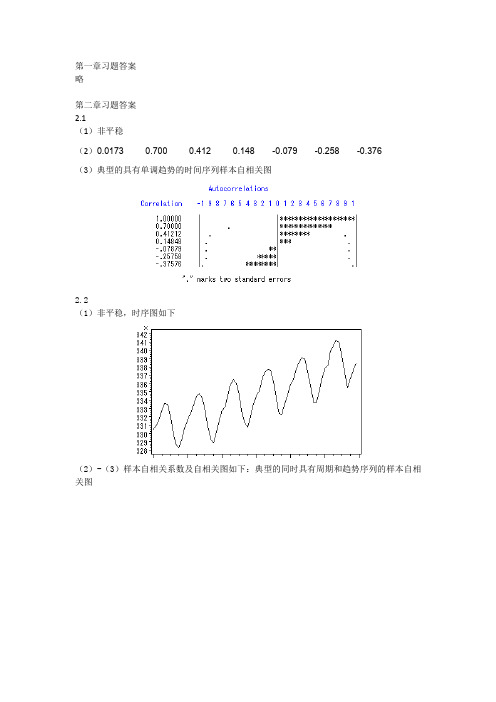
第一章习题答案略第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1）自相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）白噪声序列2.4，序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。

显著性水平=0.05不能视为纯随机序列。

2.5（1）时序图与样本自相关图如下（2） 非平稳 （3）非纯随机 2.6（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为：32--c 0c λλλ+=，解该特征方程得三个特征根：11λ=，2c λ=3c λ=-无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。

《时间序列分析——基于R》王燕，读书笔记笔记：⼀、检验：1、平稳性检验：图检验⽅法：时序图检验：该序列有明显的趋势性或周期性，则不是平稳序列⾃相关图检验：（acf函数）平稳序列具有短期相关性，即随着延迟期数k的增加，平稳序列的⾃相关系数ρ会很快地衰减向0（指数级指数级衰减），反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验：单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验（Box.test（data，type，lag=n）——lag表⽰输出滞后n阶的⽩噪声检验统计量，默认为滞后1阶的检验统计量结果）1、Q统计量：type=“Box-Pierce”2、LB统计量：type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf（），pacf（），auto.arima（）⾃动定阶1.3建模arima()1.4模型显著性检验：残差的⽩噪声检验Box.test（）；参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合：直线、曲线（⼀般是多项式，还有其它函数）2.2平滑法移动平均法：SMA()——TTR包指数平滑法：HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验，差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima（p,d,f）3.3季节模型可以叠加的模型4、残差⾃回归模型：4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型，对模型做残差⾃相关DW检验。

dwtest()——lmtest包，增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型：异⽅差检验：LM检验ArchTest（）——FinTS包，⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法：1、频域分析⽅法2、时域分析⽅法步骤：1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型，优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向：1、AR，MA，ARMA，ARIMA（Box-Jenkins模型）2、异⽅差场合：ARCH，GARCH等（计量经济学）3、多变量场合：“变量是平稳”不再是必需条件，协整理论3、⾮线性场合：门限⾃回归模型，马尔科夫转移模型第⼆章时间序列的预处理预处理内容：对它的平稳性和纯随机性进⾏检验，最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征，同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。

【分享】应用时间序列分析课后答案在学习应用时间序列分析这门课程的过程中，课后答案对于我们巩固知识、检验学习成果起着至关重要的作用。

今天，我就来和大家分享一下我所整理的应用时间序列分析课后答案，希望能对正在学习这门课程的同学们有所帮助。

首先，我们来谈谈为什么时间序列分析如此重要。

在现实生活中，许多现象都随着时间的推移而发生变化，比如股票价格的波动、气温的变化、销售量的起伏等等。

通过对这些时间序列数据的分析，我们可以揭示隐藏在数据背后的规律和趋势，从而做出更准确的预测和决策。

接下来，让我们直接进入课后答案的分享。

在第一章的课后习题中，有一道关于时间序列平稳性检验的题目。

对于这道题，我们需要先计算序列的均值和方差，如果均值和方差不随时间变化，那么初步可以判断该序列是平稳的。

然后，再通过自相关函数（ACF）和偏自相关函数（PACF）来进一步确定平稳性。

具体的计算过程和判断方法，答案中都有详细的步骤和解释。

再来看第二章关于模型识别的课后题。

在这部分，我们要根据给定的时间序列数据的自相关和偏自相关函数的特征，来判断适合的模型类型。

比如，如果 ACF 呈现拖尾，PACF 截尾，那么可能适合的模型是 AR 模型；反之，如果 ACF 截尾，PACF 拖尾，则可能是 MA 模型。

而当 ACF 和 PACF 都呈现拖尾时，就需要考虑 ARMA 模型了。

在第三章关于参数估计的习题中，涉及到了最小二乘法、极大似然估计等方法。

答案中会给出具体的计算公式和推导过程，帮助我们理解如何通过数据来估计模型的参数。

这部分的内容相对较难，需要我们认真思考和反复练习。

第四章的课后作业主要是关于模型诊断和检验。

我们需要通过残差分析来判断模型的拟合效果，如果残差是白噪声，说明模型拟合较好；否则，就需要对模型进行进一步的改进和调整。

答案中会有关于如何进行残差分析的详细示例和判断标准。

第五章则侧重于时间序列的预测。

这部分的课后题会让我们运用所建立的模型对未来的值进行预测，并计算预测误差。

应用时间序列分析（试卷一）一、 填空题1、拿到一个观察值序列之后，首先要对它的平稳性和纯随机性进行检验，这两个重要的检验称为序列的预处理。

2、白噪声序列具有性质纯随机性和方差齐性。

3、平稳AR （p ）模型的自相关系数有两个显著的性质：一是拖尾性；二是呈负指数衰减。

4、MA(q)模型的可逆条件是：MA(q)模型的特征根都在单位圆内，等价条件是移动平滑系数多项式的根都在单位圆外。

5、AR （1）模型的平稳域是{}11<<-φφ。

AR （2）模型的平稳域是{}11,12221<±<φφφφφ且，二、单项选择题1、频域分析方法与时域分析方法相比（D ）A 前者要求较强的数学基础，分析结果比较抽象，不易于进行直观解释。

B后者要求较强的数学基础，分析结果比较抽象，不易于进行直观解释。

C前者理论基础扎实，操作步骤规范，分析结果易于解释。

D后者理论基础扎实，操作步骤规范，分析结果易于解释。

2、下列对于严平稳与宽平稳描述正确的是（D）A宽平稳一定不是严平稳。

B严平稳一定是宽平稳。

C严平稳与宽平稳可能等价。

D对于正态随机序列，严平稳一定是宽平稳。

3、纯随机序列的说法，错误的是（B）A时间序列经过预处理被识别为纯随机序列。

B纯随机序列的均值为零，方差为定值。

C在统计量的Q检验中，只要Q时，认为该序列为纯随机序列，其中m为延迟期数。

D不同的时间序列平稳性检验，其延迟期数要求也不同。

4、关于自相关系数的性质，下列不正确的是（D）A. 规范性；B. 对称性；C. 非负定性；D. 唯一性。

5、对矩估计的评价，不正确的是（A）A. 估计精度好；B. 估计思想简单直观；C. 不需要假设总体分布；D. 计算量小（低阶模型场合）。

6、关于ARMA模型，错误的是（C）A ARMA模型的自相关系数偏相关系数都具有截尾性。

B ARMA模型是一个可逆的模型C 一个自相关系数对应一个唯一可逆的MA模型。

D AR模型和MA模型都需要进行平稳性检验。

时间序列分析参考答案时间序列分析参考答案时间序列分析是一种研究随时间变化的数据模式和趋势的统计方法。

它可以帮助我们理解数据的变化规律，预测未来的趋势，以及制定相应的决策。

在本文中，我们将探讨时间序列分析的基本概念、方法和应用。

一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据观测值。

它可以是连续的，比如每天的股票价格，也可以是离散的，比如每月的销售额。

时间序列分析的目标是找出数据中的模式和趋势，以便进行预测和决策。

时间序列分析的基本概念包括趋势、季节性和周期性。

趋势是指数据在长期内的整体变化方向，可以是上升、下降或平稳。

季节性是指数据在一年中周期性重复出现的变化模式，比如节假日销售额的增长。

周期性是指数据在较长时间内出现的波动，通常周期长度大于一年。

二、时间序列分析的方法时间序列分析的方法包括描述性分析、平稳性检验、模型建立和预测等。

描述性分析是对时间序列数据进行可视化和统计分析，以了解数据的基本特征。

常用的描述性分析方法包括绘制折线图、直方图和自相关图等。

折线图可以显示数据的整体趋势和季节性变化，直方图可以展示数据的分布情况，自相关图可以帮助我们发现数据的相关性。

平稳性检验是判断时间序列数据是否具有平稳性的方法。

平稳性是指数据的均值和方差在时间上保持不变。

常用的平稳性检验方法包括单位根检验和ADF检验等。

模型建立是根据时间序列数据的特征，选择合适的模型来描述数据的变化规律。

常用的模型包括AR模型、MA模型和ARMA模型等。

AR模型是自回归模型，表示当前观测值与过去观测值之间的线性关系；MA模型是移动平均模型，表示当前观测值与过去观测值的误差之间的线性关系；ARMA模型是自回归移动平均模型，综合考虑了自回归和移动平均的效果。

预测是利用已知的时间序列数据，通过建立模型来预测未来的观测值。

常用的预测方法包括滚动预测、指数平滑法和ARIMA模型等。

滚动预测是指根据当前观测值和过去观测值的模型，逐步预测未来的观测值；指数平滑法是基于历史数据的加权平均值，对未来的观测值进行预测；ARIMA模型是自回归移动平均差分整合模型，可以处理非平稳的时间序列数据。