《直角三角形》习题

解直角三角形练习题一、选择题1. 在直角三角形中，若一个锐角的度数是45°，则另一个锐角的度数是（）A. 45°B. 135°C. 90°D. 45°或135°2. 若直角三角形的两条直角边分别为3和4，则斜边的长度为（）A. 5B. 6C. 7D. 83. 在直角三角形中，若斜边长为10，一直角边长为6，则另一直角边长为（）A. 8B. 9C. 10D. 124. 已知直角三角形的斜边长为10，一个锐角的度数为30°，则该三角形的面积是（）A. 25B. 30C. 50D. 100二、填空题1. 在直角三角形中，若一个锐角的度数是60°，则另一个锐角的度数是______。

2. 若直角三角形的两条直角边分别为5和12，则斜边的长度是______。

3. 在直角三角形中，若斜边长为13，一直角边长为5，则另一直角边长为______。

4. 已知直角三角形的斜边长为10，一个锐角的度数为45°，则该三角形的面积是______。

三、解答题1. 在直角三角形ABC中，∠C=90°，∠A=30°，AC=6，求BC和AB的长度。

2. 在直角三角形DEF中，∠F=90°，DF=5，EF=12，求∠D和∠E 的度数。

3. 已知直角三角形的斜边长为15，一个锐角的度数为60°，求该三角形的面积。

4. 在直角三角形XYZ中，∠Y=90°，∠X=45°，ZY=8，求XY和XZ的长度。

5. 已知直角三角形的斜边长为10，一直角边长为6，求另一直角边长及两个锐角的度数。

6. 在直角三角形LMN中，∠N=90°，∠L=30°，LN=9，求LM和MN的长度。

7. 已知直角三角形的面积为24，斜边长为10，求两个直角边的长度。

8. 在直角三角形PQR中，∠Q=90°，∠P=60°，PQ=8，求PR和QR的长度。

解直角三角形的练习题### 解直角三角形的练习题1. 基础概念题：直角三角形中，直角的度数为多少？斜边与直角边的关系是什么？2. 简单应用题：在直角三角形ABC中，角C为直角，AB为斜边，若AC=10，BC=8，求AB的长度。

3. 勾股定理应用题：已知直角三角形的两条直角边分别为6和8，求斜边的长度。

4. 角度计算题：在直角三角形中，如果一个锐角是另一个锐角的两倍，求这两个锐角的度数。

5. 实际测量题：一座高塔与地面垂直，从塔底到塔顶的直线距离是100米。

如果从塔底到塔顶的斜线距离是120米，求塔底到塔顶的水平距离。

6. 三角函数值计算题：在直角三角形中，已知一个锐角的正切值为3，求这个角的正弦和余弦值。

7. 综合应用题：一个梯子斜靠在墙上，梯子的顶端距离地面5米，梯子与地面的夹角为60度。

求梯子的长度。

8. 相似三角形判断题：两个直角三角形，如果它们的对应边成比例，它们是否相似？为什么？9. 特殊角三角函数值应用题：在直角三角形中，如果一个角为30度，求这个角的正弦、余弦和正切值。

10. 图形变换题：一个直角三角形的直角边长分别为3和4，如果将这个三角形沿着斜边旋转90度，求旋转后的三角形的边长。

11. 实际问题解决题：一个风筝挂在树上，风筝线与地面成60度角，如果风筝线的长度为10米，求风筝到地面的垂直距离。

12. 三角函数逆运算题：已知一个角的正弦值为0.5，求这个角的度数（精确到度）。

13. 比例问题：在直角三角形中，如果斜边长度是一条直角边长度的两倍，求另一条直角边与斜边的长度比。

14. 角度变换题：一个直角三角形的两个锐角分别为α和β，如果将三角形旋转45度，求旋转后两个锐角的新值。

15. 函数图像题：画出正弦函数y=sin(x)在0到90度的图像，并标注特殊角度的函数值。

16. 几何证明题：证明在直角三角形中，斜边的中线等于斜边长度的一半。

17. 三角函数变换题：已知一个角的正弦值为1/2，求这个角的余弦值。

含30度角的直角三角形（北京习题集）（教师版）一．选择题（共5小题）1．（2019秋•西城区期末）如图，在等腰三角形中，，，为边的中点．若，则的长为 A ．3B ．4C ．6D ．82．（2018秋•东城区期末）如图，在中，，，于，是的平分线，且交于，如果，则的长为 A ．2B ．4C ．6D ．83．（2019春•昌平区校级月考）如图，若，，，则 A ．B ．C ．D ．4．（2019秋•海淀区校级月考）如图，中，，，，点是边上的动点，则的最小值为 A ．1B ．2C ．3D ．45．（2018春•海淀区校级期中）已知直角三角形中，，，若，则长为 A ．2B ．4C ．3D ．ABC BA BC =120ABC ∠=︒D AC 6BC =BD ()ABC ∆90A ∠=︒30C ∠=︒AD BC ⊥D BE ABC ∠AD P 2AP =AC ()30B ∠=︒90C ∠=︒20AC m =(AB =)25m 30m 40m ABC ∆90C ∠=︒30A ∠=︒4AB =P AC BP ()ABC 30A ∠=︒90C ∠=︒AC =AB ()二．填空题（共7小题）6．（2019秋•延庆区期末）如图，与交于点，，，，则的度数是 ．7．（2019秋•丰台区期末）如图，中，，，交于点，，则 ．8．（2019秋•延庆区期末）如图，在中，，是的平分线，垂直平分，若，则 ．9．（2019秋•海淀区校级期中）如图，在中，，，平分交于点，的垂直平分线交于点，交于点，若，则的长为 ．10．（2019秋•西城区校级期中）等腰三角形的顶角是，底边上的高是3，则腰长为 ．11．（2019秋•海淀区校级期中）已知，如图，，，则的面积为 ．12．（2019秋•海淀区校级期中）中，，，， ．三．解答题（共3小题）13．（2017秋•大兴区期末）已知：如图，在中，，，求的长．14．（2014秋•海淀区校级期末）等腰三角形中，，，求边上的高的长．EC DA B 90ACB ∠=︒60A ∠=︒BD BE =DEB ∠ABC ∆AB AC =120BAC ∠=︒AD AC ⊥BC D 3AD =BC =ABC ∆90A ∠=︒CD ACB ∠DE BC 2DE =AB =ABC ∆AB BC =30ABC ∠=︒BD ABC ∠AC D BC EF BC E BD F 6BF =AC 120︒6AB BC ==15A ∠=︒ABC ∆Rt ABC ∆90C ∠=︒2B A ∠=∠4BC cm =AB =cm ABC ∆8AB AC ==120A ∠=︒BC ABC 30A ∠=︒8AB =AB CD15．（2014•顺义区一模）如图，在四边形中，，，，，求的长．ABCD 90B D ∠=∠=︒60C ∠=︒4BC =3CD =AB含30度角的直角三角形（北京习题集）（教师版）参考答案与试题解析一．选择题（共5小题）1．（2019秋•西城区期末）如图，在等腰三角形中，，，为边的中点．若，则的长为 A ．3B ．4C ．6D ．8【分析】根据等腰三角形的性质和直角三角形的性质即可得到结论．【解答】解：，，，为边的中点，，，， 故选：．【点评】本题考查了直角三角形的性质和等腰三角形的性质，熟练掌握直角三角形的性质是解题的关键．2．（2018秋•东城区期末）如图，在中，，，于，是的平分线，且交于，如果，则的长为 A ．2B ．4C ．6D ．8【分析】易得的等边三角形，则，在直角中，利用含30度角的直角三角形的性质来求的长度，然后在等腰中得到的长度，则易求的长度．【解答】解：中，，，．又是的平分线，ABC BA BC =120ABC ∠=︒D AC 6BC =BD ()BA BC =Q 120ABC ∠=︒30C A ∴∠=∠=︒D Q AC BD AC ∴⊥6BC =Q 132BD BC ∴==A ABC ∆90A ∠=︒30C ∠=︒AD BC ⊥D BE ABC ∠AD P 2AP =AC ()AEP ∆2AE AP ==AEB ∆EB BEC ∆CE AC ABC ∆Q 90BAC ∠=︒30C ∠=︒60ABC ∴∠=︒BE Q ABC ∠，，，，．又，，则，的等边三角形，则，在直角中，，则，，．故选：．【点评】本题考查了含角的直角三角形的性质、角平分线的性质以及等边三角形的判定与性质．利用三角形外角性质得到是解题的关键．3．（2019春•昌平区校级月考）如图，若，，，则 A ．B ．C ．D ．【分析】根据含的直角三角形的性质解答即可．【解答】解：，，，，故选：．【点评】此题考查含的直角三角形，关键是根据含的直角三角形的性质解答．4．（2019秋•海淀区校级月考）如图，中，，，，点是边上的动点，则的最小值为 30EBC ∴∠=︒60AEB C EBC ∴∠=∠+∠=︒C EBC ∠=∠60AEP ∴∠=︒BE EC =AD BC ⊥60CAD EAP ∴∠=∠=︒60AEP EAP ∠=∠=︒AEP ∴∆2AE AP ==AEB ∆30ABE ∠=︒24EB AE ==4BE EC ∴==6AC CE AE ∴=+=C 30︒60AEB ∠=︒30B ∠=︒90C ∠=︒20AC m =(AB =)25m 30m 40m 30︒30B ∠=︒Q 90C ∠=︒20AC m =40AB m ∴=D 30︒30︒ABC ∆90C ∠=︒30A ∠=︒4AB =P AC BP ()A ．1B ．2C ．3D ．4【分析】先根据直角三角形30度角的性质得的长，根据垂线段最短可得是的最小值．【解答】解：，，，， 点是边上的动点，则当与重合时，的值最小为2，故选：．【点评】本题考查了直角三角形30度角的性质，点到直线的距离，熟练掌握垂线段最短是关键．5．（2018春•海淀区校级期中）已知直角三角形中，，，若，则长为 A ．2B ．4C ．3D ．【分析】根据计算． 【解答】解：，，， ， 故选：．【点评】本题考查了三角函数，熟练运用三角函数关系是解题的关键．二．填空题（共7小题）6．（2019秋•延庆区期末）如图，与交于点，，，，则的度数是 ．【分析】根据三角形的内角和和等腰三角形的性质即可得到结论．【解答】解：，，，，BC BC BP 90C ∠=︒Q 30A ∠=︒4AB =114222BC AB ∴==⨯=Q P AC P C BP B ABC 30A ∠=︒90C ∠=︒AC =AB ()cos AC A AB =∠30A ∠=︒Q 90C ∠=︒AC =∴cos cos30AC A AB =∠=︒=4AB ∴==B EC DA B 90ACB ∠=︒60A ∠=︒BD BE =DEB ∠75︒90ACB ∠=︒Q 60A ∠=︒30ABC DBE ∴∠=∠=︒BE BD ∴=， 故答案为：．【点评】本题考查了三角形的内角和，对顶角的性质，等腰三角形的性质，正确的识别图形是解题的关键．7．（2019秋•丰台区期末）如图，中，，，交于点，，则　9　．【分析】根据三角形内角和定理，等腰三角形的性质得到，根据直角三角形的性质求出，根据等腰三角形的性质求出，计算即可．【解答】解：，，，，，又，，，，，，，，故答案为：9．【点评】本题考查的是等腰三角形的性质，直角三角形的性质，掌握直角三角形中，角所对的直角边等于斜边的一半是解题的关键．8．（2019秋•延庆区期末）如图，在中，，是的平分线，垂直平分，若，则　6　．【分析】根据角平分线的性质和线段垂直平分线的性质即可得到结论．【解答】解：是的平分线，，垂直平分，1(18030)752DEB ∴∠=︒-︒=︒75︒ABC ∆AB AC =120BAC ∠=︒AD AC ⊥BC D 3AD =BC =30B C ∠=∠=︒CD BD AB AC =Q 120BAC ∠=︒30B C ∴∠=∠=︒AD AC ⊥Q 90DAC ∴∠=︒30C ∠=︒26CD AD ∴==120BAC ∠=︒Q 90DAC ∠=︒30BAD ∴∠=︒DAB B ∴∠=∠3BD AD ∴==9BC BD CD ∴=+=30︒ABC ∆90A ∠=︒CD ACB ∠DE BC 2DE =AB =CD Q ACB ∠ACD BCD ∴∠=∠DE Q BC，，，，，，，，，故答案为：6．【点评】本题考查了直角三角形的性质，线段垂直平分线的性质，角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．9．（2019秋•海淀区校级期中）如图，在中，，，平分交于点，的垂直平分线交于点，交于点，若，则的长为　6　．【分析】根据等腰三角形的性质和线段垂直平分线的性质得出，进而利用含的直角三角形的性质解答即可．【解答】解：连接，如图所示：在中，，平分交于点，，，的垂直平分线交于点，，，，，， ，BD CD ∴=DCB B ∴∠=∠2ACB B ∴∠=∠90A ∠=︒Q 30B ∴∠=︒90DEB ∠=︒Q 24BD CD DE ∴===2AD DE ==6AB ∴=ABC ∆AB BC =30ABC ∠=︒BD ABC ∠AC D BC EF BC E BD F 6BF =AC 6CF BF ==30︒CF Q ABC ∆AB BC =BD ABC ∠AC D AD DC ∴=BD AC ⊥BC Q EF BC E 6BF CF ∴==230DFC DBC ABC ∴∠=∠=∠=︒BD AC ⊥Q 90BDC ∴∠=︒132DC CF ∴==26AC DC ∴==故答案为：6．【点评】此题考查含角的直角三角形，关键是根据等腰三角形的性质和线段垂直平分线的性质得出解答．10．（2019秋•西城区校级期中）等腰三角形的顶角是，底边上的高是3，则腰长为　6　．【分析】画出图形，可求得底角为30度，结合已知，由含的直角三角形的性质可求得腰的长．【解答】解：如图，，于点，，，，． 故答案为：6．【点评】本题考查了等腰三角形的性质和含角的直角三角形的性质；求得的角是正确解答本题的关键．11．（2019秋•海淀区校级期中）已知，如图，，，则的面积为　9　．【分析】根据等腰三角形的性质得到，由三角形的外角的性质得到，过作交的延长线于，根据直角三角形的性质得到，于是得到结论． 【解答】解：，，，， 过作交的延长线于，，，的面积为， 故答案为：9．30︒CF BF =120︒30︒AB AC =AD BC ⊥D 3AD =120BAC ∠=︒120BAC ∠=︒Q AB AC =(180)230B C BAC ∴∠=∠=︒-∠÷=︒AD BC ⊥Q 1362AB ∴=÷=30︒30︒6AB BC ==15A ∠=︒ABC ∆15ACB A ∠=∠=︒30CBD A ACB ∠=∠+∠=︒C CD AB ⊥AB D 132CD BC ==6AB BC ==Q 15A ∠=︒15ACB A ∴∠=∠=︒30CBD A ACB ∴∠=∠+∠=︒C CD AB ⊥AB D 90D ∴∠=︒132CD BC ∴==ABC ∴∆1163922AB CD =⨯⨯=g【点评】本题考查了含直角三角形的性质，等腰三角形的性质，三角形的外角的性质，正确的作出辅助线是解题的关键．12．（2019秋•海淀区校级期中）中，，，，　8　．【分析】由“直角三角形的两个锐角互余”和“30度角所对的直角边等于斜边的一半”解答．【解答】解：如图，在中，，，， ，．故答案是：8．【点评】本题考查了直角三角形角所对的直角边等于斜边的一半的性质，熟记性质是解题的关键，作出图形更形象直观．三．解答题（共3小题）13．（2017秋•大兴区期末）已知：如图，在中，，，求的长．【分析】过点作于．解直角三角形求出，利用等腰三角形的性质即可解决问题．【解答】解：过点作于．，，，，30︒Rt ABC ∆90C ∠=︒2B A ∠=∠4BC cm =AB =cm Q Rt ABC ∆90C ∠=︒2B A ∠=∠190303A ∴∠=︒⨯=︒4BC cm =Q 28AB BC cm ∴==30︒ABC ∆8AB AC ==120A ∠=︒BC A AD BC ⊥D BD A AD BC ⊥D AB AC =Q 120BAC ∠=︒30B C ∴∠=∠=︒2BC BD =在中，，，，，．【点评】本题考查等腰三角形的性质、解直角三角形等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．14．（2014秋•海淀区校级期末）等腰三角形中，，，求边上的高的长．【分析】①当为底角时，首先计算出，然后再计算出的度数，再根据直角三角形的性质可得的长，再利用勾股定理计算出长即可；②当为顶角时，直接利用在直角三角形中，角所对的直角边等于斜边的一半可得答案；③当为底角，为底边，利用勾股定理以及在直角三角形中，角所对的直角边等于斜边的一半可得答案．【解答】解：①当为底角时，，，，，，，， ；②当为顶角时，，， ，，，③当为底角，为底边，则，，，，Rt ABD ∆90ADB ∠=︒30B ∠=︒8AB =cosBD B AB=cos308BD AB ∴=︒==BC ∴=ABC 30A ∠=︒8AB =AB CD A ∠60CBD ∠=︒BCD ∠BD CD A ∠30︒A ∠AB 30︒A ∠30A ∠=︒Q 8AB CB ==30ACB ∴∠=︒60CBD ∴∠=︒CD AD ⊥Q 30BCD ∴∠=︒142BD CB ∴==CD ∴===A ∠CD AB ⊥Q 12CD AC ∴=AB AC =Q 8AC ∴=4CD ∴=A ∠AB AC BC =AC BD =CD AB ⊥Q 4AD BD ∴==设，则，故，解得：， 综上：边上的高的长为4或【点评】此题主要考查了直角三角形的性质，关键是掌握在直角三角形中，角所对的直角边等于斜边的一半．15．（2014•顺义区一模）如图，在四边形中，，，，，求的长．【分析】延长，，交于点，可得出三角形与三角形相似，由相似得比例，设，利用30角所对的直角边等于斜边的一半得到，利用勾股定理表示出，由表示出，在直角三角形中，利用30度角所对的直角边等于斜边的一半得到，即可求出的长．【解答】解：延长，，交于点，，，，， 在中，，设，则有，根据勾股定理得：，DC x =2AC x =22244x x +=x=CD ∴=AB CD 30︒ABCD 90B D ∠=∠=︒60C ∠=︒4BC =3CD =AB DA CB E ABE CDE AB x =2AE x =BE BC BE +CE DCE 2DC CE =AB DA CB E E E ∠=∠Q 90ABE D ∠=∠=︒ABE CDE ∴∆∆∽∴AB AE CD EC=Rt ABE ∆30E ∠=︒AB x =2AE x =BE ==，在中，，，即， 解得：则【点评】此题考查了相似三角形的判定与性质，含30度直角三角形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．4CE BC BE ∴=+=+Rt DCE ∆30E ∠=︒12CD CE ∴=1(4)32+=x =AB =。

2022-2023学年北师大版九年级数学下册《1.4解直角三角形》同步练习题（附答案）一．选择题1．在Rt△ABC中，∠C＝90°，BC＝2，，则AC的长是（）A．B．3C．D．2．在△ABC中，∠A和∠C都是锐角，且sin A＝，tan C＝，则△ABC是（）A．直角三角形B．钝角三角形C．等边三角形D．不能确定3．在平面直角坐标系xOy中，已知点P（1，3）与原点O的连线与x轴的正半轴的夹角为α（0°＜α＜90°），那么cosα的值是（）A．3B．C．D．4．如图，在Rt△ABC中，∠C＝90°，sin A＝，BC＝，则AC的长为（）A．B．3C．D．25．在Rt△ABC中，∠B＝90°，如果∠A＝α，BC＝a，那么AC的长是（）A．a•tanαB．a•cotαC．D．6．等腰三角形底边与底边上的高的比是2：，则它的顶角为（）A．30°B．45°C．60°D．120°7．阅读理解：为计算tan15°三角函数值，我们可以构建Rt△ACB（如图），使得∠C＝90°，∠ABC＝30°，延长CB使BD＝AB，连接AD，可得到∠D＝15°，所以tan15°＝＝＝＝2﹣．类比这种方法，请你计算tan22.5°的值为（）A．+1B．﹣1C．D．8．如图，在△ABC中，AD⊥BC于点D．若BD＝9，DC＝5，cos B＝，E为边AC的中点，则cos∠ADE的值为（）A．B．C．D．9．如图，在△ABC中，AB＝AC＝10，BC＝12，点D为BC的中点，DE⊥AB于点E，则tan∠BDE的值等于（）A．B．C．D．10．如图，在△ABC中，∠BAC＝120°，AC＝8，AB＝4，则BC的长是（）A．B．C．6D．8二．填空题11．如图，Rt△ABC中，∠C＝90°，点D在AC上，∠DBC＝∠A，若AC＝4，cos A＝，则BD的长度为．12．已知等腰三角形两条边的长分别是4，6，底角为α，则cosα＝．13．如图，在△ABC中，∠ACB＝90°，点D在AB的延长线上，连接CD，若AB＝2BD，tan∠BCD＝，则的值为．14．如图，已知点A（4，3），点B为直线y＝﹣2上的一动点，点C（0，n），﹣2＜n＜3，AC⊥BC于点C，连接AB．若直线AB与x轴正半轴所夹的锐角为α，当n＝2时，则tanα＝；当tanα的值最大时，n的值为．15．如图，在△ABC中，AD⊥BC于D，点E在AC上，∠ABE＝45°，tan∠CBE＝，若AD＝BC，AC＝2，则线段BC的长是．三．解答题16．根据下列条件解直角三角形：（1）在Rt△ABC中，∠C＝90°，c＝8，∠A＝60°；（2）在Rt△ABC中，∠C＝90°，a＝3，b＝9．17．如图，在平面直角坐标系中，OB＝4，sin∠AOB＝，点A的坐标为（，0）．（1）求点B的坐标；（2）求sin∠OAB的值．18．如图，点C在线段AB上，点D，E在直线AB的同侧，∠A＝∠DCE＝∠CBE＝90°，∠ADC＝∠ABD，AC＝3，BC＝，求tan∠CDB的值．19．如图，在Rt△ABC中，∠ACB＝90°，D是边AB的中点，过B作BE⊥CD，交CD的延长线于点E，AC＝30，sin B＝，求：（1）线段CD的长．（2）cos∠BDE的值．20．如图（1），在Rt△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，以下是某同学推理证明的过程：证明：∵sin A＝，sin B＝∴c＝，c＝∴根据你掌握的三角函数知识，请在图（2）中的锐角△ABC中，求证：．参考答案一．选择题1．解：如图，在Rt△ABC中，∠C＝90°，BC＝2，∴sin A＝＝＝，∴AB＝3，∴AC＝＝＝．故选：A．2．解：∵sin A＝，∴∠A＝60°，∵tan C＝，∴∠C＝60°，∴∠B＝180°﹣∠A﹣∠C＝180°﹣60°﹣60°＝60°．∴△ABC是等边三角形．故选：C．3．解：如图，过P点作P A⊥x轴于A，则∠POA＝α，∵点P的坐标为（1，3），∴OA＝1，P A＝3，∴tan∠POA＝＝＝3，即tanα＝3．故选：D．4．解：∵∠C＝90°，sin A＝＝，BC＝，∴AB＝BC＝×＝2，∴AC＝＝＝＝．故选：C．5．解：如图：在Rt△ABC中，AC＝＝．故选：D．6．解：如图，AB＝AC，AD⊥BC，∴BD＝CD，∵BC：AD＝2：，∴tan B＝＝，∴∠B＝60°，∵AB＝AC，∴△ABC是等边三角形，∴∠BAC＝60°，故选：C．7．解：如图：在Rt△ACB中，∠C＝90°，∠ABC＝45°，延长CB使BD＝AB，连接AD，∴∠BAD＝∠D＝22.5°，设AC＝BC＝1，则AB＝BD＝AC＝，∴CD＝BC+BD＝1+，在Rt△ADC中，tan22.5°＝＝＝﹣1，故选：B．8．解：∵AD⊥BC，BD＝9，cos B＝，∴AB＝＝15，AD＝＝12，∵DC＝5，∴AC＝＝13，∵E为边AC的中点，∴ED＝，∴∠EDA＝∠DAE，∴cos∠EDA＝cos∠DAE＝，故选：D．9．解：连接AD，∵△ABC中，AB＝AC＝10，BC＝12，D为BC中点，∴AD⊥BC，BD＝BC＝6，∴AD＝，∴tan∠BAD＝．∵AD⊥BC，DE⊥AB，∴∠BDE+∠ADE＝90°，∠BAD+∠ADE＝90°，∴∠BDE＝∠BAD，∴tan∠BDE＝tan∠BAD＝，故选：C．10．解：如图，过点C作CE⊥BA交BA的延长线于E．∵∠BAC＝120°，∴∠CAE＝180°﹣120°＝60°，∴AE＝AC•cos60°＝4，EC＝AC•sin60°＝4，∵AB＝4，∴BE＝AB+AE＝8，∴BC＝＝＝4，故选：B．二．填空题11．解：∵∠C＝90°，AC＝4，cos A＝，∴AB＝5，∴BC＝＝＝3，∵∠DBC＝∠A．∴cos∠DBC＝cos∠A＝＝，∴BD＝3×＝，故答案为：．12．解：分两种情况：当等腰三角形的腰长为4，底边长为6时，如图：过点A作AD⊥BC，垂足为D，∵AB＝AC＝4，AD⊥BC，∴BD＝DC＝BC＝3，在Rt△ABD中，cos B＝＝，当等腰三角形的腰长为6，底边长为4时，如图：过点A作AD⊥BC，垂足为D，∵AB＝AC＝6，AD⊥BC，∴BD＝DC＝BC＝2，在Rt△ABD中，cos B＝＝＝，综上所述：cosα＝或，故答案为：或．13．解：过点D作DM⊥BC，交CB的延长线于点M，∵∠ACB＝∠DMB＝90°，∠ABC＝∠DBM，∴△ABC∽△DBM，∴＝＝，∵AB＝2BD，∴＝＝＝，在Rt△CDM中，由于tan∠MCD＝＝，设DM＝2k，则CM＝3k，又∵＝＝，∴BC＝2k，AC＝4k，∴＝＝2，故答案为：2．14．解：过点A作AM⊥y轴于点M，作AN⊥BG于点N，如图所示：则∠AMC＝90°，∠ANB＝90°，∵直线y＝﹣2与x轴平行，∴∠ABN＝α，∠CGB＝90°，∵AC⊥BC，∴∠ACB＝90°，∵∠ACM+∠MAC＝90°，∠ACM+∠BCG＝90°，∴∠CAM＝∠BCG，∵∠AMC＝∠CGB＝90°，∴△AMC∽△CGB，∴，设BG＝m，∵点A坐标为（4，3），点C坐标为（0，n），∴AM＝4，GC＝n+2，CM＝3﹣n，∴＝，当n＝2时，可得，解得m＝1，∴GB＝1，BN＝3，∴tanα＝＝；∵tanα＝，当BN最小，即BG最大时，tanα最大，∵＝，∴m＝﹣（n﹣3）（n+2）＝﹣（n﹣）2+，∵﹣＜0，∴当n＝时，m取得最大值，即tanα最大，故答案为：，．15．解：如图，过点A作AF⊥BE于点F，设AD与BF交于点G，∵∠ABE＝45°，∴△ABF是等腰直角三角形，∴AF＝BF，∵∠GDB＝∠AFG＝90°，∠BGD＝∠AGE，∴∠GBD＝∠F AG，∴tan∠GBD＝tan∠F AG，∴＝＝，设DG＝x，则BD＝2x，∴BG＝＝x，设FG＝a，则AF＝2a，∴BF＝AF＝2a，AG＝＝a，∴BG＝BF﹣FG＝a，∴a＝x，∴AD＝AG+DG＝a+x＝6x，∵DC＝BC﹣BD＝AD﹣BD＝a+x﹣2x＝a﹣x＝4x，在Rt△ADC中，根据勾股定理得AD2+DC2＝AC2，∴（6x）2+（4x）2＝（2）2，∴x＝1（负值舍去），∴BC＝AD＝6x＝6．故答案为：6．三．解答题16．解：（1）∵∠C＝90°，∠A＝60°，∴∠B＝90°﹣∠A＝30°，∴b＝c＝4，∴a＝b＝12，∴∠B＝30°，b＝4，a＝12；（2）在Rt△ABC中，∠C＝90°，a＝3，b＝9，∴tan A＝＝＝，∴∠A＝30°，∴∠B＝90°﹣∠A＝60°，c＝2a＝6，∴∠A＝30°，∠B＝60°，c＝6．17．解：（1）过点B作BC⊥OA于点C，在Rt△BOC中，OB＝4，sin∠AOB＝，∴BC＝OB•sin∠AOB＝4×＝3，∴，∴点B的坐标为（，3）；（2）∵点A的坐标为（，0），∴OA＝，∴AC＝OA﹣OC＝＝，∵∠ACB＝90°，∴，∴，∴sin∠OAB的值为．18．解：如图，设CE交BD于G．∵∠A＝∠A＝90°，∠ADC＝∠ABD，∴△ADC∽△ABD，∴，，解得AD＝5，∴DC＝＝，DB＝＝，∵∠A＝∠ECD＝∠CBE＝90°，∴∠ACD+∠ECB＝90°，∠ACD+∠ADC＝90°，∴∠ADC＝∠ECB，设∠DBA＝∠CDA＝α，则∠ECB＝α，∴∠GCB＝∠GBC＝α，∴CG＝GB，设CG＝GB＝x，∴DG＝﹣x，∴（）2+x2＝（﹣x）2，解得x＝，∴tan∠CDB＝＝．19．解：（1）∵∠ACB＝90°，AC＝30，sin B＝＝，∴AB＝50，∵D为直角三角形ABC斜边上的中点，∴CD＝AB＝25；（2）∵AB＝50，D为AB的中点，∴AD＝BD＝25，∵BE⊥CD，∴∠E＝90°，由勾股定理得：BC＝＝＝40，由勾股定理得：BE2＝BD2﹣DE2＝BC2﹣CE2，即252﹣DE2＝402﹣（25+DE）2，解得：DE＝7，∴cos∠BDE＝＝．20．解：过C点作CD⊥AB于D，过B点作BE⊥AC于E，∴sin A＝，sin B＝，∴CD＝b sin∠A＝a sin B，∴，同理，∴．。

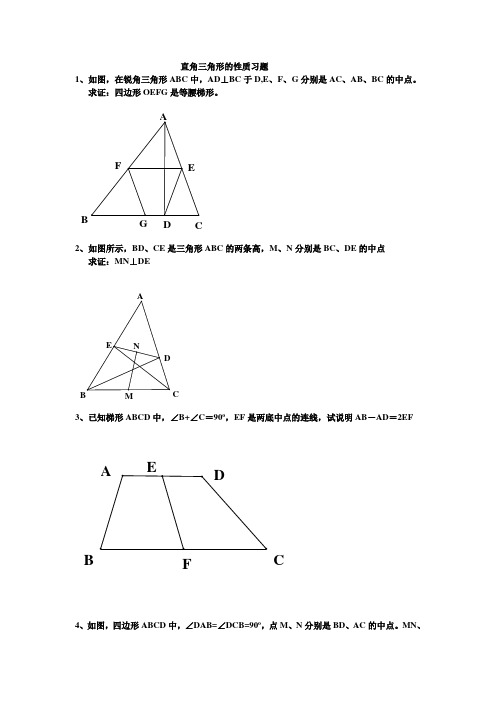
直角三角形的性质习题1、如图，在锐角三角形ABC中，AD⊥BC于D,E、F、G分别是AC、AB、BC的中点。

求证：四边形OEFG是等腰梯形。

BG D C2、如图所示，BD、CE是三角形ABC的两条高，M、N分别是BC、DE的中点求证：MN⊥DEC3、已知梯形ABCD中，∠B+∠C＝90o，EF是两底中点的连线，试说明AB－AD＝2EFBF C4、如图，四边形ABCD中，∠DAB=∠DCB=90o，点M、N分别是BD、AC的中点。

MN、AC的位置关系如何？证明你的猜想。

DAB5、过矩形ABCD对对角线AC的中点O作EF⊥AC分别交AB、DC于E、F，点G为AE 的中点，若∠AOG＝30o求证：3OG=DCFA6、如图所示；过矩形ABCD的顶点A作一直线，交BC的延长线于点E，F是AE的中点，连接FC、FD。

求证：∠FDA=∠FCBAB1：已知，Rt △ABC 中，∠ACB=90°，AB=8cm ，D 为AB 中点，DE ⊥AC 于E ， ∠A=30°，求BC ，CD 和DE 的长2：已知：△ABC 中，AB=AC=BC （△ABC 为等边三角形）D 为BC 边上的中点， DE ⊥AC 于E.求证：AC CE 41.3：已知：如图AD ∥BC ，且BD ⊥CD ，BD=CD ，AC=BC. 求证：AB=BO.4.△ABC 中，∠BAC=2∠B ，AB=2AC ，AE 平分∠CAB 。

求证：AE=2CE 。

5.已知，Rt △ABC 中，∠ACB=90°，CD ⊥AB ，CE 为AB 边上的中线，且∠BCD=3∠DCA 。

求证：DE=DC 。

6.如图：AB=AC ，AD ⊥BC 于D ，AF=FD ，AE ∥BC 且交BF 的延长线于E ，若AD=9，BC=12，求BE的长。

7.在△ABC中，∠ACB=90°，D是AB边的中点，点F在AC边上，DE与CF平行且相等。

北师大版九年级数学下册第一章《4.解直角三角形》课时练习题（含答案）一、单选题1．在△ABC中，∠B=45°，∠C=75°，AC=6，则AB的长是（）A．2(31)+ +B．3(31)+C．4(31)+D．5(31)2．如图，△AOB中，OA＝4，OB＝6，AB＝27，将△AOB绕原点O旋转90°，则旋转后点A的对应点A′的坐标是（）A．（4，2）或（﹣4，2）B．（23，﹣4）或（﹣23，4）C．（﹣23，2）或（23，﹣2）D．（2，﹣23）或（﹣2，23）3．△ABC中，若AB＝6，BC＝8，∠B＝120°，则△ABC的面积为()A．123B．12 C．243D．4834．如图，在等腰直角三角形ABC中，∠C=90°，AC=6，D是AC上一点，如果tan∠DBA=1，那么AD的长为（）5A．1 B．2 C．2D．225．如图，Rt△ABC中，∠ACB = 90°，AB = 5，AC= 3，把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C' ，则四边形ABC'A'的面积是（）A．15 B．18 C．20 D．226．如图，小明在一条东西走向公路的O 处，测得图书馆A 在他的北偏东60︒方向，且与他相距200m ，则图书馆A 到公路的距离AB 为（ ）A ．100mB ．1002mC ．1003mD ．2003m 3 7．如图，在平面直角坐标系中，将边长为1的正方形OABC 绕点O 顺时针旋转45︒后得到正方形111OA B C ，依此方式，绕点O 连续旋转2019次得到正方形201920192019OA B C ，那么点2019A 的坐标是( )A ．22,22⎛⎫- ⎪ ⎪⎝⎭B ．(1,0)C ．22,22⎛⎫-- ⎪ ⎪⎝⎭D ．(0,1)-8．如图，在BAC 中，90BAC ∠=︒，2AB AC =，将BAC 绕点A 顺时针旋转至DAE ，点D 刚好落在BC 直线上，则BDE △的面积为（ ）A ．24BD B ．22BC C ．4BC BD ⋅ D ．22AB二、填空题9．如图，在菱形ABCD 中，∠A =60°，AB =6．折叠该菱形，使点A 落在边BC 上的点M 处，折痕分别与边AB ，AD 交于点E ，F ．当点M 与点B 重合时，EF 的长为________；当点M的位置变化时，DF 长的最大值为________．10．如图，在Rt ABC 中，∠C ＝90°，sinA ＝35，AB ＝10，D 是AC 的中点，则BD ＝______．11．如图，已知四边形ABCD ，AC 与BD 相交于点O ，∠ABC =∠DAC =90°，14tan ,23BO ACB OD ∠==，则ABDCBD S S =___．12．如图是小明画的卡通图形，每个正六边形的边长都相等，相邻两正六边形的边重合，点A ，B ，C 均为正六边形的顶点，AB 与地面BC 所成的锐角为β，则tan β的值是______．13．如图，在矩形ABCD 中，AB =4，BC =43P 在线段BC 上运动（含B 、C 两点），连接AP ，以点A 为中心，将线段AP 逆时针旋转60°到AQ ，连接DQ ，则线段DQ 的最小值为____．14．如图，在矩形ABCD 中，AB=4，BC=3，E ，F 分别为AB ，CD 边的中点．动点P 从点E 出发沿EA 向点A 运动，同时，动点Q 从点F 出发沿FC 向点C 运动，连接PQ ，过点B 作BH ⊥PQ 于点H ，连接DH ．若点P 的速度是点Q 的速度的2倍，在点P 从点E 运动至点A 的过程中，线段PQ 长度的最大值为_____，线段DH 长度的最小值为_____．三、解答题15．如图，菱形ABCD 中，120D ∠=︒，F 是AD 中点，连接BF ，BE DC ⊥，垂足是E ．（1）求证：BF BE =；（2）若23BF =BEDF 的面积．16．如图，在△ABC 中，∠B ＝45°，AC ＝5，cosC ＝35，AD 是BC 边上的高线． （1）求AD 的长；（2）求△ABC 的面积．17．如图，在ABC 中，390,tan ,3C A ABC ∠==∠的平分线BD 交AC 于点.3D CD =．求AB 的长？18．如图，一艘海轮位于灯塔P 的南偏东30°方向，距离灯塔120海里的A 处，它计划沿正北方向航行，去往位于灯塔P 的北偏东45°方向上的B 处．(1)问B 处距离灯塔P 有多远？（结果精确到0.1海里）(2)假设有一圆形暗礁区域，它的圆心位于射线PB 上，距离灯塔150海里的点O 处．圆形暗礁区域的半径为50海里，进入这个区域，就有触礁的危险．①请判断海轮到达B 处是否有触礁的危险？并说明理由．②如果海轮从B 处继续向正北方向航行，是否有触礁的危险？直接写出结论，不用说明理由．2 1.4≈3 1.7≈）参考答案1．B2．C3．A4．B5．A6．A7．A8．A 9．33633-10．21311．3 3212．1931513．214．3213﹣215．（1）证明：连接BD∵四边形ABCD是菱形，∠ADC=120°，∴AB=CB=CD=AD，∠A=∠C=60°，∵F是AD中点，BE⊥DC，∴△ABD、△CBD是等边三角形，∵F是AD中点，BE⊥DC，∴BF⊥AD，∴∠AFB=∠CEB =90°，∵∠A=∠C，AB=CB，∴△ABF≌△CBE（AAS），∴BF=BE；（2）由（1）得△ABF是直角三角形，∠A=60°，∵BF=3sin60°3∴AB=CB=CD=AD=4，AF=12AB=2，∴ABCD =234S菱形=83ABF CEB1S=S=2232⨯⨯△△=23∴四边形BEDF 的面积=ABF CEB ABCD S S S --△△菱形16．解：（1）∵AD ⊥BC ，∴∠ADC ＝∠ADB ＝90°．在Rt △ACD 中，AC ＝5，cosC ＝35， ∴CD ＝AC•cosC ＝3，∴AD4．（2）∵∠B ＝45°，∠ADB ＝90°， ∴∠BAD ＝90°﹣∠B ＝45°， ∴∠B ＝∠BAD ，∴BD ＝AD ＝4，∴S △ABC ＝12AD•BC ＝12×4×（4+3）＝14．17．解：在Rt ABC 中，90,C tanA ∠== 30,60,A ABC ∴∠=∠= BD 是ABC ∠的平分线，30,CBD ABD ∴∠=∠=︒ 又3,CD =330CD BC tan ∴==， 在Rt ABC 中，90,30∠=︒∠=︒C A ， 630BC AB sin ∴==︒． 故答案为：6．18．（1）解：过点P 作PD AB ⊥交于点D ． 由题意可知，120PA =海里，903060APD ∠=︒-︒=︒，45BPD ∠=︒． 906030A ∴∠=︒-︒=︒．1602PD PA ∴==（海里）， 在Rt PBD 中，45BPD ∠=︒，PBD ∴∆是等腰直角三角形， 2602PB PD ∴==（海里）84.8≈（海里）． 答：B 处距离灯塔P 约84海里． （2）解：①海轮到达B 处没有触礁的危险，理由如下： 由题意知：150OP =海里，602PB =海里， (150602)OB OP PB ∴=-=-海里65≈海里50>海里， ∴海轮到达B 处没有触礁的危险． ②过点O 作OE AB ⊥交于E ，交AB 延长线于点E ，则90OEB ∠=︒， 45OBE PBD ∠=∠=︒， sin OE OB OBE ∴=∠ 2(150602)=-752604650=≈<， ∴海轮从B 处继续向正北方向航行，有触礁的危险．。

解直角三角形—题集1.如图，在地面上的点处测得树顶的仰角为度，米，则树高为（ ）．A.米B.米C.米D.米【答案】A【解析】米．【标注】【知识点】仰角与俯角2.如图，斜坡，坡顶到水平地面的距离为米，坡底为米，在处，处分别测得顶部点的仰角为，，求的长度．（结果保留根号）．【答案】的长度为米．【解析】设米，则米，由题意得，四边形为矩形，∴，在中，∴ ，在中，，∴，∴，解得，，∴．答：的长度为米．【标注】【知识点】仰角与俯角A.的值越小，梯子越陡B.的值越小，梯子越陡C.的值越小，梯子越陡D.陡缓程度与的函数值无关3.如图，梯子跟地面的夹角为，关于的三角函数值与梯子的倾斜程度之间，叙述正确的是（）．【答案】B【标注】【知识点】坡度4.某地的一座人行天桥如图所示，天桥高为米，坡面的坡度为，文化墙在天桥底部正前方米处（的长），为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为．（1）（2）若新坡面坡角为，求坡角度数．有关部门规定，文化墙距天桥底部小于米时应拆除，天桥改造后，该文化墙是否需要拆除？请说明理由．（参考数据：，）【答案】（1）（2）．该文化墙需要拆除，证明见解析．【解析】（1）（2）∵新坡面坡角为，新坡面的坡度为，∴，∴．作于点，则米，∵新坡面的坡度为，∴，解得，米，∵坡面的坡度为，米，∴米，∴米，又∵米，∴米米，故该文化墙需要拆除．【标注】【知识点】坡度游船港口海警船北（1）（2）5.一艘观光游船从港口以北偏东的方向出港观光，航行海里至处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东方向，马上以海里每小时的速度前往救援．求点到直线的距离．求海警船到达事故船处所需的大约时间．（温馨提示：，）【答案】（1）（2）海里．小时．【解析】游船港口海警船北（1）（2）如图，过点作交延长线于．在中，∵，，海里，∴点到直线距离海里．在中，∵，，∴（海里），∴海警船到达事故船处所需的时间大约为：（小时）．【标注】【知识点】方位角在锐角三角函数中的应用6.一副直角三角板按如图所示放置，点在的延长线上，，，，，，则的长为 ．【答案】【解析】过点作于点，在中，，，，∴．∵，∴．，在中，，，∴，∴，∴．【标注】【知识点】三角板拼接问题7.如图，是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧与墙平行且距离为米，一辆小汽车车门宽为米，当车门打开角度为时，车门是否会碰到墙？ ．（填“是”或“否”）请简述你的理由 ．（参考数据：，，）．【答案】否 ; 点到的距离小于与墙的距离【解析】过点作，垂足为点，如图．在中，∵，米，∴米，∵汽车靠墙一侧与墙平行且距离为米，∴车门不会碰到墙(点到的距离小于与墙的距离)．故答案为：否；点到的距离小于与墙的距离．【标注】【知识点】测量物体之间的距离8.小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测得地面上的影长为米，坡面上的影长为米．已知斜坡的坡角为，同一时刻，一根长为米、垂直于地面放置的标杆在地面上的影长为米，求树的高度．【答案】米．【解析】延长交延长线于点，则，作于，在中，，，∴（米），（米），在中，∵同一时刻，一根长为米、垂直于地面放置的标杆在地面上的影长为米，（米），，∴（米），∴（米），在中，（米），故答案为：米．【标注】【知识点】影子问题（1）（2）9.如图，在中，，点是边的中点，，．求和的长．求的值．【答案】（1）（2），．．【解析】（1）（2）∵点是边的中点，且∴．∵，∴．∵在中，，，∴．在中，，，∴．故，．如图，作交于点．∵在中，，，∴设，，由勾股定理可得，解得，∴．在中，∵，，∴．即．【标注】【知识点】解直角三角形的综合应用10.如图，在四边形中，，于点，已知，，，求的长．【答案】．【解析】过点作于．∵在中，，，∴，．∵，，∴，∵，∴．∴在中，，，∴，．又∵在中，，，．∴．【标注】【知识点】解直角三角形的综合应用11.如图，在中，，，=， ，求．【答案】．【解析】 在中，，，，，，由勾股定理得：，∵，∴，∵∴，，∴．【标注】【知识点】解直角三角形的综合应用。

直角三角形的边角关系练习题1、已知,AD 为等腰三角形ABC 底边上的高,且tanB=34,AC 上有一点E,满足AE:EC=2:3,那么tan ∠ADE 等于（ ） A 53 B 32 C 21 D 312、直线4-=kx y 与y 轴相交所成的锐角的正切值为21，则K 的值为3、如图，拦水坝的横断而为梯形ABCD ，坝顶宽BC=6米，高3.2米，了提高水能力，需将水坝加高2米，并且保持顶宽度不变，迎水坡CD 坡度不变，但是背水坡坡度由原来i=1：2变成i′=1：2.5（有关数据在图上已注明），求加高后底HD 长多少？3、如图，小明将一张矩形纸片ABCD 沿CD 折叠，B 点恰好落在AD 边上，设此为F ，若AB ：BC=4：5，则cos ∠DCF 的值为 。

5、山脚下有一棵树AB ，小华从点B 沿山坡向上走50米到达点D ，用高为1.5米的测角仪CD 测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB 的高．（精确到0.1米）（已知sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27．）6．如图，一游人由山脚A沿坡角为30°的山坡AB行走600m，到达一个景点B，再由B沿山坡BC行走200m到达山顶C，若在山顶C处观测到景点B的俯角为45°，则山高CD为（）A，3003+1002 B 300+1003 C 300+1002 D 4008、我们知道当人的视线与物体表面互相垂直时的视觉效果最佳．如图是小明站在距离墙壁1.60米处观察装饰画时的示意图，此时小明的眼睛与装饰画底部A 处于同一水平线上，视线恰好落在装饰画中心位置E处，且与AD垂直．已知装饰画的高度AD为0.66米，求：（1）装饰画与墙壁的夹角∠CAD的度数（精确到1°）；（2）装饰画顶部到墙壁的距离DC（精确到0.01米）．的长方体台阶来铺，需要铺几级台阶？11、旗杆、树和竹杆都垂直于地面且一字排列，在路灯下树和竹杆的影子的方位和长短如图所示．请根据图上的信息标出灯泡的位置（用点P 表示），再作出旗杆的影子（用线段字母表示）．（不写作法，保留作图痕迹）A 213-B 63C 6132-D 813+14．如图，四边形ABCD 是矩形，点E 在线段CB 的延长线上，连接DE 交AB 于点F ，∠AED=2∠CED ，点G 是DF 的中点，若BE=1，AG=4，则AB 的长为15、在等边三角形ABC 中，D 为BC 边上一点，E 为AC 边上一点，且∠ADC =60°，BD=4，CE=34 2，则△ABC 的面积（ ）16、在正方形网格中，sin ∠ABC=18、如图，正方形ABCD 中，E 是BC 边上一点，以E 为圆心，EC 为半径的半圆与以A 为圆心，AB 为半径的圆弧外切，则sin EAB 的值为（ ）A 、43 B 、34 C 、45D 、3519、如图，A 、B 、C 、三点在正方形网格线的交点处.若将△ACB 绕着点A 逆时针旋转到如图位置，得到△AC ′B ′，使A 、C 、B ′三点共线。

第一章 直角三角形的边角关系§1.1 从梯子的倾斜程度谈起（第一课时）四、随堂练习：1、如图，△ABC是等腰直角三角形，你能根据图中所给数据求出tanC 吗?2、如图，某人从山脚下的点A走了200m后到达山顶的点B，已知点B到山脚的垂直距离为55m，求山的坡度.(结果精确到0.001)3、若某人沿坡度i＝3：4的斜坡前进10米，则他所在的位置比原来的位置升高________米.4、菱形的两条对角线分别是16和12.较长的一条对角线与菱形的一边的夹角为θ，则tanθ＝______.5、如图，Rt△ABC是一防洪堤背水坡的横截面图，斜坡AB的长为12 m，它的坡角为45°，为了提高该堤的防洪能力，现将背水坡改造成坡比为1：1.5的斜坡AD，求DB的长.(结果保留根号)五、课后练习：1、在Rt△ABC中,∠C=90°,AB=3,BC=1,则tanA= _______.2、在△ABC中,AB=10,AC=8,BC=6,则tanA=_______.3、在△ABC中,AB=AC=3,BC=4,则tanC=______.4、在Rt△ABC中,∠C是直角,∠A、∠B、∠C的对边分别是a、b、c,且a=24,c= 25,求tanA、tanB的值.5、若三角形三边的比是25:24:7,求最小角的正切值.6、如图,在菱形ABCD中,AE⊥BC于E,EC=1,tanB=, 求菱形的边长和四边形AECD的周长.7、已知:如图,斜坡AB的倾斜角a,且tanα=,现有一小球从坡底A处以20cm/s 的速度向坡顶B处移动,则小球以多大的速度向上升高?§1.1从梯子的倾斜程度谈起（第二课时）四、随堂练习：1、在等腰三角形ABC中，AB=AC＝5，BC=6，求sinB，cosB，tanB.2、在△ABC中，∠C＝90°，sinA＝，BC=20，求△ABC的周长和面积.3、在△ABC中.∠C=90°，若tanA=，则sinA= .4、已知：如图，CD是Rt△ABC的斜边AB上的高，求证：BC2＝AB·BD. (用正弦、余弦函数的定义证明)五、课后练习：1、在Rt△ABC中,∠ C=90°,tanA=,则sinB=_______,tanB=______.2、在Rt△ABC中,∠C=90°,AB=41,sinA=,则AC=______,BC=_______.3、在△ABC中,AB=AC=10,sinC=,则BC=_____.4、在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论正确的是( )A.sinA=B.cosA=C.tanA=D.cosB=5、如图,在△ABC中,∠C=90°,sinA=,则等于( )A. B. C. D.6、Rt△ABC中,∠C=90°,已知cosA=,那么tanA等( )A. B. C. D.7、在△ABC中，∠C=90°,BC=5,AB=13,则sinA的值是A． B． C． D．8、已知甲、乙两坡的坡角分别为α、β, 若甲坡比乙坡更徒些, 则下列结论正确的是( )A.tanα<tanβB.sinα<sinβ;C.cosα<cosβD.cosα>cosβ9、如图,在Rt△ABC中,CD是斜边AB上的高,则下列线段的比中不等于sinA的是( )A. B. C. D.10、某人沿倾斜角为β的斜坡前进100m,则他上升的最大高度是( )mA. B.100sinβ C. D. 100cosβ11、如图,分别求∠α,∠β的正弦,余弦,和正切.12、在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求:CD,sinC.13、在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5.求sin∠ACD,cos∠ACD和tan∠ACD.14、在Rt△ABC中,∠C=90°,sinA和cosB有什么关系?15、如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD=.求：s△ABD：s△BCD§1.2 30°、45°、60°角的三角函数值三、随堂练习1.计算：(1)sin60°-tan45°； (2)cos60°+tan60°；(3) sin45°+sin60°-2cos45°； ⑷；⑸(+1)-1+2sin30°-； ⑹(1+)0-｜1-sin30°｜1+()-1；⑺sin60°+； ⑻2-3-(+π)0-cos60°-.2.某商场有一自动扶梯，其倾斜角为30°.高为7 m，扶梯的长度是多少?3．如图为住宅区内的两幢楼，它们的高AB＝CD=30 m，两楼问的距离AC=24 m，现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时，求甲楼的影子在乙楼上有多高?(精确到0.1 m，≈1.41，≈1.73)四、课后练习：1、Rt△ABC中，，则；2、在△ABC中，若,，则，面积S＝ ；3、在△ABC中，AC：BC＝1：，AB＝6，∠B＝ ，AC＝ BC＝ 4、等腰三角形底边与底边上的高的比是，则顶角为 （ ）（A）600 （B）900 （C）1200 （D）15005、有一个角是的直角三角形，斜边为，则斜边上的高为 （ ）（A） （B） （C） （D）6、在中，，若，则tanA等于（ ）． （A） （B） （C） （D）7、如果∠a是等边三角形的一个内角，那么cosa的值等于（ ）． （A） （B） （C） （D）18、某市在“旧城改造”中计划内一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a元，则购买这种草皮至少要（ ）．（A）450a元 （B）225a元 （C）150a元 （D）300a元9、计算：⑴、 ⑵、⑶、 ⑷、⑸、 ⑹、⑺、·tan60° ⑻、10、请设计一种方案计算tan15°的值。