管理运筹学讲义 第6节 网络计划(6学时)

v2 4
15 9 v3 3
1
v7
37
OR:SM
第二节 最小树问题
v1 23 v6 28 v5 25 17 16 v4 1 v7 9 v3 3
20
v2 4
15
38
OR:SM
第二节 最小树问题
v1 23 v6 28 v5 25 17 16 v4 1 v7 9 v3 3 20
v2 4
15
39
OR:SM
√ √ √
√
OR:SM
第一节 图论的概念
• 解：用图来建模。把比赛项目作为研究对象，用点 表示。如果2个项目有同一名运动员参加，在代表这 两个项目的点之间连一条线，可得下图。
在图中找到一个点序 列，使得依次排列的 两点不相邻，即能满 足要求。如： 1) A,C,B,F,E,D B D
A
F
2) D,E,F,B,C,A
1 2 1 2
e1 e2 v2 e5 e6 e7 e8 v1 e4 e3 v3
V1 V2 和E1 E 2 称G1是G2的一个子图。
e4 v2 e5 e6 e8 e6 v3 v2
e2
e4
e3 v3 e8
v4
（G图）
v5
e7
v4
v5
(a)
12
v4
(b)
v5
OR:SM
第一节 图论的概念
网络（赋权图）
第二节 最小树问题
v1 23 1 v7 4 9 28 v5 25 17 16 v4 v2 15 v3 3
v1 5 v2 8 4 3 v4 v3 7 5 v5 1 v6
8
2
6
33
OR:SM
第二节 最小树问题

A
拆迁
/
2
B
工程设计
/
3
C
土建工程设计
B
2.5
D
采购设备
B
6
E
厂房土建
C、A
20
F
设备安装
D、E
4
G
设备调试
F
2
A（2）
1
B (3)
2
C (2.5)
3
D (6)
E (20)
G (2)
F (4)
4
5
6
用箭秆删除法标号（保证箭尾号大于箭头号)
工序
A
B
C
D
EFGHIJKL
M
N
紧前工序
_
_
_
_
D
E
A
F
G
B
由本例可见：关键工序 头尾皆有
=
关键工序时间之和=工期T。
，但反之未必。
二、工程完工期的概率分析
（计划评审技术PERT）
1、PERT与 CPM的区别：
CPM工序时间是确定的
工程工期的概率分析是是时间不确定情况下PERT
的主要工作
确定平均工序时间的三点估计法：
设工序最乐观时间为aij，最悲观时间为bij，最可能时间为m ij ,
t ij
a ij 4m ij bij
- 给任意点 i 标 Li ,
Li=Min{以 i 为箭尾的各箭之 “箭头
- 箭长tij”}
16
（3）求关键路（用标号法）
6
2
8
0
0 1
3
B '(0)
3
2）计算各工序 i

9
6 3
3
4
7
2
53
4 31
5
1
7
4
4
第3节 最短路问题
一、最短路的含义
赋权有向图D (V，A)，图中各弧(vi，v j )有权wij， vs，vt为图D中任意两点，求一条路P， 使它是从vs到vt的所有路中总权最小的路，
即w(
P
)
min
wij 。
(vi，vj )P
定义：路P的权是P中所有弧的权之和，记为w(P)
习题6-3：用Dijkstra方法求解下图从v1到v9的 最短‘路’。
v2
11
v7
3 6
2
5
5
v5
8
v1
v3
v9
2 4
4
3
7
v4
4
v6
6
v8
第3节 最短路问题
三、最短路问题的应用 ✓ 设备更新问题
第3节 最短路问题
例10：某工厂使用一台设备，每年年初工厂都要作出决定， 如果继续使用旧的，要付维修费；若购买一台新设备， 要付购买费。试制定一个5年的更新计划，使总支出最 少。已知设备在各年的购买费，及不同机器役龄时的 维修费如下表所示：
5
2
5 v6
v4
v7 8
习题6-2
2、
v2
2
v5
5
1
5
1
8
v1
7
5 v4 9
v6
6
v7
2
1
12
v3
第3节 最短路问题
（二）赋权无向图的最短‘路’问题的求解方 法
赋权无向图G=(V，E)，边[vi，vj]表示既可以 从vi到达vj，也可以从vj到达vi，所以边[vi， vj]可以看作是两条弧(vi，vj)和(vj，vi)，且 它们具有相同的权ωij。

结点：表示相邻工序的时间分界点， 结点：表示相邻工序的时间分界点，称事项
连接箭尾的结点称为该工序的紧前事项 连接箭尾的结点称为该工序的紧前事项 连接箭头的结点称为该工序的紧后事项。 连接箭头的结点称为该工序的紧后事项。 紧后事项
权：工序的完成时间 相邻弧：表示工序前后衔接关系，称紧 前(后)工序； 相邻弧：表示工序前后衔接关系， 后 工序； 工序
a + 4m + b t ij = 6
p135
（1）绘制工程网络图
1 烧水（ ） 烧水（10） 3 沏茶（ ） 沏茶（2） 4
1）顺序：按工序先后从左至右； 备茶 ）顺序：按工序先后从左至右； 2）图的结构 ） 弧(箭线 ： 箭线)： 箭线 表示工序； 表示工序；
（3） 2 ）
为工序的起点、终点 为工序的起点、
G (4) 15 11 8 F (2) 15 H (2) 17 9 17
D (3) E (6) 7
工序时间参数的计算： 工序时间参数的计算：
1 计算最早开始时间 计算最早开始时间(ES)与最早完工 与最早完工(EF)时间 与最早完工 时间 从网络起点开始, 用下列公式计算最早开始时间(t 和最 从网络起点开始 用下列公式计算最早开始时间 ES)和最 早完工时间(t 早完工时间 EF): 最早开始时间 = (紧前活动的 最早结束时间的最大值 紧前活动的)最早结束时间的最大值 紧前活动的 =开始结点的最早时间 开始结点的最早时间 tES (i, j) = maxk tEF (k, i)=ETi 最早完工时间 = 最早开始时间 + 活动持续时间 tEF(i, j) = tES (i, j) + t (i, j)
工序时间（ 工序代号 紧前工序 工序时间（周） A / 2 B / 3 C / 2 D A 3 E A 4

运筹学
1
2
3
4
5
6
24
22
26
24
30
18
18
上图为一个项目的网络计划，已知用于该项目的直接成本为47800元，间接成本为18000元，该项目原订74日完成，现要缩短工期，每缩短一天，间接费用可以节省330元，试求出工期较短而成本最少的最优方案。箭线下的数字为正常持续时间，括弧内为最短持续时间。相关数据见下表。 1→3→4→6为关键线路。
工作的最迟可能开工时间与最迟可能结束的时间
02
总时差
在不影响任务总工期的条件下，某工作（i,j）可以延迟其开工时间的最大幅度称为工作的总时差R(i,j) R(i,j) =tLF(i,j)-tEF(i,j)=tLS(i,j)-tES(i,j)
工作单时差
在不影响紧后工作的最早开工时间条件下，此工作可以延迟其开工时间的最大服务，r(i,j) r(i,j)= tES(j,k)-tEF(i,j)
本工作
紧后工作
紧前工作
紧后工作
双代号网络计划
双代号网络图是以箭线及其两端节点的编号表示工作的网络图
支模2
支模1
扎筋2
扎筋1
混凝土2
混凝土1
1.双代号网络图的基本符号
运筹学
工作i—j的持续时间 -------- D i—j 节点最早时间：earliest time -------- ETi 节点最迟时间：latest time -------- LTi 工作最早开始时间earliest star time -------- ES i—j 工作最早结束时间earliest finish time -------- EF i—j 工作最迟开始时间 latest star time -------- LS i—j 工作最迟结束时间 latest finish time ------- LF i—j i—j工作的自由时差 -------- FF i—j i—j工作的总时差 -------- TF i—j

S
2
4
7
2 A
0 5
S
5 45 B
98
14
5
13
D
T
C
E
4
4
4
7
最短路线：S AB E D T
最短距离：Lmin=13
2．求任意两点间最短距离的矩阵算法
⑴ 构造任意两点间直接到达的最短距离矩阵D（0）= dij（0）
S A B D（0）= C D E T
SABCDET 0 25 4 2 02 7 5 20 1 5 3 4 1 0 4 75 0 15 3 41 0 7 5 7 0
e1 v1
e5
v0 e2
e3
v2
e4
e6 e7
v3
v4
（4）简单图：无环、无多重边的图称为简单图。
（5）链：点和边的交替序列，其中点可重复，但边不能 重复。
（6）路：点和边的交替序列，但点和边均不能重复。
（7）圈：始点和终点重合的链。
（8）回路：始点和终点重合的路。
（9）连通图：若一个图中，任意两点之间至少存在一条 链，称这样的图为连通图。 （10）子图，部分图：设图G1=｛V1,E1｝, G2={V2,E2}, 如果有V1V2，E1E2，则称G1是G2的一个子图；若 V1=V2，E1E2，则称G1是G2的一个部分图。 （11）次：某点的关联边的个数称为该点的次，以d(vi)表示。
步骤：
1. 两两连接所有的奇点，使之均成为偶点；
2. 检查重复走的路线长度，是否不超过其所在 回路总长的一半，若超过，则调整连线，改 走另一半。
v1
4
v4
4
1
4
v2
v5
5

17 17
1
5 e 8 4
9
9
g 6
23 23
6
c 2
• 参数计算
工程期望工期 TE=23 ，关键工序的方差2 =49/9，则 (x)=-1.29，查表知 P(x)=9.9%
P(x)=90% ，查表知 (x)=1.3，则可接受的合同工期为TE+ (x) =26
19 OM:SM
直接 费用
极限完 工时间
正常完 工时间
赶进度极限完工费用 正常完工作业时间
时间
赶单位时间增加的直接
费用 (费率 )
- 正常完工费用 - 极限完工作业时间
OM:SM
22
第五节
2、工期-费用优化案例
网络计划优化
某工程作业流程及其费用统计资料
作业 A B C D E 紧前作业 B B 作业时间（天） 正常完工 3 5 5 6 5 极限完工 3 3 4 3 2 作业直接费用（万元） 正常完工 8 16 20 20 5 极限完工 8 19 23 23 8.6 费率 1.5 3 1 1.2
工序时间 t a 4m b 6 ，方差
2
（
ba 6
)
2
二、计算期望工期
• 工程期望工期等于关键路线上各道工序的时间之和 。
工期 T E

i
(
a i 4 m i bi 6
)，方差
2


i
(
bi a i 6
)
2
• 设规定的工程完工时间为Tk，则完工时间的概率为 ( x )
0 0 1
6 a 6 c 4
6
15
6
OM:SM

版权所有 肖智 重庆大学经济与工商管理学院
版权所有 肖智 重庆大学经济与工商管理学院
表2.1-1 演员 1 2 3 4 节目 A B C D E F G H
5
6
7
8
9
10






版权所有 肖智 重庆大学经济与工商管理学院

分析： 把节目作为研究对象，用点表示。如果两个节目 无同一名演员参加，这说明二者可以紧排在一起，则 给相应的两点间连结一条边，得到下列图2.1-9。这 就是本例的网络模型。于是问题归结为：从图中找出 一条从A到H或从H到A且通过所有结点的链，且每一 个点只通过一次。 不难看出，这样的路有四条： （1）AFBCGDEH （2）HEDGCBFA （3）AFGCBDEH （4）HEDBCGFA 则文艺演出的节目表可按上面任一顺序安排。 肖智 版权所有
重庆大学经济与工商管理学院
B
C D E
A H G
图2.1-9
F
版权所有 肖智 重庆大学经济与工商管理学院
例2.1.2：电话线架设问题 某地7个村镇之间的现有交通道路如下图2.1-10 所示，边旁数字为各村镇之间道路的长度。现要沿交 通道路架设电话线，使各村之间均能通话。应如何架 线使总长最短?
6 1
5
最短路
1-3-2-4-6
版权所有 肖智 重庆大学经济与工商管理学院
2、标号法： 例2.3-4：以例2.3-1为例，解题步骤如下图2.3-4。
6
4 2 3 6 5
C1
8
7 4 5
5
11
B1
0
4
D1
5 12 6
3

1 a1
a2
2
3
a3 4
LOGO
5 b1 6 b2 7 b3 8
作业的合并 3
B 1A2
D
E
5G
C
F
4
LOGO
6
1A2
X
5
G
6
4.绘制网络图的基本原则
两事项间只能有一项作业
A
3
改为 A
2
B
5
2
B
C
C
4
LOGO
5
LOGO
网络图应从左向右延伸，编号应从小到大，且不 重复。箭头事项编号大于箭尾事项编号
7.3 网络优化
工期限定，资源需要平衡 资源有限，工期希望最短 工期缩短，总费用最小
LOGO
一、工期限定，资源需要平衡 LOGO
工期不变，就是关键工作时间不能调整 资源不平衡将导致资源不足 利用时差，调整非关键路线上工作的开
始时间，使资源实现平衡。
例
LOGO
2(6)
00
1 B
运筹学7
讲课教师：XXX
第七章 网络计划技术
LOGO
7.1 PERT网络图 7.2 PERT网络参数计算 7.3 PERT网络优化 7.4
7.1 PERT网络图
LOGO
一、网络计划技术的基本概念
工程计划与甘特图
– 不易表现工程全貌 – 不便于对各项工作的安排进行筹划和推敲 – 不能识别影响进度的关键工作 – 不能反映一项工作不能按进度完成时对工程进度的影
C
总费用
间接费用
直接费用
TK*
T
直接成本的处理
LOGO
按线性处理，作业的费用率为

表示。
a1
(v2)钱
a7
a2
a8
(赵v1)
a14 a15 a3
(v4) 李
a4
a9
(v3)孙
a5
a6
a12
a11
(v5) 周
a10
(v6)吴 a13
(v7)陈
图3
图（Graph）由点（Vertex）和点之间的连线所构成的集合。 不带箭头的连线称为边；带前头的连线称为弧。 点和边的集合称为无向图（Undirected graph），如图 (a)， 用G={V，E}表示；
,
d (0) SC

d (0) CB
,
d (0) SD

d
(0) DB
,
d (0) SE

d
(0) EB
,
d (0) SF

d
(0) FB
,
d
(0) ST

d (0) TB
}
一般地有：
d (1) ij

min{di(r0)

d (0) rj
}
0 2 4 4 6 1 6

2
Hale Waihona Puke 0224
3
11

v7 v6
v 3
v4 v5
v1,v2 , v4 ,v7,v3, v5,v6 , v8
§6.1 图与网络的基本概念
图论中图是由点和边构成，可以反映一些对象之间的关系。 如物质结构、电路网络、城市规划、交通运输、信息传递、物 资调配等都可以用点和线连接起来的图进行模拟。
0sssasbscsdsesfstasaaabacadaeafatbsbabbbcbdbebfbtcscacbcccdcecfctdsdadbdcdddedfdteseaebecedeeefetfsfafbfcfdfefffttstatbtctdtetfttddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddd???????????????????????????0212022420312043434071305???????????????????????????????????????6????????????????7d0为对称矩阵50160??????1sb0ss0sb0sa0ab0sb0bb0sc0cb0sd0db0se0eb0sf0fb0st0tbminddddddddddddddddd?????????因为从i到j的最短路不一定是i?j可能是i?l?ji?l?k?j

或具有类似工作的持续时间的历史统计资料时，可以根据这些资料，
采用分析对比的方法确定所需工作的持第续2时6页间/共。70页
⑵ 三时估计法。
• 在不具备有关工作的持续时间的历史资料时，在较难估计出工作持续时间时，可对工作进 行估计三个时间值，然后计算其平均值。这三个时间值是：
• 乐观时间。在一切都顺利时，完成工作需要的最少时间，记作a。 • 最可能时间。在正常条件下，完成工作所需要时间。记作m。 • 悲观时间。在不顺利条件下，完成工作需要最多时间，记作b。
第16页/共70页
6. 平行工作。
• 可与本工作同时进行的工作
第17页/共70页
7. 起始节点与终点节点。
• 在网络计划图中只能有一个起始节点和一个终点节点。当工程开始或完成时存在几个平行工作时，可以用
虚工作将它们与起始节点或终点节点连接起来。
1 s
2
第18页/共70页
8. 线路：
• 网络图中从起点节点沿箭线方向顺序通过一系列箭线与节点，最后到达终点节点的 通路。本例中有五条线路。并可以计算出各线路的持续时间，见表11-2。
• 网络计划的时间参数计算有几种类型：双代号网络 计划有工作计算法和节点计算法；单代号网络计划 有节点计算法。以下仅介绍工作计算法。其它的计 算法可参考[ 1]。
网络图中工作的时间参数。它们是：
• 工作持续时间(D)； • 工作最早开始时间（ES）； • 工作最早完成时间（EF）； • 工作最迟开始时间（LS）； • 工作最迟完成时间（LF）； • 工作总时差（TF）； • 工作自由时差（FF）。 第24页/共70页
第11页/共70页
2. 紧前工作和紧后工作
• 紧前工作是指紧排在本工作之前的工作；且开始或完

46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特
运筹学网络计划分析
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以煌。
18、敢于向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。

第一节 图的基本概念
5、子图
v1 e1 e4 e3 v3 图 1 v4 e5 v3 图 4 v4 图 5 v
2
v1
v
2
v1
e1
e4
v
2
e2
生成子图：包含图的所有顶点 （顶点）导出子图：G[V1]，其中 V1={v1 ,v2，v3}（图4） 边导出子图：G[E1]，其中 E1={e1 ,e4}（图5）
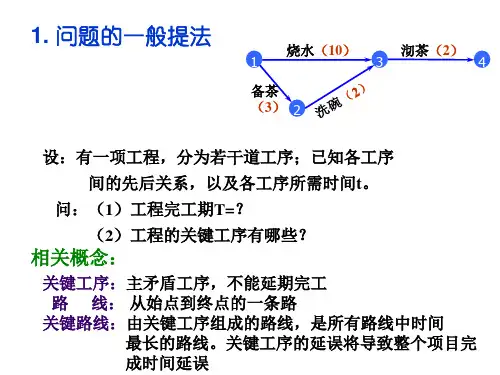
第二节 最短路问题
(5)总结
多阶段决策问题
网络模型
计算机求解
决策方案
第二节 最短路问题
三、每对顶点之间的最短路 1、实例 3（选址问题）:某城市要建立一个消防站，为该市 所属的七个区服务（图 13）.问：应设在哪个区，才能使它 至最远区的路径最短.
v1 3 v2 2 18 v3 2 3 v7 1.5 v
e7} （图17）
,
完美匹配：M={e2 , e5
e8
，
e9} （图18）
割边：e6 , e7
,
e8
，
e9 （图18）
§5.1 中国邮递员问题
二、欧拉图（Euler）
V1 e2 e1 e3 e4 V2 e5 V1 e2 e1 e4 e3 e5 V2
V3
图
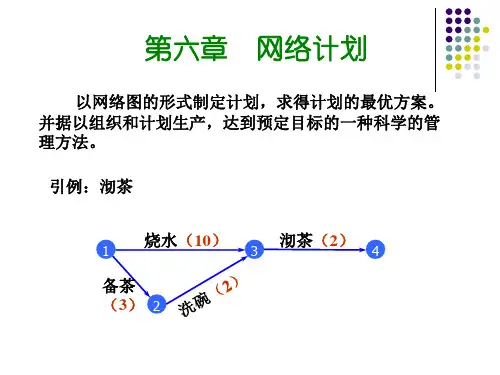
巡回:经过每条边至少一次的闭途径 欧拉巡回:经过每条边正好一次的巡回 欧拉图：存在欧拉巡回的图 欧拉路：经过每条边正好一次的路
e5 图 1 v4
图G: G=(V,E)
|V(G)|=n
|E(G)|=m
顶点集：V={v1,v2 ,v3 ,v4} 边集：E={e1,e2 ,e3 ,e4, e5}
关系：e1=v1v2，e3=v1v4，e5=v4v4