四川省成都七中2012-2013学年高二下学期入学考试数学(理)试题_Word版含答案

四川省成都七中高2012级高三入学考试试卷数学(理)注意事项：本试题分为第I 卷和第II 卷两部分，满分150分，考试时间为120分钟。

、第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分；在每小题给出的四个选项中只有一个是符合题目要求的。

1.已知全集U=R ，集合{|lg 0},{|21},()x U A x x B x A B =≤=≤U 则C =A ．(,1)-∞B ．(1,)+∞C ．(],1-∞D ．[)1,+∞ 2．设z=1+i （i 是虚数单位），则22z z+=A ．1i --B ．1i -+C ．1i -D ．1i +3．函数)(,0)(,0,)(lim ,)(lim ,),()(x f x f mn n x f m x f b a x f b x a x 则且上连续在>'<==-+→→在),(b a 内A ．没有实根B ．至少有一个实根C ．有两个实根D ．有且只有一个实根4．关于两条不同的直线m 、n 与两个不同的平面α、β，下列命题正确的是 A．m//α，n//β且α//β，则m//nB ．,,m n αβαβ⊥⊥⊥且则m//n;C ．m//α，n β⊥且,//;m n αβ⊥则D ．,////,m n m n αβαβ⊥⊥且则5．若两个非零向量,||||2||a b a b a b a +=-=r r r r r r r 满足，则向量a b a b +-r r r r 与的夹角为A ．6πB ．3π C ．23π D ．56π6．在数列{}n a 中，*111001,,(),n n a a a n n N a +=-=∈则的值为A ．5050B ．5051C ．4950D ．49517.将函数f (x )的图象沿x 轴向右平移π3个单位，再将横坐标伸长为原来的2倍(纵坐标不变)，得到的图象所对应的函数为y ＝cos x ，则f (x )为A ．y ＝cos(2x ＋π3) B ．y ＝cos(2x －π3) C ．y ＝cos(2x ＋23π)D ．y ＝cos(2x －23π)8．设36log (1)(6)()31(6)x x x f x x --+>⎧=⎨-≤⎩的反函数为118(),(),9f x f n ---=若则(4)f n +=A ．2B ．—2C ．1D ．—19.已知球的半径为5，相互垂直的两个平面分别截球面得两个圆，若两圆的公共弦长为6，则两圆的圆心距为A ．4BC．D ．110．将123)(x x +的展开式中各项重新排列，使含x 的正整数次幂的项互不相邻的排法共有多少种？A ．1013313A A ⋅B ．3111010A A +C ．99413A A ⋅D ．3111010A A ⋅11．如图所示,已知正方体1111ABCD A B C D -的棱长为2, 长为2的线段MN 的一个端点M 在棱1DD 上运动, 另一端点N在正方形ABCD 内运动, 则MN 的中点的轨迹的面积为 A ．4π B ．2πNM D 1C 1B 1A1DCC ．πD ．2π12.已知集合{(,),}U x y x R y R =∈∈，{(,)}M x y x y a =+<，{(,)()}P x y y f x ==，现给出下列函数：①x y a =②log a y x =③sin()y x a =+④cos y ax =，若01a <<时，恒有U P C M P ⋂=，则()f x 所有可取的函数的编号是A ． ①②③④B ．①②④C ．①②D ．④第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题4分，共16分）13．已知2213sin sin 23cos 22ααα-+=，则tan α=______________. 14．已知{}n a 是等比数列，41252==a a ，， 则13221++++n n a a a a a a Λ= ．15．定义在R 上的函数2()(2)3(),[0,2],()2,f x f x f x x f x x x +=∈=-满足且当时若当13[4,2],()()18x f x t t∈--≥-时恒成立，则实数t 的取值范围是 . 16. 给出定义：若2121+≤<-m x m （其中m 为整数），则m 叫做离实数x 最近的整数，记作{}x = m . 在此基础上给出下列关于函数{}x x x f -=)(的四个命题：①函数y =)(x f 的定义域为R ，值域为⎥⎦⎤⎢⎣⎡21,0；②函数y =)(x f 的图像关于直线2kx =（Z k ∈）对称； ③函数y =)(x f 是周期函数，最小正周期为1； ④函数y =)(x f 在⎥⎦⎤⎢⎣⎡-21,21上是增函数.则所有正确的命题的编号是______________.四川省成都七中高2012级高三入学考试试卷数学试题(理科)答题卷班级 姓名得分 一、第一卷答题卡: 题号 1 2 3 4 5 6 7 8 9 10 11 12答案二、填空题（本大题共4小题，每小题4分，共16分）13 _______________; 14 _____: 15 ____ 16 三、解答题：（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）17．（本题满分12分）ABC ∆中内角,,A B C 的对边分别为,,a b c，向量2(2sin ,(cos 2,2cos 1)2B m B n B ==-u r r 且//m n u r r（Ⅰ）求锐角B 的大小，（Ⅱ）如果2b =，求ABC ∆的面积ABC S ∆的最大值18.（本小题共12分）某选手进行实弹射击训练，射击中每次射击的结果是相互独立的.已知他每次射击时，命中环数ξ的分布列如下表：ξ8 9 10 P0.10.50.4该选手在训练时先射击三次，若三次射击的总环数不小于29环，则射击训练停止；若三次射击的总环数小于29环，则再射击三次，然后训练停止.（I ）求该选手在射击训练中恰好射击三次的概率；（II ）求该选手训练停止时，射击的次数η的分布列及期望. 19.（本小题满分12分）已知：如图，长方体中，、分别是棱,上的点，,.（1） 求异面直线与所成角的余弦值； （2） 证明平面； （3） 求二面角的正弦值.20．（本题满分12分）已知函数4()log (41)x f x kx =++()k R ∈是偶函数． （1）求k 的值;（2）设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点,求实数a 的取值范围．21.（本小题满分12分）已知数列{}n a 满足()111,21n n a a a n N *+==+∈ （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若数列{}n b 满足nnb n b b b b a )1(44441111321+=----Λ，证明：{}n b 是等差数列；（Ⅲ）证明：()23111123n n N a a a *++++<∈L 22．（本题满分14分）已知函数2()ln ()f x ax x a R =+∈．（1）当12a =时，求()f x 在区间[]1,e 上的最大值和最小值；（2）如果函数()g x ，1()f x ，2()f x ，在公共定义域D 上，满足12()()()f x g x f x <<，那么就称为()g x 为12(),()f x f x 的“活动函数”． 已知函数2211()()2(1)ln 2f x a x ax a x =-++-，221()22f x x ax =+．①若在区间()1,+∞上，函数()f x 是1()f x ，2()f x 的“活动函数”，求a 的取值范围；②当23a =时，求证：在区间()1,+∞上，函数1()f x ，2()f x 的“活动函数”有无穷多个．四川省成都七中高2012级高三入学考试试卷数学试题(理科)参考答案一、BDDDC D CBAD DB 二、13. 1或-3 14. 32(14)3n -- 15. ［-1,0）∪［3,+∞） 16. ①②③三、17．解：（1）n m ρρΘ// B BB 2cos 3)12cos 2(sin 22-=-∴B B 2cos 32sin -=∴ 即 32tan -=B又B Θ为锐角 ()π,02∈∴B322π=∴B3π=∴B……………………………………6分（2）得，由余弦定理acb c a B b B 2cos 2,3222-+===πΘ 又ac c a 222≥+Θ 代入上式得：4≤ac （当且仅当 2==c a 时等号成立。

一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的答案填在答题卡上）.1、下列各组几何体中全是多面体的一组是（）A．三棱柱四棱台球圆锥B．三棱柱四棱台正方体圆台C．三棱柱四棱台正方体六棱锥D．圆锥圆台球半球2．在空间直角坐标系错误！未找到引用源。

中，点错误！未找到引用源。

关于错误！未找到引用源。

轴对称的点错误！未找到引用源。

坐标是（）A．错误！未找到引用源。

B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

3．给出下列命题中，其中是正确命题的有（）①垂直于同一条直线的两条不同直线互相平行②垂直于同一条直线的两个不同平面互相平行③垂直于同一个平面的两条不同直线互相平行④垂直于同一个平面的两个不同平面互相平行A．1个B．2个C．3个D．4个4．某几何体的三视图如图所示，则它的体积是（A．错误！未找到引用源。

B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

5．过圆锥的高的三等分点作平行于底面的截面，它们把圆锥侧面分成的三部分的侧面积之比为（）A．1：2：3 B．1：3：5 C．1：2：4 D．1：3：96．设错误！未找到引用源。

是两条不同的直线，错误！未找到引用源。

是两个不同的平面，给出下列命题：①若错误！未找到引用源。

，则错误！未找到引用源。

②若错误！未找到引用源。

，则错误！未找到引用源。

③若错误！未找到引用源。

，错误！未找到引用源。

，则错误！未找到引用源。

④若错误！未找到引用源。

，则错误！未找到引用源。

或错误！未找到引用源。

其中正确命题的是（）A．①④B．②④C．②③D．③④7．设三棱锥错误！未找到引用源。

的顶点错误！未找到引用源。

在平面错误！未找到引用源。

上的射影是错误！未找到引用源。

，给出以下命题：①若错误！未找到引用源。

两两互相垂直，则错误！未找到引用源。

是错误！未找到引用源。

的垂心②若错误！未找到引用源。

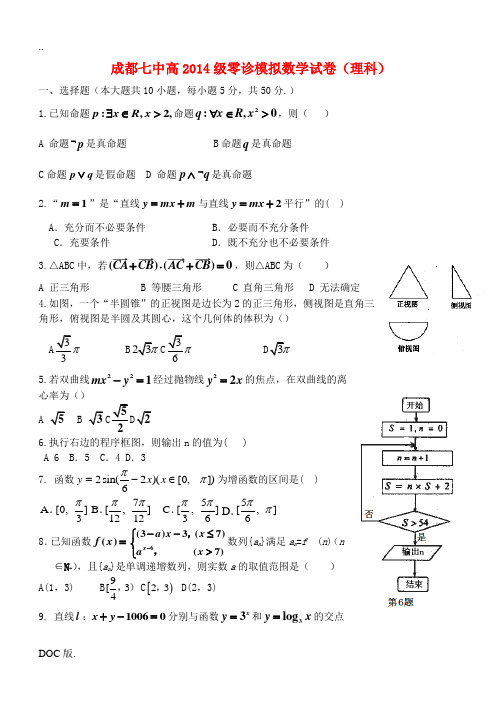
成都七中高2014级零诊模拟数学试卷（理科）一、选择题（本大题共10小题，每小题5分，共50分.） 1.已知命题:,2,p x R x ∃∈>命题2:,0q x R x ∀∈>，则（ ） A 命题p ⌝是真命题 B 命题q 是真命题 C 命题p q ∨是假命题 D 命题p q ⌝∧是真命题2.“1m =”是“直线y mx m =+与直线2y mx =+平行”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件3.△ABC 中，若()()0CA CB AC CB +⋅+=，则△ABC 为（ ） A 正三角形 B 等腰三角形 C 直角三角形 D 无法确定4.如图，一个“半圆锥”的正视图是边长为2的正三角形，侧视图是直角三 角形，俯视图是半圆及其圆心，这个几何体的体积为（） 3 B 23π3 3π5.若双曲线221mx y -=经过抛物线22y x =的焦点，在双曲线的离 心率为（） 53526.执行右边的程序框图，则输出n 的值为( ) A 6 B ．5 C ．4 D ．3 7. 函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是( )A ．]3,0[πB ．]127,12[ππC ．]65,3[ππD ．],65[ππ8．已知函数()f x =6(3)3(7)(7)x a x x a x ---≤⎧⎨>⎩，，数列{a n }满足a n =f (n )（n∈N +），且{a n }是单调递增数列，则实数a 的取值范围是（ ）A(1，3)B 9[34，） C [)23，D(2，3) 9. 直线l ：10060x y +-=分别与函数3x y =和3log y x =的交点为11(,)A x y ，22(,)B x y 则122()y y +=（ ） A 2010 B 2012 C 2014 D 不确定10.设等差数列{}n a 的前n 项和为n S ，已知320122012(1)20140a a -+=，32333320174029a a a -+=，则下列结论正确的是（）A 2014201232014,S a a =<B 2014201232014,S a a =>C 2014201232013,S a a =<D 2014201232013,S a a =>二、填空题（本大题有5小题,每小题5分,共25分.把答案填在答题卷的相应位置.） 11.为了解高2014级学生的身体发育情况，抽查了该年级100名年龄为17．5岁—18岁的男生体重（kg ），得到频率分布直方图如右图：根据上图可得这100名学生中体重在［56．5，64．5］的学生人数是___________人 12.在平面直角坐标系xoy 中，设D是由不等式组10100x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩表示的区域，E 是到原点的距离不大于1的点构成的区域，向E 中随机投一点，则所投点落在D 中的概率是________.13.正方体1111ABCD A B C D -的棱长为4，点,P Q 在棱1CC 上，且1PQ =，则三棱锥P QBD -的体积是____________________. 14. 若2221()sin cos f θθθ=+(())2k k Z πθ≠∈，则()f θ的最小值为____________ 15.设()f x 为定义在区间I 上的函数.若对I 上任意两点1212,()x x x x ≠和实数(0,1)λ∈，总有1212((1))()(1)()f x x f x f x λλλλ+-<+-，则称()f x 为I 上的严格下凸函数。

成都七中2013-2014学年度（上）期中考试试题高 二 数 学（理科）(命题人:廖学军 审题人:滕召波)考试说明:（1）考试时间:120分钟,试卷满分:150分;（2）请将选择题答案涂在答题卡上,将非选择题答在答题卡相应位置上.第Ⅰ卷(选择题,共50分)参考公式：球的表面积公式:24SR ;球的体积公式:343VR .其中R 表示球的半径. 一、选择题:(本大题有10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 下列命题正确的是( )A.有两个面平行,其余各面都是四边形的几何体叫棱柱.B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱.C.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱.D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台.2. 如图，该图是某平面图形的斜二测画法直观图，已知O’A’ = 3, O’B’ = 2,则这个平面图形的面积为( )A.6B.3C.4D.12 3. 若直线a 不平行于平面α,则下列结论成立的是( )A.α内的所有直线都与直线a 异面.B.α内不存在与a 平行的直线.C.α内的直线都与a 相交.D.直线a 与平面α有公共点. 4. 某几何体的三视图如图所示，其中俯视图是个半圆，则该几何体的表面积为( ) A.32π B.π＋ 3 C.32π＋ 3 D.52π＋ 3 5. 如图，在正方形SG 1G 2G 3中，E ，F 分别是G 1G 2及G 2G 3的中点，D 是EF 的中点，现在沿SE ，SF 及EF 把这个正方形折成一个四面体，使G 1，G 2，G 3三点重合，重合后的点记为G ，则在四面体S －EFG 中必有( )A ．SG⊥△EFG 所在平面B ．SD⊥△EFG 所在平面C ．GF⊥△SEF 所在平面D ．GD⊥△SEF 所在平面 6．已知两个平面垂直,下列命题:(1) 一个平面内已知直线必垂直于另一个平面的任意直线. (2) 一个平面内的已知直线必垂直于另一个平面的无数条直线. (3) 一个平面内的任一条直线必垂直于另一个平面.x’y ’O ’ A ’ B ’(4) 过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.其中正确命题的个数是( )A.3B.2C.1D.07．如图给出的是计算1+13+15+…+129的值的一个程序框图,则图中执行框内①处和判断框中的②处应填的语句是( ) A.n=n+2,i=15 B.n=n+2,i>15C.n=n+1,i=15D.n=n+1,i>158．已知直角三角形ABC,其三边分为a 、b 、c(a>b>c).分别以三角形的a 边,b 边,c 边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体, 其表面积和体积分别为S 1,S 2,S 3和V 1,V 2,V 3.则它们的关系为( )A ．S 1>S 2>S 3, V 1>V 2>V 3B ．S 1>S 2>S 3, V 1=V 2=V 3C ．S 1<S 2<S 3, V 1<V 2<V 3D ．S 1<S 2<S 3, V 1=V 2=V 3 9．a 和b 是两条异面直线,下列结论正确的个数是( )(1) 过不在a 、b 上的任一点,可作一个平面与a 、b 都平行.(2) 过不在a 、b 上的任一点,可作一条直线与a 、b 都相交. (3) 过a 可以并且只可以作一个平面与b 平行.(4) 过不在a 、b 上的任一点,可作一条直线与a 、b 都垂直. A.1 B.2 C.3 D.4 10．如图，正方体ABCD-A 1B 1C 1D 1的棱长为1，线段B 1D 1上有两个动点E ，F ，且EF=22， 则下列结论中错误．．的个数是( ) (1) AC ⊥BE.(2) 若P 为AA 1上的一点,则P 到平面BEF 的距离为22. (3) 三棱锥A-BEF 的体积为定值.(4) 在空间与DD 1,AC,B 1C 1都相交的直线有无数条.(5) 过CC 1的中点与直线AC 1所成角为40︒并且与平面BEF 所成角为50︒的直线有2条. A.0 B.1 C.2 D.3第Ⅱ卷(非选择题,共100分)二、 填空题:(本大题有5个小题,每小题5分,共25分)11.如图,正方体ABCD A 1B 1C 1D 1的棱长为4,M 为BD 1的中点,N 在A 1C 1上,且|A 1N|=3|NC 1|,则MN 的长为 .12．已知各顶点都在一个球面上的正四棱柱的高为2,这个球的表面积为12π,则这个正四棱柱的体积为 .13．执行如下图的程序框图,那么输出S 的值是________.结束i=i+1 否开始s=s+1n 是 ②s=0,n=1,i=1 输出s①开始2,1S k == 5?k <否1k k =+是输出S结束11S S=-14．已知圆台的上底半径为2cm,下底半径为4cm ，圆台的高为5cm,则侧面展开图所在扇形的圆心角=______.15．下面是空间线面位置关系中传递性的部分相关命题:① 与两条平行直线中一条平行的平面必与另一条直线平行; ② 与两条平行直线中一条垂直的平面必与另一条直线垂直; ③ 与两条垂直直线中一条平行的平面必与另一条直线垂直; ④ 与两条垂直直线中一条垂直的平面必与另一条直线平行; ⑤ 与两个平行平面中一个平行的直线必与另一个平面平行; ⑥ 与两个平行平面中一个垂直的直线必与另一个平面垂直; ⑦ 与两个垂直平面中一个平行的直线必与另一个平面垂直; ⑧ 与两个垂直平面中一个垂直的直线必与另一个平面平行. 其中正确命题的个数有_______个.三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 16．(本题满分12分)(1)如图,∆ABC 在平面α外,AB ∩α=P,BC ∩α=Q,AC ∩α=R,求证:P,Q,R 三点共线.(2)如图,空间四边形ABCD 中,E,F 分别是AB 和CB 上的点,G,H 分别是CD 和AD 上的点, 且EH 与FG 相交于点K. 求证:EH,BD,FG 三条直线相交于同一点.17．(本题满分12分)如图，四边形ABCD 为正方形，PD⊥平面ABCD ，PD∥QA，QA ＝AB ＝12PD.(1)证明：平面PQC⊥平面DCQ ； (2)求二面角D —PQ —C 的余弦值. 18．（本小题满分12分） 如图，直四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 为平行四边形，其中AB ＝2， BD ＝BC ＝1， AA 1＝2，E 为DC 的中点，F 是棱DD 1上的动点．(1)求异面直线AD 1与BE 所成角的正切值；(2)当DF 为何值时，EF 与BC 1所成的角为90°？ 19．（本小题满分13分）如图,AA 1、BB 1为圆柱OO 1的母线,BC 是底面圆O 的直径,D 、E 分别是AA 1、CB 1的中点, DE ⊥平面CBB 1.(1) 证明:DE ∥平面ABC;(2)求四棱锥C —ABB 1A 1与圆柱OO 1的体积比;(3)若BB 1=BC,求直线CA 1与平面BB 1C 所成角的正弦值. 20．（本小题满分13分）如图,在斜三棱柱ABC-A 1B 1C 1中,侧面AA 1B 1B ⊥底面ABC,侧棱AA 1与底面ABC 成60°的 角,AA 1=2.底面ABC 是边长为2的正三角形,其重心为G 点,E 是线段BC 1上一点,且BE=13BC 1.(1)求证:GE ∥侧面AA 1B 1B;(2)求平面B 1GE 与底面ABC 所成锐二面角的正切值; (3)求点B 到平面B 1GE 的距离.21．（本小题满分13分）如图所示，在三棱锥A —BCD 中，侧面ABD 、ACD 是全等的直角三角形，AD 是公共的斜 边，且AD ＝3，BD ＝CD ＝1，另一个侧面ABC 是正三角形.(1)当正视图方向与向量CD 的方向相同时，画出三棱锥A —BCD 的三视图;(要求标出尺寸) (2)求二面角B —AC —D 的余弦值;(3)在线段AC 上是否存在一点E ，使ED 与平面BCD 成30°角？ 若存在，确定点E 的位置；若不存在，说明理由.成都七中2013-2014学年度（上）期中考试试题高 二 数 学（理科）参考答案一、选择题：（每小题5分）1-5C B D C A 6-10B BCB A二、填空题：（每小题5分）11.6 12. 8 13. -1 14.43π 15. 2 三．解答题： 16．（1）（2）（ 每小问各6分） 17．(1)证明:如图，以D 为坐标原点，线段DA 的长为单位长，以AD 、DP 、DC 所在直线为 x 轴、y 轴、z 轴建立空间直角坐标系Dxyz.依题意有Q(1,1,0)，C(0,0,1)，P(0,2,0)，则DQ →＝(1,1,0)，DC →＝(0,0,1)，PQ →＝(1，－1,0).所以PQ →·DQ →＝0，PQ →·DC →＝0， 即PQ⊥DQ，PQ⊥DC.又DQ∩DC＝D ，所以PQ⊥平面DCQ. 又PQ ⊂平面PQC ，所以平面PQC⊥平面DCQ.(2)∠CQD 为二面角的平面角余弦值为63. （ 每小问各6分）18．（ 每小问各6分）解析：方法1：(1)连接EC 1.在直四棱柱ABCD －A 1B 1C 1D 1中，AD 1∥BC 1，则∠EBC 1为异面直线AD 1与BE 所成的角．⎭⎬⎫又底面ABCD⊥侧面DCC 1D 1⎭⎪⎬⎪⎫BD ＝BC E 为CD 的中点⇒BE ⊥CD ⇒BE ⊥侧面DCC 1D 1⇒BE ⊥EC 1. 在Rt △BEC 1中，BE ＝BC 2－EC 2＝22，EC 1＝CC 12＋CE 2＝322， 所以tan ∠EBC 1＝EC 1EB＝3. (2)当DF ＝14时，EF 与BC 1所成的角为9 0°.由(1)知，BE ⊥侧面DCC 1D 1⇒BE ⊥EF.又DE ＝EC ＝22，CC 1＝AA 1＝2. 当DF ＝14时，因为DF CE ＝1422＝24，DE CC 1＝222＝24，所以△DEF∽△CC 1E ，所以∠DEF＋∠CEC 1＝90°，所以∠FEC 1＝90°，即FE⊥EC 1.又EB∩EC 1＝E ，所以EF⊥平面BEC 1， 所以EF⊥BC 1，即EF 与BC 1所成的角等于90°.方法2：由BC 2＋BD 2＝DC 2可知BD⊥BC，分别以BC 、BD 、BB 1为x 轴、y 轴、z 轴建立空间直角坐标系，如图，则B(0，0，0)，A(－1，1，0)，D(0，1，0)，D 1 (0，1，2)，C(1，0，0)，C 1(1，0，2)，E(12，12，0)．因为AD 1→＝(1，0，2)，BE →＝(12，12，0)，EH FG K K EH EH ABD K ABD FG BCD K FG K BCD ABD BCD=BD K BD ∈⊂∈⊂∈∈∈提示：直线和相交于点；由点，平面，得平面由于平面，而，所以平面，平面平面，因此，点直线，三条直线交于同一点AB P AB ABC P ABC P P ABC Q R P Q R ααα=⊂∈∈证明：因为，平面，所以平面，，所以在平面与平面的交线上.同理可证，和均在这条交线上，所以，，三点共线.所以cos 〈AD 1→，BE →〉＝125×22＝110＝1010， 所以sin 〈AD 1→，BE →〉＝31010，所以tan 〈AD 1→，BE →〉＝3，即AD 1与BE 所成的角的正切值为3.设F(0，1，q)，则EF →＝ (－12，12，q)．又BC 1→＝(1，0，2)，由EF →·BC 1→＝(－12)×1＋0×12＋q·2＝0，得q ＝14，即DF ＝14时，EF ⊥BC 1.19．(1)如图,连接.E OA O O E 、、分别为1CB BC 、的中点,EO ∴是1BB C ∆的中位线,1//EO BB ∴且112EO BB =. 又111//,DA BB AA BB =,故11,2DA BB EO DA ==∴//EO 且DA EO =,∴四边形AOED 是平行四边形,即//DE OA ,又,,//DE ABC OA ABC DE ABC ⊄⊂∴平面平面平面. ……3分 (2)如图,连接CA .由题知1DE CBB ⊥平面,且由(1)知//DE OA ,1,AO CBB AO BC ∴⊥∴⊥平面, 2AC AB OA ∴==.BC是底面圆O 的直径,CA AB ∴⊥.又1AA 是圆柱的母线,1AA ABC ∴⊥平面,11,AA CA AA AB A ∴⊥=又,11CA AA B B ∴⊥平面,即CA 为四棱锥11C ABB A -的高.设圆柱高为h ,底面半径为r ,则()()112212=,2233C ABB A V r h V hr r hr π-=⋅=圆柱,1122223:3C ABB A hrV V r h ππ-∴==圆柱. …… 5分 (3)如图,作过C 的母线1CC ,连接11B C ,则11B C 是上底面圆1O 的直径,连接11A O ,则11//AO AO ,又111111,AO CBB C AO CBB C ⊥∴⊥平面平面,连接1CO ,则 11A CO ∠为直线1CA 与平面1BB C 所成的角.()()22221111226,AC AC AA r r r AO r =+=+==, ∴在11Rt AO C ∆中,111116sin 6A O ACO A C∠==. ∴直线1CA 与平面1BB C 所成角的正弦值为66. …… 5分20．解法1:(1)延长B 1E 交BC 于点F,11B EC ∆∽△FEB,BE=21EC 1,∴BF=21B 1C 1=21BC, 从而点F 为BC 的中点. ∵G 为△ABC 的重心,∴A、G 、F 三点共线.且11//,31AB GE FB FE FA FG ∴==,又GE ⊄侧面AA 1B 1B,∴GE//侧面AA 1B 1B. …… 4分(2)在侧面AA 1B 1B 内,过B 1作B 1H⊥AB,垂足为H,∵侧面AA 1B 1B⊥底面ABC,∴B 1H⊥底面ABC.又侧棱AA 1与底面ABC 成60°的角,AA 1=2,∴∠B 1BH=60°,BH=1,B 1H=.3 在底面ABC 内,过H 作HT⊥AF,垂足为T,连B 1T,由三垂线定理有B 1T⊥AF, 又平面B 1CE 与底面ABC 的交线为AF,∴∠B 1TH 为所求二面角的平面角. ∴AH=AB+BH=3,∠HAT=30°,∴HT=AH 2330sin =︒.在Rt△B 1HT 中,332tan 11==∠HT HB TH B , 从而平面B 1GE 与底面ABC 成锐二面角的正切值为233. …… 5分 (3)用等积可求得点B 到平面B 1GE 的距离是63. …… 4分解法2:(1)∵侧面AA 1B 1B⊥底面ABC,侧棱AA 1与底面ABC 成60°的角,∴∠A 1AB=60°, 又AA 1=AB=2,取AB 的中点O,则AO⊥底面ABC. 以O 为原点建立空间直角坐标系O —xyz 如图, 则()0,1,0A -,()0,1,0B ,()3,0,0C,()10,0,3A ,()10,2,3B ,()13,1,3C . ∵G 为△ABC 的重心,∴3,0,03G ⎛⎫ ⎪ ⎪⎝⎭.113BE BC =,∴33,1,33E ⎛⎫⎪ ⎪⎝⎭,∴1310,1,33CE AB ⎛⎫== ⎪ ⎪⎝⎭. 又GE ⊄侧面AA 1B 1B,∴GE//侧面AA 1B 1B. (2)设平面B 1GE 的法向量为(,,)a b c =n ,则由10,0.B E GE ⎧⋅=⎪⎨⋅=⎪⎩n n 得3230,3330.3a b c b c ⎧--=⎪⎪⎨⎪+=⎪⎩可取()3,1,3=-n 又底面ABC 的一个法向量为()0,0,1=m设平面B 1GE 与底面ABC 所成锐二面角的大小为θ,则21cos ||||7θ⋅==⋅m n m n . 由于θ为锐角,所以227sin 1cos 7θθ=-=,进而23tan 3θ=.故平面B 1GE 与底面ABC 成锐二面角的正切值为233.(3) 由（2）可知平面B 1GE 的法向量为 ，， 所以点B 13(,1,0)(3,1,3)3277(3,1,3)BG n d n -•-•====-3,3=-n 3(1,0)3BG =-…… 4分21．(1) 三棱锥A —BCD 的三视图如右图所示： …… 3分 (2)解设平面ABC 的法向量为n 1＝(x ，y ，z)，则由n 1⊥BC →知：n 1·BC →＝－x ＋y ＝0，同理由n 1⊥AC →知：n 1·AC →＝－x －z ＝0， 可取n 1＝(1,1，－1)， 同理，可求得平面ACD 的一个法向量为n 1＝(1,0，－1).∴cos〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝1＋0＋13×2＝63.即二面角B —AC —D 的余弦值为63. …… 5(3)解设E(x ，y ，z)是线段AC 上一点，则x ＝z>0，y ＝1，所以DE →＝(x,1，x)，设平面BCD 的一个法向量为n ＝(0,0,1)，要使ED 与平面BCD 成30°角，由图可知DE →与n 的夹角为60°，所以cos 〈DE →，n 〉＝DE →·n |DE →||n|＝co s60°＝12，所以2x ＝1＋2x 2，解得x ＝22，所以CE ＝2x ＝1. 故线段AC 上存在一点E ，使ED 与平面BCD 成30°角，且当CE ＝1时，ED 与平面BCD 成30°角. …… 5分。

四川省成都七中2012-2013学年高二下学期入学考试（数学理）————————————————————————————————作者：————————————————————————————————日期：318212921625267454DCAA 1C 1B 1成都七中2012-2013学年高二下学期入学考试数学（理）试题一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.) 1.已知221,n nC -=则n =( )(A)5 (B)6 (C)7 (D)8 2.从0,2,3,4,6,12六个数中任取两个不同数作积,则不同的积有( )个.(A)7 (B)9 (C)11 (D)153.已知椭圆的方程为22195x y +=,则此椭圆的离心率为( )(A)23 (B)53 (C)49 (D)594.某校高二年级15个班参加成都市调研考试的参考人数的茎叶图 如图,则这组数据的中位数和众数分别是( ) (A)51和51 (B)51和52 (C)52和51 (D)52和525.在四面体ABCD 中,,E F 分别是,AB CD 的中点,若AC BD ⊥,且4,3,AC BD ==则 EF =( )(A)5 (B)4 (C)3 (D)2.56.双曲线221412x y -=的一个焦点坐标是( )(A)(0,8) (B)(22,0)-(C)(0,23) (D)(4,0)- 7.右侧的程序执行后的结果是( )(A)910(B)9 (C)10 (D)1098.在面积为S 的ABC ∆内部任取一点P ,则PBC ∆的面积大于34S 的概率是( ) (A)116(B)14(C)34(D)9169.352()x x-展开式中的常数项为( ) (A)40- (B)40 (C)10- (D)1010.如图,在直三棱柱111ABC A B C -中,11,,2AB AC AB AC AA ⊥==D 是1AA 的中点,则1BC与平面BCD 所成的角正弦值为( ) (A)73 (B)147S=0 i=1DOS=S+1/(SQR(i )+SQR(i +1)) i=i+1 LOOP UNTILi>99PRINT S END(C)142 (D)2311.五个不同的元素(1,2,3,4,5)i a i =排成一列,规定1a 不许排第一,2a 不许排第二,则不同的排法种数为( )(A)48 (B)78 (C)96 (D)108 12.四边形ABCD 是正方形,MD ⊥平面ABCD ,NB ⊥平面ABCD ,且.MD NB AB == 则二面角A MN C --的余弦值为( )(A)63 (B)63- (C)13 (D)13-13.欢乐斗地主是一款QQ 游戏,其规则：两名农民为一方合作对战一名地主,使用一副共54张的扑克牌,每人17张牌,剩余的3张归地主,只要有一人出完手中的牌,则此盘游戏结束.地主最先出完牌,则地主一方赢；两农民中的任何一人最先出完牌,则农民一方赢.输赢用欢乐豆结算： (1)欢乐豆不足2000的人不能当地主.(2)若农民一方赢,则两农民都赢地主1000欢乐豆.若地主一方赢,则两农民都输1000欢乐豆给地主(欢乐豆不足1000的农民,则把所有欢乐豆都输给地主).甲乙丙三人玩欢乐斗地主,已知甲当地主时,最先出完牌的概率为1,2甲当农民时(不管谁当地主)最先出完牌的概率都为730；乙当地主时,最先出完牌的概率为13,30乙当农民时(不管谁当地主)最先出完牌的概率为16.现正进行的一盘游戏,甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,在甲乙丙三人斗地主的技术和牌运都不发生变化的前提下,抢不抢地主当?甲丙如何选择?( )(A)甲不抢地主当丙抢地主当 (B)甲抢地主当丙不抢地主当 (C)甲丙都抢地主当 (D)甲丙都不抢地主当,结束游戏14.设点1F 是椭圆221123x y +=的左焦点,弦AB 过椭圆的右焦点,则1F AB ∆的面积的最大值是( )(A)6 (B)12 (C)33 (D)6315.已知[0,10](1,2,,10),i x i ∈=L 1210,,,x x x L 的平均数为7.5,当2212(10)(10)x x -+-++L210(10)x -取得最大值时,1210,,,x x x L 这十个数中等于0的数的个数为( )(A)0 (B)1 (C)2 (D)3424ABCD成都七中2012-2013学年下期2014级入学考试数学试卷(理科)答题卷考试时间：120分钟 总分：150分命题人：巢中俊 审题人：张世永二、填空题(每小题5分,共30分.把答案填在题中横线上.)16.乘积126127125()()()a a a b b b c c c +++++++++L L L 展开后,共有 项. 17.在正四面体ABCD (各棱都相等)中,E 是BC 的中点,则异面直线AE 与CD 所成的角的余弦 值为18.已知椭圆224ax y +=与221129x y +=的焦距相等,则a = 19.将一张面值1元的人民币全部换成面值1角,2角和5角的硬币,则换法总数为 20.某项测试成绩满分10分,随机抽取若干名学生参加测试,得分统计如图所示,则得分的平均数为x =(第20题图) (第21题图)21.如图,在四边形ABCD 中,90,30,DAB ADC ∠=︒∠=︒4, 2.AB AD CD === 将四边形ABCD 绕AD 旋转一周,则所成几何体的体积为(台体的体积公式11221()3V S S S S h =++)三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)22. (1)以正方体的顶点为顶点,可以确定多少个四棱锥?(2)黑暗中从3双尺码不同的鞋子中任意摸出3只,求摸出3只中有配成一双(事件A )的概率.(3)利用二项式定理求2013143被12除所得的余数.23.已知Rt ABC ∆中,90,4,2,ABC AB BC ∠=︒==,,D E 分别是,AB AC 的中点,将ADE ∆沿着DE 翻折成1,A DE ∆使得平面1A DE ⊥平面DECB ,F 是1A B 上一点且1A E ∥平面C A 1D E DABBE C FFDC .(1)求1A F FB.(2)求三棱锥1D ACF -的体积. (3)求1A B 与平面FDC 所成角的大小.24.已知圆221:4,C x y +=圆222:25.C x y +=点O 为坐标原点,点M 是圆2C 上的一动点,线段OM 交圆1C 于,N 过点M 作x 轴的垂线交x 轴于0M ,过点N 作0M M 的垂线交0M M 于.P(1)当动点M 在圆2C 上运动时,求点P 的轨迹C 的方程.P N M 0OMxy(2)设直线:5xl y m =+与轨迹C 交于不同的两点,求实数m 的取值范围. (3)当55m =时,直线l 与轨迹C 相交于,A B 两点, 求OAB ∆的面积.成都七中2012-2013学年下期2014级入学考试数学试卷(理科)试卷参考答案一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.)14.设直线AB的方程为3x my=+,联立2211233x yx my⎧+=⎪⎨⎪=+⎩消x得22(4)630m y my++-=.设1122(,),(,)A x yB x y.则12122263,44my y y ym m+=-=-++.122121212121221133()4123.24F ABmS F F y y y y y y y ym ∆+ =-=-=+-=⋅+令21,t m=+则 1.t≥12123123123 6.3323F ABtSt tt∆=⋅=≤=++(3t=时等号成立)二、填空题(每小题5分,共30分.把答案填在题中横线上.)16. 210 17.3618.447或19. 10 20. 6 21.203(28)3π-三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)22.解(1)141248.C=…………5分CA 1D BE xyz FOOCA 1DEDABBECF(2)1134363()5C C P A C ==. …………10分 (3)2013201322013143(1441)(121)=-=- …………12分02201312201212012212012201320132013201320132013(12)(12)(1)(12)(1)(1)C C C C =+-++-+-L20132013201312(1)M C =+-(M 是整数) …………14分 12112(1)11.M M =-=-+所以2013143被12除所得的余数为11. …………15分23.解(1)连接EB 交DC 于,O 连接.FO11111.A E FDC A E BA E A E FO FDC BA E FO ⎫⎪⊂⇒⎬⎪=⎭I 平面平面平面平面∥∥ …………3分 ,D E 分别是,AB AC 的中点12DE BC ODE OCBDE BC ⇒∆∆⎧⎪⇒⇒⎨=⎪⎩∥∽12EO DE OB CB ==. 所以在1BA E ∆中,11.2A F EO FB OB == …………5分(2) 1111 . A DE DECB A DE DECB DE A D DECB A D DE ⊥⎫⎪=⇒⊥⎬⎪⊥⎭I 平面平面平面平面平面11111133D A CF C A DF C A DB A DCB V V V V ----===11224(2).3329⨯=⨯⨯⨯= …………10分(3)1.A D DECB ⊥平面又.DE DB ⊥以1,,DE DB DA u u u r u u u r u u u u r 为正交基底建立如图所示的空间直角坐标系.D xyz - 则1(0,0,0),(0,0,2),(0,2,0),(2,2,0).D A B C …………7分设(,,).F x y z 因为11.2A F FB =所以11,2A F FB =u u u u r u u u r 即1(,,2)(,2,),2x y z x y z -=---所以24(0,,).33F24(2,2,0),(0,,).33DC DF ==u u u r u u u r 设平面FDC 的法向量000(,,).n x y z =r则000000200x y n DC y z n DF ⎧+=⋅=⎧⎪⇒⎨⎨+=⋅=⎩⎪⎩u u u r r u u u r r ,令01,z =则(2,2,1).n =-r 又1(0,2,2)A B =-u u u r .设1A B 与平面FDC 所成角的大小为θ,则1112sin cos ,.2A B n A B n A B nθ⋅=〈〉==u u u r r u u u r r u u u r r 因为[0,],2πθ∈所以1A B 与平面FDC 所成角的大小4π. …………15分 24.解(1)设点(,)P x y .则(,),(,)M N M x y N x y .从而(,),(,)M N OM x y ON x y ==u u u u r u u u r因为52OM ON =u u u u r u u u r ,所以5(,)(,)2M N x y x y =.即55,.22N M x x y y ==所以5(,)2M x y . 点M 在圆2C 上,所以225()252x y +=.整理得点P 的轨迹C 的方程：22 1.254x y += …………5分(2)联立221.254 5x y x y m ⎧+=⎪⎪⎨⎪=+⎪⎩消y 得到2225200x mx m ++-=. …………7分因为直线:5x l y m =+与轨迹C 交于不同的两点,所以22(2)4(520)0,m m ∆=--> 即2 5.m <所以实数m 的取值范围为(5,5).- …………10分(3)(方法1)直线5:.55x l y =+设1122(,),(,)A x y B x y , 联立221.2545 55x y x y ⎧+=⎪⎪⎨⎪=+⎪⎩消x 得到2251905x x +-=.则121225,19.5x x x x +=-=- 22221212121255()()()[()()]5555x x AB x x y y x x =-+-=-++-+ 2212121226262686()()4.5555x x x x x x =-=+-=⨯ 直线:550.l x y -+=设O 到直线AB 的距离为,d 则d =205055.2615-⨯+=+ 112686546.2255526OAB S AB d ∆==⨯⨯⨯= …………15分。

四川省成都七中2013-2014学年高二下学期开学考试数学（理）试题Word版含答案成都七中高2015届高二下期入学考试数学试题(理)一、选择题：本大题共10小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合{|2,}xM y y x R ==∈，集合，{|lg(1)}S x y x ==-则下列各式中正确的是( )A.M S M =B.M S S =C.M S =D.M S =?2. 对四组数据进行统计，获得以下散点图，关于其相关系数比较，正确的是( )相关系数为1r相关系数为2r相关系数为3r相关系数为4rA.24310r r r r <<<<B.42130r r r r <<<<C.42310r r r r <<<<D.24130r r r r <<<<3. 已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β，直线l 满足l ⊥m ，l ⊥n ，l ?α，l ?β，则( )A ．α∥β且l ∥αB ．α⊥β且l ⊥βC ．α与β相交，且交线垂直于lD ．α与β相交，且交线平行于l 4. 阅读如图所示的程序框图，运行相应的程序，输出的s 值等于( ) A.3- B.21- C.3 D.21 5. 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点，其中18=AB ，24=BC 、30=AC ，球心到这个截面的距离为球半径的一半，则球的表面积为( ) A.1200π B.1400π C.1600π D.1800π 6. 下列判断正确的是( )A. 若命题p 为真命题，命题q 为假命题，则命题“p q ∧”为真命题B.命题“若0xy =，则0x =”的否命题为“若0xy =，则0x ≠”C. “1sin 2α=”是” 6πα=”的充分不必要条件D. .命题“,20xx ?∈>R ”的否定是“ 00,20xx ?∈≤R ”7. 将函数y ＝3cos x ＋sin x(x ∈R)的图像向左平移m(m>0)个单位长度后，所得到的图像关于y 轴对称，则m 的最小值是( )A.π12B.π6C.π3D.5π6 8. 设0x 是方程ln 4x x +=的解，则0x 属于区间( )A.（0，1）B.（1，2）C.（2，3）D.（3，4）9. 已知x,y 满足2420x x y x y c ≥??+≤??-++≥?且目标函数z=3x+y 的最小值是5，则z 的最大值是( )A.10B.12C.14D.16 10. 直线032=--y x 与圆()()22239x y -++=交于E.F 两点，则?EOF （O 是原点）的面积为( ) A.23 B.43C.52D.556二、填空题：本大题共5小题，每小题5分，共20分.11. 已知向量a →,b →不共线，若向量a →+λb →与b →+λa →的方向相反,则实数λ的值为 . 12. 在ABC ?中,角A 、B 、C 所对的边分别为a 、b 、c,且满足sin cos a B b A =,则2sin cos B C -的最大值是 .13. 如果直线()21400,0ax by a b -+=>>和函数()()110,1x f x mm m +=+>≠的图象恒过同一个定点，且该定点始终落在圆()()221225x a y b -+++-=的内部或圆上，那么ba的取值范围是______. 14. 如果不等式x a x x )1(42->-的解集为A ，且}20|{<① 已知,,a b m 都是正数，且a m ab m b+>+，则a b <；② 若函数)1lg()(+=ax x f 的定义域是}1|{③ 已知x ∈（0，π），则2sin sin y x x=+的最小值为22；④ 已知a 、b 、c 成等比数列，a 、x 、b 成等差数列，b 、y 、c 也成等差数列，则ycx a +的值等于2;⑤ 已知函数2()1,()43xf x eg x x x =-=-+-,若有()()f a g b =,则b 的取值范围为(22,22)-+.其中正确命题的序号是________.三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本，这40名学生的成绩全部在40分至100分之间，现将成绩按如下方式分成6组：第一组，成绩大于等于40分且小于50分；第二组，成绩大于等于50分且小于60分；……第六组，成绩大于等于90分且小于等于100分，据此绘制了如图所示的频率分布直方图.在选取的40名学生中，（1）求成绩在区间[80,90)内的学生人数；（2）从成绩大于等于80分的学生中随机选2名学生，求至少有1名学生成绩在区间[90,100]内的概率.17. (本小题满分12分)设数列{a n }是公差大于零的等差数列，已知12a =，23210a a =-.（1）求{a n }的通项公式；（2）设数列{b n }是以函数f(x)=4sin 2πx 的最小正周期为首项，以3为公比的等比数列，求数列{a n ?b n }的前n 项和n S .18. (本小题满分12分)(1)设函数f(x)=(sin ωx+cos ωx)2+2cos 2ωx(ω>0)的最小正周期为23π,将y=f(x)的图像向右平移2π个单位长度得到函数y=g(x)的图像,求y=g(x)的单调增区间．(2)设?ABC 的内角A 、B 、C 的对边长分别为a 、b 、c ，3cos()cos 2A CB -+=，b 2=ac ，求角B 的大小.19. (本小题满分12分)如图，建立平面直角坐标系xoy ，x 轴在地平面上，y 轴垂直于地平面，单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程221(1)(0)20y kx k x k =-+>表示的曲线上，其中k 与发射方向有关.炮的射程是指炮弹落地点的横坐标. （1）求炮的最大射程；（2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标a 不超过多少时，炮弹可以击中它？请说明理由.20.(本小题满分13分)已知几何体A BCED -的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．（1）求异面直线DE 与AB 所成角的余弦值；（2）求二面角A ED B --的正弦值.21. (本小题满分14分)已知圆C ：x 2＋y 2－2x ＋4y －4＝0．问在圆C 上是否存在两点A 、B 关于直线y ＝kx －1对称，且以AB 为直径的圆经过原点？若存在，写出直线AB 的方程；若不存在，说明理由．成都七中高2015届高二下期入学考试数学试题(理答案)一、选择题：本大题共10小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合，集合，则下列各式中正确的是( )A. B.C. D.解析：A 由题意得，，所以根据选项可得，所以选A.2.对四组数据进行统计，获得以下散点图，关于其相关系数比较，正确的是( )相关系数为相关系数为相关系数为相关系数为A. B.C. D.【答案】A【解析】由相关系数的定义以及散点图所表达的含义可知.3.已知m，n为异面直线，m⊥平面α，n⊥平面β，直线l满足l⊥m，l⊥n，l?α，l?β，则( )A．α∥β且l∥α B．α⊥β且l⊥βC．α与β相交，且交线垂直于l D．α与β相交，且交线平行于l 【答案】D [解析] 若α∥β，则m∥n与m，n为异面直线矛盾，故A错．若α⊥β且l⊥β，则由n⊥平面β知l ∥n 与l ⊥n矛盾，故B错．若α与β相交，设垂直于交线的平面为γ，则l ⊥γ，又l ⊥m，l ⊥n，m⊥平面α，n⊥平面β，故交线平行于l.故选D.4.阅读如图所示的程序框图，运行相应的程序，输出的值等于( )A. B. C. D.解析：A 程序执行循环六次，依次执行的是，，故输出值等于.5.球面上有三点、、组成这个球的一个截面的内接三角形三个顶点，其中，、，球心到这个截面的距离为球半径的一半，则球的表面积为( )A. B. C. D.解析：A ∵，，，∴，是以为斜边的直角三角形．∴的外接圆的半径为，即截面圆的半径，又球心到截面的距离为，∴，得．∴球的表面积为．6.下列判断正确的是( )A. 若命题为真命题，命题为假命题，则命题“”为真命题B.命题“若，则”的否命题为“若，则”C. “”是””的充分不必要条件D. .命题“”的否定是“”【答案】D【解析】A项中，因为真假，所以为假命题.故A项错误；B项中，“若，则”的否命题为“若，则”，故B项错误；C项中，是的必要不充分条件，故C项错误；D选项正确.7.将函数y＝cos x＋sin x(x∈R)的图像向左平移m(m>0)个单位长度后，所得到的图像关于y轴对称，则m的最小值是( )A.12πB.6πC.3πD.65π 【答案】B[解析] 结合选项，将函数y ＝cos x ＋sin x ＝2sin 3π的图像向左平移6π个单位得到y ＝2sin 2π＝2cos x ，它的图像关于y 轴对称，选B. 8. 设是方程的解，则属于区间（）A.（0，1）B.（1，2）C.（2，3）D.（3，4）【答案】C 【解析】设,因为，，所以.所以.9. 已知x,y 满足且目标函数z=3x+y 的最小值是5，则z 的最大值是( ) A.B.C.D.解析：由，则，因为的最小值为，所以，作出不等式对应的可行域，由图象可知当直线经过点时，直线的截距最小，所以直线的直线方程为，由，解得，代入直线得即直线方程为，平移直线，当直线经过点时，直线的截距最大，此时有最大值，由，得，即,代入直线得。

2012—2013学年度第二学期入学考试地理试卷第I卷选择题（共58分）一、选择题（每个题只有一个正确选项，选对一题得2分，多选、错选均不得分。

）1、下图中能正确反映热力环流原理的是A．① B．② C．③ D．④下图是某区域某时地面天气简图。

读图回答下面四题。

2、图中M地的风向是（）A. 东北B. 东南C. 西北D. 西南3、图中所示高压中心位于（）A. 亚洲B. 太平洋C. 澳大利亚D. 亚速尔群岛4、图中所示可能是（）A. 1月B. 6月C. 10月D. 4月5、此时，我国南方大部分地区容易受到________的影响。

A. 台风B. 洪涝C. 低温冻害D. 泥石流根据下面经纬网图，回答下面三题。

Array6、以下描述正确的是（）A. 图中的“150°”是西经度B. 图中B点位于东半球C. 图中点C位于中纬度D. 图中D点位于西半球7、图中A、C两点之间的距离约为（）A. 2220kmB. 1110kmC. 1923kmD. 1700km8、图中B点的对趾点（是地球同一直径的两个端点）的地理坐标是（）A. 165°W，40°SB. 15°W，50°SC. 15°W，40°SD. 165°W ,50°S读等高线地形图，回答下面三题。

9、③④两地的水平距离约为（）A. 1500米B. 2500米C. 600米D. 300米10、⑥处的陡崖高度可能是（）A. 30米B. 200米C. 145米D. 45米11、若图中要建一个大坝，若坝顶海拔为300米，则坝高可能是（）A. 40米B. 110米C. 30米D. 80米某校研究性学习小组到野外考察，下图为考察区域地形图，虚线所示为考察线路。

读图回答下面两题。

12、图中④点地形为（）A. 山谷B. 鞍部C. 洼地D.山顶13、下列描述可能与实地情况相符的是（）A. ①地附近的河流从西南流向东北B. ②地坡度最陡C. ③地分布有茶园D.④地是观赏瀑布的最佳位置14、该考察线路的高差可能是（）A. 450米B. 200米C. 550米D. 600米左图为日本及其附近海域震源深度分布示意图。

命题人： 夏祖凤一．选择题（每题5分，共60分，每小题有且仅有一个选项是正确的）1..以下角：①异面直线所成角；②直线和平面所成角；③二面角的平面角；可能为钝角的有 （ ） A ．0个 B ．1个 C ．2个 D ．3个2.如下左图，一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形， 如果直角三角形的直角边长都为1，那么这个几何体的表面积为（ ）61 B ．23 C ．32．32+3如图所示的斜二测直观图的平面图形(A′B′∥y′，B′C′∥x′∥A′D′)是( )A.直角梯形B.等腰梯形C.不可能是梯形D.平行四边形4.设c b a ，，是空间三条不同的直线，且c b b a ⊥，//，则直线a 与c 的位置关系一定是( )A.a 与c 异面B.c a //C.c a ⊥D. P c a =5.一个单位有职工800人，期中具有高级职称的160人，具有中级职称的320人，具有初级职称的200人，其余人员120人.为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是 （ ）A. 12,24,15,9B. 9,12,12,7C. 8,15,12,5D. 8,16,10,66.已知三条直线,,m n l ，三个平面,,αβγ。

下面四个命题中，正确的是（ ）A.//αγαββγ⊥⎫⇒⎬⊥⎭B.//m l l m ββ⎫⇒⊥⎬⊥⎭C.//////m m n n γγ⎫⇒⎬⎭D.//m m n n γγ⊥⎫⇒⎬⊥⎭7.执行右面的程序框图，如果输入的N 是6，那么输出的p 是( )A .120 B. 720 C. 1440 D. 508.在直二面角α－PQ －β中,直角三角形ABC 在面α内,斜边AB 在棱PQ 上,若AC 与面β成30° 的角,则BC 与面β所成角为（ ）A ．30° B.45° C.60° D.上述三个结论都不对9.P 是ΔABC 所在平面α外的一点，P 到ΔABC 三顶点的距离相等，PO ⊥α于O ，则O 是 ΔABC 的（ ） A ．外心 B.内心 C.垂心 D.重心10.如图，A 1B 1C 1—ABC 是直三棱柱，∠BCA =90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC =CA =CC 1，则BD 1与AF 1所成角的余弦值是（ ）A ．1030B ．21C ．1530D ．1015 11.在矩形ABCD 中，AB =3，BC =4，PA ⊥平面ABCD ，且PA =1，则P 到对角线BD 的距离为（ ）A ．2921 B.513 C.23 D.423 12.如图，正方体ABCD －A 1B 1C 1D 1的棱长为4，点P 、Q 在棱CC 1上，PQ ＝1，则三棱锥P －QBD的体积是( ) A. 83 B. 43C. 8D. 与P 点位置有关二．填空题（每题4分，共16分）13.运行右图所示的程序，输出的结果是_______ 14.在正方体1111ABCD A B C D -的各面的12条对角线中，与正方体的对角线1A C 垂直的共有_________条．15.正四面体侧面与底面所成二面角的余弦值为_________________________.16.已知P 为锐二面角α—1—β内一点，P 到平面α、β及棱1的距离之比为1：2：2，则此二面角的度数为_______三.解答题（第17、18、19、20、21题每题12分，第22题14分，共76分，请作出必要的图形和解题步骤）17.一个三棱柱111C B A ABC -的三视图如图所示（主视图、俯视图都是矩形，左视图是直角三角形），设E 为线段1AA 上的点．(1)画出该几何体的直观图；(2)求几何体B C B E 11-的体积和表面积；18.为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试，将所得数据整理后，画出频率分布直方图(如图)，图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12.(1) 第二小组的频率是多少？样本容量是多少？(2) 若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？(3) 在这次测试中，学生跳绳次数的中位数落在哪个小组内？请说明理由。

四川省成都七中2012届高三下期入学考试（数学理）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

共150分。

考试时间120分钟。

参考公式：如果事件A 、B 互斥，那么 球是表面积公式P(A+B)=P(A)+P(B) S=4πR 2如果事件A 、B 相互独立，那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式 如果事件A 在一次试验中发生的概率是P ，那么 334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径k n kk n n P P C k P --=)1()(一、 选择题：本大题共12个小题，每小题5分，共60分，在每小题给出的四个备选项中，只有一项是符合题目要求的． 1. 化简:1-3i (3+i)2=( )A.14+34iB.-14-34iC.12+32iD.- 12-32i 2. 过定点作圆(x-2)2+y 2=4的切线,若这样的切线有且仅有两条,则定点可能是( ) A.(2,2) B.(2,1) C.(3,2) D.(4,0)3. 将y=2cos(x 3+π6)的图象按向量→a =(-π4,-2)平移，则平移后所得图象的解析式为( )Ａ．y=2cos(x 3+π4)-2 Ｂ．y=2cos(x 3-π4)+2 Ｃ．y=2cos(x 3-π12)-2 Ｄ．y=2cos(x 3+π12)+24. 在各项均为正数的等比数列{a n }中,若a 5a 6=9,则13log a +23log a +…+103log a的值为( ) A.12 B.10 C.8 D.2+log 355. 已知lim n →∞2n-an2n +an =1(a ∈R),那么a 的取值范围是( )A.a<0B.a<2且a ≠-2C.-2<a<2D.a<-2或a>2 6. ∆ABC 中，点D 在AB 上，CD 平方∠ACB ．若→CB=→a ，→CA=→b ，|→a |=1，|→b |=2，则→CD= A.13→a +23→b B.23→a +13→b C.35→a +45→b D.45→a +35→b 7. 在平面直角坐标系中，若不等式组⎩⎪⎨⎪⎧x ＋y －1≥0，x －1≤0，ax －y ＋1≥0，(a 为常数)所表示的平面区域的面积等于2，则a 的值为( )A ．－5B ．1C ．2D ．38. 下面四个命题：①“直线a ∥直线b ”的充要条件是“a 平行于b 所在的平面”； ②“直线l ⊥平面α内所有直线”的充要条件是“l ⊥平面α”；③“直线a 、b 为异面直线”的充分不必要条件是“直线a 、b 不相交”；④“平面α∥平面β”的必要不充分条件是“α内存在不共线三点到β的距离相等．” 其中正确命题的序号是 ( )A ．①②B ．②③C ．②④D ．③④9. 如图所示，过抛物线y 2＝2px(p>0)的焦点F 的直线l 交抛物线于点A 、B ，交其准线于点C ，若|BC|＝2|BF|，|AF|＝3，则此抛物线的方程为( )A ．y 2＝32xB ．y 2＝9xC ．y 2＝92x D ．y 2＝3x10. 正四棱锥V —ABCD 的五个顶点在同一个球面上，若其底面边长为4，侧棱长为26，则( )A ．球的表面积为18πB ．AB 两点的球面距为3arccos 19C ．VA 两点的球面距为32arccos 13D ．球的体积32π11. 某班进行班干部选举，从甲、乙、丙、丁四人中选出3人分别担任班长、副班长、团支书，则上届任职的甲、乙、丙三人没有连任原职的概率是( ) A ．512 B ．1124 C ．12 D ．132412. 设f(x)是定义在R 上的奇函数，且当x ≥O 时,f -1(x)=x ，若对任意的x ∈[t ，t+2]，不等式f(x)≤12f(x+t)恒成立，则实数x 的取值范围是( )．A.[2,+∞)B.[-2,-1]∪[0,2]C. [2,+∞)D.(0,2] 二、填空题：本大题共4小题每小题4分，共16分。

成都七中2012－2013学年下期2014级入学考试理科综合试卷化学试卷第Ⅰ卷（选择题共60分）选择题（每小题4分，共60分。

每小题只有一个选项符合题意）1．下列过程或现象与盐类的水解无关的是A．加热氯化铁溶液的颜色变深B．CaCO3的饱和溶液pH约为9.3C．0.1 mol/L AlCl3溶液中c(Al3+)<0.1 mol/L D.小苏打发酵粉加入柠檬酸后效果更好2．某温度下，100 mL 0.4 mol/L醋酸溶液与足量Zn粒反应生成H2的速率v(H2)=0.01 mol/(L·min)。

为了减缓反应速率，但又不影响生成H2的总量，下列有关说法正确的是A．可向该溶液中加少量CaCO3固体B．可向该溶液中加入10 mL 0.1 mol/L醋酸溶液C．可向该溶液中加入少量NaNO3溶液D．若向该溶液中加入少量醋酸钠固体，反应速率可能变成v(H2)=0.3 mol/(L·h)3．下列说法正确的是A．氯气、硫酸钡和氨水分别属于非电解质、强电解质和弱电解质B.体积不同但pH相同的醋酸和盐酸，分别用蒸馏水稀释至原体积的m倍和n倍，稀释后两溶液的pH仍相同，而m和n无法确定相对大小C. CuCl2+2H2O Cu(OH)2+2HCl，加入少量硝酸银固体后可以增大CuCl2水解程度D.用来配制标准NaOH溶液的NaOH固体含有少量的KOH，此时中和测得盐酸的浓度数值一定偏高4．在NaHSO4溶液中离子的总浓度为0.06mol/L，若加入等体积离子浓度为0.06mol/L的Ba(OH)2溶液，混合后溶液的体积不变，则溶液的pH值为A. 2B. 1.7C. 12D. 12.35．常温下，下列溶液中可能大量共存的离子组是A．加入金属镁能产生大量H2的溶液中：Na+、NH4+、F-、SO32-B．含有大量S2-的溶液中：K+、Mg2+、ClO-、SO42-C．能使Al3+生成沉淀的溶液中：NH4+、Na+、SiO32-、HCO3-D．水电离产生的c(OH-)＝1×10-10 mol/L的溶液中：Al3+、SO42-、NO3-、Cl-6．室温下，下列变化后的溶液pH小于8的是A．pH=10的氨水稀释100倍B．pH=4的醋酸和pH=10的NaOH等体积混合C．pH=8的NaOH溶液与pH=8的氨水等体积混合D．pH=11的NaOH溶液与pH=5的盐酸等体积混合7．下列说法正确的是A．将pH=4的醋酸溶液稀释后，溶液中所有离子的浓度均降低B．中和pH与体积均相同的盐酸和醋酸溶液，消耗NaOH的物质的量相同C．已知pOH=－lg[c(OH-)]，又知体温下正常人的血液pH=7.35，则血液的pOH为6.65 D．KCN溶液中有剧毒HCN挥发出来，为了减少HCN的生成，最佳方法是加入KOH8．下列溶液均为0.100 mol/L，下列关系正确的是①NH4Cl ②NH4HSO4 ③NH4Fe(SO4)2④NH3·H2OA．①②显酸性，③④显碱性B．c(NH4+)：④＜③＜②C．溶液的pH：①＜②＜④ D．②溶液中：c(NH4+)+c(H+)= c(SO42-)+c(OH-)9．可逆反应2A(g)B(g)+3C(g)，开始在一真空容器中通入一定量的A(g)达到平衡后，下列说法正确的是A. 测得容器内压强增大p%，A 的转化率也是p%B. 恒容容器内平衡后再充入A(g)，此平衡逆向移动C. 恒容容器内平衡后再充入等量的A(g)，达到新平衡后，容器内压强p ’为原平衡容器压强p 的2倍D. 恒压容器内平衡后再充入Ar(g)，A 的转化率不变10．在25 mL 0.1 mol·L -1 NaOH 溶液中逐滴加入0.2mol·L -1 CH3COOH 溶液，曲线如右图所示，下列判断正确的是A ．B 点，a=12.5B ．D 点，c(Na ＋) = c(CH3COO-)＋c(CH3COOH)C ．在A 、B 间存在一点，此点水的电离程度最大D ．在C 点升温，CH3COOH 电离程度增大，CH3COO-的水解程度减小11．下列说法不正确的是A.等体积等浓度的Na2S 溶液和Na2SO3溶液中，离子数目以前者为多B.已知室温时0.10mol/L NH4Cl 溶液中c(H+) =7.5×10-6mol/L ，室温时0.10mol/L KCN 溶液中c (OH —) =1.3×10-3mol/L 。