1、第2讲 匀变速直线运动的规律
- 格式:doc
- 大小:168.00 KB
- 文档页数:7

2023届高考一轮复习 第一章 直线运动 第二讲 匀变速直线运动的规律 习题1(含解析)1.一个质点做方向不变的直线运动,加速度的方向始终与速度的方向相同,但加速度大小先保持不变,再逐渐减小直至为零,则在此过程中( )A.速度先逐渐增加,然后逐渐减小,当加速度减小到零时,速度达到最小值B.速度先均匀增加,然后增加得越来越慢,当加速度减小到零时,速度达到最大值C.位移逐渐增大,当加速度减小到零时,位移将不再增大D.位移先逐渐增大,后逐渐减小,当加速度减小到零时,位移达到最小值2.中国自主研发的“暗剑”无人机,速度可超过2马赫。
在某次试飞测试中,起飞前沿地面做匀加速直线运动,加速过程中连续经过两段均为120 m 的测试距离,用时分别为2 s 和1 s ,则无人机的加速度大小是( ) A.220m/sB.240m/sC.260m/sD.280m/s3.子弹恰能依次穿过3块紧贴在一起的厚度分别为32d d 、和d 的固定木板(即穿过第3块木板时子弹速度减小为零)。
假设子弹在木板里运动的加速度是恒定的,则下列说法正确的是( ) A.子弹依次进入各木板时的速度之比为3:2:1B. C.子弹依次通过各木板所需的时间之比为3:2:1D.4.汽车在平直的公路上行驶,发现险情紧急刹车,汽车立即做匀减速直线运动直到停车,已知汽车刹车时第1秒内的位移为13 m ,在最后1秒内的位移为2 m ,则下列说法正确的是( ) A.汽车在第1秒末的速度可能为10 m/s B.汽车加速度大小可能为23m/s C.汽车在第1秒末的速度一定为11 m/sD.汽车的加速度大小一定为24.5m/s5.为检测某公路湿沥青混凝土路面与汽车轮胎的动摩擦因数μ,测试人员让汽车在该公路的水平直道行驶,当汽车速度表显示40 km/h 时紧急刹车(车轮抱死),车上人员用手机测得汽车滑行3.70 s 后停下来,g 取210m /s ,则测得μ约为( ) A.0.2B.0.3C.0.4D.0.56.如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5、…所示小球运动过程中每次曝光的位置,连续两次曝光的时间间隔均为T ,每块砖的厚度为d 。



第2讲匀变速直线运动规律考点一匀变速直线运动规律的应用基本公式法1.C919大型客机是我国自主设计、研制的大型客机,最大航程为5 555千米,最多载客190人,多项性能优于波音737和波音747。
若C919的最小起飞(离地)速度为60 m/s,起飞跑道长2.5×103m。
C919起飞前的运动过程可看成匀加速直线运动,若要C919起飞,则C919在跑道上的最小加速度为( )A.0.36 m/s2B.0.72 m/s2C.1.44 m/s2D.2.88 m/s2【解析】选B。
由匀变速直线运动规律v2-=2ax可得C919的最小起飞加速度为a== m/s2=0.72 m/s2,选项B正确,A、C、D错误。
2.中国高铁以“快、准、稳”成为一张靓丽的“名片”而为国人所自豪。
2019年3月9日由北京南开往杭州东的G35次高铁上,一位男旅客在洗手间内吸烟,触发烟感报警装置,导致高铁突然降速缓行。
假设此次事件中列车由正常车速80 m/s匀减速至24 m/s后匀速行驶。
列车匀速行驶6 min后乘警通过排查解除了警报,列车又匀加速恢复至80 m/s的车速。
若列车在匀加速和匀减速过程的加速度大小均为1.4 m/s2,试求:(1)列车以非正常车速行驶的距离;(2)由于这次事件,列车到达杭州东时晚点多少秒?【解析】(1)列车正常车速为v1,减速后车速为v2,减速和加速过程位移为s1,时间均为t1,减速后匀速行驶位移为s2,时间为t2,由运动学公式可知:-=2as1,s2=v2t2,s=2s1+s2。
联立解得:s=12 800 m。
(2)设列车正常车速通过s位移所用时间为t′,则t1=,t′=,Δt=2t1+t2-t′。
联立解得:Δt=280 s。
答案:(1)12 800 m (2)280 s平均速度法【典例1】物体做匀加速直线运动,相继经过两段距离均为16 m的路程,第一段用时4 s,第二段用时2 s,则物体的加速度是( )A. m/s2B. m/s2C. m/s2D. m/s2【通型通法】1.题型特征:题中已知物体的位移和通过该段位移所用的时间。

2020年高考物理二轮温习热点题型与提分秘籍专题02 匀变速直线运动的规律及图像题型一 匀变速直线运动的规律及应用【题型解码】 (1)匀变速直线运动的基本公式(v -t 关系、x -t 关系、x -v 关系)原则上可以解决任何匀变速直线运动问题.因为那些导出公式是由它们推导出来的,在不能准确判断用哪些公式时可选用基本公式.(2)未知量较多时,可以对同一起点的不同过程列运动学方程.(3)运动学公式中所含x 、v 、a 等物理量是矢量,应用公式时要先选定正方向,明确已知量的正负,再由结果的正负判断未知量的方向.【典例分析1】(2019·安徽蚌埠高三二模)图中ae 为珠港澳大桥上四段110 m 的等跨钢箱连续梁桥,若汽车从a 点由静止开始做匀加速直线运动,通过ab 段的时间为t ,则通过ce 段的时间为( )A .t B.t 2C .(2-)t D .(2+) t22【参考参考答案】 C【名师解析】 设汽车的加速度为a ,通过bc 段、ce 段的时间分别为t 1、t 2,根据匀变速直线运动的位移时间公式有:x ab =at 2,x ac =a (t +t 1)2,x ae =a (t +t 1+t 2)2,解得:t 2=(2-)t ,故C 正确,A 、B 、D 错误。
1212122【典例分析2】(2019·全国卷Ⅰ,18)如图,篮球架下的运动员原地垂直起跳扣篮,离地后重心上升的最大高度为H 。
上升第一个所用的时间为t 1,第四个所用的时间为t 2。
不计空气阻力,则满足( )H 4H 4t 2t 1A.1<<2 B.2<<3t 2t 1t 2t 1C.3<<4 D.4<<5t 2t 1t 2t 1【参考参考答案】 C【名师解析】 本题应用逆向思维求解,即运动员的竖直上抛运动可等同于从一定高度处开始的自由落体运动,所以第四个所用的时间为t 2=,第一个所用的时间为t 1=-,因此有==2+H 42×H 4g H 42H g 2×34Hg t 2t 112-3,即3<<4,选项C 正确。
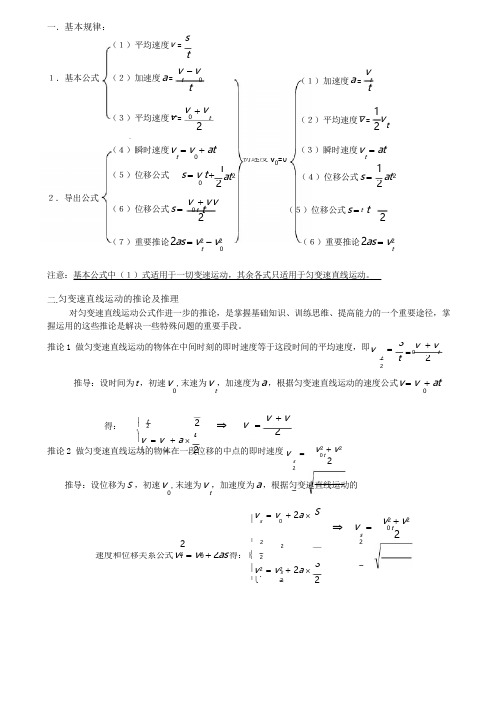
1.基本公式 (2)加速度 a = v - v初速度 v 0=0(5)位移公式 s = v t + 122推论 1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即v= St 2⇒ v = v + v ⎪ t 2 ⎪ 2 ⎨ 2 ⎪v = v + a ⨯ t ⎪⎩ t2 ⎧2速度和位移关系公式 v 2 = v 2 + 2as 得: ⎪ 2⎪v 2 = v 2+ 2 a ⨯ S⎪⎩ t 22一.基本规律:(1)平均速度 v =stvt 0(1)加速度 a = ttt(3)平均速度 v = v 0 +v2t1(2)平均速度 v = v2 t(4)瞬时速度 v = v + at(3)瞬时速度 v = attt1at 2(4)位移公式 s = at 22.导出公式(6)位移公式 s = v + v v0 t t (5)位移公式 s = t t2 2(7)重要推论 2as = v 2 - v 2t(6)重要推论 2as = v 2t注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
t v + v = 0t2推导:设时间为 t ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的速度公式 v = v + at0 t得:推论 2 做匀变速直线运动的物体在一段位移的中点的即时速度v=sv 2 + v 20 t22推导:设位移为 S ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的0 t⎪vs = v 0+ 2 a ⨯2t 0 ⎨ s 2 S⇒ v =s2v 2 + v 20 t2经过第二个时间 t 后的速度为 v =2v +at ,这段时间内的位移为 S = v t + at 2 = v t + at 22 2 经过第三个时间 t 后的速度为 v =3v +at ,这段时间内的位移为 S = v t + at 2 = v t+ at 2 2 2 2 2 3 2 32 2 2 2t推论 3 做匀变速直线运动的物体,如果在连续相等的时间间隔 t 内的位移分别为 S 、 S 、 S …… S123n ,加速度为 a,则 ∆S =S 2- S 1 = S 3 - S 2= …… = S n - S推导:设开始的速度是 vn -1= at2经过第一个时间 t 后的速度为 v = v + a t ,这一段时间内的位移为 S = v t + 1 0 1 0 1 2 at 2,1 32 0 2 1 0 1 52 032…………………经过第 n 个时间 t 后的速度为 v =nv +at ,这段时间内的位移为 S =v t +1 a t 2 =v t + n 0 n n -1 02n -1 2at 2则 ∆S = S 2 - S 1 = S 3 - S 2 = …… = S n - Sn -1= at 2点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度 a 与时间 “有关的恒量”.这也提供了一种加速度的测量的方法: 即 a =∆S,只要测出相邻的相同时间内的位移之差 ∆S 和 t ,就容易测出加速度 a 。
课时2 匀变速直线运动规律的应用1.匀变速直线运动的基本规律(1)匀变速直线运动就是加速度不变的直线运动,当v与a方向相同时,物体做加速直线运动;当v与a方向相反时,物体做减速直线运动;物体的速度变大变小与a是否变化无关,由它们之间的方向关系决定。
(2)基本运动规律①速度与时间关系公式v=v0+at。
②位移与时间关系公式x=v0t+at2。
③位移与速度关系公式2ax=v2-。
2.匀变速直线运动的常用推论(1)中间时刻的瞬时速度=(v+v0)。
(2)中间位置的瞬时速度=。
(3)连续相等时间内相邻的位移之差相等,即Δx=x2-x1=x3-x2=x4-x3=…=aT2。
3.初速度为零的匀加速直线运动比例式(1)1T末、2T末、3T末、…、nT末的瞬时速度之比v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n。
(2)1T内、2T内、3T内、…、nT内的位移之比x1∶x2∶x3∶…∶x n=12∶22∶32∶…∶n2。
(3)第一个T内、第二个T内、第三个T内、…、第n个T内的位移之比Δx1∶Δx2∶Δx3∶…∶Δx n=1∶3∶5∶…∶(2n-1)。
(4)通过连续相等的位移所用时间之比t1∶t2∶t3∶…∶t n=1∶(-1)∶(-)∶…∶(-)。
4.自由落体运动和竖直上抛运动的规律(1)自由落体运动①速度公式:v=gt。
②位移公式:x=gt2。
③位移—速度公式:2gx=v2。
(2)竖直上抛运动①速度公式:v=v0-gt。
②位移公式:x=v0t-gt2。
③位移—速度公式:-2gx=v2-。
④上升的最大高度:h=。
⑤上升到最大高度用时:t=。
1.(2019安徽安庆市第二中学开学摸底)质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位),则该质点()。
A.第1s内的位移是5mB.前2s内的平均速度是6m/sC.任意相邻的1s内位移差都是1mD.任意1s内的速度增量都是2m/s答案 D2.(2019湖南长沙1月月考)物体做匀加速直线运动,相继经过两段距离为16m的路程,第一段用时4s,第二段用时2s,则物体的加速度是()。
匀变速直线运动的基本规律 1.匀变速直线运动 (1)定义:沿着一条直线,且加速度不变的运动。 (2)分类: ①匀加速直线运动,a与v0方向相同。 ②匀减速直线运动,a与v0方向相反。 2.匀变速直线运动的规律 (1)速度公式:v=v0+at。
(2)位移公式:x=v0t+12at2。 (3)位移速度关系式:v2-v 20=2ax。
初速度为零的匀变速直线运动的四个重要推论 (1)1T末、2T末、3T末„„瞬时速度的比为: v1∶v2∶v3∶„∶vn=1∶2∶3∶„∶n
(2)1T内、2T内、3T内„„位移的比为: x1∶x2∶x3∶„∶xn=12∶22∶32∶„∶n2 (3)第一个T内、第二个T内、第三个T内„„位移的比为: xⅠ∶xⅡ∶xⅢ∶„∶xn=1∶3∶5∶„∶(2n-1) (4)从静止开始通过连续相等的位移所用时间的比为: t1∶t2∶t3∶„∶tn=1∶(2-1)∶(3-2)∶„∶(n-n-1)
1.一观察者站在第一节车厢前端,当列车从静止开始做匀加速运动时,下列说法正确的是( ) A.每节车厢末端经过观察者的速度之比是1∶2∶3„ B.每节车厢末端经过观察者的时间之比是1∶3∶5„ C.在相等时间里经过观察者的车厢数之比是1∶3∶5„ D.在相等时间里经过观察者的车厢数之比是1∶2∶3„ 解析:选AC 根据初速度为零的匀变速直线运动的推论及v2=2ax知选项A、C正确。 匀变速直线运动的重要推论
匀变速直线运动的两个重要推论 (1)物体在一段时间内的平均速度等于这段时间中间时刻的瞬时速度,还等于初末时刻
速度矢量和的一半,即:v=vt2=v0+v2。 (2)任意两个连续相等的时间间隔T内的位移之差为一恒量,即:Δx=x2-x1=x3-x2=„=xn-xn-1=aT2。 还可以推广到xm-xn=(m-n)aT2。
对匀变速直线运动规律的两点说明 (1)匀变速直线运动的基本公式均是矢量式,应用时要注意各物理量的符号,一般规定初速度的方向为正方向,当v0=0时,一般以a的方向为正方向。 (2)物体先做匀减速直线运动,速度减为零后又反向做匀加速直线运动,全程加速度不变,对这种情况可以将全程看做匀变速直线运动,应用基本公式求解。
2.一物体做匀变速直线运动,某时刻速度大小为4 m/s,1 s后速度的大小变为10 m/s,在这1 s内该物体的( ) A.位移的大小可能小于3 m B.位移的大小可能大于10 m C.加速度的大小可能小于4 m/s2 D.加速度的大小可能大于10 m/s2 解析:选D 若初、末速度同向时:
v=v0+v2=4+10
2 m/s=7 m/s,
x=v t=7 m, a=v-v0t=10-41 m/s2=6 m/s2。 若初、末速度反向时: v=v0+v2=-4+10
2 m/s=3 m/s
x=v t=3 m, a=v-v0t=10--41 m/s2=14 m/s2 因此可得出只有选项D正确。 匀变速直线运动的规律 [命题分析] 本考点是高考的热点,常以选择题或计算题的形式考查,在高考中可被单独命题,也可与v-t图象、牛顿运动定律、电场等知识综合命题。 [例1] (2013·江西五校联考)质量为m的飞机静止在水平直跑道上。飞机起飞过程可分为两个匀加速运动阶段,其中第一阶段飞机的加速度为a1,运动时间为t1。当第二阶段结束时,飞机刚好达到规定的起飞速度v0。飞机起飞过程中,在水平直跑道上通过的路程为s,受到的阻力恒为Ff。求第二阶段飞机运动的加速度a2和时间t2。 [思维流程] 第一步:抓信息关键点 关键点 信息获取 (1)起飞过程分为两个匀加速运动阶段 第一阶段的末速度即为第二阶段的初速度 (2)通过的路程为s 两个阶段的总路程为s (3)受到的阻力恒为Ff 飞机不仅受阻力作用,两个阶段加速度不同
第二步:找解题突破口 飞机的两个运动阶段情景相似,且第一阶段的末速度等于第二阶段的初速度,分别根据速度公式和位移公式对两个阶段列出方程,求解即可得出a2和t2。 第三步:条理作答 [解析] 第一、二阶段结束时飞机运动速度分别为 v1=a1t1
v0=v1+a2t2
运动距离分别为:
s1=12a1t 21
s2=v1t2+12a2t 22 总距离为s=s1+s2 解得a2=v 20-a 21t 212s-a1t 21
t2=2s-a1t 21v0+a1t1 [答案] v 20-a 21t 212s-a1t 21 2s-a1t 21v0+a1t1 ——————————————————————————————— 求解匀变速直线运动问题的一般解题步骤 (1)首先确定研究对象,并判定物体的运动性质。 (2)分析物体的运动过程,要养成画物体运动示意图的习惯。 (3)如果一个物体的运动包含几个阶段,就要分段分析,各段交接处的速度往往是联系各段的纽带。 (4)运用基本公式或推论等知识进行求解。 —————————————————————————————————————— [变式训练] 1.发射卫星一般用多级火箭,第一级火箭点火后,使卫星向上匀加速直线运动的加速度为50 m/s2,燃烧30 s后第一级火箭脱离,又经过10 s后第二级火箭启动,卫星的加速度为80 m/s2,经过90 s后,卫星速度为8 600 m/s。求在第一级火箭脱离后的10 s内,卫星做什么运动,加速度是多少?(设此过程为匀变速直线运动) 解析:第一级火箭燃烧完毕时的速度v1=a1t1=50×30 m/s=1 500 m/s。由题意知,卫星在第二级火箭燃烧过程中做匀加速直线运动,末速度v3=8 600 m/s,加速度a3=80 m/s2,时间t3=90 s,设这一过程中的初速度为v2,由v3=v2+a3t3,得v2=v3-a3t3=(8 600-80×90) m/s=1 400 m/s,可见从第一级火箭分离至第二级火箭启动,卫星速度在减小,做匀减速直
线运动,设加速度为a2,由v2=v1+a2t2,得a2=v2-v1t2=1 400-1 50010 m/s2=-10 m/s2,负号表示加速度a2的方向与速度方向相反。 答案:匀减速运动 10 m/s2 匀变速直线运动推论的应用
[命题分析] 本考点是匀变速直线运动规律的延续,是高考的重点,常结合牛顿运动定律、电场等知识进行综合考查。
[例2] 物体以一定的初速度冲上固定的光滑斜面,到达斜面最高点C时速度恰为零,如图1-2-1所示。从物体过A时开始计时,已知物体第一次运动到斜面长度3/4处的B点时,所用时间为t,求物体从B滑到C所用的时间。 图1-2-1 [解析] 方法一:比例法 对于初速度为零的匀加速直线运动,在连续相等的时间里通过的位移之比为 x1∶x2∶x3∶„∶xn=1∶3∶5∶„∶(2n-1)
现有xBC∶xBA=xAC4∶3xAC4=1∶3 通过xAB的时间为t,故通过xBC的时间tBC=t。 方法二:中间时刻速度法 利用推论:中间时刻的瞬时速度等于这段位移的平均速度。
vAC=v+v02=v0+02=v02
又v 20=2axAC① v2B=2axBC②
xBC=14xAC③
解①②③得:vB=v02。 可以看出vB正好等于AC段的平均速度,因此B点是中间时刻的位置。因此有tBC=t。
方法三:利用有关推论 对于初速度为0的匀加速直线运动,通过连续相等的各段位移所用的时间之比t1∶t2∶t3∶„∶tn=1∶(2-1)∶(3-2)∶(4-3)∶„∶(n-n-1)。 现将整个斜面分成相等的四段,如上图所示。设通过BC段的时间为tx,那么通过BD、DE、EA的时间分别为:
tBD=(2-1)tx,tDE=(3-2)tx,tEA=(2-3)tx, 又tBD+tDE+tEA=t,得tx=t。 [答案] t ——————————————————————————————— 运动学问题选择公式口诀 运动过程要搞清,已知未知心里明。 基本公式很重要,推论公式不小瞧。 平均速度a不见,纸带问题等时间。 比例公式可倒用,推论各有己特点。 —————————————————————————————————————— [变式训练] 2.一个做匀加速直线运动的物体,在前4 s内经过的位移为24 m,在第二个4 s内经过的位移是60 m,求这个物体运动的加速度和初速度各是多少? 解析:方法一:基本公式法
前4 s内经过的位移:x1=v0t+12at2 第2个4 s内经过的位移: x2=v0(2t)+12a(2t)2-(v0t+12at2) 将x1=24 m、x2=60 m代入上式, 解得a=2.25 m/s2 v0=1.5 m/s。
方法二:利用有关推论 由公式Δ x=aT2,得
a=Δ xT2=60-2442 m/s2=2.25 m/s2。
根据v=vt2得24+608 m/s=v0+4a,所以v0=1.5 m/s。 答案:2.25 m/s2 1.5 m/s
万能模型——“匀变速直线运动”模型 此模型蕴涵在日常生活、体育赛事和军事活动等具体情境中,具有形式灵活,过程多变的特点。但每个过程都符合或近似符合匀变速直线运动的规律。 [示例] “10米折返跑”的成绩反映了人体的灵敏素质。如图1-2-2所示,测定时,在平直跑道上,受试者以站立式起跑姿势站在起点终点线前,当听到“跑”的口令后,全力跑向正前方10米处的折返线,测试员同时开始计时。受试者到达折返线处时,用手触摸折返线处的物体(如木箱),再转身跑向起点终点线,当胸部到达起点终点线时,测试员停表,所用时间即为“10米折返跑”的成绩。设受试者起跑的加速度为4 m/s2,运动过程中的最大速度为4 m/s,快到达折返线处时需减速到零,减速的加速度为8 m/s2,返回时达到最大速度后不需减速,保持最大速度冲线。求受试者“10米折返跑”的成绩为多少秒?