当前位置：文档之家 › 匀变速直线运动规律及应用

匀变速直线运动规律及应用

  • 格式：ppt
  • 大小：2.22 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

匀变速直线运动规律的应用

匀变速直线运动规律的应用

能力· 思维· 方法
【解题回顾】本题分析时，有不少学生易患如下毛 病，当推出v1＞v2时假设物体匀加速，便主观地认 为若物体做匀减速运动结果就是v1＜v2.
此外，本题还有一个较好的处理方法，就是利用vt图线比较v1和v2的大小. 设物体做加速运动，其v-t图如图2-2-2，其中间时 刻的速度v2大小即为梯形OABC的中位线的长度.而中 间位置的速度大小则应是把梯形面积平分为二的线 段DE表示的长度.若物体做减速运动由图2-2-3可得 出同样的结论.
物体在AB之间作匀变速直线
运动，C为AB的中点，已知物 体在A、B的速度分别为V 1和 V2试求物体在C点的速度
要点· 疑点· 考点
二、初速度为0的匀变速直线运动的特殊规律 1.从静止出发后，在T秒内、2T秒内、3T秒内位 移之比为：12∶22∶32∶…∶n2
2.从静止出发后，在第一个T秒内、第二个T秒内、 第三个T秒内位移，即连续相等时间内位移之比为： 1∶3∶5∶…∶(2n-1). 3.从静止出发后，在T秒末、2T秒末、3T末速度 之比为：1∶2∶3∶…∶n.
二、匀变速直线运动的规律
1.基本公式.
(1)速度公式：vt=v0+at，
(2)位移公式：s=v0t+(1/2)at2. (3)速度、位移关系：v２t-v20=2as，
要点回眸
【注意】匀变速直线运动中所涉及 的物理量有五个，分别为v0、vt、s、 a、t,其中t是标量，其余均为矢量， 一般情况下，选初速度方向为正方向. 当知道五个量中的任意三个的时候， 就可以利用公式求出其余两个量.
能力· 思维· 方法
【例3】物体从A到B做匀变速直线运动，经过中间 位置时的速度为v1，它在这段时间中间时刻的速 度为v2，则(AC)

匀变速直线运动的规律及应用

匀变速直线运动的规律及应用

③
2
解①~③得：t＝5 s，x＝12.5 m.
答案：12.5 m
类型二：运动学常用的重要推论及其应用 【例 2】 一列火车做匀变速直线运动驶来，一人在轨 道旁边观察火车运动，发现在相邻的两个 10 s 内，火车 从他跟前分别驶过 8 节车厢和 6 节车厢，每节车厢长 8 m （连接处长度不计），求： （1）火车的加速度的大小； （2）人开始观察时火车速度的大小. 思路点拨：抓住相邻的两个 10 s，利用结论求解.
vt/2＝v0－aT，
解得 v0＝7.2 m/s.
答案：（1）0.16 m/s2 （2）7.2 m/s
方法技巧：正确分析题目中的条件，选择合适的公式或结
论求解是分析运动学问题的前提，再就是必要时要作出运
动草图帮助分析.
针对训练 2－1：两木块自左向右运动，现用高速摄影 机在同一底片上多次曝光，记录下木块每次曝光时的位 置，如图 1－2－3 所示，连续两次曝光的时间间隔是相等 的，由图可知（ ）
匀变速直线运动flash
2.匀变速直线运动中几个常用的结论
（1）Δx＝aT2，即任意相邻相等时间内的位移之差相 等.可以推广到 xm－xn＝（m－n）aT2.判断匀变速直线运动
的实验依据.
（2）vt/2＝ v0 v ＝ x ，即某段时间中间时刻的瞬时
2 t
速度等于该段时间内的平均速度.
（3）某段位移中点的瞬时速度：v ＝
v＝v gt，上升时间 t 上＝v / g
0
0
h＝v t 1 gt 2
2 0
v2－v02＝
2gh，上升最大高度
Hmax＝
v2 0
2g
下降过程：自由落体运动（a＝g） v＝ gt

高一物理 匀变速直线运动规律的应用

高一物理 匀变速直线运动规律的应用

1．v2－v02＝2ax此式不涉及时间，若题目中已知量 和未知量都不涉及时间，利用此式往往比较简单；
2用．于x匀＝变vt普速遍直适线用运于动各，种两运者动相，结而合可v＝以v轻02+v松＝地v2t求只出适 中间时刻的瞬时速度或者初、末速度．
3．x2－x1＝aT2适用于匀变速直线运动， 进一步的推论有xm－xn＝(m－n)aT2(其中T为连续 相等的时间间隔，xm为第m个时间间隔内的位移， xn为第n个时间间隔内的位移)．
目标定位
预习导学
课堂讲义
对点练习
课堂讲义
匀变速直线运动的规律总结
三、初速度为零的匀变速直线运动的比例式
1．初速度为零的匀加速直线运动，按时间等分(设相
等的时间间隔为T)
(1)1T末、2T末、3T末…、nT末瞬时速度之比
v1∶v2∶v3∶…∶vn＝1∶2∶3∶…∶n
(2)1T内、2T内、3T内、…、nT内的位移之比 x1∶x2∶x3∶…∶xn＝12∶22∶32∶…∶n2
(3)第一个T内，第二个T内，第三个T内，…，
第n个T内位移之比 xⅠ∶xⅡ∶xⅢ∶…∶xn＝1∶3∶5∶…∶(2n－1)
目标定位
预习导学
课堂讲义
对点练习
课堂讲义
匀变速直线运动的规律总结
2．初速度为零的匀加速直线运动，按位移等分(设相等的 位移为x) (1)通过前x、前2x、前3x…时的速度之比
v1∶v2∶v3∶…∶vn＝1: 2: 3:......: n
第2s、第3s、第4s内，通过
的路程分别为1m、2m、3m、
4m，有关其运动的描述正
确A．的4是s内( 的A平B)均速度是
2.5m/s B．在第3、4两秒内平均速 度是3.5m/s

匀变速直线运动的公式及其应用方法

匀变速直线运动的公式及其应用方法

匀变速直线运动的公式及其应用方法一、匀变速直线运动的速度公式设物体在t时刻的速度为v，t时刻的位移为s，则匀变速直线运动的速度公式可以表示为：v = v₀ + at其中，v₀是初始速度，a是加速度。

二、匀变速直线运动的位移公式设物体在t时刻的位移为s，则匀变速直线运动的位移公式可以表示为：s = s₀ + v₀t + 1/2at²其中，s₀是初始位移。

三、利用速度公式求物体的位移考虑一个物体从t₁时刻到t₂时刻的运动过程。

根据速度公式可知：v₂=v₁+a(t₂-t₁)将该等式两边积分得：∫v₂ dt = ∫(v₁ + a(t₂ - t₁)) dt即：s₂-s₁=v₁(t₂-t₁)+1/2a(t₂-t₁)²可见，通过速度公式和积分可求得物体在t₁到t₂时刻的位移。

四、利用位移公式求物体的速度当物体的初速度v₀、加速度a和位移s已知时，我们可以从位移公式中解出t，再代入速度公式中可以求得物体在任意时刻的速度。

五、匀变速直线运动的应用方法1.求解物体的时间、速度和位移关系：通过速度公式和位移公式，可以求解物体在任意时刻的速度和位移，并了解物体在不同时间段的运动情况。

2.物体的竖直自由落体运动：自由落体运动是一种匀变速直线运动，其中加速度为重力加速度g，可以利用匀变速直线运动的公式求解自由落体运动的速度和位移。

3.汽车加速度和制动距离计算：通过测量汽车的加速时间和制动距离，可以利用匀变速直线运动的公式反推汽车的加速度。

4.抛体运动的分析：抛体运动是一种由初速度引起的匀变速直线运动，可以利用匀变速直线运动的公式求解抛体运动中的速度和位移等参数。

5.跳伞运动的分析：跳伞运动是一种由初速度引起的匀变速直线运动，可以应用匀变速直线运动的公式分析跳伞运动中的速度、位移和时间等参数。

综上所述，匀变速直线运动的公式和应用方法对于研究运动物体的速度、位移和时间等参数具有重要意义，它在物理学和工程学等领域有着广泛的应用。

匀变速直线运动的规律及应用

匀变速直线运动的规律及应用
S1:S2:S3:…:Sn=1:4:9:…:n2
（3）第1s内、第2s内、第3s内、…第ns内的位移之比
SI:SII:SIII:…:SN=1:3:5:…:(2n-1)
注意：（1）如何描述这几个规律 （2）时间间隔可扩展到任意t秒
5、做匀变速直线运动的物体，在任意相邻相等时间间隔
例3、一汽车在水平路面上行驶时以v=20m/s，遇到障碍刹车， 加速度的大小为4m/s2，求汽车在6s内通过的位移为多少？ （汽车距刹车点多远）
解： S=v0t+ at2=20×6+ ×（-4）×36＝48m
注意，以上解法是错误的。原因是刹车过程的最后状态是停下 来，即：vt＝0。这类题在解的过程中，应首先判断在所给时 间内，物体是否停下来。如果物体没有停下来，所求过程为匀 变速直线运动，直接代公式求解；如果已经停下来了，过程应 该分为两部分：匀变速过程（停下来以前）和静止过程（停下 来以后），整个过程不再是匀变速直线运动。这种情况下，直 接代公式就不行了。但是前一个过程还是匀变速，可以代公式 求前一个过程的位移（注意这时所代时间不再是全部时间而是 匀变速过程的时间）。我们又知道，后一个过程的位移为0， 所以前一个过程的位移与整个过程的位移相同
设物体运动的初速度为v0，加速度为a，则由位移公式有：
S1=v0t1+
at12
7.2=3v0+ a×32 ①
对后3s，v2=v0+at=v0+2a
②
S2=v2t2+
at22
16.8=3v2+ a×32 ③
三式联立可求得：v0=0 a=1.6m/s2 ∴由S= at2有S总= ×1.6×52=20（m）
可以求出a=－2.5m/s2

高中物理精品课件：匀变速直线运动规律应用

高中物理精品课件：匀变速直线运动规律应用

（二）解匀变速直线运动问题的步骤
1、正确判断研究对象的运动性质
2、作草图，并找出已知量
3、分析已知量和所求量之间的关系，选用
适当的公式
4、求得结果后必须分析答案的合理性
一、典型例题
一个滑雪的人，从85m长的山坡上匀变速滑下，
初速度是1.8m/s，末速度是5m/s，他通过这段山坡
需要多长时间？
• 2、做匀加速直线运动的物体途中依次经过A、B、C三点，
2T
x2
（n-1）T
3T
x3
Xn-1
nT
xn
(3)第一个T内，第二个内，第三个T内，…位移之
比
xⅠ：xⅡ：xⅢ：…xN=1：3：5： …（2N-1）xⅡxⅠ来自0xⅢT
2T
xN
3T
（n-1）T
nT
（4）第一个L，第二个L，第三个L，…
所用时间之比
tⅠ：tⅡ：tⅢ：…tN=1：（ 2 1 ）：（ 3 2 ）：
2a
故 6 s 内的位移为 x＋x1＝25 m.
重点探究
变式 如图Z1-1所示是某同学研究匀变速直线运动规律时得到的一条纸带(实验
中交流电源的频率为50 Hz),依照打点的先后顺序取计数点1、2、3、4、5、6、
7,相邻两计数点间还有4个点未画出,测得x1=1.42 cm,x2=1.91 cm,x3=2.40 cm,
（一）匀变速直线运动规律：
速度公式：
v v 0 at
（Ⅰ）
位移公式：
1 2
x v0 t at
2
（Ⅱ）
速度位移关系式：
v v 2ax
（Ⅲ）
平均速度：
v0 v
v

第1章 第2节 匀变速直线运动规律及应用


3.(2011•新课标)甲乙两辆汽车都从静止出发做加速 直线运动，加速度方向一直不变．在第一段时间间 隔内，两辆汽车的加速度大小不变，汽车乙的加速 度大小是甲的两倍；在接下来的相同时间间隔内， 汽车甲的加速度大小增加为原来的两倍，汽车乙的 加速度大小减小为原来的一半．求甲乙两车各自在 这两段时间间隔内走过的总路程之比．
解法二：(极值法)利用判别式求解，由解法一可知xA 1 1 2 2 ＝x＋xB，即v0t＋ ×(－2a)×t ＝x＋ at 2 2 整理得3at2－2v0t＋2x＝0 这是一个关于时间t的一元二次方程，当根的判别式Δ ＝(2v0)2－4×3a×2x＜0时，t无实数解，即两车不相撞， 所以要使两车不相撞，A车的初速度v0应满足的条件是v0＜ 6ax
2
点评： 解决匀变速直线运动的常用方法有如 下几种： (1)一般公式法 一般公式法是指选用速度、位移和时间的关系 式，它们均是矢量式，使用时应注意方向性．一般 以v0的方向为正方向，其余与正方向相同者取正， 与正方向相反者取负．
2 平均速度法
x 定义式v ，对任何性质的运动都适用，而公式 t 1 v (v0 v )只适用于匀变速直线运动． 2 3中间时刻速度法 利用“在一段时间t的中间时刻的瞬时速度等于这段时间 t的平均速度”，即v t v.此公式适用于任何一个匀变速
【解析】在0～5s，物体向正向运动，5s～6s向负 向运动，故5s末离出发点最远，sm=35m，A错； 由面积法求出0～5s的位移s1=35m,5s～6s的位移 s2=-5m，总路程为：40m，B对；由面积法求出 0～4s的位移s=30m，平均速度为：v=s/t=7.5m/s， C对；由图象知5s～6s过程物体加速，合力和位移 同向，合力做正功，D错．

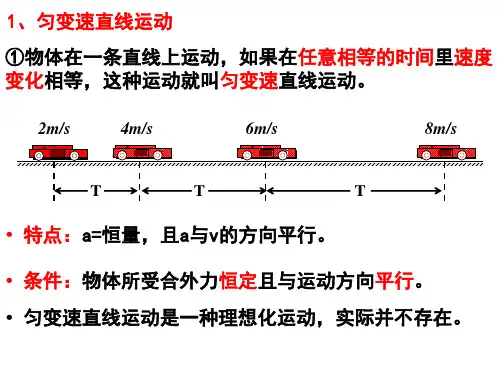
专题二匀变速直线运动的规律及其应用ppt课件


• 条件：物体所受合外力恒定且与运动方向平行。 • 匀变速直线运动是一种理想化运动，实际并不存在。
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
v
• 图象 a
s
s t
t
t
2、匀变速直线运动的规律 为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
（4）比例法
s1 : s2 : s3 : …… = 12 : 22 : 32 : …… v1 : v2 : v3 : …… = 1 : 2 : 3 : …… sⅠ : sⅡ : sⅢ :……=1 : 3 : 5 : ……
t1 : t2 : t3 : …… = 1 : ( 2 ― 1) : ( 3 ― 2 ):……
无初速度地释放一颗，在连续释放若干钢球后，对准斜面
上正在滚动的若干小球拍摄到如图所示的照片，测得AB=
15cm，BC=20cm.求： （1）拍摄照片时B球的速度
CBA
（2）A球上面还有几颗正在滚动的钢球 答案： （1）VB=1.75m/s （2）2个
例4、如图所示，为了测定某辆轿车在平直路上启动时的 为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
-2m/s2
（1）刹车后2s内前进的距离及刹车过程中的加速度
（2）刹车后前进9m所用的时间 1s （3）刹车后8s内前进的距离 25m
➢“速度”的误区 为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益 例9、一物体作匀变速直线运动，某时刻速度的大小4m/s ，1s后速度的大小变为10m/s，在这1s内该物体的( AD ) (A)位移的大小可能小于4m (B)位移的大小可能大于10m (C)加速度的大小可能小于4m/s2 (D)加速度的大小可能大于10m/s2.

匀变速直线运动的规律及应用


由x2-x1=aT2得
a= x2 x1 64 24 m/s2=2.5 m/s2 2 2
再由x1=v0t+ 答案
T 4 1 at2解得v =1 0 2
m/s.
1 m/s
2.5 m/s2
方法提炼 如何合理地选取运动学公式解题? (1)注意公式中涉及的物理量及题目中的已知量 之间的对应关系,根据题目的已知条件中缺少的 量去找不涉及该量的公式. (2)若题目中涉及不同的运动过程,则应重点寻 找各段运动的速度、位移、时间等方面的关系. (3)利用匀变速直线运动的四个推论往往能使解 题过程简化. (4)运动学公式众多,同一题目可以选用不同公 式解题,在学习中应加强一题多解训练,加强解 题规律的理解,提高自己运用所学知识解决实际 问题的能力,促进发散思维的发展.
图1
③能量对称性 物体从A→B和从B→A重力势能变化量的大小相 等,均等于mghAB.
(2)多解性
当物体经过抛出点上方某个位置时,可能处于上 升阶段,也可能处于下降阶段,造成双解.
题型探究
题型1 匀变速运动公式的灵活选用 【例1】一个做匀加速直线运动的物体,在连续相 等的两个时间间隔内,通过的位移分别是24 m和
第2课时 匀变速直线运动的规
律及应用
考点自清
一、匀变速直线运动 1.定义:沿着一条直线,且 加速度 不变的运动. 2.分类:
匀加速直线运动：a与v 同向
匀减速直线运动：a与v 反向
二、匀变速直线运动的规律 1.三个基本公式 v=v 速度公式： 0+at 位移速度关系式： 2-v02=2ax v 2.两个推论 (1)做匀变速直线运动的物体在一段时间内的平 均 速 度 等 于 这 段 时 间 初 末时 刻 速 度矢 量 和 的

第1章 1.2 匀变速直线运动的规律及其应用

第2课时：匀变速直线运动的规律及其应用读基础知识基础回顾：一、匀变速直线运动的规律1．匀变速直线运动沿一条直线且加速度不变的运动．2．匀变速直线运动的基本规律(1)速度公式：v＝v0＋at.(2)位移公式：x＝v0t＋12at2.(3)位移速度关系式：v2－v02＝2ax.二、匀变速直线运动的推论1．三个推论(1)连续相等的相邻时间间隔T内的位移差相等．即x2－x1＝x3－x2＝…＝x n－x n－1＝aT2.(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初、末时刻速度矢量和的一半，还等于中间时刻的瞬时速度．平均速度公式：v＝v0＋v2＝2v t.(3)位移中点速度2xv＝v02＋v22.2．初速度为零的匀加速直线运动的四个重要推论(1)T末、2T末、3T末、…、nT末的瞬时速度之比为v1∶v2∶v3∶…∶v n＝1∶2∶3∶…∶n.(2)T内、2T内、3T内、…、nT内的位移之比为x1∶x2∶x3∶…∶x n＝12∶22∶32∶…∶n2.(3)第1个T内、第2个T内、第3个T内、…、第n个T内的位移之比为xⅠ∶xⅡ∶xⅢ∶…∶x N＝1∶3∶5∶…∶(2n－1)．(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶t n＝1∶(2－1)∶(3－2)∶(2－3)∶…∶(n－n－1)．自查自纠：(1)匀变速直线运动是加速度均匀变化的运动。

()(2)匀变速直线运动是速度均匀变化的运动。

()(3)匀加速直线运动的位移是均匀增大的。

()(4)某物体从静止开始做匀加速直线运动，速度由0到v运动距离是由v到2v运动距离的2倍。

() (5)对任意直线运动，其中间时刻的瞬时速度一定等于其平均速度。

()(6)在匀变速直线运动中，中间时刻的速度一定小于该段时间内位移中点的速度。

()答案(1)×(2)√(3)×(4)×(5)×(6)√研考纲考题要点1匀变速直线运动规律的基本应用1.匀变速直线运动公式为矢量式，一般规定初速度v0的方向为正方向(当v0＝0时，一般以加速度a的方向为正方向)，与正方向同向的物理量取正值，反向的物理量取负值。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【解析】(1)先求粉笔与皮带间的动摩擦因数 μ，皮 带开始以 v0＝5 m/s 匀速运动， 粉笔对地以μg 的加速度 匀加速运动，划痕 L＝5 m 为相对位移， 2 v0 v2 v 0 0 则 v0· － ＝L，即 a＝ ＝2.5 m/s2＝μg a 2a 2L μ＝0.25 第二阶段，因皮带受阻，做 a0＝5 m/s2 的匀减速运 动． 粉笔还能在皮带上做相对滑动，粉笔相对皮带滑行 距离 2 v2 v 25 25 0 0 L′＝ － ＝ m－ m＝2.5 m. 2a 2a0 2×2.5 2×5
( n - n -1) .
1 ∶ ( 2 -1) ∶ ( 3 - 2) ∶„∶
题型一：匀变速直线运动规律的应用 例1 摩托车在平直公路上从静止开始起动，a1＝ 1.6 m/s2 ，稍后匀速运动，然后减速， a2 ＝ 6.4 m/s2 ， 直到停止，共历时130 s，行程1 600 m．试求： (1)摩托车行驶的最大速度vm； (2)若摩托车从静止起动，a1、a2不变，直到停止，行 程不变，所需最短时间为多少？
时间最短，则其运动时间可以表示为C、D两种形式；另 一种可能是木块先加速，当达到与传送带相同速度后，摩
擦力消失，木块再做匀速运动到右端，此时其运动时间是
选项A，所以不可能的就是B.
4.做匀加速直线运动的物体在时间 T 内通过位移 x1 到达 A 点，接着在时间 T 内又通过位移 x2 到达 B 点， 则以下判断正确的有( AD ) x1＋x2 A．物体经 A 点的速度大小为 2T x1＋x2 B．物体运动的加速度为 2 T x1＋x2 C．物体到达 B 点的速度大小为 T x2－x1 D．物体运动的加速度为 2 T
【解析】依加速度的意义式，可知 A对， C错，依速度 公式，可得B对，D错．
*
3．如图所示，传送带的水平部分长为L，传送速率为v，
在其左端无初速释放一小木块，若木块与传送带间的 动摩擦因数为μ，则木块从左端运动到右端的时间不可
能是(
)B
【解析】当在传送带的左端无初速释放一木块后，木块在
传送带上的运动有两种可能，一种可能是木块一直加速其
求解匀变速直线运动问题常见方法 方 法 分析说明 一般公式法指速度公式、位移公式及推 论三式．它们均是矢量式，使用时要注 意方向性．一般以v0的方向为正方向， 其余与正方向相同者为正，与正方向相 反者取负
x 定义式 v 1＝ t 对任何性质的运动都适 v0 + v 用，而 v ＝ 只适用于匀变速直线 2 运动
Δx
Δx
2．正在匀加速沿平直轨道行驶的长为 L 的列车， 保持加速度不变通过长度为 L 的桥．车头驶上桥时的速 度为 v1，车头经过桥尾时的速度为 v2，则列车过完桥时 的速度为( D ) A. v1v2
题型二：运动的多过程问题 例3 短跑名将博尔特在北京奥运会上创造了100 m和200 m 短跑项目的新世界纪录 ，他的成绩分别是 9.69 s 和 19.30 s．假定他在100 m比赛时从发令到起跑的反应时 间是 0.15 s ，起跑后做匀加速运动，达到最大速率后做 匀速运动.200 m比赛时，反应时间及起跑后加速阶段的 加速度和加速时间与 100 m比赛时相同，但由于弯道和 体力等因素的影响，以后的平均速率只有跑 100 m时最 大速率的96%.求： (1)加速所用时间和达到的最大速率； (2)起跑后做匀加速运动的加速度．(结果保留两位小数) 【思路点拨】首先要根据题意作出物体运动的草图，建立 一幅清晰的运动图景，然后找出各段运动中各物理量的关 系．
*
【巩固基础】 1．一物体作匀加速直线运动，通过一段位移 Δx 所 用的时间为 t1， 紧接着通过下一段位移 Δx 所用时间为 t2. 则物体运动的加速度为 ( A ) 2Δ x（t1－t2） A. t1t2（t1＋t2） 2Δ x（t1＋t2） C. t1t2（t1－t2） Δ x（t1－t2） B. t1t2（t1＋t2） Δx（t1＋t2） D. t1t2（t1－t2）
2．1T内，2T内，3T内„位移之比为： s1∶s2∶s3∶„∶sn＝ 个T内的位移之比为： sⅠ∶sⅡ∶sⅢ∶„∶sN＝ 1∶3∶5∶„∶(2N－1).
12∶22∶32∶„∶n2 .
Байду номын сангаас
3 ．第一个 T 内，第二个 T 内，第三个 T 内，„„第 N
4．从静止开始通过连续相等的位移所用时间之比为： t1∶t2∶t3∶„∶tn＝
66 m/s 【解析】(1)a＝ ＝0.3 m/s2 220 s (2)D301 次列车减速到与 D3115 次列车速度相等所 v2－ v1 需的时间为 t＝ ＝200 s a 此过程 D3115 次列车位移为 x1＝v1t＝1200 m 1 2 D301 次列车位移为 x2＝v2t－ at ＝7200 m 2 要避免追尾 D301 次列车制动时距离 D3115 次列车 至少为 s＝x2－x1＝6000 m
一般公式法
平均速度法
中间时刻 速度法
利用“任一时间t中间时刻的瞬时速度 等于这段时间t内的平均速度”即 vt/2＝v ，适用于任何一个匀变速直线运 动 对于初速度为零的匀加速直线运动与 末速度为零的匀减速直线运动，可利 用初速度为零的匀加速直线运动的比 例关系求解 把运动过程的“末态”作为“初态” 的反向研究问题的方法．一般用于末 态已知的情况 应用v－t图象，可把较复杂的问题转变 为较为简单的数学问题解决
.
1．在任意两个连续相等的时间间隔内通过的位移之差 为一恒量，即： sⅡ － sⅠ ＝ sⅢ － sⅡ ＝„＝ sN － sN － 1 ＝ Δs ＝ aT2 . 进一步推论：sn＋m－sn＝ 时间间隔． maT2 ，其中sn、sn＋m分别
表示第 n段和第 (n＋ m) 段相等时间内的位移， T为相等
第2节 匀变速直线运动规律及应用
一、匀变速直线运动： 在任意相等的时间内 速度的
变化 相等的直线运动，即 速直线运动．
加速度
恒定的变
二、匀变速直线运动规律(基本公式) 1．速度公式：v＝ v0＋at 2．位移公式：x＝ 3．速度平方公式：
1 2 v0t＋ at 2 v2－v02＝2ax
. . .
4．位移、平均速度关系式：x＝ 三、匀变速直线运动中的几个重要推论
【方法与知识感悟】求解匀变速直线运动问题的一般
解题步骤：
(1)首先确定研究对象，并判定物体的运动性质． (2)分析物体的运动过程，要养成画物体运动示意 (草 ) 图的习惯． (3)如果一个物体的运动包含几个阶段，就要分段分析， 各段交接处的速度往往是联系各段的纽带． (4)运用基本公式或推论等知识进行求解．
【方法与知识感悟】应用匀变速直线运动规律应注意的 问题
1．正负号的规定：匀变速直线运动的基本公式均是矢 量式，应用时要注意各物理量的符号，一般情况下，我 们规定初速度的方向为正方向，与初速度同向的物理量 取正值，反向的物理量取负值．
2．在匀变速直线运动中若物体先做匀减速直线运动， 减速为零后又反向做匀加速直线运动，全程加速度不 变．对这种情况可以将全程看做匀减速直线运动，应用 基本公式求解． 3．刹车类问题：匀减速直线运动，要注意减速为零后 停止，加速度变为零的实际情况，注意题目给定的时间 若大于刹车时间，计算时应以刹车时间为准．
例4 某传动装置的水平传送带以恒定的速度v0＝ 5 m/s运行，将一块底面水平的粉笔轻轻放在传送带 上，发现粉笔在传送带上留下一条长度L＝5 m的白 色划线，稍后，因传动装置受阻碍，传送带做匀减 速运动，其加速度的大小为5 m/s2.传动装置受阻后， 粉笔是否能在传送带上继续滑动？若能，它沿皮带 继续滑动的距离L′为多少？(g取10 m/s2)
比例法
逆向思维法 图象法
推论法 (Δx＝at2)
对一般的匀变速直线运动问题，若出 现相等的时间间隔问题，应优先考虑 用Δx＝at2求解
例 2 2011 年 7 月 23 日发生了震惊全国的 D301 次列车与 D3115 次列车追尾事故，我们应当吸取这一惨痛的教 训．假设事故发生前， D3115 次列车以 6 m/s 的速度沿 甬温线向福州方向匀速运动， D301 次列车以 66 m/s 的 速度也沿甬温线向福州方向行驶，已知 D301 次列车制 动后需要220 s才能停止运动． (1)D301次列车制动后产生的加速度为多大？ (2)要避免此次事故发生，则D301次列车至少应在距离 D3115次列车多远处开始制动减速？
【解析】(1)作 v－t 图线如图，设匀加速时间为 t1，则 t1 匀减速时间为 ，匀速时间为 130－ 4 5t1 1 2 5t1 ，依题意有： a1t1＋a1t1(130－ ) 4 2 4 1 t1 ＋ a1t1 ＝1 600，解得 t1＝8 s，t1＝ 2 4 200 s(舍去)，∴vm＝a1t1＝12.8 m/s. (2)当不存在匀速运动这个阶段时，所用时间最短， 5t t 设加速时间 t，减速时间则为 ，总时间则为 ，依题意 4 4 2 1 2 （a1t） 有： a1t ＋ ＝1 600，解得 t＝40 s，∴总时间为 2 2a2 50 s.
【解析】(1)设 100 m 比赛时加速所用时间为 t(以 s 为单位)，匀速运动的速度为 v(以 m/s 为单位)， 1 则有 vt＋(9.69－0.15－t)v＝100 ① 2 1 vt＋ (19.30－0.15－t)×0.96v＝200 ② 2 由①②得：t＝1.29 s ③ v＝11.24 m/s ④ v (2)设加速度大小为 a，则 a＝ ＝8.71 m/s2 ⑤ t
元贝驾考 元贝驾考2016科目一 科 目四 驾考宝典网 / 驾考宝典2016科目一 科目四
【方法与知识感悟】运动学公式较多，同一题目可以
选用不同公式解题．如何选择公式进行解题：首先要
牢记基本公式，理解推导公式；审题时弄清题中已知 哪些物理量；选择与已知量相关的公式进行解题．一 般情况下利用基本公式可以解答所有的运动学问题， 但灵活运用推导公式可使解题过程简单．在学习中应 加强一题多解的训练，加强解题规律的理解，提高自 己运用所学知识解决实际问题的能力，促进发散思 维．