下载文档原格式
第七章轴向拉伸和压缩一、内容提要轴向拉伸与压缩是杆件变形的基本形式之一，是建筑工程中常见的一种变形。
(一)、基本概念1. 内力 由于外力的作用，而在构件相邻两部分之间产生的相互作用力。
这里要注意产生内力的前提条件是构件受到外力的作用。
2. 轴力 轴向拉（压）时，杆件横截面上的内力。
它通过截面形心，与横截面相垂直。
拉力为正，压力为负。
3. 应力 截面上任一点处的分布内力集度称为该点的应力。
与截面相垂直的分量σ称为正应力，与截面相切的分量τ称为切应力。
轴拉（压）杆横截面上只有正应力。
4. 应变 单位尺寸上构件的变形量。
5. 轴向拉（压） 杆件受到与轴线相重合的合外力作用，产生沿着轴线方向的伸长或缩短的变形，称为轴向拉（压）。
6. 极限应力 材料固有的能承受应力的上限，用σ0表示。
7. 许用应力与安全系数 材料正常工作时容许采用的最大应力，称为许用应力。
极限应力与许用应力的比值称为安全系数。
8. 应力集中 由于杆件截面的突然变化而引起局部应力急剧增大的现象，称为应力集中。
(二)、基本计算1. 轴向拉（压）杆的轴力计算求轴力的基本方法是截面法。
用截面法求轴力的三个步骤：截开、代替和平衡。
求出轴力后要能准确地画出杆件的轴力图。
画轴向拉（压）杆的轴力图是本章的重点之一，要特别熟悉这一内容。
2. 轴向拉（压）杆横截面上应力的计算任一截面的应力计算公式 AF N =σ 等直杆的最大应力计算公式 AF max N max =σ 3. 轴向拉（压）杆的变形计算虎克定律 A E l F l N =∆εσE =或 虎克定律的适用范围为弹性范围。
泊松比 εε=μ'4. 轴向拉（压）杆的强度计算强度条件塑性材料：σma x ≤[σ] 脆性材料： σt ma x ≤[σt ]σ c ma x ≤[σc ]强度条件在工程中的三类应用（1）对杆进行强度校核在已知材料、荷载、截面的情况下，判断σma x是否不超过许用值[σ]，杆是否能安全工作。
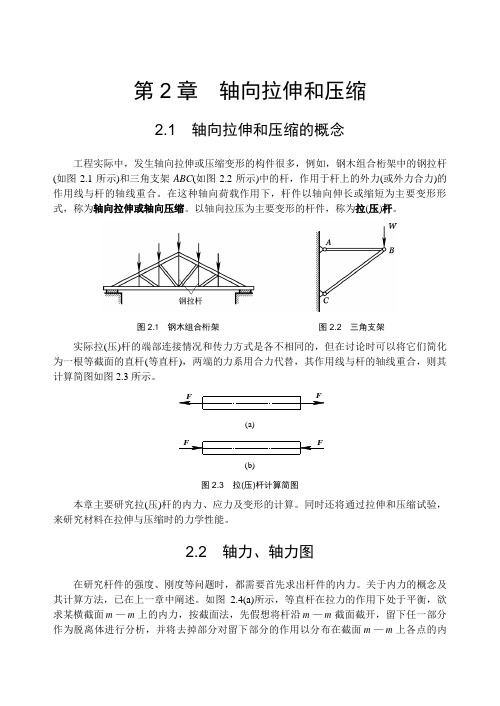
第2章 轴向拉伸和压缩2.1 轴向拉伸和压缩的概念工程实际中，发生轴向拉伸或压缩变形的构件很多，例如，钢木组合桁架中的钢拉杆(如图2.1所示)和三角支架ABC (如图2.2所示)中的杆，作用于杆上的外力(或外力合力)的作用线与杆的轴线重合。
在这种轴向荷载作用下，杆件以轴向伸长或缩短为主要变形形式，称为轴向拉伸或轴向压缩。
以轴向拉压为主要变形的杆件，称为拉(压)杆。
图2.1 钢木组合桁架 图2.2 三角支架实际拉(压)杆的端部连接情况和传力方式是各不相同的，但在讨论时可以将它们简化为一根等截面的直杆(等直杆)，两端的力系用合力代替，其作用线与杆的轴线重合，则其计算简图如图2.3所示。
F (b)(a)(a)(b)(a)(b)图2.3 拉(压)杆计算简图本章主要研究拉(压)杆的内力、应力及变形的计算。
同时还将通过拉伸和压缩试验，来研究材料在拉伸与压缩时的力学性能。
2.2 轴力、轴力图在研究杆件的强度、刚度等问题时，都需要首先求出杆件的内力。
关于内力的概念及其计算方法，已在上一章中阐述。
如图 2.4(a)所示，等直杆在拉力的作用下处于平衡，欲求某横截面m —m 上的内力，按截面法，先假想将杆沿m —m 截面截开，留下任一部分作为脱离体进行分析，并将去掉部分对留下部分的作用以分布在截面m —m 上各点的内第2章 轴向拉伸和压缩9力来代替(如图 2.4(b)所示)。
对于留下部分而言，截面m —m 上的内力就成为外力。
由于整个杆件处于平衡状态，杆件的任一部分均应保持平衡。
于是，杆件横截面m —m 上的内力系的合力(轴力)N F 与其左端外力F 形成共线力系，由平衡条件0xF=∑，N 0F F -=得 N F F =(b)(a)mmNF }FF (a)(b)(a)m m }{FFFNF(b) (b)(a)mm NF }{FF F(c)图2.4 轴力N F 为杆件任一横截面上的内力，其作用线与杆的轴线重合，即垂直于横截面并通过其形心。
