一个神经网络控制系统的稳定性判据的方法
- 格式:doc
- 大小:1.25 MB
- 文档页数:17

基于神经网络的电力系统安全稳定性预测与控制近年来,随着电力系统规模的不断扩大和新能源的不断发展,电力系统的可靠性和稳定性越来越受到重视。
而神经网络技术,作为一种模拟人脑神经系统的计算模型,已经被广泛应用于电力系统安全稳定性预测与控制领域。
首先,我们来介绍一下电力系统安全稳定性的定义。
电力系统安全稳定性是指在电力系统各种扰动(如瞬时故障、负荷扰动、天气变化等)作用下,系统继续保持其正常工作状态的能力,以及在发生故障等意外情况时,系统尽可能迅速地恢复到正常工作状态的能力。
因此,电力系统安全稳定性预测与控制就是指通过各种手段,对电力系统的运行状态进行监控和预测,并采取相应的控制措施,在最小的损失下保证电力系统的安全稳定运行。
在电力系统的安全稳定性预测与控制领域中,神经网络技术具有独特的优势。
传统的电力系统安全稳定性预测模型往往需要大量的经验和数据,而且往往只能考虑相对简单的情况下的预测,而神经网络技术则可以通过学习大量的历史数据和经验,来预测并适应不同的运行条件和扰动情况。
其次,我们来分析一下基于神经网络的电力系统安全稳定性预测与控制的具体实现方法。
首先,需要建立一个合适的神经网络模型。
这个神经网络模型一般包括输入层、隐藏层和输出层三个部分。
输入层主要是对电力系统运行状态和扰动进行输入,隐藏层则是通过神经网络的非线性映射关系,来建立电力系统运行状态和扰动之间的关系,输出层则是输出电力系统的安全稳定性指标或控制指令。
接着,需要根据实际情况收集大量的历史数据和经验,并对这些数据进行预处理和特征提取。
这些历史数据和经验可以包括电力系统运行数据、天气数据、负荷数据等。
我们可以通过对这些数据进行统计分析、特征提取和数据清洗等操作,来为神经网络提供更准确和有效的输入数据。
然后,需要对神经网络进行训练和调整,以提高其预测和控制的准确度和稳定性。
神经网络的训练一般采用反向传播算法或其他类似的优化算法来实现。
在训练的过程中,需要根据具体的实验结果和误差分析,对神经网络的结构和参数进行调整和优化,来提高其预测和控制性能。

神经元网络的稳定性分析神经元网络是生物学的一个重要领域,经过多年的研究,我们已经逐渐掌握了大量生物神经元网络的特性和运作机制。
神经元的连接具有高度的稳定性,这是神经元网络能够长时间保存信息的基础。
然而,由于生物神经元网络的复杂性和不确定性,研究其稳定性仍然存在困难。
本文旨在探讨神经元网络的稳定性分析。
1. 神经元网络的模型神经元网络是由神经元节点和它们之间的连接构成的。
神经元节点是生物体内信息传递的基本单元,其内部由细胞膜、胞质和核等构成。
而神经元之间的连接则是通过突触实现的。
在神经元网络中,各个节点之间的信号传递以及连接的形式均对网络的稳定性产生影响。
2. 神经元网络的稳定性分析是指在一定的输入和自身参数下,网络的响应是否会收敛到一定的状态。
通常情况下,稳定性的分析可以通过计算神经元网络的特征值或计算微分方程的解析解来实现。
此外,还可以使用神经元网络的仿真模拟来分析其稳定性。
3. 神经元网络的稳定性机制神经元网络的稳定性机制主要包括同步、决策和适应性。
同步机制是指网络中的神经元具有相似的行为,从而使得整个网络产生同步现象。
决策机制是指网络中的神经元会根据一定的规则进行判断和决策。
适应性机制是指网络中的神经元在不同的环境和刺激下会进行适应性调节。
4. 神经元网络稳定性分析的应用神经元网络稳定性分析是神经科学、计算机科学和工程学等众多领域的重要应用研究方向。
其中,神经科学领域的研究主要集中在生物神经元网络的模拟和仿真,以及神经退行性疾病的诊断和治疗等方面。
计算机科学领域的研究则主要关注基于神经元网络的智能系统和算法。
在工程学领域,神经元网络稳定性分析也被广泛应用于控制系统、电力系统、交通系统等领域。
总结:神经元网络是生物体内信息传递的基本单元,其稳定性分析是神经科学、计算机科学和工程学等众多领域的重要应用研究方向。
神经元网络的稳定性分析主要包括模型构建、参数计算、信号仿真等重要环节。
除此之外,神经元网络稳定性机制还包括同步机制、决策机制和适应性机制等方面。


稳定性分析与控制器设计一、稳定性分析稳定性是控制系统分析和设计的一个重要指标。
在控制系统中,稳定性分析主要是用来判断系统在不同参数、边界条件和干扰下的稳定性问题。
控制系统的稳定性主要包括稳定性的定义、分析方法、稳定性分析的应用。
1. 稳定性的定义在控制系统中,稳定性是指系统在输入和参数满足一定条件时,输出信号不会无限增长,而是趋于稳定的状态。
如果系统的输出信号一直增长,系统就失去了稳定性。
2. 稳定性分析方法稳定性分析在控制系统中是非常重要的,主要的分析方法有:(1)特征根法特征根法又称为极点法,是判断系统稳定性的一种方法。
通过计算系统的特征方程,可以得到系统的特征根,如果特征根都在稳定的区域内,则系统是稳定的。
(2)频域法频域法是一种通过分析系统在不同频率下的响应特性来判断稳定性的方法。
通过分析系统在不同频率下的幅频特性、相频特性和群延时,可以得出系统的稳定性特性。
(3)时域法时域法是一种通过分析系统在时间轴上的响应特性来判断稳定性的方法。
通过分析系统的阶跃响应、冲击响应等,可以判断系统的稳定性。
3. 稳定性分析的应用(1)控制系统设计在控制系统设计中,稳定性分析是非常重要的。
在设计控制系统时需要根据系统的特性,选取合适的系统结构,选择合适的控制算法,以保证系统的稳定性。
(2)控制系统维护在控制系统维护中,稳定性分析也是非常重要的。
通过对控制系统的稳定性进行分析,可以判断系统是否存在故障,以及系统的稳定性是否受到影响。
二、控制器设计控制器是控制系统中的一个重要组成部分。
控制器的设计是控制系统设计的核心之一。
控制器设计的目标是使系统具有合适的控制性能,如精度、响应速度、稳定性等。
1. PID控制器PID控制器是控制系统中常见的一种控制器。
PID控制器的主要作用是根据系统的误差信号,计算出输出信号,从而改变系统的控制量。
PID控制器的三个部分分别是比例、积分、微分控制器,输在控制量的线性组合。
2. 模糊控制器模糊控制器是一种基于模糊逻辑的控制器,可以用来处理一些非线性、模糊的控制问题。


控制系统稳定性判据控制系统稳定性是控制工程中一个重要而关键的问题。
对于一个控制系统来说,稳定性是指当系统受到扰动时,系统输出能够以有限的幅度、有限的时间内收敛到期望的状态。
因此,对于控制系统的稳定性进行判断和分析是非常必要的。
在控制系统的稳定性判据中,有几个重要的指标被广泛应用。
这些判据不仅可以用于传统的模拟控制系统,也可以用于现代的数字控制系统。
第一个判据是零极点位置判据。
零极点分布是控制系统的重要性质之一,它直接关系到系统的稳定性。
当系统的极点全部位于左半平面时,即全部具有负的实部,系统就是稳定的。
如果出现了至少一个极点位于右半平面,那么系统就是不稳定的。
通过计算系统的传递函数,可以获得系统的零极点信息,从而进行稳定性判断。
第二个判据是根轨迹判据。
根轨迹是由系统的传递函数所决定的一条曲线。
当系统的开环传递函数的参数发生变化时,根轨迹会随之变化。
根据根轨迹的形状和位置,可以判断系统的稳定性。
如果根轨迹全部位于左半平面,系统就是稳定的。
如果根轨迹有点位于右半平面,那么系统就是不稳定的。
通过绘制根轨迹图,可以直观地了解系统的稳定性。
第三个判据是频率响应判据。
频率响应是指系统输出对输入信号频率变化的响应情况。
通常采用频率响应曲线来表示系统的特性。
对于稳定系统来说,频率响应曲线应该是有界的,即曲线不会出现无限增长或无限衰减的情况。
当频率响应曲线无界时,系统就是不稳定的。
通过分析频率响应曲线,可以评估系统的稳定性。
另外一个重要的判据是李雅普诺夫稳定性判据。
李雅普诺夫稳定性判据是基于系统的能量函数进行判断的。
如果系统的能量函数对时间的导数为负,则系统是稳定的。
通过构造适当的李雅普诺夫函数,可以进行稳定性判断。
综上所述,控制系统稳定性判据涵盖了零极点位置判据、根轨迹判据、频率响应判据和李雅普诺夫稳定性判据。
这些方法可以有效地进行控制系统的稳定性分析和判断。
在实际工程中,一般会综合运用这些判据来确保控制系统的稳定性,从而保证系统的正常运行。

神经元网络模型及其稳定性分析神经元网络模型是神经科学领域中的一个重要研究方向。
该模型通过对神经元及其之间的相互作用关系进行建模,可以更加深入地了解神经系统的运作机理,并对神经系统的许多重要现象进行解释和预测。
本文将从神经元网络模型的基础入手,介绍神经元的动力学行为和网络拓扑结构;然后从稳定性分析的角度探讨神经元网络的同步和异步行为,讨论网络的稳定性以及如何设计控制策略来维持稳定性。
一、神经元的动力学行为神经元是神经系统的基本单位,其通过神经突触与其他神经元之间相互作用。
神经元的动力学行为可以被模拟成一些基本的数学方程,最常用的是Hodgkin-Huxley模型。
该模型描述了神经元膜电势的变化及其影响因素,包括细胞膜的电容、离子通道的电导和电流等。
在Hodgkin-Huxley模型中,神经元的膜电势随着时间的推移而发生变化。
初试时,神经元的膜电势为静息电位,当该神经元受到外部刺激时,膜电势将会随之变化。
变化的大小和方向取决于外部刺激的强度和类型,以及神经元本身的特征参数。
在经历一个周期之后,神经元的膜电势会重新返回静息电位。
神经元的动力学行为还有其他的模型,包括FitzHugh-Nagumo 模型和Izhikevich模型等。
这些模型可以用来描述神经元的不同类型及其行为,如兴奋型和抑制型神经元,周期性放电和临界放电等。
二、神经元网络的拓扑结构神经元网络的拓扑结构是指神经元之间的连接方式和关系。
不同的拓扑结构对神经网络的动态行为产生了不同的影响。
最简单的神经元网络拓扑结构是全连接结构,即所有神经元之间都有相互作用。
这种拓扑结构可以有效地传递信息,但同时也容易产生不稳定的行为,如神经网络的自发震荡。
另一种常见的拓扑结构是层次结构,即神经元按照层次分组。
类似于神经系统的分层结构,这种网络拓扑结构的优点是具有层次性和稳定性,但也存在信号传输效率低和信息处理能力不足等问题。
还有一些其他的神经元网络拓扑结构,如小世界网络、无标度网络等。

网络控制系统的稳定性分析1、引言人类社会是不断向前发展的,促使这种发展最大的动力莫过于人类的创造力,人类利用自己这种特有的能力在改造着自然,同时也在不断改变着人类社会和人们的思维方式。
正是由于人类在自身发展过程中不断的创造和探索,特别是随着科学技术的不断发展,这种变革的速度也越来越快。
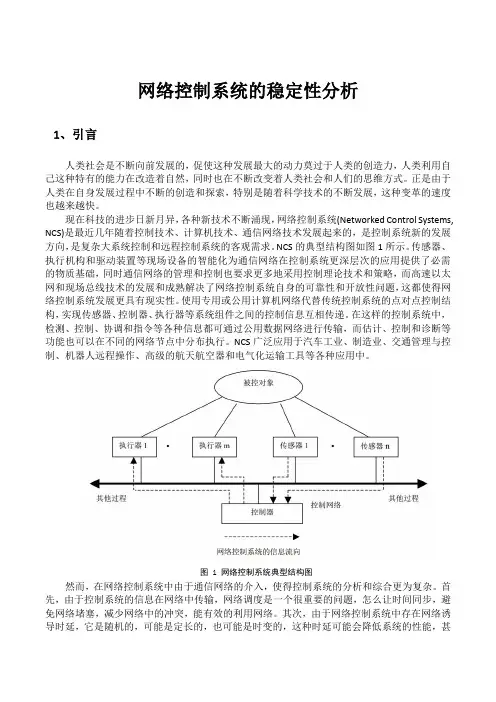
现在科技的进步日新月异,各种新技术不断涌现,网络控制系统(Networked Control Systems, NCS)是最近几年随着控制技术、计算机技术、通信网络技术发展起来的,是控制系统新的发展方向,是复杂大系统控制和远程控制系统的客观需求。
NCS的典型结构图如图1所示。
传感器、执行机构和驱动装置等现场设备的智能化为通信网络在控制系统更深层次的应用提供了必需的物质基础,同时通信网络的管理和控制也要求更多地采用控制理论技术和策略,而高速以太网和现场总线技术的发展和成熟解决了网络控制系统自身的可靠性和开放性问题,这都使得网络控制系统发展更具有现实性。
使用专用或公用计算机网络代替传统控制系统的点对点控制结构,实现传感器、控制器、执行器等系统组件之间的控制信息互相传递。
在这样的控制系统中,检测、控制、协调和指令等各种信息都可通过公用数据网络进行传输,而估计、控制和诊断等功能也可以在不同的网络节点中分布执行。
NCS广泛应用于汽车工业、制造业、交通管理与控制、机器人远程操作、高级的航天航空器和电气化运输工具等各种应用中。
图 1 网络控制系统典型结构图然而,在网络控制系统中由于通信网络的介入,使得控制系统的分析和综合更为复杂。
首先,由于控制系统的信息在网络中传输,网络调度是一个很重要的问题,怎么让时间同步,避免网络堵塞,减少网络中的冲突,能有效的利用网络。
其次,由于网络控制系统中存在网络诱导时延,它是随机的,可能是定长的,也可能是时变的,这种时延可能会降低系统的性能,甚至导致系统的不稳定,其次,在网络中传输的数据包还可能在传输中丢失,在多包传输中可能有数据包乱序等问题,这也是导致系统性能下降甚至不稳定的因素。

具时变时滞的神经网络的稳定性分析在研究神经网络系统中,我们经常会采用一些常用的方法和技巧,比如说:线性矩阵不等式技巧、Lyapunov稳定性的理论都是比较基本的技巧。
对于随机神经网络的稳定性分析中,随机分析技巧也是一个必须要掌握的。
同时也要巧妙的运用不等式放缩技巧和处理不等式的一些引理等,合理并灵活的运用这些基本的技巧,能够降低论文结论的保守性。
在这篇论文中,主要是讨论了两类神经网络的稳定性问题。
一类是对时变时滞神经网络的稳定性判定,另一类是对具有时变时滞和分布时滞的随机神经网络的稳定性进行分析。
并分别得到了这两类神经网络系统的稳定性判定的结论以及改进条件。
这篇文章的主要研究成果如下:首先对单时滞的神经网络模型的稳定性给出了推断,然后将单时滞的情况扩张为两个的情况。
对于两个时滞的神经网络的稳定性的判定在论文中主要讨论了两种情况,一种是针对两个时滞在限制条件0≤d<sub>11</sub>≤d<sub>1</sub>(t)≤d<sub>12</sub>,d<sub>1</sub>(t)≤μ<sub>1</sub>和0≤d<sub>21</sub>≤d<sub>2</sub>(t)≤d<sub>22</sub>, d<sub>2</sub>(t)t)≤μ<sub>2</sub>下的稳定性分析,另一种是针对上面限制条件当d<sub>11</sub>=d<sub>21</sub>=0的情况下的稳定性进行了分析。
论文中讨论的两个系统在判定李雅普洛夫泛函上界时考虑了时变时滞及其上下界对其的影响,而不仅仅是考虑其时变时滞下界为零的情况。

判断系稳定性的方法一、稳定性判据(时域)1、赫尔维茨判据系统稳定的充分必要条件:特征方程的各项系数全部为正 将系统特征方程各项系数排列成如下行列式;当主行列式及其对角线上的各子行列式均大于零时,即A = a >01 n -1a a >0A =n -n -3 2 a a n n -2a a an -n -3 n -5 A = a a a >0 3 n n -2 n -4a an -1 n -3A > 0n则方程无正根,系统稳定。
赫尔维茨稳定判据之行列式直接由系数排列而成,规律简单明 确,使用也比较方便,但是对六阶以上的系统,很少应用。
例;若已知系统的特征方程为S 4+8S 3+18S 2+16S +5=0试判断系统是否稳定。
解:系统特征方程的各项系数均为正数。
81600人11850an -1anan -3an -2an -5an -A= 0a a n• nn -20 00000 00 00 :00a 01aa20000实用标准1A二08160根据特征方程,列写系统的赫尔维茨行列式。
01185由△得各阶子行列式;A1 =8=8 >08 16=128 >0A2 —1 188 1 6 0A=1 18 5=1728>030 8 16A4=A=8690>0各阶子行列式都大于零,故系统稳定。
2、劳思判据(1)劳思判据充要条件:A、系统特征方程的各项系数均大于零,即a>0;iB、劳思计算表第一列各项符号皆相同。
满足上述条件则系统稳定,否则系统不稳定,各项符号变化的次数就是不稳定根的数目。
(2)劳思计算表的求法:A、列写劳思阵列,并将系统特征方程的系数按如下形式排列成列首两行,即:s n an anananS n-1 a a a an n—n—n S n— b b b b1 2 3 4 s n-3 c c c c1 2 3 4S2 u1 u 2S1 v1 S0 wB 、计算劳思表b = 1 aa —aa —n~1_n~2n_n~3- an -1b = 2 aa —aa —n~1~n_4n_n~5- an -1b = 3aa —aa—n~1_n~6n_n~7a系数b 的计算要一直进行到其余的b 值都等于零为止。
神经元网络的稳定性研究神经元网络是一种广泛存在于生物和非生物领域的网络结构。
在人类神经系统中,神经元网络是大脑思维和感知处理的基础,而在人工智能领域,神经元网络已经广泛应用于语音识别、图像识别、自然语言处理等领域。
在神经元网络中,神经元之间的连接具有动态性和非线性性,这就使得神经元网络的稳定性成为了一个非常重要的问题。
神经元网络稳定性的相关研究早已有之,而其中一类常用的稳定性研究方法是线性稳定性分析。
线性稳定性分析是一种通过数学方法分析神经元网络是否稳定的方法,其基本思想是对神经元网络进行微小的扰动分析,通过分析扰动的演化轨迹来判断神经元网络的稳定性。
然而,在实际应用中,神经元网络的非线性特性使得线性稳定性分析方法显得比较乏力。
因此,近年来,研究人员提出了一系列新的稳定性分析方法,以更好地解决神经元网络稳定性问题。
其中一种比较新的稳定性分析方法是解析稳定性分析方法,其基本思想是直接对神经元网络的动力学系统进行分析,通过解析方程来判断系统的稳定性。
这种方法可以更直观地理解神经元网络的稳定性问题,且在数据抽样较少时也具有更好的适应性。
另一种比较有代表性的稳定性分析方法是基于李雅普诺夫稳定性理论的非线性稳定性分析方法。
该方法是一种综合性的稳定性研究方法,其基本思想是通过寻找适当的李雅普诺夫函数,建立非线性李雅普诺夫方程,并对方程的稳定性进行分析。
通过该方法,研究人员可以更全面地了解神经元网络的稳定性特性。
除了上述方法外,还有一些新的稳定性研究方法正在不断涌现,这些方法不仅能够更加全面地解决神经元网络的稳定性问题,而且还能够引发研究人员对神经元网络稳定性的更深入探讨。
总之,神经元网络稳定性是神经元网络领域中的一个重要问题,而各种新的稳定性研究方法的涌现也在推动神经元网络稳定性研究的不断深入。
未来,我们可以期待更多的全面、深入的神经元网络稳定性研究成果的涌现。
基于不等式的几类神经网络稳定性判据的开题报告1. 研究背景神经网络是一种由神经元相互连接而成的计算模型,又称为人工神经网络。
近年来,神经网络在图像识别、语音识别、自然语言处理等领域取得了广泛应用。
然而,神经网络存在稳定性问题,即神经网络的输出结果不稳定,容易受到数据噪声、初始状态等因素的影响,导致网络的鲁棒性较差。
为了解决神经网络的稳定性问题,学者们提出了许多稳定性判据。
其中,基于不等式的稳定性判据较为常见,采用数学不等式来对网络的稳定性进行分析和判定。
这类判据具有判定精度高、计算速度快等优点,已广泛应用于神经网络的设计和优化中。
2. 研究目的本论文旨在研究基于不等式的神经网络稳定性判据,分析其应用范围、稳定性分析原理和优缺点,探究其在神经网络设计中的应用。
3. 研究内容研究内容包括以下几个方面:(1)基于不等式的神经网络稳定性判据的理论分析和研究,包括Lyapunov稳定性判据、多项式不等式稳定性判据、线性矩阵不等式稳定性判据等。
(2)采用MATLAB等数值计算工具,对各类神经网络稳定性判据进行仿真实验,分析其稳定性判定精度和计算效率。
(3)探究基于不等式的神经网络稳定性判据在神经网络设计中的应用,包括网络结构设计、参数优化等方面,比较其与其他稳定性判据的优劣。
(4)以某个典型神经网络应用领域为例,如图像识别、语音识别等,探索基于不等式的神经网络稳定性判据在该领域中的应用和优化方案。
4. 研究意义该论文的研究可为神经网络的稳定性分析和优化提供新思路和方法,有利于改善神经网络的鲁棒性和性能表现,同时也可扩展基于不等式的稳定性判据的应用范围,促进其在工程实践中的推广和应用。
控制系统的稳定性分析方法控制系统的稳定性是指在不同输入情况下,系统输出是否会趋于稳定状态。
稳定性分析在控制系统设计和优化中起着重要的作用。
本文将介绍几种常用的控制系统稳定性分析方法。
一、传递函数法传递函数法是一种常用的控制系统稳定性分析方法。
传递函数是控制系统输入与输出之间的关系表示,通过对传递函数进行分析,可以得到系统的特性以及稳定性。
传递函数法的具体步骤如下:1. 将系统表示为传递函数的形式,传递函数通常表示为H(s),其中s为复变量。
2. 利用传递函数的特性,计算系统的极点和零点。
极点是传递函数的分母为零的根,零点是传递函数的分子为零的根。
3. 分析系统的极点位置以及极点的实部和虚部。
根据极点的位置可以判断系统的稳定性。
二、根轨迹法根轨迹法是一种图形法,通过绘制传递函数的根轨迹图来分析系统的稳定性。
根轨迹图是传递函数极点随参数变化过程中的轨迹。
根轨迹法的具体步骤如下:1. 将传递函数表示为参数的函数形式。
2. 寻找参数的变化范围,通常选择参数的范围使得系统保持稳定。
3. 计算传递函数的极点随参数变化的轨迹,将其画在复平面上。
4. 根据根轨迹图的形状和位置判断系统的稳定性。
三、Nyquist稳定判据Nyquist稳定判据是通过分析控制系统的传递函数在Nyquist轨迹上的特性来判断系统的稳定性。
具体步骤如下:1. 绘制传递函数的Nyquist轨迹。
2. 通过Nyquist轨迹上的幅角和极点位置判断系统的稳定性。
如果幅角为负且极点位于原点右侧,则系统稳定。
四、Bode图法Bode图法是一种常用的频域分析方法,通过绘制传递函数的幅频特性图和相频特性图来分析系统的稳定性。
具体步骤如下:1. 将传递函数表示为分子和分母的形式。
2. 计算传递函数在频域上的幅频特性和相频特性。
3. 根据幅频特性和相频特性的特征判断系统的稳定性。
以上是几种常用的控制系统稳定性分析方法。
在实际应用中,根据系统的特点和需求,选择合适的方法进行稳定性分析。
生物神经网络的稳定性分析生物神经网络是一类模拟生物学中生物神经系统的计算机模型,在人工智能领域中有着广泛的应用。
与传统计算机程序所采用的算法不同,生物神经网络是基于神经元之间的联系和通信机制进行计算的。
因而,相较于传统程序,生物神经网络有着更加优异的性能,在诸多领域中得到了广泛运用。
随着生物神经网络的应用越来越广泛,对其稳定性的分析和评估也显得尤为必要。
在生物神经网络的实际应用中,其稳定性直接决定了其在系统性任务中的可靠性和鲁棒性。
因此,对生物神经网络的稳定性进行分析和评估,可以进一步改进生物神经网络的设计和优化,提高其稳定性和可靠性。
生物神经网络的稳定性分析可以从多个方面入手。
首先,我们可以从结构上对生物神经网络的稳定性进行考察。
生物神经网络的稳定性和其结构紧密相关,因为网络的结构组成了神经元之间的联系和通信路径,这直接影响了神经元之间的交流和信息处理能力。
通过分析生物神经网络中节点之间的连接方式和连接强度等结构属性,可以评估网络的稳定性。
例如,在一些基于生物神经网络的识别系统中,连接强度同步化策略的应用可以提高网络的稳定性,保证了网络的可靠性和鲁棒性。
除了结构上的分析,我们还可以利用动力学和控制理论的方法对生物神经网络的稳定性进行探究。
生物神经网络是一个动态系统,因此动力学是一种常用的分析方法。
通过对生物神经网络的动态行为进行分析,我们可以更全面地了解网络的稳定性。
例如,在生物神经网络中,每个神经元都呈现出周期性振荡的神经活动,这些活动的稳定性可以反映网络的稳定性。
另一方面,控制理论的方法也可以用于生物神经网络的稳定性分析中。
通过设计相应的控制策略,我们可以控制生物神经网络的稳定性,提高网络的可靠性和鲁棒性。
除了结构、动力学和控制理论等方面的分析,我们还可以从数据集的角度考虑生物神经网络的稳定性。
在实际应用中,我们通常会使用大量的数据集进行生物神经网络的训练,这些数据集的质量和数量会影响网络的稳定性。
一个神经网络控制系统的稳定性判据的方法摘要:本文讨论了基于李雅普诺夫方法分析神经网络控制系统的稳定性。
首先,文章指出神经网络系统的动态可以由视为线性微分包含(LDI)的一类非线性系统表示。
其次,对于这类非线性系统的稳定条件是推导并利用单神经系统和反馈神经网络控制系统的稳定性分析。
此外,用图形方式显示非线性系统参数位置的这种参数区域表示方法(PR)提出了通过引入新的顶点和最小值的概念。
从这些概念上可以推导出一个能有效地找到李雅普诺夫函数的重要理论。
单个神经的神经系统的稳定性标准时由参数区域来决定的。
最后,分析了包括神经网络设备和神经网络控制器为代表的神经网络控制系统的稳定性。
1.介绍最近,已经有很多关于神经网络的自适应控制的研究,例如:在机器人领域,川户提出了一种使用的学习控制系统,控制系统的一项关键指标就是他的稳定性,然而分析像基于神经网络的控制系统这样的非线性系统的稳定性是非常难的。
Nguyen和Widrow 设计了一种在电脑上模拟卡车拖车的神经网络控制器。
这个设计主要分为两大部分。
第一部分是通过神经网络来学习设备的动态,这一部分被称为“仿真器”。
第二部分是通过最小化的性能函数来计算出神经网络网络控制器的参数(权值)。
但是,他们没有分析神经网络控制系统的稳定性。
一项稳定性分析标准工具讲有利于神经网络控制应用到许多实际问题中。
最近,这类可被视为线性微分包含(LDI)的非线性系统的稳定条件已经被作者推导出来,再引用的[7][8]中讨论了。
其中一项保证LDI稳定的充分条件与李雅普诺夫稳定性定理是相一致的。
本文应用LDI的稳定条件和Nguyen与Widrow的方法来分析神经网络系统的稳定性。
文中选取了一种代表神经网络状态的方法。
此外,我们表明包含由近似于神经网络设备和神经网络控制器组成的神经网络反馈控制系统也可以分析神经网络是否能稳定。
这意味着,本文提出的稳定条件可以分析神经网络反馈控制系统。
本文的构成如下:第二节展示了一种文中的神经网络系统。
摘要:本文讨论了基于李雅普诺夫方法分析神经网络控制系统的稳定性。
首先,文章指出神经网络系统的动态可以由视为线性微分包含(LDI)的一类非线性系统表示。
其次,对于这类非线性系统的稳定条件是推导并利用单神经系统和反馈神经网络控制系统的稳定性分析。
此外,用图形方式显示非线性系统参数位置的这种参数区域表示方法(PR)提出了通过引入新的顶点和最小值的概念。
从这些概念上可以推导出一个能有效地找到李雅普诺夫函数的重要理论。
单个神经的神经系统的稳定性标准时由参数区域来决定的。
最后,分析了包括神经网络设备和神经网络控制器为代表的神经网络控制系统的稳定性。
1.介绍最近,已经有很多关于神经网络的自适应控制的研究,例如:在机器人领域,川户提出了一种使用的学习控制系统,控制系统的一项关键指标就是他的稳定性,然而分析像基于神经网络的控制系统这样的非线性系统的稳定性是非常难的。
Nguyen和Widrow 设计了一种在电脑上模拟卡车拖车的神经网络控制器。
这个设计主要分为两大部分。
第一部分是通过神经网络来学习设备的动态,这一部分被称为“仿真器”。
第二部分是通过最小化的性能函数来计算出神经网络网络控制器的参数(权值)。
但是,他们没有分析神经网络控制系统的稳定性。
一项稳定性分析标准工具讲有利于神经网络控制应用到许多实际问题中。
最近,这类可被视为线性微分包含(LDI)的非线性系统的稳定条件已经被作者推导出来,再引用的[7][8]中讨论了。
其中一项保证LDI稳定的充分条件与李雅普诺夫稳定性定理是相一致的。
本文应用LDI的稳定条件和Nguyen与Widrow的方法来分析神经网络系统的稳定性。
文中选取了一种代表神经网络状态的方法。
此外,我们表明包含由近似于神经网络设备和神经网络控制器组成的神经网络反馈控制系统也可以分析神经网络是否能稳定。
这意味着,本文提出的稳定条件可以分析神经网络反馈控制系统。
本文的构成如下:第二节展示了一种文中的神经网络系统。
第三节给出了LDI的稳定条件。
第四节提出了一个以图形方式显示LDI参数的参数区域表示方法(PR)并推导出一个有效导出李雅普诺夫函数的重要定理。
第五节阐述了神经网络系统的LDI表示方法。
第六节介绍了用PR方法表示单神经系统和神经网络反馈系统的稳定标准。
2.神经控制系统假设一个神经网络函数是x(k + I) =P( x ( k )u, (k)),他的神经网络反馈控制系统的函数是:x(k + 1) = P(x(k),u(k)) 和u(k) = C(x(k)),其中x(k)是实属范围内的状态向量,u(k)是实属范围内的输入向量。
P和C分别表示神经网络设备和神经网络控制器的非线性传递函数。
如图1,显示了一个单一的神经网络系统和神经网络反馈控制系统。
假设每个神经元的输出函数f ( u )都是可微分的,在k > 0的情况下,我们可以得到:f ( 0 ) = 0,f(v)∈[-k,k],对于所有的v都成立此外,假设所有的传递权重都已经被学习方法所确定了,例如反向传播神经网络在神经网络控制稳定性分析之前。
在一个单一的神经网络系统中,因为我们分析神经网络系统的动态平衡稳定性,所以设定. u(k) = 0。
图1.神经网络:(a )单一神经网络,(b )反馈神经网络3.一类非线性系统的稳定条件让我们分析以下这类非线性系统1x(k + 1) = ((k))x(k),((k))=(())ri i i h k =∑A z A z z A (1)其中r 是一个正实数,在z (k )是一个向量,同时:T12()[n x k x k x k x k =(),(),…,()],1()~()n x k x k 是状态变量。
1(())((k))=1.ri i i h z k h z =≥0, ∑注3.1:像公式(1)代表的这类非线性系统我们可以把它看做LDI 。
大多数情况,对于LDI 的特性,我们可以用代替(())i h z k ,因此我们后面用()i h k ()i h k 来表示。
这类系统还包含了在模糊控制领域中流行的Takagi 和Sugeno 的模型,所以下面的稳定性条件 讨论也适用于模糊控制。
下面给出了一个满足公示(1)的稳定条件。
定理3.1:公式(1)描述的LDI 的稳定平衡在大范围内渐进稳定的条件是存在一个通用正定矩阵满足:A P T i i -<A P 0 (2)对于i=1,2,···,r 成立。
这个定理简化了李雅普诺夫稳定性定理对于r=1是的线性离散系统的情况。
当然,定理3.1给出了一个是公式(1)的系统稳定的充分条件。
我们可以直观的认为当所有的i A 都是稳定矩阵,公式(1)的系统是全局稳定的。
但是,一般情况下这是不正确的,因为公式(1)的系统不总是大范围渐进稳定的,即使所有的i A 都是稳定矩阵。
为了使公式(1)代表的系统稳定,我们必须找到一个通用矩阵P 满足A P Tii -<A P 0,对于所有的 i 都成立。
通过研究我们已经可以找到这样的通用正定矩阵P 。
接下来,我们就要给出这个满足公式(2)的正定矩阵P 存在的必要条件。
定理3.2;假设存在一个稳定矩阵矩阵i A ,其中i=1,2,···,r 。
存在一个正定矩阵P 使得A P T i i -<A P 0,对于所有 i 都成立,则i A A j为稳定矩阵,其中i ,j=1,2,···,r ,。
反过来,这个定理说明:只要i A A j中存一个不是稳定矩阵,就不存在满足公示(2)的矩阵P 。
4. 参数区域表示方法(PR )我们提出对于公示(1)系统的PR 的概念。
PR 可以通过图表显示出LDI 的参数。
下面是两个例子。
例4.1: 让我们分析下面的LDI (LDI-1)31(1)()()i i i k h k x k =+=∑x A其中:31T 123()1,0.10.10.30.10.10.3101010()()[()(1)],,,i i i h h k k k x k x k ==≥0,=-⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑x A A A .这个LDI 系统也可以表示为:∑=-+=+31)}1()(){()1(i i i i k x b k x a k h k x其中:a1 = 0.1,bl = 0.1, a2 = 0.3,b2 = 0.1, a3 = 0.1,b3 = 0.3.图2显示了LDI 的参数区域数值,其中其中点1,2,3分别代表了321A A A ,, 例4.2:让我们假设另一个LDI 系统LDI-2,∑==+51)()()1(x i i k k h k x A i ,其中:,0115.015.0,012.02.0,013.01.0,011.03.0,011.01.0)],1()([)(,1)(,0)(543251⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=-==≥∑=A A A A A x 1T k x k x k k h k h i i i 相似的,LSI 可以等效为:∑=-+=+51)}1()(){()1(i i i i k x b k x a k h k x ,此时:a1= 0.1, bl = 0.1, a2 = 0.3, b2 = 0.1, a3 = 0.1, b3 = 0.3, a4 = 0.2, b4 = 0.2, a5 = 0.15, b5 = 0.15.这个LDI 系统的区域参数表示如图3所示。
我们发现,尽管图2和图3中区域参数的区域是相同的的,但是LDI-1和LDI-2区域参数是不同的。
在图2中,每个点正好对应一个顶点。
但是在图3中,点1,2,3构成了参数区域,而点4,5包含在区域内。
注解4.1: 在2*2的矩阵A 中,PR 一般是四维的,因为在每个这样的矩阵中都有四个要素,例如:⎥⎦⎤⎢⎣⎡=i i i id c b a i APR 的例4.1和4.2是二维的,因为0d 1c i i ==,,对于所有的i 都成立。
下面定义顶点和最小单位。
定义4.1(顶点): 图2中PR 的顶点1,2,3就是被定义为顶点的321A A A ,,。
定义4.2(最小单位):一个有且只有顶点的非线性系统被称为最小单位。
明显的,前面的LDI-1是最小单位,LDI-2不是最小单位。
下面,给出一个检查是否为最小单位系统的稳定性的重要定理。
定理4.1:假设存在一个正定矩阵。
如果A P T i i -<A P 0,其中i=1,2,…,r ,那么 **A P T -<A P 0,其中=1.0,,∑∑==≥=ri i i ri i s s 11i *s A A证明过程已经在附录中给出。
可以注意到*A 并不是一个顶点矩阵。
定理4.1指出LDI系统的稳定性可以通过对一个最小单位应用定理3.1而检验得出。
3240.5A A 5.0A +=32150.25A 0.25A 0.5A A ++=因此,LDI-2的最小单位与LDI-1的相同。
从定理4.1可以得出如果LDI-1稳定则LDI-2也稳定。
后面将定理4.1应用到例子6.4和6.6中。
5.神经网络的LDI 表示方法A.简单的神经网络用LDI 来表示神经网络系统的动力并应用定理3.1来分析神经网络的稳定性是非常重要的。
在这一章节中,提出了用LDI 表示神经网络动力系统的过程。
接下里以图4中的简单神经网络为例。
这个神经网络是由一个单一的层组成,函数是: (5) (4))()1(),1()(21v f k x k w k x w v =+-+=其中21w w 和是权值。
假定输出函数f (v )是一个Sigmoid 函数。
⎪⎪⎪⎪⎭⎫ ⎝⎛--+=1)ex p(12)(q v v f λ其中q 和x 是函数的参数并且 q 和v>0.图5表示的是sigmoid 函数。
在本文中,稳定性准则适用于一切x>0的情况,于是假设x=1。
如图5,输出函数满足:)(0)(1221≤≤≤≥≤≤v v g v f v g v v g v f v g 图2.LDI-1的参数区域其中21g g 和分别是)(v f '的最小值和最大值,所以:qv f g v f g vv/5.0)(max ,0)(min 21='=='=当.)()(dvv df v f ≡'的时候。
所以神经网络的输入输出关系可以被表示为如下的LDI :∑=-+=+==+21212211))1()(()())()(()()1(i i i k x w k x w g k h v g k h g k h v f k x 其中满足0)(),(21≥k h k h 和1)()(21=+k h k h 。