滑动轴承设计与计算
- 格式:ppt
- 大小:978.00 KB
- 文档页数:48


第八章滑动轴承8.1 重点、难点分析本章的重点内容是滑动轴承轴瓦的材料及选用原则;非液体摩擦滑动轴承的设计准则及设计计算;液体动力润滑径向滑动轴承的设计计算。
难点是液体动力润滑径向滑动轴承的设计计算及参数选择。
8.1.1 轴瓦材料及其应用对轴瓦材料性能的要求:具有良好的减摩性、耐磨性和咬粘性;具有良好的摩擦顺应性、嵌入性和磨合性;具有足够的强度和抗腐蚀的能力和良好的导热性、工艺性、经济性等。
常用轴瓦材料:金属材料、多孔质金属材料和非金属材料。
其中常用的金属材料为轴承合金、铜合金、铸铁等。
8.1.2 非液体摩擦滑动轴承的设计计算对于工作要求不高、转速较低、载荷不大、难于维护等条件下的工作的滑动轴承,往往设计成非液体摩擦滑动轴承。
这些轴承常采用润滑脂、油绳或滴油润滑,由于轴承得不到足够的润滑剂,故无法形成完全的承载油膜,工作状态为边界润滑或混合摩擦润滑。
非液体摩擦轴承的承载能力和使用寿命取决于轴承材料的减摩耐磨性、机械强度以及边界膜的强度。
这种轴承的主要失效形式是磨料磨损和胶合;在变载荷作用下,轴承还可能发生疲劳破坏。
因此,非液体摩擦滑动轴承可靠工作的最低要求是确保边界润滑油膜不遭到破坏。
为了保证这个条件,设计计算准则必须要求:p≤[p],pv≤[pv],v≤[v]限制轴承的压强p,是为了保证润滑油不被过大的压力挤出,使轴瓦产生过度磨损;限制轴承的pv值,是为了限制轴承的温升,从而保证油膜不破裂,因为pv值是与摩擦功率损耗成正比的;在p及pv值经验算都符合要求的情况下,由于轴发生弯曲或不同心等引起轴承边缘局部压强相当高,当滑动速度高时,局部区域的pv值可能超出许用值,所以在p较小的情况下还应该限制轴颈的圆周速度v。
8.1.3液体动力润滑径向滑动轴承设计计算液体动力润滑的基本方程和形成液体动力润滑(即形成动压油膜)的条件已在第一章给出,这里不再累述。
1.径向滑动轴承形成动压油膜的过程径向滑动轴承形成动压油膜的过程可分为三个阶段:(1)起动前阶段,见图8-1a;(2)起动阶段,见图8-1b;(3)液体动力润滑阶段,见图8-1c;图8-1 径向滑动轴承形成液体动力润滑的过程对于这一形成过程应掌握如下要点:(1)从轴颈开始转动到轴颈中心达到静态平衡点的过程分析;(2)在给定载荷、轴颈转动方向及偏心距e的大小时,如何确定轴颈的平衡位置;(3)确定轴颈平衡位置后,油膜压力分布的大致情况以及最小油膜厚度h min的位置;(4)影响轴颈静态平衡点位置的主要因素有外载荷F,润滑油粘度η和轴颈转速n。





液体动力润滑径向滑动轴承设计计算流体动力润滑的楔效应承载机理已在第四章作过简要说明,本章将讨论流体动力润滑理论的基本方程(即雷诺方程)及其在液体动力润滑径向滑动轴承设计计算中的应用。
(一)流体动力润滑的基本方程流体动力润滑理论的基本方程是流体膜压力分布的微分方程。
它是从粘性流体动力学的基本方程出发,作了一些假设条件后得出的。
假设条件:流体为牛顿流体;流体膜中流体的流动是层流;忽略压力对流体粘度的影响;略去惯性力及重力的影响;认为流体不可压缩;流体膜中的压力沿膜厚方向不变。
图12-12中,两平板被润滑油隔开,设板A 沿x 轴方向以速度v 移动;另一板B 为静止。
再假定油在两平板间沿 z 轴方向没有流动(可视此运动副在z 轴方向的尺寸为无限大)。
现从层流运动的油膜中取一微单元体进行分析。
作用在此微单元体右面和左面的压力分别为p 及p p dx x ∂⎛⎞+⎜∂⎝⎠⎟,作用在单元体上、下两面的切应力分别为τ及dy y ττ⎛⎞∂+⎜⎟∂⎝⎠。
根据x 方向的平衡条件,得:整理后得根据牛顿流体摩擦定律,得,代入上式得 该式表示了压力沿x 轴方向的变化与速度沿y 轴方向的变化关系。
下面进一步介绍流体动力润滑理论的基本方程。
1.油层的速度分布将上式改写成(a)对y 积分后得(c)根据边界条件决定积分常数C1及C2:当y=0时,v= V;y=h(h为相应于所取单元体处的油膜厚度)时,v=0,则得:代入(c)式后,即得 (d)由上可见,v由两部分组成:式中前一项表示速度呈线性分布,这是直接由剪切流引起的;后一项表示速度呈抛物线分布,这是由油流沿x方向的变化所产生的压力流所引起的。
2、润滑油流量当无侧漏时,润滑油在单位时间内流经任意截面上单位宽度面积的流量为:将式(d)代入式(e)并积分后,得(f)设在 p=p max处的油膜厚度为h0(即时当润滑油连续流动时,各截面的流量相等,由此得 :整理后得该式为一维雷诺方程。


动载滑动轴承轴心轨迹计算在往复式机械中,作用在连杆大小端及曲轴的滑动轴承上的载荷,无论大小和方向都随时间作周期性变化。
动载轴承由于油膜动压受旋转效应和挤压效应的综合作用,其轴心轨迹是变化的。
在正常的工况下,其轴心轨迹收敛于固定的轨迹曲线。
动载轴承的轴心轨迹的计算可以估计出轴承的失效形式及失效位置,从而在设计时可作有效的预防。
对轴心轨迹的计算,不能用稳态下的计算方法来确定,这是因为其油膜动压涉及挤压效应和旋转效应的综合作用,因而要采用非稳态下的计算方法才能确定。
本文主要采用Holland方法并通过计算机模拟进行计算。
图1 轴承模型示意图1.建立模型在进行轴心轨迹的计算之前,对有限宽的动载轴承作以下假设:(1)轴承的间隙中充满润滑油介质,流动服从雷诺方程,不考虑润滑油的涡动现象;(2)整圆轴承,轴承的轴线和轴颈平行;(3)轴承外表面光整;(4)不考虑温度场变化引起的油粘度变化。
求解轴心轨迹的基本思路如下,在油膜力和载荷互相平衡的情况下(由于轴颈惯性力相对较小,因此可以忽略不计),轴心都会逐渐收敛于一个确定的轨迹,所以可在轴颈的任意初始位置上根据力平衡关系确定轴心变化速度。
由此得到经过一微小时间间隔后的新的轴颈位置。
从这个位置再确定新的轴心变位速度,又得到另一时间间隔后的另一个轴颈位置。
如此不断进行下去,直到收敛于一个封闭的轴心轨迹。
分析动载轴承轴心轨迹的具体方法有Holland法、和Hahn法和移动率(Mobility)法。
为了克服对动载Reynolds方程在数学上求通解的困难,采用Holland法进行分析。
图1为物理模型的受力关系示意。
图中,F为动载荷,γ为动载荷与Y轴的方向角,δ为偏位角,Ωb为轴承角速度,Ωj为轴颈角速度,轴颈中心O j绕轴承中心O b的回转变位角速度为δ’,偏心率随时间的增长速率为ε’,R为轴承的内径。
P D是由轴颈和轴承相对油楔的旋转角速度引起的油膜动压,P V是由轴颈与轴承之间的挤压引起的油膜动压,称为挤压油压。

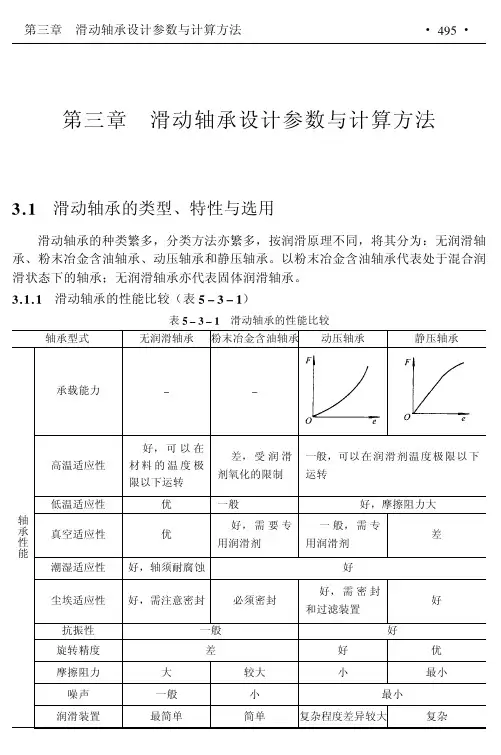
第三章滑动轴承设计参数与计算方法!"#滑动轴承的类型、特性与选用滑动轴承的种类繁多,分类方法亦繁多,按润滑原理不同,将其分为:无润滑轴承、粉末冶金含油轴承、动压轴承和静压轴承。
以粉末冶金含油轴承代表处于混合润滑状态下的轴承;无润滑轴承亦代表固体润滑轴承。
!"#"#滑动轴承的性能比较(表$%!%#)表$%!%#滑动轴承的性能比较轴承型式无润滑轴承粉末冶金含油轴承动压轴承静压轴承轴承性能承载能力!!高温适应性好,可以在材料的温度极限以下运转差,受润滑剂氧化的限制一般,可以在润滑剂温度极限以下运转低温适应性优一般好,摩擦阻力大真空适应性优好,需要专用润滑剂一般,需专用润滑剂差潮湿适应性好,轴须耐腐蚀好尘埃适应性好,需注意密封必须密封好,需密封和过滤装置好抗振性一般好旋转精度差好优摩擦阻力大较大小最小噪声一般小最小润滑装置最简单简单复杂程度差异较大复杂w w w.bz f x w.c om!"#"$滑动轴承的承载能力与极限转速几种主要滑动轴承的极限承载能力和极限转速曲线见图!"#"$和图!"#"%。
可供选择滑动轴承类型时参考。
对动压轴承,按中等粘度润滑油进行计算;对无润滑轴承和混合润滑轴承,按磨损寿命为$&’(计算;对静压轴承,理论上在材料强度允许图%&!&#径向轴承的极限载荷与转速""""无润滑轴承—·—液体动压轴承—··—粉末冶金含油轴承—滚动轴承图%&!&$推力轴承的极限载荷与转速""""无润滑轴承—·—液体动压轴承—··—粉末冶金含油轴承—滚动轴承w w w.bz f x w.c om的载荷和转速范围内均可应用。
为了便于比较,还将疲劳寿命为!"#$的滚动轴承的极限承载能力和极限转速曲线画出。
摩擦:滚动摩擦滚动摩擦轴承滚动轴承滑动摩擦滑动摩擦轴承滑动轴承第十二章滑动轴承第一节概述1、滑动轴承应用场合:1)工作转速特高轴承,如汽轮发电机;2)要求对轴的支撑位置特别精确的轴承,如精密磨床;3)特重型的轴承,如水轮发电机;4)承受巨大的冲击和振动,如轧钢机;5)根据工作要求必须做成剖分式的轴承,如曲轴轴承;6)在特殊的工作条件下(如在水中或腐蚀性介质中)工作的轴承,如军舰推进器的轴承;7)在安装轴承处的径向空间尺寸受到限制时,也常采用滑动轴承,如多辊轧钢机。
2、分类①按载荷方向:径向(向心)轴承、止推轴承、向心止推②按接触表面之间润滑情况:液体滑动轴承、非液体滑动轴承液体滑动轴承:完全是液体非液体滑动轴承:不完全液体润滑轴承、无润滑轴承不完全液体润滑轴承(表面间处于边界润滑或混合润滑状态)无润滑轴承(工作前和工作时不加润滑剂)③液体润滑承载机理:液体动力润滑轴承(即动压轴承)液体静压润滑轴承(即液体静压轴承)3、如何设计滑动轴承(设计内容)1)轴承的型式和结构2)轴瓦的结构和材料选择3)轴承的结构参数4)润滑剂的选择和供应5)轴承的工作能力及热平衡计算4.特点:承载能力大,工作平稳可靠,噪声小,耐冲击,吸振,可剖分等特点。
第二节滑动轴承的典型结构一、整体式径向滑动轴承:特点:结构简单,易于制造,端部装入,装拆不便,轴承磨损后无法调整。
应用:低速、轻载或间歇性工作的机器中。
二、对开式径向滑动轴承:装拆方便,间隙可调,应用广泛。
特点:结构复杂、可以调整磨损而造成的间隙、安装方便。
应用场合:低速、轻载或间歇性工作的机器中。
三、止推式滑动轴承:多环式结构,可承受双向轴向载荷。
第三节滑动轴承的失效形式及常用材料一、失效形式1、磨粒磨损:硬颗粒对轴颈和轴承表面起研磨作用。
2、刮伤:硬颗粒划出伤痕。
3、胶合:轴承温度过高,载荷过大,油膜破裂或供油不足时,轴颈和轴承相对运动表面材料发生粘附和迁移,从而造成轴承损坏。
可倾瓦径向滑动轴承计算在工程设计中,可倾瓦径向滑动轴承是一种常用的轴承类型,可用于承受横向负载和旋转运动的轴向负载。
其设计和计算涉及多个参数和步骤,包括轴承尺寸、负载计算、材料选取等。
本文将介绍可倾瓦径向滑动轴承的设计原理和计算方法。
###1.可倾瓦径向滑动轴承的设计原理可倾瓦径向滑动轴承是一种采用滚动摩擦方式来支撑旋转机件的轴承,其设计原理是利用轴承之间的滑动摩擦力来支撑和传递负载。
其主要特点是可以承受较大的径向负载和轴向负载,并且具有自调心功能,能够适应轴承与轴的不规则相对运动。
###2.可倾瓦径向滑动轴承的计算步骤(1)确定轴承尺寸:首先需要确定轴承的内径、外径和宽度等尺寸参数,这些参数通常由设计工程师根据实际工程需求和负载条件来确定。
(2)计算负载:根据设计条件和负载要求,计算轴承所承受的径向负载和轴向负载,包括静载和动载条件。
(3)选取材料:选择适当的轴承材料,通常为高强度、高耐磨性的合金材料,以满足负载和使用寿命要求。
(4)计算润滑参数:确定润滑方式和参数,包括滑动摩擦系数、润滑膜厚度等,以确保轴承在运行时不受损伤。
(5)进行稳定性计算:进行轴承的稳定性分析,确定轴承在各种工况下的稳定性和可靠性。
###3.可倾瓦径向滑动轴承的设计案例例如设计一个直径为200mm、宽度为50mm的可倾瓦径向滑动轴承,承受径向负载为10kN,轴向负载为5kN,滑动摩擦系数为0.1,轴承采用耐磨合金材料,润滑膜厚度为0.02mm的设计案例。
根据上述设计参数和计算步骤,可以依次进行轴承尺寸确定、负载计算、材料选取、润滑参数计算和稳定性分析,得到最终的设计方案。
###4.结论通过以上设计案例,可倾瓦径向滑动轴承的设计和计算是一个复杂的工程任务,需要设计工程师充分理解轴承的原理和参数,合理选择材料和润滑方式,确保轴承在不同工况下都能稳定可靠地工作。
在实际工程设计中,需要结合具体情况和要求进行综合考虑和优化,以确保轴承的性能和可靠性。