电子电路中的对偶原理分析

对偶原理及其在电路教学中的运用对偶原理是一种数学定理，它指出两个等价的问题在解决方式上是对偶的。

这意味着，解决原问题的方法也可以用来解决对偶问题，反之亦然。

在电路教学中，对偶原理常常被用来简化电路设计和分析过程。

例如，在寻找最短路径时，我们可以使用对偶原理来把最短路径问题转化为最长路径问题，这样就可以使用最长路径算法来解决问题。

对偶原理还可以用来帮助我们解决网络流问题。

网络流是一种模型，用于描述从一个源点流向多个汇点的资源。

通过使用对偶原理，我们可以将求解网络流问题转化为求解最大匹配问题，这样就可以使用最大匹配算法来解决问题。

总之，对偶原理在电路教学中有很多应用，可以帮助我们简化问题的解决方式，并提供更多的解决选择。

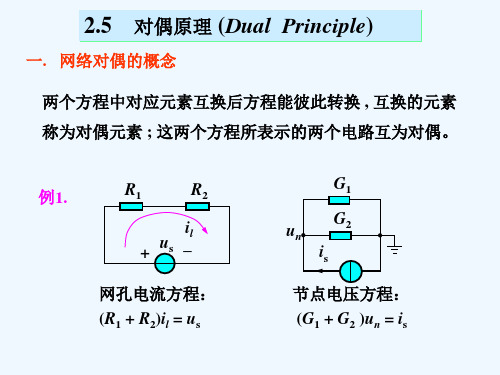
☐如果电路的节点方程与电路的网孔方程不仅形式相同，各项系数以及激励的数值相同，那么电路方程的解也分别相等，称这样的两个电路互为对偶电路(dual circuit)。

☐在电路理论中，电路的结构、连接方式、定律、元件、参数、名词、变量及其关系式等都存在互相对偶性。

2
5
方程比较：
136
63
1666246
426634
34535m S m S m S R R R R R i R i R R R R R i R i R R R R R i u ++---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-++-=⎢⎥⎢⎥⎢
⎥⎢⎥⎢⎥⎢⎥--++⎣
⎦⎣⎦⎣⎦
136636616
2464
2663534345ˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆS n n S n S G G G G G G u u G G G G G u G u u i G G G G G ⎡⎤⎡⎤++---⎡⎤
⎢
⎥⎢⎥
⎢⎥-++-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--++⎣⎦⎢⎥⎢⎥⎣
⎦⎣⎦
有缘学习更多关注桃报：奉献教育（店铺）或＋谓ｙｇｄ３０７６
电压电流
有缘学习更多关注桃报：奉献教育（店铺）或＋谓ｙｇｄ３０７６
☐电压源的极性沿着顺时针方向升高时,对偶电流源的电流方向指向该网孔对应的节点方向.
☐电压源的极性沿着逆时针方向升高时,对偶电流源的电流方向指向该网孔对应的节点的反方向.
☐电流源的电流与网孔电流的方向相同时,对偶电压源的正极性落在该网孔对应的节点上.
☐电流源的电流与网孔电流的方向相反时,对偶电压源的负极性落在该网孔对应的节点上.
13。

对偶原理在电路基础课程中的应用探索对偶原理是电路理论中常用的重要原理之一，它可以帮助我们在分析和设计电路时进行转化和简化。

在电路基础课程中，对偶原理的应用有以下几个方面的探索：
1. 对偶性质的介绍
首先需要介绍对偶性质的基本概念，即对于任意电路，都存在一种对偶电路，它与原电路具有相同的拓扑结构，但是其中的元件被互换了，即电源和负载的位置互换，电阻与电容互换，电感与电容互换等。

2. 对偶原理的具体应用
对偶原理的具体应用包括：
(1) 电路简化：将复杂的电路通过对偶转化为简单的电路，便于分析和计算。

(2) 电路设计：通过对偶原理设计出相应的电路，实现不同的功能和特性。

(3) 电路优化：利用对偶原理将电路转化为更容易优化的形式，实现电路的最小化、最大化等优化目标。

(4) 电路等效：通过对偶原理将电路转化为等效的形式，方便比较和分析不同电路的性能和特性。

3. 对偶原理在实际电路中的应用
在实际电路设计和分析中，对偶原理可以应用于各种电路拓扑结构的转化和简化，如滤波器、放大器、振荡器、计数器等。

例如，在振荡器设计中，通过对偶原理可以将电感电容振荡器转化为电容电感振荡器，实现振荡频率的调节和稳定。

总之，对偶原理在电路基础课程中具有重要的应用价值，可以帮助学生更好地理解电路原理，提高电路设计和分析的能力。

第29卷　第5期2007年10月电气电子教学学报J OURNAL OF EEEVol.29　No.5Oct.2007对偶原理在电力电子电路中的应用伍小杰,董　瑶,戴　鹏,周　娟(中国矿业大学信息与电气工程学院,江苏徐州221008)收稿日期:2007204228;修回日期:2007207220作者简介:伍小杰(19662),男,湖南衡阳人,博士,教授,主要从事电力电子技术、交流电机控制、风力发电等方面的教学与科研工作董　瑶(832),女,山东威海人,硕士研究生,研究方向为电力电子与电力传动戴　鹏(32),男,安徽淮南人,博士,副教授,主要从事大功率电力传动的教学与科研工作周　娟(62),女,江苏睢宁人,硕士,讲师,主要从事电力电子与电力传动的教学与科研工作摘　要:对偶原理是分析电力电子电路拓扑结构的有力工具。

本文根据图论中图的对偶概念,对电力电子电路进行了对偶性分析,介绍了电力电子电路对偶变换的方法。

由于对偶原理只适用于平面电路,本文还通过新的概念定义以及适当的变换方法将对偶原理的应用扩展到了非线性电力电子器件与非平面电路中。

文中最后举例说明了对偶原理在电力电子拓扑结构中的重要作用。

关键词:对偶原理;电力电子电路;拓扑结构;非平面电路中图分类号:TN7 文献标识码:A 文章编号:100820686(2007)0520033205Application of Duality Pr inciple in Pow er Electr onic Cir cuit sW U Xiao 2j ie ,DONG Y a o ,DAI Peng ,ZH O U Juan(S chool of In f ormat i on and Elect rical En gi neeri n g ,Chi na Uni vers it y of Mini ng an d Technol og y ,Xuzhou 221008,Chi na )Abstract :Dualit y p ri ncipl e is a powerf ul tool for t he analysi s of topological st ruct ure of power elect ronic ci rcui t s.The dualit y of power el ect ronic ci rcui t s ha s been anal yzed usi ng t he concept of dualit y in graph t heory and t he met hods of dual t ransform i n power elect ronic circuit s are al so i nt roduced i n t hi s paper.Traditionall y ,dualit y pri nciple is limit ed t o li near ci rcui t s.In t hi s paper ,t he application of dualit y p ri nci 2pl e has been ext ended to non 2li near power el ect ronic device s a nd non 2pl anar ci rcuit s usi ng new co ncept s a nd appropriate t ransform met hods.Exa mples are gi ven to illust rat e t he i mport ance of dual t heory i n t he topo 2logy of power elect ro nic s.K eyw or ds :duali t y pri nciple ;power elect ro nic circuit s ;t opologi cal st ruct ure ;non 2plana r circuit s0　引言电力电子电路的拓扑结构种类繁多,各种不同的电路结构都可以归结为多个电力电子基本拓扑单元的组合,或者是经过一定简化后的组合,按照这一思路还可以派生出一些新结构。

第1篇一、实验目的1. 理解电路对偶原理的基本概念和原理。

2. 掌握如何通过电路对偶原理分析电路的特性。

3. 应用对偶原理解决实际电路问题。

二、实验原理电路对偶原理是指在电路中，如果将电压源与电流源、短路与开路、串联与并联、电阻与电导、电容与电感等元件进行对偶替换，电路的输入输出特性将保持不变。

对偶原理在电路分析中具有重要作用，可以简化电路的复杂度，提高分析效率。

三、实验仪器与设备1. 电路实验箱2. 电阻3. 电容4. 电感5. 电压表6. 电流表7. 电源四、实验步骤1. 搭建电路：根据实验要求，搭建相应的电路，如串联电路、并联电路、电阻分压电路等。

2. 测量数据：使用电压表和电流表测量电路中各个元件的电压和电流值，记录实验数据。

3. 对偶替换：根据对偶原理，将电路中的电压源替换为电流源，电阻替换为电导，电容替换为电感，进行对偶替换。

4. 重新测量数据：对对偶替换后的电路进行测量，记录电压和电流值。

5. 对比分析：对比对偶替换前后的实验数据，分析电路对偶原理在实际电路中的应用。

五、实验结果与分析1. 串联电路对偶替换：- 原电路：电压U = IR，其中R为电阻，I为电流。

- 对偶替换后：电流I = UR，其中U为电压，R为电导。

通过对偶替换，我们可以发现，电路的输入输出特性并未改变，只是元件的参数发生了变化。

2. 并联电路对偶替换：- 原电路：电压U = I1R1 + I2R2，其中R1、R2为电阻，I1、I2为电流。

- 对偶替换后：电流I = UR1 + UR2，其中U为电压，R1、R2为电导。

同样地，对偶替换后的电路输入输出特性并未改变，只是元件的参数发生了变化。

3. 电阻分压电路对偶替换：- 原电路：电压U = I1R1 + I2R2，其中R1、R2为电阻，I1、I2为电流。

- 对偶替换后：电流I = UR1 + UR2，其中U为电压，R1、R2为电导。

通过对偶替换，我们可以发现，电阻分压电路的输入输出特性并未改变，只是元件的参数发生了变化。

电路对偶原理
电路对偶原理是电路理论中一个重要的概念，它指的是通过互换电路中的电源和电阻的位置，可以得到一个等效的电路。

换句话说，如果一个电路能够满足一定的电路特性，那么交换其中的电源和电阻的位置后，新得到的电路也将满足相同的电路特性。

电路对偶原理的应用非常广泛，例如在逻辑电路设计中，我们可以通过对偶原理来简化电路设计和分析。

以与门和或门为例，它们的逻辑功能是互补的，通过应用对偶原理，我们可以很容易地从一个门的逻辑功能推导出另一个门的逻辑功能。

同时，电路对偶原理也可以用于简化电路分析的过程。

通过交换电源和电阻的位置，我们可以将电源视为电阻，电阻视为电源，进而将电路转化为等效电路，从而简化分析的过程。

需要注意的是，电路对偶原理只适用于一些特定的电路特性和性质。

因此，在应用电路对偶原理时，需要明确电路所具有的特性，并合理选择是否使用对偶原理进行简化或分析。

总而言之，电路对偶原理是一个重要的电路理论概念，通过互换电路中的电源和电阻的位置，可以得到等效的电路。

它在电路设计和分析中有着广泛的应用，可以简化电路设计和分析的过程。