数学建模对偶问题和灵敏度分析
对偶问题
例题1：某养鸡场所用的混合饲料由n 种天然饲料配合而成。
要求在这批配合饲料中必须含有m 种不同的营养成分，且第i 种营养成分的含量不低于bi 。
已知第i 种营养成分在每单位第j 种天然饲料中的含量为a ij ，每单位第j 天然饲料的价格为c j 。
试问，应如何对这n 种饲料配方，使这批饲料的费用最小? 解 设x j 为第j 种天然饲料的用量。
显然，a ij x j 即为所用第j 种天然饲料中第i 种营养成分的含量，1n
ij j j a x =∑为这批混
合饲料中第i 种营养成分的总含量；它不应低于bi 。
于是，我们得下列线性规划模型(1—1)：
1
min n
j j
j f c x ==∑
1
1,,..01,,n
ij j i j j a x b i m s t x j n
=⎧≥=⎪⎨⎪≥=⎩
∑
现设想有一个饲料加工厂欲把这m 种营养成分分别制成m 种营养丸。
设第i 种营养丸的价格为ui(i ＝1，…，m)。
则养鸡场采购一个单位的第j 种天然饲料，就相当于对这m 种营养丸分别采购数量a 1j ，…a mj ，所化费用为1m
ij i i a u =∑养
鸡场自然希望在用营养丸代替天然饲料时，在价格上能相对地比较便宜，故而饲料加工厂为了能与天然饲料供应者竞争，在制订价格时必然满足下述条件：
1
1,
,m
ij i
j i a u
c j n =≤=∑
另一方面，养鸡场如果全部采购营养丸来代替天然饲料进行配料，则第i 种营养丸就需采购bi 个单位，所化费用为b i u i ，总费用为z=∑b i u i
饲料加工厂面临的问题是：应把这m 种营养丸的单价ui(f=1，…，m)定为多少，才能使养鸡场乐意全部采用该厂生产的营养丸来取代这批天然饲料，且使本厂在竞争中得到最大收益。
为该问题建立数学模型，即得如下线性规划(1—2)：
1
max m
i i i z b u ==∑
1
1,,..01,,m
ij i j i i
a u c j n s t u i m =⎧≤=⎪⎨⎪≥=⎩∑
我们称问题(1—2)为原有问题 (1—1)的对偶问题(记为(D))。
,n
影子价格（Shadow Price ）
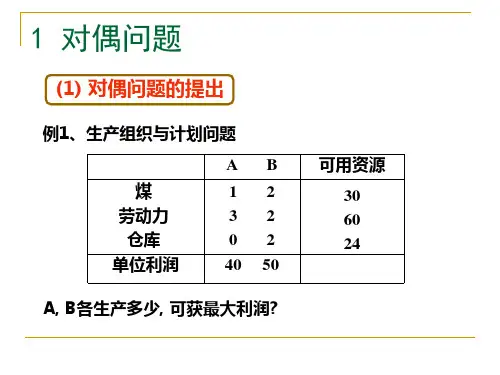
例题2：某工厂计划在下一生产周期生产
3种产品A 1, A 2, A 3，这些产品都要在甲、乙、丙、丁4种设备上加工，根据设备性能和以往的生产情况知道单位产品的加工工时、各种设备的最大加工工时限制，以及每种产品的单位利润，如下表。
问如何安排生产计划，才能使工厂得到最大利润？
解：设x1, x2, x3为产品A1, A2, A3的产量
线性规划模型为：
Max f=8x1+10x2+2x3
s.t. 2x1+x2+3x3≤70
4x1+2x2+2x3≤80
3x1 + x3≤15
2x1+2x2 ≤50
最优单纯形表为：
最优方案为：x1＝0，x2＝25， x3＝15， x4＝0
最大利润为280千元
现在从另一个角度来讨论问题
假设工厂考虑不安排生产，而准备将所有设备出租，收取租费。
于是需要为每种设备的台时进行估价。
设y1, y2, y3, y4分别表示甲、乙、丙、丁4种设备的台时估价。
由例1中的表可知，生产一件产品A1需要各设备台时分别为2h，4h，3h，2h，如果将2h，
4h ，3h ，2h 不用于生产产品A 1，而是用于出租，租费应满足（为了不蚀本，租费不能少于利润） 2 y 1+4y 2+3 y 3+2 y 4≥8，依次可分析得线性规划模型如下
123412341
23123
12370801550243282210..322,,0
Min f y y y y y y y y y y y s t y y y y y y =++++++≥⎧⎪++≥⎪⎨++≥⎪⎪≥⎩
说明：企业为了能够得到租用设备的用户，使出租设备的计划成交，在价格满足约束条件下，应将设备价格定得尽可能低（why ？）
最优解：y 1＝2/3， y 2＝0， y 3＝0， y 4＝14/3 最小租费：280千元 定义：
,n
设***
*12ˆ(,,,)T
m y
y y y =为对偶问题（D ）的最优解，则称*i y 为原有问题（P ）
第i 个约束对应的影子价格（Shadow Price ）
由例2知*i y 是对第i 种资源（设备台时）的一种估价，这个价格不是市场价格，而是针对具体企业在一定时期内存在的一种特殊价格，它蕴含在求最大利润的生产计划模型中。
影子价格的经济含义：
（1）影子价格是对现有资源实现最大效益的一种估价。
根据例2的讨论，企业可以根据现有资源的影子价格，对资源的使用有两种考虑：第一，是否将设备用于外加工或出租，若租费高于某设备的影子价格，可考虑出租该设备，否则不宜出租；第二，是否将投资用于购买设备，以扩大生产能力，若市价低于某设备的影子价格，可考虑买进该设备，否则不宜买进。
（2）影子价格表明资源增加对总效益产生的影响。
易见有
****
*
1122m m f z b y b y b y ==++
+
从而，如果i b 增加一个单位，目标函数值的增量将是*i y ，据此，由影子价格的大小可以知道哪种资源的增加可以给企业带来较大的收益。
如例2中四种设备的影子价格分别为2/3，0，0，14/3，因此，在同样的条件下，增加设备丁是最有利的，不应增加设备乙和丙。
例3：某外贸公司准备购进两种产品A 1, A 2。
购进产品A 1每件需要10元，占用5m 3的空间，待每件A 1卖出后，可获纯利润3元；购进产品A 2每件需要15元，占用3m 3的空间，待每件A 2卖出后，可获纯利润4元。
公司现有资金1400元，有430 m 3的仓库空间存放产品，从而可得线性规划模型如下：
12
1212123410151400
..53430,0Max z x x x x s t x x x x =++≤⎧⎪
+≤⎨⎪≥⎩ 最优单纯形表
最优方案：x 1＝50，x 2＝60
最大利润：390
现在公司有另外一笔资金585元，准备用于投资，到底是购买产品呢？还是增加仓库容量？（假设增加1m3的仓库空间需要0.8元）
由上表知，仓库的影子价格y2＝1/9，即增加1m3的仓库空间，公司可多获利1/9元，又增加1m3的仓库空间需要0.8元，从而，每增加1元投资可多获利
10/72元，近似为0.14元；购买产品的资金的影子价格y1＝11/45，每增加1元购买产品可多获利11/45元，近似为0.24元。
因此，投资应该用于购买产品而不是增加仓库容量。
585元进行投资之后，最大利润为585 y1＝143元（？？？？？？？）
灵敏度分析（Sensitivity Analysis）
最优解是在参数cj、bi、aij都固定不变的条件下取得的。
但是，在实际问题中，对一个具体的企业来说，参数cj、bi、aij不是固定不变的。
例如，产品的市场价格可能有所变动；国家分配的原材料可能有所增减；动力供应情况可能随季审而变化f添置新设备而使生产台时增加；由于产品设计结构有所改进，使单位产品的原材料消耗定额有所增减……，现实诸因素的种种变化都会引起已建立的数学模型的参数变化。
或者，当运用线性规划编制完生产计划并即将付诸应用时，又发生了新的情况，某些原来未加限制的资源现在有了限制，从而出现一个新的追加约束条件。
或者，企业准备增加新产品，使工厂的生产计划发生整个变化。
从而，我们面临这样的问题：上述种种情况的发生，将对已求得的最优解产生什么影响?或者说，我们如何在原有的最优单纯形表的基础上用最少的计算量，去获得修改后的线性规划问题的最优解?这就是下面我们要讨论的灵敏度分析问题。
一般分下面几个问题来进行灵敏度分析（Sensitivity Analysis）：
1．变量x s的目标函数系数c s在何范围内变动，问题(LP)的最优基(最优解)不变?如果超出这个范围，如何求最优解?
2．第s种资源bs在何范围内变动，最优基不变?如果bs超出这个范围，如何求最优解?
3．变量x s在矩阵A中的系数列向量发生变化，如何求新问题的最优解?
4．追加新的约束条件，如何求新的线性规划的最优解?
5．增加新的变量x s，如何求新问题的最优解?。
