当前位置：文档之家 › 《管理运筹学》第四版第6章单纯形法灵敏度分析与对偶课后习题解析

《管理运筹学》第四版第6章单纯形法灵敏度分析与对偶课后习题解析

  • 格式：docx
  • 大小：11.43 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

第6章单纯形法的灵敏度分析与对偶

第6章单纯形法的灵敏度分析与对偶

这个约束条件的对偶价格就和这个剩余变量的
z
有关了。这将使得最优目
j
标值特别“恶化”而不是改进，故这时约束条件的对偶价格应取 z j 值的相反
数- z j。
对于含有等于号的约束条件，其约束条件的对偶价格就和该约束方
程的人工变量有关了。其约束条件的对偶价格就等于此约束方程的人工变
量的 z j值。
管理运筹学
XB
bb12
5
5
,
X
B
5
5
b3 15
15
对于b1：比值的分母取B－1的第一列，这里只有β11=1，而β21=β31=0，则
1
max
b1
11
5 1
5
Δb1无上界，即Δb1≥－5，因而b1在[35,+∞) 内变化时对偶价格不变。
管理运筹学
18
§1 单纯形表的灵敏度分析
对于b2：比值的分母取B－1的第二列，β12＜0，β22＞0，则
§1 单纯形表的灵敏度分析
一、目标函数中变量Ck系数灵敏度分析
1.在最终的单纯形表里，X k是非基变量 由于约束方程系数增广矩阵在迭代中只是其本身的行的初等变换与Ck没有任何关系， 所以当Ck变成Ck+ Ck时，在最终单纯形表中其系数的增广矩阵不变，又因为Xk是非 基变量，所以基变量的目标函数的系数不变，即CB不变，可知Zk也不变，只是Ck变
xBi di1
|
d 'i1
0
50
而Min
xBi di1
|
d 'i1
0
25,故有当 50
b1
25,即250
b
b
325第一个
约束条件的对偶价格不变。

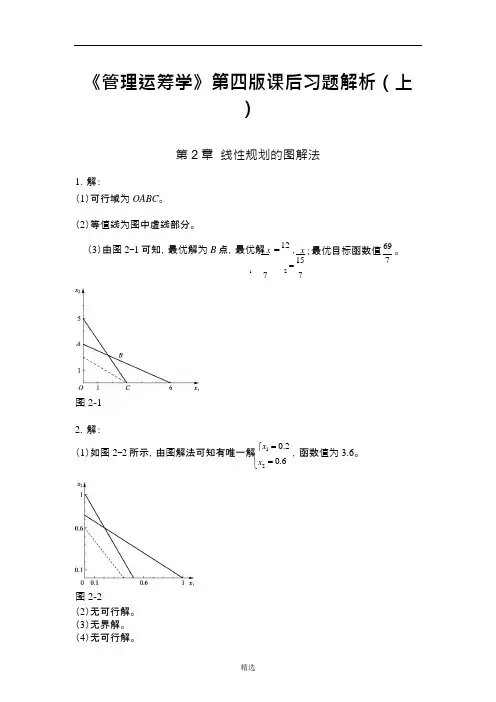
《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题答案

精选⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。

（2）等值线为图中虚线部分。

（3）由图2-1可知，最优解为B 点，最优解 x =12， x = 15 1727图2-1；最优目标函数值 69。

72．解：（1）如图2-2所示，由图解法可知有唯一解 ⎧x 1 = 0.2，函数值为3.6。

⎩x 2图2-2（2）无可行解。

（3）无界解。

（4）无可行解。

⎨ （5）无穷多解。

⎧x = （6）有唯一解 ⎪ 1⎪ 203 ，函数值为 92 。

8 3 x = ⎪⎩ 2 33．解： （1）标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4．解： 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。

管理运筹学 第6章 目标规划

管理运筹学 第6章 目标规划

目标规划问题及模型
∵正负偏差不可能同时出现，故总有：
x1－x2+d--d+ =0
若希望甲的产量不低于乙的产量，即不希望d->0,用目标约束可
表为:
min{d }
x1
x2
d
d
0
若希望甲的产量低于乙的产量，即不希望d＋>0,用目标约束可
表为:
min{d }
x1
x2
d
d
0
若希望甲的产量恰好等于乙的产量，即不希望d＋>0,也不希望
2x1 2x2 12
s.t
4
x1 x1
2x2
8 16
4x2 12
x1 , x2 0
其最优解为x1＝4，x2＝2，z＊＝14元
目标规划问题及模型
但企业的经营目标不仅仅是利润，而且要考虑多个方面，如： (1) 力求使利润指标不低于12元； (2) 考虑到市场需求，甲、乙两种产品的生产量需保持1:1的比
标决策的需要而由线性规划逐步发展起来的一个分支。 由于现代化企业内专业分工越来越细，组织机构日益复
杂，为了统一协调企业各部门围绕一个整体的目标工作，产 生了目标管理这种先进的管理技术。目标规划是实行目标管 理的有效工具，它根据企业制定的经营目标以及这些目标的 轻重缓急次序，考虑现有资源情况，分析如何达到规定目标 或从总体上离规定目标的差距为最小。
min Z = f（ d ++ d - ）
（2） 要求不超过目标值，但允许达不到目标值，即只有使 正偏差量要尽可能地小（实现最少或为零）
min Z = f（ d +）
目标规划问题及模型
例1. 某企业计划生产甲，乙两种产品，这些产品分别要在 A,B,C,D四种不同设备上加工。按工艺文件规定，如表所示。

管理运筹学ppt6第六章 单纯形法的灵敏度分析与对偶ok

管理运筹学ppt6第六章 单纯形法的灵敏度分析与对偶ok

§ 1 单纯形表的灵敏度分析
解：首先求出x3在最终表上的系数列B−1P'6，zj,σj
迭代 基变
x1
x2
s1
s2
s3
x3
次数 量
cB
50 100
0
0
0
160
x1
50
1
0
1
0
-1
10.5
s2
0
0
0
-2
1
1
20
2
x2
100
0
1
0
0
1
1
zj
50
100
50
0
50 125
σj=cj-zj
0
0
-50
0
-50 35
➢ 基变量系数cB变化 ➢ 对所有的zj都变化，包括zk
z j cB p j
假设cB=(cB1, cB2,…, ck ,…,cBm)
(cB1, cB2,…, ck+ck ,…,cBm)
§ 1 单纯形表的灵敏度分析
原最优单纯形表可表示如下。
迭代 基变
…
xk
…
xj
…
次数 量
cB
…
ck
…
cj
…
xB1
若要最优解不变
j = j ck akj
当j≠k时， j
0
akj 0
ck
j
akj
akj 0
ck
j
akj
当j=k时， k ck ck zk
xk为基变量 k 0, akk 1
k = 0
=ck ck zk ck akk
max{
j

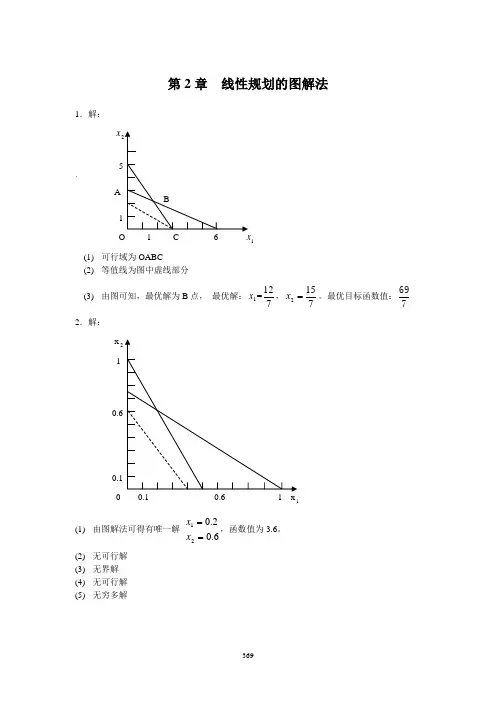
管理运筹学课后习题答案

管理运筹学课后习题答案

第2章 线性规划的图解法1．解：x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知，最优解为B 点， 最优解：1x =712，7152=x 。

最优目标函数值：7692．解： x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ，函数值为3.6。

(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ，函数值为392。

3．解：(1). 标准形式：3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式：21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式：21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4．解：标准形式：212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量（0，0） 最优解为 1x =1，x 2=3/2.标准形式：32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量（0.0.13） 最优解为 x 1=1，x 2=5.6．解：(1) 最优解为 x 1=3，x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8，x 2=0. (6) 不变化。

管理运筹学单纯形法的灵敏度分析与对偶对偶问题课件

管理运筹学单纯形法的灵敏度分析与对偶对偶问题课件
参数灵敏度分析关注的是模型中参数变化对最优解的影响 。通过分析参数变化对最优解的影响，可以了解参数变化 对模型最优解的影响程度和方向，从而为决策者提供有关 参数调整的建议。
参数灵敏度分析的方法包括局部灵敏度分析和全局灵敏度 分析。局部灵敏度分析关注单个参数的小幅度变化对最优 解的影响，而全局灵敏度分析则考虑多个参数同时变化对 最优解的影响。
结合的必要性
解决复杂优化问题
单纯形法在处理线性规划问题时具有高效性，而灵敏度分析和对偶问题则提供了分析和解决非线性规划问题的 工具。将两者结合，可以更好地解决复杂的优化问题。
提高决策准确性
通过灵敏度分析，可以对决策变量的微小变化对最优解的影响进行量化分析，从而更准确地预测和应对各种情 况。对偶问题则提供了从另一个角度审视问题的机会，有助于发现潜在的优化空间。
灵敏度分析与对偶对偶问题的概述
灵敏度分析是线性规划中研究最优解的敏感性的分析方法。它主要关注当模型参数发生变化时，最优 解和最优值的变化情况。通过灵敏度分析，可以了解模型参数对最优解的影响程度，从而更好地理解 和预测实际问题的变化趋势。
对偶对偶问题是线性规划中的一类重要问题。它主要研究原问题和对偶问题的关系，以及如何利用对 偶理论求解原问题。对偶对偶问题在理论研究和实际应用中都具有重要的意义，如资源分配、投资组 合优化等问题。
感谢您的观看
THANKS
通过建立线性规划模型，将物流配送 路径问题转化为求取最小成本的问题 。约束条件包括车辆路径限制、运输 成本限制等，目标函数为最小化总成 本。
灵敏度分析与对偶对 偶问题应用
在物流配送路径调整过程中，需要考 虑客户需求变化、运输成本变化等因 素对最优解的影响。通过灵敏度分析 ，可以确定最优解对不同因素变化的 敏感性，从而制定出更加合理的配送 路径。同时，通过对偶对偶问题的研 究，可以更好地理解配送路径的性质 和结构，进一步优化配送路径。

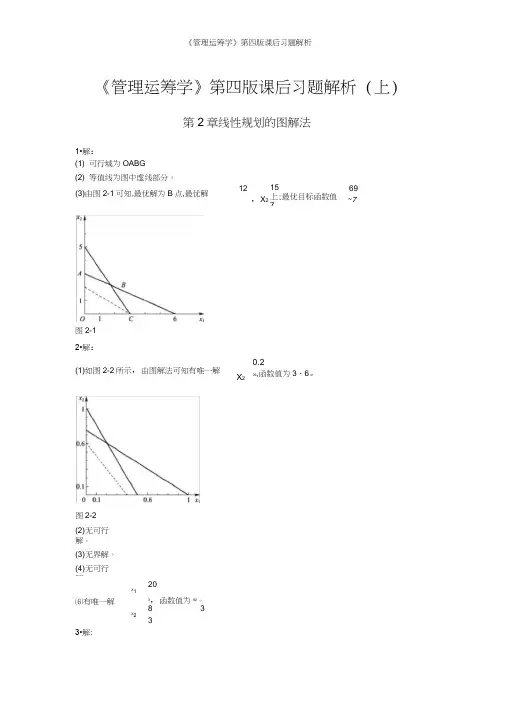
《管理运筹学》第四版课后习题解析

《管理运筹学》第四版课后习题解析

《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1•解：(1) 可行域为OABG(2) 等值线为图中虚线部分。

图2-1 2•解：3•解:12，X215上;最优目标函数值769~7X20.206,函数值为3、6。

X1⑹有唯一解X2 203，函数值为92。

8 3 3(3)由图2-1可知,最优解为B点,最优解图2-2(2) 无可行解。

(3) 无界解。

(4) 无可行解。

(1)如图2-2所示，由图解法可知有唯一解(1) 标准形式max 3x1 2x2 0s1 0s2 0s39x1 2x2 s1 303x1 2x2 s2 132x1 2x2 s3 9X i，X2，®,S2，S3 > 0(2) 标准形式min f 4X1 6X2 0S1 0S23X1 X2 S1 6X1 2X2 S2 107X1 6X2 4X1, X2，S1, S2》(3) 标准形式min f X1 2X2 2X2 0S1 0S23X1 5X2 5X2 S1 702X1 5X2 5X2 503X1 2X2 2X2 S2 30X i，X2，X2，q,S2 > 0 4.解: 标准形式maX z 10X1 5X2 0S1 0S23X1 4X2 S1 95X1 2X2 S2 8X1, X2,s1,s2> 0松弛变量(0，0)最优解为X1=1,X2=3/2。

5.解: 标准形式min f 11X1 8X2 0S1 0S2 0S310X1 2X2 S1 203X1 3X2 S2 184X1 9X2 S3 36X i，X2，S i，S2，S3 > 0剩余变量(0, 0, 13)最优解为X i=1,X2=5。

6•解：(1) 最优解为X I=3,X2=7。

(2) 1 q 3。

⑶ 2 C2 6。

Xi 6。

⑷4X 4。

⑸最优解为X1=8,X2=0。

(6)不变化。

因为当斜率1 < 9 < 1,最优解不变,变化后斜率为1,所以最优解不变。

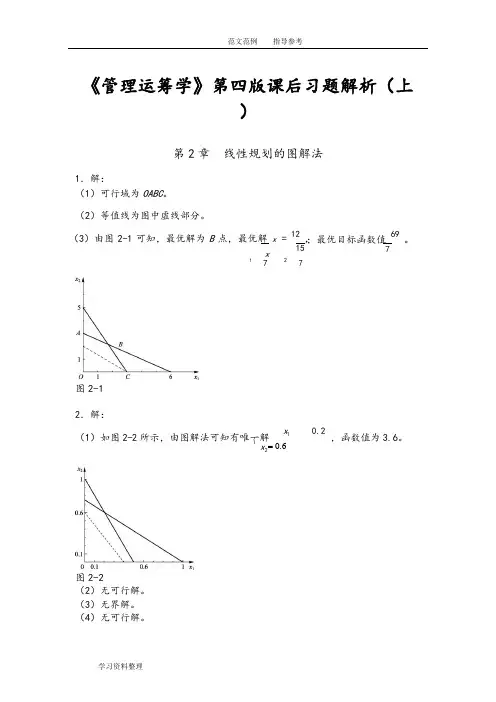
《管理运筹学》第四版课后习题答案解析

《管理运筹学》第四版课后习题答案解析

学习资料整理⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。

（2）等值线为图中虚线部分。

（3）由图2-1可知，最优解为B 点，最优解 x =12， x15 1727图2-1；最优目标函数值 69。

72．解：（1）如图2-2所示，由图解法可知有唯一解 x 10.2，函数值为3.6。

x 2图2-2（2）无可行解。

（3）无界解。

（4）无可行解。

⎨ （5）无穷多解。

x（6）有唯一解 120 3，函数值为 92 。

8 3x2 33．解：（1）标准形式max f3x 12x 20s 10s 20s 39x 1 2x 2 s 1 30 3x 1 2x 2 s 2 13 2x 12x 2s 39x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f4x 16x 20s 10s 23x 1x 2 s 16 x 12x 2s 210 7x 16x2 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min fx 12x 22x 20s 1 0s 23x1 5x 25x 2s 1702x 15x 25x 250 3x 12x 22x 2s 230x 1, x 2, x 2, s 1, s 2 ≥ 04．解： 标准形式max z10x 15x 20s 10s 2范文范例 指导参考学习资料整理3x 14x 2s 19 5x 12x 2s 28x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。

5．解： 标准形式min f11x 18x 20s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4x 19x 2s 336x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量（0, 0, 13）最优解为 x 1=1，x 2=5。

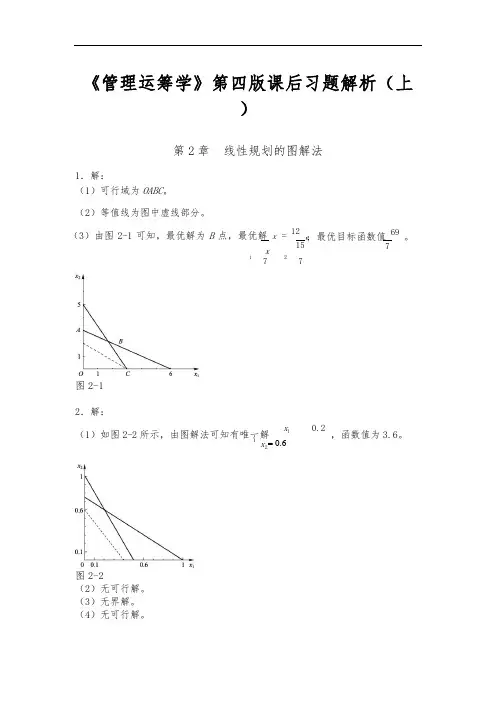
《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题答案

⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。

（2）等值线为图中虚线部分。

（3）由图2-1可知，最优解为B 点，最优解 x=12， x15 1727图2-1；最优目标函数值 69。

72．解：（1）如图2-2所示，由图解法可知有唯一解 x 10.2，函数值为3.6。

x 2图2-2（2）无可行解。

（3）无界解。

（4）无可行解。

⎨ （5）无穷多解。

x（6）有唯一解 120 3，函数值为 92 。

8 3x2 33．解：（1）标准形式max f3x 12x 20s 10s 20s 39x 1 2x 2 s 1 30 3x 1 2x 2 s 2 13 2x 12x 2s 39x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f4x 16x 20s 10s 23x 1x 2 s 16 x 12x 2s 210 7x 16x 2 4x 1,x 2, s 1, s 2 ≥ 0（3）标准形式min fx 12x 22x 20s 1 0s 23x 15x25x 2s 170 2x15x 25x 250 3x 12x 22x 2s 230x 1, x 2, x 2, s 1, s 2 ≥ 04．解： 标准形式max z10x 15x 20s 10s 23x 1 4x 2s915x1 2x 2 s2 8 x, x2 , s1, s2 ≥01≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。

5．解： 标准形式min f11x 18x 20s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4x 19x 2s 336x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量（0, 0, 13）最优解为 x 1=1，x 2=5。

6．解：（1）最优解为 x 1=3，x 2=7。

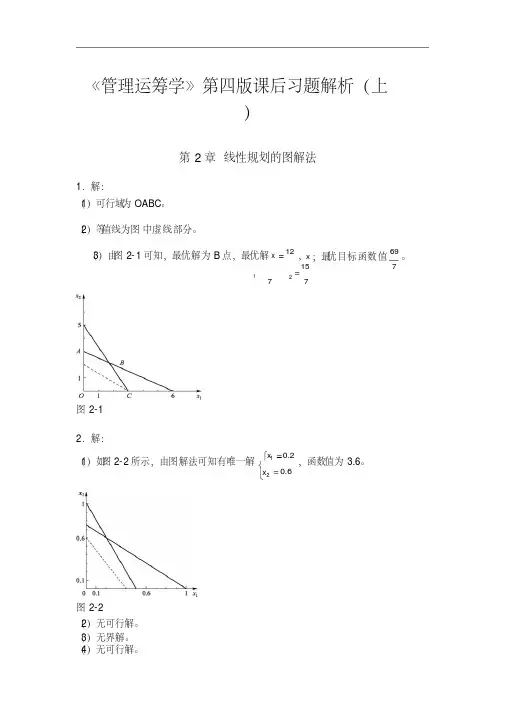
《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题答案
（2）标 准形式
min f 4 x1 6x2 0s1 0s2
3x1 x2 s1 6 x1 2 x2 s2 10 7 x1 6 x2 4 x1, x2 , s1, s2 ≥ 0
（3）标 准形式
min f x1 2 x2 2 x2 0s1 0s2
3x1 5x2 5x2 s1 70 2 x1 5 x2 5x2 50 3x1 2 x2 2x2 s2 30 x1, x2 , x2 , s1 , s2 ≥ 0
推 导 出 x1 18000 ，x2 3000 ，故基金 A 投 资 90 万元，基金 B 投 资 30 万元。
第 3 章 线性规划问题的计算机求 解
1．解： ⑴甲、乙两种柜的日 产量是分 别是 4 和 8，这时 最大利 润 是 2720 ⑵每多生 产一件乙柜，可以使 总利润 提高 13.333 元 ⑶常数 项 的上下限是指常数 项在指定的范 围内 变化时，与其对应 的约 束条件的 对 偶价格不 变。比如油漆时间变为 100，因为 100 在 40 和 160 之间，所以其对偶价格 不 变仍为 13.333 ⑷不 变，因为还 在 120 和 480 之间。
《管理运筹学》第四版课后习题解析（上 ）
第 2 章 线性规划的图解法
1．解： （1）可行域为 OABC。
（2）等值线为图 中虚 线 部分。
（3）由图 2- 1 可知，最优解为 B 点，最优解 x = 12 ，x ；最优目标 函数 值 69 。
15
7
1
7
2
7
图 2-1
2．解：
（1）如图 2- 2 所示，由图 解法可知有唯一解
（8）总 利润增加了 100×50=5 000，最优产 品组 合不 变。 （9）不能，因为对 偶价格 发生变 化。

广西大学MBA 管理运筹学 第六章 单纯形法的灵敏度分析与对偶

广西大学MBA 管理运筹学 第六章 单纯形法的灵敏度分析与对偶

迭代 次数
基变 量 CB x1 S2 x2 zj σj=cj-zj 50 0 100
x1 50 1 0 0 50 0
x2 100 0 0 1
s1 0 1 -2 0
s2 0 0 1 0 0 0
s3 0 -1 1 1 50 -50 b 50 50 250
Z= 27500
2
100 50 0 -50
先对非基变量s 的目标函数的系数C 先对非基变量 1的目标函数的系数 3进行灵敏度 分析。这里σ 分析。这里 3=-50，所以当 3 的增量 3≤-(-50)即 ，所以当C 的增量∆C 即 ∆C3≤50时，最优解不变，也就是说 1的目标函数的系数 时 最优解不变，也就是说S C′3=C3+△C3≤0+50=50时，最优解不变。 △ 时 最优解不变。 再对基变量x 的目标函数的系数C 进行灵敏度分析。 再对基变量 1的目标函数的系数 1进行灵敏度分析。
变成变成bbjj时由于表的迭代实际是约时由于表的迭代实际是约束方程的增广矩阵行的初等变换束方程的增广矩阵行的初等变换bbjj的变化并不影响系的变化并不影响系数矩阵的迭代故其最终表中的系数矩阵没有变化要数矩阵的迭代故其最终表中的系数矩阵没有变化要使其对偶价格不变只要原来最终表中的所有使其对偶价格不变只要原来最终表中的所有zzjj值都不值都不值是由基变量的系数与系数矩阵中值是由基变量的系数与系数矩阵中j列对应元素列对应元素相乘所得即相乘所得即zzjjbbpptt
从对偶价格的定义，可以知道当对偶价格为正时， 它将改进目标函数值。对于求目标函数最大值的线性 规划来说改进就是增加其目标函数值，而对求目标函 数最小值的线性规划来说改进却是减少其目标函数值。 当对偶价格为负时，它将“恶化”目标函数值， 对求目标函数最大值的线性规划来说恶化就是减少其 目标函数值，而对求目标函数最小值的线性规划来说 “恶化”却是增加其目标函数值。 在第三章我们已提及过影子价格，对于求目标函 数最大值的线性规划中对偶价格等于影子价格，而对 求目标函数最小值的线性规划中影子价格为对偶价格 的相反数。

《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题解析（上）第2章线性规划的图解法1 •解：1 ）可行域为OABC2）等值线为图中虚线部分2•解：『X =0 21）女图2-2所示，由图解法可知有唯一解X1 _ . ,函数值为3.6凶=°.6图2-22） 无可行解。

3） 无界解。

4） 无可行解。

3）由图2-1可知，最优解为B 点，最优解辿=12，丿 最优目标函数值 _152 _ 76975）无穷多解3•解:1）标准形式max f =3x i 2x 2 0s i - 0s 2 - 0s 39xi 2x 2 si =303x 1 亠2X 2 亠s =132x i 亠2x 2 亠S 3 =9x i , x 2 ,S 1, S 2, S 3》02） 标准形式min f =4x 1 亠6x 2 亠0$ 亠0s 23x i - X 2 - Si — 6x 1 2x 2 S 2 =i07x i -6x 2 =4x i , x , S i , S 2 A 03） 标准形式min f =xi —2X 2 亠2X 2 亠0s 1 亠0S 2-3x i 5x 2 -5x 2 S i =702x i -5x 2 5X 2： =503x i 2x 2 —2x 2 -S 2 =30x i , xl X 2： Si, S 2 A 0 4•解：标准形式max z =10x i ' 5x 2 ' 0s i 0S 23x 1 4x 2 Si =95xi 2x 2 S 2 =8x i , x , S i , S 2 A 06）有唯一解■: X 2=20 3，函数值为 83 92 3松弛变量0,0） 最优解为x i =1, X 2=3/2。

5•解：标准形式min f =11x i 8x 2 - 0s i - 0s 2 - 0S 310X 1 2X 2 -s 1 =203X I 亠 3X2 -S 2 =184X1 9X2 —S3 =36X 1, X 2 , S 1, S 2 , S3》0剩余变量0, 0, 13)最优解为X 1=1 , X 2=5。

《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题答案

《电路理论》课程教学大纲⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。

（2）等值线为图中虚线部分。

（3）由图2-1可知，最优解为B 点，最优解 x=12， x = 15 1727图2-1；最优目标函数值 69。

72．解：（1）如图2-2所示，由图解法可知有唯一解⎧x 1 = 0.2，函数值为3.6。

⎩x 2图2-2（2）无可行解。

（3）无界解。

《电路理论》课程教学大纲（4）无可行解。

⎨ （5）无穷多解。

⎧x = （6）有唯一解 ⎪ 1⎪ 203 ，函数值为 92 。

8 3 x = ⎪⎩ 2 33．解： （1）标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4．解： 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。

管理运筹学--单纯形法的灵敏度分析与对偶对偶问题讲课讲稿

管理运筹学--单纯形法的灵敏度分析与对偶对偶问题讲课讲稿
2. 初始单纯表中的基变量Xs=b，迭代后的单 纯形表中为XB= B-1b
3. 初始单纯表中的约束系数矩阵为：
[A,I]=[B,N,I] 迭代后的单纯形表中约束系数矩阵为：
[B-1A, B-1I]=[B-1B, B-1N, B-1I]=[I , B-1N, B-1] 4. 若初始矩阵中变量xj的系数向量为Pj，迭代
x4
x5 值
0 x3
8
1
0
1
0
0
0 x4 12 0 2 0 1 0
0 x5 36 3 4 0 0 1
检验数j
3 50 0 0
• 最优基和最优基的逆
Cj
3 5 0 0 0比
CB XB
b
x1
x2 x3
x4
x5 值
0 x3 4 0 0 1 2/3 -1/3
5 x2 6 0 1 0 1/2 0
3 x1 4 1 0 0 -2/3 1/3
0
0
1
表
j
0
0 -50
0
-50
初始单纯形表为:
Cj
CB
CN
0
XB
XN
XS
0
X S
b
B
N
I
检验数j
CB
CN
0
当迭代若干步，基变量为X B时，新的单纯形表:
Cj
CB
CN
0
XB
XN
XS
CB
b X B
B-1
I
检验数j
0
B-1N CN- CB B-1N
B-1 - CB B-1
小结
1. 对应初始单纯表中的单位矩阵I，迭代后的 单纯形表中为B-1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《管理运筹学》第四版第6章单纯形法的灵敏度分析与
对偶课后习题解析
《管理运筹学》第四版第6章单纯形法的灵敏度分析与对
偶课后习题解析
《管理运筹学》第四版课后习题解析
第6章单纯形法的灵敏度分析与对偶
1(解：
(l)cl?24
⑵ c2?6
(3)cs2?8
2(解：
(1)cl??0.5
(2)?2?c3?0
(3)cs2?0.5
3(解：
(1)bl?250
(2)0?b2?50
(3)0?b3?150
4(解：
(1)bl??4
(2)0?b2?10
(3)b3?4
最优基矩阵和其逆矩阵分别为:B???
最优解变为xl?10??10??l??, B????41??;41?????x2?0, x3?13,最小值变为-78;
?0, x2?14, x3?2,最小值变为-96;最优解没有变化;最优解变为xl
6(解：
⑴利润变动范围cl?3,故当cl=2时最优解不变。

⑵根据材料的对偶价格为1判断，此做法有利。

(3)0?b2?45o
(4)最优解不变，故不需要修改生产计划。

(5)此时生产计划不需要修改，因为新的产品计算的检验数为?3小于零，对原生产计划没有影响。

7.解：
⑴设xl,x2,x3为三种食品的实际产量，则该问题的线性规划模型为
max z?2.5xl?2x2?3x3
约束条件:8xl?16x2?10x3?350
10xl?5x2?5x3?450
2xl?13x2?5x3?400
xl,x2,x3?0
解得三种食品产量分别为xl?43.75,x2?x3?0,这时厂家获利最大为109.375万
ye©
(2)如表中所示，工序1对于的对偶价格为0.313万元，由题意每增加
10工时可以多获利3.13万元，但是消耗成本为10万元，所以厂家这样做不合算。

(3)B食品的加工工序改良之后，仍不投产B,最大利润不变;
若是考虑生产甲产品，则厂家最大获利变为169.7519万元，其中
xl?14.167,x2?0, x3?ll, x4?31.667;
(4)若是考虑生产乙产品，则厂家最大获利变为163.1万元，其中xl?ll,x2?0, x3?7.2, x4?38;
所以建议生产乙产品。

8(解：
均为唯一最优解，根据从计算机输出的结果看出，如果松弛或剩余变量为零且对应的对偶价格也为零，或者存在取值为零的决策变量并且其相差值也为零时，可知此线性规划有无穷多组解。

9(解：
(1)minf= 10yl+20y2.
s.t.yl+y2?2
yl+5y2?l
yl+y2?l
yi,y2?0
(2)max JL— 1 OOyl +200y2.
s.t. l/2yl+4y2?4
2yl+6y2?4
2yl+3y2?2
yl,y2?0
10(解
(l)min f=?10yl+50y2+20y3.
s.t. ?2yl +3y2+y3?l
?yl+y2+y3 =5
yl, y2?0, y3没有非负限制。

(2)max z= 6yl?3y2+2y3.
s.t.yl?y2?y3?l
2yl+y2+y3 =3
?3yl+2y2?y3??2
yl, y2?o, y3没有非负限制
11.解：
max z?6y 1 ?7y2?8y3?9y4?l Oy5
约束条件:yl?y5?l
yl?y2?l
y2?y3?l
y3?y4?l
y4?y5?l
yl,y2,y3,y4,y5?0
用对偶问题求解极大值更简单，因为利用单纯形法计算时省去了人工变量。

12.解：
⑴该问题的对偶问题为
max f?4yl?12y2
约束条件:3yl ?y2?2
2yl?3y2?3
yl?y2?5
求解得maxf=12,如下所示：
(2)该问题的对偶问题为min Z?2yl?3y2?5y3约束条件:2yl?3y2?y3??3
3yl?y2 ?4y3 ??8 5yl?7y2 ?6y3 ??10
yl,y2,y3?0
求得求解得min z=24,如下所示：
思考：
在求解
min f?CX 约束条件:AX?b X?0
max 2?CX 约束条件:AX?b X?0
以上两种线性规划时一般可以选取对偶单纯形法。

13.解：
其中:C为非负行向量，列向量b中元素的符号没有要求
其中:C为非正行向量，列向量b中元素的符号没有要求
⑴错误。

原问题存在可行解，则其对偶问题可能存在可行解，也
可能无可行解；
(2)正确;
(3)错误。

对偶问题无可行解，则原问题解的情况无法判定，可能无可行解，可能有可行解，甚至为无界解;(4)正确；
14(解：
maxz??xl ?2x2?3x3
??4??xl?x2?x3?sl
?x2?x3?s3??2?
?xi?04?l,?,3；sj?0,j?l,?,3?
用对偶单纯形法解如表6-1所示。

表6-1
续表
最优解为xl=6, x2=2, x3=0,目标函数最优值为10。

15.解:原问题约束条件可以表示为AX?b?ta,其中a和b为常数列向量。

令t?0,将问题化为标准型之后求解，过程如下：
其中最优基矩阵的逆矩阵为
?100????1
B???ll?l?,
?001???
则
B*b???ll?l??10???2?
，001 »3»3冲»»
♦ vx VZ d •♦♦♦♦♦•
?100??t??l??t?????????
B?1 *ta???l 1 ?1 ???t??t??3????3t?
?001??t??l??t?????????
?5?t???
(b?ta)??2?3t?则B?l*
?3?t???
从而，1)当
时，最优单纯形表为2?3t?0, 3?t?0,此0^ 5?t?0,线性规划问题的最优解为(xl,x2)?(5?t,3?t^,
目标函数最大值为ll?3t;
37
2)当?t?时，由2?3t?0可知，(xl,x2)?(5?&3?t)并非最优解，利用对偶
22
此时7?2t?0, ?2?3t?0, 3?t?0,从而线性规划问题的最优解为
(xl,x2)?(7?2t,3?t),目标函数的最大值为13; 3)当
7
?t?10 时，，由7?2t?0 可知,(xl,x2)?(7?2t,3?t)并非最优解,利用 2
此时?7?2t?0, 5?t?0, 10?t?0,从而线性规划问题的最优解为
(xl,x2)?(0,10?t),目标函数的最大值为20?2t;
16解先写出原问题的对偶问题
min f?20yl ?20y2
约束条件:yl?4y2?2⑴
2yl?3y2?2 (2) 3yl?2y2?l
(3)4yl?y2?l (4)
yl,y2?0
13
将yl?,y2?代入对偶问题的约束条件，得有且只有(2)、(4)式等式成立，105
也就是说，其对应的松弛变量取值均为0,⑴和(3)式对应的松弛变量不为0,
从而由互补松弛定理有xl?x3?0;又因为yl?0,y2?0,从而原问题中的
两个约束应该取等式，把xl?x3?0代入其中，得到
2x2?4x4?20
3x2 ?x4?20
解方程组得到x2?6,x4?2o经验证xl?0,x2?6,x3?0,x4?2满足原问题约
束条件，从而其为原问题的最优解，对应的目标函数最大值为14;。