向量及向量的加减法
- 格式:ppt
- 大小:226.00 KB
- 文档页数:19
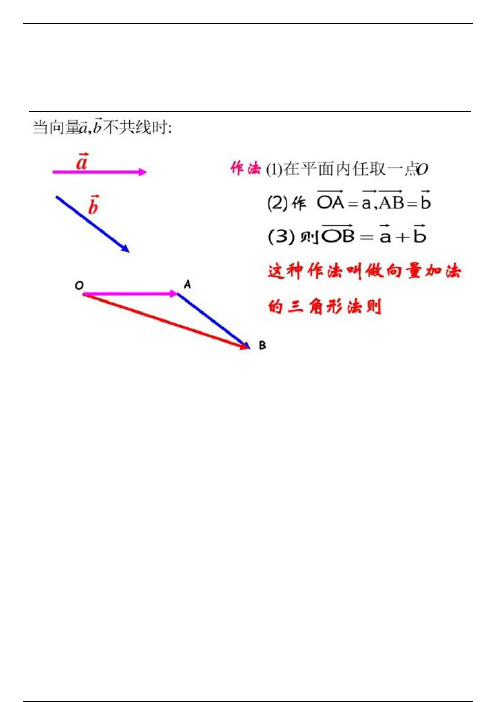
向量的加法口诀: 首尾相连,首连尾,方向指向末向量。
以第一个向量的起点为起点,以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算,图像如下图所示:向量的减法口诀: 首首相连,尾连尾,方向指向被减向量。
以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容,要求同学们会向量的基本运算,其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算,学会运用图像解决向量加减法,向量的数乘等问题。
向量的相关题目难度也不是很大,只要大家认真学习,认真做好笔记,认真做做题目,总结做题规律,那么当我们遇到类似题目时就会似曾相识,做起来也很顺手,再细心点的话,得满分也没有问题。
学习方法很多,重要的事找到适合自己的方法,当然适合自己方法就是最好的方法。
附一;三角形定则解决向量加减的方法将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减,则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的λ∣倍;当∣λ∣<1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义:已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义:两个向量的数量积(内积、点积)是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示:a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a(交换律);(λa)·b=λ(a·b)(关于数乘法的结合律);(a+b)·c=a·c+b·c(分配律);向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即:由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b.若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积.。


向量的加减法3、向量的加法求两个向量的和向量的运算叫做向量的加法.法则:①三⾓形法则;②平⾏四边形法则.运算律:交换律+=+,结合律(+)+=+(+).4、向量的减法向量的加法和减法互为逆运算.已知两个向量的和及其中⼀个向量,求另⼀个向量的运算叫做向量的减法.差向量:向量加上的相反向量,叫做与的差(向量)求差向量的⽅法:向量减法的三⾓形法则,即减向量的终点指向被减向量的终点.⼆、重难点知识剖析1、的字母是有顺序的,起点在前终点在后,所以我们说有向线段有三个要素:起点、⽅向、长度;既有⼤⼩⼜有⽅向的量,我们叫做向量,有⼆个要素:⼤⼩、⽅向.向量不能⽐较⼤⼩;实数与向量不能相加减,但实数与向量可以相乘.向量与有向线段的区别:向量是⾃由向量,只有⼤⼩和⽅向两个要素;与起点⽆关:只要⼤⼩和⽅向相同,则这两个向量就是相同的向量;有向线段有起点、⼤⼩和⽅向三个要素,起点不同,尽管⼤⼩和⽅向相同,也是不同的有向线段2、已知向量、在平⾯内任取⼀点,作,,则向量叫做与的和,记作,即3、向量减法的三⾓形法则:两个向量相减,则表⽰两个向量起点的字母必须相同(否则⽆法相减),这样两个向量的差向量是以减向量的终点的字母为起点,以被减向量的终点的字母为终点.在平⾯内任取⼀点O,作,则向量.4、多边形法则:⼀般地,⼏个向量相加,可把这⼏个向量顺次⾸尾相接,那么它们的和向量是以第⼀个向量的起点为起点、最后⼀个向量的终点为终点的向量.只要你理解法则内容,那么解起向量加减法的题来就会更加得⼼应⼿了,尤其遇到向量的式⼦运算题时,⼀般不⽤画图就可迅速求解,如下⾯例题:(1)化简-+-=(+)-(+)=-=(2)化简+++=.特殊情况:两向量平⾏对于零向量与任⼀向量,有三、例题讲解例1、化简下列各式:(1);(2).分析:利⽤向量加法、减法的运算律。
解:(1)原式= =;(2)原式==;点评:⼀般地,我们总有因此在涉及到向量的有关运算时,要注意围绕上述基本结论进⾏变形。

一、空间向量的定义
在空间中,我们把具有大小和方向的量叫做向量。
二、空间向量的坐标表示:
如图给定空间直角坐标系和向量,设为坐标向量,则存在唯一的有序实数组,使,有序实数组叫作向量在空间直角坐标系中的坐标,记作。
三、空间向量的理解:
(1)向量一般用有向线段表示,同向等长的有向线段表示同一或相等的向量;
(2)空间的两个向量可用同一平面内的两条有向线段来表示。
四、空间向量的加法、减法的定义:
与平面向量运算一样,空间向量的加法、减法如下:
运算律:
(1)加法交换律:;
(2)加法结合律:;
(3)数乘分配律:λ=λ+λ
坐标表示:
若,,则。
五、向量加法的几个重要结论:
①和向量的模满足当同向时右等号成立,当反向时左等号成立,当中有零向量时两等号成立,当不共线时,上式的几何意义是三角形任意一边小于另两边之和,大于另两边之差;
②几个向量相加,可通过平移将它们转化为首尾相接的向
量.
③首尾相接的若干个向量构成一个封闭图形,则它们的和为零向量.。

如何求解向量的加减法和数量积向量在数学和物理学中有着广泛的应用,了解如何求解向量的加减法和数量积是掌握向量运算的基础。
本文将介绍向量的概念,并详细说明如何进行向量的加减法和数量积运算。
一、向量的概念及表示方法向量是具有大小和方向的量,常用箭头标记表示。
向量可以表示位移、速度、力以及其它物理量。
在二维平面中,向量可以表示为一个有序数对 (a,b),其中 a 是横坐标分量,b 是纵坐标分量。
在三维空间中,一个向量可以表示为一个有序数组 (a,b,c),即 (a,b,c)。
二、向量的加法向量的加法是指将两个向量相加得到一个新的向量。
向量的加法满足交换律和结合律。
对于两个二维向量 A(a1, a2) 和 B(b1, b2),它们的加法计算方式如下:(A + B)(a1 + b1, a2 + b2)三、向量的减法向量的减法是指将一个向量从另一个向量中减去得到一个新的向量。
对于两个二维向量 A(a1, a2) 和 B(b1, b2),它们的减法计算方式如下:(A - B)(a1 -b1, a2 - b2)四、向量的数量积向量的数量积也称点积或内积,是一种运算方式,其运算结果为一个标量(即一个实数)。
对于两个二维向量 A(a1, a2) 和 B(b1, b2),它们的数量积计算方式如下:A ·B = a1b1 + a2b2五、向量的运算性质1. 向量的加法满足交换律和结合律,即 A + B = B + A,(A + B) + C = A + (B + C)。
2. 向量的减法需要使用负向量来表示,即 A - B = A + (-B)。
3. 向量的数量积满足交换律,即 A · B = B · A。
4. 向量的数量积满足分配律,即 A · (B+C) = A · B + A · C。
六、向量的加减法和数量积的应用向量的加减法和数量积在物理学、工程学等领域有着广泛的应用。

1向量及向量的加减法5.1 向量及向量的加减法要点透视:1.由于«Skip Record If...»的方向是任意的,且规定«Skip Record If...»平行于任何向量,故在有关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件.2.向量不能比较大小,但向量的模可以比较大小.3.数学中研究的向量是自由向量,只有大小、方向两个要素,起点可以任意选取,现在必须区分清楚共线向量中的“共线”与几何中的“共线”、的含义,要理解好平行向量中的“平行”与几何中的“平行”是不一样的.4.向量的几何加法有两种法则:平行四边形法则和三角形法则.当两个向量的起点公共时,用平行四边形法则;当两向量是首尾连接时,用三角形法则.向量加法的三角形法则可推广至多个向量相加:«Skip Record If...»,但这时必须“首尾相连”.活题解析:例1.给出下列命题:①若|«Skip Record If...»|=|«Skip Record If...»|,则«Skip Record If...»=«Skip Record If...»;②若A,B,C,D是不共线的四点,则«Skip Record If...»是四边形ABCD为平行四边形的充要条件:③若«Skip Record If...»=«Skip Record If...»,«Skip Record If...»=«Skip Record If...»,则«Skip Record If...»=«Skip Record If...»,④«Skip Record If...»=«Skip Record If...»的充要条件是|«Skip Record If...»|=|«Skip Record If...»|且«Skip Record If...»//«Skip Record If...»;⑤若«Skip Record If...»//«Skip Record If...»,«Skip Record If...»//«Skip Record If...»,则«Skip Record If...»//«Skip Record If...»,其中正确的序号是。
高考数学中的向量运算及其应用技巧向量是高中数学中非常重要的一部分,它不仅有着广泛的应用,而且在高考中也是不可或缺的一部分。
在高考数学中,向量作为基础知识,被广泛应用于解析几何、平面几何、三角函数等领域。
本文将为大家介绍高考数学中的向量运算及其应用技巧,帮助同学们更好地掌握这一知识点。
一、向量运算1. 向量的加减法向量的加减法是向量运算中的基本操作。
向量的减法要用到相反向量。
向量的相反向量是指与其大小相等,方向相反的向量。
设向量 $\vec{a}$ 与 $\vec{b}$,则它们的加法与减法运算如下:$$\vec{a}+\vec{b}=\vec{c}$$$$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})=\vec{d}$$其中 $\vec{c}$ 为向量的和, $\vec{d}$ 为向量的差。
2. 向量的数量乘法向量的数量乘法是指向量与一个实数的积,用来改变向量的大小和方向。
设向量$\vec{a}$,实数$k$,则它们的数量乘法如下:$$k\vec{a}=\vec{b}$$其中 $\vec{b}$ 的大小是 $\vec{a}$ 的大小的 $|k|$ 倍,如果$k$ 是正数,方向与 $\vec{a}$ 方向相同;如果 $k$ 是负数,方向与 $\vec{a}$ 方向相反。
3. 向量的数量积向量的数量积是指两个向量相乘,得到的是一个实数。
设向量$\vec{a}$,$\vec{b}$,则它们的数量积如下:$$\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos \theta $$其中 $\theta$ 是 $\vec{a}$ 与 $\vec{b}$ 的夹角。
由于 $\cos\theta$ 的范围是 $[-1,1]$,如果 $\vec{a}$ 与 $\vec{b}$ 的夹角小于$90^{\circ}$,那么它们的数量积是正数;如果夹角是$90^{\circ}$,那么数量积是 $0$;如果 $\vec{a}$ 与 $\vec{b}$ 的夹角大于$90^{\circ}$,那么数量积是负数。
向量加减法的原理
向量加减法是在向量空间中对向量进行操作的一种方法。
向量是有方向和大小的量,可以表示为一组有序数。
在加减法中,我们对向量的对应分量进行相加或相减。
假设有两个向量A和B,可以表示为:
A = (a₁, a₂, a₃, ..., aₙ)
B = (b₁, b₂, b₃, ..., bₙ)
其中a₁, a₂, ..., aₙ和b₁, b₂, ..., bₙ是向量的对应分量。
向量加法的原理是将两个向量的对应分量相加,得到一个新的向量C:
C = A + B = (a₁+ b₁, a₂+ b₂, a₃+ b₃, ..., aₙ+ bₙ)
向量减法的原理是将第二个向量的对应分量取相反数,然后与第一个向量相加,得到一个新的向量C:
C = A - B = (a₁- b₁, a₂- b₂, a₃- b₃, ..., aₙ- bₙ)
向量加减法遵循向量的代数运算性质,例如,满足交换律和结合律。
这些性质使
得向量加减法在物理学、几何学、计算机图形学等领域中得到广泛应用。
需要注意的是,两个向量进行加减法的前提是它们的维度相同,即两个向量拥有相同的分量个数。
否则,加减法操作是没有定义的。
向量的加减法教案第一章:向量简介1.1 向量的定义向量的概念:具有大小和方向的量向量的表示方法:用箭头表示,例如→a 或<a, b>1.2 向量的性质向量的大小:向量的长度或模向量的方向:向量的起点到终点的线段单位向量:大小为1的向量1.3 向量的坐标表示二维空间中的向量:用(x, y) 表示三维空间中的向量:用(x, y, z) 表示第二章:向量的加法2.1 向量加法的定义向量加法:将两个向量的对应分量相加得到新的向量2.2 向量加法的几何意义向量加法:起点相同的两个向量,终点相加得到一个新的向量2.3 向量加法的坐标表示二维空间中的向量加法:(a, b) + (c, d) = (a+c, b+d)三维空间中的向量加法:(a, b, c) + (d, e, f) = (a+d, b+e, c+f) 第三章:向量的减法3.1 向量减法的定义向量减法:将两个向量的对应分量相减得到新的向量3.2 向量减法的几何意义向量减法:起点相同的两个向量,终点相减得到一个新的向量3.3 向量减法的坐标表示二维空间中的向量减法:(a, b) (c, d) = (a-c, b-d)三维空间中的向量减法:(a, b, c) (d, e, f) = (a-d, b-e, c-f)第四章:向量的数乘4.1 向量数乘的定义向量数乘:将一个向量与一个实数相乘得到新的向量4.2 向量数乘的几何意义向量数乘:将向量的大小乘以实数,方向不变4.3 向量数乘的坐标表示二维空间中的向量数乘:(a, b) c = (ac, bc)三维空间中的向量数乘:(a, b, c) c = (ac, bc, cc)第五章:向量加减法的应用5.1 向量加减法的几何应用向量加减法在几何图形中的应用,例如计算向量位移、速度等5.2 向量加减法的物理应用向量加减法在物理学中的应用,例如计算力的合成和分解5.3 向量加减法的实际应用向量加减法在计算机图形学中的应用,例如计算图像的位移和旋转第六章:向量加减法的运算律6.1 向量加法的运算律交换律:向量a + 向量b = 向量b + 向量a结合律:(向量a + 向量b) + 向量c = 向量a + (向量b + 向量c)6.2 向量减法的运算律减法与加法的关联:向量a 向量b = 向量a + (-向量b)结合律:(向量a 向量b) 向量c = 向量a (向量b + 向量c)第七章:向量的数乘运算7.1 向量数乘的运算律分配律:向量a (向量b + 向量c) = (向量a 向量b) + (向量a 向量c) 结合律:向量a (向量b 向量c) = (向量a 向量b) 向量c7.2 标量与向量的运算标量与向量相乘:标量向量= 向量标量第八章:向量加减法的应用举例8.1 二维空间中的向量加减法应用例题:计算物体在两个力的作用下的位移8.2 三维空间中的向量加减法应用例题:计算飞机在两个推力的作用下的位移第九章:向量的数乘应用举例9.1 二维空间中的向量数乘应用例题:计算物体在力的大小变化后的加速度9.2 三维空间中的向量数乘应用例题:计算飞机在推力大小变化后的加速度向量加减法的基本概念、运算律及应用10.2 向量加减法的拓展向量加减法在其他领域的应用,例如生物学、经济学等10.3 向量加减法的练习题及解答提供一些向量加减法的练习题,帮助学生巩固所学知识重点和难点解析一、向量简介1.1 向量的定义与表示方法:理解向量的基本概念,以及向量的大小和方向。