苏科版七年级上册数学第五章5.3展开与折叠(1).docx

苏科版数学七年级上册教学设计《5-3展开与折叠（第1课时）》一. 教材分析《5-3展开与折叠（第1课时）》是苏科版数学七年级上册的一部分，本节课的主要内容是让学生理解并掌握展开与折叠的概念，能够运用展开与折叠的方法解决一些实际问题。

教材通过丰富的实例和直观的图片，引导学生探索和发现展开与折叠的规律，培养学生的空间想象能力和抽象思维能力。

二. 学情分析七年级的学生已经具备了一定的空间想象能力和抽象思维能力，他们对平面图形和立体图形有一定的了解。

但学生在解决实际问题时，往往缺乏将实际问题转化为数学问题的能力。

因此，在教学过程中，教师需要注重培养学生的转化能力和解决问题的能力。

三. 教学目标1.了解展开与折叠的概念，能够正确进行展开与折叠操作。

2.能够运用展开与折叠的方法解决一些实际问题。

3.培养学生的空间想象能力和抽象思维能力。

4.提高学生的转化能力和解决问题的能力。

四. 教学重难点1.展开与折叠的概念及其应用。

2.将实际问题转化为数学问题。

五. 教学方法1.情境教学法：通过丰富的实例和直观的图片，引导学生探索和发现展开与折叠的规律。

2.启发式教学法：教师提出问题，引导学生思考和讨论，培养学生的问题解决能力。

3.合作学习法：学生分组进行讨论和实践，培养学生的团队合作能力。

六. 教学准备1.准备相关的实例和图片，用于引导学生探索和发现展开与折叠的规律。

2.准备一些实际问题，用于学生练习和巩固展开与折叠的方法。

3.准备黑板和粉笔，用于板书和展示。

七. 教学过程1.导入（5分钟）教师通过展示一些实例和图片，引导学生观察和思考，提出问题：“你们看过地图吗？地图是如何展开的？如果将地图折叠起来，会是怎样的形状？”让学生发表自己的看法，引出展开与折叠的概念。

2.呈现（10分钟）教师通过展示更多的实例和图片，引导学生探索和发现展开与折叠的规律。

例如，展示一个圆柱体展开后的图形，让学生观察和思考，引导学生发现圆柱体的展开图是由一个矩形和两个圆组成的。

5.3 展开与折叠
1、侧面展开图是扇形的是（）
A、圆柱
B、棱柱
C、圆锥
D、棱锥
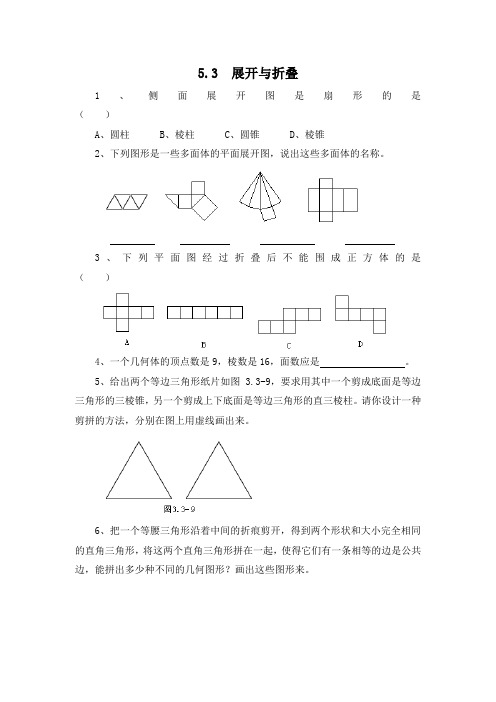
2、下列图形是一些多面体的平面展开图，说出这些多面体的名称。

3、下列平面图经过折叠后不能围成正方体的是（）
4、一个几何体的顶点数是9，棱数是16，面数应是。

5、给出两个等边三角形纸片如图 3.3-9，要求用其中一个剪成底面是等边三角形的三棱锥，另一个剪成上下底面是等边三角形的直三棱柱。

请你设计一种剪拼的方法，分别在图上用虚线画出来。

6、把一个等腰三角形沿着中间的折痕剪开，得到两个形状和大小完全相同的直角三角形，将这两个直角三角形拼在一起，使得它们有一条相等的边是公共边，能拼出多少种不同的几何图形？画出这些图形来。

7、如图3.3-10，是一个边长为4cm的正方体木块，在它的表面涂上颜色，然后切成边长为1cm的小正方体木块，没有涂上颜色的有多少块？
参考答案
5.3 展开与折叠（第二课时）
1、C；
2、三棱锥，三棱柱，四棱锥，四棱柱；
3、B；
4、9；
5、剪拼方法如下图：
6、三种，如下图所示：
7、4个。

初中数学试卷
鼎尚图文**整理制作。

5.3 展开与折叠教学目标知识技能目标：了解简单几何体的表面展开图形。

能想象并画出简单几何体的表面展开图形。

过程性目标：经历展开的过程，感受立体图形与平面图形的关系，体验图形的变化过程，积累数学学习的经验。

情感与态度目标：经历合作与探索、竞赛的学习过程，养成学生研究性学习、合作学习的习惯，培养学生的合作学习的精神，激发学生对数学的兴趣。

教学重难点重点：经历数学活动的过程，感受平面图形与立体图形的关系，发展空间想象力。

难点：想象简单几何体表面展开图形的形状，由简单几何体的表面展开图形，想象其折叠成立体图形的过程。

教学过程：一、自主先学1.课前与你的小伙伴探讨将我们学过几何体（如：圆柱、圆锥、三棱柱、三棱锥）展开成平面图形吗？展示你自学的成果2.学以致用：如图，第一行的几何体表面展开后得到第二行的某个平面图形，请用线连一连．二、探究合作：1.如何将一个正方体纸盒沿棱剪开，并展开成一个平面图形？（借助下面的网格纸把你的展开图画下来）2．要将一个正方体纸盒的表面展开成一个平面图形，要剪开多少条棱？归纳：_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________三．演练空间 1.出示PPT 练习一2.如果“你”在前面，那么谁在后面？3.如图所示的立方体，如果把它展开，可以是下列图形中的小结：这节课你最大的收获是什么？ 课后作业：1．请你将一个长方体纸盒沿棱剪开展开成平面图形，试画出展开后的平面图形并与同学交流．当堂检测：1、请写出图中，各个几何体的展开图是什么几何体的展开图。

5.3 展开与折叠(1)一、基础训练1.圆锥的侧面展开图是 ( )A．长方形 B．正方形 C．圆 D．扇形2.在如图所示的图形中，是三棱柱的平面展开图的是( )A B C D3.下列各图经过折叠后不能围成一个正方体的是( )A B C D4.一个正方体，六个面上分别写着六个连续的整数，且每个相对面上的两个数之和相等，如图所示，你能看到的数为7、10、11，则六个整数的和为（）A．51 B．52 C．57 D．58二、综合应用5.如图2, 已知正方体的各个侧面分别标上字母a，b，c，d，e，f；其中a在后面，b在下面，c在左面，则下列结论错误的是（）（A）d在上面（B）e在前面（C）f在右面（D）d在前面6.用一张长方形的纸，可围成种不同的圆柱．7.三棱锥的展开图是由个形组成的, 圆锥的展开图是由一个和一个形组成的图形．8.若要使如图3所示的平面展开图按虚线折叠成正方体后，相对面上两个数之和为6，则x=_____，y=_____。

9.如图4所示是一多面体的展开图形，每个面都标有字母，请根据要求回答提问：（1）如果面A在多面体的底部，那么面在上面.（2）如果面F在前面，从左面看是面B，则面在上面.（3）从右面看是面C，面D在后面，面在上面.10.下列图形中，哪些图形通过折叠可以围成一个棱柱？先想一想，然后动手折一折．不能围成棱柱的，如何变化图形使得它能围成四棱柱?⑴⑵⑶11.如图所示图是长方体的表面展开图，折叠成一个长方体，那么与字母 J重合的点是哪几个？12.已知平面上连结两点的所有连线中，线段最短．现有一只虫子从圆柱上A点处绕圆柱侧面爬到B点处，你能画出它爬行的最短路线吗？请画出圆柱的侧面展开示意图和侧面展开示意图上小虫爬行的最短路线.三、思维拓展13.现有一个正方体，一只蚂蚁从点A沿正方体的表面爬到点B，请你在图中画出由A爬到B的最短途径. (画法至少3种，越多越好,看谁画法多！)§5．3 展开与折叠(1)一．选择题1．D 2. D 3. D 4. C 5. D二．填空题6．两 7．四三角形圆扇形8．5 3 9．（1）F，（2）E，（3）F三．解答题10．图②11．N和H12．长方形及其对角线(图略)13．14．初中数学试卷桑水出品。

5.3 展开与折叠第一课时教学目标一、教学重难点重点：经历数学活动的过程，感受平面图形与立体图形的关系，发展空间想象力。

难点：想象简单几何体表面展开图形的形状，由简单几何体的表面展开图形，想象其折叠成立体图形的过程。

二、学情分析七年级的学生对自己身边的事充满好奇，他们非常乐意动手操作，有很强的好胜心和表现欲。

小学已学习过一些正方体、长方体、圆柱、圆锥、棱锥等基础知识。

因此完全可以在教师的引导下，展开合作与探究的学习活动，完成本课的学习任务。

本课针对青少年学生的身心发展的特点，以活动为主线，创设情境，让学生经历观察、操作、想象、交流与合作的过程，激发学生的学习兴趣和探究的欲望。

采用多媒体演示与学生实物操作相结合的方式，发展学生的空间观念。

三、教学准备学生准备：用卡纸做成的正方体模型（用六个面拼成，胶带粘接便于展开）及圆柱、圆锥、棱柱、棱锥（只有侧面供剪开用），画出剪裁线的卡纸（图见图5），小刀，剪刀、胶带。

教师准备：墨水瓶盒（剪去多余部分），学生用的模型一套。

课件视频展台。

五、教学教程（一）情境导入T．生活中有些东西是不可缺少的，如果让你来选，商品能够入选吗？S．能。

T.对于大多数商品来说，都离不开它的“外衣”——包装。

（放映几幅精美的包装盒的图片）。

你们想知道这些精美的包装盒是怎样制作出来的吗？S.想。

T．（实物展示），那就让我们先来探索最常见的墨水瓶盒的设计秘密吧！（二）教师活动，学生观察，感受课题T.（演示墨水瓶盒的展开成平面图形与折叠围成立体盒子的过程）一只墨水瓶盒可以展开成平面图形，反过来，这个平面图形也可以折叠围成立体盒子，本节课我们就来探索展开与折叠的奥秘。

（三）学生活动之一——几何体的侧面展开图。

T．放映问题：图（1）中纸筒纸盒沿红线或侧棱剪开，能展开成平面图形吗？会是什么形状呢？S ．想象，猜测T ．放映图（2），问题：把上面的立体图形与下面的平面图形用线连结起来。

S ．口答T ．生1的回答是否正确呢？请各小组拿出手中的模具按要求剪开并相互传看。