广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题： (17) Word版含答案

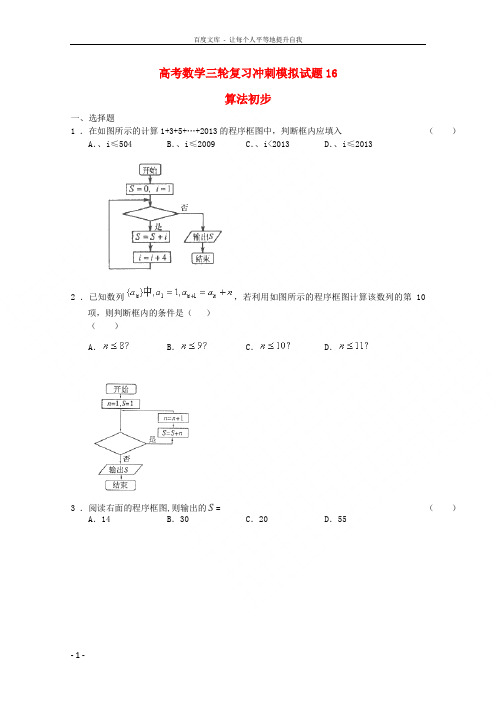
高考数学三轮复习冲刺模拟试题16算法初步一、选择题1 ．在如图所示的计算1+3+5+…+2013的程序框图中，判断框内应填入（）A．、i≤504 B．、i≤2009 C．、i<2013 D．、i≤20132 ．已知数列，若利用如图所示的程序框图计算该数列的第10项，则判断框内的条件是（）（）A．B．C．D．3 ．阅读右面的程序框图,则输出的S= （）A．14 B．30 C．20 D．554 ．如图,若框图所给的程序的输出结果是S=990,那么判断框中应填入的关于的判断条件是（）A．k≥9?B．k≥8?C．k≤8?D．k≤7?5 ．阅读下边的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为（）A．-1 B．1 C．3 D．96 ．执行如图所示的程序框图，输出的S值为（）-A．3B．6-C．10D．157 ．阅读如图的程序框图,若运行相应的程序,则输出的S的值是（）A．39B．21C． 81D．1028 ．执行右图所示的程序框图,则输出的S 的值是（ ）A ．-1B ．23C ．32D ．49 ．某程序框图如图所示，该程序运行后输出的k 的值是（ ）开始,1==S n 3n S S n =+⋅4?n <1+=n n输出S结束是 否A．4 B．5 C．6 D．7二、填空题10．如果执行下面的程序框图,输入正整数n=4,m=3,那么输出的p等于___________参考答案一、选择题 1. D 2. 【答案】B【解析】通过分析，本程序框图为“当型“循环结构.判断框内为满足循环的条件 第1次循环，s=1+1=2 n=1+1=2；第2次循环，s=2+2=4 n=2+1=3；当执行第10项时，11n =， n 的值为执行之后加1的值，所以，判断条件应为进入之前的值。

故答案为：9n ≤或10n <,选B. 3. B 4. C 5. C 6. C7. 【答案】D 第一次循环，3,2S n ==;第二次循环，232321,3S n =+⨯==;第三次循环，32133102,4S n =+⨯==;第四次循环，不满足条件，输出32133102S =+⨯=，选D.8. 【答案】D解:第一次循环,21,224S i ==-=-;第二次循环,22,32(1)3S i ===--;第三次循环,23,42223S i ===-;第四次循环,24,5322S i ===-;所以该循环是周期为4的周期循环,所以当9i =时,和第四次循环的结果相同,所以4S =.选D.9. 【答案】A解：第一次循环为00,021,1S S k ==+==;第二次循环为11,123,2S S k ==+==;第三次循环为33,3211,3S S k ==+==;第四次循环为1111,112100,4S S k ==+>=;第五次循环，不满足条件，输出4k =.选A.二、填空题 10. 24。

高考数学三轮复习冲刺模拟试题10立体几何01一、选择题1 ．已知正四棱柱ABCD —A 1B 1C l D 1中，AA 1=2AB ，E 是AA 1的中点，则异面直线DC 1与BE 所成角的余弦值为 （ ）A ．15B C D ．352 ．某几何体的三视图如图所示,则它的体积是（ ）A ．283π-B ．83π-C ．82π-D ．23π3 ．几何体的三视图如图所示,则该几何体的体积为（ ）A ．223π+B ．423π+C ．2πD ．4π+4 ．已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC为球O 的直径，且2SC =，则此棱锥的体积为 （ ）A ．6B ．6C ．3D ．25 ．设b a ,是两条直线，βα,是两个平面，则b a ⊥的一个充分条件是（ ）A ．βαβα⊥⊥,//,b aB ．βαβα//,,⊥⊥b aC ．βαβα//,,⊥⊂b aD ．βαβα⊥⊂,//,b a6 ．如图，E 、F 分别是三棱锥P-ABC 的棱AP 、BC 的中点，PC=10，AB=6，EF=7，则异面直线AB 与PC 所成的角为（ ） （ ） A ．90° B ．60° C ．45° D ．30°二、填空题7 ．某几何体的三视图如图所示,则该几何体的体积为__________.8．一个几何体的三视图如上图所示,且其侧视图为正三角形,则这个几何体的体积为 .9 ．一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为________.10．一个几何体的三视图如图所示，则该几何体的表面积与体积分别为___________11．如图为一个几何体的三视图，其中俯视为正三角形，A1B1=2,AA1=4，则该几何体的表面积为_______。

12．右图是一个空间几何体的三视图,则该几何体的体积大小为___________________.13．已知直线m,n 与平面α,β,给出下列三个命题:①若m∥α,n∥α,则m∥n; ②若m∥α,n⊥α,则n⊥m; ③若m⊥α,m∥β,则α⊥β. 其中真命题的个数是______个14．已知某几何体的三视图如图所示,则该几何体的体积为___________.15．已知一个几何体的三视图如下图所示(单位：cm)，其中正视图是直角梯形，侧视图和俯视图都是矩形，则这个几何体的体积是________cm 3.16．一个几何体的三视图如图所示，则该几何体的体积为____________；参考答案 一、选择题 1. B 2. A3. 【答案】C解:由三视图可知,该几何体下面是半径为1,高为2的圆柱.上面是正四棱锥.真四棱锥的=,所以四棱锥的体积为213⨯=,圆柱的体积为2π,所以该几何体的体积为23π+,选C. 4. 【答案】A【解析】因为ABC ∆为边长为1的正三角形，且球半径为1，所以四面体O ABC -为正四面体，所以ABC ∆的外接圆的半径为，所以点O 到面ABC 的距离3d ==,所以三棱锥的高23SF OE ==,所以三棱锥的体积为1132236⨯⨯=，选A.5. 【答案】C【解析】若b β⊥，//αβ，所以b α⊥，又a α⊂，所以b a ⊥，即a b ⊥，所以选C. 6. 【答案】B【解析】,取AC 的中点M,连结EM,MF ，因为E,F 是中点，所以16//,322MF AB MF AB ===,110//,522ME PC ME PC ===,所以MF 与ME 所成的角即为AB 与PC 所成的角。

高考数学三轮复习冲刺模拟试题09不等式一、选择题1 ．设x,y 满足约束条件⎪⎩⎪⎨⎧≥≥≥≤0y ,0x 0y -x 02-y -x 3,若目标函数z=ax+by(a>0,b>0)的最大值为2,则a1+b1的最小值为 （ ）A ．625 B ．38 C ．2 D ．42 ．,,x y z 均为正实数,且22lo g xx =-,22lo g yy -=-，22lo g zz-=，则 （ ）A ．x y z <<B ．z x y <<C ．z y x <<D ．y x z <<3 ．设动点),(y x P 满足⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00502402y x y x y x ，则y x z 25+=的最大值是（ ）A ．50B ．60C ．70D ．1004 ．设3=2a lo g ，=2b ln ，12=5c -，则（ ）A ．<<a b cB ．<<b c aC ．<<c a bD ．<<c b a5 ．9831lo g ,lo g 24a b c ===,则,,a b c 的大小关系是（ ）A ．a b c >>B ．b a c >>C ．a c b >>D ．b c a >>6 ．已知实数x y ，满足2203x y x y y +≥⎧⎪-≤⎨⎪≤≤⎩，，，则2z x y =-的最小值是（ ）A ．7B ．-5C ．4D ．-77 ．若0,,>c b a 且324)(-=+++bc c b a a ，则c b a ++2的最小值为（ ）A ．13-B ．13+C ．232+D ．232-8 ．设x ，y 满足⎪⎩⎪⎨⎧≤--≥-≥+22142y x y x y x ，则y x z +=（ ）A ．有最小值2，最大值3B ．有最小值2，无最大值C ．有最大值3，无最小值D ．既无最小值，也无最大值二、填空题9．已知的最小值是5，则z 的最大值是______.10．已知变量x,y 满足约束条件⎪⎩⎪⎨⎧≤-≥+≤142y x y x y ,则y x z +=3的最大值为__________.11．已知函数2()()f x x a x b a b =++∈R ，的值域为[0)+∞，，若关于x 的不等式()f x c <的解集为(6)m m+，，则实数c 的值为 ．12．若关于x 的不等式211+()022n x x -≥对任意*n N ∈在(-,]x λ∈∞上恒成立，则实 常数λ的取值范围是 ；13．已知132l o g a =,062b =.,43c =l o g ,则,,a b c 的大小关系为______________.14．非负实数x,y 满足⎩⎨⎧≤-+≤-+03042y x y x,则3x y +的最大值为_______.三、解答题15．已知函数f （x ）=x 2+2x+a （共10分）（1）当a=21时，求不等式f （x ）>1的解集；（4分）（2）若对于任意x ∈[1，+∞），f （x ）>0恒成立，求实数a 的取值范围；（6分）参考答案一、选择题 1. C 2. 【答案】A【解析】因为,,x y z 均为正实数，所以22lo g 1xx =->，即2lo g 1x <-，所以102x <<。

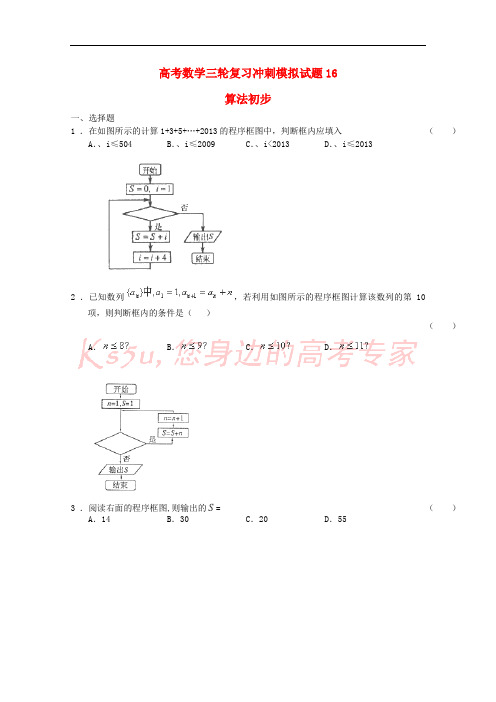
高考数学三轮复习冲刺模拟试题16算法初步一、选择题1 ．在如图所示的计算1+3+5+…+2013的程序框图中，判断框内应填入（）A．、i≤504 B．、i≤2009 C．、i<2013 D．、i≤20132 ．已知数列，若利用如图所示的程序框图计算该数列的第10项，则判断框内的条件是（）（）A．B．C．D．3 ．阅读右面的程序框图,则输出的S= （）A．14 B．30 C．20 D．554 ．如图,若框图所给的程序的输出结果是S=990,那么判断框中应填入的关于的判断条件是（）A．k≥9?B．k≥8?C．k≤8?D．k≤7?5 ．阅读下边的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为（）A．-1 B．1 C．3 D．96 ．执行如图所示的程序框图，输出的S值为（）-A．3B．6-C．10D．157 ．阅读如图的程序框图,若运行相应的程序,则输出的S的值是（）A．39B．21C． 81D．1028 ．执行右图所示的程序框图,则输出的S 的值是（ ）A ．-1B ．23C ．32D ．49 ．某程序框图如图所示，该程序运行后输出的k 的值是（ ）A．4 B．5 C．6 D．7二、填空题10．如果执行下面的程序框图,输入正整数n=4,m=3,那么输出的p等于___________参考答案一、选择题 1. D 2. 【答案】B【解析】通过分析，本程序框图为“当型“循环结构.判断框内为满足循环的条件 第1次循环，s=1+1=2 n=1+1=2；第2次循环，s=2+2=4 n=2+1=3；当执行第10项时，11n =， n 的值为执行之后加1的值，所以，判断条件应为进入之前的值。

故答案为：9n ≤或10n <,选B. 3. B 4. C 5. C 6. C7. 【答案】D 第一次循环，3,2S n ==;第二次循环，232321,3S n =+⨯==;第三次循环，32133102,4S n =+⨯==;第四次循环，不满足条件，输出32133102S =+⨯=，选D.8. 【答案】D解:第一次循环,21,224S i ==-=-;第二次循环,22,32(1)3S i ===--;第三次循环,23,42223S i ===-;第四次循环,24,5322S i ===-;所以该循环是周期为4的周期循环,所以当9i =时,和第四次循环的结果相同,所以4S =.选D.9. 【答案】A解：第一次循环为00,021,1S S k ==+==;第二次循环为11,123,2S S k ==+==;第三次循环为33,3211,3S S k ==+==;第四次循环为1111,112100,4S S k ==+>=;第五次循环，不满足条件，输出4k =.选A.二、填空题 10. 24。

高考数学三轮复习冲刺模拟试题05三角函数02三、解答题 1． 已知函数.（1）求函数图象的对称轴方程； （2）求的单调增区间.（3）当时,求函数的最大值，最小值.2． 如图，在平面直角坐标系中，以轴为始边作两个锐角，它们的终边分别与单位圆交于两点．已知的横坐标分别为．（1）求的值；（2）求的值．3．设函数22()(sin cos )2cos(0)f x x x x ωωωω=++>的最小正周期为23π.(Ⅰ)求ω的值; (Ⅱ)求()f x 在区间-63ππ⎡⎤⎢⎥⎣⎦，上的值域; (Ⅲ)若函数()y g x =的图像是由()y f x =的图像向右平移2π个单位长度得到,求()y g x =的单调增区间.4．在△ABC中,a,b,c 分别为角A,B,C 的对边,A 为锐角,已知向量→p =(1,3cos 2A ),→q =(2sin 2A,1-cos2A),且→p ∥→q .(1)若a 2-c 2=b 2-mbc,求实数m 的值;(2)若a=3,求△ABC 面积的最大值,以及面积最大是边b,c 的大小.5．设函数22()cos()2cos ,32xf x x x R π=++∈.(Ⅰ) 求()f x 的值域;(Ⅱ) 记△ABC 的内角A 、B 、C 的对边长分别为a 、b 、c,若()1f B =,1b =,3c =求a 的值.6．已知向量⎪⎭⎫⎝⎛-=-=21,cos 3),1,(sin x x ,函数()b a x f +=)(·2- (1)求函数)(x f 的最小正周期T 及单调减区间(2)已知c b a ,,分别是△ABC 内角A,B,C 的对边,其中A 为锐角,4,32==c a 且1)(=A f ,求A,b 和△ABC 的面积S7．已知函数1sin cos )2sin sin 32()(2+⋅-=xx x x x f .（Ⅰ）求()f x 的定义域及最小正周期； （Ⅱ）求()f x 在区间[,]42ππ上的最值.8． (本小题满分13分)在△ABC 中，A ，C 为锐角，角A ，B ，C 所对应的边分别为a ，b ，c ，且32=,=510cos A sinC 。

高考数学三轮复习冲刺模拟试题12解析几何01一、选择题1．若直线1l ：280ax y +-=与直线2l ：(1)40x a y +++=平行 ，则a 的值为（ ）A ．1B ．1或2C ．-2D ．1或-22．倾斜角为135︒，在y 轴上的截距为1-的直线方程是（ ）A ．01=+-y xB ．01=--y xC ．01=-+y xD ．01=++y x3．若抛物线y 2=a x 上恒有关于直线x +y-1=0对称的两点A ，B ，则a 的取值范围是（ ）A ．(43-，0) B ．(0，34) C ．(0，43) D ．403(,)(,)-∞+∞ 4．己知抛物线方程为2=2y px (>0p ),焦点为F ,O 是坐标原点, A 是抛物线上的一点,FA与x 轴正方向的夹角为60°,若OAF ∆3则p 的值为 （ ）A ．2B ．3C ．2或23D ．225．已知椭圆2222:1(0)x y C a b a b+=>>的离心率为32.双曲线221x y -=的渐近线与椭圆C有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C 的方程为（ ）A ．22182x y += B ．221126x y += C ．221164x y += D ．221205x y += 6．已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为12,F F ,在双曲线右支上存在一点P 满足12PF PF ⊥且126PF F π∠=,那么双曲线的离心率是（ ）AB C 1D 17．设F 是抛物线)0(2:21>=p px y C 的焦点，点A 是抛物线与双曲线22222:by a x C -=1)0,0(>>b a 的一条渐近线的一个公共点，且x AF ⊥轴，则双曲线的离心率为（ ）A ．2B ．3C ．25 D ．5二、填空题 8．若⊙5:221=+y x O 与⊙)(20)(:222R m y m x O ∈=+-相交于A 、B 两点，且两圆在点A 处的切线互相垂直，则线段AB 的长度是____________________；9．已知双曲线)0,0(12222>>=-b a by a x 的左右焦点为21,F F ,P 为双曲线右支上的任意一点,若||||221PF PF 的最小值为8a,则双曲线的离心率的取值范围是_________. 10．已知抛物线的参数方程为⎩⎨⎧==ty t x 882(t 为参数),焦点为F ,准线为l ,P 为抛物线上一点,l PA ⊥,A 为垂足,如果直线AF 的斜率为3-,那么=PF _________ .参考答案一、选择题 1. 【答案】A【解析】直线1l 的方程为42ay x =-+，若1a =-，则两直线不平行，所以1a ≠-，要使两直线平行，则有282114a a -=≠=-+，由211a a =+，解得1a =或2a =-。

高考数学三轮复习冲刺模拟试题14排列、组合、二项式定理一、选择题1 ．如图,用四种不同的颜色给图中的P A B C D 、、、、五个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共有( )种 （ ）A ．72B ．86C ．106D ．1202 ．现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是 (A)152 (B)126 (C)90 (D)543 ．试题）在1012x x ⎛⎫- ⎪⎝⎭的二项展开式中,4x 的系数为（ ）A ．-120B ．120C ．-15D ．154 ．试题）92)21(xx -的展开式中的常数项为 （ ）A ．1B ．3C ．1621 D ．8155 ．二项式8312⎪⎪⎭⎫⎝⎛-x x 的展开式中的常数项是（ ）A ．-28B ．-7C ．7D ．286 ． 2521(2)(1)x x+-的展开式的常数项是（ ） （ ）A ．－3B ．－2C ．2D ．37 ．若51()ax x-(0)a >展开式中3x 的系数为581-,则a 的值为 （ ）A ．13B ．19C ．127D ．18 ．91x ⎫⎪⎭展开式中的常数项是（ ）A ．36-B ．36C ．84-D ．84二、填空题9 ．（天津市六校2013届高三第二次联考数学理试题（WORD 版））在(1+x)2(1-x2)3的展开式中,含x 项的系数是 .参考答案一、选择题 1. A 2. B 3. C 4. C 5. C 6. D7. 【答案】A 二项展开式的通项为55521551()()(1)kkk k k k k k T C ax C a x x---+=-=-，由523k -=得1k =，所以14325(1)T C a x =-，即3x 的系数为45a -，即45581a -=-，所以4181a =，解得13a =，选A.8. 【答案】C解:展开式的通项公式为93921991()(1)kkkk k kk T C C x x --+=-=-,令9302k -=得3k =.所以常数项为3349(1)84T C =-=-,选C二、填空题 9. 4-。

高考数学三轮复习冲刺模拟试题18导数01一、选择题1 ．函数 的图象与x 轴所围成的封闭图形的面积为（ ）（ ）A ．B ．1C ．2D ．2 ．已知函数2()=f x x cos x -，则(0.6),(0),(-0.5)f f f 的大小关系是（ ）A ．(0)<(0.6)<(-0.5)f f fB ．(0)<(-0.5)<(0.6)f f fC ．(0.6)<(-0.5)<(0)f f fD ．(-0.5)<(0)<(0.6)f f f3 .定义在R 上的可导函数f(x),且f(x)图像连续,当x ≠0时,1'()()0f x x f x -+>,则函数1()()g x f x x -=+的零点的个数为（ ）A ．1B ．2C ．0D ．0或24 ．已知函数))((R x x f ∈满足1)1(=f ，且)(x f 的导函数21)('<x f ，则212)(+<x x f 的解集为（ ） A ．{}11<<-x x B ．{}1-<x xC ．{}11>-<x x x 或D ．{}1>x x二、填空题5 ．若f(x)在R 上可导,f(x)=x 2+2f’(2)+3,则⎰=3dx）x （f .6 ．若不等式1|ln |3≥-x ax 对任意]1,0(∈x 都成立,则实数a 取值范围是________.7 ．计算1-1(2+)x x e dx ⎰= ；8 ．曲线1xy =与直线y=x 和y=3所围成的平面图形的面积为_________.9 ．设1x m e dx =⎰,11en x dx -=⎰,则m 与n 的大小关系为______.10．已知函数d cx bx x x f +++=23)(在区间[1,2]-上是减函数，那么b c +的最大值为________________；参考答案一、选择题 1. 【答案】A【解析】根据积分的应用可求面积为02211()(1)cos S f x dx x dx xdx ππ--==++⎰⎰⎰2021113()sin 1222x x xπ-=++=+=，选A.2. 【答案】B【解析】因为函数2()=f x x cos x -为偶函数，所以(0.5)(0.5)f f -=，()=2f 'x x sin x +，当02x π<<时，()=20f 'x x s i n x +>，所以函数在02x π<<递增，所以有(0)<(0.5)<(0.6)f f f ，即(0)<(0.5)<(0.6)f f f -，选B.3. 【答案】C【解析】由1'()()0f x x f x -+>，得'()()0x f x f x x+>，当0x >时，'()()0xf x f x +>，即(())'0xf x >，函数()xf x 此时单调递增。