当前位置：文档之家 › 第五章、势能面

第五章、势能面

  • 格式：ppt
  • 大小：786.00 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

第五章分子模拟

第五章分子模拟
这说明: 得到一个过渡态不能证明它就是连接反应物和产物的 过渡态，通过分析虚频的简正振动情况可以判断其是 不是所要的过渡态。
表征驻点的性质
驻点: 势能面上梯度为零的点,它既可能是极小值, 也可能是鞍点。 极小值: 在势能面的各个方向都是极小的.
鞍点: 是在某些方向上是极小的,但在某一个方向 上是极大的,因为鞍点是连接两个极小值的点。
IRC计算在输出文件末尾对计算进行总结,列出能量和优化的变 量的值。第一个值和最后一个值是整条路径的起点和终点。
在起点上，得到了一个类似甲醛分子的结构,可以认定该 反应路线是通向甲醛的；在终点上,得到了一个C-H键伸长 的结构,C-O键略微缩短，通向解离分子。
计算活化能：
IRC计算确认了所得到的就是我们所要的过渡态,下面就可 以计算活化能了。 注意 IRC得到的产物的能量不一定等于两个单独的体系的 和,因为当IRC计算得到分子配合物的极小值,与两个分离 体系的能量和有些差别。
1,2氢迁移反应（第二个反应）
寻找过渡态： 猜测过渡态在碳原子上的一个氢原子象氧原子方向迁移 , 处于同时与碳原子和氧原子作用的位置 , 对其进行的频率分 析表明其为一阶鞍点,包含零点能的总能量为-113.67941。 反应路径分析：
IRC分析得到的两个结构,一个类似于HCOH,一个类似于 H2CO,说明该结构为该反应的过渡态 。
H2 CO H2 + CO H2CO
计算过渡态的能量的方法
* 过渡态几何构型优化，计算SCF能量 首 先 猜 测 过 渡 态 几 何 构 型 。 计 算 中 设 置 Opt=(TS, CalcFC)。 * 频率分析,计算零点能 频率分析表明其有一个虚频，表明它是一个过渡态。 * IRC计算,确认为本反应的过渡态 IRC计算需要优化好的过渡态和相应的力矩阵，得到的 方法是： 从临时文件中获得(IRC=RCFC)或 在IRC计算的初始进行计算(IRC=CalcFC)

第五章_固体表面吸附(固-气界面吸附)

第五章_固体表面吸附(固-气界面吸附)
De : 一孤对粒子从无穷远至键合离子间的平衡距离 re 的结合能； r: 孤对原子中表面一原子与吸附质原子间任意的距离。 a:双原子分子的弹力系数。
③化学吸附具有选择性
如：CO在金属表面上的吸附
O C MM
OO CC MM
NO + 1/2O2 CH2=CH2 + 1/2O2
NO2 O
NO只在Pt上吸附 只用Ag作催化剂。
无选择性；吸附热与气体凝聚热相近；吸附速度快；多层吸附。
（2）相互作用势能
设 f 代表作用力，r 为粒子间距离，U(r)为粒子间相互作用势能，有：
f U (r) r
或
r
U(r)
f dr
永久偶极矩相互作用势能为：
U (r)
2 3
12 22
3k Tr 6
诱导偶极矩相互作用势能为：
Ui(r)
( i 2 12
使体相中某些组分在表面区产生富集的现象。 其特点为组成随表面吸附质不同而变化。
如：Ag-Pd合金，吸附CO时，体相中的Pd可通过扩散到达 表面与CO形成羰基键，从而使表面富Pd。除去CO后，表面 组成由回到原来的状态。
第二节 物理吸附和化学吸附
1、物理吸附与Lennard-Jone势能曲线
（1）物理吸附特点
S
RT
则：
p
或： bp
b(1 )
1 bp
若有两种气体存于表面而发生竞争吸附时：
则：
A
பைடு நூலகம்
bA pA 1 bA pA bB
pB
B
bB pB 1 bA pA bB
pB
如果吸附解离成两个碎片，且各占据一个吸附位置，则：
f ( ) (1 )2 f '( ) 2

2022物理第五章机械能第3节机械能守恒定律及其应用学案

2022物理第五章机械能第3节机械能守恒定律及其应用学案

第3节机械能守恒定律及其应用必备知识预案自诊知识梳理一、重力做功与重力势能1。

重力做功的特点(1)重力做功与路径无关，只与物体始末位置的有关。

（2）重力做功不引起物体的变化。

2.重力势能（1）公式:E p=。

(2）矢标性:重力势能是，但有正、负，其意义是表示物体的重力势能比它在参考平面上大还是小,这与功的正、负的物理意义不同。

(3）系统性:重力势能是物体和共有的。

(4）相对性:重力势能的大小与的选取有关。

重力势能的变化是的,与参考平面的选取。

3.重力做功与重力势能变化的关系(1)定性关系：重力对物体做正功,重力势能就;重力对物体做负功,重力势能就。

(2）定量关系:重力对物体做的功等于物体重力势能的减少量.即W G=—（E p2-E p1)=。

二、弹性势能1.弹性势能(1）定义:发生弹性形变的物体之间,由于有弹力的相互作用而具有的势能,叫弹性势能。

（2）弹性势能的大小与形变量及有关。

(3）矢标性：。

（4）没有特别说明的情况下,一般选弹簧形变为零的状态为弹性势能零点。

2.弹力做功与弹性势能变化的关系弹力做功与弹性势能变化的关系类似于重力做功与重力势能变化的关系，用公式表示为W=。

三、机械能守恒定律1.机械能和统称为机械能，其中势能包括和。

2。

机械能守恒定律(1)内容:在只有做功的物体系统内，动能与势能可以相互转化,而总的机械能。

（2）机械能守恒的条件①只有重力或弹力做功。

①注:（1）机械能守恒的条件不是合外力做的功等于零，更不是合外力为零；中学阶段可理解为“只有重力或弹簧的弹力做功”，但要明确不是“只受重力或弹力作用”。

（2）利用守恒观点列机械能守恒的方程时一定要选取零势能面，而且系统内不同的物体必须选取同一零势能面。

(3)守恒表达式考点自诊1.判断下列说法的正误.(1）克服重力做功,物体的重力势能一定增加.(）（2）发生弹性形变的物体都具有弹性势能。

（）(3）弹簧弹力做正功时，弹性势能增加。

（）(4)物体所受合外力为零时，机械能一定守恒.（）(5）物体受到摩擦力作用时，机械能一定要变化。

势能面的局部优化和全局优化

势能面的局部优化和全局优化

势能⾯的局部优化和全局优化导师Gilles的Computational Chemistry第⼀课。

总结的⾮常好。

I. 势能⾯ Potential Energy Surface, PES,原⼦坐标的势能函数。

N原⼦体系有3N个Cartesian坐标变量，有3N-6内坐标变量，线性分⼦则是3N-5内坐标；任何物理体系都倾向于采取⾃由能最⼩的构象。

⾃由能最⼩处构象的熵近似相等，所以最⼩⾃由能近似等于最⼩能量。

最⼩能量的构象对应于势能梯度0点。

在最⼩能结构附近的展开可以研究分⼦⼏何，光谱(IR, UV, NMR, etc.)，热化学(ΔH, ΔS, 反应热，活化能垒)II. 势能⾯最⼩值的局部优化技术1. 最Robust的：Newton-Raphson Optimization在最⼩点处做Harmonic近似，V = (1/2)*K*(r-r0)^2梯度向量: g = dV/dr = K*(r-r0)⼆阶导(⼒常数矩阵): F = K = [d^2V/dr^2] 元Fij = d^2V/dXi*dYi (F⼜称Hessin矩阵)则Newton-Raphson法的迭代式为: (r0-r) = -g/F(推导: 将F的表达式代⼊g的表达式，并移项即可。

)虽然Newton-Raphson是最Robust的⽅法，但是(1) 计算⼒常数矩阵F占据了主要的计算耗费(2) 对于⼤的分⼦的计算过于昂贵(3) 在接近最⼩点的时候收敛很快2. 最快的⽅法: Steepest descent method既然F计算过于耗时，那么我们把它⽤⼀个常数矩阵F0替代，即迭代式为: (r0-r) = -g/F0这样的搜索极快，不过会在最⼩点处来回震荡。

3. ⼆者结合的⽅法: Fletcher fowell Method先做⼏步Steepest descent，然后切换到Newton-Raphson⽅法；切换到Newton-Raphson⽅法时，采⽤估计的初始Hessin矩阵，此矩阵使⽤⼀阶导g对坐标的⼀阶差商构造，即F = (g-new - g-old)/(r-new - r-old)4. 最适中的⽅法: Conjugate gradient method (GC)这个⽅法是⾸先沿坐标的⼀个⽅向优化，搜索到最⼩值后，则向着与该⽅向共轭的或正交的⽅向搜索，不断循环，直⾄全部坐标收敛。

第五章 第3讲 机械能守恒定律及其应用

第五章 第3讲 机械能守恒定律及其应用

基础知识·自主梳理 高频考点·分类突破 学科素养提升 课时作业•巩固提升
首页 上页 下页 尾页
高频考点·分类突破
2．机械能是否守恒的三种判断方法 (1)利用机械能的定义判断：若物体动能、势能之和不变，机械能守恒． (2)用做功判断：若物体或系统只有重力(或弹簧的弹力)做功，或有其他力做功，但其 他力做功的代数和为零，则机械能守恒． (3)利用能量转化判断：若物体系统与外界没有能量交换，物体系统内也没有机械能 与其他形式能的转化，则物体系统机械能守恒．
第五章 机械能及其守Hale Waihona Puke 定律 第3讲 机械能守恒定律及其应用
C
目录
ONTENTS
基础知识·自主梳理 高频考点·分类突破 学科素养提升 4 课时作业·巩固提升
基础知识·自主梳理 高频考点·分类突破 学科素养提升 课时作业•巩固提升
首页 上页 下页 尾页
基础知识·自主梳理
一、重力做功与重力势能
1．重力做功的特点 (1)重力做功与 路径 无关，只与始、末位置的 高度差 有关． (2)重力做功不引起物体 机械能 的变化． 2．重力做功与重力势能变化的关系 (1)定性关系：重力对物体做正功，重力势能就 减小 ；重力对物体做负功，重力势 能就 增大 ．
基础知识·自主梳理 高频考点·分类突破 学科素养提升 课时作业•巩固提升
首页 上页 下页 尾页
高频考点·分类突破
解析：b 球从水平位置下摆到最低点的过程中，a 球升至最高点，重力势能增加，动 能也增加，机械能增加．由于 a、b 系统只有重力做功，则系统机械能守恒，既然 a 球机械能增加，b 球机械能一定减小．可见，杆对 a 球做了正功，杆对 b 球做了负功．所 以，本题正确答案为 B、C. 答案：BC

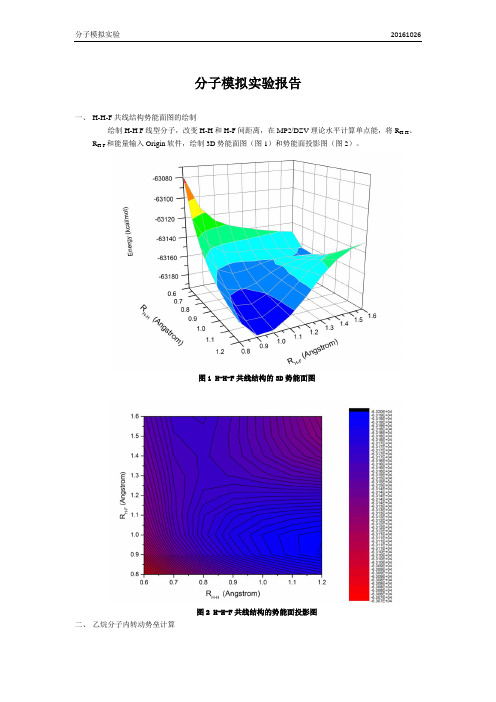
分子模拟实验-势能面

分子模拟实验-势能面

分子模拟实验报告
一、H-H-F共线结构势能面图的绘制
绘制H-H F线型分子，改变H-H和H-F间距离，在MP2/DZV理论水平计算单点能，将R H-H、R H-F 和能量输入Origin软件，绘制3D势能面图（图1）和势能面投影图（图2）。

图1 H-H-F共线结构的3D势能面图
图2 H-H-F共线结构的势能面投影图
二、乙烷分子内转动势垒计算
在Chem3d中画出NO分子，点击Surfaces-ChooseSurface-MolecularOrbital绘制分子轨道等值面图，通过SelectMolecularOrbital选择不同的分子轨道，截图如下。

LUMO+1 （163.115 eV）LUMO（-2.832 eV）
HOMO（-2.832 eV）HOMO-1 （-12.846 eV）
HOMO-2 （-21.326 eV）HOMO-3 （-21.326 eV）
HOMO-4 （-23.922 eV）HOMO-5 （-52.100 eV）
图3NO分子的八个分子轨道等值面图
按轨道的能量从低到高的顺序排列，使用Origin软件绘制NO的分子轨道能级图（图4）。

图3NO分子的分子轨道能级图
三、自我测评
本次实验继续练习了Chem3D中的扫描操作，学习了Origin软件中三维势能面图和势能面图的绘制和
Chem3D中分子轨道相关功能。

沪科版(上海)物理高一第二学期(试用版)第五章 D 重力势能 课件 _2精品课件

（增加、 减少）
减少
增加
重力做功和重 力势能变化的
关系
重力做的功等 于重力势能的
减少
物体克服重力 做的功等于重 力势能的增加
三、重力势能的系统性
• 重力势能属于物体和地球组成的系统共有的. • 平常所说的“物体”的重力势能，只是一种习
惯简化的说法。
思考：
1. 一块砖平放、侧放、竖放在水平地面上， 三者的重力势能大小关系是什么？
二、重力做功与重力势能变化的关系 WG = mgh1-mgh2= Ep1 - Ep2
三、重力势能的系统性 重力势能属于物体和地球组成的系统的.
每个人都会有自己的特长。一个人做某些事会比其他事做的更好。但许多人从未找到最适合自己的事情，其根本原因往往是他们没有进行足够的思考。如果你对一切都随遇而安，那总是会有一天你会后悔莫及的。心，只有一 生，不要追逐的太累。心灵的愉悦，来自精神的富有；简单的快乐，来自心态的知足。家，很平淡，只要每天都能看见亲人的笑脸，就是幸福的展现。爱，很简单，只要每天都会彼此挂念，就是踏实的温暖。幸福并不缥缈， 于两心知的默契。人与人之间，尊重是相互的，心与心相交，尊重是必须的，尊重，是一个人教养，体现在做人做事，尊重，是一个人的人品尊重，让人与人走近。人无所舍，必无所成。心无所依，必无所获。自己的路只有 度。能抓住希望的只有自己，能放弃自己的也只有自己。能怨恨嫉妒的是自己，能智慧温暖的还是自己。心中有岸，才会有渡口，心有所持，才能行之安然。每个人都会有自己的想法、做法、活法。理念不同，做法不同，活 人，影响别人，甚至攻击别人。他好，不会嫉妒，不会报复；他不好，不去打击，不去鄙视。人人都有自尊，人人都有苦衷，生活中没有谁，不希望自己活得更好，走得更顺。学会理解、尊重与帮助。每一个优秀的人，都有 份学业，一份工作，一段爱情，离开了爸爸妈妈，去了一座别的城市。当你倦了厌了时，想想你的父母正在为你打拼，这就是你必须坚强的理由。不管发生什么，记住不是只有你一个人在努力不要轻易放弃。一个人在外面， 每一个闪光的人，都在不为人知的地方默默努力。穿越孤独，战胜恐惧，完善自己。可以流泪，可以休憩，可以抱怨，但绝不放弃。酸甜苦辣，阴晴圆缺，都会途经，也都将过去。内心的宁静，是最有力量的修行。佛说，人 常常，我们苦苦的追逐，又执着的放不下。殊不知，有些不甘放下的，往往不是值得争取的，有些苦苦追逐的，往往不是生命需要的。我们要做的是让心静下来，心静下来才知道自己到底想要的是什么，让心静下来，静观自 要么像白菜一样有层次。要么像莲藕一样有心眼。可我做不到！我就像一根甘蔗，直，不会拐弯抹角，一就是一，二就是二。虽然这样的性格吃不开，容易得罪人，但我还是喜欢这样的自己，不虚伪，不算计别人，喜欢做真 人的善良一定要有底线，大度要讲原则，道德讲底线。你不发脾气，别人就以为你没脾气，你不争取，别人就会占尽你的便宜。宁愿你有点心机，也不要活得太单纯。不要别人跟你说几句好听的，你就不管不顾地对人家好， 生活是自己的，你的每一天，每一份快乐，都得靠自己去感受，去捕捉。改变别人是事倍功半，改变自己是事半功倍。相信自己，美好的生活从改变自己开始！自信，是走向成功的伴侣，是战胜困难的利剑，是达向理想彼岸 的第一步；有了它，就走上了义无反顾的追求路。诚信是人最美丽的外套，是心灵最圣洁的鲜花。人有见识，就不轻易发怒。宽恕人的过失，便是自己的荣耀。青春赚的钱，难赚回青春；生命赚的钱，难买回生命；幸福换来 钱，难索回爱情；时间挣来的钱，难挣回时间。即使用一生得到全世界的钱，全世界的钱也买不回你的一生，请记住金钱不是万能的。该休息的时候要休息，该放松的时候要放松，快乐生活才是最给力的。人这一辈子，不可 的事情；要学会自己化解，要时时拥有快乐的心境和乐观的心态。前行路上，遇见烦恼的时候，不妨学说三句话，第一句话：“算了吧”；第二句话：“不要紧”；第三句话：“一切都会过去的”。没有过不去的事情，只有 便没有雨天。别人拥有的，不必羡慕；只要努力，时间都会给你。总想赢者必输，不怕输者必赢。令狐冲说：“有些事情本身我们无法控制，只好控制自己。”考前两个月就是冲刺。养兵千日，用兵一时更快、更高、更强。 成功的父亲是汗水面对目标，信心百倍，人生能有几次搏？面对成绩，心胸豁达，条条大陆通罗马。如果敌人让你生气，那说明你还没有胜他的把握，如果朋友让你生气，那说明你仍然在意他的友情高考试卷是一把刻度不均 题的分值不一定高。既然目标是地平线留给世界的就只能是背影 。没有平日的失败，就没有最终的成功。重要的是分析失败原因并吸取教训。能冲刷一切的除了眼泪，就是时间，以时间来推移感情，时间越长，冲突越淡， 就怕不敢考。积一时之跬步，臻千里之遥程在冷峻的雪山上很多朝圣者倒在半路上 。学习与坐禅相似，须有一颗恒心。时间太瘦，指缝太宽调节好兴奋期，学习一浪高一浪名列前茅是银，日新月异是金怨言是上天得至人类 诚的部分不必每分钟都学习，但求学习中每分钟都有收获人非要经历一番不同平时的劫难才能脱胎换骨，成为真正能解决问题的人。务须咬牙厉志，蓄其气而长其志，切不可恭然自馁也生活比电影狠多了，从来不给弱者安排 界，却失去了自己，又有什么意义呢？不要把时间、财力和劳动，浪费在空洞多余的话语上。永远以用心乐观的心态去拓展自我和身外的世界。人的一生，有许多事情，是需要放在心里慢慢回味的，过去的就莫要追悔，一切 你堕落的借口，即使你改变不了这个世界，你却依然可以改变自己，选择条正确的路永远走下去。不肯下一点功夫，永远不会明白自己从何而来，又将立足于何处。. 凡事不要想得太复杂，手握的太紧，东西会碎，手会疼。 便成了路。通过云端的道路，只亲吻攀登者的足迹。不是每个人都适合与你白头偕老。有的人是拿来成长的，有的人是拿来生活的，有的人是�

沪科版(上海)物理高一第二学期(试用版)第五章 D 重力势能 课件 _2优秀课件

功地把自己推销给别人之前，你必须百分之百的把自己推销给自己。即使爬到最高的山上，一次也只能脚踏实地地迈一步。
（增加、 减少）
减少
增加
重力做功和重 力势能变化的
关系
重力做的功等 于重力势能的
减少
物体克服重力 做的功等于重 力势能的增加
三、重力势能的系统性
• 重力势能属于物体和地球组成的系统共有的. • 平常所说的“物体”的重力势能，只是一种习
惯简化的说法。
思考：
1. 一块砖平放、侧放、竖放在水平地面上， 三者的重力势能大小关系是什么？
二、重力做功与重力势能变化的关系 WG = mgh1-mgh2= Ep1 - Ep2
三、重力势能的系统性 重力势能属于物体和地球组成的系统的.
用微笑告诉别人，今天的我，比昨天更强。瀑布跨过险峻陡壁时，才显得格外雄伟壮观。勤奋可以弥补聪明的不足，但聪明无法弥补懒惰的缺陷。孤独是 每个强者必须经历的坎。有时候，坚持了你最不想干的事情之后，会得到你最想要的东西。生命太过短暂，今天放弃了明天不一定能得到。只有经历人生 的种种磨难，才能悟出人生的价值。没有比人更高的山，没有比脚更长的路学会坚强，做一只沙漠中永不哭泣的骆驼！一个人没有钱并不一定就穷，但没 有梦想那就穷定了。困难像弹簧，你强它就弱，你弱它就强。炫丽的彩虹，永远都在雨过天晴后。没有人能令你失望，除了你自己人生舞台的大幕随时都 可能拉开，关键是你愿意表演，还是选择躲避。能把在面前行走的机会抓住的人，十有八九都会成功。再长的路，一步步也能走完，再短的路，不迈开双 脚也无法到达。有志者自有千计万计，无志者只感千难万难。我成功因为我志在成功！再冷的石头，坐上三年也会暖。平凡的脚步也可以走完伟大的行程。 有福之人是那些抱有美好的企盼从而灵魂得到真正满足的人。如果我们都去做自己能力做得到的事，我们真会叫自己大吃一惊。只有不断找寻机会的人才 会及时把握机会。人之所以平凡，在于无法超越自己。无论才能知识多么卓著，如果缺乏热情，则无异纸上画饼充饥，无补于事。你可以选择这样的“三 心二意”：信心恒心决心；创意乐意。驾驭命运的舵是奋斗。不抱有一丝幻想，不放弃一点机会，不停止一日努力。如果一个人不知道他要驶向哪个码头， 那么任何风都不会是顺风。行动是理想最高贵的表达。你既然认准一条道路，何必去打听要走多久。勇气是控制恐惧心理，而不是心里毫无恐惧。不举步， 越不过栅栏；不迈腿，登不上高山。不知道明天干什么的人是不幸的！智者的梦再美，也不如愚人实干的脚印不要让安逸盗取我们的生命力。别人只能给 你指路，而不能帮你走路，自己的人生路，还需要自己走。勤奋可以弥补聪明的不足，但聪明无法弥补懒惰的缺陷。后悔是一种耗费精神的情绪，后悔是 比损失更大的损失，比错误更大的错误，所以，不要后悔！复杂的事情要简单做，简单的事情要认真做，认真的事情要重复做，重复的事情要创造性地做。 只有那些能耐心把简单事做得完美的人，才能获得做好困难事的本领。生活就像在飙车，越快越刺激，相反，越慢越枯燥无味。人生的含义是什么，是奋 斗。奋斗的动力是什么，是成功。决不能放弃，世界上没有失败，只有放弃。未跌过未识做人，不会哭未算幸运。人生就像赛跑，不在乎你是否第一个到 达终点，而在乎你有没有跑完全程。累了，就要休息，休息好了之后，把所的都忘掉，重新开始！人生苦短，行走在人生路上，总会有许多得失和起落。 人生离不开选择，少不了抉择，但选是累人的，择是费人的。坦然接受生活给你的馈赠吧，不管是好的还是坏的。现在很痛苦，等过阵子回头看看，会发 现其实那都不算事。要先把手放开，才抓得住精彩旳未来。可以爱，可以恨，不可以漫不经心。我比别人知道得多，不过是我知道自己的无知。你若不想 做，会找一个或无数个借口；你若想做，会想一个或无数个办法。见时间的离开，我在某年某月醒过来，飞过一片时间海，我们也常在爱情里受伤害。1、 只有在开水里，茶叶才能展开生命浓郁的香气。人生就像奔腾的江水，没有岛屿与暗礁，就难以激起美丽的浪花。别人能做到的事，我一定也能做到。不 要浪费你的生命，在你一定会后悔的地方上。逆境中，力挽狂澜使强者更强，随波逐流使弱者更弱。凉风把枫叶吹红，冷言让强者成熟。努力不不一定成 功，不努力一定不成功。永远不抱怨，一切靠自己。人生最大的改变就是去做自己害怕的事情。每一个成功者都有一个开始。勇于开始，才能找到成功的 路。社会上要想分出层次，只有一个办法，那就是竞争，你必须努力，否则结局就是被压在社会的底层。后悔是一种耗费精神的情绪后悔是比损失更大的 损失，比错误更大的错误所以不要后悔。每个人都有潜在的能量，只是很容易:被习惯所掩盖，被时间所迷离,被惰性所消磨。与其临渊羡鱼，不如退而结网。 生命之灯因热情而点燃，生命之舟因拼搏而前行。世界会向那些有目标和远见的人让路。不积跬步，无以至千里；不积小流，无以成江海。骐骥一跃，不 能十步；驽马十驾，功在不舍。锲而舍之，朽木不折；锲而不舍，金石可镂。若不给自己设限，则人生中就没有限制你发挥的藩篱。赚钱之道很多，但是 找不到赚钱的种子，便成不了事业家。最有效的资本是我们的信誉，它小时不停为我们工作。销售世界上第一号的产品——不是汽车，而是自己。在你成

计算材料学第五章电子结构理论

模拟原子的运动在模拟原子的运动在bornoppenheimer势能面上的分子动力学的分子动力学carparrinello方法势能面上方法模拟模拟方法方法第一性原理计算的能量量级与单位换算第一性原理计算的能量量级与单位换算homo和和lumo?highestoccupiedmolecularorbitalhomo最高占据分子轨道通常最高占据分子轨道通常为束缚态能量为负值为束缚态能量为负值?lowestunoccupiedmolecularorbtaillumo最低未占分子轨道最低未占分子轨道?homolumo之间的能隙之间的能隙gap反映分子电子结构的相对稳定性往往对分子电子结构的相对稳定性往往对应于结构稳定性和化学惰性应于结构稳定性和化学惰性在固体中homo和反映?在固体中和lumo扩展为价带带valenceband和导带扩展为价和导带conductionband能隙扩展为带隙能隙扩展为带隙bandgap电子的基态与激发态电子的基态与激发态?材料的电子结构可以归为两大类
A QM Code
Input atom positions and types
Choose sensible basis functions
1. J. M. Thijssen, Computational Physics, (Cambridge University Press, 1999). 2. K. Ohno, K. Esfarjani, K. Kawazoe, Computational Materials Science, (Springer, 1999). 3. M. Springborg, Method of Electronic-Structure Calculations, (Wiley, 2000). 4. E. Kaxiras, Atomic and Electronic Structure of Solids, (Cambridge University Press, 2003). 5. R. M. Martin, Electronic Structure, (Cambridge University Press, 2004).

第五章 趋势面分析

第五章趋势面分析1趋势面分析：就是根据G上的已知点Mi(xi,yi,zi),(i=1，2…..n)拟合一个数学曲面L，以此研究地质变量Z在区域上和局部范围内变化特征的一种统计分析方法。

2趋势面拟合度：是指观测点上的趋势值与实测值在总体上的逼近程度。

1趋势面分析的模型？答：二维一次模型：z=b1+b2x+b3y二维二次模型：z=b1+b2x+b3y+b4x2+b5xy+b6y22趋势面的拟合度是不是越高越好，为什么？答：对于一组给定的数据，一般说采用趋势面的次数越高则其拟合度也越高。

但并不是拟合度越高越好。

这是因为对有些问题，我们既要求显示某地质参数的区域性变化规律，同时还想得到在此区域背景下的局部异常，过高的拟合度会漏掉有价值的异常带。

另外，拟合度很高时，所得的趋势面在观测点上吻合的较好，但在非观测点上可能产生很大的偏差，因此，应该根据具体情况来适当的选择拟合度。

3趋势面偏差图的意义？答：引入剩余以后，原始数据原始数据即被分解成为趋势值和剩余值两部分。

趋势值反应区域性大范围内的变化情况，剩余值反应局部变化特点。

二者结合起来可以帮助人们深入的做地质分析。

比如，石油勘查中以趋势面拟合地质构造数据时，趋势面图反映了区域构造背景，剩余图则反映了在这一背景下的局部异常，从它可发现低缓异常带，这对研究该区域的油气分布和查找实测构造图可能漏掉的构造圈闭是十分有用的。

此外，剩余图零值线的区域走向往往反映了区域断裂的分布，这对研究油气藏的形成条件也十非常重要的。

又如用趋势面拟合物探资料和地球化学指标时，利用剩余图可以找出异常带，这些异常带往往与特定的地质条件，特别是与许多成矿条件（比如石油、储油、条件等）有关。

因此剩余图是找矿的重要手段。

第八章因子分析1因子分析：是研究变量间相关关系、样品间相似关系、变量与样品间成因联系以及探索它们之间产生上述关系之你在原因的一些多元统计分析方法总称。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Ψ* ψ0
不相交 —— 净正重叠较小
从势能面和分子结构的角度分析，有利于无辐射跃迁发 生的因素包括：
1）始态与终态的势能面相互靠近
2）始态与终态具有类似的电子特征
2）对于涉及自选改变的跃迁（如ISC），始态与终态彼此
间具有很强的旋轨耦合
5、 势能面与光化学反应的关系
对光化学有意义的势能面上的特征： 1）S0、S1、T1势能面上的极小值的位置 2）S0、S1、T1势能面上的极大值的位置 3）引起势能面分离的相互作用 4）两个势能面接近处的分子几何构型
被分子吸收的每个光子，以一个确定的概率产生最低 的激发单重态（ S1 ）或最低的激发三重态（ T1 ）
S1和T1态是绝大多数有机光化学过程开始的能级
光化学反应的特点
易于生成高能产物和不稳定的产物 体系温度对光化学反应的影响较小，初级光化
学反应一般可以在较低温度下进行 低的活化能和高的反应速率常数 一般化学反应总是向自由能降低的方向进行，
S0
C
A
B
r0
量子力学解释
跃迁概率 ∝ < χi∣χj > 2 —— Franck-Conden因子
0-2 Abs
0-3 0-1 0-0
HIGH HIGH Medium LOW
FL
0-2 0-3
0-1 0-0
4、 无辐射跃迁
交叉
弱避免
强避免
匹配
接触
势能面的几种经典情况
无辐射跃迁
经典解释
发生无辐射跃迁的概率为：
(b) 重原子和弱键
谐振子的振动波函数χv 及概率函数χv2 的图示
2 1 0
(a) χv
2 1 0
(b1) χv2
2 1 0
(b2) χv2
Χv2 —— 概率函数，表示分子在某一振动能级时的某一给定核间距r处存在的概率
根据波函数 χv 及概率函数 χv2 的性质，可得以下结论：
1）积分∫χiχjdτ≡ <χi ∣χj > ，将决定两个电子振动态之间跃迁的概率。
其平均动能≠0 ，在每个振动能级上，总能Ev=Ep+Ek =常数， a) 在平衡位置时， Ek=0， Ep=max; b) 在极点时， Ek=max， Ep=0.
5) 与本征值对应的函数χv，它的数学形式将影响各电子振动能级之间的跃迁。
✓ 双原子分子谐振子的振动函数
双原子分子 的势能曲线
(a) 轻原子和强键
光化学反应的分类：
1）绝热光反应
R* P*
P R
二聚苯的激发波长为335nm,即其 激发能为357kJ/mol,经它分解生 成的苯激发态的激发能为460kJ/ mol。激发态苯行程的一部分能量 来自于化学反应的化学能.
2）非绝热光反应
R* P
R
hν
1，4-环己二烯
苯
hν
降冰片烯
苯
（从S1态发生的） （从T1态发生的）
由式 Ev=hν ( V+1/2 ) 可以看出：
1）做谐振子运动的分子的总能量是量子化的，只有V取整数时，其相应的能 量Ev才是允许的。
2）分子的可能的最低振动势能≠0，=1/2 hν 3) 振动能级之间是等间距的，其间距为hν 4）原子决不会停止围绕平衡位置的振动，即势能Ep和动能Ek都在不停地变化，
连续 B
F
ED
过 量 的 Ek
C
量子化
G
H
I 真实分子势能曲线的形状以及碰撞对分子势能的影响
从双原子分子推广到多原子分子
how简化?
多原子分子
“双原子”分子
未受 扰动
受 扰 动
未受 扰动
3、 辐射跃迁
经典模 型 S1
S0
经典而量子化的模型 S1
能隙E(L-D)=Ev (零点振动能）
H
I
D
G
L J r0* K
4）分子的能量永远≠0 ，分子存在概率最大的是V=0的振动能级。 —— V=0的振动能级对于光化学或光物理过程是最为重要的。
5）随着振动能级的提高，经典模型与量子力学模型越来越接近 （a:概率， b:能级连续化）
双原子分子的非谐振子模型
势能曲线不对称 振动能级不等间距
A
dEp/dr=0
分子解离 J
P∝1/e∆E/(νδs)
∆E——两势能面间的能差 ν —— 与两个势能面接近时的速率
相关 δs—— 与两个势能面接近处的斜率
之差相关
∆E↓
ν↑
P↑
δs ↑
量子力学解释
根据量子力学观点：由激发态势
能面ψ0向基态势能面ψ*的无辐射跃 迁，要求基态与激发态波函数的净正
重叠。
ψ0
Ψ*
相交 —— 净正重叠较大
（Ep为体系的势能，r是偏离平衡位置的距离）
谐振子的运动遵从Hooke定律，体系的能量为：
E = (1/2) k r2
其薛定谔方程的解为：
Ev=hν ( V+1/2 )
Ev ——本征值，对应于该函数的特定能量，是该动态体系的总能量（动能+势能） V—— 振动量子数，只能为0、1、2等整数 ν—— 经典振子的振动频率 h —— Planck常数
第五章、势能面
定义：电子状态确定的体系的势能随其核位置改变 的图形称为势能面
核位置
势能
1、 光化学反应的特点
所有光化学反应都遵从以下光化学规律：
只有能量足够的光被体系吸收时，光化学反应才能发 生
一个被吸收的光子在初级光化学反应过程（非自由基 过程）中仅能活化一个分子，即仅能产生一个激发态 分子
途径 激发态势能面上的某些活性中间体（对应于势能面的极
小值）不一定总能用发射或吸收技术来检测 化学反应发生的途径依赖于竞争的光物理和光化学过程
2、 势能曲线
谐振子的量子力学模型
✓ 双原子分子的谐振子振动模型
把双原子分子看成是用一只弹簧连接起来的小球，体系向平衡位置的回复力F为：
F = dEp / dr
而光化学反应却可以向自ห้องสมุดไป่ตู้能增加的方向进行。 存在基态与激发态势能面之间的跃迁
基态与激发态势能面的图示
ψR*
R*
P * ψP*
1
2
3
+hν -hν
4
6
-hν +hν
ψR
R 光物理
5
ψP
P 光化学
从图中看出：
吸收与发射都倾向在基态或激发态势能面的最低处发生 无辐射跃迁最易在两个势能面最靠近的区域发生 两个势能面上能垒的位置和高度将决定化学反应发生的
两个状态的波函数越相近，其重叠积分↑，跃迁容易↑
2) V=0时，分子在平衡键长处的概率max，在键长极大和极小处概率min; V=1时,分子在平衡键长与键长极大和极小处的概率都↓，而在平衡键长 和极端键长之间位置出现的概率↑
3）总的来说，在低振动能级，分子构型处于平衡位置的概率较大；在高振 动能级，分子构型处于各种位置的概率趋向平均化，但在极端位置的概 率较大。