4.2.3 纯滞后控制--大林控制算法
- 格式:ppt
- 大小:384.00 KB
- 文档页数:30



引言随着现代科学技术水品格发展,与其是近年来,电力工业的迅速发展,工业电阻炉尤其是钟罩式真空电阻炉越来越受人们的青睐。
工业钟罩式真空电阻炉是一种重要的热处理设备,它能使被加热零件脱气、脱氧、脱硫,以及能使有害杂质蒸发分离,避免零件氧化污染,而且它的温度容易调节,相对其它电阻炉来讲热惯性小升温时间短,它在工业中被广泛采用。
他一般具有较大的时间常数和一定的纯滞后时间,且滞后时间比较长,我们知道这样的系统村不利于现代化工业生产自动化水平提高,不利于产品质量和生产效率的提高。
但是一般来讲,对这样的系统在工业生产中要求没有超调量或超调量很小,调节时间希望在确定的采样时间内结束(虽然也希望尽快结束过渡过程,但是这是第二位的)。
因此超调试主要的设计目标,用一般的控制系统设计方法是不行的,用模拟仪表控制算法效果也欠佳。
IBM公司的大林于1968年提出一种针对工业生产过程中含有纯滞后的控制对象的控制算法,即大林算法。
它具有良好的效果,采用大林算法的意义在于大林控制算法能在一些具有纯滞后环节的系统中兼顾动静两方面的性能,可做到小超调小稳态误差。
控制效果比较理想。
对工程实际应用具有很大的意义。
第一章钟罩式真空电阻炉1.1钟罩式真空电阻炉钟罩式真空电阻炉所谓钟罩式系指炉膛位于工作台面以上,钟罩可以升降,由侧面装卸工件,所以又称侧装式。
图1-1所示为双位钟罩式真空炉。
这种型式的炉子其加热器有两种安装方式:一种是装在钟罩内,随钟罩升降,这时,固定在炉盖上的电极汇流排5也要随盖运动。
另一种是固定在静止的台面板上,电极汇流排需从机架下方引入。
钟罩式真空电阻炉的基本参数见表1-1所示。
图1-1 双位钟罩式真空电阻炉1-机架;2-真空系统;3-观察孔;4炉体;5-汇流排;6-电气部分;7-变压器;8-升降机构。
表1-1 钟罩式真空电阻炉的基本参数(SJ861-74)最高温度(℃)炉膛尺寸(工位直径高)(毫米)热态真空度(毫米汞柱)额定功率及相数恒温区尺寸及温差功率(千瓦)相数恒温区尺寸(沿高度方向)(毫米)温差(℃)100030020025101103 100 20350250215130030020025101153 100 203502502201.2钟罩式真空电阻炉的结构1.2.1钟罩式真空电阻炉的隔热屏隔热屏是一种炉衬形式,常用于周期作业真空电阻炉,其特点是热惯性很小而透热性很大。


⼤林算法实验六⼤林算法⼀、实验⽬的1.掌握⼤林算法的特点及适⽤范围。
2.了解⼤林算法中时间常数T对系统的影响。
⼆、实验仪器1.EL-AT-III型计算机控制系统实验箱⼀台2.PC计算机⼀台三、实验内容1.实验被控对象的构成:(1)惯性环节的仿真电路及传递函数G(S)=-2/(T1+1)T1=0.2 (2)纯延时环节的构成与传递函数G(s)=e-Nττ=采样周期 N为正整数的纯延时个数由于纯延时环节不易⽤电路实现,在软件中由计算机实现。
图6-1 被控对象电路图(3)被控对象的开环传函为:G(S)=-2e-Nτ/(T1+1)2.⼤林算法的闭环传递函数:Go(s)=e-Nτ/(Ts+1) T=⼤林时间常数3.⼤林算法的数字控制器:D(Z)=(1-eτ/T)(1-e-τ/T1Z-1)/[k(1-e-τ/T1)[1-e-τ/TZ-1-(1-e-τ/T)Z-N-1] ]设k1=e-τ/T K2=e-τ/T1 T1=0.2 T=⼤林常数 K=2(K-Kk2)Uk=(1-k1)ek-(1-k1)k2ek-1+(k-kk2)k1Uk-1+(k-kk2)(1-k1)Uk-N-1四、实验步骤1.启动计算机,双击桌⾯“计算机控制实验”快捷⽅式,运⾏软件。
2.测试计算机与实验箱的通信是否正常,通信正常继续。
如通信不正常查找原因使通信正常后才可以继续进⾏实验。
3.量对象的模拟电路(图6-1)。
电路的输⼊U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输⼊。
检查⽆误后接通电源。
4.在实验项⽬的下拉列表中选择实验六[六、⼤林算法], ⿏标单击按钮,弹出实验课题参数设置对话框,在参数设置窗⼝设置延迟时间和⼤林常数,点击确认在观察窗⼝观测系统响应曲线。
测量系统响应时间Ts和超调量 p。
5.复步骤4,改变参数设置,将所测的波形进⾏⽐较。
并将测量结果记⼊下表中:延迟时间Td=2,⼤林常数T=0.5延迟时间Td=3,⼤林常数T=0.8延迟时间Td=2,⼤林常数T=0.4延迟时间Td=2,⼤林常数T=0.5五、实验分析1.分析开环系统下的阶跃响应曲线。

目录第1章引言 (1)1.1、Dahllin算法介绍 (1)1.2、Dahllin算法的内容 (1)1.2.1系统结构 (1)1.2.2 算法内容及公式 (2)第二章设计内容 (4)2.1 设计目的 (4)2.2 设计内容 (4)2.1.1 数字控制器D(z)的表达式 (4)2.2.2 振铃现象 (5)第3章 MATLAB仿真 (7)3.1 MATLAB的介绍 (7)基本应用 (8)MATLAB 产品族可以用来进行以下各种工作: (8)3.2 仿真及输出图像 (8)3.2.1 Dahllin算法的MATLAB程序 (9)3.2.2 u(k)的单位阶跃响应波形图 (11)第4章设计总结 (12)第1章引言1.1、Dahllin算法介绍一般具有较大的时间常数和一定的纯滞后时间,且滞后时间比较长的系统不利于现代化工业生产自动化水平提高,不利于产品质量和生产效率的提高。
在生产过程中,大多数工业对象具有较大的纯滞后时间,对象的纯滞后时间τ对控制系统的控制性能极为不利,它使系统的稳定性降低,过渡过程特性变坏。
对这样的系统在工业生产中要求没有超调量或超调量很小,调节时间希望在确定的采样时间内结束(虽然也希望尽快结束过渡过程,但是这是第二位的)。
因此超调试主要的设计目标,用一般的控制系统设计方法是不行的,用模拟仪表控制算法效果也欠佳。
当对象的纯滞后时间τ与对象的惯性时间常数T1之比,即τ/T1≥0.5时,采用常规的比例积分微分(PID)控制,很难获得良好的控制性能。
IBM公司的大林于1968年提出一种针对工业生产过程中含有纯滞后的控制对象的控制算法,即大林算法。
它具有良好的效果,采用大林算法的意义在于大林控制算法能在一些具有纯滞后环节的系统中兼顾动静两方面的性能,可做到小超调小稳态误差。
控制效果比较理想。
对工程实际应用具有很大的意义。
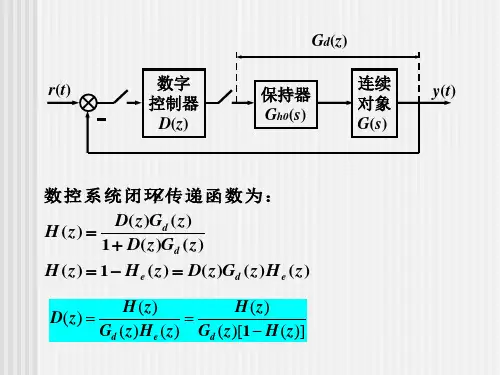
1.2、Dahllin算法的内容1.2.1系统结构大林算法要求在选择闭环Z传递函数时,采用相当于连续一节惯性环节的D (z)来代替最少拍多项式。

一、实验目的1. 理解纯滞后控制系统的概念及其在工业控制系统中的应用。
2. 掌握大林算法在纯滞后控制系统中的应用原理。
3. 通过实验验证大林算法在纯滞后控制系统中的控制效果。
二、实验原理1. 纯滞后控制系统:纯滞后控制系统是指被控对象具有纯滞后特性,即输入信号到输出信号的传递过程中存在一定的时间延迟。
这种时间延迟会使得控制作用不及时,从而影响系统的稳定性和动态性能。
2. 大林算法:大林算法是一种针对纯滞后控制系统的控制策略,其基本思想是在设计闭环控制系统时,采用一阶惯性环节代替最少拍多项式,并在闭环控制系统中引入与被控对象相同的纯滞后环节,以补偿系统的滞后特性。
三、实验设备1. MATLAB 6.5软件一套2. 个人PC机一台四、实验步骤1. 设计实验模型:根据实验要求,设计一个具有纯滞后特性的被控对象模型,并确定其参数。
2. 构建大林算法控制器:根据大林算法的原理,设计一个大林算法控制器,并确定其参数。
3. 进行仿真实验:在MATLAB软件中搭建实验平台,将设计的被控对象模型和大林算法控制器进行联接,进行仿真实验。
4. 分析实验结果:观察实验过程中系统的动态性能,分析大林算法在纯滞后控制系统中的应用效果。
五、实验结果与分析1. 实验结果(1)无控制策略:在无控制策略的情况下,被控对象的输出信号存在较大的超调和振荡,系统稳定性较差。
(2)大林算法控制:在采用大林算法控制的情况下,被控对象的输出信号超调量明显减小,振荡幅度减小,系统稳定性得到提高。
2. 分析(1)无控制策略:由于被控对象具有纯滞后特性,系统动态性能较差,导致输出信号存在较大超调和振荡。
(2)大林算法控制:大林算法通过引入与被控对象相同的纯滞后环节,有效补偿了系统的滞后特性,使得控制作用更加及时,从而提高了系统的动态性能和稳定性。
六、实验结论1. 纯滞后控制系统在实际工业生产中普遍存在,对系统的稳定性、动态性能和抗干扰能力具有较大影响。

实验4 大林算法工业设计和调试实验目的:1.认识和理解大林控制算法控制大时延系统的机理和效果。
2掌握实际控制系统的大林控制算法的设计、实现和调试方法及技术。
实验内容:1.测试系统开环阶跃响应求得被控对象的近似传递函数。
2.对被控对象近似传递函数进行等效离散化。
3.基于被控对象等效离散化模型设计大林控制算法,编写出实现程序,将其嵌入到实验软件中。
4.将设计的大林算法投入运行,并经过调试获得预期控制性能。
5.记下大林控制算法的控制效果。
实验原理及说明:大林算法是针对工业生产过程中含有纯滞后的被控对象所研究的控制算法,即在调节时间允许的情况下,要求系统没有超调量或只有在允许范围中的很小的超调量。
大林算法的设计目标是设计一个数字调节器,使整个闭环系统所期望的传递函数相当于一个延迟环节和一个惯性环节的串联,并期望整个闭环系统的纯滞后时间和被控对象的滞后时间相同,并且,纯滞后时间与采样周期是整数倍关系。
实验中采样周期为1秒,k=0.15,t=22秒,t1=55秒。
.大林算法中涉及的被调对象的参数:对象是一阶惯性滞后环节,<1>对象的放大倍数Kp:Kp=△PV/△OP 阶跃比,这是开环的静态参数,与PID的放大倍数K不是一回事;<2>对象的时间常数T:干扰阶跃引起PV变化,从变化起到稳定值约2/3处的时间值,不包括滞后时间;<3>滞后时间T2:干扰阶跃开始到PV开始变化这一段滞后时间,包括:纯滞后时间及容量过渡滞后时间;2. 整个系统的闭环传递函数相当于是一阶惯性环节, 这是大林算法的期望环节:<1> 输入R(t)是回路的设定值SP;输出Y(t)是回路的PV值;<2> 此一阶惯性环节的放大倍数为1,即稳定时PV=SP; 最终偏差接近零;<3>此期望环节的纯滞后时间应等于被调节对象的纯滞后时间;<4>此期望环节的闭环时间常数:这是待定的期望参数,为不引起回路的小幅振荡,这个时间值应选用大于等于被调对象的时间常数,3. 这些参数如果不精确,将引起大林算法的不稳定性,导致调节质量变坏;。

一、实验目的1. 理解大林算法的基本原理和设计过程。
2. 掌握大林算法在计算机控制系统中的应用。
3. 分析大林算法对控制系统性能的影响。
二、实验仪器1. PC计算机一台2. MATLAB 6.5软件一套3. EL-AT-III型计算机控制系统实验箱一台三、实验原理大林算法是一种针对具有纯滞后特性的控制系统而设计的控制算法。
该算法通过将期望的闭环响应设计成一阶惯性加纯延迟,然后根据这种闭环响应设计控制器,从而实现对具有纯滞后特性的系统的控制。
四、实验内容1. 实验被控对象的构成:(1)惯性环节的仿真电路及传递函数。
(2)纯延时环节的构成与传递函数。
(3)被控对象的开环传递函数。
2. 大林算法的闭环传递函数:闭环传递函数为:\[ G(s) = \frac{K}{T_{s}^{N} \left( \frac{s}{T} + 1 \right)} \]其中,\( K \)为增益,\( T \)为时间常数,\( N \)为纯滞后时间。
3. 大林算法的数字控制器:数字控制器为:\[ D(z) = \frac{(1 - e^{-\frac{1}{T}})(1 - e^{-\frac{1}{T_{1}}z^{-1}})}{K \left(1 - e^{-\frac{1}{T_{1}}}z^{-1}\right) \left[1 - e^{-\frac{1}{T}}z^{-1} - (1 - e^{-\frac{1}{T}})z^{-N}\right]} \]其中,\( K \)为增益,\( T \)为时间常数,\( T_{1} \)为时间常数,\( N \)为纯滞后时间。
五、实验步骤1. 启动计算机,打开MATLAB软件。
2. 编写程序,搭建被控对象模型。
3. 根据被控对象模型,设计大林算法控制器。
4. 对大林算法控制器进行仿真,观察控制效果。
5. 分析大林算法对控制系统性能的影响。
六、实验结果与分析1. 仿真结果:(1)大林算法控制器的阶跃响应。

摘要在许多实际工程中 , 经常遇到一些纯滞后调节系统,往往滞后时间比较长。
对于这样的系统, 人们较为感兴趣的是要求系统没有超调量或很少超调量, 超调成为主要的设计指标。
尤其是具有滞后的控制系统, 用一般的随动系统设计方法是不行的, 而且 PID 算法效果往往也欠佳。
在温度控制技术领域中, 普遍采用控制算PID法。
但是在一些具有纯滞后环节的系统中, PID控制很难兼顾动、静两方面的性能, 而且多参数整定也很难实现最佳控制。
IBM公司的大林于1968年提出一种针对工业生产过程中含有纯滞后的控制对象的控制算法,即大林算法。
它具有良好的效果,采用大林算法的意义在于大林控制算法能在一些具有纯滞后环节的系统中兼顾动静两方面的性能,若采用大林算法, 可做到无或者小超调,无或小稳态误差,控制效果比较理想。
对工程实际应用具有很大的意义。
下面就PID设计和大林算法设计比较,发现二者的不同之处,然后用Matlab的GUI功能将两者制作成可简单操作的用户图形界面。
关键词:大林算法;PID控制;GUI界面;Matlab;目录第一章大林算法在炉温控制中的应用 (2)1.1大林算法简介 (2)1.2大林算法在炉温控制中的设计思路 (2)1.3大林算法实现炉温控制中的代码算法及波形图 (4)第二章 PID实现炉温控制的仿真 (6)2.1 PID的原理及介绍 (6)2.2 PID炉温控制算法程序设计 (7)第三章大林算法和PID实现炉温控制的SIMULINK仿真 (10)3.1 大林算法SIMULINK仿真结构图及波形 (10)3.2 PID的SIMULINK仿真 (10)3.3 大林算法和PID的比较 (11)第四章 GUI图形用户界面编程设计 (12)4.1 GUI简介 (12)4.2 GUI界面的建立 (12)4.2.1编写pushButton回调函数 (15)4.2.2仿真波形 (16)致谢 (17)参考文献 (18)第一章 大林算法在炉温控制中的应用1.1大林算法简介大林算法是由美国IBM 公司的大林(Dahllin)于1968年针对工业生产过程中含纯滞后的控制对象的控制算法。
2. Gs=e-1ss(s+1)采样周期T=0.5s,试用达林算法设计数字控制器D(z)。
写出设计过程,对比输出与给定的效果波形,并显示控制器输出波形。
解:广义对象的脉冲传递函数:Gz=Z1-e-TssGs=Z1-e-Tss e-1sss+1 =Z[e-s-e-s1+T1s2s+1]=z-21-z-1Z[1s2-1s+1s+1]=z-21-z-1[0.5z-11-z-12-11-z-1+11-e-0.5z-1]=z-30.1065(1+0.8474z-1)1-z-1(1-0.6065z-1)根据达林算法,构成的惯性环节与滞后时间τ=1s的纯滞后环节串联而成的理想闭环系统。
设Tτ=0.5sΦs=1Tτs+1e-τs=e-1s0.5s+1它所对应的理想闭环脉冲传递函数:Φz=Z1-e-TssΦs=Z[1-e-Tss e-NTsTτs+1]=z-N-11-e-TTτ1-e-TTτz-1因为N=τT=2, T=0.5s,Tτ=0.5s所以:Φz=0.632z-31-0.368z-1所求数字控制器为:Dz= Φz Gz [1- Φz]=0.632z-31-0.368z-1z-30.10651+0.8474z-11-z-11-0.6065z-1(1-0.632z-31-0.368z-1)=5.9341-z-1(1-0.6065z-1)1+0.8474z-1(1-0.368z-1-0.632z-3)在Gz中可以看到有一个零点z=-0.8474靠近z=-1,所以如果不对达林算法进行修正必会产生振铃现象,令因子(1+0.8474z-1)中的z=1即Gz=0.1967z-31-z-1(1-0.6065z-1)修正后的数字控制器为:Dz=3.2121-z-1(1-0.6065z-1)1-0.368z-1-0.632z-3仿真图如下:3.已知某过程对象的传递函数为:Gs=3e-0.5s0.6s+1期望的闭环系统时间常数Tτ=0.25s,采样周期T=0.5s 。
《计算机控制》课程设计报告题目: Dahlin算法控制器设计**: ***学号: *********2012年7月13日《计算机控制》课程设计任务书指导教师签字:系(教研室)主任签字:2012年7 月5 日一.课题名称Dahlin 算法控制器设计二.课程设计目的课程设计是课程教学中的一项重要内容,是达到教学目标的重要环节,是综合性较强的实践教学环节,它对帮助学生全面牢固地掌握课堂教学内容、培养学生的实践和实际动手能力、提高学生全面素质具有很重要的意义。
《计算机控制技术》是一门理论性、实用性和实践性都很强的课程,课程设计环节应占有更加重要的地位。
计算机控制技术的课程设计是一个综合运用知识的过程,它需要控制理论、程序设计、硬件电路设计等方面的知识融合。
通过课程设计,加深对学生控制算法设计的认识,学会控制算法的实际应用,使学生从整体上了解计算机控制系统的实际组成,掌握计算机控制系统的整体设计方法和设计步骤,编程调试,为从事计算机控制系统的理论设计和系统的调试工作打下基础。
三.提供的实验条件(1)软件:Matlab, Altium Designer ,KEIL (2)仪器和设备:计算机、单片机四.课程设计内容被控对象为s e s s s G 12)110)(2.0(20)(-++=,T=0.5s ,6=τT ,采用Dahlin算法设计消除振铃的数字控制器。
五.工作原理在控制系统应用中,纯滞后环节往往是影响系统动态特性的不利因素。
工业过程中如钢铁,热工和化工过程中往往会有纯滞后环节。
对这类系统,控制器如果设计不当,常常会引起系统的超调和持续振荡。
由于纯延迟的存在,使被控量对干扰、控制信号不能即时的反映。
即使调节机构接受控制信号后立即动作,也要经过纯延时间t 后才到达被控量,使得系统产生较大的超调量和较长的调节时间。
当t >=0.5T (T 为对象的时间常数)时,实践证明用PID 控制很难获得良好的控制品质。