2003年中考数学试题分类汇编

2003-2012年江苏省无锡市中考数学试题分类解析汇编专题10：圆锦元数学工作室编辑一、选择题1. （江苏省无锡市2003年3分）已知⊙O1的半径为5cm，⊙O2的半径为3cm，且圆心距O1O2＝7cm，则⊙O1与⊙O2的位置关系是【】A.外离B.外切C.相交D.内含【答案】C。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

根据题意，得R=5cm，r=3cm，d=7cm，∴R＋r=8cm，R－r=2cm。

∵2＜7＜8，即R－r＜d＜R＋r，∴两圆相交。

故选C。

2. （江苏省无锡市2004年3分）已知⊙O1与⊙O2内切，它们的半径分别为2和3，则这两圆的圆心距d满足【】A、d=5B、d=1C、1<d<5D、d>5【答案】B。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

因此，根据两圆内切时，圆心距等于两圆半径的差，则圆心距d=3－2=1。

故选B。

3. （江苏省无锡市2005年3分）已知⊙O1与⊙O2的半经分别为2和4，圆心距O1 O2=6，则这两圆的位置关系是【】A、相离B、外切C、相交D、内切【答案】B。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

2003年安徽省中考试题数学试题一、选择题（本题共10个小题，每小题4分，共40分）1、冬季某天我国三个城市的最高气温分别是－10℃、1℃、－7℃，把它们从高到低排列正确的是（ ） A ：－10℃、－7℃、1℃ B ：－7℃、－10℃、1℃ C ：1℃ 、－7℃、－10℃ D ：1℃ 、－10℃、－7℃2、下列运算正确的是（ ）A ：a 2·a 3=a 6 B ：a 3÷a=a 3 C ：(a 2)3=a 5 D ：(3a 2)2=9a 43、函数xxy -=1中自变量x 的取值范围是（ ）A ：x ≠0 B ：x ≠1 C ：x>1 D ：x<1且x ≠0 4、下列多项式能因式分解的是（ ） A ：x 2-y B ：x 2+1 C ：x 2+y+y 2D ：x 2-4x+4 5、如图，AB ∥CD ，AC ⊥BC ，图中与∠CAB 互余的角有（ ） A ：1个 B ：2个 C ：3个 D ：4个ABC D第5题图5、下面是空心圆柱体在指定方向上的视图，正确的是（试验区试题）（ ）6、一种花边是由如图的弓形组成的， 弧ACB 的半径为5，弦AB=8，则弓形的高CD 为……（ ） A ：2 B ：25 C ：3 D ：316ABCD 第6题图7、点P （m ，1）在第二象限内，则点Q （-m ，0）在（ ）A ：x 轴正半轴上B ：x 轴负半轴上C ：y 轴正半轴上D ：y 轴负半轴上8、如图，⊙O 1与⊙O 2相交，P 是⊙O 1上的一点，过P 点作两圆的切线，则切线的条数可能是…（ ） A ：1，2 B ：1，3 C ：1，2，3 D ：1，2，3，49、党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到2020年比2000年翻两番。

在本世纪的头二十年（2001年～2020年），要实现这一目标，以十年为单位计算，设每个十年的国民生产总值的增长率都是x ，那么x 满足的方程为（ ）A ：(1+x)2=2B ：(1+x)2=4 C ：1+2x=2 D ：(1+x)+2(1+x)=410、如图，在平行四边形ABCD 中，AC=4，BD=6，P 是BD 上的任一点，过P 作EF ∥AC ，与平行四边形的两条边分别交于点E ，F 。

中考数学试题分类分析汇编（12专题） 专题3：方程（组）和不定式（组）一．选择题1. （2001年福建福州4分）随着计算机技术的迅猛发展，电脑价格不断降低。

某品牌电脑按原售价降低m 元后，又降价20%，现售价为n 元，那么该电脑的原售价为【 】 A. 4(n m )5+元B. 5(n m )4+元 C. (5m n)+元D. (5n m)+元【答案】B 。

【考点】一元一次方程的应用。

【分析】设电脑的原售价为x 元，则()()x m 120%n --=，∴x=5n m 4+。

故选B 。

2. （2003年福建福州4分）不等式组2x 4x 30≥⎧⎨+>⎩的解集是【 】（A ） x>－3 （B ）x≥2 （C ）－3<x≤2 （D ） x<－3 【答案】B 。

【考点】解一元一次不等式组。

【分析】解一元一次不等式组，先求出不等式组中每一个不等式的解集，再利用口诀求出这些解集的公共部分：同大取大，同小取小，大小小大中间找，大大小小解不了（无解）。

因此，2x 4x 2x 2x 30x 2≥≥⎧⎧⇒⇒≥⎨⎨+>>-⎩⎩。

故选B 。

3.（2003年福建福州4分）已知α、β满足α+β=5，且αβ=6，则以α、β为两根的一元二次方程是【 】（A ）2x 5x 60++= （B ）2x 5x 60-+= （C ）2x 5x 60--= （D ）2x 5x 60+-=【答案】B 。

【考点】一元二次方程根与系数的关系。

【分析】∵所求一元二次方程的两根是α、β，且α、β满足α+β=5、αβ=6，∴这个方程的系数应满足两根之和是b 5a-=，两根之积是c 6a =。

当二次项系数a=1时，一次项系数b=－5，常数项c=6。

故选B 。

4. （2005年福建福州大纲卷3分）如图，射线OC 的端点O 在直线AB 上，∠AOC 的度数比∠BOC 的2倍多10度．设∠AOC 和∠BOC 的度数分别为x ，y ，则下列正确的方程组为【 】A 、x+y=180x=y+10⎧⎨⎩错误！未找到引用源。

2003-2014安徽中考数学试题分类11.圆数学工作室 编辑1. （2003安徽省4分）一种花边是由如图的弓形组成的， 弧ACB 的半径为5，弦AB=8，则弓形的高CD 为【 】A ：2B ：25C ：3D ：3162. （2003安徽省4分）如图，⊙O 1与⊙O 2相交，P 是⊙O 1上的一点，过P 点作两圆的切线，则切线的条数可能是【 】A ：1，2B ：1，3C ：1，2，3D ：A、32B、33C、32D、335. （2005安徽省课标4分）如图所示，圆O的半径OA=6，以A为圆心，OA为半径的弧交圆O 于B、C点，则BC为【】A. 63B. 6233D. 326. （2006安徽省大纲4分）如图，用两道绳子捆扎着三瓶直径均为8cm的酱油瓶，若不计绳子接头（π取3），则捆绳总长是【】A．24 cm B．48 cm C．96 cm D．192 cm∵两道绳子，∴绳长=48×2=96c m。

故选C。

7. （2006安徽省课标4分）如图△ABC的内接圆于⊙O，∠C=45°，AB=4，则⊙O的半径为【】A．22 B．4 C．23 D．58. （2007安徽省4分）挂钟分针的长10cm，经过45分钟，它的针尖转过的弧长是【】A．152πcm B．15πcm C．752πcmD．75πcm9. （2007安徽省4分）如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠A OQ=【】A．60° B．65° C．72° D．75°【答案】D。

【考点】正多边形和圆，等边三角形和正方形的性质，圆周角定理，平行线的性质。

10. （2008安徽省4分）如图，在⊙O中，∠ABC=50°，则∠AOC等于【】A.50°B.80°C.90°D. 100°【答案】D。

【考点】圆周角定理。

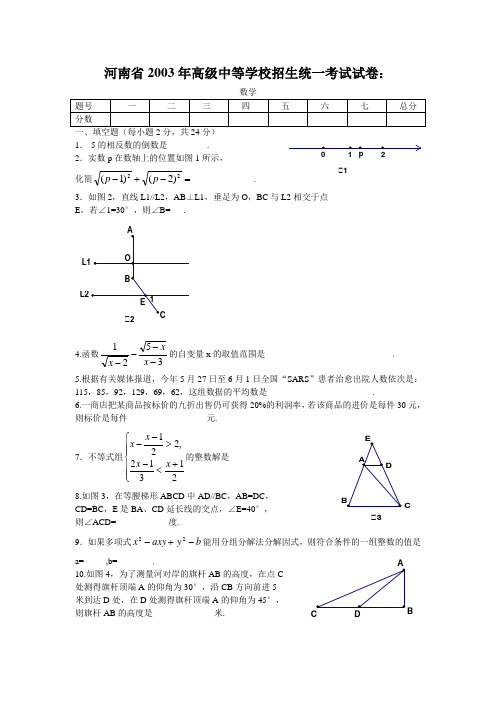
河南省2003年高级中等学校招生统一考试试卷：一、填空题（每小题2分，共24分） 1．-5的相反数的倒数是_________.2．实数p 在数轴上的位置如图1所示，化简=-+-22)2()1(p p ______________.3．如图2，直线L1//L2，AB ⊥L1，垂足为O ，BC 与L2相交于点E ，若∠1=30°，则∠B=___.ͼ2L24.函数3521----x xx 的自变量x 的取值范围是_____________________________. 5.根据有关媒体报道，今年5月27日至6月1日全国“SARS ”患者治愈出院人数依次是：115，85，92，129，69，62，这组数据的平均数是________________________. 6.一商店把某商品按标价的九折出售仍可获得20%的利润率，若该商品的进价是每件30元，则标价是每件__________________元.7．不等式组⎪⎪⎩⎪⎪⎨⎧+<->--21312,221x x x x 的整数解是8.如图3，在等腰梯形ABCD 中AD//BC ，AB=DC ，CD=BC ，E 是BA 、CD 延长线的交点，∠E=40°， 则∠ACD=____________度.9．如果多项式b y axy x -+-22a=_____,b=________.10.如图4，为了测量河对岸的旗杆AB 的高度，在点C 处测得旗杆顶端A 的仰角为30°，沿CB 方向前进5 米到达D 处，在D 处测得旗杆顶端A 的仰角为45°， 则旗杆AB 的高度是______________米.11．点P （m ，n ）既在反比例函数)0(2>-=x xy 的图象上，又在一次函数2--=x y 的图象上，则以m 、n 为根的一元一次方程为___________________. 12.如图5，某燃料公司的院内堆放着10个外 径为1米的空油桶，为了防雨需搭建简易防 雨蓬，这个防雨棚的高度最低应为___________ （3取1.73，结果精确到0.1米）.二、选择题（每小题3分，只有一个正确答案，共15分） 13．若单项式752222b a b am n nm 与+-+是同类项，则m n 的值是（ ）（A ）-3 （B ）-1 （C ）1/3 （D ）314．某专卖店在统计2003年第一季度的销售额时发现，二月份比一月份增加10%，三月份比二月份减少10%，那么三月份比一月份 ( ) (A) 增加10% （B ）减少10% （C ）不增不减 （D ）减少1% 15．用两块完全重合的等腰三角形纸片拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）正方形；（4）等边三角形；（5）等腰直角三角形，一定能拼成的图形是（ ） （A ）（1）（2）（3） （B ）（1）（3）（5） （C ）（2）（3）（5） （D ）（1）（3）（4）（5） 16．在学校对学生进行的晨检体温测量中，学生甲连续10天的体温与36°C ，的上下波动数据为0.2，0.3，0.1，0.1，0，0.2，0.1，0.1，0，0.1，在这十天中该学生的体温波动数据中不正确的是（ ）（A ）平均数为0.12 （B ）众数为0.1 （C ）中位数为0.1 （D ）方差为0.02 17．已知如图6，ABCD 是⊙O 内接正方形，AB=4，F 是BC 的中点，AF 的延长线交⊙O 于点E ，则AE的长是（ ）（A ）5512 （B ）554 （C ）55 （D ）556 三、（第18、19小题各5分，第20、21小题各6分，共22分） 18．已知2231-=x ，2231+=y ，求4-+xyy x 的值.19．已知，如图7是两个同心圆被两条半径截得的一个扇形图，请你画出一个以O 为对称中心的扇形的对称图（保留作图痕迹，写出画法）ͼ7B20．已知关于x 的方程012)14(2=-+++k x k x . （1）求证：该方程一定有两个不相等的实数根；（2）若x 1、x 2是两个实数根，且32)2)(2(21-=--k x x ，求k 的值.21．已知：如图8，在Rt △ABC 中，∠ACB=90°，AC=BC ，点D 是BC 的中点，CE ⊥AD ，垂足为点E ，BF//AC 交CE 的延长线于点F. 求证：AB 垂直平分DF.ͼ8B四、（每小题7分，共14分） 22．解方程31234222=----x x x x .23．已知：如图9，在直角梯形ABCD 中AB//CD ，AD ⊥AB ，以腰BC 为直径的半圆O 切AD 于点E ，连结点BE ，若BC=6，∠EBC=30°. 求梯形ABCD 的面积.ͼ9E A五、（8分）24．在防治“SARS ”的战役中，为防止疫情扩散，某制药厂接到了生产240箱过氧乙酸消毒液的任务.在生产了60箱后，需要加快生产，每天比原来多生产15箱，结果6天就完成了任务.求加快速度后每天生产多少箱消毒液.六、（8分）25．已知：如图10，⊙O 1与⊙O 2相交，⊙O 1的弦AB 交⊙O 2于点C 、D ，O 1O 2⊥AB 于点F ，过点B 作⊙O 2切线BE ，切点为E ，连结EC 、DE.若BE=DE ，∠BED=30°，AC 、CE 的长是方程016102=+-x x 的两个根，（AC<CE ）. （1）求证：BC=EC ；（2）求⊙O 2的半径.（该题是一个错题）ͼ10七、（9分）26．已知：如图11，在平面直角坐标系中，以BC 为直径的圆M 交x 轴于正半轴于点A 、B ，交y 轴于点E 、F ，过点C 作CD 垂直y 轴于点D ，连结AM 并延长交⊙M 于点P ，连结PE.（1）求证：∠FAO=∠EAM ；（2）若二次函数q px x y ++-=2的图象经过B 、C 、E 三点，且以点C 为顶点，当点B 的横坐标等于2时，四边形OECB 的面积是411，求这个二次函数的解析式.。

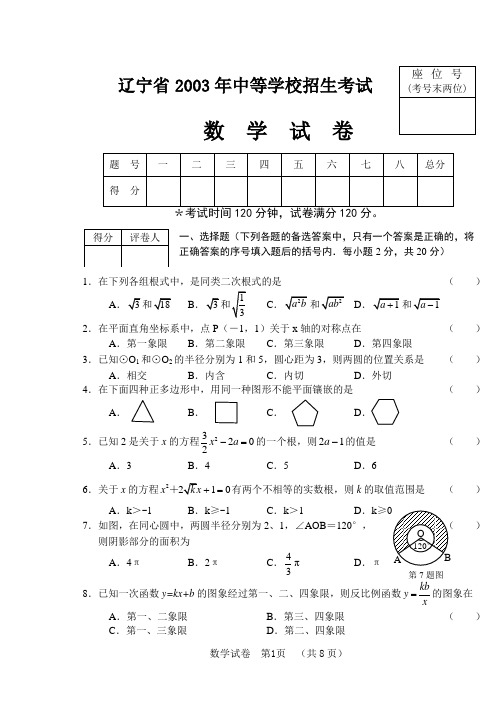
一、选择题（下列各题的备选答案中，只有一个答案是正确的，将正确答案的序号填入题后的括号内．每小题2分，共20分）1．在下列各组根式中，是同类二次根式的是（）A B C D2．在平面直角坐标系中，点P（－1，1）关于x轴的对称点在（）A．第一象限B．第二象限C．第三象限D．第四象限3．已知⊙O1和⊙O2的半径分别为1和5，圆心距为3，则两圆的位置关系是（）A．相交B．内含C．内切D．外切4．在下面四种正多边形中，用同一种图形不能平面镶嵌的是（）A．B．C．D．5．已知2是关于x的方程23202x a-=的一个根，则21a-的值是（）A．3 B．4 C．5 D．66．关于x的方程210x+=＋有两个不相等的实数根，则k的取值范围是（）A．k＞-1 B．k≥-1 C．k＞1 D．k≥7．如图，在同心圆中，两圆半径分别为2、1，∠AOB＝120°，）则阴影部分的面积为A．4πB．2πC．43πD．π8．已知一次函数y=kx+b的图象经过第一、二、四象限，则反比例函数kbyx=的图象在A．第一、二象限B．第三、四象限（）C．第一、三象限D．第二、四象限第7题图9．已知圆锥的侧面展开图的面积是15πcm 2，母线长是5cm ，则圆锥的底面半径为 （ ）A ．32cm B ．3cm C ．4cm D ． 6cm10．如图，射线l 甲、l 乙分别表示甲、乙两名运动员在自行车 比赛中所走路程与时间的函数关系，则他们行进的速度 关系是 （ ）A ．甲比乙快B ．乙比甲快C ．甲、乙同速D ．不一定二、填空题（每小题2分，共20分） 11．在函数y =中，自变量x 的取值范围是 ． 12．若方程210x x +-=的两根分别为12x x 、，则2212x x += ．13．一组数据9，5，7，8，6，8的众数和中位数依次是 ．14．如图，AB 是⊙O 的直径，弦CD ⊥AB ，E 为垂足，若AB=9， BE=1，则CD ＝ ．15．如果一个正多边形的内角和是900°，则这个多边形是正 边形． 16．已知圆的直径为13cm ，圆心到直线l 的距离为6cm ，那么直线l 和这个圆的公共点 的个数是 ．17．用换元法解方程2220383x x x x+-=+，若设23x x y +=，则原方程可化成关于y 的整式方程为 ．18．如图，在△ABC 中，∠C ＝90°，AB ＝10，AC ＝8，以AC 为 直径作圆与斜边交于点P ，则BP 的长为 ． 19．如图，施工工地的水平地面上，有三根外径都是1米的水泥管， 两两相切地堆放在一起，则其最高点到地面的距离是 ．20．在半径为1的⊙O 中，弦AB 、AC 则∠BAC 的度数为 ．第10题图19题图ABE DC O 第14题图． A BPCO第18题图．三、（第21题6分,第22题6分,第23题10分,共22分）21．当x =2，y =3的值．22．如图，已知：AB． 求作：（1）确定AB 的圆心O ． （2）过点A 且与⊙O 相切的直线． （注：作图要求利用直尺和圆规， 不写作法，但要求保留作图痕迹）23．为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题： （1）填充频率分布表中的空格； （2）补全频率分布直方图；（3）在该问题中的样本容量是多少？ 答： ．（4）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由） 答： ．（5）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？ 答： ．⌒ ⌒A B第22题图四、（10分）24．如图，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且建筑物周围没有开阔平整地带．该建筑物顶端宽度AD和高度DC都可直接测得，从A、D、C三点可看到塔顶端H．可供使用的测量工具有皮尺、测倾器．（1）请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶端到地面高度HG的方案．具体要求如下：①测量数据尽可能少．．．．；②在所给图形上，画出你设计的测量平面图，并将应测数据标记在图形上（如果测A、D间距离，用m表示；如果测D、C间距离，用n表示；如果测角，用α、β、γ表示）．（2）根据你测量的数据，计算塔顶端到地面的高度HG（用字母表示，测倾器高度忽略不计）．第24题图五、（10分）25．某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程．下面的二次函数图象（部分）刻画了该公司年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s与t之间的关系）．根据图象提供的信息，解答下列问题：（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系式；（2）求截止到几月末公司累积利润可达到30万元；（3）求第8个月公司所获利润是多少万元？)第25题图六、（12分）26．某博物馆每周都吸引大量中外游客前来参观．如果游客过多，对馆中的珍贵文物会产生不利影响．但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入．因此，博物馆采取了涨浮门票价格的方法来控制参观人数．在该方法实施过程中发现：每周参观人数与票价之间存在着如图所示的一次函数关系．在这样的情况下，如果确保每周4万元的门票收入，那么每周应限定参观人数是多少？门票价格应是多少元？第26题图人数 （人）七、（12分）27．（1）如图（a ），已知直线AB 过圆心O ，交⊙O 于A 、B ，直线AF 交⊙O 于F （不与B 重合），直线l 交⊙O 于C 、D ，交AB 于E ，且与AF 垂直，垂足为G ，连结AC 、AD ．求证：①∠BAD ＝∠CAG ；②AC ²AD ＝AE ²AF ．（2）在问题（1）中，当直线l 向上平行移动，与⊙O 相切时，其他条件不变．①请你在图（b ）中画出变化后的图形，并对照图（a ），标记字母； ②问题（1）中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．图(a) BO AF DC G E l² BO A图(b)第27题图²八、（14分）28．已知：如图，⊙D 交y 轴于A 、B ，交x 轴于C ，过点C的直线：8y =--与y 轴交于P ． （1）求证：PC 是⊙D 的切线；（2）判断在直线PC 上是否存在点E ，使得S △EOP ＝4S △CDO ，若存在，求出点E 的坐标；若不存在，请说明理由；（3）当直线PC 绕点P 转动时，与劣弧AC交于点F （不与A 、C 重合），连结OF ，设PF ＝m ，OF ＝n ，求m 、n 之间满足的函数关系式，并写出自变量n 的取值范围．辽宁省2003年中等学校招生考试数学试题参考答案及评分标准一、（选两个或两个以上答案不给分） 1．B 2．C 3．B 4．C 5．C 6．C7．B8．D 9．B10．A二、 11．x ≥1且x ≠2 12．313．8，7.5 14．15．七16．2 17．y 2-8y -20=0（或写成y 2-20=8y ） 18．3.619．（1+）米 20．15°或75°⌒ 第28题图（注：13题错1个扣1分，顺序错不给分；17题写成分式方程不给分；19题不写单位扣1分；20题只写对一解扣1分）三、21．=-············································ 2分x yx y+=-···················································································································· 4分当x=2，y=3时，原式23523+==--········································································ 6分（注：不化简，直接代数求值，按相应步骤给分）22．如图（O点找对） ································································ 3分（切线画对）································································ 6分（注：不用尺规作图，不给分，没有保留作图痕迹不给分）23．（1）（频数）12，（频率）0.24 ··············································································· 2分（2）补全频率分布直方图 ····················································································· 4分（3）50 ···················································································································· 6分（4）80.5～90.5······································································································· 8分（5）216人 ··········································································································· 10分（注：（1）中每空1分，（2）中直方图1个1分，（3）中样本容量写单位的扣1分）四、说明：本题给分点由两部分组成，一部分是图形设计（满分5分），按设计合理性和测量数据多少给分（5分、3分、1分、0分）；另一部分是依据图形计算（满分5分）。

2003年绍兴市中考数学试卷和参考答案(共150分，考试时间120分钟)【目录】一、选择题（本题有12小题,每小题4分，共48分）下列各题所附的四个选项中，有且只有一个是正确的,请把正确选项前面的字母填在题后的括号内 .......................................................................................................... 1 二、填空题（本题有6小题，每小题5分，共30分） ............................................................ 2 三、解答题（本题有7小题，共72分）下列各小题都必须写出解答过程 ............................ 3 2002年中考数学试卷参考答案 .. (5)一、选择题（本题有12小题,每小题4分，共48分）下列各题所附的四个选项中，有且只有一个是正确的,请把正确选项前面的字母填在题后的括号内1．21的倒数是（ ） A ．2B ．－2C ．21 D ．－21 2．化简:33a a ∙等于（ ）A ．23aB ．6aC ．9aD ．0a3．一元二次方程0132=--x x 的两根为1x ,2x ,则1x +2x 的值是（ ） A ．3B ．－3C ．－1D ．14．2003年3月末,我国城乡居民储蓄存款余额达94600亿元，用科学记数法表示为（ ） A ．94.6×102亿元B ．9.46×103亿元 C ．9.46×104亿元D ．0.946×105亿元5．若点(－1,2)是反比例函数xky =图象上一点,则k 的值是（ ） A ．－21 B ．21 C ．－2D ．26．如果梯形一底边长为6,中位线长为8,那么另一底边长为（ ） A ．4B ．7C ．10D ．147．圆锥的母线长为13cm,底面半径为5cm,则此圆锥的高线长为（ ） A ．6 cm B ．8 cmC ．10 cmD ．12 cm8．小明测得一周的体温并登记在下表(单位:℃)其中星期四的体温被墨迹污染.根据表中数据,可得此日的体温是（ ） A ．36.7:℃ B ．36.8:℃C ．36.9:℃D ．37.0:℃9．已知2=x ,则代数式12--x x的值为（ ） A ．－2B ．2C ．32D ．4210．已知点G 是△ABC 的重心,GP ∥BC 交AB 边于点P,BC=33,则GP 等于（ ）A ．33B ．3C ．23 D ．332 11．身高相等的三名同学甲、乙、丙参加风筝比赛，三人放出风筝线长、线与地面交角如右表（假设风筝线是拉直的），则三人所放的风筝中（ ）A ．甲的最高B ．丙的最高C ．乙的最低D ．丙的最低12．如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 以DE 为折痕向右折叠，AE 与BC 交于点F ，则△CEF 的面积为（ ）A ．4B ．6C ．8D ．10二、填空题（本题有6小题，每小题5分，共30分）13.如果节约16度水记作+16度，那么浪费6度水记作 度. 14.若正六边形的边长为2㎝，则此正六边形的外接圆半径为 ㎝. 15写出和为6的两个无理数 （只需写出一对）.16.若半径不相等的两个圆有唯一公共点，则此两圆的公切线有 条.17.若某人沿坡度ⅰ=3：4的斜坡前进10m ，则他所在的位置比原来的位置升高 m.18.抛物线c bx x y ++=2与x 轴的正半轴交于A ，B 两点，与y 轴交于C 点，且线段AB 的长为1，△ABC 的面积为1，则b 的值是 .三、解答题（本题有7小题，共72分）下列各小题都必须写出解答过程19.（本题8分）计算：()3122101-+--⎪⎭⎫⎝⎛-.20. （本题8分）已知关于x 的方程0122=-+-k x x 有两个不相等的实数根，求k 的取值范围.21. （本题10分）如图，在正方形网络上有一个△ABC.（1） 作△ABC 关于直线MN 的对称图形（不写作法）； （2） 若网络上的最小正方形的边长为1，求△ABC 的面积.22. （本题10分）已知二次函数的图象的顶点坐标为（－2，－3），且图象过点（－3，－2）.（1） 求此二次函数的解析式；（2） 设此二次函数的图象与x 轴交于A ，B 两点，O 为坐标原点，求线段OA ，OB 的长度之和.23. （本题10分）改革开放以来，我国国民经济保持良好发展势头，国内生产总值持速较快增长，下图是1998年－2002年国内生产总值统计图：A BC M N第21题根据图中信息，解答下列问题：（1）1999年国内生产总值是 ；（2）已知2002年国内生产总值比2000年增加12956亿元，2001年比2000年增加6491亿元，求2002年国内生产总值比2001年增长的百分率（结果保留两个有效数字） 24. （本题12分）如图，BC 是半圆的直径，O 是圆心，P 是BC 延长线上一点，PA 切半圆于点A ，AD ⊥BC 于点D.（1） 若∠B=30°，问：AB 与AP 是否相等？请说明理由；（2） 求证：PD ·PO=PC ·PB ；（3） 若BD ：DC=4：1，且BC=10，求PC 的长.25. （本题14分）已知∠AOB=90°，OM 是∠AOB 的平分线，按以下要求解答问题： （1）将三角板的直角顶点P 在射线OM 上移动，两直角边分别与边OA ，OB 交于点C ，D.① 在图甲中，证明：PC=PD ；② 在图乙中，点G 是CD 与OP 的交点，且PG=23PD ，求△POD 与△PDG 的面积之比. （2） 将三角板的直角顶点P 在射线OM 上移动，一直角边与边OB 交于点D ，OD=1，另一直角边与直线OA ，直线OB 分别交于点C ，E ，使以P ，D ，E 为顶点的三角形与△OCD 相似，在图丙中作出图形，试求OP 的长.（第24题）P（第25题）ABOM图丙AB COPMD图乙?图甲D MPOCB A2002年中考数学试卷参考答案一、选择题（本题有12小题,每小题4分，共48分） 1．A 2．B 3．A 4．C 5．C 6．C7．D8．A9．B10．B11．B12．C二、填空题（本题有6小题，每小题5分，共30分）13.－6 14.2 15.略 16.1或3 17.6 18.－3 三、解答题（本题有7小题，共72分） 19. （本题8分）原式=2－1+3=4. 20. （本题8分）△=4－4（k －1）=8－4k ， 令△＞0，得8－4k ＞0， 解得 k ＜2，∴ 所求k 的取值范围是k ＜2. 21. （本题10分）（1） 作图略.（2） 此三角形面积为：25232631212121232=--=⨯⨯-⎪⎭⎫ ⎝⎛⨯⨯⨯-⨯=∆ABC S .22. （本题10分）（1）∵ 函数图象的顶点坐标为（－2，－3）G∴ 设此二次函数的解析式为()322-+=x a y .又∵ 图象过点（－3，－2）， ∴ ()32322-+-=-a ，∴ a=1.∴ 此二次函数的解析式为()322-+=x y .（3） 设点A ，B 的横坐标分别为1x ，2x ，则1x ，2x 是方程0142=++x x 的两根， ∴ 1x +2x =－4，1x ·2x =1， ∴ 1x ＜0，2x ＜0，∴ OA+OB=-=--=+2121x x x x （1x +2x ）=4. 23. （本题10分）（1） 82067亿元.（2） 设2000年国内生产总值为x 亿元，则2001年，2002年分别为（x+6491）亿元，（x+12956）亿元. 由题意得：10239812956=+x ， 解得 89442=x ， 则 x+6491=95933， ∴ 增长率=%7.69593395933102398≈-.答 ：2002年国内生产总值比2001年增长%7.6. 24. （本题12分） （1） 相等. 连结AO ， ∵PA 是半圆的切线，∴∠OAP=90°. ∵OA=OB ， ∴∠B=∠OAB ， ∴∠AOD=2∠B=60°， ∴∠APO=30°， ∴∠B=∠APO ，（第24题）POC∴AB=AP.（2） 在Rt △OAP 中， ∵AD ⊥OP, ∴PA 2=PD ·PO. ∵PA 是半圆的切线， ∴PA 2=PC ·PB ， ∴PD ·PO= PC ·PB.（3）∵BD ：DC=4：1，且BC=10， ∴BD=8，CD=2， ∴OD=3.∵OA 2=OD ·OP ， ∴25=3×OP ， ∴OP=325， ∴PC=325－5=310. 25. （本题14分）（1） ①过P 作PH ⊥OA ，PN ⊥OB ，垂足分别为H ，N ，得∠HPN=90°， ∴∠HPC+∠CPN=90°. 而∠CPN+∠NPD=90°， ∴∠HPC=∠NPD.∵OM 是∠AOB 的平分线，∴PH=PN ，又∵∠PHC=∠PND=90°， ∴△PCH ≌△PDN ， ∴PC=PD.②∵PC=PD ， ∴∠PDG=45°， 而∠POD=45°，∴∠PDG=∠POD. 又∵∠GPD=∠DPO ， ∴△POD ～△PDG.∴342=⎪⎭⎫ ⎝⎛=∆∆PG PD S S PDG POD . NH 图甲D MPOCBA EGABCOPMDE NH A BCO P MDABCOPM D图乙?G（2）若PC 与边OA 相交， ∵∠PDE ＞∠CDO ， ∴△PDE ～△OCD ， ∴∠CDO=∠PED ， ∴CE=CD ，而CO ⊥ED ， ∴OE=OD ， ∴OP=21ED=OD=1. 若PC 与边OA 的反向延长线相交，过P 作PH ⊥OA ，PN ⊥OB ，垂足分别为H ，N ， ∵∠PDE ＞∠EDC ， ∴△PDE ～△ODC ， ∴∠PDE=∠ODC.∵∠OEC ＞∠PED ，∴∠PDE=∠HCP. 而PH=PN ，∴Rt △PHC ≌Rt △PND ， ∴HC=ND ，PC=PD ， ∴∠PDC=45°， ∴∠PDO=∠PCH=22.5°，∴OP=OC.设OP=x ， 则OH=ON=x 22， ∴HC=DN=OD －ON=1－x 22，而HC=HO+OC=x 22+x ， ∴1－x 22=x 22+x ， ∴x=12-，即OP=12-。

2003年河北省初中升学统一考试数 学 试 卷一、选择题：（每小题2分，共20分）1、如果水位下降3m ，记作－3m ，那么水位上升4 m ，记作（ ）A 、1 mB 、7 mC 、4 mD 、－7 m 2、下列计算中，正确的是（ ）A 、B 、C 、D 、3、一学员在广场上练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（ ）A 、第一次向左拐300，第二次向右拐300B 、第一次向右拐500，第二次向左拐1300C 、第一次向右拐500，第二次向右拐1300D 、第一次向左拐500，第二次向左拐13004、化简的结果是（）A 、B 、C 、D 、5、下列图案中，有且只有三条对称轴的是（ ）6、赵强同学借了一本书，共280页，要在两周借期内读完，当他读了一半时，发现平均每天要多读21页才能在借期内读完，他读前一半时，平均每天读多少页？如果设读前一半时，平均每天读页，则下面所列方程中，正确的是（ ）A 、B 、C 、D 、7、如图：这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图，已知桌面的直径为1.2米，桌面距离地面1米，若灯泡距离地面3米，则地面上阴影部分的面积为（ ）A 、平方米B 、平方米C 、平方米D 、平方米8、在平面直角坐标系中，若一个点的横坐标与纵坐标互为相反数，则该点一定不在（ ）A 、直线＝上B 、直线＝－上C 、抛物线＝上D 、双曲线上33=--725)(a a =02.02.022=-b a b a 4)4(2-=-2293m mm --3+m m 3+-m m 3-m m m m-3B C D x 1421140140=-+x x 1421280280=++x x 1421140140=++x x 1211010=++x x π36.0π81.0π2π24.3y x y x y 2x x y 1=A9、如图：E 是边长为1的正方形ABCD 的对角线BD 上一点，且BE ＝BC ，P 为CE 上任意一点，PQ ⊥BC 于点Q ，PR ⊥BE 于点R ，则PQ ＋PR 的值是（ ）A 、B 、C 、D 、10、如图：向放在水槽底部的烧杯注水（流量一定），注满烧杯后，继续注水，直至注满水槽，水槽中水面上升高度与注水时间之间的函数关系大致是下列图象中的（ ）二、填空题：（每小题2分，共20分）11、－2的倒数是 。

2003-2012年江苏省无锡市中考数学试题分类解析汇编专题1：实数锦元数学工作室编辑一、选择题1.（江苏省无锡市2003年3分）的结果是【】A. B. C. D.【答案】A。

【考点】分母有理化。

【分析】即可：故本题选A。

2.（江苏省无锡市2004年3分）下列各式中的最简二次根式是【】A、5B、12C、18D、91【答案】A。

【考点】最简二次根式【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式中的两个条件（被开方数不含分母，也不含能开的尽方的因数或因式）是否同时满足，同时满足的就是最简二次根式，否则就不是。

因此。

13，∴12、18和91都不是最简二次根式。

故选A。

3.（江苏省无锡市2005年3分）比较41,31,21--的大小，结果正确的是【】A、413121<-<-B、314121-<<-C、213141-<-<D、412131<-<-【答案】A。

【考点】有理数大小比较。

【分析】根据有理数大小比较的方法即可求解： ∵12-＜0，13-＜0，14＞0，∴14最大； 又∵1123>，∴1123-<-。

∴413121<-<-。

故选A 。

4.（江苏省无锡市2006年3分） 】A B ．24 C D 【答案】C 。

【考点】同类二次根式。

【分析】将四个选项化简，找出被开方数为3的选项即可：A 、 = 与B 、24不是二次根式与被开方数不同，故不是同类二次根式；C 、=D 、与故选C 。

5.（江苏省无锡市2006年3分）如图，O 是原点，实数a 、b 、c 在数轴上对应的点分别为A 、B 、C ，则下列结论错误的是【 】A ．a －b ＞0B ．ab ＜0C ．a ＋b ＜0D ．b （a －c ）＞0【答案】B 。

【考点】实数与数轴，不等式的性质。

【分析】根据数轴可以得到b ＜a ＜0＜c ，然后据此即可确定哪个选项正确：∵b ＜a ＜0＜c ，∴a －b ＞0，a ＋b ＜0，故选项A 、C 正确；∴ab ＞0，故选项B 错误；∵a －c ＜0，b ＜0，∴b （a －c ）＞0，故选项D 正确。

2003武汉中考数学试题及答案武汉市2003年初中毕业、升学考试数 学本试卷分为1卷和2卷两部分，1卷为A 卷选择题；2卷为B 卷非选择题,A 卷（毕业试卷）共60分，B 卷共90分；21A ＋B 为升学成绩，满分120分．考试时间120分钟．参考公式：在半径为R 的圆中，圆心角为n °的扇形面积的计算公式是：2360R n S π=扇形。

1卷（A 卷 第1－20题，共60分）一、判断题（共10小题，每小题2分，共20分）下列各题请你判断正误，正确的填“A ”，错误的填“B ”．l ．方程x （x ＋5）＝150化成一般形式为015052=-+x x ．（ ）2．y ＝3x －1是一次函数．（ ） 3．函数5-=x y 的自变量x 的取值范围是x ≥5．（ ）4．数据2，l ，3，9，5的平均数是4．（ ）5．在直角坐标系中，x 轴上的点的纵坐标都为0．（ ）6．tan45°＝1。

（ ）7．在同圆或等圆中，相等的圆心角所对的弧相等．（ ）8．圆的切线垂直于该圆的半径．（ ）9．两圆内切时，这两圆的公切线只有一条．（ ）10．三角形的内切圆的圆心叫做三角形的内心．（ ）二、选择题（共10小题．每小题4分，共40分）下列各题均有四个备选答案，其中有且只有一个是正确的．11．一元二次方程012=-x的根为（ ） （A ）x ＝1 （B ）x ＝－1 （C ）1x ＝1，2x ＝－1 （D ）1x ＝0，2x ＝1 12．用换元法解方程061512=+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-x x x x 时，设y x x =-1，则原方程化为关于y 的方程是（ ） （A ）0652=++y y （B ）0652=+-y y（C ）0652=-+y y （D ）0652=--y y13．不解方程，判别方程05752=+-x x的根的情况是（ ） （A ）有两个相等的实数根（B ）有两个不相等的实数根（C ）只有一个实数根（D ）没有实数根14．函数11+=x y 中自变量x 的取值范围是（ ） （A ）x ≠－1（B ）x ＞－1（C ）x ≠1（D ）x ≠015．已知圆的半径为6.5cm ，如果一条直线和圆心的距离为9cm ，那么这条直线和这个圆的位置关系是（ ）（A ）相交 （B ）相切（C ）相离 （D ）相交或相离16．如图，已知圆心角∠BOC ＝100°，则圆周角∠BAC 的度数为（A ）100° （B ）130° （C ）50°（D ）80°17．如果两圆外切，那么它们的公切线的条数为（ ） （A ）1条 （B ）2条 （C ）3条（D ）4条18．已知两圆的半径分别为3cm 和4cm ，两个圆的圆心距为10cm ，则两圆的位置关系是（ ）（A ）内切 （B ）相交 （C ）外切（D ）外离19．过⊙O 内一点M 的最长弦长为10cm ，最短弦长为8cm ，那么OM 的长为 （ ）（A ）3cm （B ）6cm （C ）41cm （D ）9cm20．若二次函数c axy +=2，当x 取（1x ≠2x ）时，函数值相等，则当x 取1x +2x 时，函数值为（ ）（A ） a ＋c （B ） a －c （C ）－c （D ）c1卷（B1卷 第21－32题，共 36分）三、选择题（共12小题，每小题3分，共36分） 下列各题中均有四个备选答案，其中有且只有一个是正确的．21．计算⎪⎭⎫ ⎝⎛-÷-a a a a11的正确结果是（ ） （A ）11+a （B ）1 （C ）11-a （D ）－122．若b＜0，化简3ab-的结果是（）（A）abb-（C）ab-b-b-（B）ab（D）abb23．商店出售下列形状的地砖：①正方形；②长方形；③正五边形；＠正六边形．若只选购其中某一种地砖镶嵌地面，可供选择的地砖共有．（）（A）1种（B）2种（C）3种（D）4种24．今年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制．下图是某同学记载的5月1日至30日每天全国的SARS新增确诊病例数据日．将图中记载的数据每5天作为一组，从左至右分为第一组至第六组，下列说法：①第一组的平均数最大，第六组的平均数最小；②第二组的中位数为138；③第四组的众数为28．其中正确的有（）（A ）0个 （B ）1个 （C ）2个 （D ）3个25．据（武汉市2002年国民经济和社会发展统计公报）报告：武汉市2002年国内生产总值达1493亿元，比2001年增长11.8％．下列说法：① 2001年国内生阐总值为1493（1－11.8％）亿元；②2001年国内生产总值为%8.1111493-亿元；③2001年 国内生产总值为%8.1111493+亿元；④若按11.8％的年增长率计算，2004年的国 内生产总值预计为1493（1＋11.8％）2亿元．其中正确的是（ ） （A ）③④ （B ）②④ （C ）①④ （D ）①②③26．某天同时同地，甲同学测得1m 的测竿在地面上影长为0.8m ，乙同学测得国旗旗杆在地面上的影长为9.6m ，则国旗旗杆的长为（ ）（A ）10m （B ）12m （C ）13m （D ）15m27．如图，已知直线BC 切⊙O 于点C ，PD 为⊙O 的直径，BP 的延长线与CD 的延长线交于点A ，∠A ＝28°，∠B ＝26°，则∠PDC等于（ ）（A ）34° （B ）36° （C ）38°（D ）40°28．一次函数y ＝－kx ＋4与反比例函数x k y =的图像有两个不同的交点，点（－21，1y ）、（－1，2y ）、（21，3y ）是函数x k y 922-=图像上的三个点，则1y 、2y 、3y 的大小关系是（ ） （A ）y 2＜y 3＜y 1 （B ）y 1＜y 2＜y 3（c ）y 3＜y 1＜y 2 （D ）y 3＜y 2＜y 1．29. 如图，已知⊙1O 、⊙2O 相交于A 、B 两点．且点1O 在⊙2O 上．过A 作⊙1O 的切线AC 交B 1O 的延长线于点P ，交⊙2O 于点C ，BP 交⊙1O 于点D ．若PD ＝1．PA ＝5．则AC 的长为（ ）（A ）5 （B ）52 （C ）2+5 （D ）5330．小李以每千克0．8元的价格从批发市场购进若干千克西瓜到市场去销售，在销售了部分西瓜之后，余下的每千克降价0.4元．全部售完．销售金额与卖瓜的千克数之间的关系如图所示，那么小李赚了（）（A）32元（B）36元（C）38元（D）44元31．已知：抛物线cy+=2（a＜0)经过点（－1，+axbx0），且满足4a＋2b＋c＞0．以下结论：①a＋b＞0；②a＋c＞0；③－a＋b＋c＞0；④2-c＞25a．其中正确的个数有（）b2ac（A）1个（B）2个（C）3个（D）4个32．已知：如图，AB为⊙O的直径，CD、CB 为⊙O的切线，D、B为切点．OC交⊙O于点E，AE的延长线交BC于点F，连接AD、BD．以下结论：①AD∥OC；②点E为△CDB的内心；③FC＝FE；④CE·FB＝AB ·CF 其中正确的只有（ ）（A ）①②（B ）②③④（C ）①③④（D ）①②④2卷（B2卷 第33－41题．共54分） 四、填空题（共4小题．每小题2分．共8分）33．因式分解：=-+-ab b a2122 。