(完整)SAR合成孔径雷达图像点目标仿真报告(附matlab代码)

合成孔径雷达图像目标识别方法研究的开题报告一、选题背景及研究意义合成孔径雷达（Synthetic Aperture Radar，SAR）是一种利用微波信号获取地面信息的主要遥感手段，其具有无视天气和昼夜变化等特点，并且能够获取高精度、高分辨率的图像数据，因此在国防、地质勘探、环境监测等领域得到了广泛应用。

但是，SAR图像数据的解译和目标识别一直是一个挑战性问题，如何设计有效的目标识别方法来解决这个问题是当前SAR研究的重要方向之一。

现阶段，SAR目标识别方法主要基于图像处理、特征提取和分类器的设计。

其中，特征提取是SAR目标识别的关键环节，而合成孔径雷达图像数据具有高维、高斯噪声、不完整性等特点，传统的特征提取方法不能满足需求。

因此，需要探索新的特征提取方法和分类算法，提高SAR目标识别的准确性和实时性。

二、研究内容和研究方法本课题的研究内容是合成孔径雷达图像目标识别方法的设计与实现，具体包括以下几个方面：1. 探索基于深度学习的SAR目标识别方法。

深度学习是近年来兴起的一种基于人工神经网络的机器学习方法，其在图像识别、语音识别等领域取得了显著的成果。

本课题将尝试将深度学习方法应用于SAR目标识别，以期获得更高的准确率和鲁棒性。

2. 提出新的特征提取方法。

本课题将探索一些新的特征提取方法，如基于稀疏表示的特征提取方法和基于卷积神经网络的特征提取方法。

这些方法将充分利用SAR图像的空间域和频谱域信息，提取具有区分度和稳定性的特征集，为后续的分类器提供更可靠的输入数据。

3. 针对SAR目标识别的分类器设计。

本课题将研究不同的分类算法，如支持向量机、朴素贝叶斯、随机森林等，并将与提出的特征提取方法进行融合，探索最佳的分类器设计。

研究方法主要采用实验方法和理论分析相结合的方式。

首先，通过收集和整理大量的SAR图像数据集，建立适合本课题的数据集，评估不同方法的性能和效果；其次，利用MATLAB、TensorFlow等工具，实现和验证所提出方法和算法的有效性和可行性；最后，结合理论分析、实验结果和实际应用需求，进一步优化和完善所提出的方法与算法。

11目录1. 设计的基本骤 (1)1.1 雷达信号的产生 (1)1.2 噪声和杂波的产生 (1)2. 信号处理系统的仿真 (1)2.1 正交解调模块 (2)2.2 脉冲压缩模块 ...............................................2.3 回波积累模块 ...............................................2.4 恒虚警处理（CFAR）模块 (4)结论 (11)1 设计的基本骤雷达是通过发射电磁信号，再从接收信号中检测目标回波来探测目标的。

再接收信号中，不但有目标回波，也会有噪声（天地噪声，接收机噪声）；地面、海面和气象环境(如云雨)等散射产生的杂波信号；以及各种干扰信号（如工业干扰，广播电磁干扰和人为干扰）等。

所以，雷达探测目标是在十分复杂的信号背景下进行的，雷达需要通过信号处理来检测目标，并提取目标的各种信息，如距离、角度、运动速度、目标形状和性质等。

图3-6 设计原理图2 信号处理系统的仿真雷达信号处理的目的是消除不需要的信号（如杂波）及干扰，提取或加强由目标所产生的回波信号。

雷达信号处理的功能有很多，不同的雷达采用的功能也有所不同，本文是对某脉冲压缩雷达的信号处理部分进行仿真。

一个典型的脉冲压缩雷达的信号处理部分主要由A/D 采样、正交解调、脉冲压缩、视频积累、恒虚警处理等功能组成。

因此，脉冲压缩雷达信号处理的仿真模型.2.1 正交解调模块雷达中频信号在进行脉冲压缩之前，需要先转换成零中频的I 、Q 两路正交信号。

中频信号可表示为:0()()cos(2())IF f t A t f t t πϕ=+ (3.2)式(3.2)中， f 0 为载波频率。

令:00()()cos 2()sin 2IF f t I t f t Q t f t ππ=- (3.3)则00()()cos 2()sin 2IF f t I t f t Q t f t ππ=- (3.4)在仿真中，所有信号都是用离散时间序列表示的，设采样周期为T ,则中频信号为 f IF (rT ) ，同样，复本振信号采样后的信号为f local =exp(?j ω 0rT ) (3.5)则数字化后的中频信号和复本振信号相乘解调后，通过低通滤波器后得到的基带信号f BB (r ) 为:11000{()cos()}(){()sin()}()N N BB IF IF n n f f r n r n T h n j f r n r n T h n ωω--==-----∑∑ (3.6)式(3.6)中， h (n ) 是积累长度为N 的低通滤波器的脉冲响应。

第21章合成孔径（SAR）雷达L.J.Cutrona21.1 基本原理和早期历史对于机载地形测绘雷达，一个日益迫切的问题是要求其具有更高的分辨力，并通过“强力”技术来达到高分辨力。

通常这种类型的雷达系统是通过辐射短脉冲来获得距离分辨力，通过辐射窄波束来获得方位分辨力。

有关距离分辨力和脉冲压缩技术的一些问题已在第10章中讨论过了。

在第10章中已经表明，若发射信号的带宽足够宽，则采用适当的技术可获得比相应脉宽要好得多的分辨力。

由于脉冲压缩已在第10章中进行了广泛地讨论，因此本章将讨论直接应用于合成孔径技术中的脉冲压缩技术，特别是讨论对于同时完成脉冲压缩和方位压缩的技术，而不讨论顺序地完成距离压缩和方位压缩的技术。

本章所要讨论的基本原理是利用合成孔径技术来改善机载地形测绘雷达的方位分辨力，使其值比辐射波束宽度所能达到的方位分辨力要高得多。

SAR是采用信号处理的方法产生一个等效的长天线，而非真正采用物理的长天线。

事实上，在绝大多数场合，使用的仅是一根较小的实际天线。

在考虑合成孔径时人们以长线性阵列物理天线的特性为参考。

在阵列天线中，许多辐射单元沿直线配置在适当的位置上，并利用这种实际的线性阵列天线，使信号同时馈给天线阵的每个单元；同样地，当天线用于接收时，可使各个单元同时接收信号。

在发射和接收工作模式下，用波导或其他传输线连接，利用干涉现象得到有效的辐射方向图。

若辐射单元相同，则线性阵列天线的辐射方向图是单个单元的方向图和阵列因子两个量的积。

在线性阵列天线中，阵列因子比单元的方向图具有尖锐得多的波瓣（较窄波束），这种天线阵因子的半功率波束宽度β（rad）可由下式给出，即β=（21.1）L/λ式中，L为实际阵列天线的长度；λ为波长。

合成孔径天线往往仅用单个辐射单元。

天线沿一直线依次在若干个位置平移，且在每一个位置发射一个信号，接收相应发射位置的雷达回波信号并储存起来。

储存时，必须同时保存所接收信号的幅度和相位。

合成孔径雷达第一次作业姓名：xxx 学号：xxx一题目：1.LFM信号分析：（1）仿真LFM信号；（2）观察不同TBP的LFM信号的频谱。

（3）观察不同过采样率下的DFT结果，注意频谱混叠情况。

2.脉冲压缩仿真：针对“基带LFM信号”:（1）实现无误差的脉冲压缩；（2）通过频域补0实现时域十倍以上的过采样率，得到光滑的时域波形，通过观察给出指标（IRW,PSLR）；（3）阅读资料，按照公式实现3阶（-20dB）,6阶（-40 dB）泰勒加权，观察加窗效果，分析指标（IRW,PSLR），并对比MATLAB TAYLORWIN函数的一致性；（4）在3阶泰勒加权下实现15.30.45.60.90.135度QPE下的脉冲压缩，显示输出波形，观察记录QPE的影响。

3.一维距离向仿真:（1）输入参数：目标参数：RCS=1，分别位于10km,11km,11km+3m,11km+50m处。

LFM信号参数：中心频率1.0GHz,脉冲宽度30us,带宽30MHz。

（2）输出：设计采样波门，仿真回波，完成脉冲压缩，检测各峰值位置，判断每个目标是否得以分辨，分析各出现在相应位置及幅度的原因。

二题目分析与解答：1.问题分析：由基础知识知，决定LFM信号的主要参数有中心频率fc(此处仿真取fc=0)，带宽B，脉冲宽度Tp, 调频斜率K，其中K=B/Tp。

对LFM信号进行傅里叶变换时，不同的时宽带宽积（TBP）会对频谱有不同的影响。

主要程序段(源程序见附件)：%参数设置Tp=5e-6; B=10e6; K=B/Tp；Fs=2*B; Ts=1/Fs;N=Tp/Ts;TBP=Tp*B%波形产生t=linspace(-Tp/2,Tp/2,N);St=exp(j*pi*K*t.^2); Phase=pi*K*t.^2;Fre=2*pi*K*t;f=linspace(-Fs/2,Fs/2,N);figure(2)plot(f*1e-6,fftshift(abs(fft(St))),'k'); xlabel('Frequency/MHz');ylabel('Magnitude');title('Frequence Response'); legend('TBP=50')fft_St=fftshift(abs(fft(St)));（1）不同脉宽和带宽下的LFM 信号：（2）不同TBP 下的信号频谱：分析：LFM 信号的频谱类似矩形窗，随着TBP 的增大，其越接近矩形窗，当TBP<100时，近似效果较差，当TBP>100时，近似效果较好，但随着TBP 的增大，频域上会产生吉布斯现象。

MATLAB雷达信号处理仿真5.2 噪声和杂波的产⽣在实际的雷达回波信号中，不仅仅有⽬标的反射信号，同时还有接收机的热噪声、地物杂波、⽓象杂波等各种噪声和杂波的叠加。

由于噪声和杂波都不是确知信号，只能通过统计特性来分析。

本节将讨论⼀些常见的噪声和杂波的产⽣⽅法。

5.2.1 随机热噪声随机热噪声有多种，常见有概率密度函数服从⾼斯分布、均匀分布、指数分布以及τ分布的热噪声。

1. 服从⾼斯（Guass ）分布的热噪声（随机序列）标准⾼斯分布的概率密度为：)2exp(1)(22σσπx x p -= (5.2.1)均值为0x 的⾼斯分布的概率密度函数为：)2)(exp(1)(220σσπx x x p --= (5.2.2) Matlab7.0本⾝⾃带了标准⾼斯分布的内部函数randn ，调⽤格式如下:Y = randn(n)Y = randn(m,n) Y = randn([m n]) Y = randn(size(A)) s = randn('state')randn 函数产⽣的随机序列服从均值为m=0，⽅差σ2＝1的⾼斯分布。

Y = randn(n)产⽣的是⼀个n ×n 的随机序列矩阵，⽽Y = randn(m,n) 和Y = randn([m n])产⽣的m ×n 的随机序列矩阵，Y = randn(size(A))产⽣的是⼤⼩与矩阵A 同样⼤⼩的随机序列矩阵。

s = randn('state') 返回的是⼀个具有两个元素的向量，该向量显⽰的是当前正态随机数产⽣器的状态。

randn('state',s) 指令可以将产⽣器的状态设置到s ，⽽randn('state',0) 则可以将正态随机数产⽣器的状态恢复到初始状态。

因此，利⽤randn 函数可以⾮常简单快捷地产⽣出服从⾼斯分布的随机序列，如图5.7。

图5.7服从⾼斯分布的随机序列及其直⽅图2. 服从均匀分布的热噪声（随机序列） (a-b)均匀分布的概率密度函数为：ab x p -=1)( (5.2.3) 根据（a-b ）均匀分布的概率密度函数和（0-1）均匀分布的概率密度函数可以推导出它们之间的关系为：a u ab ba au +?-=--=)(ζζ或 (5.2.4)其中u 服从（0-1）单位均匀分布，ζ服从（a-b ）分布所以根据上式，可以先产⽣⼀个服从（0-1）单位均匀分布的信号，然后再将其经过上式的变换，就可以得到⼀个服从（a-b ）均匀分布的信号了。

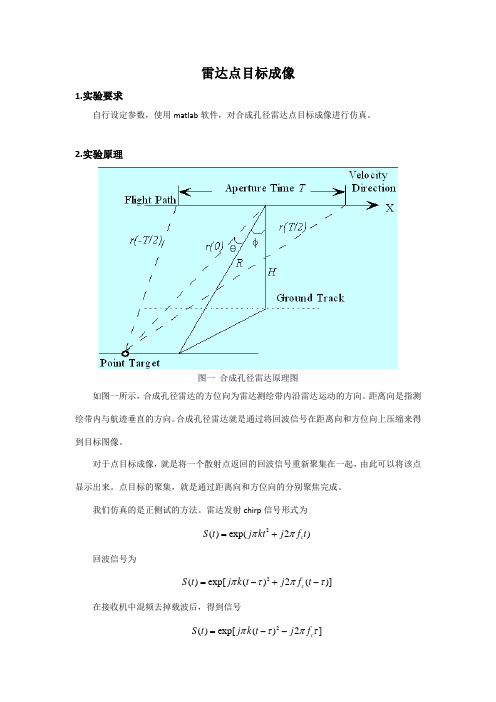
雷达点目标成像1.实验要求自行设定参数，使用matlab 软件，对合成孔径雷达点目标成像进行仿真。

2.实验原理图一 合成孔径雷达原理图如图一所示，合成孔径雷达的方位向为雷达测绘带内沿雷达运动的方向。

距离向是指测绘带内与航迹垂直的方向。

合成孔径雷达就是通过将回波信号在距离向和方位向上压缩来得到目标图像。

对于点目标成像，就是将一个散射点返回的回波信号重新聚集在一起，由此可以将该点显示出来。

点目标的聚集，就是通过距离向和方位向的分别聚焦完成。

我们仿真的是正侧试的方法。

雷达发射chirp 信号形式为2()exp(2)c S t j kt j f t ππ=+回波信号为2()exp[()2()]c S t j k t j f t πτπτ=-+-在接收机中混频去掉载波后，得到信号2()exp[()2]c S t j k t j f πτπτ=--可得信号的距离向信号形式为2exp[(2/)]j k t r c π-方位向信号形式为exp[4/]c j f r c π-其中()r t =当v t R 时有2()()2vt r t R R ≈+，知回波信号在方位向上也是线性调频信号，其调频率为22v Rλ，λ为载波波长。

对于成像算法，我们采用经典的距离多普勒算法，即SD 算法。

他的基本思想是基本思想是将二位处理分解为两个一维处理的级联方式，即分别压缩距离向和方位向。

由于雷达的飞行线路接近直线，所以方位向和距离向相互有影响，要对数据进行徙动校正。

但是由于机载SAR 飞行范围小，距离弯曲量很小，故可以不用考虑徙动校正。

SD 算法的具体流程图如图二所示。

图二 SD 算法的具体流程图4.实验过程参数设置：飞机飞行高度：10000m下视角：45度飞机的飞行速度：100m/s合成孔径时间：1sPRF ：500HzK ：113010⨯Hz/s脉冲宽度:10us载波频率: 10510Hz ⨯回波点阵大小：501X501对数据进行距离向压缩，得到图一。

超声合成孔径成像 matlab
（原创版）
目录
1.超声合成孔径成像简介
2.Matlab 在超声合成孔径成像中的应用
3.超声合成孔径成像的优点
4.面临的挑战和未来发展方向
正文
一、超声合成孔径成像简介
超声合成孔径成像（Synthetic Aperture Imaging，SAI）是一种基于合成孔径雷达（Synthetic Aperture Radar，SAR）的成像技术。

它利用雷达在不同位置接收到的回波信号，通过数据处理方法合成一个大孔径的天线，从而获得高分辨率的图像。

这种技术在环境观测、灾害监测、地图测绘以及战场态势侦察等领域有着广泛应用。

二、Matlab 在超声合成孔径成像中的应用
Matlab 是一种广泛应用于科学计算和工程设计的软件，它可以方便地实现超声合成孔径成像。

通过 Matlab，可以模拟雷达回波信号的接收过程，并进行数据处理，最终生成合成孔径成像的结果。

三、超声合成孔径成像的优点
超声合成孔径成像技术具有以下几个优点：
1.高分辨率：通过合成大孔径的天线，可以获得高分辨率的图像，提高目标识别的准确性。

2.穿透性：超声波可以穿透一定深度的物体，因此合成孔径成像可以应用于各种材料的探测和成像。

3.全天时、全天候工作：合成孔径成像不受气象条件影响，可以在任何时间、任何天气情况下进行工作。

4.灵活性：合成孔径成像可以灵活地调整雷达的参数，例如工作频率、脉冲重复频率等，以适应不同的应用场景。

四、面临的挑战和未来发展方向
尽管超声合成孔径成像技术具有许多优点，但仍然面临着一些挑战，例如如何提高成像速度、如何降低系统成本等。

合成孔径雷达概述1合成孔径雷达简介 (2)1.1 合成孔径雷达的概念 (2)1.2 合成孔径雷达的分类 (3)1.3 合成孔径雷达(SAR)的特点 (4)2合成孔径雷达的发展历史 (5)2.1 国外合成孔径雷达的发展历程及现状 (5)2.1.1 合成孔径雷达发展历程表 (6)2.1.2 世界各国的SAR系统 (9)2.2 我国的发展概况 (11)2.2.1 我国SAR研究历程表 (11)2.2.2 国内各单位的研究现状 (12)2.2.2.1 电子科技大学 (12)2.2.2.2 中科院电子所 (12)2.2.2.3 国防科技大学 (13)2.2.2.4 西安电子科技大学 (13)3 合成孔径雷达的应用 (13)4 合成孔径雷达的发展趋势 (14)4.1 多参数SAR系统 (15)4.2 聚束SAR (15)4.3极化干涉SAR（POLINSAR） (16)4.4合成孔径激光雷达（Synthetic Aperture Ladar） (16)4.5 小型化成为星载合成孔径雷达发展的主要趋势 (17)4.6 性能技术指标不断提高 (17)4.7 多功能、多模式是未来星载SAR的主要特征 (18)4.8 雷达与可见光卫星的多星组网是主要的使用模式 (18)4.9 分布SAR成为一种很有发展潜力的星载合成孔径雷达 (18)4.10 星载合成孔径雷达的干扰与反干扰成为电子战的重要内容 (19)4.11 军用和民用卫星的界线越来越不明显 (19)5 与SAR相关技术的研究动态 (20)5.1 国内外SAR图像相干斑抑制的研究现状 (20)5.2 合成孔径雷达干扰技术的现状和发展 (20)5.3 SAR图像目标检测与识别 (22)5.4 恒虚警技术的研究现状与发展动向 (25)5.5 SAR图像变化检测方法 (27)5.6 干涉合成孔径雷达 (31)5.7 机载合成孔径雷达技术发展动态 (33)5.8 SAR图像地理编码技术的发展状况 (35)5.9 星载SAR天线方向图在轨测试的发展状况 (37)5.10 逆合成孔径雷达的发展动态 (38)5.11 干涉合成孔径雷达的发展简史与应用 (38)合成孔径雷达概述1合成孔径雷达简介合成孔径雷达(Synthetic Aperture Radar,简称SAR)是一种全天候、全天时的现代高分辨率微波成像雷达。

合成孔径雷达目标识别与仿真研究合成孔径雷达目标识别与仿真研究摘要：合成孔径雷达（Synthetic Aperture Radar，SAR）是一种以主动方式获取地面图像的遥感技术，具有高分辨率、全天候、全天时等优点，被广泛应用于土地资源调查、灾害监测、军事侦察等领域。

本文针对合成孔径雷达的目标识别与仿真问题进行了研究。

文章首先介绍了合成孔径雷达的基本原理和特点，接着详细分析了合成孔径雷达图像中的目标特征，包括散射机制、杂波和布告等。

然后，本文通过仿真实验，从目标尺度、角度等方面对合成孔径雷达的目标识别效果进行了研究。

最后，本文探讨了合成孔径雷达技术的发展趋势和应用前景。

关键词：合成孔径雷达；目标识别；仿真研究；散射机制；目标特征；应用前景一、引言合成孔径雷达是一种重要的地面目标识别技术，具有高分辨率、全天候、全天时等优点，被广泛应用于土地资源调查、灾害监测、军事侦察等领域。

为了实现高效率的目标识别与仿真，需要对合成孔径雷达的原理和目标特征进行深入研究。

本文旨在通过对合成孔径雷达目标识别与仿真的研究，为相关领域的科研人员提供参考。

二、合成孔径雷达的基本原理和特点合成孔径雷达是利用累积多个狭窄波束的回波信号进行综合处理的一种无源遥感技术。

它的工作原理是通过发射连续的微波脉冲，然后接收并记录脉冲回波信号，通过对这些信号进行处理和合成，得到高分辨率的图像信息。

合成孔径雷达具有全天候、全天时的能力，无论昼夜、晴雨、云雾，都能够实现高质量的成像。

三、合成孔径雷达图像中的目标特征合成孔径雷达图像中的目标特征主要包括散射机制、杂波和布告。

目标的散射机制决定了其回波信号的功率、相位和极化等特性，通过分析和处理这些特性可以实现目标的识别。

杂波是合成孔径雷达图像中除目标信号外的无用信号，其强度的大小和分布规律会影响目标的分辨率和识别性能。

布告是由于合成孔径雷达的工作方式和地面杂波等因素造成的频谱失真，对目标探测和识别造成一定的影响。

多普勒雷达仿真代码下面是一个简单的多普勒雷达仿真代码的示例，使用 Python 编写。

这个示例代码模拟了多普勒雷达的基本工作原理，并生成了一些模拟的雷达回波数据。

```pythonimport numpy as npimport matplotlib.pyplot as plt# 定义多普勒雷达的参数c = 3e8 # 光速（m/s）f = 1e9 # 雷达频率（Hz）v = 300 # 目标速度（m/s）theta = np.radians(30) # 雷达波束与目标速度之间的夹角# 生成时间序列t = np.linspace(0, 2 * np.sqrt(v**2 * np.sin(theta)**2 / (2 * c * f)), 1000) # 计算多普勒频移fd = 2 * v * np.sin(theta) * np.cos(2 * np.pi * f * t / c)# 生成模拟的雷达回波数据echo = np.sin(2 * np.pi * f * t + fd)# 绘制结果plt.plot(t, echo)plt.xlabel('Time (s)')plt.ylabel('Amplitude')plt.title('Doppler Radar Simulation')plt.show()```在这个示例代码中，我们首先定义了一些多普勒雷达的参数，包括光速`c`、雷达频率`f`、目标速度`v`和雷达波束与目标速度之间的夹角`theta`。

然后，我们生成了一个时间序列`t`，表示雷达发射和接收信号的时间。

接下来，我们根据多普勒效应的公式计算了多普勒频移`fd`，并生成了模拟的雷达回波数据`echo`。

在这里，我们使用了一个简单的正弦函数来模拟回波信号的形状。

最后，我们使用`matplotlib`绘制了结果，显示了时间`t`和回波信号`echo`的关系图。