常见雷达图像自适应滤波算法对比分析

雷达低空探测算法是用来检测和跟踪低空目标的一种技术，主要应用于军事和民用领域。

雷达低空探测面临的主要挑战是地面和低空目标的杂波干扰，以及目标与地面、建筑物之间的遮挡。

以下是一些常用的雷达低空探测算法：
1. CFAR算法：CFAR（Constant False Alarm Rate）算法是一种自适应杂波抑制算法，通过计算每个像素的杂波功率水平，调整门限电平，以保持恒定的虚警概率。

在低空探测中，CFAR算法可以有效抑制地面和低空杂波，提高目标检测概率。

2. MTI算法：MTI（Moving Target Indicator）算法是一种基于运动目标与固定杂波在多普勒频移上存在差异的算法。

通过滤波器组对回波信号进行滤波处理，去除固定杂波，保留运动目标信号。

MTI算法可以降低杂波干扰，提高运动目标检测能力。

3. DPC算法：DPC（Doppler Power Coherence）算法是一种基于多普勒频移的检测算法。

该算法通过分析多普勒频谱，检测出具有高功率谱密度的目标信号。

DPC算法对低空目标的探测具有一定的鲁棒性，能够克服地面和建筑物遮挡的影响。

4. 协同探测算法：协同探测算法是一种利用多个雷达站进行低空目标探测的算法。

该算法通过多个雷达站的信号处理和信息融合，提高低空目标的检测概率和定位精度。

协同探测算法可以降低单个雷达站面临的杂波干扰和遮挡问题。

这些算法各有特点，可以根据具体应用场景选择适合的算法进行低空目标探测。

同时，还需要注意雷达系统的参数设置，如波束宽
度、脉冲宽度、采样率等，以获得更好的低空探测性能。

常见雷达脉冲分选算法
雷达脉冲分选算法是雷达信号处理中的重要技术之一，用于从接收到的雷达回波信号中提取出目标的信息。

常见的雷达脉冲分选算法包括MTI（Moving Target Indication）和CFAR（Constant False Alarm Rate）等。

首先，让我们来看看MTI算法。

MTI算法通过比较连续两个脉冲回波信号的相位差异，来检测目标的运动状态。

当目标运动时，其回波信号的相位会发生变化，MTI算法可以利用这种相位变化来区分目标和杂波。

MTI算法可以有效地抑制地面回波和其他静止杂波，从而提高目标检测的性能。

另一个常见的雷达脉冲分选算法是CFAR算法。

CFAR算法主要用于检测雷达回波信号中的目标，并且能够抑制地面回波和其他干扰。

CFAR算法通过对每个脉冲回波信号的幅度进行统计分析，然后根据统计结果来判断该回波信号是否来自目标。

CFAR算法能够根据环境的变化自适应地调整检测门限，从而保持恒定的误警率。

除了MTI和CFAR算法外，还有一些其他的雷达脉冲分选算法，如动态门限算法、多时延脉冲压缩算法等。

这些算法在不同的雷达
应用场景中发挥着重要作用，可以根据具体的需求选择合适的算法来实现雷达信号处理和目标检测。

总的来说，雷达脉冲分选算法在雷达信号处理中起着至关重要的作用，能够有效地提取目标信息并抑制干扰，从而实现准确的目标检测和跟踪。

不同的算法有着各自的特点和适用场景，需要根据具体的应用需求来选择合适的算法进行应用。

InSAR 干涉图滤波方法比较王兴旺,张启斌,杨勇,侯争光,姜家庆(天津市政工程设计研究院,天津300201)摘要 干涉条纹图滤波是合成孔径雷达干涉测量处理中不可缺少的重要环节。

对干涉条纹图滤波的一个重要要求是在有效抑制噪声的同时尽可能地保持条纹的纹理信息。

首先对干涉合成孔径雷达(In SAR)滤波方法进行分类,然后对基于局部统计自适应滤波中的4种算法:G o lds te in 滤波、I N SAR 干涉条纹图的复数空间自适应滤波、鲁棒加权圆周期滤波和正余弦滤波法滤波进行了研究,每种算法都给出了真实数据的处理结果,以比较各种处理算法的优缺点。

并且用5种定量的评价指标比较和评价上述4种滤波方法的优劣。

关键词 合成孔径雷达;干涉图滤波;评价指标;中图分类号 S126 文献标识码 A 文章编号 0517-6611(2009)17-08095-03C om pa rison Am o n g F ilte rin g M e th o rd s o f In SAR In te rfe ro g ram W ANG X in g -w a n g e t a l (T ian jin M u n icipa l E n g in ee rin gD e sign &R esea rch In stitu te ,T ian jin 300201)A b s tra c t F ilte r in g th e in te rfe rom e tric frin g es is on e o f th e k ey p ro ce ss in g p rocedu re s in vo lv ed in syn th e tic ape r tu re rada r i n te r fe ro m e try.T h e p rin cipa l requ irem en t o f th e filte rin g is to m ak e th e be st m a in ten an ce to th e fr in ge ’s tex tu re w h ile a t th e sam e ti m e filter ou t th e n o ise s .Inth is pape r ,first ,th e fil-ter in g m e th ods o f rada r in te rferog ramw e re class ified .T h en,fou r adaptiv e in te r fe rog ramfilter s ,i .e.,th e G o lds te in filte r ,In te r fe rom e tric ph a se com p lex adap tive filter ,R obu s t w e igh ted pe r iod ic p ivo tin g filte r ,S i n e o r cos in e in te rfe rog ramfilte r ,w e re s tud ied.In o rde r to m ak e a com pa r ison be tw eenth e d if-feren t filter s ,re a l da ta w e re u sed fo r e xper i m en ts an d re su lts w e re p ro v ided .In add ition ,five qu an tita tive m easu re s fo r th e qu a lity o f SARin te rfe rog ram s w e re pro v i ded an d u sed to eva lu a te th e fou r in te rfe rog ramfilte rs .K e y w o rd s S yn th e tic ape r tu re rada r (SAR );SARin ter fe rog ramfilte rin g ;C rite r ion o f eva lu a tion基金项目 天津市市政工程设计研究院项目资助。

基于自适应滤波的雷达目标检测算法优化研究随着雷达技术的不断发展和应用领域的拓展，雷达目标检测技术逐渐成为研究的热点之一。

在雷达目标检测过程中，自适应滤波算法被广泛用于提高目标检测的性能。

本文将围绕基于自适应滤波的雷达目标检测算法进行优化研究。

自适应滤波是一种信号处理方法，通过根据信号的统计特性来选择合适的滤波器参数，以提高信号的质量和抑制噪声等干扰。

在雷达目标检测中，自适应滤波算法可以用于抑制杂波和噪声，使得目标的信号能够更加明显地显现出来。

首先，我们需要对自适应滤波算法进行优化。

传统的自适应滤波算法通常基于最小均方误差原则，选择滤波器参数。

然而，该方法在存在较强干扰的情况下容易出现过度收敛或者误收敛的情况，从而影响到目标检测的准确性。

因此，本文将研究新的自适应滤波算法，以解决传统算法的不足。

其次，我们将研究目标检测算法与自适应滤波算法的融合，以提高目标检测的性能。

目标检测算法可以利用自适应滤波算法得到的滤波结果，进一步提取目标的特征信息，从而实现更精确的目标检测。

我们将探索如何合理地融合这两种算法，在保证目标检测准确性的同时，尽量减小计算复杂度和存储空间。

另外，我们将考虑如何适应多变的环境。

雷达目标检测往往面临多种干扰和复杂的噪声环境，如天气变化、多路径效应等。

针对这些问题，我们将尝试设计一种适应性较强的自适应滤波算法，使得该算法能够有效地应对各种复杂环境，并保持较好的目标检测性能。

另外，我们将结合深度学习技术来改进目标检测算法。

近年来，深度学习在图像处理和目标检测领域取得了突破性的进展。

我们将探索如何将深度学习的思想和算法引入到自适应滤波算法中，以进一步提升雷达目标检测的准确性和稳定性。

最后，我们将通过实验证明优化后的基于自适应滤波的雷达目标检测算法的有效性。

通过采集真实的雷达信号和目标数据，我们将对算法进行验证和评估。

同时，我们将与其他现有的目标检测算法进行对比分析，以证明所研究的算法的优越性。

自适应滤波法自适应滤波法是一种最佳滤波方法，它是在维纳滤波和Kalman滤波等线性滤波基础上发展起来的。

由于具有更强的适应性和更优的滤波性能，自适应滤波法在工程实际中，尤其在信息处理技术中得到了广泛的应用。

自适应滤波存在于信号处理、控制、图像处理等多个不同领域，它是一种智能且有针对性的滤波方法，通常用于去噪。

自适应滤波法的核心思想是根据输入信号的统计特性来调整滤波器的参数，使其能够更好地适应信号的变化。

通常情况下，自适应滤波器会根据输入信号的均值、方差等统计指标来更新滤波器的权值。

通过不断迭代优化，自适应滤波器能够逐渐收敛到最优解，从而实现对信号的准确滤波。

常见的自适应滤波方法包括最小均方差（LMS）算法、最小二乘法（LS）算法、递归最小二乘法（RLS）算法等。

这些方法在不同的应用场景下有着不同的适用性和性能表现。

LMS算法是最简单且最常用的自适应滤波方法，它通过不断调整滤波器的权值，使得滤波器的输出信号与期望信号之间的均方误差最小化。

LS算法是一种经典的线性回归方法，通过最小化输入信号与输出信号之间的均方误差来估计滤波器的权值。

RLS算法是一种递推的最小二乘法算法，通过不断更新滤波器的权值来逼近最小均方误差。

在实际应用中，自适应滤波方法被广泛应用于语音信号处理中的降噪和回声消除、图像处理中的边缘增强和去噪等领域。

通过对输入信号进行分析，自适应滤波器能够准确地去除噪声和回声，提高语音信号的清晰度和可懂度。

同时，自适应滤波器还可以应用于图像处理中，通过对图像进行自适应滤波，可以准确地提取图像的边缘特征，并去除图像中的噪声，提高图像的质量和细节。

此外，自适应滤波方法还被应用于雷达信号处理、生物医学信号处理等领域。

以上内容仅供参考，如需更多关于自适应滤波法的信息，可查阅相关的学术文献或咨询该领域的专家学者。

SAR图像滤波方法比较与分析作者：王宇航范文义张金虎来源：《森林工程》2015年第03期摘要：相干斑噪声是SAR系统的固有原理缺陷，其阻碍了SAR图像的后续分类应用。

针对传统滤波方法在噪声去除及边缘保持方面的不足，提出适用于同质区域和边缘区域的自适应滤波方法对SAR图像进行滤波处理。

首先描述SAR图像斑点噪声的产生机理及统计特性，其次根据图像后续分类的应用目的，对常用滤波器进行分析并将福建将乐林场RADARSAT-2图像数据分别进行LEE与增强LEE滤波、FROST与增强FROST滤波、GAMMA滤波、KUAN 滤波、LOCAL SIGMA滤波处理，以有效视数、图像边缘保持指数等作为评价指标。

最后将实验结果依据评价指标进行对比分析。

结果表明，增强型LEE自适应滤波综合效果最好，能在较好去除斑点噪声的同时又保持图像的边缘信息。

通过系统比较分析不同的滤波方法，从理论上为SAR图像后续森林类型分类应用前滤波方法的选择提供了理论依据。

关键词：SAR；相干斑噪声；滤波处理；RADARSAT-2中图分类号：S 771 文献标识码：A 文章编号：1001-005X（2015）03-0081-04合成孔径雷达（Synthetic Aperture Radar）是一种主动式微波成像传感器。

因为SAR系统是有源遥感技术，所以其探测目标时依靠自身发射电磁波而不受太阳辐射条件的限制，并且SAR成像系统具有全天候、全天时、多波段、多极化、可变侧视角及高分辨率等优点，而利用微波回波信号中的极化信息可用于提高对目标的分类和识别能力[1]。

斑点噪声是由一个分辨单元内众多散射体的反射波叠加形成的，表现为图像灰度的剧烈变化，即在SAR图像同一片均匀的粗糙区域内，有的分辨单元呈亮点，有的呈暗点，直接影响了SAR图像的灰度分辨率[2]，模糊了图像的纹理信息，使SAR图像不能正确的反映地物目标的散射特性从而对图像的应用造成了一定阻碍，所以斑点噪声的抑制即图像滤波是SAR图像处理的一个重要研究课题。

自适应滤波法自适应滤波法是一种常用的数字信号处理技术，主要用于去除噪声、提取信号以及增强图像等应用中。

它可以根据信号的特性和噪声的特点，自动调整滤波器的参数，从而达到最佳的信号处理效果。

本文将介绍自适应滤波法的基本原理和常用算法，并通过实例演示其应用。

自适应滤波法的基本原理是根据信号和噪声的统计特性，利用滤波器自身的调整机制，来使滤波效果更好。

传统的滤波器往往采用固定的参数来对信号进行处理，不管信号的特性如何，滤波器的参数都是不变的。

而自适应滤波器则能够针对不同的信号和噪声特性，动态地调整滤波器的参数，从而提高信号处理的效果。

自适应滤波法主要分为线性自适应滤波器和非线性自适应滤波器两种。

线性自适应滤波器是指滤波器的输出值与输入值之间存在线性关系，而非线性自适应滤波器则没有这个限制。

线性自适应滤波器较为简单，常用的算法有LMS（最小均方）算法和RLS（递推最小二乘）算法等。

非线性自适应滤波器突破了线性关系的限制，能够更好地适应复杂的信号和噪声环境。

LMS算法是自适应滤波器中最简单且最常用的一种算法。

它的基本思想是通过调整滤波器的权值来最小化滤波器的输出信号与期望信号之间的均方误差。

LMS算法的核心是更新权值，通过不断迭代使误差最小化。

具体的计算过程是，根据当前输入信号和滤波器的输出信号计算出误差，然后根据误差调整滤波器的权值。

通过多次迭代，滤波器的权值逐渐收敛到最佳值，使滤波器的输出信号尽可能接近期望信号。

RLS算法是另一种常用的自适应滤波算法，它的特点是拥有更好的收敛性能和跟踪性能。

RLS算法的基本原理是通过递归的方式计算滤波器的权值，使滤波器的输出与期望信号之间的均方误差最小。

与LMS算法相比，RLS算法的计算复杂度较高，但在一些要求较高的应用中，如语音处理和雷达信号处理等，RLS算法更能胜任。

除了LMS算法和RLS算法外，还有其他一些自适应滤波算法，如NLMS（归一化最小均方）算法、AP（逐次逼近）算法、SAF（选择性自适应）算法等。

中值滤波与自适应中值滤波的比较和应用一、引言在图像处理领域，滤波是一种常用的技术，其主要目的是消除图像中的噪声。

其中，中值滤波和自适应中值滤波是两种重要的滤波方法。

二、中值滤波中值滤波是一种非线性滤波方法，它的基本思想是用一个像素邻域中所有像素值的中值来替代该像素的值。

这种方法可以有效地去除椒盐噪声，同时保持边缘信息不被破坏。

然而，中值滤波器的一个主要缺点是对高斯噪声的抑制效果较差。

三、自适应中值滤波自适应中值滤波是一种改进的中值滤波方法，它根据每个像素点周围像素的灰度分布特性自动调整滤波窗口大小。

这种方法既保留了中值滤波的优点，又克服了对高斯噪声抑制效果差的问题。

然而，由于需要计算每个像素周围的灰度分布特性，因此计算量较大。

四、中值滤波与自适应中值滤波的比较中值滤波和自适应中值滤波的主要区别在于滤波窗口的大小。

中值滤波使用固定大小的滤波窗口，而自适应中值滤波则根据每个像素点周围像素的灰度分布特性自动调整滤波窗口大小。

因此，自适应中值滤波在保持边缘信息的同时，能更好地去除噪声。

五、应用中值滤波和自适应中值滤波广泛应用于图像处理领域，如医学图像处理、遥感图像处理、视频监控等。

它们可以帮助我们提高图像的质量，提取有用的图像特征，从而进行更深入的图像分析和理解。

六、结论总的来说，中值滤波和自适应中值滤波都是有效的图像滤波方法。

选择哪种方法取决于具体的图像处理任务和需求。

如果图像中的噪声主要是椒盐噪声，并且对计算效率有较高的要求，那么中值滤波可能是一个更好的选择。

如果图像中的噪声包括高斯噪声，并且对图像质量有较高的要求，那么自适应中值滤波可能更适合。

雷达影像是一种利用雷达信号获取地表信息的遥感技术。

在雷达影像处理的过程中，滤波方法是非常重要的一环，它可以有效地提高雷达影像的质量，并且在后续的特征提取和目标识别过程中起到至关重要的作用。

在众多的滤波方法中，ENVi是一款常用的遥感图像处理软件，它提供了多种滤波方法，如中值滤波、高斯滤波、维纳滤波等。

本文将针对ENVi对雷达影像的滤波方法进行详细介绍和分析。

一、中值滤波中值滤波是一种常见的非线性滤波方法，它的原理是将像素点周围的邻域像素灰度值进行排序，然后取中值作为该像素点的灰度值。

在ENVi软件中，中值滤波可以有效地去除图像中的椒盐噪声和斑点噪声，同时保持图像的边缘信息。

该方法适用于雷达影像中含有较多噪声的情况，能够有效地提高图像的质量和清晰度。

二、高斯滤波高斯滤波是一种常用的线性滤波方法，它基于高斯函数对像素点周围邻域的像素进行加权平均，以达到平滑图像的目的。

在ENVi软件中，可以通过设置滑动窗口的大小和标准差来调节高斯滤波的效果。

该方法可以有效地去除雷达影像中的高频噪声，同时能够保持图像的整体灰度分布特性，使得图像更加平滑自然。

三、维纳滤波维纳滤波是一种基于统计模型的滤波方法，它通过估计图像中信号和噪声的功率谱密度来进行滤波处理。

在ENVi软件中，维纳滤波可以根据输入图像的特性自适应调整滤波参数，能够有效地消除雷达影像中的噪声，并且保持图像的边缘和细节信息。

该方法适用于要求较高图像质量和清晰度的场景，能够有效地提高雷达影像的识别和分析能力。

四、多通道滤波多通道滤波是一种基于多波段信息的滤波方法，它可以利用雷达影像中不同波段的特性进行组合和处理。

在ENVi软件中，可以通过组合不同波段的滤波结果来增强图像的特定信息，比如边缘信息、纹理信息等。

该方法适用于需要综合利用多波段信息的场景，能够有效地提高雷达影像的数据融合和分析能力。

ENVi提供了多种有效的雷达影像滤波方法，包括中值滤波、高斯滤波、维纳滤波和多通道滤波等。

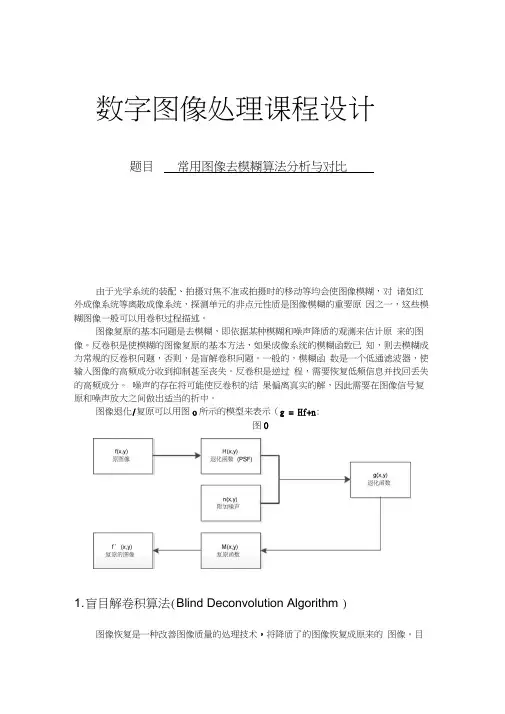
数字图像处理课程设计题目常用图像去模糊算法分析与对比由于光学系统的装配、拍摄对焦不准或拍摄时的移动等均会使图像模糊，对诸如红外成像系统等离散成像系统，探测单元的非点元性质是图像模糊的重要原因之一，这些模糊图像一般可以用卷积过程描述。

图像复原的基本问题是去模糊，即依据某种模糊和噪声降质的观测来估计原来的图像。

反卷积是使模糊的图像复原的基本方法，如果成像系统的模糊函数已知，则去模糊成为常规的反卷积问题，否则，是盲解卷积问题。

一般的，模糊函数是一个低通滤波器，使输入图像的高频成分收到抑制甚至丧失。

反卷积是逆过程，需要恢复低频信息并找回丢失的高频成分。

噪声的存在将可能使反卷积的结果偏离真实的解，因此需要在图像信号复原和噪声放大之间做出适当的折中。

图像退化/复原可以用图o所示的模型来表示（g = Hf+n:图01. 盲目解卷积算法(Blind Deconvolution Algorithm )图像恢复是一种改善图像质量的处理技术，将降质了的图像恢复成原来的图像。

目前, 图像恢复的方法很多, 然而在图像恢复过程中, 最难解决的问题之一是如何获得恢复算法中PSF勺恰当估计,那些不以PSF知识为基础的图像恢复方法统称为盲去卷积算法。

盲去卷积的方法已经受到了人们的极大重视, 对于给定的原图像, 使其退化, 得到退化图像, 再利用盲去卷积的方法使其恢复, 得到视觉质量上更好的图像。

盲解卷积的方法是以最大似然估计(MLE )为基础的，即一种用被随机噪声所干扰的量进行估计的最优化策略。

似然函数用g ( x, y ) f ( x, y )和h( x, y来加以表达, 然后问题就变成了寻求最大似然函数。

在盲解卷积中, 最优化问题用规定的约束条件并假定收敛时通过迭代来求解,得到的最大f( x, y 和 h (x, y就是还原的图像和PSF。

【函数】deconvblind【功能】使用盲解卷积算法对图像进行去模糊[J,PSF] = DECONVBLIND(I,INITPSF) deconvolves image I using maximum likelihood algorithm, returning both deblurred image J and a restoredpoint-spread function PSF. The resulting PSF is a positive array of the same size as the INITPSF, normalized so its sum adds to 1. The PSF restoration is affected strongly by the size of its initial guess, INITPSF, and less by its values (an array of ones is a safer guess).使用盲解卷积对图像I进行去模糊，得到去模糊后的图像J和重建点扩散函数矩阵PSF参量INITPS为矩阵，表示重建点扩散函数矩阵的初始值。

相控阵雷达空时自适应处理相控阵雷达是一种发射与接收都采用相位调控技术的雷达，其具有发射功率高、目标识别能力强、抗干扰能力强等优点。

随着雷达技术的不断发展，相控阵雷达在军事和民用领域中的应用越来越广泛。

相控阵雷达的空时自适应处理技术是相控阵雷达中的一项重要技术，它通过实时自适应校正信号的相位和幅度来提高雷达的功率和性能，适应复杂干扰和复杂信号环境。

相控阵雷达的空时自适应处理技术基于雷达接收到的信号，采用自适应滤波算法对信号进行处理，以提高信噪比和瞬时动态范围，以便更好地识别目标。

该技术主要包括以下几个方面：1. 算法基本原理空时自适应处理技术利用自适应滤波器对输入信号进行实时处理，以最大化滤波器响应的信号功率，同时最小化非信号功率以减小噪声干扰。

具体来说，该算法通过计算输入信号的自相关矩阵，得到信号的统计特性，进而实现自适应滤波器系数的调整，以提高目标信号的信噪比。

2. 自适应滤波器结构自适应滤波器结构包括一个输入端和一个输出端，其内部由多个加权系数和延迟单元组成。

这些加权系数是由自适应算法计算得出的，用来在滤波器中加权输入信号的不同分量。

输入信号通过滤波器后，产生一个输出信号，该输出信号的功率被最大化。

通过适当的加权策略，自适应滤波器可以对目标信号的不同特征进行处理，得到更加准确的目标信号。

3. 自适应算法空时自适应处理算法通常采用LMS（最小均方）算法或NLMS（归一化最小均方）算法。

LMS算法的特点是快速收敛和较小的计算量，但其在处理非稳态信号时可能出现饱和现象。

NLMS算法则能够避免饱和现象，但其收敛速度较慢。

4. 应用范围空时自适应处理技术广泛应用于雷达、通信等系统中，特别是在噪声干扰严重、信道复杂的情况下，能够大大提高系统的性能和可靠性。

在相控阵雷达中，空时自适应处理技术能够帮助系统更好地适应各种复杂的雷达信号环境，提高雷达的目标检测和跟踪能力，有助于提升雷达系统的实用性和可靠性。

综上所述，相控阵雷达空时自适应处理技术是一项十分重要的雷达技术，其能够实现即时信号的自适应校正，并利用自适应滤波器抑制干扰和噪声，从而提高雷达的性能和可靠性。

雷达信号处理中的降噪算法研究与优化摘要：随着雷达技术的快速发展，雷达信号的质量对于正确识别和跟踪目标变得尤为重要。

然而，雷达系统常常会受到各种噪声的干扰，这会极大地影响信号的清晰度和目标的探测能力。

因此，降噪算法的研究和优化成为了雷达信号处理中的重要课题。

本文将综述目前常用的雷达信号降噪算法，并探讨如何进一步优化这些算法以提高降噪效果。

1. 引言雷达信号降噪是指通过一系列数字信号处理算法，提取而信号中的有用信息并抑制不相关的噪声干扰。

常见的噪声干扰包括热噪声、杂散噪声、多径噪声等。

降噪算法在雷达系统中的应用十分广泛，可以有效提高目标的检测和跟踪性能。

2. 常用的降噪算法2.1 均值滤波算法均值滤波是最简单和最常用的降噪算法之一。

它通过计算窗口内像素值的平均值来抑制噪声。

然而，均值滤波算法对于高斯噪声的抑制效果较差，会导致图像模糊。

2.2 中值滤波算法中值滤波算法通过计算窗口内像素值的中值来抑制噪声。

相比于均值滤波算法，中值滤波算法对于椒盐噪声和胡椒噪声具有较好的抑制效果。

然而，在存在较强噪声时，中值滤波算法会导致图像细节的丢失。

2.3 维纳滤波算法维纳滤波算法是一种最优化的降噪算法，通过根据噪声和信号的统计特性，建立数学模型并求解最优滤波器。

维纳滤波算法在理论上能够达到最好的降噪效果。

然而，在实际应用中，维纳滤波算法对噪声和信号统计特性的准确估计是一个难题。

3. 降噪算法的优化为了进一步提高降噪算法的效果，研究者在传统算法基础上进行了一系列优化工作。

3.1 自适应滤波算法自适应滤波算法能够根据信号和噪声的特性以及背景噪声的功率谱进行自适应调整。

最常用的自适应滤波算法有LMS算法和RLS算法。

这些算法通过不断调整滤波器系数来实现对噪声的抑制，适应不同场景下的信号处理需求。

3.2 小波变换降噪算法小波变换降噪算法是近年来得到广泛应用的一种算法。

通过将信号转换到小波域进行分析，选择适当的阈值来实现对噪声的抑制。

LMSAPANLMSFRLS算法分析
LMS算法是最常用的自适应滤波算法之一，它是基于最小均方差(MSE)原则的一种加权最小二乘算法。

它的基本思想是以期望和观察误差之间的均方差作为一个指标，试图最小化误差，从而获得一个最优滤波器设计。

LMS算法可以快速而高效地调整滤波器系数，以最大化信号的抑制噪声的能力，是一种逐步增加信号的方法。

APA算法是另一种常用的自适应滤波器算法。

它基于最大似然准则，试图估计出使得观测值合理和自相关系数最大的滤波器。

APA算法不仅考虑了噪声的强度，而且考虑了噪声的自相关性，从而更有效地抑制噪声。

在大多数情况下，APA算法比LMS算法更有效，更稳定，滤波器系数的更新也更平滑。

NLMS算法是一种非线性自适应滤波算法，其基本思想是受到距离准
则的启发，以希尔伯特误差函数作为最小化准则，从而来寻求最优的滤波器设计。

NLMS算法的主要优势在于它的精确度高，收敛速度快，在噪声
多的情况下也有良好的表现。

它也比其他算法更容易实现，因为它只需要计算一个最小二乘系数来计算中间变量，而不需要逆矩阵的计算。

FRLS算法是一种近似最小二乘的自适应滤波算法，它基于利用逆维
费雪滤波器的思想，可以有效地处理一些求逆复杂的情况。

雷达遥感图像分类与解译方法要点与案例分析1. 引言在遥感领域中，雷达遥感图像分类与解译技术具有重要的应用价值。

通过对雷达遥感图像进行分类与解译，可以获取地表覆盖信息、地形特征和目标检测等关键数据，为资源管理、环境监测和军事侦察等领域提供有力支持。

本文将重点讨论雷达遥感图像分类与解译的方法要点，并通过案例分析来进一步说明其实际应用。

2. 雷达遥感图像分类方法要点2.1 数据预处理在进行雷达遥感图像分类之前，首先需要对原始图像进行预处理。

预处理的主要目的是去除图像中的噪声和伪迹，提高图像质量，从而为后续的分类工作奠定基础。

常见的数据预处理方法包括滤波、辐射校正和几何校正等。

2.2 特征提取与选择特征提取是雷达遥感图像分类的关键步骤。

通过将原始图像转化为适合分类的特征表示形式，可以提高分类的准确性和可靠性。

在特征提取时，需要考虑图像的统计特性、空间分布特性和频率成分等。

同时，为了避免维度灾难和提高计算效率，还需要进行特征选择，选择具有较高辨别能力的特征子集。

2.3 分类器设计与训练分类器的选择和设计是雷达遥感图像分类的关键环节。

常用的分类器包括支持向量机（SVM）、人工神经网络（ANN）和决策树等。

在选择分类器时，需要考虑其分类性能、泛化能力和计算复杂度等指标。

同时，还需要进行分类器的训练和调优，以提高分类效果。

3. 雷达遥感图像解译方法要点3.1 目标检测与提取雷达遥感图像解译的首要任务是目标的检测与提取。

通过利用雷达图像的回波特征和空间信息，可以准确地提取出感兴趣目标，并进行形状分析和属性提取等。

常见的目标检测方法包括基于阈值的分割、基于模型的匹配以及基于机器学习的分类等。

3.2 地物类型识别与分类地物类型识别与分类是雷达遥感图像解译的重要内容。

通过对目标的形状、背景和回波特性进行分析和判别，可以实现地物的识别与分类。

常用的地物分类方法包括基于像元的分类、基于对象的分类以及基于语义信息的分类等。

3.3 地物变化监测与分析地物变化监测与分析是雷达遥感图像解译的关键任务之一。

LMS与RLS自适应滤波算法性能比较LMS(最小均方)自适应滤波算法和RLS(递推最小二乘)自适应滤波算法是两种常见的自适应滤波算法。

它们都可用于滤波器自适应参数的更新，以便满足所需的滤波器性能。

以下是对LMS和RLS自适应滤波算法性能进行比较的一些主要方面。

1.算法原理和复杂度LMS算法是一种梯度下降法，基于误差信号和输入信号的乘积构建更新过程。

它的更新过程简单，易于实现，并且具有较低的计算复杂度。

相比之下，RLS算法不仅考虑了误差信号和输入信号的乘积，还包括过去输出和输入信号的一些特定值，以构建更准确的更新过程。

这导致了更复杂的计算，因此RLS算法的计算复杂度较高。

2.收敛速度和稳定性LMS算法的收敛速度通常较慢，这是因为它只使用局部梯度信息来进行参数更新。

它可能需要更多的迭代次数才能达到所需的滤波器性能。

相反，RLS算法具有更快的收敛速度，这是因为它利用全局信息进行参数更新。

然而，RLS算法对计算误差更敏感，当计算误差较大时，参数更新可能会变得不稳定。

3.对突变信号的适应性LMS算法通常对突变信号有较好的适应性，这是因为它每次只使用部分信息进行参数更新。

当输入信号突然发生变化时，LMS可以相对更快地适应。

与之相反，RLS算法对突变信号的适应性较差，因为它更关注整个信号的统计特性。

当输入信号发生突变时，RLS可能需要更长的时间来重新估计滤波器参数。

4.计算复杂度由于LMS算法只使用局部信息进行参数更新，其计算复杂度较低。

通常，LMS算法的计算复杂度与滤波器长度成正比。

相反，RLS算法会使用全局信息进行参数更新，因此其计算复杂度较高。

通常情况下，RLS算法的计算复杂度与滤波器长度的平方成正比。

综上所述，LMS算法和RLS算法在性能方面有一些明显的区别。

LMS 算法适用于计算资源有限的应用，但它的收敛速度相对较慢。

相反，RLS 算法具有更快的收敛速度，但计算复杂度较高。

因此，对于不同的应用需求，可以选择适合的算法来实现自适应滤波器的性能优化。

不同Alpha-Beta滤波算法的精度分析及改进刘常娟;王运锋;杨玲【摘要】机动目标跟踪是雷达应用系统的一个重要组成部分,在机动目标跟踪中,目标的跟踪精度作为一项能够反映跟踪算法好坏的指标,是大部分人所关注的重点内容.通过对四种传统的Alpha-Beta滤波算法进行精度分析和比较,总结出四种算法的滤波特点,根据这些特点,改进得出了一种自适应Alpha-Beta滤波算法.该算法相对于传统的Alpha-Beta滤波算法来说,整体滤波效果是最优的,精度也是整体最高的.%Maneuvering target tracking is an important part of radar application system,target tracking accuracy is regarded as an important index w hen evaluating an algorithm's performance for the maneuve-ring target tracking,it is the focus of attention of most people.The characteristics were summarized through the analysis and comparison of four traditional Alpha-Beta filtering algorithms,and according to these characteristics,an Adaptive alpha-beta filter algorithm was obtained by improving traditional pared with the traditional Alpha-Beta filtering algorithm,the Adaptive Alpha-Beta filter al-gorithm is best in overall filtering results,and also has the highest accuracy.【期刊名称】《四川大学学报（自然科学版）》【年(卷),期】2018(055)002【总页数】6页(P265-270)【关键词】机动目标跟踪;自适应alpha-beta滤波算法;增益;精度分析【作者】刘常娟;王运锋;杨玲【作者单位】国家空管自动化系统技术重点实验室,成都610065;四川大学计算机学院,成都610065;电子信息控制重点实验室,成都610036【正文语种】中文【中图分类】TP3911 引言雷达目标跟踪技术作为雷达技术中的一个重要组成部分,随着目标机动性的增强和平台的多样化,对雷达目标跟踪技术的要求也越来越高.Alpha-Beta跟踪滤波算法作为目标跟踪中的一种较成熟、简单的滤波算法,因为其计算复杂度相对简单,所以广泛应用于军事和民用的各个相关方面[1,2].又因为其应用领域的特殊性,安全性和精确度要求都比较高,所以目标跟踪中滤波算法的处理精度很重要.传统的Alpha-Beta跟踪滤波算法在匀速或者机动的目标状态下能够较好的跟踪目标,但是面对当前复杂变化的机动目标,目标跟踪效果并不是很理想.本文通过实验分析传统方法,新得出了一种自适应Alpha-Beta滤波算法,该方法从总体上来说提高了目标的跟踪精度.2 不同Alpha-Beta滤波算法2.1 Alpha-Beta滤波算法Alpha-Beta滤波器的主要工作由下面的方程式构成[3-7]：增益为K(k+1)=[α,β/T]′(1)状态进一步预测方程为(2)新息为(3)状态更新方程(4)其中，增益的α值控制位置滤波值偏向位置预测值的权重,根据状态更新方程可知,α值越大,位置滤波值越偏离位置预测值.反之,位置滤波值越靠近位置预测值.β/T 值控制速度滤波值偏向上一时刻速度值的权重,同样根据状态更新方程,β/T越大,速度滤波值越偏离上一时刻的速度值,反之,则速度滤波值越靠近上一时刻的速度值.从上述方程式可以看出,增益值的确定在很大程度上会对滤波结果造成影响,从而影响目标跟踪的精度.新息本质上是量测值和预测值的差值,它可能反映了两种情况,第一种情况可能反映了真值因受高斯白噪声的影响而偏离真实轨迹,第二种情况可能反映了目标的机动性运动.以下五种Alpha-Beta滤波算法的本质区别就在于增益的计算方法不同.所以重点描述增益的计算方法[3].2.1.1 Alpha-Beta值随雷达扫描次数变化的滤波算法Alpha-Beta值随雷达扫描次数变化的滤波算法使用雷达扫描次数来确定α和β值,用符号k来表示雷达扫描次数,α和β的确定方程式为[1,2,8](5)当滤波开始后(雷达扫描次数为3),由α和β公式可以看出,随着雷达扫描次数k的逐步增大,α和β都越来越小,逐步趋向于零.2.1.2 Alpha-Beta值随雷达扫描次数和门限调整的滤波算法Alpha-Beta值随雷达扫描次数和门限调整的滤波算法在增益α和β的计算方法上与Alpha-Beta 值随雷达扫描次数变化的滤波算法相同,计算公式为(5),但是k值不再唯一的由雷达扫描次数确定,还需要判断横纵坐标方向上的量测值与预测值差值的大小是否满足某个取值范围,从而再确定k值是加1还是减1.若满足取值范围,k值就加1,反之,则k值减1.实际上在目标的匀速运动部分,预测值和量测值的差值和机动部分预测值和量测值的差值比起来,相对较小,通过这个特性设置门限来改变k值,从而改变增益大小,达到优化滤波值的目的.2.1.3 Alpha-Beta值固定的滤波算Alpha-Beta值固定的滤波算法的增益采用常数来表示,α=0.5,β =0.3[4,9].这样α和β的值就是固定的.由α可知该方法的滤波值恒定在量测值和预测值的中间位置.2.1.4 残差累积的Alpha-Beta滤波算法残差累积的Alpha-Beta滤波算法是根据当前时刻之前的n次量测值和预测值差值的平方的平均值来计算增益的,这个n 由实验者自己决定,它会影响到实验结果的精度,本实验设n=3,也就是取前三次量测值和预测值差值的平方的平均值[2,4,9,10].这个平均值就是残差增益的值就是利用计算后的残差和测量误差方差来确定的.测量误差方差是雷达的固有误差,一般为恒定值,本实验的取值为25.根据这些已知条件,可以得出α和β的计算公式如式(8)～式(11).(6)(7)(8)(9)(10)(11)将计算得到的增益代入式(1)～式(4),从而得到滤波结果数据.2.1.5 自适应Alpha-Beta滤波算法通过对前面几种Alpha-Beta滤波算法的分析发现,Alpha-Beta值固定的滤波算法在匀速运动状态下滤波效果优于残差累积的Alpha-Beta滤波算法,而在机动状态下,残差累积的Alpha-Beta滤波算法优于Alpha-Beta值固定的滤波算法.根据这个特点,该自适应Alpha-Beta滤波算法的思想就是在模拟场景的匀速运动部分采用Alpha-Beta值固定的滤波算法,在模拟场景的机动部分采用残差累积的Alpha-Beta滤波算法.如何确定目标的运动状态是本方法的重点,通过实验分析发现,不同运动状态下,新息是有差别的,所以我们可以根据新息的大小来区分目标不同的运动状态.通过设置门限值,当新息大于当前门限值,认为目标处于机动状态,当新息小于等于门限值,认为目标处于匀速运动状态.本算法需要确定两个门限值,其中一个是横坐标方向量测值和预测值差的绝对值的门限值limitX,另一个是纵坐标方向量测值和预测值差的绝对值的门限值limitY.当横坐标方向和纵坐标方向的量测值与预测值差的绝对值都小于门限值时,增益的确定方法和Alpha-Beta值固定的滤波算法相同,此时增益为固定值.当横坐标方向和纵坐标方向的量测值与预测值差的绝对值有一个大于门限值或者两个都大于门限值时,增益的确定方法和残差累积的Alpha-Beta滤波算法相同[11-13],如式(12)～式(15).(12)(13)(14)(15)通过分析比较匀速运动部分和机动部分的量测值和预测值在X方向和Y方向的差值,综合考虑,我们将两个门限值都设置为19 m.当X方向和Y方向的量测值和预测值差值的绝对值都小于19 m,采用Alpha-Beta值固定的滤波算法,其它情况采用残差累积的Alpha-Beta滤波算法.3 实验结果及分析3.1 实验数据参数实验数据参数如表1所示[14].表1 实验数据参数Tab.1 Parameter参数数值目标初始位置(m)(533，389)目标初始速度(m/s)150目标初始方位角(°)45目标曲线运动圆半径(m)9000雷达采样周期(s)2采样次数80误差系数(μ，σ)(0，5)3.2 自适应Alpha-Beta滤波算法的滤波效果分析3.2.1 自适应Alpha-Beta滤波算法的门限值确定模拟场景的目标在前30个周期做匀速运动,之后开始转弯运动,经过15个周期后继续匀速运动.理论上，在匀速运动部分，预测值接近真实目标运动轨迹的可能性大一点，在机动部分，量测值接近真实目标运动轨迹的可能性大一点.通过图1可以看出,在匀速运动部分,残差累积的Alpha-Beta滤波算法的滤波效果没有Alpha-Beta值固定的滤波算法的滤波效果好,但是在机动部分,残差累积的Alpha-Beta滤波算法的滤波效果比Alpha-Beta 值固定的滤波算法的滤波效果好.当残差是取前三次量测值和预测值差值平方的平均值时,α的值由残差和测量误差方差来决定,由α的计算公式我们可以知道,当前三次量测值和预测值差值越大,残差越大,α的值就越大,此时滤波值就越偏向量测值.当的时候,α=0.5,滤波值位于量测值和预测值的中间位置,从另一个角度来说,只要前三次量测值和预测值差值中,有一个的差值大于等于那么α的值就大于0.5.而在场景出现机动的时候,量测值和预测值差值是远远大于的,此时,α的值近似等于1,所以在机动的时候,滤波值与量测值很逼近,滤波效果很好.从图2可以看出,残差累积的Alpha-Beta滤波算法在匀速运动部分横纵坐标的α值大部分大于0.5,滤波结果也就偏向测量值.导致其滤波效果没有Alpha-Beta值固定的滤波算法的滤波效果好.自适应Alpha-Beta滤波算法的思想是在匀速运动状态下使用Alpha-Beta值固定的滤波算法,在机动状态下使用残差累积的Alpha-Beta滤波算法.通过对Alpha-Beta值固定的滤波算法的实验分析,发现Alpha-Beta值固定的滤波算法横纵坐标方向上量测值和预测值差的绝对值在匀速运动部分和机动部分存在一定的规律.如图3和图4,在匀速运动部分,横纵坐标的量测值和预测值差值的绝对值大多数在19 m以下,而机动部分的差值较多次的超过19 m.据此我们将横纵坐标方向的门限值都设为19 m.滤波过程中,如果量测值与预测值差值的绝对值较大并且超过19 m,我们就认为此时可能处于机动状态,从而用残差累积的Alpha-Beta滤波算法来确定增益的值,反之则用Alpha-Beta值固定的滤波算法来确定增益的值.图1 2.1.3Alpha-Beta值固定的算法和2.1.4残差累积的Alpha-Beta滤波算法的距离误差比较效果图Fig.1 Comparison effect Diagram of the distance of filter data and realvalue Between algorithm 2.1.3 and 2.1.4图2 Alpha曲线图Fig.2 Alpha Diagram图3 横坐标新息效果图Fig.3 Innovation Diagram of horizontalaxis图4 纵坐标新息效果图Fig.4 Innovation Diagram of verticalaxis3.2.2 自适应Alpha-Beta滤波算法与各传统Alpha-Beta滤波算法的比较为了验证自适应Alpha-Beta滤波算法的滤波效果和精度,将该方法与各传统Alpha-Beta滤波算法进行了比较.滤波结果可以从滤波数据和真值数据对比效果图、滤波值与真值的距离效果图看出,如图5和图6.图5 滤波数据和真值数据效果对比图Fig.5 Effect Diagram of filter data and realvalue图6 滤波值与真值的距离效果图Fig.6 Effect Diagram of the distance of filter data and realvalue从图5和图6可知,Alpha-Beta值随雷达扫描次数变化滤波算法的滤波结果出现发散的情况,该方法不太适用于机动目标.Alpha-Beta值随雷达扫描次数和门限调整的滤波算法在计算增益的时候,当量测值横坐标与预测值横坐标的差值大于70 m,或者量测值纵坐标与预测值纵坐标的差值大于70 m,我们就认为目标处于机动状态,从而将雷达扫描次数k的值减1,从图2中的方法2.1.2曲线可以看出，α值开始变大,滤波值相对偏向了量测值一点.图5中显示该方法出现了慢慢收敛的现象.虽然Alpha-Beta值随雷达扫描次数和门限调整的滤波算法在量测值和预测值的差值较大时会自动调整k值来达到收敛的效果，但是由于每次调整时，k值只是减1，收敛的幅度太小，滤波效果并不是最好的.从图5和图6的效果图中来看,自适应Alpha-Beta滤波算法、Alpha-Beta值固定的滤波算法和残差累积的Alpha-Beta滤波算法的效果相对较好.实验3.2.3分析了自适应Alpha-Beta滤波算法相对于Alpha-Beta值固定的滤波算法和残差累积的Alpha-Beta滤波算法的优势.3.2.3 自适应Alpha-Beta滤波算法与Alpha-Beta值固定的滤波算法和残差累积的Alpha-Beta滤波算法的比较本实验对比了自适应Alpha-Beta滤波算法和另外两种算法的距离误差结果，结果如图7和图8所示.图7 2.1.5自适应Alpha-Beta滤波算法和2.1.3 Alpha-Beta值固定算法的距离误差比较效果图Fig.7 Comparison effect Diagram of the distance of filter data and realvalue Between 2.1.5 and 2.1.3图8 2.1.5自适应Alpha-Beta滤波算法和2.1.4残差累积的Alpha-Beta滤波算法距离误差比较效果图Fig.8 Comparison effect Diagram of the distance of filter data and realvalue Between 2.1.5 and 2.1.4由图7和图8可以看出,本文改进实现的自适应Alpha-Beta滤波算法结合了前四种算法各自的优点,使滤波结果整体上达到最优,精度也是最高.在匀速运动部分,它的整体滤波效果比残差累积的Alpha-Beta滤波算法好.在机动部分,它的滤波效果比Alpha-Beta值固定的滤波算法好.从图2中可以看出,在匀速运动部分,自适应Alpha-Beta滤波算法的alpha取值绝大多数是0.5.而机动部分alpha的取值多数采用残差累积方法.由此证明自适应Alpha-Beta滤波算法通过设置门限值来确定增益值,从而达到优化滤波效果的方法是可行的.4 结论本文分析了传统Alpha-Beta滤波算法的滤波特点,得到了改进的自适应Alpha-Beta滤波算法,相对于传统的滤波算法,该算法的精度和滤波效果实现了整体最优.当然从中我们也可以得到,一个算法并不完全适用于所有的运动情况,针对一个特定场景,必须根据该场景的特性来选择合适的滤波算法.参考文献:[1] 何友, 修建娟, 关欣, 等. 雷达数据处理及应用[M]. 3版. 北京: 电子工业出版社, 2013.[2] 卢海进, 徐琳. 自适应α-β滤波算法的研究和应用[J]. 大众科技, 2012, 12: 73.[3] 王红亮, 李枫, 赵亦工. 一种机动目标跟踪的自适应α-β滤波算法[J]. 雷达科学与技术, 2007, 5: 278.[4] 贺利文, 李彦鹏, 范波. 一种改进的α-β滤波算法[J]. 现代电子技术, 2012, 35: 28.[5] 冉元进, 李浩, 李浩泷. 船用雷达ARPA中的自适应α-β滤波研究[J]. 火控雷达技术, 2012, 41: 39.[6] Yoo J, Kim Y. Alpha-beta-tracking index (α-β-Λ) tracking filter[J]. Signal Proces, 2003, 83: 169.[7] 陈福喜, 杨大宁. 船用雷达ARPA系统中α-β算法研究[J]. 电子设计工程, 2016, 23: 13.[8] 张明友, 汪学刚. 雷达系统[M]. 4版. 北京：电子工业出版社, 2013.[9] 宋绪栋, 李晓花, 陈晓, 等. 贝叶斯目标跟踪方法性能分析[J]. 声学技术, 2013, 31: 101.[10] 袁德诚, 王运锋. 杂波环境下雷达新建航迹处理方法分析[J]. 四川大学学报: 自然科学版, 2017, 54: 89.[11] Wu C, Chang C, Chu T. A new EP-based α-β-γ-δ filter for target tracking[J]. Math Comput Simul, 2011, 81: 1785.[12] Dahmani M, Meche A, Keche M, et al. An improved fuzzy alpha-beta filter for tracking a highly maneuvering target[J]. Aerosp Scie Tech, 2016, 58: 298.[13] Mohammed D, Mokhtar K, Abdelaziz O, et al. A new IMM algorithm using fixed coefficients filters (fastIMM)[J]. AEU-INT J Electron C, 2010, 64: 1123.[14] 李若晨, 周刚.一种组合核函数的自适应目标跟踪算法[J]. 四川大学学报: 自然科学版, 2017, 54: 55.。

常见雷达图像自适应滤波算法对比分析摘要综合运用目视评价与各种评价因子依次对Sigma滤波,增强Lee滤波算法,增强Kuan滤波算法,增强Frost滤波算法,最大后验概率(MAP)滤波算法,边缘保持最优化(EPOS)滤波算法进行性能校验与评价,对比分析各滤波算法优缺点。

关键词自适应滤波算法;目视效果;评价因子0 引言在雷达图像滤波方面有大量雷达滤波算法,本文研究成像后SAR图像的滤波处理,采用局域统计自适应滤波算法,以局域的灰度统计特性为基础决定参与滤波的邻域像素点及其权值,在平滑噪声的同时较有效保持边缘特征。

1 滤波算法目视效果评价对雷达图像的滤波,应使在滤波消除斑点噪声同时较好保持边缘和纹理细节特征。

目视效果评价具有其重要实用性,就目前而言,大部分雷达图像解译还是需人工进行,目视效果很大程度上影响解译人员判读准确性,下面通过对滤波处理图像对比分析各滤波算法不同,窗口均设为5×5:2 利用评价因子对滤波效果进行评价实验选用两幅雷达图像,1图为HH极化,大小500×500,分辨率10m,成像于武汉地区。

2幅为HH极化,大小217×213,分辨率1.2m,地点加拿大多伦多市市区。

对两图进行各种滤波处理后,计算相应评价因子,排序可得:从均值看,其为整个图像平均强度,反映图像包含目标平均后向散射系数。

两图滤波结果Sigma滤波均值最小,整体色调表现较暗,均值滤波均值最大,色调较亮。

方差代表图像中所有点偏离均值程度,反映图像不均匀性。

两影像处理结果均为Lee滤波方差最大,即图像不均匀性最大,与Lee滤波结果中大量白色斑点的出现相符。

从等效视数看,图1均值滤波与Sigma滤波分别对应为最大最小值,Sigma滤波纹理保持较好,平滑效果不行,均值滤波平滑效果最好,但纹理损失最严重。

图2Lee滤波等效视数最大,纹理保持最好,但图像上产生白色斑点。

这种差异主要是由于两幅图像所在地区的地表粗糙程度及地表物体反射系数分布均匀程度所决定的。

雷达图像处理ENVIENVI提供基本的雷达图像处理功能，包括雷达数据格式支持、雷达文件定标、消除天线增益畸变、斜距校正、入射角图像生成、斑点噪声压缩、合成彩色图像等。

多标准ENVI图像处理功能也可以用于处理雷达数据的处理，如图像显示功能、图像拉伸、颜色处理、图像分类、几何校正、图像配准、卷积滤波、图像融合等。

目前，大所述雷达成像系统都是侧视成像，这种雷达系统所测量的距离是目标物到平台一侧的距离（倾斜距离），基于这种几何系统获得的图像叫斜距图像。

雷达斜距数据在侧向范围有系统几何畸变，实际上，由于入射角的变化使得垂直侧向范围的地距和像素大小发生变化。

因此，要使用雷达图像，必须经过从斜距到地距的校正处理。

自适应滤波器被设计成对斑点噪声压缩的同时，对图像分辨率的减少是微笑的。

自适应滤波器运用围绕每个像元值标准差来计算一个新的像元值。

不同于传统的低通平滑滤波，自适应滤波器在抑制噪声的通透式保留了图像的高频信息和细节。

Lee滤波器用于平滑亮度各图像密切相关的噪声数据以及附加或倍增类型的噪声。

增强型Lee滤波器可以在保持雷达图像纹理信息的同时减少斑点噪声。

Frost滤波器能在保留边缘的情况下，减少斑点噪声。

增强型Frost滤波器可以在保持雷达图像纹理信息的同时减少斑点噪声。

Gamma滤波器可以用于在雷达图像中保留边缘信息的同时减少斑点噪声。

Kuan滤波器用于在雷达图像中保留边缘的情况下，减少斑点噪声。

Local Sigma滤波器能很好地保留细节并有效地减少斑点噪声，及时是在对比度较低的区域。

Bit Error Filters比特误差误差滤波器可以消除图像中的”bit-error”噪声。