线面、面面平行的判定、性质定理

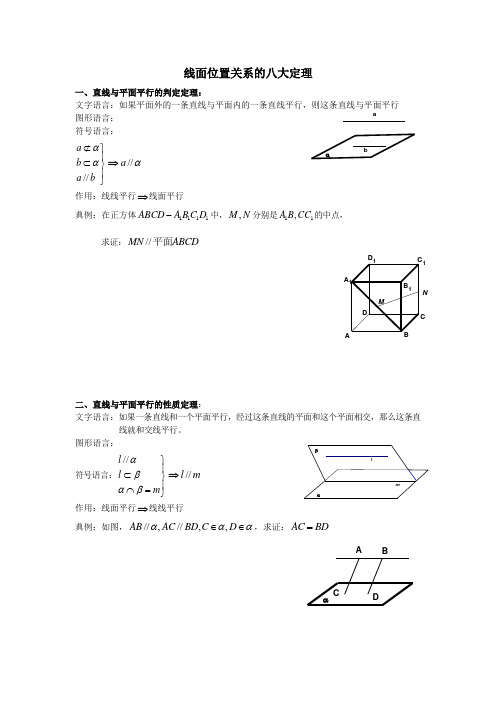
立体几何（线面平行、垂直的有关结论）空间中线面平行、垂直关系有关的定理：1、【线面平行的判定】平面外的一条直线和平面内的一条直线平行，则这条直线和这个平面平行。

2、【线面平行的性质】如果一条直线和一个平面平行，经过这条直线的平面和这平面相交，那么这条直线就和两平面的交线平行。

3、如果一个平面内有两条相交直线分别平行于另一个平面，那么这两个平面平行。

4、如果两个平面平行，其中一个平面内的任意一条直线平行于另一个平面。

5、如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。

6、如果两个平行平面同时与第三个平面相交，那么它们的交线平行。

7、一条直线与两条平行直线中的一条直线相垂直，则这条直线也与另一条直线垂直。

8、与同一条直线都垂直的两条直线相互平行。

（）9、与同一个平面都垂直的两条直线相互平行。

10、两条平行直线中的一条直线与一个平面相垂直，则另一条直线也垂直于这个平面。

11、两条相互垂直的直线中的一条平行于一个平面，则另一条直线垂直于这个平面。

（）12、两条相互垂直的直线中的一条垂直于以个平面，则另一条直线平行于这个平面。

（）13、平面外的两条相互垂直的直线中的一条垂直于一个平面，则另一条直线平行于这个平面。

14、一条直线垂直于两个平行平面中的一个平面，那么该直线也垂直于另一个平面。

15、如果两个平面垂直于同一条直线，那么这两个平面平行。

16、两个平面都与另一个平面相垂直，则这两个平面平行。

（）17、一个平面垂直于两平行平面中的一个平面，则此平面也垂直于另一个平面。

18、如果一条直线与平面内的两条相交直线都垂直，则这条直线与这个平面垂直。

19、如果一条直线垂直于一个平面，那么这条直线垂直于该平面内的任意一条直线。

20、如果一个平面过另一个平面的一条垂线，则这两个平面互相垂直。

21、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

【知识归纳】：【典型例题】：【高考小题】：。

空间点、直线、平面的位置关系（1）平面① 平面的概念： A.描述性说明； B.平面是无限伸展的；② 平面的表示：通常用希腊字母α、β、γ表示，如平面α（通常写在一个锐角内）；也可以用两个相对顶点的字母来表示，如平面BC 。

③ 点与平面的关系：点A 在平面α内，记作A α∈；点A 不在平面α内，记作A α∉点与直线的关系：点A 的直线l 上，记作：A ∈l ； 点A 在直线l 外，记作A ∉l ；. 直线与平面的关系：直线l 在平面α内，记作l ⊂α；直线l 不在平面α内，记作l ⊄α。

（2）公理1：如果一条直线的两点在一个平面内，那么这条直线是所有的点都在这个平面内。

（即直线在平面内，或者平面经过直线） 应用：判断直线是否在平面内用符号语言表示公理1：,,,A l B l A B l ααα∈∈∈∈⇒⊂ （3）公理2：经过不在同一条直线上的三点，有且只有一个平面。

推论：一直线和直线外一点确定一平面；两相交直线确定一平面；两平行直线确定一平面。

公理2及其推论作用：①它是空间内确定平面的依据 ②它是证明平面重合的依据 （4）公理3：如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线符号：平面α和β相交，交线是a ，记作α∩β＝a 。

符号语言：,P A B A B l P l ∈⇒=∈ 公理3的作用：①它是判定两个平面相交的方法。

②它说明两个平面的交线与两个平面公共点之间的关系：交线必过公共点。

③它可以判断点在直线上，即证若干个点共线的重要依据。

（5）公理4：平行于同一条直线的两条直线互相平行 （6）空间直线与直线之间的位置关系① 异面直线定义：不同在任何一个平面内的两条直线 ② 异面直线性质：既不平行，又不相交。

③ 异面直线判定：过平面外一点与平面内一点的直线与平面内不过该点的直线是异面直线④ 异面直线所成角：直线a 、b 是异面直线，经过空间任意一点O ，分别引直线a ’∥a ，b ’∥b ，则把直线a ’和b ’所成的锐角（或直角）叫做异面直线a 和b 所成的角。

线面平行的判定定理：如果存在平面外的一条直线和平面内的一条直线平行，则这条直线和这个平面平行面面平行的判定定理：如果一个平面内存在两条相交直线和另外一个平面平行，则这两个平面平行线面垂直的判定定理：如果存在平面外一条直线和平面内的两条相交直线都垂直，则这条直线和这么平面垂直面面垂直的判定定理：如果一个平面经过另外一个平面的垂线，则这两个平面互相垂直直线和圆相交的判定：如果圆心到直线的距离小于半径，则这条直线和这个圆相交线面平行的性质定理：如果一条直线和一个平面平行，则经过这条直线的平面和这个平面相交，得到的绞线平行面面平行的性质定理：如果两个平面平行，则第三个平面和这两个平面相交，得到的绞线平行线面垂直的性质定理：如果一条直线和一个平面垂直，则这条直线垂直于这个平面内的任意一条直线面面垂直的性质定理：如果两个平面互相垂直，则在其中一个平面内和脚线垂直的直线垂直于另外一个平面直线和圆相交的性质：如果直线和圆相交，则圆心到直线的距离小于半径1、函数零点判断：函数在区间[a,b]上的图象是连续的，且f(a)f(b)<0，则函数在区间上必有零点。

2、增函数：函数在区间(a,b）内，如果导函数大于零，则函数在区间内单调递增。

3、减函数：函数在区间(a,b）内，如果导函数小于零，则函数在区间内单调递减。

4、若两直线异面，则两直线没有公共点。

5、异面直线定理：连结平面内一点与平面外一点的直线，和这个平面内不经过此点的直线是异面直线。

必要条件的性质定理：1、平面与平面平行的性质定理（1）：两个平面平行，则任意一个平面与这两个平面相交所得的交线相互平行2、平面与平面平行的性质定理（2）：两个平面平行，其中一个平面内的直线必平行于另一个平面。

3、直线与平面垂直的性质定理：垂直于同一个平面的两条直线平行。

4、平面与平面垂直的性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。

5、线面垂直的性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行。