人教版高中数学必修二第一章基础训练

第一章 空间几何体一、选择题1．有一个几何体的三视图如下图所示，这个几何体可能是一个( )．主视图 左视图 俯视图 (第1题) A ．棱台 B ．棱锥 C ．棱柱 D ．正八面体2．如果一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是( )．A ．2＋2B ．221＋C ．22＋2 D ．2＋13．棱长都是1的三棱锥的表面积为( )．A ．3B ．23C ．33D ．434．长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是( )．A ．25πB ．50πC ．125πD ．都不对 5．正方体的棱长和外接球的半径之比为( )． A ．3∶1 B ．3∶2 C ．2∶3 D ．3∶36．在△ABC 中，AB ＝2，BC ＝1.5，∠ABC ＝120°，若使△ABC 绕直线BC 旋转一周，则所形成的几何体的体积是( )．A ．29πB ．27πC ．25πD ．23π7．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )．A ．130B ．140C ．150D ．1608．如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的正方形，EF ∥AB ，EF ＝23，且EF 与平面ABCD 的距离为2，则该多面体的体积为( )．A ．29 B ．5 C ．6 D ．2159．下列关于用斜二测画法画直观图的说法中，错误．．的是( )． A ．用斜二测画法画出的直观图是在平行投影下画出的空间图形B ．几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C ．水平放置的矩形的直观图是平行四边形D ．水平放置的圆的直观图是椭圆10．如图是一个物体的三视图，则此物体的直观图是( )．(第8题)(第10题)二、填空题11．一个棱柱至少有______个面，面数最少的一个棱锥有________个顶点，顶点最少的一个棱台有________条侧棱．12．若三个球的表面积之比是1∶2∶3，则它们的体积之比是_____________．13．正方体ABCD－A1B1C1D1 中，O是上底面ABCD的中心，若正方体的棱长为a，则三棱锥O－AB1D1的体积为_____________．14．如图，E，F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是___________．(第14题)15．已知一个长方体共一顶点的三个面的面积分别是2、3、6，则这个长方体的对角线长是___________，它的体积为___________．16．一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为_________厘米．三、解答题17．有一个正四棱台形状的油槽，可以装油190 L，假如它的两底面边长分别等于60 cm 和40 cm，求它的深度．18 *．已知半球内有一个内接正方体，求这个半球的体积与正方体的体积之比．[提示：过正方体的对角面作截面]19．如图，在四边形ABCD中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝22，AD＝2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积．(第19题)20．养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用)，已建的仓库的底面直径为12 m，高4 m，养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4 m(高不变)；二是高度增加4 m(底面直径不变)．(1)分别计算按这两种方案所建的仓库的体积；(2)分别计算按这两种方案所建的仓库的表面积；(3)哪个方案更经济些？第一章 空间几何体参考答案A 组一、选择题 1．A解析：从俯视图来看，上、下底面都是正方形，但是大小不一样，可以判断可能是棱台．2．A解析：原图形为一直角梯形，其面积S ＝21(1＋2＋1)×2＝2＋2．3．A解析：因为四个面是全等的正三角形，则S 表面＝4×43＝3． 4．B解析：长方体的对角线是球的直径， l ＝2225＋4＋3＝52，2R ＝52，R ＝225，S ＝4πR 2＝50π． 5．C解析：正方体的对角线是外接球的直径． 6．D解析：V ＝V 大－V 小＝31πr 2(1＋1.5－1)＝23π．7．D解析：设底面边长是a ，底面的两条对角线分别为l 1，l 2，而21l ＝152－52，22l ＝92－52，而21l ＋22l ＝4a 2，即152－52＋92－52＝4a 2，a ＝8，S 侧面＝4×8×5＝160． 8．D解析：过点E ，F 作底面的垂面，得两个体积相等的四棱锥和一个三棱柱，V ＝2×31×43×3×2＋21×3×2×23＝215．9．B解析：斜二测画法的规则中，已知图形中平行于 x 轴的线段，在直观图中保持原长度不变；平行于 y 轴的线段，长度为原来的一半．平行于 z 轴的线段的平行性和长度都不变．10．D解析：从三视图看底面为圆，且为组合体，所以选D. 二、填空题11．参考答案：5，4，3．解析：符合条件的几何体分别是：三棱柱，三棱锥，三棱台．12．参考答案：1∶22∶33．r 1∶r 2∶r 3＝1∶2∶3，31r ∶32r ∶33r ＝13∶(2)3∶(3)3＝1∶22∶33．13．参考答案：361a ．解析：画出正方体，平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点， 三棱锥O －AB 1D 1的高h ＝33a ，V ＝31Sh ＝31×43×2a 2×33a ＝61a 3． 另法：三棱锥O －AB 1D 1也可以看成三棱锥A －OB 1D 1，它的高为AO ，等腰三角形OB 1D 1为底面．14．参考答案：平行四边形或线段．15．参考答案：6，6．解析：设ab ＝2，bc ＝3，ac ＝6，则V = abc ＝6，c ＝3，a ＝2，b ＝1， l ＝1＋2＋3＝6． 16．参考答案：12．解析：V ＝Sh ＝πr 2h ＝34πR 3，R ＝32764×＝12． 三、解答题 17．参考答案：V ＝31(S ＋S S ′＋S )h ，h ＝S S S S V ′＋′＋3＝6001＋4002＋60030001903×＝75．18．参考答案：如图是过正方体对角面作的截面．设半球的半径为R ，正方体的棱长为a ，则CC'＝a ，OC ＝22a ，OC'＝R ．(第18题)在Rt △C'CO 中，由勾股定理，得CC' 2＋OC 2＝OC' 2，即 a 2＋(22a )2＝R 2． ∴R ＝26a ，∴V 半球＝26πa 3，V 正方体＝a 3． ∴V 半球 ∶V 正方体＝6π∶2． 19．参考答案：S 表面＝S 下底面＋S 台侧面＋S 锥侧面＝π×52＋π×(2＋5)×5＋π×2×22 ＝(60＋42)π． V ＝V 台－V 锥 ＝31π(21r ＋r 1r 2＋22r )h －31πr 2h 1 ＝3148π．20．解：(1) 参考答案：如果按方案一，仓库的底面直径变成16 m ，则仓库的体积V 1＝31Sh ＝31×π×(216)2×4＝3256π(m 3)．如果按方案二，仓库的高变成8 m ，则仓库的体积COAV 2＝31Sh ＝31×π×(212)2×8＝3288π(m 3)．(2) 参考答案：如果按方案一，仓库的底面直径变成16 m ，半径为8 m ． 棱锥的母线长为l ＝224＋8＝45， 仓库的表面积S 1＝π×8×45＝325π(m 2)． 如果按方案二，仓库的高变成8 m ．棱锥的母线长为l ＝226＋8＝10，仓库的表面积S 2＝π×6×10＝60π(m 2)．(3) 参考答案：∵V 2＞V 1，S 2＜S 1，∴方案二比方案一更加经济些．。

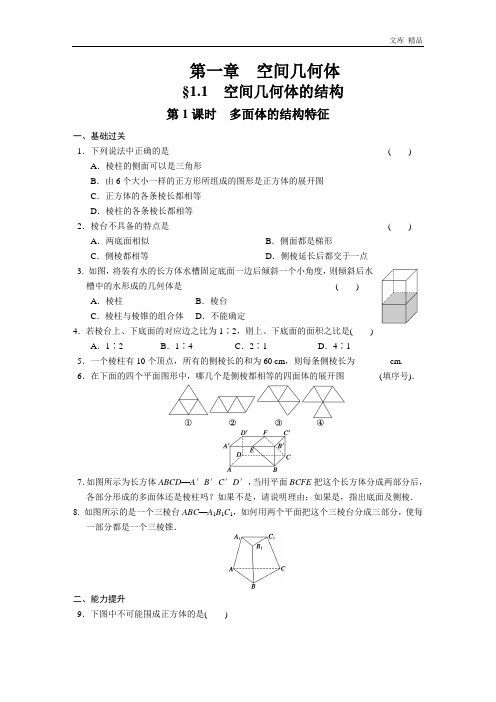
第一章空间几何体§1.1空间几何体的结构第1课时多面体的结构特征一、基础过关1．下列说法中正确的是() A．棱柱的侧面可以是三角形B．由6个大小一样的正方形所组成的图形是正方体的展开图C．正方体的各条棱长都相等D．棱柱的各条棱长都相等2．棱台不具备的特点是() A．两底面相似B．侧面都是梯形C．侧棱都相等D．侧棱延长后都交于一点3. 如图，将装有水的长方体水槽固定底面一边后倾斜一个小角度，则倾斜后水槽中的水形成的几何体是()A．棱柱B．棱台C．棱柱与棱锥的组合体 D．不能确定4．若棱台上、下底面的对应边之比为1∶2，则上、下底面的面积之比是() A．1∶2 B．1∶4 C．2∶1 D．4∶15．一个棱柱有10个顶点，所有的侧棱长的和为60 cm，则每条侧棱长为________cm. 6．在下面的四个平面图形中，哪几个是侧棱都相等的四面体的展开图________(填序号)．7．如图所示为长方体ABCD—A′B′C′D′，当用平面BCFE把这个长方体分成两部分后，各部分形成的多面体还是棱柱吗？如果不是，请说明理由；如果是，指出底面及侧棱．8. 如图所示的是一个三棱台ABC—A1B1C1，如何用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．二、能力提升9．下图中不可能围成正方体的是()10．在正方体上任意选择4个顶点，它们可能是如下各种几何体的4个顶点，这些几何体是________(写出所有正确结论的编号)．①矩形；②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；④每个面都是等边三角形的四面体；⑤每个面都是直角三角形的四面体．11．根据下列对于几何体结构特征的描述，说出几何体的名称．(1)由八个面围成，其中两个面是互相平行且全等的正六边形，其它各面都是矩形；(2)由五个面围成，其中一个面是正方形，其它各面都是有一个公共顶点的全等三角形．三、探究与拓展12．正方体的截面可能是什么形状的图形？答案1．C 2.C 3.A 4.B 5.12 6.①②7．解截面BCFE右侧部分是棱柱，因为它满足棱柱的定义．它是三棱柱BEB′—CFC′，其中△BEB′和△CFC′是底面．EF，B′C′，BC是侧棱，截面BCFE左侧部分也是棱柱．它是四棱柱ABEA′—DCFD′.其中四边形ABEA′和四边形DCFD′是底面．A′D′，EF，BC，AD为侧棱．8．解过A1、B、C三点作一个平面，再过A1、B、C1作一个平面，就把三棱台ABC—A1B1C1分成三部分，形成的三个三棱锥分别是A1—ABC，B—A1B1C1，A1—BCC1.9．D10.①③④⑤11．解(1)该几何体有两个面是互相平行且全等的正六边形，其他各面都是矩形，可满足每相邻两个面的公共边都相互平行，故该几何体是六棱柱．(2)该几何体的其中一个面是四边形，其余各面都是三角形，并且这些三角形有一个公共顶点，因此该几何体是四棱锥．12．解本问题可以有如下各种答案：①截面可以是三角形：等边三角形、等腰三角形、一般三角形；②截面三角形是锐角三角形；③截面可以是四边形：平行四边形、矩形、菱形、正方形、梯形、等腰梯形；截面为四边形时，这个四边形中至少有一组对边平行；④截面可以是五边形；⑤截面可以是六边形；⑥截面六边形可以是等角(均为120°)的六边形．特别地，可以是正六边形．截面图形举例.....................................使用本文档删除后面的即可致力于打造全网一站式文档服务需求，为大家节约时间文档来源网络仅供参考欢迎您下载可以编辑的word文档谢谢你的下载本文档目的为企业和个人提供下载方便节省工作时间，提高工作效率，打造全网一站式精品需求!欢迎您的下载，资料仅供参考!（本文档收集于网络改编，由于文档太多，审核难免疏忽，如有侵权或雷同，告知本店马上删除）。

人教版高中数学必修二第一章测试题及答案高一数学人教版必修二第一章测试题及答案一、选择题1.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是()．答案：C．2＋2/22.棱长都是1的三棱锥的表面积为()．答案：B．2√23.长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是()．答案：B．50π4.正方体的棱长和外接球的半径之比为()．答案：B．3∶25.在△ABC中，AB＝2，BC＝1.5，∠ABC＝120°，若使△ABC绕直线BC旋转一周，则所形成的几何体的体积是()．答案：A．π/96.若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是()．答案：D．1607.如图，在多面体ABCDEF中，已知平面ABCD是边长为3的正方形，EF∥AB，EF＝3/2，且EF与平面ABCD的距离为2，则该多面体的体积为()．答案：B．58.下列关于用斜二测画法画直观图的说法中，错误的是()．答案：D．水平放置的圆的直观图是椭圆二、填空题9.若三个球的表面积之比是1∶2∶3，则它们的体积之比是1∶2∶3.10.正方体ABCD－A1B1C1D1中，O是上底面ABCD的中心，若正方体的棱长为a，则三棱锥O－A1BD1的体积为a^3/6.11.已知一个长方体共一顶点的三个面的面积分别是2、3、6，则这个长方体的对角线长是√29，它的体积为√108.12.一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为4厘米.三、解答题暂无。

解析：V = Sh = πr²h = πR³，其中R = 364 × 27 = 12.三、解答题13.参考答案：V = (S + SS' + S')h，其中h =14.参考答案：V = 1/3( S + SS' + S')h = 1/3 × × 75 = xxxxxxx/3.S表面积 = S下底面积 + S台侧面积 + S锥侧面积 = π×5² + π×(2+5)×5 + π×2²×2 = (60+42)π.V台= 1/3πr₁²h = 1/3π(5²+5×2+2²)×5 = 148π/3.V锥 = 1/3πr₁²h = 1/3π5²×5 = 25π/3.V = V台 - V锥= 148π/3 - 25π/3 = 123π/3 = 41π.。

第一章 空间几何体一、选择题1．有一个几何体的三视图如下图所示，这个几何体可能是一个( )．主视图 左视图 俯视图 (第1题)A ．棱台B ．棱锥C ．棱柱D ．正八面体2．如果一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是( )．A ．2＋2B ．221＋ C ．22＋2 D ．2＋13．棱长都是1的三棱锥的表面积为( )． A ．3B ．23C ．33D ．434．长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是( )．A ．25πB ．50πC ．125πD ．都不对5．正方体的棱长和外接球的半径之比为( )． A ．3∶1B ．3∶2C ．2∶3D ．3∶36．在△ABC 中，AB ＝2，BC ＝1.5，∠ABC ＝120°，若使△ABC 绕直线B C 旋转一周，则所形成的几何体的体积是( )．A ．29π B ．27π C ．25π D ．23π7．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )．A ．130B ．140C ．150D ．1608．如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的正方形，EF ∥AB ，EF ＝23，且EF与平面ABCD 的距离为2，则该多面体的体积为( )．A ．29 B ．5 C ．6 D ．2159．下列关于用斜二测画法画直观图的说法中，错误．．的是( )． A ．用斜二测画法画出的直观图是在平行投影下画出的空间图形 B ．几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同 C ．水平放置的矩形的直观图是平行四边形 D ．水平放置的圆的直观图是椭圆10．如图是一个物体的三视图，则此物体的直观图是( )．(第10题)二、填空题11．一个棱柱至少有______个面，面数最少的一个棱锥有________个顶点，顶点最少的一个棱台有________条侧棱．12．若三个球的表面积之比是1∶2∶3，则它们的体积之比是_____________．13．正方体ABCD －A 1B 1C 1D 1 中，O 是上底面ABCD 的中心，若正方体的棱长为a ，则三棱锥O －AB 1D 1的体积为_____________．14．如图，E ，F 分别为正方体的面ADD 1A 1、面BCC 1B 1的中心，则四边形BFD 1E 在该正方体的面上的射影可能是___________．(第8题)(第14题)15．已知一个长方体共一顶点的三个面的面积分别是2、3、6，则这个长方体的对角线长是___________，它的体积为___________．16．一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为_________厘米．三、解答题17．有一个正四棱台形状的油槽，可以装油190 L，假如它的两底面边长分别等于60 cm和40 cm，求它的深度．18 *．已知半球内有一个内接正方体，求这个半球的体积与正方体的体积之比．[提示：过正方体的对角面作截面]19．如图，在四边形ABCD中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝22，AD＝2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积．20．养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用)，已建的仓库的底面直径为12 m，高4 m，养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4 m(高不变)；二是高度增加4 m(底面直径不变)．(1)分别计算按这两种方案所建的仓库的体积；(2)分别计算按这两种方案所建的仓库的表面积；(3)哪个方案更经济些？第二章 点、直线、平面之间的位置关系A 组一、选择题1．设 α，β为两个不同的平面，l ，m 为两条不同的直线，且l ⊂α，m ⊂β，有如下的两个命题：①若 α∥β，则l ∥m ；②若l ⊥m ，则 α⊥β．那么( )．A ．①是真命题，②是假命题B ．①是假命题，②是真命题C ．①②都是真命题D ．①②都是假命题2．如图，ABCD －A 1B 1C 1D 1为正方体，下面结论错误．．的是( )． A ．BD ∥平面CB 1D 1 B ．AC 1⊥BD C ．AC 1⊥平面CB 1D 1D ．异面直线AD 与CB 1角为60°3．关于直线m ，n 与平面 α，β，有下列四个命题： ①m ∥α，n ∥β 且 α∥β，则m ∥n ； ②m ⊥α，n ⊥β 且 α⊥β，则m ⊥n ； ③m ⊥α，n ∥β 且 α∥β，则m ⊥n ； ④m ∥α，n ⊥β 且 α⊥β，则m ∥n ．其中真命题的序号是( )． A ．①②B ．③④C ．①④D ．②③4．给出下列四个命题：①垂直于同一直线的两条直线互相平行 ②垂直于同一平面的两个平面互相平行 ③若直线l 1，l 2与同一平面所成的角相等，则l 1，l 2互相平行 ④若直线l 1，l 2是异面直线，则与l 1，l 2都相交的两条直线是异面直线 其中假．命题的个数是( )． A ．1B ．2C ．3D ．45．下列命题中正确的个数是( )．①若直线l 上有无数个点不在平面 α 内，则l ∥α②若直线l 与平面 α 平行，则l 与平面 α 内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行，那么另一条直线也与这个平面平行 ④若直线l 与平面 α 平行，则l 与平面 α 内的任意一条直线都没有公共点 A ．0个B ．1个C ．2个D ．3个(第2题)6．两直线l1与l2异面，过l1作平面与l2平行，这样的平面()．A．不存在B．有唯一的一个C．有无数个D．只有两个7．把正方形ABCD沿对角线AC折起，当以A，B，C，D四点为顶点的三棱锥体积最大时，直线BD和平面ABC所成的角的大小为()．A．90°B．60°C．45°D．30°8．下列说法中不正确的．．．．是()．A．空间中，一组对边平行且相等的四边形一定是平行四边形B．同一平面的两条垂线一定共面C．过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内D．过一条直线有且只有一个平面与已知平面垂直9．给出以下四个命题：①如果一条直线和一个平面平行，经过这条直线的一个平面和这个平面相交，那么这条直线和交线平行②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面③如果两条直线都平行于一个平面，那么这两条直线互相平行④如果一个平面经过另一个平面的一条垂线，那么些两个平面互相垂直其中真命题的个数是()．A．4 B．3 C．2 D．110．异面直线a，b所成的角60°，直线a⊥c，则直线b与c所成的角的范围为()．A．[30°，90°]B．[60°，90°]C．[30°，60°]D．[30°，120°]二、填空题11．已知三棱锥P－ABC的三条侧棱PA，PB，PC两两相互垂直，且三个侧面的面积分别为S1，S2，S3，则这个三棱锥的体积为．12．P是△ABC所在平面 α 外一点，过P作PO⊥平面 α，垂足是O，连PA，PB，PC．(1)若PA＝PB＝PC，则O为△ABC的心；(2)PA⊥PB，PA⊥PC，PC⊥PB，则O是△ABC的心；(3)若点P到三边AB，BC，CA的距离相等，则O是△ABC的心；(4)若PA＝PB＝PC，∠C＝90º，则O是AB边的点；(5)若PA＝PB＝PC，AB＝AC，则点O在△ABC的线上．J 13．如图，在正三角形ABC中，D，E，F分别为各边的中点，G，H ，I ，J 分别为AF ，AD ，BE ，DE 的中点，将△ABC 沿DE ，EF ，DF 折成三棱锥以后，GH 与IJ 所成角的度数为 ．14．直线l 与平面 α 所成角为30°，l ∩α＝A ，直线m ∈α，则m 与l 所成角的取值范围 是 ．15．棱长为1的正四面体内有一点P ，由点P 向各面引垂线，垂线段长度分别为d 1，d 2，d 3，d 4，则d 1＋d 2＋d 3＋d 4的值为 ．16．直二面角 α－l －β 的棱上有一点A ，在平面 α，β 内各有一条射线AB ，AC 与l 成45°，AB ⊂α，AC ⊂β，则∠BAC ＝ ．三、解答题17．在四面体ABCD 中，△ABC 与△DBC 都是边长为4的正三角形． (1)求证：BC ⊥AD ；(2)若点D 到平面ABC 的距离等于3，求二面角A －BC －D 的正弦值； (3)设二面角A －BC －D 的大小为 θ，猜想 θ 为何值时，四面体A －BCD 的体积最大．(不要求证明)18． 如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝2，BB 1＝BC ＝1，E 为D 1C 1的中点，连结ED ，EC ，EB 和DB ．(1)求证：平面EDB ⊥平面EBC ； (2)求二面角E －DB －C 的正切值.(第18题)(第17题)19*．如图，在底面是直角梯形的四棱锥Ｓ－ABCD 中，AD ∥BC ，∠ABC ＝90°， SA ⊥面ABCD ，SA ＝AB ＝BC ＝１，AD ＝21．(1)求四棱锥S —ABCD 的体积；(2)求面SCD 与面SBA 所成的二面角的正切值． (提示：延长 BA ，CD 相交于点 E ，则直线 SE 是 所求二面角的棱.)(第19题)20*．斜三棱柱的一个侧面的面积为10，这个侧面与它所对棱的距离等于6，求这个棱柱的体积．(提示：在 AA 1 上取一点 P ，过 P 作棱柱的截面，使 AA 1 垂直于这个截面.)（第20题)第三章 直线与方程一、选择题1．若直线x ＝1的倾斜角为 α，则 α( )． A ．等于0B ．等于πC ．等于2π D ．不存在2．图中的直线l 1，l 2，l 3的斜率分别为k 1，k 2，k 3，则( )． A ．k 1＜k 2＜k 3B ．k 3＜k 1＜k 2C ．k 3＜k 2＜k 1D ．k 1＜k 3＜k 23．已知直线l 1经过两点(－1，－2)、(－1，4)，直线l 2经过两点(2，1)、(x ，6)，且l 1∥l 2，则x ＝( )．A ．2B ．－2C ．4D ．14．已知直线l 与过点M (－3，2)，N (2，－3)的直线垂直，则直线l 的倾斜角是( )． A ．3π B ．32π C ．4π D ．43π5．如果AC ＜0，且BC ＜0，那么直线Ax ＋By ＋C ＝0不通过( )． A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．设A ，B 是x 轴上的两点，点P 的横坐标为2，且|P A |＝|PB |，若直线P A 的方程为x －y ＋1＝0，则直线PB 的方程是( )．A ．x ＋y －5＝0B ．2x －y －1＝0C ．2y －x －4＝0D ．2x ＋y －7＝07．过两直线l 1：x －3y ＋4＝0和l 2：2x ＋y ＋5＝0的交点和原点的直线方程为( )． A ．19x －9y ＝0B ．9x ＋19y ＝0C ．19x －3y ＝ 0D ．3x ＋19y ＝08．直线l 1：x ＋a 2y ＋6＝0和直线l 2 : (a －2)x ＋3ay ＋2a ＝0没有公共点，则a 的值 是( )．A ．3B ．－3C ．1D ．－19．将直线l 沿y 轴的负方向平移a (a ＞0)个单位，再沿x 轴正方向平移a ＋1个单位得直线l'，此时直线l' 与l 重合，则直线l' 的斜率为( )．(第2题)A ．1＋a a B ．1＋－a a C ．aa 1＋ D ．aa 1＋－10．点(4，0)关于直线5x ＋4y ＋21＝0的对称点是( )． A ．(－6，8) B ．(－8，－6) C ．(6，8) D ．(－6，－8)二、填空题11．已知直线l 1的倾斜角 1＝15°，直线l 1与l 2的交点为A ，把直线l 2绕着点A 按逆时针方向旋转到和直线l 1重合时所转的最小正角为60°，则直线l 2的斜率k 2的值为 ．12．若三点A (－2，3)，B (3，－2)，C (21，m )共线，则m 的值为 ．13．已知长方形ABCD 的三个顶点的坐标分别为A (0，1)，B (1，0)，C (3，2)，求第四个顶点D 的坐标为 ．14．求直线3x ＋ay ＝1的斜率 ．15．已知点A (－2，1)，B (1，－2)，直线y ＝2上一点P ，使|AP |＝|BP |，则P 点坐标为 ． 16．与直线2x ＋3y ＋5＝0平行，且在两坐标轴上截距的和为6的直线方程是 ． 17．若一束光线沿着直线x －2y ＋5＝0射到x 轴上一点，经x 轴反射后其反射线所在直线的方程是 ．三、解答题18．设直线l 的方程为(m 2－2m －3)x ＋(2m 2＋m －1)y ＝2m －6(m ∈R ，m ≠－1)，根据下列条件分别求m 的值：①l 在x 轴上的截距是－3； ②斜率为1．19．已知△ABC 的三顶点是A (－1，－1)，B (3，1)，C (1，6)．直线l 平行于AB ，交AC ，BC 分别于E ，F ，△CEF 的面积是△CAB 面积的41．求直线l 的方程．20．一直线被两直线l1：4x＋y＋6＝0，l2：3x－5y－6＝0截得的线段的中点恰好是坐标原点，求该直线方程．.21．直线l过点(1，2)和第一、二、四象限，若直线l的横截距与纵截距之和为6，求直线l的方程．第四章圆与方程一、选择题1．若圆C的圆心坐标为(2，－3)，且圆C经过点M(5，－7)，则圆C的半径为()．A．5B．5 C．25 D．102．过点A(1，－1)，B(－1，1)且圆心在直线x＋y－2＝0上的圆的方程是()．A．(x－3)2＋(y＋1)2＝4 B．(x＋3)2＋(y－1)2＝4C．(x－1)2＋(y－1)2＝4 D．(x＋1)2＋(y＋1)2＝43．以点(－3，4)为圆心，且与x轴相切的圆的方程是()．A．(x－3)2＋(y＋4)2＝16 B．(x＋3)2＋(y－4)2＝16C．(x－3)2＋(y＋4)2＝9 D．(x＋3)2＋(y－4)2＝194．若直线x＋y＋m＝0与圆x2＋y2＝m相切，则m为()．A．0或2 B．2 C．2D．无解5．圆(x－1)2＋(y＋2)2＝20在x轴上截得的弦长是()．A．8 B．6 C．62D．436．两个圆C1：x2＋y2＋2x＋2y－2＝0与C2：x2＋y2－4x－2y＋1＝0的位置关系为()．A．内切B．相交C．外切D．相离7．圆x2＋y2－2x－5＝0与圆x2＋y2＋2x－4y－4＝0的交点为A，B，则线段AB的垂直平分线的方程是()．A．x＋y－1＝0 B．2x－y＋1＝0C．x－2y＋1＝0 D．x－y＋1＝08．圆x2＋y2－2x＝0和圆x2＋y2＋4y＝0的公切线有且仅有()．A．4条B．3条C．2条D．1条9．在空间直角坐标系中，已知点M(a，b，c)，有下列叙述：点M关于x轴对称点的坐标是M1(a，－b，c)；点M关于y oz平面对称的点的坐标是M2(a，－b，－c)；点M关于y轴对称的点的坐标是M3(a，－b，c)；点M关于原点对称的点的坐标是M4(－a，－b，－c)．其中正确的叙述的个数是()．A．3 B．2 C．1 D．010．空间直角坐标系中，点A(－3，4，0)与点B(2，－1，6)的距离是()．A．243B．221C．9 D．86二、填空题11．圆x2＋y2－2x－2y＋1＝0上的动点Q到直线3x＋4y＋8＝0距离的最小值为．12．圆心在直线y＝x上且与x轴相切于点(1，0)的圆的方程为．13．以点C(－2，3)为圆心且与y轴相切的圆的方程是．14．两圆x2＋y2＝1和(x＋4)2＋(y－a)2＝25相切，试确定常数a的值．15．圆心为C(3，－5)，并且与直线x－7y＋2＝0相切的圆的方程为．16．设圆x2＋y2－4x－5＝0的弦AB的中点为P(3，1)，则直线AB的方程是．三、解答题17．求圆心在原点，且圆周被直线3x＋4y＋15＝0分成1∶2两部分的圆的方程．18．求过原点，在x轴，y轴上截距分别为a，b的圆的方程(ab≠0)．19．求经过A(4，2)，B(－1，3)两点，且在两坐标轴上的四个截距之和是2的圆的方程．20．求经过点(8，3)，并且和直线x＝6与x＝10都相切的圆的方程．数学必修2综合测试题考试时间：90分钟 试卷满分：100分一、选择题：本大题共14小题，每小题4分，共56分．在每小题给出的四个选项中，只有一项是符合要求的．1．在直角坐标系中，已知A (－1，2)，B (3，0)，那么线段AB 中点的坐标为( )． A ．(2，2)B ．(1，1)C ．(－2，－2)D ．(－1，－1)2．右面三视图所表示的几何体是( )．A ．三棱锥B ．四棱锥C ．五棱锥D ．六棱锥3．如果直线x ＋2y －1＝0和y ＝kx 互相平行，则实数k 的值为( )． A ．2B ．21 C ．－2 D ．－214．一个球的体积和表面积在数值上相等，则该球半径的数值为( )． A ．1B ．2C ．3D ．45．下面图形中是正方体展开图的是( )．ABCD(第5题)6．圆x 2＋y 2－2x －4y －4＝0的圆心坐标是( )． A ．(－2，4)B ．(2，－4)C ．(－1，2)D ．(1，2)7．直线y ＝2x ＋1关于y 轴对称的直线方程为( )． A ．y ＝－2x ＋1 B ．y ＝2x －1 C ．y ＝－2x －1D ．y ＝－x －1正视图 侧视图俯视图(第2题)8．已知两条相交直线a ，b ，a ∥平面 α，则b 与 α 的位置关系是( )． A ．b ⊂平面α B ．b ⊥平面αC ．b ∥平面αD ．b 与平面α相交，或b ∥平面α9．在空间中，a ，b 是不重合的直线，α，β是不重合的平面，则下列条件中可推出 a ∥b 的是( )．A ．a ⊂α，b ⊂β，α∥βB ．a ∥α，b ⊂βC ．a ⊥α，b ⊥αD ．a ⊥α，b ⊂α10． 圆x 2＋y 2＝1和圆x 2＋y 2－6y ＋5＝0的位置关系是( )． A ．外切B ．内切C ．外离D ．内含11．如图，正方体ABCD —A'B'C'D'中，直线D'A 与DB 所成的角可以表示为( )．A ．∠D'DB B ．∠AD' C'C ．∠ADBD ．∠DBC'12． 圆(x －1)2＋(y －1)2＝2被x 轴截得的弦长等于( )． A ． 1B ．23 C ． 2 D ． 313．如图，三棱柱A 1B 1C 1—ABC 中，侧棱AA 1⊥底面A 1B 1C 1，底面三角形A 1B 1C 1是正三角形，E 是BC 中点，则下列叙述正确的是( )．A ．CC 1与B 1E 是异面直线 B ．AC ⊥平面A 1B 1BAC ．AE ，B 1C 1为异面直线，且AE ⊥B 1C 1D ．A 1C 1∥平面AB 1E14．有一种圆柱体形状的笔筒，底面半径为4 cm ，高为12 cm ．现要为100个这种相同规格的笔筒涂色(笔筒内外均要涂色，笔筒厚度忽略不计)． 如果每0.5 kg 涂料可以涂1 m 2，那么为这批笔筒涂色约需涂料．A ．1.23 kgB ．1.76 kgC ．2.46 kgD ．3.52 kg二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上． 15．坐标原点到直线4x ＋3y －12＝0的距离为 ．C BAD A 'B 'C 'D '(第11题)A 1B 1C 1ABEC(第13题)16．以点A (2，0)为圆心，且经过点B (－1，1)的圆的方程是 ．17．如图，在长方体ABCD —A 1B 1C 1D 1中，棱锥A 1——ABCD 的体积与长方体的体积之比为_______________．18．在平面几何中，有如下结论：三边相等的三角形内任意一点到三边的距离之和为定值．拓展到空间，类比平面几何的上述结论，可得：四个面均为等边三角形的四面体内任意一点_______________________________________．三、解答题：本大题共3小题，共28分．解答应写出文字说明，证明过程或演算步骤． 19．已知直线l 经过点(0，－2)，其倾斜角是60°． (1)求直线l 的方程；(2)求直线l 与两坐标轴围成三角形的面积．A BC DD 1C 1B 1A 1(第17题)20．如图，在三棱锥P —ABC 中，PC ⊥底面ABC ， AB ⊥BC ，D ，E 分别是AB ，PB 的中点．(1)求证：DE ∥平面PAC ； (2)求证：AB ⊥PB ；(3)若PC ＝BC ，求二面角P —AB —C 的大小．21．已知半径为5的圆C 的圆心在x 轴上，圆心的横坐标是整数，且与直线4x ＋3y －29＝0相切． (1)求圆C 的方程；(2)设直线ax －y ＋5＝0与圆C 相交于A ，B 两点，求实数a 的取值范围；(3) 在(2)的条件下，是否存在实数a ，使得过点P (－2，4)的直线l 垂直平分弦AB ？若存在，求出实数a 的值；若不存在，请说明理由．ACPBDE(第20题)。

1.1.1柱、锥、台、球的的结构特征练习一一、选择题1、下列命题中，正确命题的个数是（）（1）桌面是平面；（2）一个平面长2 米，宽3 米；（3）用平行四边形表示平面，只能画出平面的一部分；（4）空间图形是由空间的点、线、面所构成。

A 、1 B、 2 C、 3 D、 42、下列说法正确的是（）A、水平放置的平面是大小确定的平行四边形B、平面ABCD 就是四边形ABCD 的四条边围来的部分C、100 个平面重叠在一起比10 个平面重叠在一起厚D、平面是光滑的，向四周无限延展的面3、下列说法中表示平面的是（）A、水面B、屏面C、版面D、铅垂面4、下列说法中正确的是（）A、棱柱的面中，至少有两个面互相平行B、棱柱的两个互相平行的平面一定是棱柱的底面C、棱柱的一条侧棱的长叫做棱柱的高D、棱柱的侧面是平行四边形，但它的底面一定不是平行四边形5、长方体的三条棱长分别是AA/=1，AB=2，AD=4，则从A 点出发，沿长方体的表面到C/的最短距离是（）A、 5B、7C、D、37296、若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是（）A、三棱锥B、四棱锥C、五棱锥D、六棱锥]7、过球面上两点可能作出球的大圆（）A、0 个或1 个B、有且仅有1 个C、无数个D、一个或无数个8、一个圆柱的母线长为5，底面半径为2，则圆柱的轴截面的面积为（）A、10B、20C、40D、15二、填空题9、用一个平面去截一个正方体，截面边数最多是------------- 条。

10、正三棱台的上、下底面边长及高分别为1、2、2，则它的斜高是 --------------。

11、一个圆柱的轴截面面积为Q，则它的侧面面积是 ------------- 。

12、若圆锥的侧面面积是其底面面积的2 倍，则这个圆锥的母线与底面所成的角为 ------------ ，圆锥的侧面展开图扇形的圆心角为 ---------- 。

13、在赤道上，东经1400 与西经1300 的海面上有两点A、B，则A、B 两点的球面距离是多少海里---------------。