当前位置：文档之家 › 第二章 2 两个重要极限和利用等价无穷小求极限

第二章 2 两个重要极限和利用等价无穷小求极限

  • 格式：ppt
  • 大小：489.00 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

等价无穷小求极限

等价无穷小求极限

证明 因为0→x 时，01→-x e .解 令x tan =α，x sin =β. 在0→x 时， αα'==x x sin ~tan ，ββ'==x x tan ~sin .解 令x tan =α，x sin =β，32x =γ ．在0→x 时，有αα'==x x sin ~tan ，当α、β为无穷小量，αα'~，ββ'~，且()A =+βα11lim ．则()()ββαα111lim 1lim +='+'A =．证 ()()()()ββαββααα111ln 1ln 1ln lim1ln lim +⋅'⋅+'+='+'()()()βααααααα11ln 1ln 1ln lim +⋅⋅+'⋅''+= ()βααα11ln lim +⋅'=()βα11ln lim +=A ln lim =．所以 ()()ββαα111lim 1lim +='+'A =．例14 求()xx x sin 31021lim +→．其中，当α、β为无穷小量，αα'~，ββ'~，且βα⎪⎭⎫⎝⎛1lim 存在．则ββαα'⎪⎭⎫⎝⎛'=⎪⎭⎫ ⎝⎛1lim 1lim ．证 βα⎪⎭⎫ ⎝⎛1ln lim βααβαβ'⎪⎭⎫ ⎝⎛'⋅''--=1ln ln ln lim βααα'⎪⎭⎫ ⎝⎛'⋅'=1ln 11lim βα'⎪⎭⎫⎝⎛'=1ln lim所以 ββαα'⎪⎭⎫⎝⎛'=⎪⎭⎫ ⎝⎛1lim 1lim .例15 ()xx x ln 1cot lim +→ （它是0∞型）解 当0→x 时，x x ~tan ．根据4.1.2可知，()xx x ln 10cot lim +→=xx x xx xx ex x 1ln ln 10ln 10ln 10lim 1lim tan 1lim +→→→=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=1ln ln 1lim -⋅-→=+e ex xx ．当0→x 时，越计算过程越复杂．这时，我们可以把洛必达法则和等价无穷小的代换结合起来使用，这样就可以简化计算，方便问题求出．我们通过大量的例题，分别从等价无穷小的概念及其重要性质，等价无穷小的应用这几个方面研究了等价无穷小在求函数极限中的作用，通过我们做题可知：计算函数极限的方法是多种多样的，但是方法的选择是否恰当，直接关系到计算过程是否简洁和计算结果是否正确．本文通过对大量例题的分析和做题方法的比较，体现了等价无穷小代换求极限是一种行之而有效的方法．用无穷小量的等价代换来计算极限虽然很方便，但在计算过程中并非所有的无穷小量都能用其等价无穷小量来代换．而在做题的过程中，相当一部分学生往往不清楚在什么情况下才能进行代换，以至于不可避免地会出现这样或那样的错误，所以我在本文针对这些问题给出了大量的例题来解释．参考文献：[1] 华东师范大学数学系编．数学分析[M]．北京：高等教育出版社，1991[2] 田婷．等价无穷小求极限问题的探讨[J]．苏州工业职业技术学院．2007，06[3] 李秀敏，王灵色．等价无穷小代换在求极限过程中的应用[J]．高等数学研究，2002，03[4] 杨明顺．利用等价无穷小求极限方法的一个推广[J]．商洛师范专科学校学报，2003，01[5] 伍华健．在求函数极限过程中使用等价无穷小[J]．广西师范学校（自然学科）.1999，02[6] 王建平．无穷小量的等价代换在代数和极限运算中的应用[J]．河南教育学院报（自然科学版），2005，04[7] 姜玉秋．巧用等价无穷小替换求解复杂极限的研究[J]．吉林师范大学学报（自然科学版），2005，04[8] 胡景明．用等价无穷小代换求极限时常犯的错误[J]．河北工程技术高等专科学校学报，1997，01[9] 同济大学数学教研室主编．高等数学[M]．北京：高等教育出版社，1988[10] 吕祥凤，王艳．等价无穷小的性质及应用[J]．重庆师范学院学报（自然科学版），2000，06[11]Walter Rudin．Principles of Mathematical Analysis [M]．McGraw-Hill PublishingCo，197611。

函数极限的运算

函数极限的运算

1 2 x 1 cos x 1 2 解 : lim lim x 0 x si n x x 0 x x 2
25
例17设
x 2x k lim 4， 求k的 值 。 x 3 x3
2
解:由题意可知，当x→3时，x2-2x+k和x-3是 同阶无穷小．
即 lim( x 2 2 x k ) 0
9
例8
3x 2 x 1 lim 2 x 2 x x 5
3
解 因为当x→∞时，类型为“
大与无穷小的关系，
”型未定式，
且分子中的x指数大于分母中x的指数．根据无穷
2 1 5 2 2 3 2x x 5 0 x x x lim 0 lim 3 x 2 5 x 3 x 2 x 5 3 3 2 3 x x 3x3 2 x 1 所 以 lim 2 x 2 x x 5
12
sin 3x 例 9 lim x 0 x
解:
sin3 x sin 3 x sin3 x 3 lim （ 3 ） 3 lxim lim 0 x 0 x 0 3x x 3x
tan x 例10 lim x 0 x 0 解 这个极限是“0 ”型未定式，且含有三角函 sin x 数tanx，要想用公式，就要化为 的形式． x tan x sin x 1 lim lim( ) 1 x 0 x 0 x x cos x
x 2
x2 所以 lim x2 x 2
5
例4
x3 lim 2 x 3 x 9
解 因为当x→3时，分母、分子的极限都为0，称 为“ 0
0
”型未定式．对于这种类型的极限，常
用消去“零因式”的方法．

应用数学第4讲---两个重要的极限

应用数学第4讲---两个重要的极限

应用数学 问题一：圆的面积公式问题
要想回答这个问题，我们需要知道，圆的面积公式是怎么来的！
公元263年，我国数学家刘徽 为了精确计算圆周率，使 用了一种“割圆术”的方 法：割之弥细 , 所失弥小, 割之又割 , 以至于不可割 , 则与圆合体而无所失矣 .
应用数学 问题一：圆的面积公式问题
要想回答这个问题，我们需要知道，圆的面积公式是怎么来的！
应用数学 求下列极限 解
(4)
sin x sin x 1 1 lim x sin x x 0 x x 2 lim lim x 0 x 0 2 x sin x sin x sin x 2 2 lim x 0 x x
(5)
1 1 u arctan x 1 lim lim lim u 0 tan u x 0 u 0 tan u tan u x lim u 0 u u

3
e 3
应用数学 例 2 求下列极限
2 (1) lim 1 x x
x
3 (2) lim 1 x x
x
x 1 (3) lim x x 1
解
x
(4) lim 1 tan x
x 0
应用数学
第四讲——
两 个 重 要 的 极 限
( Two important Limits)
应用数学 理解两个重要的极限概念
知识目标
理解复利计算的最终趋势 掌握分割求和从细微到宏观的思想
会利用两个重要的极限公式求极限 能力目标
会建立复利金融公式并预测其走势
能举一反三进行极限的计算
应用数学 问题一：圆的面积问题
2 (1) lim 1 x x

两个重要极限教案

两个重要极限教案

两个重要极限教案公开课教案教者龚桂琼科目数学班级12级数一班课题两个重要极限（一）课型时间地点教材分析《两个重要极限》是在学生学习了数列的极限、函数的极限以及函数极限的四则运算法则的基础上进行研究的，它是解决极限计算问题的一个有效工具，也是今后研究初等函数求导公式的一个工具，所以两个重要极限是后继学习的重要基础。

学情分析一方面，学生已经学习了函数的极限以及函数极限的运算法则，会用因式分解约去非零因子、有理化分子或分母这两种方法计算“0型”函数的极限，具备了接受新知识的基础；另一方面，学生理性思维能力相对较弱，对函数极限概念的理解还比较浅显，运用极限思维解决问题的能力有限。

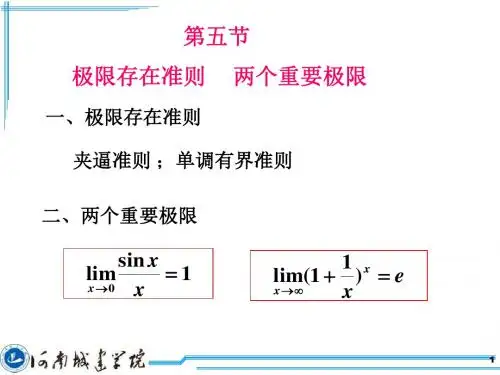
教学目标知识与技能：让学生了解公式1sinlim=→xxx的证明过程，正确理解公式，知道公式应用的条件，熟练运用公式及其变形式解决有关函数极限的计算。

过程与方法：通过教师引导，学生观察、实验、猜想、分析讨论和练习，培养学生观察、归纳、举一反三的能力，进一步认识换元法、转化思想、数型结合思想在数学解题中的重要作用。

情感态度与价值观：通过对这一重要极限公式的研究，进一步认识数学的美，激发学生的学习兴趣；养成细心观察、认真分析、善于总结的良好思维品质。

教学重点正确理解公式1sinlim=→xxx，并能运用公式及其变形式解决有关函数极限的计算。

教学难点公式1sin lim0=→xxx 的证明、公式及其变形式灵活运用。

教法学法本节课采用实验法、讨论法以及讲练结合的教学方法。

通过复习函数极限的定义以及函数极限的运算法则，配以适当的练习，强化学生对极限概念的理解和运算能力。

在公式的引入上通过设疑引导学生尝试、讨论、猜想，并借助多媒体动画帮助学生理解结论，锻炼学生运用数学工具解决数学问题的意识，提高学生的学习兴趣。

对于公式的证明，所涉及的内容比较多，逻辑性较强，在老师的引导下了解论证过程。

在公式的运用上按照循序渐进的原则，设计梯度、降低难度，留出学生的思考空间，让学生去尝试、联想、探索，以独立思考和相互交流相结合的形式，在教师的指导下分析和解决问题，帮助学生获得成功的体验。

极限存在准则 两个重要极限

极限存在准则 两个重要极限

∴ {xn } 是单调递增的 ;
1 1 1 1 xn < 1 + 1 + + L + < 1 + 1 + + L + n −1 2! n! 2 2 1 = 3 − n − 1 < 3, ∴ {xn } 是有界的 ; 2 1n ) ∴ lim x n 存在. 记为lim(1 + ) = e (e = 2.71828L n→∞ n→∞ n
x → +∞
)
= lim (9
x → +∞
x
1 x x
)
1 x + 1 3
0
1 x
3 1 = 9 ⋅ lim 1 + x x → +∞ 3

1 3x ⋅x
= 9⋅e = 9
∴ lim cos x = 1,
x→0
∴ lim(1 − cos x ) = 0,
x→0
又 Q lim 1 = 1,
x→0
sin x ∴lim = 1. x→0 x
例3
1 − cosx . 求 lim 2 x→0 x
x 2sin2 2 lim 2 x→0
解: 原式 =
x
1 sin = lim x 2 x→0 2
1 令t= , x
x→0
1t lim(1 + x) = lim(1 + ) = e. x→0 t →∞ t
1 x
1 x
lim(1 + x) = e
例.
解: 令 t = −x, 则
t →∞
lim(1+ 1)−t t
1
= lim

高等数学中的两个重要极限

高等数学中的两个重要极限
x
1 x lim (1 ) ? x x
1000 10000 100000 …
2.717 2.718
-1000 -10000
2.71827
-100000 …
X
x
-10
-100
1 2.868 2.732 (1 ) x
2.720 2.7183
2.71828
1 x lim (1 ) e x x
sin t 所以 , 原式 5lim 5 1 5 t 0 t
注：在运算熟练后可不必代换，直接计算：
sin 5 x sin 5 x lim 5lim 5 1 5 x 0 x 0 5x x
推广： 设 为某过程中的无穷小量 ,
某过程
lim
sin

1
练习1. 求下列极限:
x 0 u0
u0
2 x

2 u
1 u 2
lim[(1 u) ]
[lim(1 u) ]
u0 1 u 2
e 2
方法二 掌握熟练后可不设新变量
lim 1 x lim[(1 x ) ]2
x 0 x 0 1 x 2 2 x
1 x
[lim(1 x )
O x B
C D A
sin x lim 1. ＋ x 0 x
tan x 例 1 求 lim x0 x tan x sin x 1 解 lim lim( ) x 0 x 0 cos x x x sin x 1 lim( ) x 0 x cos x sin x 1 lim lim x 0 x 0 cos x x
当 x 时 1 0 且 | sin x | 1 x

第2章 7-利用无穷小量代换求极限

上面性质说明:在求某些无穷小乘除运算的极限时,可 使用其等价无穷小量代换,不影响极限值的结果,从而
简化计算步骤.
第二章 极限与连续
利用等价无穷小量代换求极限
等价无穷小量的性质
设1, 1, , 1, 为同一极限过程中的无穷小量, 且 ~ 1, ~ 1 , 则
lim f ( x) lim1 f ( x).
tan x ln(1 x ) lim x 0 sin x 2
例1.求极限
解:因为
sin x ~ x ( x 0) sin x 2 ~ x 2 ( x 2 0)
tan x ~ x ( x 0) ln(1 x ) ~ x ( x 0)
所以
tan x ln(1 x ) x x lim lim 2 lim1 1 2 x 0 x 0 x x 0 sin x
第二章 极限与连续
利用等价无穷小量代换求极限
等价无穷小量的性质
若在同一极限过程中, α, β, γ 均为无穷小量, 则
(1) α ~ α;
(2) 若α ~ β; 则 β ~ α; (3) 若α ~ β, β ~ γ ; 则 α ~ γ ;
(反身性)
(对称性) (传递性)
(4) 若α ~ β; 则 αγ ~ γ β .
例3 求极限
sin x ~ x ( x 0) sin x 2 ~ x 2 ( x 2 0) 解:因为 x2 tan x ~ x ( x 0) 1 cos x ~ ( x 0) 2 sin x 1 sin x 1 tan x sin x 所以 lim lim cos x 3 lim cos x x 0 x 0 x 0 sin 2 x sin3 x sin x x2 1 cos x 1 1 1 2 lim lim lim x 0 cos x sin 2 x x 0 cos x x 2 x 0 cos x 2 2

两个重要极限、无穷小的比较


例如
0 4.无穷小的比较是 型极限的另外一种说法； 0 （）和 lim lim 5.有两个重要的符号 0 0
x2 2 2 2 (1) lim 0， 当 x 0 时 , 3 x x 是比 3 x x 低 高阶的无穷小; 即 x o (3 x ) ( x 0). x 0 3 x sin x (2) lim 1， 当 x 0x 时， sin 与 x 是等价无穷小． 即 sin x~ (x x0). x0 x 1 2 1 cos x 1 2 ( 3) lim 1 ， 当 x 0 时， 1 cos x 与 x (3) ， 0 时， 1 cos x 是 x 是同阶无穷小． 的二阶无穷小． 即 1 cos x ~ x ( x 0). 2 x 0 1x 2 2 2 x 2 19
形状一致.
1 sin sin 2 x x 1 如： lim 1 u 2 x （令 ） lim x0 2x x 1 x 即 lim x sin 1 1 sin(sin x ) sin( x 1) lim 1 lim 1 x + x x 1 x 0 x 1 sin x 0 可以解决含有三角函数的 型的极限问题. 0 2) 作用： 0 , 0 都适用
又 x1 3 3,假定 xk 3, x k 1 3 x k
x n 存在. xn 是有界的; lim n
3 3 3,
xn1 3 xn , x
2 n1
3 x n , lim x
n
2 n1
lim( 3 x n ),
（1 ）
11

3 x 2x m n mn 补例.1.求 lim( ) . (a ) a 1 x 2 x 2x 1 2( x 2) 4 （1+ 3 ） 解: 原式 lim(1 ) x x x 原式 2 lim 2 2x 1 2( x 2 1 x lim(1 ) ) (1 )4 (1 x ) x x2 x 2 3 x *6 3 1 x 2 2 2 （1+ ） 2 lim[(1 ) ]e . x e . lim x x2 x x 2 2 *4 1 (1 ) x 1 x 2.求 lim x 1

教学内容极限存在准则与两个重要极限(精)


若 limk C 0, 则称 是关于 的 k 阶无穷小;
若 lim 1, 则称 是 的等价无穷小, 记作 ~

或 ~
例如 , 当x 0 时
x3 o( 6x2 ) ; sin x～ x ; tan x ～ x arcsin x～x
又如 ，
lim
即
xn a
,
故
lim
n
xnLeabharlann a.例1. 证明
证: 利用夹逼准则 . 由
n

n2
1


n2
1
2

n2
1
n


n2
n2
且
lim
n
n2 n2


lim n1
1


n2
1

lim n
n

1
n2

n2
1
2

n2
1
n

xn

a xn

a
xn1 xn

1 (1 2
a xn 2
)

1 (1 2
a) a
1
∴数列单调递减有下界，故极限存在，设
lim
n
xn

A
则由递推公式有 A 1 ( A a )
A a
2A

x1 0,

xn 0, 故
lim
n
xn

a
2. 设
证明下述数列有极限 .
证: 显然 xn xn1 , 即
(1 ) 1
单调增, 又

1.4两个重要极限


x
于是
3 x lim (1 + ) = lim(1 + t ) t = lim[(1 + t ) t ]3= [lim(1 + t ) t ]3 = e 3 x →∞ t →0 t →0 t →0 x x 3 x 3 3 3 或 lim(1 + ) = [lim(1 + ) ] = e3 x →∞ x →∞ x x
π
ESC
一. 极限的四则运算法则 二.第一个重要 极限 第一个重要
x 1 2 cos 另一方面， x = 1 − 2 sin > 1 − x ，于是有 另一方面， 2 2 1 2 sin x 1 − x < cos x < <1． 2 x
2
1 2 由准则Ⅰ 因为 lim (1 − x ) = 1 ，由准则Ⅰ可得 x →0 2 sin x =1． lim x →0 x
n →∞
ESC
二.第一个重要 极限 第一个重要
sin x =1 1. lim x→0 x
(1.4.1)
证 因为 sin( − x) = − sin x = sin x ，所以 −x −x x 由正值趋于零的情形． 只讨论 x 由正值趋于零的情形． 作单位园O 作单位园O， 设圆心角 ∠AOB = x ,延长 OB交过 A点的切线于于 D ， 面积＜ 则 ∆AOB 面积＜扇形 AOB 面积＜ 面积． 面积＜ ∆AOD 面积．即 ESC
ESC
一. 极限的四则运算法则 二.第二个重要 极限 第二个重要
lim x 2. x→∞(1+ 1)x = e
表1
(1.4.7)
1 x x → ∞ 时 (1 + ) 之值的变化情况 x
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。