十六进制 二进制

进制的认识二进制八进制十六进制的基本概念在计算机科学和信息技术领域，进制是一个重要的概念。

进制是一种数制法，用于表示数字和字符。

常见的进制有十进制、二进制、八进制和十六进制。

本文将介绍这些进制的基本概念以及它们在计算机领域中的应用。

一、基础概念1. 二进制（Binary）二进制是一种使用两个数字0和1来表示数值的进制。

在二进制中，每个数字位都是2的幂次加权的。

例如，二进制数1101表示（1×2³）+（1×2²）+（0×2¹）+（1×2⁰）= 13。

2. 八进制（Octal）八进制是一种使用八个数字0-7来表示数值的进制。

在八进制中，每个数字位都是8的幂次加权的。

例如，八进制数725表示（7×8²）+（2×8¹）+（5×8⁰）= 477。

3. 十六进制（Hexadecimal）十六进制是一种使用十六个数字0-9和字母A-F来表示数值的进制。

在十六进制中，每个数字位都是16的幂次加权的。

例如，十六进制数1D2表示（1×16²）+（13×16¹）+（2×16⁰）= 466。

二、进制转换计算机中常用的进制是二进制，而人类常用的进制是十进制。

在计算机科学中，经常需要在不同进制之间进行转换。

1. 十进制转二进制十进制转二进制的方法是通过除2取余法。

将十进制数逐次除以2，直到商为0为止，然后将所得余数从低位到高位依次排列，即可得到二进制数。

例如，将十进制数13转换为二进制数：13 ÷ 2 = 6 ... 余数1，6 ÷ 2 = 3 ... 余数0， 3 ÷ 2 = 1 ... 余数1， 1 ÷ 2 = 0 ... 余数1，所得的余数序列为1101。

2. 二进制转十进制二进制转十进制的方法是将二进制数的每一位与相应的权重相乘，然后将乘积相加。

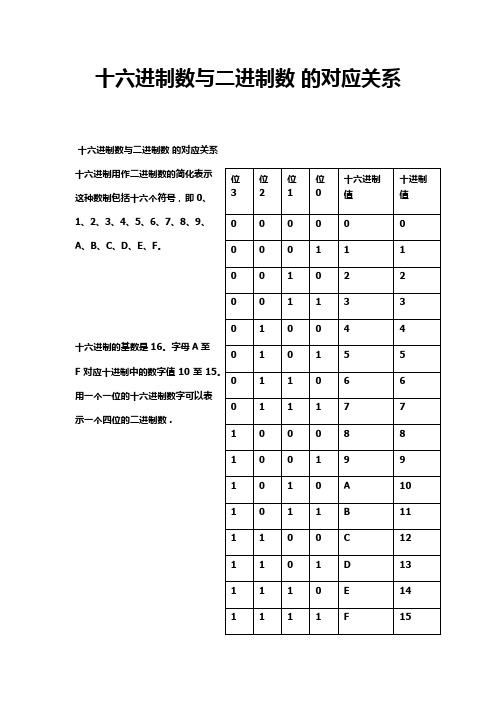
十六进制数与二进制数的对应关系十六进制数与二进制数的对应关系十六进制用作二进制数的简化表示Array这种数制包括十六个符号，即0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。

十六进制的基数是16。

字母A至F对应十进制中的数字值10至15用一个一位的十六进制数字可以表示一个四位的二进制数 .从二进制数值转换成十六进制数值时，把二进制数值的各个四位组转换成十六进制数值，然后连在一起书写即可。

例如，将二进制数值1101 0111转换成十六进制数值时，第1个四位组（1101）对应于十六进制数值D；第2个四位组（0111）对应于十六进制数值7。

把这两个结果合并在一起，就可以得到十六进制数字D7。

教学程序及设想1引入把教学内容转化为具有潜在意义的问题，让学生产生强烈的问题意识，使学生的整个学习过程成为“猜想”继而紧张的沉思2 由实例得出本课新的知识点3 讲解例题。

在讲例题时，不仅在于怎样解，更在于为什么这样解，而及时对解题方法和规律进行概括，有利于学生的思维能力。

4 能力训练。

课后练习使学生能巩固羡慕自觉运用所学知识与解题思想方法。

5 总结结论，强化认识。

知识性的内容小结，可把课堂教学传授的知识尽快化为学生的素质，数学思想方法的小结，可使学生更深刻地理解数学思想方法在解题中的地位和应用，并且逐步培养学生良好的个性品质目标。

6 变式延伸，进行重构，重视课本例题，适当对题目进行引申，使例题的作用更加突出，有利于学生对知识的串联，累积，加工，从而达到举一反三的效果。

8布置作业。

针对学生素质的差异进行分层训练，既使学生掌握基础知识，又使学有余力的学生有所提高，。

二进制和十六进制算法二进制和十六进制是计算机科学中常用的进制表示方法，可以用来表示数字、字符和图像等数据。

这两种进制在计算机领域有着广泛的应用，掌握它们的算法对理解计算机系统和编程非常重要。

下面将详细介绍二进制和十六进制的算法和应用。

一、二进制算法1.二进制表示法二进制是一种由0和1组成的进制系统，它是一种基于二的进制系统。

二进制数的每一位称为一个比特（bit），由于二进制每一位只有两个可能的取值0或1，所以在计算机中更容易处理和存储。

2.二进制到十进制的转换算法二进制转换为十进制是将二进制数按位展开，根据权值相加得到十进制数。

具体转换公式为：二进制数B的第n位×2的n次方相加，其中n为该位数的位置，从右向左依次为0、1、2、3等。

举例说明：1011(二进制)=1×2^3+0×2^2+1×2^1+1×2^0=8+0+2+1=11(十进制)3.十进制到二进制的转换算法十进制转换为二进制是将十进制数不断除以2，直到商为0为止，然后把每次的余数倒序排列即可。

举例说明：11(十进制)=1×2^3+0×2^2+1×2^1+1×2^0=1011(二进制)4.二进制运算算法二进制运算包括加法、减法、乘法和除法等基本运算。

其运算规则与十进制运算类似，只不过操作数和结果都是用二进制表示的。

举例说明：1011(二进制)+1100(二进制)___________如果两个二进制数位数不同，则需要在较短的数前面补零，然后才能进行运算。

5.二进制逻辑运算算法二进制逻辑运算主要包括与、或、非和异或等运算。

这些运算是基于逻辑的，常用于电路设计和位操作。

例如：0010(二进制)AND1011(二进制)_______________0010(二进制)1.十六进制表示法十六进制是一种由0-9和A-F（A、B、C、D、E、F分别对应10-15）组成的进制系统，它是一种基于十六的进制系统。

二进制十六进制转换方法1、二进制转换为十六进制方法：取四合一法，即从二进制的小数点为分界点，向左（向右）每四位取成一位，接着将这四位二进制按权相加，得到的数就是一位十六位二进制数，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的十六进制数。

如果向左（向右）取四位后，取到最高（最低）位时候，如果无法凑足四位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足四位。

（1）例：将二进制11101001.1011转换为十六进制得到结果：将二进制11101001.1011转换为十六进制为E9.B（2）例：将101011.101转换为十六进制得到结果：将二进制101011.101转换为十六进制为2B.A2、将十六进制转换为二进制方法：取一分四法，即将一位十六进制数分解成四位二进制数，用四位二进制按权相加去凑这位十六进制数，小数点位置照旧。

（1）例：将十六进制6E.2转换为二进制数得到结果：将十六进制6E.2转换为二进制为01101110.0010即110110.001 附上十进制、二进制、十六进制转化的对照表。

扩展资料：二进制与八进制之间的转换：首先，我们需要了解一个数学关系，即2^3=8，2^4=16，而八进制和十六进制是用这个关系衍生而来的，即用三位二进制表示一位八进制，用四位二进制表示一位十六进制数。

接着，记住4个数字8、4、2、1（2^3=8、2^2=4、2^1=2、2^0=1）。

现在我们来练习二进制与八进制之间的转换。

1、二进制转换为八进制方法：取三合一法，即从二进制的小数点为分界点，向左（向右）每三位取成一位，接着将这三位二进制按权相加，得到的数就是一位八位二进制数，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数。

如果向左（向右）取三位后，取到最高（最低）位时候，如果无法凑足三位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足三位。

1.十六进制与二进制数的相互转换。

（我们先从熟悉的十进制说起，十进制即逢十进一，由0－9组成，它的每一位都是十的幂，比如123，个位是10的0次方，十位是10的1 次方，百位是10的2次方，因此123其实就相当于1×10(2)+2×10(1)+3×10(0)=1×100＋2*10＋3＝123（注：括号内的数表示次方），对于二进制和十六进制，转成十进制也是同样的道理，二进制的每一位是2的幂，十六进制的每一位是16的幂，把十进制转换中的10换成2或16即可。

通常将二进制，十六进制转换成十进制的方法叫安全展开法。

比如：（1）二进制——>十进制：二进制数1101＝1×2（3）＋1×2（2）＋0×2（1）＋1×2（0）＝8＋4＋0＋1＝13（2）十六进制——>十进制：十六进制数12＝1×16（1）＋2×16（0）＝16＋2＝18反过来：十进制转二进制和十六进制，分别用除2取余法和除16取余法。

比如：十进制数13 除以2，商为6，余数为1，将得到的商6继续除以2，商为3，余数为0，将得到的商3继续除以2，商为1，余数为1，将得到的商1继续除以2，商为0，余数为0。

当算到商为0时，结束。

结果从下往上看，应该为1101。

十六进制转十进制一样的，只是是除以16。

）2.空穴是如何产生的？（在电子挣脱价键的束缚成为自由电子后，其价键中所留下的空位。

一个空穴带一个单位的正电子电量）3.半导体的正确定义。

（材料的电阻率界于金属与绝缘材料之间的材料。

这种材料在某个温度范围内随温度升高而增加电荷载流子的浓度，电阻率下降）4.二极管最主要的特性是什么？（正向性）5.二极管的电流方程式。

6.正确的桥式整流电路图中二极管的方向。

7.温升与二极管的正确降压的关系。

8.晶体二极管的单项导电性可以实现滤波吗？（不能）（能实现检流、滤波）9.已知放大电路输入及输出功率，如何求其放大倍数。

二进制和十六进制怎么转换一、二进制转十六进制各种进制之间的转换方法：一、不同的进位制数转化为十进制数：按权展开相加十进制是权是10；二进制是权是2；十六进制是权是16；八进制是权是8；例：110011(二进制数)=1*2^5+1*2^4+0*2^3+0*2^2+1*2^1+1*2^0=32+16+2+1=51 1507(八进制数)=1*8^3 + 5*8^2 + 0*8^1 + 7*8^0 = 8392AF5（十六进制数）=2*16^3 + A*16^2+ F*16^1 + 5*16^0 = 10997二、十进制数化为不同进制数整数部分：除权取余；小数部分：乘权取整例：十进制数13转化成二进制数13/2=6 余16/2=3 余03/2=1 余11/2=0 余1结果：1101三、二进制换算八进制将二进制数从右到左，三位一组，不够补0例：二进制数10110111011换八进制数：010 110 111 011结果为：2673四、二进制转换十六进制二进制数转换为十六进制数的方法也类似，从右到左，四位一组，不够补0如上题：0101 1011 1011结果为：5BB二、简介进制在基数b的位置记数系统(其中b是一个正自然数，叫做基数)，b个基本符号(或者叫数字)对应于包括0的最小b个自然数。

要产生其他的数，符号在数中的位置要被用到。

最后一位的符号用它本身的值，向左一位其值乘以b。

一般来讲，若b是基底，我们在b进制系统中的数表示为的形式，并按次序写下数字a0a1a2a3...ak。

这些数字是0到b-1的自然数 [3] 。

一般来讲，b进制系统中的数有如下形式：数和是相应数字的比重 [3] 。

二进制计数17世纪至18世纪的德国数学家莱布尼茨，是世界上第一个提出二进制记数法的人。

用二进制记数，只用0和1两个符号，无需其他符号 [4] 。

二进制数据也是采用位置计数法，其位权是以2为底的幂。

例如二进制数据110.11，逢2进1，其权的大小顺序为2²、2¹、2º、、。

十六进制数与二进制数的相互转换篇一：哎呀，同学们，你们知道吗？在数学的奇妙世界里，有个超级有趣又有点让人头疼的东西，那就是十六进制数和二进制数的相互转换！这就好像是一个神秘的密码游戏，等着我们去解开呢！比如说，二进制数，那一堆的0 和1 ，看起来是不是像一群调皮的小蚂蚁在乱跑？而十六进制数呢，有0 到9 ，还有A 、B 、C 、D 、E 、F ，这简直就是一群穿着不同衣服的小伙伴！那怎么把二进制数变成十六进制数呢？咱们就拿一个例子来说吧，比如二进制数10101010 ，这可咋办呀？我们把它从右往左，每4 位分成一组，就像把一堆糖果分成一小堆一小堆的。

那这个数就分成了1010 和1010 。

1010 对应的十六进制数是A ，那两个A 拼起来，不就是AA 嘛！这是不是很神奇？反过来，十六进制数变成二进制数也不难哟！比如说十六进制数5F ，5 对应的二进制数是0101 ，F 对应的是1111 ，合起来不就是01011111 嘛！老师上课讲这些的时候，我一开始真的是晕头转向，心里想：“这都是啥呀，怎么这么难！” 可是后来，我多做了几道题，多琢磨了琢磨，突然就发现，其实也没那么可怕！就好像我们刚开始学骑自行车，觉得摇摇晃晃要摔倒，可一旦掌握了技巧，就能骑得飞快啦！同学们，你们刚开始学的时候是不是也觉得很难呀？不过别怕，只要我们多练习，多思考，一定能把这个神秘的密码游戏玩得特别溜！我的观点就是：虽然十六进制数与二进制数的相互转换一开始让人觉得很复杂，但是只要我们用心去学，多练习，就一定能掌握这个神奇的技能，在数学的世界里畅游！篇二：哎呀！同学们，你们知道吗？在数学的奇妙世界里，有个超级有趣的东西叫十六进制数和二进制数的相互转换！这可真是个神奇的魔法呢！比如说二进制数，就像是一群排排站的小士兵，只有0 和1 两种状态。

而十六进制数呢，就像是一个更有组织的大部队，有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F 这16 个小伙伴。

二进制和十六进制算法
二进制和十六进制算法是计算机科学中非常重要的概念。

它们是计算机中最基本的数值表示法，也是编程中最常用的数值表示法之一。

二进制是一种计算机使用的数制，它只包含两个数字：0和1。

在计算机中，所有的数据都以二进制的形式存储和处理。

二进制数的每一位只能是0或1。

每个二进制数字位表示一个权值，这个权值是2的幂，从右到左依次增加。

例如，二进制数1001表示的值是
1*23+0*22+0*21+1*20，即9。

十六进制是另一种常用的数值表示法，它包含16个数字：0-9
和A-F。

在计算机科学中，十六进制数常用于表示颜色、内存地址和编程中的常量等。

十六进制数的每一位表示一个权值，这个权值是
16的幂，从右到左依次增加。

例如，十六进制数1A2B表示的值是
1*163+10*162+2*161+11*160，即6683。

二进制和十六进制之间可以很方便地相互转换。

将一个二进制数转换为十六进制数，可以先将二进制数按照4位一组进行分组，然后将每组二进制数转换为十六进制数即可。

例如，二进制数10101110
可以分为两组：1010和1110，转换为十六进制数就是AE。

将一个十六进制数转换为二进制数，可以将每个十六进制数字转换为4位二进制数字，然后将所有的二进制数字拼接在一起即可。

例如，十六进制数3F转换为二进制数就是0011 1111。

掌握二进制和十六进制算法是计算机科学中的基础知识，它们在计算机硬件设计、计算机网络、数字电路等领域都有广泛的应用。