人教版九年级数学学案：22.1.3 二次函数y=a(x-h)2+k的图象与性质(3)

第3课时二次函数y=a（x-h）2+k的图象和性质教材分析之前学生已经学过一次函数、反比例函数的图像和性质，以及会建立二次函数的模型和理解二次函数的图像相关概念和性质基础之上进行的。

是前面知识的应用和拓展，又为今后学习二次函数的应用及一元二次方程与二次函数之间的关系作预备。

充分体现了数形结合的思想，因此本课无论在知识上还是培养学生动手能力上都起了很大的作用。

学生已经会了上一节的二次函数图像及性质。

课标要求会用描点法画出二次函数的图像，通过图像了解二次函数的性质。

学情分析可能有些学生对二次函数还不理解，甚至还不会描点法画出函数图像，看图能力差，不能类比一次函数的一些观察图像的方法来学习二次函数的图像。

不能从图中获取相关的信息。

由于放假的原因，学生对上下平移和左右平移的知识有很多淡忘，所以完成本节知识在理解方面会有难点。

教学目标来源:Z#xx#k.Com 知识目标：让学生经历二次函数y＝a(x－h)2+k性质探究的过程，理解函数y＝a(x－h)2+k的性质，理解二次函数y＝a(x－h)2+k的图象与二次函数y＝ax2的图象的关系能力目标：通过画图象独立去探索交流图象的性质培养分析解决问题的能力。

能说出二次函数y＝a(x－h)2+k的图象与二次函数y＝ax2的图象的关系。

情意目标：在学习中体会知识之间的联系，体会知识的发生发展过程和知识体系。

教学重点：会用描点法画出二次函数y＝a(x－h)2+k的图象，理解二次函数y＝a(x－h)2+k的性质。

能说出顶点坐标。

教学难点：理解二次函数y＝a(x－h)2+k的性质，理解二次函数y＝a(x－h)2+k的图象与二次函数y＝ax2关系。

教学导学案手段教学方法问答法、练习法、讨论法教学过程1、创设情境：:（组织方法）复习两个上下平移及左右平移的二次数学图像，对照图像说出开口方向、对称轴、顶点坐标、最值、性质。

详见导学案。

解决哪些教学目标：在学习中体会知识之间的联系，体会知识的发生发展过程和知识体系。

22.1.3二次函数y=a(x-h)2+k的图象和性质（1）预习案一、预习目标及范围：1.会画二次函数y=ax2+k的图象.2.掌握二次函数y=ax2+k的性质并会应用.3.比较函数y=ax2与y=ax2+k的联系.二、预习要点1.上下平移规律：平方项，常数项上下 .2.把抛物线y=2x2向平移1个单位长度，就得到抛物线；把抛物线y=2x2向平移1个单位长度，就得到抛物线y=2x2-1.三、预习检测1.说出下列二次函数的开口方向、对称轴及顶点坐标(1) y=2(x+3)2(2) y=-3(x-1)2(3) y=5(x+2)2(4) y=-(x-6)2(5) y=7(x-8)22.抛物线y=-3(x+2)2开口向，对称轴为，顶点坐标为________.3.抛物线y=3x2+0.5可以看成由抛物线向平移个单位得到的.4.写出一个开口向上，对称轴为x=-2，并且与y轴交于点（0，8）的抛物线解析式____________.探究案一、合作探究活动内容1：活动1：小组合作情景问题：二次函数y=ax2的图象是什么形状呢？什么确定y=ax2的性质？通常怎样画一个函数的图象？在同一直角坐标系中，画出二函数y=2x2+1与y=2x2-1的图象．解：先列表：(1)抛物线y=2x2+1,y=2x2-1的开口方向、对称轴和顶点各是什么？(2) 抛物线y=2x2+1,y=2x2-1与抛物线y=2x2有什么关系？可以发现，把抛物线y=2x2向平移1个单位长度，就得到抛物线；把抛物线y=2x2向平移1个单位长度，就得到抛物线y=2x2-1.归纳：二次函数y=ax2+k的图象可以由y=ax2的图象平移得到：当k > 0 时,向上平移k个单位长度得到.当k < 0 时,向下平移-k个单位长度得到.活动2：探究归纳上下平移规律：平方项不变，常数项上加下减.活动内容2：典例精析例题:：把抛物线y = 2x2向上平移5个单位，会得到哪条抛物线？向下平移2个单位呢？归纳：1.画抛物线y=ax2+k的图象有几步？第一种方法：平移法，两步即第一步画y=ax2的图象，再向上（或向下）平移︱k︱单位.第二种方法：描点法，三步即列表、描点和连线.2.抛物线y=ax2+k中的a决定什么？怎样决定的？k决定什么？它的对称轴是什么？顶点坐标怎样表示？a决定开口方向和大小；k决定顶点的纵坐标.二、随堂检测1、抛物线y=2x2向下平移4个单位，就得到抛物线。

22.1.3二次函数y=a(x －h)2＋k 的图象和性质学案学习目标：1.会画二次函数y ＝a （x －h ）2的图象并掌握它的开口方向、对称轴、顶点坐 标及增减性等；2.掌握二次函数y ＝a （x －h ）2的图象的平移规律。

3．会应用二次函数y ＝a (x －h)2＋k 的性质解题．.一、复习引入1.抛物线23(2)y x =-+的开口 ，对称轴为 ，顶点坐标为 ，它是由抛物线2-3y x =向 平移 个单位长度所得。

二、自主学习,合作探究画出函数y ＝－12 (x ＋1)2－1的图象，指出它的开口方向、对称轴及顶点、最值、增减2.221-x y =怎样得到的？ 归纳总结：1.二次函数k h x a y +-=2)(的图象和性质： （1）（2）（3）2.k h x a y +-=2)(的图象和2ax y =图象的关系：三、理一理知识点 1.23.各种形式的二次函数的关系2()y a x h k =-+ax =四、练习3．一抛物线和抛物线y ＝－2x 2的形状、开口方向完全相同，顶点坐标是(－1，3)，则该抛物线的解析式为( ) A ．y ＝－2(x －1)2＋3 B ．y ＝－2(x ＋1)2＋3 C ．y ＝－(2x ＋1)2＋3 D ．y ＝－(2x －1)2＋3 4．二次函数y ＝(x －1)2＋2的最小值为__________________．5．将抛物线y ＝5(x －1)2＋3先向左平移2个单位，再向下平移4个单位后，得到抛物线的解析式为_______________________．6.抛物线1)3(212-+-=x y 有最______点，其坐标是______．当x ＝______时，y 的最______值是______；当x ______时，y 随x 增大而增大．7．若抛物线y ＝a (x －1)2＋k 上有一点A （3，5），则点A 关于对称轴对称点A’的坐标为。

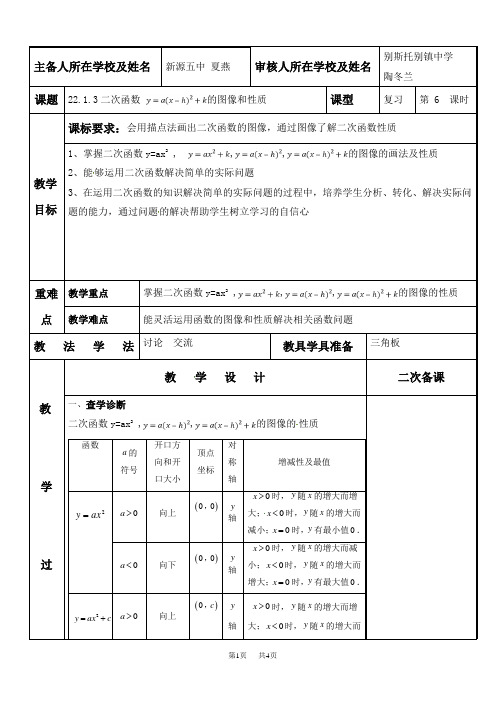
主备人所在学校及姓名新源五中夏燕审核人所在学校及姓名别斯托别镇中学陶冬兰课题22.1.3二次函数的图像和性质课型复习第 6 课时教学目标课标要求：会用描点法画出二次函数的图像，通过图像了解二次函数性质1、掌握二次函数y=ax2 , ,,的图像的画法及性质2、能够运用二次函数解决简单的实际问题3、在运用二次函数的知识解决简单的实际问题的过程中，培养学生分析、转化、解决实际问题的能力，通过问题的解决帮助学生树立学习的自信心重难点教学重点掌握二次函数y=ax2 ,,,的图像的性质教学难点能灵活运用函数的图像和性质解决相关函数问题教法学法讨论交流教具学具准备三角板教学过教学设计二次备课一、查学诊断二次函数y=ax2 ,,的图像的性质函数a的符号开口方向和开口大小顶点坐标对称轴增减性及最值2axy=0a>向上()00，y轴x>时，y随x的增大而增大；0x<时，y随x的增大而减小；0x=时，y有最小值0．a<向下()00，y轴x>时，y随x的增大而减小；0x<时，y随x的增大而增大；0x=时，y有最大值0．2y ax c=+0a>向上()0c，y轴x>时，y随x的增大而增大；0x<时，y随x的增大而向下()2y a x h k=-+二、导学施教知识点1：二次函数y=ax2, y=ax2+c, y=a(x-h)2, y=a(x-h)2+k的性质：1、己知抛物线y=a(x-2)2的的形状和开口方向与抛物线y=-2x2的形状和开口方向相同，则抛物线y=a(x-2)2的开口方向______，对称轴是_____，顶点是_____2、已知抛物线y=-2(x-2)2上有两点（x1,y1）和（x2,y2）,且x1>x2>2,则y1 _ y23、抛物线y=3(x-2)2+1与y=3(x+2)2+1的关系是_____4、若二次函数y=ax2+c(a≠0)的图像上有两点（x1,5）(x2,5),且x1≠x2，则当x取x1+x2时，函数值为_____5、抛物线y=-6x2+5可以看作是由抛物线y=-6x2_____平移变换得到.6、把抛物线向左平移2个单位长度得到抛物线y=2x2,则原抛物线的解析式是_____7、抛物线和y=2x2的图像形状相同，对称轴平行于y轴，并且顶点坐标是（-1，0），则此抛物线的解析式为_____知识点2：二次函数y=ax2, y=ax2+c, y=a(x-h)2, y=a(x-h)2+k的解析式的确定8、已知一条抛物线的开口方向和形状大小与抛物线y=3x2都相同,顶点在抛物线y=(x+2) 2的顶点上。

第二十二章二次函数第一节《二次函数y=a(x-h)2+k的图像和性质（3）》教学设计——人教版九年级上授课科目：数学授课课题：二次函数的图像和性质（3）授课时间：授课人：教学过程设计一． 课前热身1.请说出二次函数y=-2x 2的开口方向、顶点坐标、2.把y=-2x 2的图像223y=-2x +32y=-2(x+2)⎧⎪⎨⎪⎩向上平移个单位 向左平移个单位3.请猜测一下，二次函数y=-2(x+2)2+3的图像是否可以由y=-2x 2平移得到？你认为该如何平移呢？解析：用课件直观的演示两种平移的过程及结果，通过图象观察y=-2(x+2)2+3的性质，并板书。

二．例题讲解备注：让学生说出函数是由哪个函数如何平移得到，教师画草图演示。

三．研学教材y=a(x-h)2+k22(2)4y x =−−+总结：y=a(x-h)2+k 是由y=ax 2如何平移得到的？ 顶点式y=a(x-h)2+k 的三种特殊形式()()()22220,000,,000h k y ax h k k h y y a x h y a x h k k a ax =≠→===≠→=−=−+≠⎧⎪+→=⎨=⎪⎪⎪⎩四．练习1.把抛物线y=-3x 2先向上平移2个单位，再向右平移1个单位，那么所得抛物线的解析式为23(1)2y x =−−+2.抛物线y=-3x 2+2的图像向右平移2个单位，再向上平移1个单位，得到抛物线的解析式为()2323y x =−−+3.抛物线y=-3(x-1)2+2的图像如何得到y=-3x 24.已知一个二次函数的顶点为A(-1,3),且它是由二次函数y=5x 2平移得到，请直接写出该二次函数的解析式 五．应用举例例：要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高，高度为3米，水柱落地处距离池中心3米，水管应多长？解析：将实际问题转化成数学问题，让学生先读题，根据思路做出动画演示，建模。

22.1.3 二次函数y=a（x-h）2+k的图象和性质第3课时二次函数y=a（x-h）2+k的图象和性质教学目标：1．使学生理解函数y=a(x－h)2＋k的图象与函数y=ax2的图象之间的关系。

2．会确定函数y=a(x－h)2＋k的图象的开口方向、对称轴和顶点坐标。

3．让学生经历函数y=a(x－h)2＋k性质的探索过程，理解函数y=a(x－h)2＋k的性质。

重点难点：重点：确定函数y=a(x－h)2＋k的图象的开口方向、对称轴和顶点坐标，理解函数y=a(x－h)2＋k的图象与函数y=ax2的图象之间的关系，理解函数y=a(x－h)2＋k的性质是教学的重点。

难点：正确理解函数y=a(x－h)2＋k的图象与函数y=ax2的图象之间的关系以及函数y=a(x －h)2＋k的性质是教学的难点。

教学过程：一、提出问题1．函数y=2x2＋1的图象与函数y=2x2的图象有什么关系?(函数y=2x2＋1的图象可以看成是将函数y=2x2的图象向上平移一个单位得到的)2．函数y=2(x－1)2的图象与函数y=2x2的．图象有什么关系?(函数y=2(x－1)2的图象可以看成是将函数y=2x2的图象向右平移1个单位得到的，见P10图26.2.3)3．函数y=2(x－1)2＋1图象与函数y=2(x－1)2图象有什么关系?函数y=2(x－1)2＋1有哪些性质?二、试一试你能填写下表吗?y=2x2向右平移的图象1个单位y=2(x－1)2向上平移1个单位y=2(x－1)2＋1的图象开口方向向上对称轴y轴顶点(0，0)问题2：从上表中，你能分别找到函数y=2(x－1)2＋1与函数y=2(x－1)2、y=2x2图象的关系吗? 问题3：你能发现函数y=2(x－1)2＋1有哪些性质?对于问题2和问题3，教师可组织学生分组讨论，互相交流，让各组代表发言，达成共识；函数y＝2(x－1)2＋1的图象可以看成是将函数y=2(x－1)2的图象向上平称1个单位得到的，也可以看成是将函数y=2x2的图象向右平移1个单位再向上平移1个单位得到的。