2017春季-线性代数与概率论-平时作业
- 格式:doc
- 大小:1.28 MB
- 文档页数:10

《线性代数》在线作业一一、单选题1. 题面见图片A. AB. BC. CD. D正确答案:C2. 题面见图片A. AB. BC. CD. D正确答案:A3. 题面见图片A. AB. BC. CD. D正确答案:C4. 题面见图片A. AB. BC. CD. D正确答案:A5. 题面见图片A. AB. BC. CD. D正确答案:A6. 题面见图片A. AB. BC. CD. D正确答案:A7. 题面见图片A. AB. BC. CD. D正确答案:C8. 题面见图片A. AB. BC. CD. D正确答案:A9. 题面见图片A. AB. BC. CD. D正确答案:C10. 题面见图片A. AB. BC. CD. D正确答案:B11. 题面见图片A. AB. BC. CD. D正确答案:B12. 题面见图片A. AC. CD. D正确答案:B13. 题面见图片A. AB. BC. CD. D正确答案:D14. 题面见图片A. AB. BC. CD. D正确答案:D15. 题面见图片A. AB. BC. CD. D正确答案:D16. 题面见图片A. AB. BC. CD. D正确答案:D17. 题面见图片A. AB. BC. CD. D正确答案:A18. 题面见图片A. AB. BC. C正确答案:C19. 题面见图片A. AB. BC. CD. D正确答案:D20. 题面见图片A. AB. BC. CD. D正确答案:C。
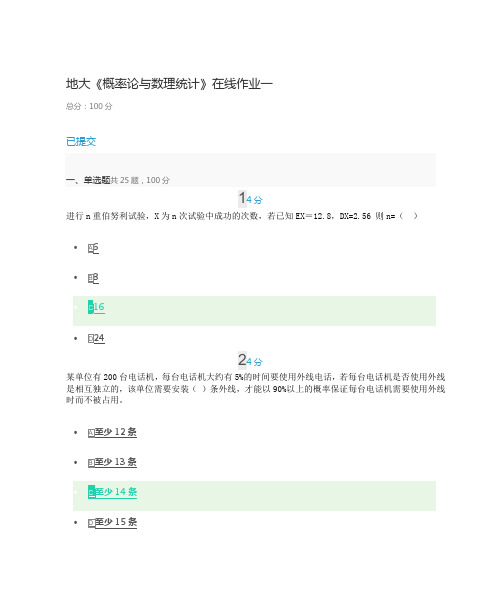
地大《概率论与数理统计》在线作业一总分:100分已提交一、单选题共25题,100分14分进行n重伯努利试验,X为n次试验中成功的次数,若已知EX=12.8,DX=2.56 则n=()是相互独立的,该单位需要安装()条外线,才能以90%以上的概率保证每台电话机需要使用外线时而不被占用。
34分设随机变量X服从正态分布,其数学期望为10,均方差为5,则以数学期望为对称中心的区间(),使得变量X在该区间内概率为0.9973。
44分设A,B为两个互斥事件,且P(A)>0,P(B)>0,则下列结论正确的是()。
有10辆发生事故的概率是()64分现考察某个学校一年级学生的数学成绩,现随机抽取一个班,男生21人,女生25人。
则样本容量为( )74分已知事件A与B相互独立,且P(B)>0,则P(A|B)=()94分一个螺丝钉重量是一个随机变量,期望值是1两,标准差是0.1两。
求一盒(100个)同型号螺丝钉的重量超过10.2斤的概率()。
104分有一袋麦种,其中一等的占80%,二等的占18%,三等的占2%,已知一、二、三等麦种的发芽率分别为0.8,0.2,0.1,现从袋中任取一粒麦种,则它发芽的概率为()。
114分对敌人的防御地段进行100次轰炸,每次轰炸命中目标的炸弹数目是一个随机变量,其期望值为2,方差为1.69。
求在100次轰炸中有180颗到220颗炸弹命中目标的概率()。
现的结果为( )144分从a,b,c,d,...,h等8个字母中任意选出三个不同的字母,则三个字母中不含a与b的概率为()。
,甲、乙、丙产品的合格率分别为90%、85%、和95%,则顾客买到这种产品为合格品的概率是()194分设随机变量X在区间(a,b)的分布密度f(x)=c,在其他区间为f(x)=0,欲使变量X服从均匀分布则c的值为( )装()台分机才能以90%的把握使外线畅通。
214分设袋中有k号的球k只(k=1,2,…,n),从中摸出一球,则所得号码的数学期望为()234分设试验E为的投掷一枚骰子,观察出现的点数。


《线性代数与概率统计》作业题一、计算题1 231.计算行列式 D 3 12.2 31解:x 1332.计算行列式3x53.66x41 2 1 4 01 2 1 3.计算行列式 D 01 .1 3 01 3 14.设 A1 2 , B 1 0,求AB 与BA . 1 3 1 25.设f (x)2x2x 1,A1 1,求矩阵A的多项式 f ( A). 012631136.设矩阵A 111, B112,求 AB.0110111 017.设A 1 1 1 ,求逆矩阵 A1.2 1 12 2 4 1 141 1 3 0 21 8.求的秩.A 1 21 1 133 122114 22 6 082x1x2x31 9.解线性方程组4x12x25x3 4 .2x1x22x352x1x23x31 10.解线性方程组4x12x25x3 4 .2x1 2 x3611.甲、乙二人依次从装有7 个白球, 3 个红球的袋中随机地摸1个球,求甲、乙摸到不同颜色球的概率.12.一箱中有 50 件产品,其中有 5 件次品,从箱中任取 10件产品,求恰有两件次品的概率 .13.设有甲、乙两批种子,发芽率分别为0.9 和 0.8,在两批种子中各随机取一粒,求:(1)两粒都发芽的概率;(2)至少有一粒发芽的概率;(3)恰有一粒发芽的概率 .14.某工厂生产一批商品,其中一等品点1,每件一等品获利 3 元;二等品占1,23每件二等品获利 1 元;次品占1 ,每件次品亏损2 元。
求任取 1 件商品获利X 的6数学期望 E(X) 与方差 D(X)。
二、应用题15.甲、乙两工人在一天的生产中,出现次品的数量分别为随机变量X1, X2,且分布列分别为:X10123X 20123P k0.40.30.20.1P k0.30.50.20若两人日产量相等,试问哪个工人的技术好?。


线 性 代 数 试 卷(A)一、选择题(每题3分,共15分)1._____________,2)(2101210211的值为则的秩若矩阵a A r a a A =⎪⎪⎪⎭⎫ ⎝⎛---=11-(D)1-(C)1-0(B)0(A)或者或 2._____________,1||*=-=A A A 则,且为正交矩阵设 A -(D)•••A •(C)A -(B)••A (A)T T3.设βα,是n 维列向量,0≠βαT ,n 阶方阵T E A αβ+=,3≥n ,则在A 的n 个特征值中,必然______________(A) 有n 个特征值等于1 (B) 有1-n 个特征值等于1(C) 有1个特征值等于1 (D) 没有1个特征值等于14.______________,)()(,则阶方阵,且秩相等,既为设B r A r n B A = B)(A)(B),r(A (D)r(A)2B),r(A (C)r(A)2B)(A (B)0B)r(A (A)r r r +≤==+=-5._____________,)(b Ax n A r A n m ==⨯则非齐次线性方程组的秩设矩阵 )(A 一定无解 )(B 可能有解)(C 一定有唯一解 )(D 一定有无穷多解二、填空题(每题3分,共15分)1.设*A 是n 阶方阵A 的伴随矩阵,行列式2||=A ,则|2|*A =_____________2. D 中第二行元素的代数余子式的和∑=412j j A =__________ ,其中 D = 1111111*********---3. 已知实二次型321123122132,12224),(x x x ax x x x x x x f ++++=正定,则实常数a 的取值范围为________________4. 2n 阶行列式 ________________=A B B A ,其中n 阶矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=a a a A 0000000 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=000000 b b b B5. 设A=,⎪⎪⎪⎭⎫ ⎝⎛101020101而n ≥2为正整数,则______21=--n n A A 三、计算题(每题9分,共54分)1. 计算n 阶行列式•m x x x x x x m x x x x x m x •D n n nn ---=3213213212. 求矩阵X 使⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-==-+--120210006,100010002,011B A BX A BA AX ,其中3. 设非齐次线性方程组⎪⎩⎪⎨⎧=-++=++-=+++3432211244332114433213222d x x x c x c d x b x b x x d x a x a x x 有三个解向量 1η=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-1211, 2η=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-1112, 3η=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2423求此方程组系数矩阵的秩,并求其通解(其中t k j i d c b a ,,,为已知常数)4. 已知实二次型 ),,(321x x x f =)0(233232232221>+++λλx x x x x 经过正交变换QY X =,化为标准形23222152y y y ++,求实参数λ及正交矩阵Q5. 设线性方程组为⎪⎪⎩⎪⎪⎨⎧=-+-=+++=+++=+++b x x x x x x a x x x x x x x x x x 432143214321432131723153203,问a ,b 各取何值时,线性 方程组无解,有唯一解,有无穷多解?在有无穷多解时求出其通解6. 在四元实向量构成的线性空间4R 中,求a 使4321,,,ββββ为4R 的基,并求由基43214321,,,,,,ββββαααα到的过渡矩阵P ,其中⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00011α ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00112α ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=01113α ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=11114α ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=1111a β ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=12112a β ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=00113β ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00014β四、证明题(每题8分,共16分)1. 设 321,,ααα 是欧氏空间V 的标准正交基,证明:112321233123111(22)(22)(22)333βαααβαααβααα=+-=-+=--也是V 的标准正交基2. 设=f AX X T 是n 元实二次型,有n 维实列向量21,X X ,使,证明:存在维列实向量,使=0。
‘10 0、1. 已知正交矩阵 p 使得P T AP= 0-10 ,则 P / A 2006(A _1+A )P =J ) 0 -2,,人是A 的几个特征根,ffl det ( A T ) =-1 …0 02. 对矩阵A 沁“施行一次列变换相当丁-( )。
A 左乘一个m 阶初等矩阵B 右乘一个m 阶初等知阵C 左乘一个n 阶初等矩阵D 右乘一个n 阶初等矩阵 3. 若 A 为 mXn 矩阵,r (A ) = /*</?, M = {X \ AX = 0, XE R11}。
则()oAM 是加维向最空间B, M 是〃维向量空间c, M 是mr 维向量空间D, M 是nr 维向量空间 4. 若n 阶方阵A 满足,A 2 =E,则以下命题哪一个成立()。
A, r (A ) = n B,广(4) = % C,广(4)'%, D,厂(A )<% 5. 若A 是n 阶正交矩阵,则以下命题那一个不成立( )。
A 矩阵-A r 为正交炬阵B 炬阵-为正交雉阵C 知(阵A 的行列式是实数D 知(阵A 的特征根是实数4、求向量纽q = (1,2丄2)严(1,0丄2),也=(1丄0,0),«4= (1丄2,4)的的秩。
5、向量69在基a = (1,1,1), 0 = (0」」),厂=(1,一1,1)卜的坐标(4, 2, -2),求。
在a + 0,0 + ”y + a2.设A 为n 阶方阵,人,易3. 4.设八是mxn 矩阵,则方程组AX =B 对于任意的m若向量组 5.DMa = (0, 4, 2), B1 5 1 31 X 52 27X 2 5 4 39 X 35 8 3维列向屋B 都冇无数多个解的充分必要条件是: 3)的秩不为3,则恬,则D (x ) = 0的全部根为:1. n 阶行列式-1…-1 0 的值为(川(斤_1))A-l B, (一1)" C, (一1)丁n (”+i ) D ,(-1尸1.若A 为3阶正交矩阵,求det (E-A 2)2.计算行列式a b b bb b b abb b a b b b a<0 2 0、3.设 A =2 0 0 ,.0 \0 1丿AB = A-B 9 求矩阵 A-Bo 卜•的坐标。
18春福师《线性代数与概率统计》在线作业电路由元件A与两个并联的元件B、C串联而成,若A、B、C损坏与否是相互独立的,且它们损坏的概率依次为0.3,0.2,0.1,则电路断路的概率是A0.325B0.369C0.496D0.314设试验E为的投掷一枚骰子,观察出现的点数。
试判别下列事件是随机事件的为( )A点数大于7B点数小于1C点数为9D点数为4概率的统计定义不满足下列性质()C有限可加性D可列可加性点估计( )给出参数值的误差大小和范围D以上都不对在长度为a的线段内任取两点将其分成三段,则它们可以构成一个三角形的概率是设试验E为某人打靶,连续射击二次,观察射击的过程及结果。
我们用“+”表示射中,“-”表示没射中。
试判别E的样本空间为(A{+,-}B{-,+}C{++,+-,-+,--}D{--,+-,++}假设有100件产品,其中有60件一等品,30件二等品,10件三等品,如果每次随机抽取一件,连续两次,(有放回抽样)则两次取到的产品等级相同的概率是()A29/330B0.09C0.46D5/11在某医院,统计表明第一季度出生1000个婴儿中,有3个婴儿死亡,则我们认为这个医院的婴儿死亡率为()一个袋内装有10个球,其中有4个白球,6个红球,采取不放回抽样,每次取1件,则第二次取到的是白球的概率是()在古典概型中,事件A是由全部n个基本事件中的某m个基本事件复合成的,则P(A)=()C1-m/nD1-n/m某学校二年级的数学成绩统计如下:90分以上12人,80分以上28人,70分以上35人,60分以上23人,60分以下2人。
则该班此次考试的不及格率为()C0.75D0.25以A表示事件“甲种产品畅销,乙种产品滞销”,则A的对立事件为A甲滞销,乙畅销B甲乙均畅销D甲滞销或乙畅销由概率的公理化定义可推知两个对立事件的概率之和为()安培计是以相隔0.1为刻度的,读数时选取最靠近的那个刻度,允许误差为0.02A,则超出允许误差的概率是()设X,Y为两个随机变量,则下列等式中正确的是AE(X+Y)=E(X)+E(Y)BD(X+Y)=D(X)+D(Y)CE(XY)=E(X)E(Y)DD(XY)=D(X)D(Y)设试验E为袋中有编号为1,2,3,4,5的五个球,从中任取一个,观察编号的大小问这个试验E的样本空间是( )A{1,2,3,4,5}B{1,3,5C{2,4,6}设随机试验E为投掷一枚硬币,随机变量X代表出现正面的次数,则X服从()A单点分布B二点分布C二项分布D泊淞分布设在某种工艺下,每25平方米的棉网上有一粒棉结,今从某台梳棉机上随机取得250平方厘米棉网,则其中没有棉结的概率是()A0.000045B0.01114C0.03147D0.36514设P(A)=a,P(B)=b,P(A+B)=C,则B的补集与A相交得到的事件的概率是Ca(1-b)Da(1-c)市场上某种商品由三个厂家同时供货,其供应量,第一个厂家为第二个厂家的2倍,第二、三两个厂家相等,而且各厂产品的次品率依次为2%、2%、4%,则市场上供应的该商品的次品率为()A0.784B0.862C0.975D0.964已知事件A与B相互独立,且P(B)>0,则P(A|B)=()AP(A)BP(B)CP(A)/P(B)DP(B)/P(A)一台仪表是以0.2为刻度的,读数时选取最靠近的那个刻度,则实际测量值与读数之偏差小于0.04概率为()正态分布的概率密度曲线下面所围成的面积为()用机器包装味精,每袋味精净重为随机变量,期望值为100克,标准差为10克,一箱内装200袋味精,则一箱味精净重大于20500克的概率为()A0.0457B0.009C0.0002设一个系统上100个互相独立起作用的部件所组成,每个部件损坏的概率为0.1,必须有85个以上的部件工作才能使整个系统工作,则整个系统工作的概率为()A0.95211B0.87765C0.68447D0.36651设A,B为任意两事件,且A包含于B(不等于B),P(B) 0,则下列选项必然成立的是AP(A)BP(A)≤P(AB)CP(A) P(AB)DP(A)≥P(AB)设随机事件A,B及其和事件A∪B的概率分别是0.4,0.3和0.6,则B的对立事件与A 的积的概率是将一枚匀称的硬币连续掷两次,则正面只出现一次的概率为()如果有试验E:投掷一枚硬币,重复1000次,观察正面出现的次数。
《线性代数、概率论》期末考试试卷答案一、选择题(每小题后均有代号分别为A, B, C, D的被选项, 其中只有一项是正确的, 将正确一项的代号填在横线上,每小题2分,共40分):1.行列式G的某一行中所有元素都乘以同一个数k得行列式H,则------------C-------------;(A) G=H ;(B) G= 0 ;(C) H=kG ;(D) G=kH 。
2.在行列式G中,A ij是元素a ij的代数余子式,则a1j A1k+ a2j A2k+…+a nj A nk--------D------;(A) ≠G (j=k=1,2,…,n时) ;(B) =G(j, k=1,2,…,n; j≠k时) ;(C) =0 (j=k=1,2,…,n时) ;(D) =0(j, k=1,2,…,n ;j≠k时) 。
3.若G,H都是n⨯ n可逆矩阵,则----------B------------;(A) (G+H)-1=H-1+G-1;(B) (GH)-1=H-1G-1;(C) (G+H)-1=G-1+H-1;(D) (GH)-1=G-1H-1。
4.若A是n⨯ n可逆矩阵,A*是A的伴随矩阵, 则--------A----------;(A) |A*|=|A|n-1;(B) |A*|=|A|n ;(C) |A*|=|A|n+1;(D) |A*|=|A|。
5.设向量组α1, α2,…,αr (r>2)线性相关, 向量β与α1维数相同,则------------C----------- (A) α1, α2,…,αr-1 线性相关;(B) α1, α2,…,αr-1 线性无关;(C) α1, α2,…,αr ,β线性相关;(D) α1, α2,…,αr ,β线性无关。
6.设η1, η2, η3是5元齐次线性方程组AX=0的一组基础解系, 则在下列中错误的是D-------------------(A) η1, η2, η3线性无关;(B) X=η1+η2+ η3是AX=0的解向量;(C) A的秩R(A)=2;(D) η1, η2, η3是正交向量组。
16春季福师《线性代数与概率统计》在线作业⼆福师《线性代数与概率统计》在线作业⼆⼀、单选题(共 50 道试题,共 100 分。
)1. 在⼗个整数0,1,2,3,4,5,6,7,8,9中任取四个不不同的数字,能够组成⼀个四位偶数的概率是(). 45/90. 41/720. 53/720. 41/90正确答案:2. 设,为两事件,且P()=0,则. 与互斥. 是不可能事件. 未必是不可能事件. P()=0或P()=0正确答案:3. 如果X与Y这两个随机变量是独⽴的,则相关系数为(). 0. 1. 2. 3正确答案:4. 进⾏n重伯努利试验,X为n次试验中成功的次数,若已知X=12.8,X=2.56则试验的成功率p=(). 0.5. 0.6. 0.8. 0.9正确答案:5. 设随机事件,及其和事件∪的概率分别是0.4,0.3和0.6,则的对⽴事件与的积的概率是. 0.2. 0.5. 0.6. 0.3正确答案:6. ⼀个装有50个球的袋⼦中,有⽩球5个,其余的为红球,从中依次抽取两个,则抽到的两球均是红球的概率是(). 0.85正确答案:7. 现有⼀批种⼦,其中良种占1/6,今任取6000粒种⼦,则以0.99的概率推断,在这6000粒种⼦中良种所占的⽐例与1/6的差是(). 0.0124. 0.0458. 0.0769. 0.0971正确答案:8. 某⼈进⾏射击,设每次射击的命中率为0.02,独⽴射击150次,则最可能命中次数为(). 1. 3. 5. 8正确答案:9. 甲、⼄同时向⼀敌机炮击,已知甲击中敌机的概率为0.6⼄击中敌机的概率为0.5,则敌机被击中的概率是(). 0.92. 0.24. 0.3. 0.8正确答案:10. 安培计是以相隔0.1为刻度的,读数时选取最靠近的那个刻度,允许误差为0.02,则超出允许误差的概率是(). 0.6. 0.2. 0.8. 0.4正确答案:11. 由概率的公理化定义可推知两个对⽴事件的概率之和为(). 0. 0.5. 0.6. 1正确答案:12. 甲、⼄、丙三⼈同时向⼀架飞机射击,它们击中⽬标的概率分别为0.4,0.5,0.7。
1 《线性代数与概率统计》 作业题 第一部分 单项选择题 1.计算11221212xxxx?(A )
A.12xx B.12xx C.21xx D.212xx
2.行列式111111111D?(B ) A.3 B.4 C.5 D.6
3.设矩阵231123111,112011011AB,求AB=?(B ) A.-1 B.0 C.1 D.2
4.齐次线性方程组123123123000xxxxxxxxx有非零解,则=?(C ) A.-1 2
B.0 C.1 D.2
5.设50906791A,67356300B,求AB=?(D ) A.1041106084 B.1041116280 C.1041116084 D.1041116284
6.设A为m阶方阵,B为n阶方阵,且Aa,Bb,00ACB,则C=?(D ) A.(1)mab B.(1)nab C.(1)nmab D.(1)nmab
7.设343122321A,求1A=?(D ) 3
A.13235322111 B.13235322111 C.13235322111 D.13235322111 8.设,AB均为n阶可逆矩阵,则下列结论中不正确的是(B ) A.111[()]()()TTTABAB B.111()ABAB C.11()()kkAA(k为正整数) D.11()(0)nkAkAk (k为正整数)
9.设矩阵mnA的秩为r,则下述结论正确的是(D ) A.A中有一个r+1阶子式不等于零 B.A中任意一个r阶子式不等于零 C.A中任意一个r-1阶子式不等于零 D.A中有一个r阶子式不等于零
10.初等变换下求下列矩阵的秩,321321317051A的秩为?(C ) 4
A.0 B.1 C.2 D.3
11.写出下列随机试验的样本空间及下列事件的集合表示:掷一颗骰子,出现奇数点。(D) A.样本空间为{1,2,3,4,5,6},事件“出现奇数点”为{2,4,6}
B.样本空间为{1,3,5},事件“出现奇数点”为{1,3,5} C.样本空间为{2,4,6},事件“出现奇数点”为{1,3,5} D.样本空间为{1,2,3,4,5,6},事件“出现奇数点”为{1,3,5}
12.向指定的目标连续射击四枪,用iA表示“第i次射中目标”,试用iA表示四枪中至少有一枪击中目标( C ): A.1234AAAA
B.12341AAAA C.1234AAAA D.1
13.一批产品由8件正品和2件次品组成,从中任取3件,则这三件产品中至少有一件不是正品的概率为( B ) A.25
B.715 C.815 D.35
14.甲乙两人同时向目标射击,甲射中目标的概率为0.8,乙射中目标的概率是0.85,两人同时射中目标的概率为0.68,则目标被射中的概率为(C ) 5
A.0.8 B.0.85 C.0.97 D.0.96
15.袋中装有4个黑球和1个白球,每次从袋中随机的摸出一个球,并换入一个黑球,继续进行,求第三次摸到黑球的概率是(D )
A.16125
B.17125 C.108125 D.109125
16.设A,B为随机事件,()0.2PA,()0.45PB,()0.15PAB,(|)PAB=?(B ) A.16 B.13 C.12 D.23
17.市场供应的热水瓶中,甲厂的产品占50%,乙厂的产品占30%,丙厂的产品占20%,甲厂产品的合格率为90%,乙厂产品的合格率为85%,丙厂产品的合格率为80%,从市场上任意买一个热水瓶,则买到合格品的概率为(D ) A.0.725 B.0.5 C.0.825 D.0.865
18.有三个盒子,在第一个盒子中有2个白球和1个黑球,在第二个盒子中有3个白球和1个黑球,在第三个盒子中有2个白球和2个黑球,某人任意取一个盒子,再从中任意取一个球,则取到白球的概率为(C ) 6
A.3136 B.3236 C.2336 D.3436
19.观察一次投篮,有两种可能结果:投中与未投中。令1,;0,X投中未投中. 试求X的分布函数()Fx。( C )
A.0,01(),0121,1xFxxx B.0,01(),0121,1xFxxx
C.0,01(),0121,1xFxxx D.0,01(),0121,1xFxxx 20.设随机变量X的分布列为(),1,2,3,4,515
kPXkk,则或(12)PXX?(C)
A.115 B.215 C.15 D.415
第二部分 计算题 1.设矩阵231123111,112011011AB,求AB. 7
解:错误!未找到引用源。=错误!未找到引用源。 =错误!未找到引用源。=-(24-24)=0
2.已知行列式2512371446125927,写出元素43a的代数余子式43A,并求43A的值. 解:43A=错误!未找到引用源。 =错误!未找到引用源。=(-2)*(-14+42)-5*(6-28)=54
3.设1100010000100021A,求2A. 解:错误!未找到引用源。=错误!未找到引用源。*错误!未找到引用源。=错误!未找到引用源。
4.求矩阵25321585431742041123A的秩. 解:A错误!未找到引用源。→错误!未找到引用源。→错误!未找到引用源。
=错误!未找到引用源。 ,所以矩阵的秩为2。
5.解线性方程组12312312331331590xxxxxxxxx. 解: (A,B)=错误!未找到引用源。→错误!未找到引用源。→错误!未找到8
引用源。 →错误!未找到引用源。,故方程组无解。
6..解齐次线性方程组123412341234123424023450413140750xxxxxxxxxxxxxxxx. 解: A=错误!未找到引用源。→错误!未找到引用源。→错误!未找到引用源。
→错误!未找到引用源。→错误!未找到引用源。 与原方程组同解的方程组为:
所以方程组的一般解为: 错误!未找到引用源。 (其中,错误!未找到引用源。
7.袋中有10个球,分别编有号码1到10,从中任取一球,设A={取得球的号码是偶数},B={取得球的号码是奇数},C={取得球的号码小于5},问下列运算表示什么事件: (1)A+B;(2)AB;(3)AC;(4)AC;(5)BC;(6)A-C.
解:(1)A+B={取得球的号码是1至10的整数}; (2)AB={取得球的号码既是偶数又是奇数}=Φ; (3)AC={取得球的号码是2、4}; (4)错误!未找到引用源。={取得球的号码是1、3、5、6、7、8、9、10}; (5)错误!未找到引用源。={取得球的号码是6、8、10}; (6)A-C={取得球的号码是6、8、10}
8.一批产品有10件,其中4件为次品,现从中任取3件,求取出的3件产品中有次品的概率。
解:设B表示所取3件产品中有次品(至少有一件次品)的事件,错误!9
未找到引用源。表示所取的3件产品中恰有k件次品的事件(k=0,1,2,3),因为错误!未找到引用源。=错误!未找到引用源。(错误!未找到引用源。表示无次品的事件),所以有: P(B) = 1 - P(错误!未找到引用源。) = 1 - P(错误!未找到引用源。) = 1 -错误!未找到引用源。= 错误!未找到引用源。
9.设A,B,C为三个事件,1P(A)=P(B)=P(C)=4,()()0PABPBC,1()8PAC,求事件A,B,C至少有一个发生的概率。
解:因为1P(A)=P(B)=P(C)=4,()()0PABPBC,1()8PAC,所以A,B和B,C是独立事件,A,C之间有相交,所以P(A,B,C至少有一个发生的概率) =1-错误!未找到引用源。= 错误!未找到引用源。
10.一袋中有m个白球,n个黑球,无放回地抽取两次,每次取一球,求: (1)在第一次取到白球的条件下,第二次取到白球的条件概率; (2)在第一次取到黑球的条件下,第二次取到白球的条件概率。
解:设A表示“第一次取到白球”,B表示“第二次取到白球” (1)袋中原有m+n个球,其中白球m个,第一次取到白球后,袋中还有m+n-1个球,其中白球m-1个,故:P(B∣A) =错误!未找到引用源。 ; (2)袋中原有m+n个球,其中白球m个,第一次取到黑球后,袋中还有m+n-1个球,其中白球m个,故:错误!未找到引用源。 .
11.设A,B是两个事件,已知()0.5PA,()0.7PB,()0.8PAB,试求:()PAB与()PBA。 解:由于P(A+B)=P(A)+P(B)-P(AB),得P(AB)=0.5+0.7-0.8=0.4, 因为 P(A-B)=P(A)-P(AB),所以P(A-B)=0.5-0.4=0.1; 因为P(B-A)=P(B)-P(AB),所以P(B-A)=0.7-0.4=0.3.
12.某工厂生产一批商品,其中一等品点12,每件一等品获利3元;二等品