考点跟踪突破32 图形的平移

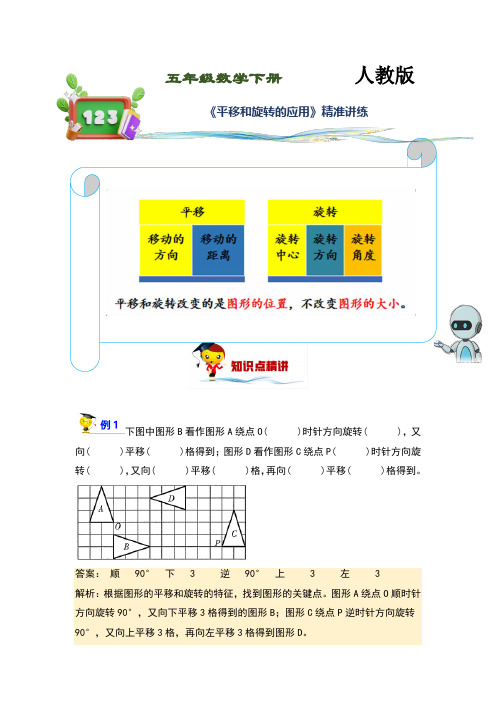
下图中图形B看作图形A绕点O( )时针方向旋转( )，又向( )平移( )格得到；图形D看作图形C绕点P( )时针方向旋转( )，又向( )平移( )格，再向( )平移( )格得到。

答案：顺 90°下 3 逆 90°上 3 左 3解析：根据图形的平移和旋转的特征，找到图形的关键点。

图形A绕点O顺时针方向旋转90°，又向下平移3格得到的图形B；图形C绕点P逆时针方向旋转90°，又向上平移3格，再向左平移3格得到图形D。

五年级数学下册人教版《平移和旋转的应用》精准讲练根据观察，图形B看作图形A绕O点顺时针方向旋转90°，又向下平移3格得到；图形D看作图形C绕点P逆时针方向旋转90°，又向上平移3格，再向左平移3格得到。

顺时针旋转90°，得到的图形是。

( )答案：×解析：将这个图形顺时针旋转90°得到的图形先画出来，再对比判断即可。

顺时针旋转90°，得到的图形应该是。

所以判断错误。

下列各组图形，只通过平移或旋转，不能形成长方形的是（）。

A．B．C．D．答案：C解析：根据题意，逐项进行旋转平移，然后解答。

A．可以绕两个三角形的交点顺时针旋转180度，形成长方形；B．先向上平移一格，再绕两个图形的相交点逆时针旋转90度，形成长方形；C．通过平移旋转无法形成长方形；D．可以把右下的图形先向上平移4格，再向左平移5格，左下的图形先向上平移4格，再向右平移5格就得到了长方形。

故答案为：C按要求作图。

（每小格边长表示2米）（1）B点在A点的（）面的（）米处。

A点在C点（）偏（）（）°方向上。

（2）把梯形先向右平移4格，再把梯形绕B点逆时针旋转90度，用数对表示旋转后梯形D点的位置是（）（画出图形）。

（3）把这个梯形按3∶1的比画出放大后的图形，放大后图形的面积是（）。

答案：（1）通过观察图形可知，B点在A点的南面的2×2＝4米处。

《图形的平移与旋转》考点点拨考点一：平移概念及其特征1、概念：在平面内，将一个图形 ，这样的图形运动称为平移.2、特征：（1）平移不改变图形的 ；（2）经过平移，对应点所连的线段 ；对应线段 ，对应角 . 例1（温州市）如图1，点A(1,2)向右平移2个单位得到对应点A ’,则点A ’的坐标是( )A.(1．4)B.(1．0) C ．(-l ，2) D.(3，2)解析：由题意知，点A(1,2)向右平移2个单位，所以横坐标向右平移2个单位，而纵坐标不变.因此平移后的对应点A′的坐标为（3，2）.故应选D.例2（武汉市）如图2，在直角坐标系中，右边的图案是由左边的图案经过平移得到的，左图案中左右眼睛的坐标分别是（－4，2），（－2，2），右图案中左眼的坐标是（3，4），则右图案中的右眼的坐标是 .解析：由题意知，左图案中左眼睛的坐标是（－4，2），右图案中左眼的坐标是（3，4），所以右边的图案是由左边的图案向右平移7个单位后，再向上平移2个单位得到的.所以左图案中右眼睛的坐标（－2，2），同样是向右平移7个单位后，再向上平移2个单位.因此右图案中的右眼的坐标是（7，4）. 例3（海南省）△ABC 在平面直角坐标系中的位置如图3所示.将△ABC 向右平移6个单位，作出平移后的△A 1B 1C 1，并写出△A 1B 1C 1各顶点的坐标.解析：根据平移原理作图如图所示.△A 1B 1C 1各顶点的坐标为：A 1（6，4），B 1（4，2），C 1（5，1）.（图1）图3评注：平移的最显著特征就是平移不改变图形的形状和大小，只是位置发生了变化.利用其特征，进行简单的平移作图，注重考查学生知识的理解和应用.考点二、旋转的概念及特征1、概念：在平面内，将一个图形绕 一个角度，这样的图形运动称为旋转，这个定点称为 ，转动的角称为 .2、特征：（1）经过旋转，图形上的每一个点都绕旋转中心延相同方向转动了 ；（2）任意一对对应点与旋转中心的连线所成的角都是旋转角，且 ；（3）对应线段 ，对应点到旋转中心的 . 例4（四川眉山）数学课上，老师让同学们观察如图4所示的图形，问：它绕着圆心O 旋转多少度后和它自身重合？甲同学说：45°；乙同学说：60°；丙同学说：90°；丁同学说：135°。

第29讲《图形的平移》要点梳理知识点1.平移的概念把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后所得到的，这两个点是对应点．连接各组对应点的线段____________．图形的这种移动叫做平移变换，简称_________________．知识点2.平移的条件确定一个平移运动的条件是平移的_________________和__________________．知识点3.平移的规则图形上的每一个点都沿同一个方向移动相同的距离．知识点4.平移的性质(1) 平移不改变图形的形状与大小；(2)连接各组对应点的线段平行且相等；(3)对应线段________________；(4)对应角__________________________．知识点5.画平移图形画平移图形,必须找出平移方向和距离,其依据是平移的性质．1．平移的作图以局部带整体，先找出图形的关键点，将原图中的关键点与移动后的对应点连接起来，确定平移距离和平移方向，再过其他关键点分别作线段与前面所连接的线段平行且相等，得到关键点的对应点，将对应点连接，所得的图形就是平移后的新图形．2．图形经过两次轴对称(两对称轴相互平行)得到的图形，可以看作是由原图形经过平移得到的，也就是说两次翻折相当于一次平移．命题点1：平移的性质1.(台州)如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C 平移的距离CC ′＝_______________．2.(东营)如图,把△ABC 沿着BC 的方向平移到△DEF 的位置,它们重叠部分的面积是△ABC 面积的一半,若BC=3 ,则△ABC 移动的距离是（ ）A.23 B.33 C.26 D.26-3命题点2：坐标系中的平移3.(西宁)在平面直角坐标系中,将点A(-1，-2)向右平移3个单位长度得到点B,则点B 关于x 轴的对称点B'的坐标为( )A.(－3，－2)B.(2，2)C.(－2，2)D.(2，－2)4.(安顺)如图，将△PQR 向右平移2个单位长度，再向下平移3个单位长度，则顶点P 平移后的坐标是( )A ．(－2，－4)B ．(－2，4)C ．(2，－3)D ．(－1，－3)命题点3：利用平移设计图案5．(本溪)下列各网格中的图形是用其图形中的一部分平移得到的是( )典例精析考点1.判断图形的平移【例1】(济南)如图,在6×6方格中有两个涂有阴影的图形M,N,①中的图形M 平移后位置如②所示,以下对图形M 的平移方法叙述正确的是( )A ．向右平移2个单位，向下平移3个单位B ． B ．向右平移1个单位，向下平移3个单位C ．向右平移1个单位，向下平移4个单位D ．向右平移2个单位，向下平移4个单位点考点2.求平移变换后对应点的坐标【例2】(海南)如图，在平面直角坐标系中，△ABC 位于第二象限，点A 的坐标是(－2，3)，先把△ABC 向右平移4个单位长度得到111C B ΔA ，再作与111C B ΔA 关于x 轴对称的222C B ΔA ，则点A 的对应点A2的坐标是( )A ．(－3，2)B ．(2，－3)C.(1，－2) D ．(－1，2)【例3】(雅安)已知△ABC 顶点坐标分别是A(0,6),B(－3,－3),C(1,0),将△ABC 平移后顶点A 的对应点A 1的坐标是(4,10),则点B 的对应点B 1的坐标为( )A ．(7，1)B ．(1，7)C ．(1，1)D ．(2，1)考点3.作已知图形的平移图形【例3】(临夏州)如图，在平面直角坐标系中，△ABC 的顶点A(0，1)，B(3，2)，C(1，4)均在正方形网格的格点上．(1) 画出△ABC 关于x 轴的对称图形111C B ΔA(2) 将111C B ΔA 沿x 轴方向向左平移3个单位后得到222C B ΔA ，写出顶点A 2，B 2，C 2的坐标．【达标测试】 1.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC 平移到△DEF 的位置,下面正确的平移步骤是( )A ．先把△ABC 向左平移5个单位，再向下平移2个单位；B ．先把△ABC 向右平移5个单位，再向下平移2个单位C ．先把△ABC 向左平移5个单位，再向上平移2个单位D ．先把△ABC 向右平移5个单位，再向上平移2个单位2.如图，在平面直角坐标系:xOy 中，已知点,0)2A(,B(1,1)。

人教版七年级数学下册期考重难点突破、典例剖析与精选练习：图形的平移知识网络重难突破知识点一图形平移平移的概念：在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做平移变换 (简称平移)，平移不改变物体的形状和大小。

【典型例题】1．（2019·北京市鲁迅中学初三期中）下面生活中的实例,不是旋转的是( )A．传送带传送货物B．螺旋桨的运动C．风车风轮的运动D．自行车车轮的运动2．（2019·哈尔滨市第一一三中学校初一期中）第七届世界军人运动会（7th CISM Military World Games），于2019年10月18日至27日在中国武汉举行，图中是吉祥物“兵兵”，将左图中的“兵兵”通过平移可得到图为（）A．B．C．D．3．（2020·沈阳市第一一一中学初一期中）如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标，其中，可以看作由“基本图案”经过平移得到的是()A．B．C．D．4．（2019·射阳县第二初级中学初一期中）下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是（）A．B．C．D．5．（2020·泉州第十六中学初一期中）如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则( )A．乙比甲先到B．甲和乙同时到C．甲比乙先到D．无法确定6．（2018·招远市期末）如图，在边长为1的正方形网格中，两个三角形的顶点都在格点（网线的交点）上，下列方案中不能把△ABC平移至△DEF位置的是（）A．先把△ABC沿水平方向向右平移4个单位长度，再向上平移3个单位长度B．先把△ABC向上平移3个单位长度，再沿水平方向向右平移4个单位长度C．把△ABC沿BE方向移动5个单位长度D．把△ABC沿BE方向移动6个单位长度7．（2019·衡水市期中）在图示的四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）A．B．C．D．.8．（2018·扬州市期末）观察下面图案，在A，B，C，D四幅图案中，能通过图1平移得到的是（）A．B．C．D．知识点二平移的性质：1、把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同.2、新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点3、连接各组对应点的线段平行且相等。

考点跟踪突破23 图形的对称、平移、旋转与位似一、选择题1．(2016·哈尔滨)下列图形中，既是轴对称图形又是中心对称图形的是( D )2.(2016·雅安)已知△ABC 顶点坐标分别是A(0，6)，B(－3，－3)，C(1，0)，将△ABC 平移后顶点A 的对应点A 1的坐标是(4，10)，则点B 的对应点B 1的坐标为( C )A ．(7，1)B ．(1，7)C ．(1，1)D ．(2，1)3．(2016·绥化)把一张正方形纸片如图①、图②对折两次后，再按如图③挖去一个三角形小孔，则展开后图形是( C )4．(2016·株洲)如图，在三角形ABC 中，∠ACB ＝90°，∠B ＝50°，将此三角形绕点C 沿顺时针方向旋转后得到三角形A′B′C ，若点B′恰好落在线段AB 上，AC ，A ′B ′交于点O ，则∠COA′的度数是( B )A ．50°B ．60°C ．70°D ．80°,第4题图) ,第5题图)5．(2016·海南)如图，AD 是△ABC 的中线，∠ADC ＝45°，把△ADC 沿着直线AD 对折，点C 落在点E 的位置．如果BC ＝6，那么线段BE 的长度为( D )A ．6B ．6 2C ．2 3D ．3 26．已知两点A(5，6)，B(7，2)，先将线段AB 向左平移一个单位，再以原点O 为位似中心，在第一象限内将其缩小为原来的12得到线段CD ，则点A 的对应点C 的坐标为( A ) A ．(2，3) B ．(3，1)C ．(2，1)D ．(3，3)二、填空题7．如图，在平面直角坐标系中， 将点P(－4，2)绕原点顺时针旋转90°， 则其对应点Q 的坐标为__(2，4)__．,第7题图),第8题图)8．(2016·泰州)如图，△ABC中，BC＝5 cm，将△ABC沿BC方向平移至△A′B′C′的位置时，A′B′恰好经过AC的中点O，则△ABC平移的距离为__2.5__cm.9．在平面直角坐标系中，点A的坐标是(2，－3)，作点A关于x轴的对称点，得到点A′，再作点A′关于y轴的对称点，得到点A″，则点A″的坐标是__(－2，3)__．10.(2016·梅州)如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB＝4，BC＝2，那么线段EF的长为．,第10题图),第11题图) 11．(导学号30042218)(2016·福州)如图，在Rt△ABC中，∠ABC＝90°，AB＝BC＝2，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，则BM的长是．三、解答题12．(2016·临夏州)如图，在平面直角坐标系中，△ABC的顶点A(0，1)，B(3，2)，C(1，4)均在正方形网格的格点上．(1)画出△ABC关于x轴的对称图形△A1B1C1；(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2，写出顶点A2，B2，C2的坐标．解：(1)图略(2)图略，点A2(－3，－1)，B2(0，－2)，C2(－2，－4)13．(2016·荆门)如图，在Rt△ABC中，∠ACB＝90°，点D，E分别在AB，AC上，CE＝BC，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CF，连接EF.(1)补充完成图形；(2)若EF∥CD，求证：∠BDC＝90°.解：(1)补全图形，如图所示 (2)由旋转的性质得：∠DCF ＝90°，∴∠DCE ＋∠ECF ＝90°，∵∠ACB ＝90°，∴∠DCE ＋∠BCD ＝90°，∴∠ECF ＝∠BCD ，∵EF ∥DC ，∴∠EFC ＋∠DCF ＝180°，∴∠EFC ＝90°，在△BDC 和△EFC 中，⎩⎨⎧DC ＝FC ，∠BCD ＝∠ECF ，BC ＝EC ，∴△BDC ≌△EFC (SAS )，∴∠BDC ＝∠EFC ＝90°14.(导学号 30042219)(2016·十堰)如图，将矩形纸片ABCD(AD ＞AB)折叠，使点C 刚好落在线段AD 上，且折痕分别与边BC ，AD 相交，设折叠后点C ，D 的对应点分别为点G ，H ，折痕分别与边BC ，AD 相交于点E ，F.(1)判断四边形CEGF 的形状，并证明你的结论；(2)若AB ＝3，BC ＝9，求线段CE 的取值范围．解：(1)∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠GFE ＝∠FEC ，∵图形翻折后点G 与点C 重合，EF 为折线，∴∠GEF ＝∠FEC ，∴∠GFE ＝∠GEF ，∴GF ＝GE ，∵图形翻折后EC 与GE 完全重合，∴GE ＝EC ，GF ＝FC ，∴GF ＝FC ＝EC ＝GE ，∴四边形CEGF 为菱形(2)由(1)得四边形CEGF 是菱形，当点F 与点D 重合时，CE 取最小值．此时，CE ＝CD ＝AB ＝3；如图，当点G 与点A 重合时，CE 取最大值，由折叠的性质得AE ＝CE ，∵∠B ＝90°，∴AE 2＝AB 2＋BE 2，即CE 2＝32＋(9－CE )2，∴CE ＝5，∴线段CE 的取值范围3≤CE ≤5。

考点跟踪突破、选择题（每小题5分，共25分）A B32图形的相似1. （20佃重庆）如图，△ ABC DEF ,相似比为1 : 2,若BC = 1 ,则EF的长是（B ）A. 1B. 2C. 3D. 42. （2019 泰安）在厶ABC和厶A1B1C1中，下列四个命题：①若AB = A1B1, AC = A1C1,从=Z A1,则A ABC 也△汩1&;②若AB = A1B1, AC =A1C1, /B = / B1,则△ABC =△ A1B1C1;③若 / A = / A1, ZC= / C1,则△ ABC A1B1C1;④若AC : A£1= CB : C1B1, ZC= / C1,则厶ABC A1B1C1.其中真命题的个数为(B )A. 4B. 3C. 2D. 13. （2019宁波）如图，梯形ABCD3,则厶ABC与厶DCA的面积比为（C ）=90° , AB = 2, DC =A. 2 : 3B. 2 : 5C. 4 : 9 D/.2 : .34. （20佃孝感）在平面直角坐标系中，已知点E（-4, 2）, F（—2, —2）,以原点O为位1似中心,相似比为-,把厶EFO缩小，则点E的对应点E'的坐标是（D ）A. (—2, 1) B . (—8, 4)C. ( —8, 4)或(8, —4) D . (—2, 1)或(2, —1)5. (20佃河北)在研究相似问题时，甲、乙两同学的观点如下:甲：将边长为3, 4, 5的三角形按图中的方式向外扩张，得到新三角形，它们的对应边间距均为1,则新三角形与原三角形相似.乙：将邻边为3和5的矩形按图②的方式向外扩张，得到新的矩形，它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点，A.两人都对B .两人都不对C.甲对，乙不对D.甲不对，乙对二、填空题（每小题5分，共25分）6. （20佃邵阳）如图，在?ABCD中，F是BC上的一点，直线DF与AB的延长线相交于点E, BP // DF ,且与AD相交于点P,请从图中找出一组相似的三角形: △ABP，第7题图）7. （20佃 滨州）如图，平行于BC 的直线DE 把厶ABC 分成的两部分面积相等，则右=AB 2 -.8. （2019安徽）如图，P 为平行四边形 ABCD 边AD 上一点，E , F 分别为PB , PC 的中 点，△ PEF , △ PDC , △ PAB 的面积分别为 S , S i , S 2,若 S = 2,贝U S i + S 2 = __8__.9. （20佃娄底）如图，小明用长为3 m 的竹竿CD 做测量工具，测量学校旗杆 AB 的高 度，移动竹竿，使竹竿与旗杆的距离 DB = 12 m ,则旗杆AB 的高为__9__m.10.（2019苏州）如图，在平面直角坐标系中，四边形OABC 是边长为2的正方形，顶 点A , C 分别在x , y 轴的正半轴上.点 Q 在对角线 OB 上，且QO = OC ,连接CQ 并延长 CQ 交边AB 于点P 则点P 的坐标为_（2 , 4 - .三、解答题（共 50分）11. （10分）（20佃南通）如图，点E 是菱形ABCD 对角线CA 的延长线上任意一点，以 线段AE 为边作一个菱形 AEFG ,且菱形AEFG s 菱形ABCD ,连接EB , GD.(1) 求证：EB = GD ;⑵若/ DAB = 60° , AB = 2, AG = '. 3,求 GD 的长.解：(1)证明：•••菱形 AEFG s 菱形 ABCD , /-Z EAG =Z BAD , /-Z EAG +Z GAB = / BAD+Z GAB , /.Z EAB =Z GAD , •/ AE = AG , AB = AD , AEB ◎△ AGD , /• EB =GD (2)解：连接 BD 交 AC 于点 P ,则 BP 丄AC , vZ DAB = 60° ,:丄 PAB = 30° , /• BP = 1,又 AB = 2，•/ AP =AB 2- BP 2= 3 , AE = AG = . 3，•/ EP = 2.3 , /• EB = . EP 2+ BP 2 =12 + 1= 13 , /• GD = 1312. （10分）（20佃巴中）如图，在平面直角坐标系 xOy 中，△ ABC 三个顶点坐标分别为 A （ - 2 , 4） , B （ - 2 , 1） , C （- 5 , 2）.（1）请画出△ ABC 关于x 轴对称的厶A 1B 1C 1；⑵将△ A 1B 1C 1的三个顶点的横坐标与纵坐标同时乘以一 2,得到对应的点A 2 , B 2 , C 2 , 请画出△ A 2B 2C 2；⑶求△ A 1B 1C 1与厶A 2B 2C 2的面积比，即S A A 1B 1C 1： S A A 2B 2C 2= 1 : 4 （不写解答 过程，直接写出结果）.，第8题图）B(2) 如图所示：△ A 2B 2C 2即为所求(3) •••将△ A 1B 1C 1的三个顶点的横坐标与纵坐标同时乘以一 2,得到对应的点 A 2, B 2,C 2, •••△ A 1B 1C 1 与厶 A 2B 2C 2 的相似比为 1 : 2, ••• SAA I B I C I : SAA 2B 2C 2= 1 : 413. (10分)(20佃德宏州)如图，是一个照相机成像的示意图.(1)如果像高 MN 是35 mm ,焦距是50 mm ,拍摄的景物高度 AB 是4.9 m ,拍摄点离景 物有多远？⑵如果要完整的拍摄高度是 2 m 的景物，拍摄点离景物有4 m ,像高不变，贝肪目机的焦距应调整为多少毫米？35 2(2) 拍摄高度是2 m 的景物，拍摄点离景物有4 m ,像高不变，• LC =：，解得LC = 70, •相机的焦距应调整为 70 mm14. (10 分)(20佃遵义)如图，?ABCD 中，BD 丄AD , / A = 45° , E , F 分别是 AB , CD 上的点，且BE = DF ,连接EF 交BD 于点O.(1) 求证：BO = DO ;(2) 若EF 丄AB ,延长EF 交AD 的延长线于点 G ,当FG = 1时，求AD 的长.r:解：根据物体成像原理知：△ LMN LBA , LCLD.(1)•••像高 MN 是 35 mm , 距是50 mm ,拍摄的景物高度AB 是4.9 m ，:亦LD ，解得LD = 7, •••拍摄点距离景物 米焦 J \ \1:阴1 9- H ---- T0^~~~"I ■ ■ k I I I 1 I 4■ I 叫解：⑴如图所示：△ A I B I C I 即为所求i~i - -b —r-r _ r - r1 4 I * 1 1 1 r - f —-n --------------- r - r - rB解：(1)证明：•••四边形ABCD 是平行四边形，••• DC = AB , DC // AB , /-Z ODF =Z OBE ,j-Z ODF = Z OBE ,在厶ODF 与厶OBE 中，Z DOF = Z BOE , /.△ ODFOBE(AAS), • BO = DO-DF = BE,(2)解：T BD 丄AD , /.Z ADB = 90° , vZ A = 45 °, DBA =Z A = 45° , •/ EF 丄AB , /.Z G=Z A = 45° , ODG 是等腰直角三角形，•/ AB // CD , EF 丄AB , • DF 丄OG, • OF = FG, △ DFG 是等腰直角三角形，•/△ ODF ◎△ OBE(AAS), •• OE= OF , /.GF =OF = OE,即卩2FG = EF, DFG 是等腰直角三角形，•/ DF = FG= 1, • DG = DF2+ FG2 =2, v AB // CD，• DG=EG,即A[2=2，•/AD=2 一215. （10分）（20佃衢州）（1）提出问题如图①，在等边△ ABC中，点M是BC上的任意一点（不含端点B, C）,连接AM ,以AM 为边作等边△ AMN ,连接CN.求证：Z ABC =Z ACN.（2）类比探究如图②，在等边△ ABC中，点M是BC延长线上的任意一点（不含端点C）,其他条件不变，（1）中结论Z ABC =Z ACN还成立吗？请说明理由.（3）拓展延伸如图③，在等腰△ ABC中，BA = BC,点M是BC上的任意一点（不含端点B , C），连接AM ,以AM 为边作等腰△ AMN ,使顶角Z AMN =Z ABC.连接CN.试探究Z ABC 与Z ACN的数量关系，并说明理由.解: (1)证明：•/△ ABC , △ AMN 是等边三角形，•/ AB = AC , AM = AN , Z BAC =Z MAN•AB = AC ,=60 ° , ./Z BAM =Z CAN , •.•在厶BAM 和厶CAN 中，＜Z BAM =Z CAN , BAM 也AM = AN ,△CAN( SAS, /.Z ABC = Z ACN(2)解：结论Z ABC =Z ACN仍成立.理由如下：vA ABC , △ AMN 是等边三角形，•/ AB = AC ,AM = AN , Z BAC =Z MAN = 60 ° , /Z BAM =Z CAN ,：在厶BAM 和厶CAN AB = AC ,中，Z BAM =Z CAN , /.△BAM ◎△ CAN( SA$ , /-Z ABC = Z ACNAM = AN ,⑶解：Z ABC =Z ACN.理由如下：v BA = BC , MA = MN ,顶角Z ABC =Z AMN，/•底角Z BAC =Z MAN , /•△ABC AMN , /• AB = AC,又vZ BAM =Z BAC -Z MAC , Z，，AM AN' ，CAN =Z MAN -Z MAC , /Z BAM =Z CAN , /•△BAM CAN , /Z ABC = Z ACN。

考点跟踪突破30图形的平移一、选择题（每小题6分，共30分）1. （2019呼和浩特）已知线段CD是由线段AB平移得到的，点A（—1 , 4）的对应点为C （4, 7）,则点B（—4, —1）的对应点D的坐标为（A ）A. （1 , 2）B. （2, 9）C. （5, 3） D . （—9, —4）Aa—7L2. （2019滨州）如图，如果把△ ABC的顶点A先向下平移3格，再向左平移1格到达A' 点，连接A'B,则线段A'B与线段AC的关系是（D ）A.垂直B.相等C.平分D •平分且垂直3. （2019邵阳）某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是（D ）A. 甲种方案所用铁丝最长B. 乙种方案所用铁丝最长C. 丙种方案所用铁丝最长D .三种方案所用铁丝一样长4. （20佃舟山）如图，将厶ABC沿BC方向平移2 cm得到△ DEF ,若厶ABC的周长为16 cm,则四边形ABFD的周长为（C ）A. 16 cmB. 18 cmC. 20 cmD. 22 cm5. （2019滨州）如图，等边△ ABC沿射线BC向右平移到△ DCE的位置，连接AD , BD , 则下列结论：①AD = BC ;②BD , AC互相平分；③四边形ACED是菱形.其中正确的个数有（D ）A. 0个B. 1个C. 2个D . 3个二、填空题（每小题6分，共30分）b ~甲H C E6. （20佃陕西模拟）如图，△ ABC 的三个顶点均在方格纸的格点上分别用有序数对（0，— 2）、（3, — 1）表示，将△ ABC 平移后，点C 的对应点C i 的位置为（1 , 2）,则点A 的对应点A i 的位置为__（— 1, 3）__.7. 如图，将等腰直角△ ABC 沿BC 方向平移得到△ A i B i C i •若BC = 3 .2, △ ABC 与 △ A i B i C i 重叠部分的面积为 2,则BB i = —一.& （2019 无锡）如图，△ ABC 中，/ ACB = 90° , AB = 8 cm ,D 是 AB 的中点.现将△ BCD 沿BA 方向平移i cm ,得到△ EFG , FG 交AC 于点H ,则GH 的长等于__3__ cm.9.如图①，两个等边厶ABD , △ CBD 的边长均为1,将厶ABD 沿AC 方向向右平移到 △ A B' 的位置得到图②，则阴影部分的周长为 __2__.1 r 一0（0, 0）,它的顶点为P ,它的对称轴与抛物线 y = ?X 2交于点Q ,则图中阴影部分 的面积为__27 . 2 —三、解答题（共 40分）11. （10分）（20佃云南）如图，下列网格中，每个小正方形的边长都是 1 ,图中“鱼”的 各个顶点都在格点上.（1） 把“鱼”向右平移 5个单位长度，并画出平移后的图形；（2） 写出A , B , C 三点平移后的对应点 A', B ' , C '的坐标.,B ，C 两点的位置10. 0）和原点C抛物线m 经过点A （ — 6, （2019广安）如图，12. (10分)(20佃湘潭)在边长为1的小正方形网格中，△ AOB 的顶点均在格点上. (1) B 点关于y 轴的对称点坐标为(—3, 2);(2) 将厶AOB 向左平移3个单位长度得到厶 A 1O 1B 1,请画出△ A 1O 1B 1； (3) 在⑵的条件下，A 1的坐标为__(— 2, 3)__.解：(1)B 点关于y 轴的对称点坐标为(一3, 2)13. (10 分)(2019 珠海)如图，在 Rt A ABC 中，/ BAC = 90° , AB = 4, AC = 3,线段 AB 为半圆O 的直径，将Rt A ABC 沿射线AB 方向平移，使斜边与半圆 O 相切于点G ,得 到厶DEF , DF 与BC 交于点H.(1)求BE 的长；⑵求Rt A ABC 与厶DEF 重叠(阴影)部分的面积.(2)结合坐标系可得 A'(5, 2), B ' (0, 6), C ' (1 , 0)1 1 "T'Yy~I!l b i 1il1—I - 1 11 . b1 1 J k 1 S111■“jr M 11 if43III1 1 1 4I I■(3)A 1的坐标为(—2, 3)解：(1)如图所示:⑵△ A 1O 1B 1如图所示:A DOB E解：(1)连接OG,如图，•••/ BAC = 90° , ••• Rt A ABC沿射线AB方向平移，使斜边与半圆AB = 4, AC = 3, ••• BC = , AB 2+ AC2= 5, O相切于点G,得厶DEF,••• AD = BE , DF = AC = 3, EF = BC = 5, / EDF = Z BAC = 90° , •/ EF 与半圆 O 相切 于点 G , • OG 丄 EF , •/ AB = 4,线段 AB 为半圆 O 的直径，• OB = OG = 2, v/ GEO =Z118 8 8S ABDH =尹D-DH = 2X 3x 2 = 3,即Rt A ABC 与厶DEF 重叠（阴影）部分的面积为-14. （10分）（2019绍兴）如图，矩形ABCD 中，AB = 6,第1次平移将矩形 ABCD 沿AB 的方向向右平移 5个单位，得到矩形A 1B 1C 1D 1,第2次平移将矩形 A 1B 1C 1D 1沿A 1B 1的方 向向右平移5个单位，得到矩形A 2B 2C 2D 2,…，第n 次平移将矩形A n - 1B n -1C n -1D n -1沿A n -1B n - 1的方向平移5个单位，得到矩形A n B n C n D n （n > 2）.DL h CL hCn-1CnAi J5A2 iAnBrf-l L(1)求AB 1和AB 2的长； ⑵若AB n 的长为56,求n.解：(1) •/ AB = 6,第1次平移将矩形 ABCD 沿AB 的方向向右平移 5个单位，得到矩 形A 1B 1C 1D 1,第2次平移将矩形 A 1B 1C 1D 1沿A 1B 1的方向向右平移 5个单位，得到矩形 A 2B 2C 2D 2…• AA 1= 5, A 1A 2= 5, A 2B 1 = A 1B 1 — A 1A 2= 6 — 5= 1, • AB 1 = AA 1 + A 1A 2 + A 2B 1 =5 + 5 + 1 = 11, • AB 2 的长为 5+ 5+ 6 = 16⑵■/ AB 1 = 2X 5+ 1 = 11, AB 2= 3 X 5 + 1 = 16, • AB n = (n + 1) X 5 + 1 = 56,解得 n = 10• Rt A EOG s Rt A EFD , • O E • E F OG DF ，OE ~5 2 10 2，解得 OE = 10, • BE = OE - OB =罟 3 (2)BD = DE — BE = 4 — 4= |.v DF // AC ,DH • A C 8AD ,即DH = 3，解得 DH = 2. • S 阴影=DEF ,。

考点跟踪突破32主谓一致1．Neither Li Hua nor I __A__ good at writing.(2016，永州)A．am B．is C．are2．This pair of shoes __B__ me well，but the shoes ________ expensive.(导学号：38122191)(2016，长沙模拟)A．fit；are B．fits；are C．fits；is3．Look！A woman with three children __A__ crossing the street.Let's help them.(2016，郴州)A．is B．are C．was4．One of my friends __A__ moved to America.I miss her so much.(2016，邵阳)A．has B．have C．are5．Everybody except Mike and Linda __B__ there when the meeting began.(导学号：38122192)(2016，巴中)A．are B．was C．were6．There __A__ a pencil and some pens in the box.(导学号：38122193)(2016，绥化)A．is B．are C．aren't7．About __A__ of the land ________ covered with trees and grass.(2016，龙东)A．three fifths；is B．three fifths；are C．three fifth；are8．Both Kate and I __C__ ready for the new high school life.(2016，孝感)A．am B．is C．are D．be9．Alice prefers stories that __A__ short and funny.(2016，南充) A．are B．is C．was D．were10．—What would you like to have for supper，Jack?—Either noodles or rice __C__ OK.I don't mind.(导学号：38122194)(2016，安顺)A．are B．were C．is D．was11．The number of the volunteers in our city __B__ 2，000.And sixty percent of them ________ teachers and students.(导学号：38122195)(2016，荆门)A．is；is B．is；are C．are；is D．are；are12．—Do you need more time to complete the task?—Yes.Another ten days __A__ enough.(导学号：38122196)(2017，预测)A．is B．was C．are D．were13．Andy，you'd better not eat meat only.You should know milk and fruit __B__ good for you.A．is B．are C．was D．were14．Physics，as well as English，__A__ very important for us.(导学号：38122197)(2017，预测)A．is B．are C．was D．were15．—What would you like，coffee or tea?—Either __A__ OK.I don't mind.A．is B．are C．was D．were16．There __C__ still some apple juice in the fridge.It's not necessary for us to go to the supermarket now.A．was B．were C．is D．are17．—Maths __A__ my favorite subject.What about you?—Physics ________.I think it's very interesting.A．is；is B．are；are C．are；is D．is；are18．As the proverb says，early to bed and early to rise __B__ a man healthy，wealthy and wise.A．make B．makesC．made D．is making19．Not only my friends but also I __B__ interested in football and Messi is our favorite star.A．be B．am C．is D．are20．A number of tourists __A__ Yangzhou many times because it is such a beautiful city.(导学号：38122198)(2016，武汉模拟)A．have been to B．has been toC．has gone to D．have gone to21．—Do you know Jim well?—No.I only know that he is one of the boys in our class who __D__ from England.A．has come B．have comeC．comes D．come22．—Bill's family __D__ having supper at seven this evening.—Oh？How do you know that ?(导学号：38122199)(2016，安徽模拟)A．is B．was C．were D．are23．—__C__ there any sheep on your farm now?—Yes.And I also raise some cows this year.A．Is B．Was C．Are D．Were24．The shoes __A__ mine.This pair of shoes ________ mybrother's.(2016，内江模拟)A．are；is B．is；are C．are；are D．are；am。

第03讲图形的平移 (核心考点讲与练)一．平行线之间的距离（1）平行线之间的距离从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离．（2）平行线间的距离处处相等．二．生活中的平移现象1、平移的概念在平面内，把一个图形整体沿某一的方向移动，这种图形的平行移动，叫做平移变换，简称平移．2、平移是指图形的平行移动，平移时图形中所有点移动的方向一致，并且移动的距离相等．3、确定一个图形平移的方向和距离，只需确定其中一个点平移的方向和距离．三．平移的性质（1）平移的条件平移的方向、平移的距离（2）平移的性质①把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同．②新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．四．作图-平移变换（1）确定平移后图形的基本要素有两个：平移方向、平移距离．（2）作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．五．利用平移设计图案确定一个基本图案按照一定的方向平移一定的距离，连续作图即可设计出美丽的图案．通过改变平移的方向和距离可使图案变得丰富多彩．一．平行线之间的距离（共3小题）1．（2019春•桂平市期末）如图，AB∥DC，ED∥BC，AE∥BD，那么图中和△ABD面积相等的三角形（不包括△ABD）有（）A．1个B．2个C．3个D．4个【分析】根据两平行直线之间的距离相等，再根据等底等高的三角形的面积相等，找出与△ABD等底等高的三角形即可．【解答】解：∵AB∥DC，∴△ABC与△ABD的面积相等，∵AE∥BD，∴△BED与△ABD的面积相等，∵ED∥BC找不到与△ABD等底等高的三角形，∴和△ABD的面积相等的三角形有△ABC、△BDE，共2个．故选：B．【点评】本题主要考查了平行线间的距离相等，等底等高的三角形面积相等的性质，找出等底等高的三角形是解题的关键．2．（2021春•宁德期末）如图，MN⊥AB，垂足为M点，MN交CD于N，过M点作MG⊥CD，垂足为G，EF过点N点，且EF∥AB，交MG于H点，其中线段GM的长度是点M到直线CD的距离，线段MN的长度是点M到直线EF的距离，又是平行线AB、EF间的距离，点N到直线MG的距离是线段GN的长度．【分析】点到直线的距离是指直线外一点到这条直线的垂线段的长度，根据这一定义结合图形进行填空即可．【解答】解：线段GM的长度是点M到直线CD的距离；线段MN的长度是点M到直线EF的距离，又是平行线AB、EF间的距离；点N到直线MG的距离是线段GN的长度．【点评】正确理解点到直线的距离的定义是解决此类问题的关键．3．（2019春•如东县期末）如图，两条平行线间依次有三个图形：△ABC，▱CDEF和梯形DGMN．根据图中所标数据比较它们的面积，其中面积最大的是（）A．△ABC B．▱CDEF C．梯形DGMN D．无法比较【分析】根据两条平行线之间的距离处处相等，分别算出三个图形的面积进行比较，即可得出答案．【解答】解：设平行线之间的距离为x，三角形ABC的面积＝＝6x，平行四边形CDEF的面积＝7x，梯形DGMN的面积＝＝5.5x，∴面积最大的是平行四边形CDEF．故选：B．【点评】此题考查三角形、平行四边形、梯形的面积公式，利用平行线之间的距离处处相等是解决问题的关键．二．生活中的平移现象（共10小题）4．（2021春•大丰区月考）下列现象是数学中的平移的是（）A．树叶从树上落下B．电梯从底楼升到顶楼C．骑自行车时轮胎的滚动D．钟摆的摆动【分析】根据平移的概念：在平面内，把一个图形整体沿某一的方向移动，这种图形的平行移动，叫做平移变换，简称平移，即可选出答案．【解答】解：A、树叶从树上落下，不是平移，故此选项不符合题意；B、电梯从底楼升到顶楼是平移，故此选项符合题意；C、骑自行车时的轮胎滚动是旋转，故此选项不符合题意；D、钟摆的摆动，不是平移，故此选项不符合题意；故选：B．【点评】本题主要考查了图形的平移，在平面内，把一个图形整体沿某一的方向移动叫平移，学生混淆图形的平移与旋转或翻转，而误选．5．（2021春•海州区期末）如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则（）A．甲和乙同时到B．甲比乙先到C．乙比甲先到D．无法确定【分析】根据平移可得出两蚂蚁行程相同，结合二者速度相同即可得出结论．【解答】解：∵甲、乙两只蚂蚁的行程相同，且两只蚂蚁的速度相同，∴两只蚂蚁同时到达．故选：A．【点评】本题考查了生活中的平移现象，结合图形找出甲、乙两只蚂蚁的行程相等是解题的关键．6．（2021春•许昌期末）下列运动属于平移的是（）A．小朋友荡秋千B．自行车在行进中车轮的运动C．地球绕着太阳转D．小华乘手扶电梯从一楼到二楼【分析】在平面内，把一个图形整体沿某一的方向移动，这种图形的平行移动，叫做平移变换，简称平移．根据平移的概念进而得出答案．【解答】解：A、小朋友荡秋千，属于旋转变换，此选项错误；B、行驶的自行车的车轮，属于旋转变换，此选项错误；C、地球绕着太阳转，属于旋转变换，此选项错误；D、小华乘手扶电梯从一楼到二楼，属于平移变换，此选项正确；故选：D．【点评】此题主要考查了生活中的平移，正确掌握平移的概念是解题关键．7．（2021春•徐州期末）木匠有32m的木板，他想要在花圃周围做围栏．他考虑将花圃设计成以下的造型上述四个方案中，能用32m的木板来围成的是①③④（写出所有可能的序号）．【分析】根据平移的性质以及矩形的周长公式分别求出各图形的周长即可得解．【解答】解：①周长＝2（10+6）＝32（m）；②∵垂线段最短，∴平行四边形的另一边一定大于6m，∵2（10+6）＝32（m），∴周长一定大于32m；③周长＝2（10+6）＝32（m）；④周长＝2（10+6）＝32（m）；故答案为：①③④．【点评】本题考查了矩形的周长，平行四边形的周长公式，平移的性质，根据平移的性质第一个图形，第三个图形的周长相当于矩形的周长是解题的关键．8．（2021春•南开区期末）一个长方形花园，长为a，宽为b，中间有两条互相垂直的宽为c的路，则可种花的面积为ab﹣ac﹣bc+c2．【分析】将路平移到花园的两边，即可找到种花的两边的长度即可求面积．【解答】解：将路平移到花园两边，所得种花的两边的长度分别为：（a﹣c）、（b﹣c）．∴种花的面积为：（a﹣c）（b﹣c）＝ab﹣ac﹣bc+c2故答案为：ab﹣ac﹣bc+c2．【点评】本题考查了列代数式，以及平移的知识，能根据题意正确列出代数式是解此题的关键．9．（2021春•江都区校级期末）白云宾馆在装修时，准备在主楼梯上铺上红地毯．已知这种地毯每平方米售价30元，主楼梯宽2米，其侧面如图所示，则购买这种地毯至少需要504元．【分析】根据题意，结合图形，先把楼梯的横竖向上向右平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．【解答】解：如图，利用平移线段，把楼梯的横竖向上向右平移，构成一个矩形，长宽分别为5.8米，2.6米，即可得地毯的长度为2.6+5.8＝8.4（米），地毯的面积为8.4×2＝16.8（平方米），故买地毯至少需要16.8×30＝504（元）．故答案为：504．【点评】此题考查了平移的应用，解决此题的关键是要利用平移的知识，把要求的所有线段平移到一条直线上进行计算．10．（2021春•依安县期末）如图是某公园里一处矩形风景欣赏区ABCD，长AB＝50米，宽BC＝25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那么小明沿着小路的中间出口A到出口B所走的路线（图中虚线）长为98米．【分析】根据已知可以得出此图形可以分为横向与纵向分析，横向距离等于AB，纵向距离等于（AD﹣1）×2，求出即可．【解答】解：利用已知可以得出此图形可以分为横向与纵向分析，横向距离等于AB，纵向距离等于（AD﹣1）×2，∴图是某公园里一处矩形风景欣赏区ABCD，长AB＝50米，宽BC＝25米，为50+（25﹣1）×2＝98米，故答案为：98．【点评】此题主要考查了生活中的平移现象，根据已知得出所走路径是解决问题的关键．11．（2020秋•海州区校级期中）某公园准备修建一块长方形草坪，长为30米，宽为20米，并在草坪上修建如图所示的十字路，已知十字路宽x米，请回答下列问题：（1）草坪（阴影部分）的面积是多少平方米？（2）修建十字路的面积是多少平方米？（3）如果十字路宽4米，那么草坪（阴影部分）的面积是多少平方米？【分析】（1）阴影面积等于矩形面积减去道路面积；（2）根据修建的十字路面积＝两条路的面积和﹣重叠部分的面积得出；（3）根据长方形草坪的面积﹣十字路的面积＝草坪（阴影部分）的面积得出．【解答】解：（1）30×20﹣（30x+20x﹣x2）＝600﹣50x+x2（平方米），答：草坪（阴影部分）的面积是（600﹣50x+x2）平方米；（2）30x+20x﹣x2＝50x﹣x2（平方米），答：修建十字路的面积是（50x﹣x2）平方米；（3）600﹣50x+x2＝600﹣50×4+4×4＝416（平方米），答：草坪（阴影部分）的面积416平方米．【点评】本题考查了列代数式及代数式求值的问题，解题的关键是灵活运用公式：整体面积＝各部分面积之和，阴影部分面积＝原面积﹣空白的面积．12．（2020秋•江阴市校级月考）根据图中标示的数据，计算图形的周长（单位：mm）【分析】经过线段的平移，该图形可变为一个长为（29+14），宽为（10+11+2）的长方形．【解答】解：如图形的周长＝（29+14+10+11+2）×2＝132mm．【点评】本题主要考查的是平移的性质，经过线段的平移将原图形转化为一个矩形的周长是解题的关键．13．（2015春•宝应县期中）在长为12m，宽为9m的长方形空地上，沿平行于长方形各边的方向分别割出三个大小完全一样的小长方形花圃，其示意图如图所示，求其中一个小长方形花圃的长和宽．【分析】由图形可看出：小矩形的2个长+一个宽＝12m，小矩形的2个宽+一个长＝9m，设出长和宽，列出方程组即可得答案．【解答】解：设小矩形的长为xm，宽为ym，由题意得：，解得：，即小矩形的长为5m，宽为2m．答：小矩形花圃的长和宽分别为5m，2m．【点评】本题考查了二元一次方程组的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程组求解．三．平移的性质（共10小题）14．如图，△ABC向右平移2cm得到△DEF，如果△ABC的周长是16cm，那么四边形ABFD的周长是（）A．16cm B．18cm C．20cm D．22cm【分析】根据平移的性质得到BE＝AD＝CF，DF＝AC，根据四边形的周长公式计算，得到答案．【解答】解：∵△ABC向右平移2cm得到△DEF，∴BE＝AD＝CF＝2（cm），DF＝AC，∵△ABC的周长是16cm，∴AB+AC+BC＝16cm，∴四边形ABFD的周长＝AB+BF+DF+AD＝AB+BC+CF+AC+AD＝16+2+2＝20（cm），故选：C．【点评】本题考查的是平移的性质，根据平移的性质求出AD和CF以及DF＝AC是解题的关键．15．如图，在△ABC中，BC＝7，∠A＝80°，∠B＝70°，把△ABC沿RS的方向平移到△DEF 的位置，若CF＝4，则下列结论中错误的是（）A．DF＝7B．∠F＝30°C．AB∥DE D．BE＝4【分析】根据平移的性质，平移只改变图形的位置，不改变图形的大小与形状，平移后对应点的连线互相平行，对各选项分析判断后利用排除法．【解答】解：∵把△ABC沿RS的方向平移到△DEF的位置，BC＝7，∠A＝80°，∠B＝70°，∴EF＝BC＝7，CF＝BE＝4，∠F＝∠ACB＝180°﹣∠A﹣∠B＝180°﹣80°﹣70°＝30°，AB∥DE，∴B、C、D正确，A错误，故选：A．【点评】本题考查了平移的性质，熟练掌握平移性质是解题的关键．16．（2021春•凤山县期末）如图，△ABC沿着BC方向平移到△DEF，已知BC＝6、EC＝2，那么平移的距离为（）A．2B．4C．6D．8【分析】观察图象，发现平移前后，B、E对应，C、F对应，根据平移的性质，易得平移的距离＝BE＝6﹣2＝4，进而可得答案．【解答】解：由题意平移的距离为BE＝BC﹣EC＝6﹣2＝4，故选：B．【点评】本题考查平移的性质，经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等，本题关键要找到平移的对应点．17．（2021春•罗湖区校级期末）如图，若图形A经过平移与下方图形拼成一个长方形，则正确的平移方式是（）A．向右平移4格，再向下平移4格B．向右平移6格，再向下平移5格C．向右平移4格，再向下平移3格D．向右平移5格，再向下平移3格【分析】根据图形A与下方图形中空白部分的位置解答即可．【解答】解：由图可知，正确的平移方式向右平移4格，再向下平移4格．故选：A．【点评】本题考查了平移的性质，比较简单，准确识图是解题的关键．18．（2021春•河源期末）如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B＝90°，AB＝8，DH＝3，平移距离为4，求阴影部分的面积为（）A．20B．24C．25D．26【分析】由S△ABC＝S△DEF，推出S四边形ABEH＝S阴即可解决问题；【解答】解：∵平移距离为4，∴BE＝4，∵AB＝8，DH＝3，∴EH＝8﹣3＝5，∵S△ABC＝S△DEF，∴S四边形ABEH＝S阴∴阴影部分的面积为＝×（8+5）×4＝26故选：D．【点评】此题主要考查了平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等，要熟练掌握．19．（2021春•江都区期中）如图，直线m与∠AOB的一边射线OB相交，∠3＝120°，向上平移直线m得到直线n，与∠AOB的另一边射线OA相交，则∠2﹣∠1＝60°．【分析】作OC∥m，如图，利用平移的性质得到m∥n，则判断OC∥n，根据平行线的性质得∠1＝∠OBC＝30°，∠2+∠AOC＝180°，从而得到∠2+∠3的度数．【解答】解：作OC∥m，如图，∵直线m向上平移直线m得到直线n，∴m∥n，∴OC∥n，∴∠1＝∠BOC，∠2+∠AOC＝180°，∠AOC＝∠3﹣∠1，∴∠2+∠3﹣∠1＝180°，∴∠2﹣∠1＝180°﹣120°＝60°，故答案为：60°．【点评】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同．新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．20．（2021春•兴化市期末）把一副直角三角尺如图摆放，∠C＝∠F＝90°，∠CAB＝60°，∠FDE＝45°，斜边AB、DE在直线l上，△ABC保持不动，△DEF在直线l上平移，当以点A、E、F三点为顶点的三角形是直角三角形时，则∠CAF的度数是15或30．【分析】有两种情形，当点D运动到与A重合时，△AEF是直角三角形，当点D运动到A是DE中点时，△AEF是直角三角形．【解答】解：当点D运动到与A重合时，△AEF是直角三角形，此时∠CAF＝60°﹣45°＝15°当点D运动到A是DE中点时，△AEF是直角三角形，此时∠CAF＝90°﹣60°＝30°，∴∠CAF的度数为15或30，故答案为：15或30．【点评】本题考查平移的性质，直角三角形的性质等知识，解题的关键是学会用分类讨论的思想解决问题，属于中考常考题型．21．（2021春•镇江期末）如图，在三角形ABC中，∠ABC＝90°，BC＝7，把△ABC向下平移至△DEF后，AD＝CG＝4，则图中阴影部分的面积为20．【分析】先根据平移的性质得到AD＝BE＝4，EF＝BC＝6，S△ABC＝S△DEF，则BG＝3，由于S阴影部分＝S梯形BEFG，所以利用梯形的面积公式计算即可．【解答】解：如图，∵△ABC向下平移至△DEF，∴AD＝BE＝4，EF＝BC＝6，S△ABC＝S△DEF，∵BG＝BC﹣CG＝7﹣4＝3，∴S梯形BEFG＝（3+7）×4＝20，∵S阴影部分+S△DBG＝S△DBG+S梯形BEFG，∴S阴影部分＝S梯形BEFG＝20．故答案为：20．【点评】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．22．（2020春•惠来县期末）如图，AD∥BC，∠B＝∠D＝50°，点E、F在BC上，且满足∠CAD ＝∠CAE，AF平分∠BAE．（1）∠CAF＝65°；（2）若平行移动CD，那么∠ACB与∠AEB度数的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；（3）在平行移动CD的过程中，是否存在某种情况，使∠AFB＝∠ACD？若存在，求出∠ACD 度数；若不存在，说明理由．【分析】（1）证明∠CAF＝∠BAD，求出∠BAD即可．（2）证明∠EAC＝∠ECA，再利用三角形的外角的性质解决问题即可．（3）设∠ACD＝x，∠CAD＝y．则有x+y＝130°，构建方程组解决问题即可．【解答】解：（1）∵AD∥BC，∴∠B+∠BAD＝180°，∵∠B＝50°，∴∠BAD＝130°，∵AF平分∠BAE，∴∠BAF＝∠EAF，∵∠CAD＝∠CAE，∴∠CAF＝∠BAE+∠DAE＝∠BAD＝65°，故答案为65．（2）结论：∠ACB与∠AEB度数的比值不变．理由：∵AD∥BC，∴∠CAD＝∠ACE，∵∠CAD＝∠CAE，∴∠ACE＝∠CAE，∵∠AEB＝∠ACE+∠CAE＝2∠ACB，∴∠ACB：∠AEB＝1：2．（3）设∠ACD＝x，∠CAD＝y．则有x+y＝130°，∵∠AFB＝∠ACD＝∠ACB+∠CAF，∴x＝65°+y，解得x＝97.5°，∴∠ACD＝97.5°．【点评】本题考查平行线的性质，平移变换，三角形内角和定理，三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．23．（2019春•江宁区期中）如图1，已知直线a∥b，点A、E在直线a上，点B、F在直线b上，∠ABC＝100°，BD平分∠ABC交直线a于点D，线段EF在线段AB的左侧．若将线段EF沿射线AD的方向平移，在平移的过程中BD所在的直线与EF所在的直线交于点P．试探索∠1的度数与∠EPB的度数有怎样的关系？为了解决以上问题，我们不妨从EF的某些特殊位置研究，最后再进行一般化．【特殊化】（1）如图2，当∠1＝40°，且点P在直线a、b之间时，求∠EPB的度数；（2）当∠1＝70°时，求∠EPB的度数；【一般化】（3）当∠1＝n°时，求∠EPB的度数．（直接用含n的代数式表示）【分析】（1）利用外角和角平分线的性质直接可求解；（2）分三种情况讨论：①当交点P在直线b的下方时；②当交点P在直线a，b之间时；③当交点P在直线a的上方时；分别画出图形求解；（3）结合（2）的探究，分两种情况得到结论：①当交点P在直线a，b之间时；②当交点P 在直线a上方或直线b下方时．【解答】解：（1）如图2，作PG∥a，∴∠EPG＝∠EFC＝40°∵a∥b∴PG∥b∴∠GPB+∠CBD＝180°，又∵BD是∠ABC平分线，且∠ABC＝100°，∴∠GPB＝180°﹣2（1）∠ABC＝130°∴∠EPB＝∠EPG+∠GPB＝170°，（2）①当交点P在直线b的下方时：∠EPB＝∠1﹣50°＝20°；②当交点P在直线a，b之间时：∠EPB＝50°+（180°﹣∠1）＝160°；③当交点P在直线a的上方时：∠EPB＝∠1﹣50°＝20°；（3）①当n＞50°时，交点P在直线a上方，∠EPB＝n﹣50°，交点P在直线a、b之间，∠EPB＝230°﹣n交点P在直线b下方，∠EPB＝n﹣50°，②当n＜50°时，交点P在直线a上方，∠EPB＝50°﹣n交点P在直线a、b之间，∠EPB＝130°+n交点P在直线b下方，∠EPB＝50°﹣n．【点评】本题考查了平行线的性质；三角形外角性质．根据动点P的位置，分类画图，结合图形求解是解决本题的关键．数形结合思想的运用是解题的突破口．四．作图-平移变换（共2小题）24．（2009春•宿豫区期中）将图中的三角形ABC向右平移6格．略．【分析】分别作出点A、B、C的对应点，顺次连接即可．【解答】解：【点评】本题需注意，作平移图形时，找关键点的对应点是主要的一步．25．（2021春•睢宁县月考）如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点．在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．（1）请在图中画出△ABC向上平移3个单位后的△A1B1C1；（2）图中AC与A1C1的关系是：AC＝A1C1，AC∥A1C1．（3）画出△ABC的AB边上的高CD；垂足是D；（4）图中△ABC的面积是8．【分析】（1）将各点的横坐标不变、纵坐标加3可得；（2）根据平移的性质解答即可．（3）从C点向AB的延长线作垂线，垂足为点D，CD即为AB边上的高；（4）根据三角形面积公式即可求出△ABC的面积．【解答】解：（1）如图所示：（2）AC＝A1C1，AC∥A1C1；故答案为：AC＝A1C1，AC∥A1C1；（3）如图所示；（4）△ABC的面积＝；故答案为：8．【点评】本题主要考查了根据平移变换作图，以及三角形的中线，高的一些基本画图方法．平移作图的一般步骤为：①确定平移的方向和距离，先确定一组对应点；②确定图形中的关键点；③利用第一组对应点和平移的性质确定图中所有关键点的对应点；④按原图形顺序依次连接对应点，所得到的图形即为平移后的图形．五．利用平移设计图案（共3小题）26．（2021春•江都区期中）下列所示的车标图案，其中可以看作由“基本图案”经过平移得到的是（）A．B．C．D．【分析】根据平移的概念；在平面内，将一个图形整体沿某一方向移动，这种图形移动，叫做平移，即可选出答案．【解答】解：根据平移的概念，观察图形可知C符合题意，故选：C．【点评】本题主要考查了图形的平移，注意区分图形的平移、旋转、翻折是解题的关键．27．（2021春•鼓楼区校级月考）平移小平行四边形◇可以得到美丽的“中国结”图案，下面四个图案是由小平行四边形◇平移后得到的类似“中国结”的图案，按图中规律，在第n个图案中，小平行四边形◇的个数是2n2个【分析】仔细观察图形发现第一个图形有2×12个小平行四边形，第二个图形有2×22个小平行四边形，第三个图形有2×32个小平行四边形，…由此规律得到第n个图形有2n2个小平行四边形，可求得答案．【解答】解：第一个图形有2×12＝2个小平行四边形，第二个图形有2×22＝8个小平行四边形，第三个图形有2×32＝18个小平行四边形，…第n个图形有2n2个小平行四边形．故答案为：2n2．【点评】此题考查了图形的变化类规律，解题的关键是仔细观察图形的变化，并找到图形的变化规律，利用规律解决问题．28．（2021春•新吴区月考）请把下面的小船图案先向上平移3格，再向右平移4格．【分析】分别作出△MNE和梯形ABCD向上平移3格，再向右平移4格的对应位置即可．【解答】解：如图所示：．【点评】此题主要考查了图形的平移，关键是掌握平移后图形的大小和形状不发生改变．题组A 基础过关练一．选择题（共4小题）1．（2021春•高邮市期末）现实世界中，平移现象无处不在，中国的方块字中有些也具有平移性，下列汉字是由平移构成的是（）A．B．C．D．【分析】根据平移的基本性质，汉字只需由两或三个完全相同的部分组成即可．【解答】解：根据题意，由两或三个完全相同的部分组成的汉字即可，∴“朋”可以通过平移得到．故选：B．【点评】本题考查了平移的基本性质的运用，熟知图形平移不变性的性质是解答此题的关键．2．（2020•如皋市一模）如图，△ABC沿着由点B到点E的方向，平移到△DEF．若BC＝5，EC ＝3，则平移的距离为（）A．7B．5C．3D．2分层提分【分析】根据平移的性质即可解决问题．【解答】解：由题意得平移的距离为：BE＝BC﹣EC＝5﹣3＝2，故选：D．【点评】本题考查平移的性质，经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等，本题关键要找到平移的对应点．3．（2021春•汉阳区期末）下列生活现象中，属于平移的是（）A．足球在草地上滚动B．拉开抽屉C．把打开的课本合上D．钟摆的摆动【分析】根据平移的定义，对选项进行一一分析，排除错误答案．【解答】解：A．足球在草地上滚动方向变化，不符合平移的定义，不属于平移，故本选项错误；B．拉开抽屉符合平移的定义，属于平移，故本选项正确；C．把打开的课本合上，不符合平移的定义，不属于平移，故本选项错误；D．钟摆的摆动是旋转运动，不属于平移，故本选项错误；故选：B．【点评】本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状、大小和方向，学生易混淆图形的平移与旋转或翻转，而选择错误．注意平移是图形整体沿某一直线方向移动．4．（2021春•郫都区校级期中）如图，在△ABC中，BC＝5，∠A＝80°，∠B＝70°，把△ABC 沿RS的方向平移到△DEF的位置，若CF＝4，则下列结论中错误的是（）A．BE＝4B．∠F＝30°C．AB∥DE D．DF＝5【分析】根据平移的性质，平移只改变图形的位置，不改变图形的大小与形状，平移后对应点的连线互相平行，对各选项分析判断后利用排除法．【解答】解：∵把△ABC沿RS的方向平移到△DEF的位置，BC＝5，∠A＝80°，∠B＝70°，∴CF＝BE＝4，∠F＝∠ACB＝180°﹣∠A﹣∠B＝180°﹣80°﹣70°＝30°，AB∥DE，∴A、B、C正确，D错误，故选：D．【点评】本题考查了平移的性质，熟练掌握平移性质是解题的关键．二．填空题（共10小题）5．（2020•蠡县一模）如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为20cm．【分析】先根据平移的性质得到CF＝AD＝2cm，AC＝DF，而AB+BC+AC＝16cm，则四边形ABFD的周长＝AB+BC+CF+DF+AD，然后利用整体代入的方法计算即可．【解答】解：∵△ABC沿BC方向平移2cm得到△DEF，∴CF＝AD＝2cm，AC＝DF，∵△ABC的周长为16cm，∴AB+BC+AC＝16cm，∴四边形ABFD的周长＝AB+BC+CF+DF+AD＝AB+BC+AC+CF+AD＝16cm+2cm+2cm＝20cm．故答案为：20cm．【点评】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同．新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．6．（2021春•鼓楼区期中）如图，这个图形的周长是18．【分析】本题可将图形的边长拆分、拼成一个矩形，从而求得周长．【解答】解：将图形的上面部分的边都向上和向左右、平移，可得一个长为5、宽为4的矩形，∴这个图形的周长为4+4+5+5＝18．故答案为：18．【点评】解答本题的关键是将这个图形拼成学过的简单图形，从而求解．7．（2018春•新沂市期中）如图，在△ABC中，BC＝5cm，把△ABC沿直线BC的方向平移到△DEF的位置，若EC＝2cm，则平移的距离为3cm．【分析】根据平移的性质可得对应点连接的线段是AD、BE和CF，结合图形可直接求解．【解答】解：观察图形可知，对应点连接的线段是AD、BE和CF．∵BC＝5cm，CE＝2cm，∴平移的距离＝BE＝BC﹣EC＝3cm．故答案为：3．【点评】本题主要考查了平移的基本性质：经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．8．（2018春•镇江期末）如图所示，一块长为m，宽为n的长方形地板中间有一条裂缝，若把裂缝右边的一块向右平移距离为d的长度，则由此产生的裂缝面积是dn．【分析】利用新长方形的面积减去原长方形的面积得到产生的裂缝的面积．【解答】解：产生的裂缝的面积＝（m+d）n﹣mn＝dn．答：产生的裂缝的面积是dn．故答案为：dn．【点评】本题考查了生活中的平移现象．解题的关键是掌握平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同．新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．9．（2021春•姜堰区期末）如图，在△ABC中，D是BC的中点，将△ABC沿BC向右平移得△A'DC'，若点A平移的距离AA'＝4cm，则BC＝8cm．。