吉林省长春市农安县靠山镇中考数学复习反比例函数专题训练(,精选资料)

中考数学复习《反比例函数》专项综合练习及答案一、反比例函数1．如图，反比例函数y1=的图象与一次函数y2= x 的图象交于点A、 B，点 B 的横坐标是 4，点 P（ 1，m）在反比例函数 y1= 的图象上．（1）求反比例函数的表达式；（2）观察图象回答：当 x 为何范围时， y1＞ y2；（3）求△ PAB的面积．【答案】（1）解：把 x=4 代入 y2=x，得到点 B 的坐标为（ 4， 1），把点B（4，1）代入 y1= ，得 k=4．反比例函数的表达式为 y1=（2）解：∵点 A 与点 B 关于原点对称，∴ A 的坐标为（﹣ 4，﹣ 1），观察图象得，当x＜﹣ 4 或 0＜ x＜ 4 时， y1＞ y2（3）解：过点 A 作 AR⊥y 轴于 R，过点 P 作 PS⊥ y 轴于 S，连接 PO，设 AP 与 y 轴交于点 C，如图，∵点 A 与点 B 关于原点对称，∴OA=OB，△AOP △ BOP∴S=S，∴S△PAB=2S△AOP．y1=中，当x=1时，y=4，∴P（ 1， 4）．设直线 AP 的函数关系式为y=mx+n ，把点 A（﹣ 4，﹣ 1）、 P（1 ，4）代入 y=mx+n ，则，解得．故直线 AP 的函数关系式为 y=x+3，则点 C 的坐标（ 0，3）， OC=3，∴S △AOP =S △ AOC +S △ POC= OC?AR+ OC?PS= ×3×4+ ×3×1= ，∴S △PAB =2S △AOP =15．【解析】 【分析】（ 1）把x=4 代入 y 2= x ，得到点 B 的坐标，再把点 B 的坐标代入 y 1=，求出 k 的值，即可得到反比例函数的表达式；（2）观察图象可知，反比例函数的图象在一次函数图象上方的部分对应的自变量的取值范围就是不等式 y 1＞ y 2 的解集；（ 3）过点A 作 AR ⊥y 轴于 R ，过点 P 作 PS ⊥ y 轴于 S ，连接 PO ，设 AP 与 y 轴交于点 C ，由点 A 与点B 关于原点对称，得出 △AOP =S △BOP ， S △PAB =2S △AOP ． 求出 P 点坐标，利用OA=OB ，那么 S待定系数法求出直线AP 的函数关系式，得到点 C 的坐标，根据 S △ AOP △AOC △ POC 求出=S+SS △AOP =，则 S △ PAB =2S △ AOP =15．2．已知点 A ， B 分别是 x 轴、 y 轴上的动点，点 C ， D 是某个函数图象上的点，当四边形ABCD （ A ， B ， C ， D 各点依次排列）为正方形时，称这个正方形为此函数图象的伴侣正方形．例如：如图，正方形 ABCD 是一次函数 y=x+1 图象的其中一个伴侣正方形．（1）若某函数是一次函数 y=x+1，求它的图象的所有伴侣正方形的边长；（2）若某函数是反比例函数y= （ k＞ 0），他的图象的伴侣正方形为ABCD，点 D（ 2，m）（ m＜ 2）在反比例函数图象上，求m 的值及反比例函数解析式；（3）若某函数是二次函数y=ax2+c（ a≠0），它的图象的伴侣正方形为ABCD， C、D 中的一个点坐标为（ 3， 4）．写出伴侣正方形在抛物线上的另一个顶点坐标________，写出符合题意的其中一条抛物线解析式________，并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数 ________．【答案】（1）解：如图1，当点 A 在 x 轴正半轴，点 B 在 y 轴负半轴上时，∵O C=0D=1，∴正方形 ABCD的边长 CD=；∠ OCD=∠ ODC=45，°当点 A 在 x 轴负半轴、点 B 在 y 轴正半轴上时，设小正方形的边长为a，易得 CL=小正方形的边长=DK=LK，故 3a=CD=．解得 a=，所以小正方形边长为，∴一次函数y=x+1 图象的伴侣正方形的边长为或（2）解：如图2，作 DE， CF分别垂直于x、 y 轴，易知△ ADE≌ △ BAO≌△ CBF此时， m＜ 2， DE=OA=BF=m， OB=CF=AE=2﹣ m，∴O F=BF+OB=2，∴C 点坐标为（ 2﹣m， 2），∴2m=2 （ 2﹣ m），解得 m=1．反比例函数的解析式为y=．（3）（ 3， 4）； y=﹣x2+ ；偶数【解析】【解答】解：（3）实际情况是抛物线开口向上的两种情况中，另一个点都在（3， 4）的左侧，而开口向下时，另一点都在（3，4）的右侧，与上述解析明显不符合①当点 A 在 x 轴正半轴上，点 B 在 y 轴正半轴上，点 C 坐标为（ 3， 4）时：另外一个顶点为（ 4， 1），对应的函数解析式是y=﹣ x2+ ；②当点 A 在 x 轴正半轴上，点 B 在 y 轴正半轴上，点 D 坐标为（ 3， 4）时：不存在，③当点 A 在 x 轴正半轴上，点 B 在 y 轴负半轴上，点 C 坐标为（ 3，4）时：不存在④当点 A 在 x 轴正半轴上，点 B 在 y 轴负半轴上，点 D 坐标为（ 3， 4）时：另外一个顶点C 为（﹣⑤ 当点1， 3），对应的函数的解析式是A 在 x 轴负半轴上，点B 在 yy= x2+ ；轴负半轴上，点 D 坐标为（3， 4）时，另一个顶点C的坐标是（ 7，﹣ 3）时，对应的函数解析式是y=﹣⑥当点 A 在 x 轴负半轴上，点 B 在 y 轴负半轴上，点；C 坐标为（3， 4）时，另一个顶点D的坐标是（﹣ 4， 7）时，对应的抛物线为y= x2+；∵由抛物线的伴侣正方形的定义知，一条抛物线有两个伴侣正方形，是成对出现的，∴所求出的任何抛物线的伴侣正方形个数为偶数．【分析】解答此题时，要特别注意认真读题，分析题意，注意已知条件点 A， B 分别是 x 轴、 y 轴上的动点，点 C， D 是某个函数图象上的点。

中考数学复习《反比例函数》专项练习题--带有答案一、单选题1．关于反比例函数y＝﹣3x，下列说法错误的是（）A．图象经过点（1，﹣3）B．图象分布在第一、三象限C．图象关于原点对称D．图象与坐标轴没有交点2．已知反比例函数y=kx的图象经过点(m，3m)，则此反比例函数的图象在（）A．第一、二象限B．第一、三象限C．第二、四象限D．第三、四象限3．当k＞0时，反比例函数y= kx和一次函数y=kx+2的图象大致是（）A．B．C．D．4．如图，已知点A，B分别在反比例函数y= 2x （x＞0），y= −8x（x＞0）的图象上且OA⊥OB，则OA：OB为（）A．√2B．12C．√3D．135．如图，正比例函数y=k1x与反比例函数y=k2x 的图象交于A(1，m)、B两点，当k1x≤k2x时，x的取值范围是（）A．−1≤x<0或x≥1B．x≤−1或0<x≤1C．x≤−1或x≥1D．−1≤x<0或0<x≤16．如图，在平面直角坐标系中，矩形OABC的面积为10，反比例函数y=kx(x>0)与AB、BC分别交于点D、E，若AD=2BD，则k的值为（）A．53B．103C．203D．527．如图所示的二次函数y=ax2+bx+c的图象中，刘星同学观察得出了下面四条信息：(1) b2−4ac＞0；(2) c＞1；(3) a−b+c＞0；(4) a+b+c＜0.你认为其中错误的有（）A．2个B．3个C．4个D．1个8．如图，在平面直角坐标系中，点P（ 1 ， 4 ）、Q （m ，n ）在函数y=kx(x>0)的图象上．当m>1时，过点P分别作x轴、y轴的垂线，垂足为点A、B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E．随着m的增大，四边形ACQE的面积（）A．减小B．增大C．先减小后增大D．先增大后减小二、填空题9．若反比例函数y=k的图象经过点A(4,1)，则当y<1时，x的取值范围是．x10．已知平行四边形的面积是12cm2，它的一边是acm，这边上的高是hcm，则a与h的函数关系式为，它位于第象限．11．如图，在平面直角坐标系中，OB在x轴上，∠ABO＝90°，点A的坐标为（2，4），将△AOB绕点A逆时针旋转90°，点O的对应点C恰好落在反比例函数y＝k的图象上，则k的值为．x的图象上，观察图象可知，当x＞1时，y的取值范围12．如图，已知点P（1，2）在反比例函数y=kx是.13．如图，四边形OABC是矩形，ADEF是正方形，点A，D在x轴的正半轴，点C在y轴的正半轴上，点F的图象上，OA=2，OC=6，则正方形ADEF的边长为．再AB上，点B，E在反比例函数y= kx三、解答题(k≠0)的图象在第一象限交于A(2，3)和14．如图，一次函数y=ax+b(a≠v)与反比例函数y=kxB(3，m)两点，与x轴交于点C．（1）求反比例函数和一次函数的解析式；（2）连接OA，OB求△OAB的面积．(k≠0)的图象交于A(a，3)，B(3，b)两点，过点A作AC⊥x 15．如图，直线y=−x+2与反比例函数y=kx轴于点G，过点B作BD⊥x轴于点D．（1）求a，b的值及反比例函数的解析式；（2）若点P在直线y=−x+2上，且S△ACP=S△BDP，请求出此时点P的坐标．（m＜0）图象的两个交16．如图，已知A（﹣4，0.5），B（﹣1，2）是一次函数y=ax+b与反比例函数y=mx点，AC⊥x轴于C，BD⊥y轴于D．（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？（2）求一次函数解析式及m的值；（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．17．如图，在平面直角坐标系中，直线AB与函数y= k（x＞0）的图象交于点A（m，2），B（2，n）．过xOC，且△ACD的面积是6，连接点A作AC平行于x轴交y轴于点C，在y轴负半轴上取一点D，使OD= 12BC．（1）求m，k，n的值；（2）求△ABC的面积．18．为预防传染病，某校定期对教室进行“药熏消毒”．已知某种药物在燃烧阶段，室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例；一次性燃烧完以后，y与x成反比例（如图所示）．在药物燃mg．烧阶段，实验测得在燃烧5分钟后，此时教室内每立方米空气含药量为72（1）若一次性燃烧完药物需10分钟．①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式．mg时，对人体方能无毒害作用，那么从消毒开始，在哪个时间段学生②当每立方米空气中的含药量低于75不能停留在教室里？（2）已知室内每立方米空气中的含药量不低于0.7mg时，才能有效消毒，如果有效消毒时间要持续120分钟，问要一次性燃烧完这种药物需多长时间？答案1．B 2．B 3．C 4．B 5．A 6．C 7．D 8．B 9．x<0或x>4 10．a=12ℎ；一 11．12 12．0＜y ＜2 13．√13 ﹣114．（1）解：∵点A(2，3)在反比例函数y =kx 的图象上∴k =2×3=6∴反比例函数的解析式为y =6x又∵B(3，m)在反比例函数y =6x 的图象上∴m =2∴点B(3，2)由于直线y =ax +b 过点A(2，3)，B(3，2)∴{2k +b =33k +b =2解得{k =−1b =5∴一次函数的解析式为y =−x +5答：反比例函数的解析式为y =6x ，一次函数的解析式为y =−x +5； （2）解：如图，分别过点A 、B 分别作x 轴垂线，垂足分别为D ，E直线y=−x+5与x轴的交点C(5，0)即OC=5∴S△AOB=S△AOC−S△BOC=12×5×3−12×5×2=52．15．（1）解：∵直线y=−x+2与反比例函数y=kx(k≠0)的图象交于A(a，3)，B(3，b)两点∴−a+2=3，−3+2=b∴a=−1，b=−1∴A(−1，3)，B(3，−1)∵点A(−1，3)在反比例函数y=kx上∴k=−1×3=−3∴反比例函数解析式为y=−3x．（2）解：设点P(n，−n+2)∵A(−1，3)∴C(−1，0)∵B(3，−1)∴D(3，0)∴S△ACP=12AC×|x P−x A|=12×3×|n+1|S△BDP=12BD×|x B−x P|=12×1×|3−n|∵S△ACP=S△BDP∴12×3×|n+1|=12×1×|3−n|∴n=0或n=−3∴P(0，2)或(−3，5)．16．解：（1）当﹣4＜x＜﹣1时，一次函数大于反比例函数的值；（2）把A （﹣4，0.5），B （﹣1，2）代入y=kx+b 得 {−4k +b =0.5−k +b =2，解得{k =12b =52 所以一次函数解析式为y=12x+52；把B （﹣1，2）代入y=mx ，得m=﹣1×2=﹣2； （3）连接PC 、PD ，如图，设P 点坐标为（t ，12t+52）． ∵△PCA 和△PDB 面积相等 ∴12•12•（t+4）=12•1•（2﹣12t ﹣52） 解得t=﹣52∴P 点坐标为（﹣52，54）．17．（1）解：∵点A 的坐标为（m ，2），AC 平行于x 轴，∴OC=2，AC ⊥y 轴，∵OD= 12 OC ，∴OD=1，∴CD=3，∵△ACD 的面积为6，∴12 CD •AC=6 ∴AC=4，即m=4则点A 的坐标为（4，2），将其代入y= kx 可得k=8 ∵点B （2，n ）在y= 8x 的图象上，∴n=4； （2）解：如图，过点B 作BE ⊥AC 于点E ，则BE=2∴S △ABC = 12AC •BE= 12×4×2=4即△ABC 的面积为4．18．（1）解：①设药物燃烧时的函数解析式为y =k 1x ，药物燃烧后的解析式为y =k 2x把(5，72)代入y =k 1x 中得：72=5k 1 ∴k 1=710∴药物燃烧时的函数解析式为y =710x(0≤x ≤10)∴药物刚好燃烧完时教室内每立方米空气含药量为10×710=7mg 把(10，7)代入y =k 2x 中得：7=k210∴k 2=70∴药物燃烧后的解析式为y =70x(x ≥10)；②在y =710x(0≤x ≤10)中，当y =75时x =2 ∵710>0∴当0≤x ≤10时，y 随x 增大而增大 ∴当2≤x ≤10时，学生不能在教室停留； 在y =70x (x ≥10)中，当y =75时x =50 ∵70>0∴当x ≥10时，y 随x 增大而减小∴当10≤x ≤50时，学生不能在教室停留； 综上所述，当2≤x ≤50时，学生不能在教室停留； （2）解：设要一次性燃烧完这种药物需t 分钟 同理可得当0≤x ≤t 时y =710x(0≤x ≤t)当药物刚好燃烧完时教室内每立方米空气含药量为t×710=7t10mg同理可得x≥t时y=7t 210x(x≥t)在y=710x(0≤x≤t)中，当y=0.7时x=1∴当1≤x≤t时为有效消毒时间；在y=7t 210 x (x≥t)中，当y=7t10x=0.7时x=t2∴当t≤x≤t2时为有效消毒时间；综上所述，当1≤x≤t2时为有效消毒时间∵有效消毒时间为120分钟∴t2−1=120解得t=11（负值舍去）∴要一次性燃烧完这种药物需11分钟第11 页共11 页。

中考数学《反比例函数》专项复习综合练习题-附含答案一、单选题1．已知反比例函数y=- 12x,则（）A．y随x的增大而增大B．当x>-3且x≠0时，y>4C．图象位于一、三象限D．当y<-3时，0<x<42．甲、乙、丙三位同学分别正确指出了某一个函数的一个性质．甲：函数图象经过第一象限；乙：函数图象经过第三象限；丙：每第一个象限内 y值随x值的增大而减小．根据他们的描述这个函数表达式可能是（）A．y=2x B．y= 2x C．y=﹣1xD．y=2x23．反比例函数y=kx(k>0)在第一象限内的图象如图，点M是图象上一点 MP垂直x轴于点P 如果△MOP 的面积为1 那么k的值是( )A．1 B．2 C．4 D．√24．如图，反比例函数y=kx(x<0)交边长为10的等边△ OAB的两边于C、D两点，OC＝3BD，则k的值（）A．−9√3B．9√3C．－10√3D．10√35．抛物线y=ax2+bx+c图象如图所示，则一次函数y=﹣bx﹣4ac+b2与反比例函数y= a+b+cx在同一坐标系内的图象大致为（）A．B．C．D．√3 6．如图，点D是▱OABC内一点，AD与x轴平行，BD与y轴平行，BD=√3∠BDC=120°S△BCD=92 (x<0)的图象经过C、D两点，则k的值是（）若反比例函数y=kxA．−6√3B．-6 C．−12√3D．-127．如图，已知在平面直角坐标系xOy中，O是坐标原点，点A是函数y=1（x＜0）图象上一点，AO的延长x（x＞0 k是不等于0的常数）的图象于点C，点A关于y轴的对称点为A′，点C关于x 线交函数y=k2x轴的对称点为C′，交于x轴于点B 连结AB AA′、 A′C′．若△ABC的面积等于6，则由线段AC CC′C′A′ A′A所围成的图形的面积等于（）A．8 B．10 C．3√10D．4√68．如图，反比例函数y=kx与一次函数y=kx﹣k+2在同一直角坐标系中的图象相交于A B两点其中A（﹣1 3）直线y=kx﹣k+2与坐标轴分别交于C D两点下列说法：①k＜0；②点B的坐标为（3 ﹣1）；③当x＜﹣1时kx ＜kx﹣k+2；④tan∠OCD=﹣1k其中正确的是（）A．①③B．①②④C．①③④D．①②③④二、填空题9．已知反比例函数y=﹣2x若y≤1，则自变量x的取值范围是．10．在平面直角坐标系中若一条平行于x轴的直线l分别交双曲线y=﹣6x 和y= 2x于A B两点 P是x轴上的任意一点，则△ABP的面积等于11．如图，在平面直角坐标系中正方形ABCD的面积为20 顶点A在y轴上顶点C在x轴上顶点D在双曲线y=kx(x>0)的图象上边CD交y轴于点E 若CE=ED，则k的值为.12．如图，点 P 是反比例函数图象上的一点 过点 P 向 x 轴作垂线 垂足为 M 连结 PO 若阴影部分面积为 6 ，则这个反比例函数的关系式是 ．13．如图，已知A （ 12 y 1） B （2 y 2）为反比例函数y ＝ 1x 图象上的两点 动点P （x 0）在x 轴正半轴上运动 当线段AP 与线段BP 之差达到最大时 点P 的坐标是 .三、解答题14．如图，反比例函数y =kx (x >0)的图像分别交正方形OABC 的边AB 、BC 于点D 、E 若A 点坐标为(1，0) 若△ODE 是等边三角形 求k 的值.15．某水果生产基地在气温较低时 用装有恒温系统的大棚栽培一种新品种水果 如图是试验阶段的某天恒温系统从开启到关闭后 大棚内的温度y(℃)与时间x(ℎ)之间的函数关系 其中线段AB 、BC 表示恒温系统开启后阶段 双曲线的一部分CD 表示恒温系统关闭阶段．．．．．．．．．．． 请根据图中信息解答下列问题：（1）这个恒温系统设定的恒定温度为多少℃；（2）求全天的温度y(℃)与时间x(ℎ)之间的函数表达式；（3）若大棚内的温度低于10℃时 蔬菜会受到伤害．问：这天内恒温系统最多可以关闭多少小时 才能避免水果生长受到影响？16．如图，已知点A在反比函数y=kx(k<0)的图象上点B在直线y=x−3的图象上点B的纵坐标为－1 AB⊥x轴且S△OAB=4．（1）求点A的坐标和k的值；（2）若点P在反比例函数y=kx(k<0)的图象上点Q在直线y=x−3的图象上P、Q两点关于y轴对称设点P的坐标为(m，n)求nm +mn的值．17．如图，点A在反比例函数y=kx(x>0)的图象上AB⊥x轴于点B AB的垂直平分线PD交双曲线与点P．（1）若点A的坐标为(1 8)，则点P的坐标为．（2）若AP⊥BP点A的横坐标为m．①求k与m之间的关系式；②连接OA OP若△AOP的面积为6 求k的值．18．如图，一次函数y＝k1x+b与反比例函数y＝k2x的图象交于A（2 m） B（n ﹣2）两点．过点B作BC⊥x轴垂足为C 且S△ABC＝5．（1）求一次函数与反比例函数的解析式；（2）根据所给条件请直接写出不等式k1x+b＞k2x的解集；（3）若P（p y1） Q（﹣2 y2）是函数y＝k2x 图象上的两点且y1≥y2求实数p的取值范围．答案1．D 2．B 3．B 4．A 5．D 6．C 7．B 8．C9．x ≤﹣2或x ＞0 10．4 11．4 12．y =−12x 13．(52, 0)14．解：由题意可得△OAD ≅△OCE 设AD =x ，则：DB =EB =1−x 因为OD 2=x 2+1 且△ODE 是等边三角形所以 x 2+1=(1−x)2+(1−x)2 x 1=2+√3 x 2=2−√3 2+√3>1舍去 所以x =2−√3则K =1∗(2−√3)=2−√315．（1）解：设线段AB 表达式为y =kx +b(k ≠0) ∵线段AB 过点(0，10) (2，14)∴{b =102k +b =14解得{b =10k =2∴线段AB 的表达式为：y =2x +10(0≤x ≤5) 当x =5时 y =2×5+10=20 ∴恒定温度为：20℃； （2）解：由（1）可知：线段AB 的表达式为：y =2x +10(0≤x ≤5) B 坐标为(5，20) ∴根据图象可知线段BC 的表达式为：y =20(5<x ≤10)设双曲线CD 解析式为：y =m x(m ≠0)∵C(10，20)∴可得：m10=20 解得：m =200∴双曲线CD 的解析式为：y =200x(10<x ≤24)∴y 关于x 的函数表达式为：y ={2x +10(0≤x ≤5)20(5<x ≤10)200x (10<x ≤24)；（3）解：把y =10代入y =200x中得10=200x解得：x =20∴20−10=10（小时）∴恒温系统最多可以关闭10小时． 16．（1）解：由题意B(2，−1)∵12×2×AB =4 ∴AB =4∵AB//y 轴∴A(2，−5)∵A(2，−5)在y =kx 的图象上 ∴k =−10.（2）解：设P(m ，−10m )，则Q(−m ，−10m ) ∵点Q 在y =x −3上∴−10m=−m −3 整理得：m 2+3m −10=0 解得m =−5或2 当m =−5 n =2时 n m +m n =−2910 当m =2 n =−5时 nm +m n=−2910故n m +m n=−2910.17．（1）（2 4）（2）解：①由题意得 点A 的纵坐标为km 即AB ＝km ∵PD 垂直平分AB ∴PA ＝PB ∵AP ⊥BP∴△PAB 是等腰直角三角形 ∴∠PAB ＝∠PBA ＝45° ∵PD ⊥AB∴△DAP 和△DBP 是等腰直角三角形 ∴DA ＝DB ＝DP ＝k2m ∴P （m +k2m ，k 2m ）将P （m +k2m ，k2m ）代入y =kx 可得：(m +k2m )⋅k2m =k 整理得：k =2m 2；②过点P 作PC ⊥x 轴于点C ，则四边形PABC 是梯形∵S △AOB ＝S △POC ＝k2 ∴S △AOE ＝S 四边形PEBC ∴S △AOP ＝S 梯形PABC ＝6 ∴(k 2m +k m )⋅k2m2=6 整理得：k 2=16m 2∵k =2m 2 ∴k 2=8k解得：k =8或k =0（舍去） ∴k =8．18．（1）把 A(2，m) B(n ，−2) 代入 y =k 2x得： k 2=2m =−2n即m=−n则A(2，−n)过A作AE⊥x轴于E过B作BF⊥y轴于F延长AE、BF交于D ∵A(2，−n)B(n，−2)∴BD=2−n AD=−n+2BC=|−2|=2∵SΔABC=12·BC·BD∴12×2×(2−n)=5解得：n=−3即A(2，3)B(−3，−2)把A(2，3)代入y=k2x得：k2=6即反比例函数的解析式是y=6x；把A(2，3)B(−3，−2)代入y=k1x+b得：{3=2k1+b−2=−3k1+b解得：k1=1b=1即一次函数的解析式是y=x+1；（2）∵A(2，3)B(−3，−2)∴不等式k1x+b>k2x的解集是−3<x<0或x>2；（3）分为两种情况：当点P在第三象限时要使y1⩾y2实数p的取值范围是p⩽−2当点P在第一象限时要使y1⩾y2实数p的取值范围是p>0即P的取值范围是p⩽−2或p>0。

中考数学《反比例函数》专项复习综合练习题-附带答案一、单选题1．已知函数y=kx的图象经过点（2，3 ），下列说法正确的是（）A．y随x的增大而增大B．函数的图象只在第一象限C．当x<0时必y<0D．点（-2 -3）不在此函数的图象上2．点A（x1， y1） B（x2， y2） C（x3， y3）在反比例函数y＝πx的图象上，若x1＜x2＜0＜x3，则y1 y2 y3的大小关系是（）A．y1＞y2＞y3B．y3＞y2＞y1C．y2＞y1＞y3D．y3＞y1＞y23．研究发现近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系小明佩戴的400度近视镜片的焦距为0.25米经过一段时间的矫正治疗加之注意用眼健康现在镜片焦距为0.5米，则小明的近视镜度数可以调整为（）A．200度B．250度C．300度D．500度4．如图，点M为反比例函数y＝1x上的一点过点M作x轴 y轴的垂线分别交直线y＝-x+b于C D 两点若直线y＝-x+b分别与x轴 y轴相交于点A、B，则AD·BC的值是（）A．3 B．2 √2C．2 D．√55．如图，在菱形OABC中，点A的坐标为(10,0)，对角线OB、AC相交于点D,OB⋅AC=160 .双曲线y=kx(x>0)经过点D，交BC的延长线于点E，则过点E的双曲线表达式为（）A．y=20x B．y=24xC．y=28xD．y=32x6．如图，已知一次函数y 1=kx+b 的图象与反比例函数y 2= 4x 的图象交于（2 m ）和（n ﹣1）两点 观察图象 下列判断正确的是（ ）A ．当x ＞2时 y 1＜y 2B ．当x ＜2时 y 1＜y 2C ．当x ＞n 时 y 1＜y 2D ．当x ＜n 时 y 1＜y 27．如图，在函数y 1=k1x （x ＜0）和y 2=k2x （x ＞0）的图象上 分别有A 、B 两点 若AB ∥x 轴 交y 轴于点C 且OA ⊥OB S △AOC =32 S △BOC =272，则线段AB 的长度是（ ）A ．8B ．9C ．10D ．118．如图，直线y= √3 x ﹣6分别交x 轴 y 轴于A B M 是反比例函数y= kx （x ＞0）的图象上位于直线上方的一点 MC ∥x 轴交AB 于C MD ⊥MC 交AB 于D AC •BD=4 √3 ，则k 的值为（ ）A ．﹣3B ．﹣4C ．﹣5D ．﹣6二、填空题9．当n= 时 函数y=2x n ﹣1是反比例函数．(k<0)的图象上，则y1，y2，y3的从小10．若点A(−3，y1)，B(−1，y2)，C(2，y3)都在反比例函数y=kx到大的关系是．有一个关于x的函数不论x取何值 y的解析式总是取y1、y2、y3中11．已知函数y1=x y2=x2和y3=1x的值的较小的一个，则y的最大值等于12．如图，已知函数y=−3与y=ax2+bx+c（a＞0 b＞0）的图象相交于点P 且点P的纵坐标为1，则关于x=0的解是x的方程ax2+bx+3x（k＞0）与长方形OABC在第一象限相交于D、E两点 OA=2 OC=4 连结OD、13．如图，反比例函数y=kxOE、DE．记△OAD、△OCE的面积分别为S1、S2．填空：①点B坐标为；②S1S2（填“＞”、“＜”、“=”）；三、解答题14．如图，根据小孔成像的科学原理当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时火焰的像高y(单位：cm)是物距(小孔到蜡烛的距离)x(单位：cm)的反比例函数当x=6时y=2．（1）求y 关于x 的函数解析式．（2）若火焰的像高为3cm 求小孔到蜡烛的距离．15．某学校的自动饮水机 开机加热时水温每分钟上升20℃ 水温到100℃时停止加热．此后水温开始下降．水温y(℃)与开机通电时间x(min)成反比例关系．若水温在20℃时接通电源．一段时间内 水温y 与通电时间x 之间的函数关系如图所示．（1）水温从20℃加热到100℃ 需要 min ；（2）求水温下降过程中 y 与x 的函数关系式 并写出自变量取值范围； （3）如果上午8点接通电源 那么8：20之前 不低于80℃的时间有多少？ 16．如图，在平面直角坐标系xOy 中 一次函数y1=ax+b （a b 为常数 且a ≠0）与反比例函数y2 = mx （m为常数 且m ≠0）的图象交于点A （-2 1）、B （1 n ）．（1）求反比例函数和一次函数的解析式； （2）连结OA 、OB 求△AOB 的面积；（3）直接写出当y 1＜y 2＜0时 自变量x 的取值范围．17．你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面 面条的总长度y （m ）是面条的粗细（横截面积）S （mm 2）的反比例函数 其图象如图所示．（1）写出y与S的函数关系式：．（2）当面条粗 1.6mm 2时面条总长度是 m．18．如图，在平面直角坐标系xOy中已知四边形DOBC是矩形且D(0 4) B(6 0).若反比例函数y＝k1(x>0)的图象经过线段OC的中点A 交DC于点E 交BC于点F.设直线EF的表达式为y＝k2x＋b.x（1）求反比例函数和直线EF的表达式；（2）求△OEF的面积；（3）请结合图象直接写出不等式k2x＋b－k1>0的解集.x参考答案1．C2．D3．A4．C5．D6．D7．C8．A9．010．y3<y1<y211．112．x=﹣3 y=113．（4 2）；=14．（1）解：由题意设：y=kx把x=6y=2代入得k=6×2=12∴y关于x的函数解析式为：y=12x；（2）解：把y=3代入y=12x得x=4∴小孔到蜡烛的距离为4cm．15．（1）4（2）解：如图设函数解析式为y=kx代入点(4，100)可得∴y=400 x当y=20时x=40020=20∴水温下降过程中y与x的函数关系式是y=400x(4⩽x⩽20)（3）解：由计算可知水温从20∘C开始加热到100∘C再冷却到20∘C 需4+20=24分钟水温从20∘C加热到80∘C所需要时间为：80−2020=3（分钟）令y =80，则x =40080=5∴水温不低于80∘C 的时间为5−3=2（分钟） 答：不低于80∘C 的时间有2分钟. 16．（1）解：∵A （-2 1）∴将A 坐标代入反比例函数解析式y 2= mx 中 得m=-2 ∴反比例函数解析式为y=- 2x ； 将B 坐标代入y=- 2x 得n=-2 ∴B 坐标（1 -2）将A 与B 坐标代入一次函数解析式中 得 {−2a +b =1a +b =−2解得a=-1 b=-1∴一次函数解析式为y 1=-x-1 （2）解：设直线AB 与y 轴交于点C 令x=0 得y=-1 ∴点C 坐标（0 -1）∴S △AOB =S △AOC +S △COB = 12 ×1×2+ 12 ×1×1= 32 ；（3）解：由图象可得 当y 1＜y 2＜0时 自变量x 的取值范围x ＞1．17．（1）y= 128S（2）8018．（1）∵四边形DOBC 是矩形 且D （0 4） B （6 0） ∴C 点坐标为（6 4） ∵点A 为线段OC 的中点 ∴A 点坐标为（3 2） ∴k 1=3×2=6∴反比例函数解析式为y= 6x ；把x=6代入y= 6x 得y=1，则F 点的坐标为（6 1） 把y=4代入y= 6x 得x= 32 ，则E 点坐标为（ 32 4） 把F 、E 的坐标代入y=k 2x+b 得 {6k 2+b ＝132k 2+b ＝4 解得 {k 2＝−23b ＝5∴直线EF 的解析式为y=- 23 x+5；（2）△OEF 的面积=S 矩形BCDO -S △ODE -S △OBF -S △CEF= 4×6−12×4×32−12×6×1−12×（6−32）×（4−1） = 454 .（3）结合函数图象 写出直线在反比例函数图象上方所对应的自变量的范围 即可得到不等式k 2x ＋b －k 1x >0的解因为E 点坐标为（ 324） F 点的坐标为（6 1），则k 2x ＋b － k1x>0解是： 32<x<6。

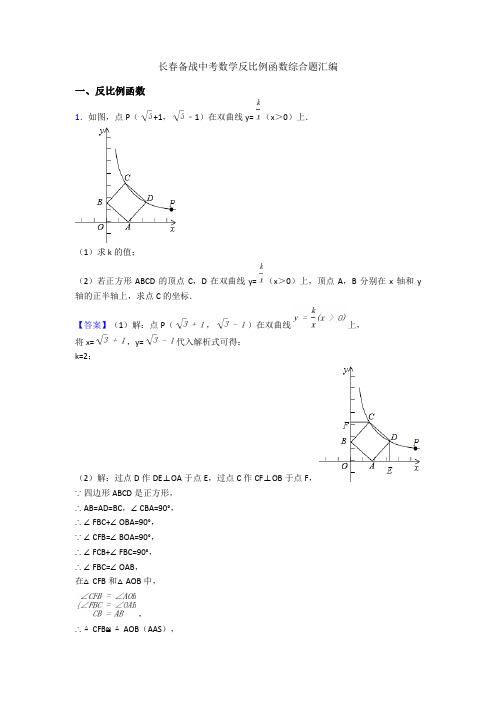
长春备战中考数学反比例函数综合题汇编一、反比例函数1．如图，点P（ +1，﹣1）在双曲线y= （x＞0）上．（1）求k的值；（2）若正方形ABCD的顶点C，D在双曲线y= （x＞0）上，顶点A，B分别在x轴和y 轴的正半轴上，求点C的坐标．【答案】（1）解：点P（，）在双曲线上，将x= ，y= 代入解析式可得：k=2；（2）解：过点D作DE⊥OA于点E，过点C作CF⊥OB于点F，∵四边形ABCD是正方形，∴AB=AD=BC，∠CBA=90°，∴∠FBC+∠OBA=90°，∵∠CFB=∠BOA=90°，∴∠FCB+∠FBC=90°，∴∠FBC=∠OAB，在△CFB和△AOB中，，∴△CFB≌△AOB（AAS），同理可得：△BOA≌△AED≌△CFB，∴CF=OB=AE=b，BF=OA=DE=a，设A（a，0），B（0，b），则D（a+b，a）C（b，a+b），可得：b（a+b）=2，a（a+b）=2，解得：a=b=1．所以点C的坐标为：（1，2）．【解析】【分析】（1）由待定系数法把P坐标代入解析式即可；（2）C、D均在双曲线上，它们的坐标就适合解析式，设出C坐标，再由正方形的性质可得△CFB≌△AOB△BOA≌△AED≌△CFB，代入解析式得b（a+b）=2，a（a+b）=2，即可求出C坐标.2．如图，在平面直角坐标系中，平行四边形的边，顶点坐标为，点坐标为 .（1）点的坐标是________，点的坐标是________（用表示）；（2）若双曲线过平行四边形的顶点和，求该双曲线的表达式；（3）若平行四边形与双曲线总有公共点，求的取值范围.【答案】（1）；（2）解：∵双曲线过点和点，∴，解得，∴点的坐标为，点的坐标为，把点的坐标代入，解得，∴双曲线表达式为（3）解：∵平行四边形与双曲线总有公共点，∴当点在双曲线，得到，当点在双曲线，得到，∴的取值范围 .【解析】【分析】（1）由四边形ABCD为平行四边形，得到A与B纵坐标相同，C与D纵坐标相同，横坐标相差2，得出B、C坐标即可；（2）根据B与D在反比例图象上，得到C与D横纵坐标乘积相等，求出b的值确定出B坐标，进而求出k的值，确定出双曲线解析式；（3）抓住两个关键点，将A坐标代入双曲线解析式求出b的值；将C坐标代入双曲线解析式求出b的值，即可确定出平行四边形与双曲线总有公共点时b的范围．3．如图，在平面直角坐标系中，矩形OADB的顶点A，B的坐标分别为A（﹣6，0），B （0，4）．过点C（﹣6，1）的双曲线y= （k≠0）与矩形OADB的边BD交于点E．（1）填空：OA=________，k=________，点E的坐标为________；（2）当1≤t≤6时，经过点M（t﹣1，﹣ t2+5t﹣）与点N（﹣t﹣3，﹣ t2+3t﹣）的直线交y轴于点F，点P是过M，N两点的抛物线y=﹣ x2+bx+c的顶点．①当点P在双曲线y= 上时，求证：直线MN与双曲线y= 没有公共点；②当抛物线y=﹣ x2+bx+c与矩形OADB有且只有三个公共点，求t的值；③当点F和点P随着t的变化同时向上运动时，求t的取值范围，并求在运动过程中直线MN在四边形OAEB中扫过的面积．【答案】（1）6；-6；（﹣，4）（2）解：①设直线MN解析式为：y1=k1x+b1由题意得：解得∵抛物线y=﹣过点M、N∴解得∴抛物线解析式为：y=﹣ x2﹣x+5t﹣2∴顶点P坐标为（﹣1，5t﹣）∵P在双曲线y=﹣上∴（5t﹣）×（﹣1）=﹣6∴t=此时直线MN解析式为：联立∴8x2+35x+49=0∵△=352﹣4×8×48=1225﹣1536＜0∴直线MN与双曲线y=﹣没有公共点．②当抛物线过点B，此时抛物线y=﹣ x2+bx+c与矩形OADB有且只有三个公共点∴4=5t﹣2，得t=当抛物线在线段DB上，此时抛物线与矩形OADB有且只有三个公共点∴，得t=∴t= 或t=③∵点P的坐标为（﹣1，5t﹣）∴y P=5t﹣当1≤t≤6时，y P随t的增大而增大此时，点P在直线x=﹣1上向上运动∵点F的坐标为（0，﹣）∴y F=﹣∴当1≤t≤4时，随者y F随t的增大而增大此时，随着t的增大，点F在y轴上向上运动∴1≤t≤4当t=1时，直线MN：y=x+3与x轴交于点G（﹣3，0），与y轴交于点H（0，3）当t=4﹣时，直线MN过点A．当1≤t≤4时，直线MN在四边形AEBO中扫过的面积为S=【解析】【解答】解：（1）∵A点坐标为（﹣6，0）∴OA=6∵过点C（﹣6，1）的双曲线y=∴k=﹣6y=4时，x=﹣∴点E的坐标为（﹣，4）故答案为：6，﹣6，（﹣，4）【分析】（1）根据A点的坐标即可得出OA的长，将C点的坐标代入双曲线y=，即可求出k的值，得出双曲线的解析式，根据平行于x轴的直线上的点的坐标特点得出点E的纵坐标为4，将y=4代入双曲线的解析式即可算出对应的自变量的值，从而得出E点的坐标；（2）①用待定系数法求出直线MN解析式，将M,N两点的坐标代入抛物线y=﹣x2+bx+c，得出关于b,c的方程组，求解得出b,c的值，根据顶点坐标公式表示出P点的坐标，再将P点的坐标代入双曲线即可求出t的值，从而得出直线MN解析式，解联立直线MN解析式与双曲线的解析式组成的方程组，根据根的判别式的值小于0，得出直线MN与双曲线没有公共点；②当抛物线过点B，此时抛物线y=﹣x2+bx+c与矩形OADB有且只有三个公共点，故4=5t﹣2，求解得出t的值，当抛物线在线段DB上，此时抛物线与矩形OADB有且只有三个公共点，故,求解得出t的值，综上所述得出答案；③根据P点的坐标判断出当1≤t≤6时，y P随t的增大而增大，此时，点P在直线x=﹣1上向上运动进而表示出F点的坐标，将F点的纵坐标配成顶点式，得出当1≤t≤4时，随者y F随t的增大而增大，此时，随着t的增大，点F在y轴上向上运动，故1≤t≤4，当t=1时，直线MN：y=x+3与x轴交于点G（﹣3，0），与y轴交于点H（0，3），当t=4﹣时，直线MN过点A．根据割补法算出当1≤t≤4时，直线MN在四边形AEBO中扫过的面积。

吉林省长春市数学中考复习综合专题：反比例函数应用姓名:________ 班级:________ 成绩:________一、综合题 (共30题；共360分)1. （10分） (2020八下·杭州期末) 已知一次函数y=3x+m的图象与反比例函数y= 的图象交于点A(1，a)，B(-2，-3)。

（1）求一次函数，反比例函数的表达式。

（2）设点C(t，y1)，D(t、y2)分别是一次函数和反比例函数图象上的点，当y1>y2时，求t的取值范围。

（3）设点E(x1 ， 2)，F(x2 ， 2)分别是一次函数和反比例函数图象上的点，点G是反比例函数图象上与点F成中心对称的点，求△GEF的面积。

2. （10分） (2017九上·温江期末) 如图，直线y= x+2与双曲线相交于点A（m，3），与x轴交于点C．（1）求双曲线解析式；（2）点P在x轴上，如果△ACP的面积为3，求点P的坐标．3. （10分）(2017·湖州模拟) 阅读下面材料：如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2= 交于A（1，3）和B（﹣3，﹣1）两点．观察图象可知：当x=﹣3或1时，y1=y2 ．（1）通过观察函数的图象，可以得到不等式ax+b＞的解集________．（2）参考观察函数的图象方法，解决问题：关于x的不等式x2+a﹣＜0（a＞0）只有一个整数解，则a 的取值范围________．4. （10分）如图，直线y=2x与反比例函数y=（k≠0，x＞0）的图象交于点A（1，a），点B是此反比例函数图形上任意一点（不与点A重合），BC⊥x轴于点C．（1）求k的值；（2）求△OBC的面积.5. （11分）(2019·陇南模拟) 如图，在平面直角坐标系中，函数的图象经过点P（4，3）和点B（m，n）（其中0＜m＜4），作BA⊥x轴于点A，连接PA，PB，OB，已知S△AOB＝S△PAB ．（1）求k的值和点B的坐标．（2）求直线BP的解析式．（3）直接写出在第一象限内，使反比例函数大于一次函数的x的取值范围是________．6. （10分） (2017九上·黑龙江月考) 如图一次函数y=kx+b与反比例函数y= （x＞0）的图象交于A（1，6），B（n，2）两点．（1）求一次函数和反比例函数的解析式（2）求△AOB的面积．7. （15分）(2019·萧山模拟) 已知一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于点A（2，2），B（﹣1，a）（1）求一次函数和反比例函数的表达式；（2）设点P（h，y1），Q（h，y2）分别是两函数图象上的点；①试直接写出当y1＞y2时h的取值范围；②若y1﹣y2＝2，试求h的值.8. （10分）如图是某一蓄水池的排水速度与排完水池中的水所用的时间t（h）之间的函数关系图象．（1）请你根据图象提供的信息求出此蓄水池的蓄水量；（2）写出此函数的表达式；（3）若要6 h排完水池中的水，那么每小时的排水量应该是多少？（4）如果每小时排水量是，那么水池中的水要用多少小时排完？9. （15分） (2020八下·射阳期中) 某气象研究中心观测到一场沙尘暴从发生到减弱的过程，开始一段时间风速平均每小时增加2千米，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米，然后风速不变，当沙尘暴遇到绿色植被区时，风速y（千米/小时），时间x（小时）成反比例关系地慢慢减弱，结合风速与时间的图象，回答下列问题：（1）这场沙尘暴的最高风速是多少？最高风速维持了多长时间；（2）求出当x≥20时，风速y（千米/小时）与时间x（小时）之间的函数关系？（3）在这次沙尘暴的形成过程中，当风速不超过10千米/小时称为“安全时刻”，其余时刻是“危险时刻”.问这次风暴的整个过程中，“危险时刻”一共有多长时间？10. （15分）某小学为每个班级配备了一种可以加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10℃，待加热到100℃，饮水机自动停止加热，水温开始下降，水温y（℃）和通电时间x（min）成反比例关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温为20℃，接通电源后，水温和时间的关系如下图所示，回答下列问题：（1）分别求出当0≤x≤8和8＜x≤a时，y和x之间的关系式；（2）求出图中a的值；（3）李老师这天早上7：30将饮水机电源打开，若他想再8：10上课前能喝到不超过40℃的开水，问他需要在什么时间段内接水．11. （15分）(2018·宁晋模拟) 为了筹款支持希望工程，某“爱心”小组决定利用暑假销售一批进价为10元的小商品，为寻求合适的销售价格，他们进行了试销，试销情况如表：第1天第2天第3天第4天……日单价x（元）20304050……日量y（个）30201512……（1）若y是x的反比例函数，请求出这个函数关系式；（2）若该小组计划每天的销售利润为450元，则其单价应为多少元？12. （6分） (2017八下·简阳期中) 如图，反比例函数y= 的图象与一次函数y=x+b的图象交于点A（1，4）、点B（﹣4，n）．（1）求一次函数和反比例函数的解析式；（2）求△OAB的面积；（3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．13. （11分） (2017九上·江津期中) 如图，一次函数y=ax -2(a¹0)的图象与反比例函数 y= (k¹0)的图象交于A、B两点，且与x轴、y轴分别交于点C、D．已知tan∠AOC= ，AO= ．（1）求这个一次函数和反比例函数的解析式；（2）若点 F 是点D 关于 x 轴的对称点，求△ABF 的面积．14. （10分）(2017·淅川模拟) 如图，在平面直角坐标系xOy中，矩形OEFG的顶点E的坐标为（4，0），顶点G的坐标为（0，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．（1）求图象经过点A的反比例函数的解析式；（2）设（2）中的反比例函数图象交EF于点B，直接写出直线AB的解析式．15. （11分）(2017·苏州模拟) 如图，在平面直角坐标系中，函数y= （x＞0，k是常数）的图象经过A（2，6），B（m，n），其中m＞2．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，AC与BD交于点E，连结AD，DC，CB．（1）若△ABD的面积为3，求k的值和直线AB的解析式；（2）求证： = ；（3）若AD∥BC，求点B的坐标．16. （15分）(2018·柘城模拟) 如图，∠AOB=90°，反比例函数y=﹣（x＜0）的图象过点A（﹣1，a），反比例函数y= （k＞0，x＞0）的图象过点B，且AB∥x轴．（1）求a和k的值；（2）过点B作MN∥OA，交x轴于点M，交y轴于点N，交双曲线y= 于另一点C，求△OBC的面积．17. （15分）(2018·高邮模拟) 如图，在平面直角坐标系中，一次函数y=ax+b的图象与反比例函数y= 的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，-2），tan∠BOC= ．（1）求该反比例函数和一次函数的解析式．（2）求△BOC的面积．（3） P是x轴上的点，且△PAC的面积与△BOC的面积相等，求P点的坐标．18. （15分） (2020八下·长兴期末) 如图，已知一次函数y=3x的图象与反比例函数y= 的图象交于点A(a，3)。

长春中考数学备考之反比例函数压轴突破训练∶培优篇一、反比例函数1．如图，在平面直角坐标系中，反比例函数y= 的图象与一次函数y=ax+b的图象交于点A（﹣2，3）和点B（m，﹣2）．（1）求反比例函数和一次函数的解析式；（2）直线x=1上有一点P，反比例函数图象上有一点Q，若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形，直接写出点Q的坐标．【答案】（1）解：∵点A（﹣2，3）在反比例函数y= 的图形上，∴k=﹣2×3=﹣6，∴反比例函数的解析式为y=﹣，∵点B在反比例函数y=﹣的图形上，∴﹣2m=﹣6，∴m=3，∴B（3，﹣2），∵点A，B在直线y=ax+b的图象上，∴，∴，∴一次函数的解析式为y=﹣x+1（2）解：∵以A、B、P、Q为顶点的四边形是以AB为边的平行四边形，∴AB=PQ，AB∥PQ，设直线PQ的解析式为y=﹣x+c，设点Q（n，﹣），∴﹣ =﹣n+c，∴c=n﹣，∴直线PQ的解析式为y=﹣x+n﹣，∴P（1，n﹣﹣1），∴PQ2=（n﹣1）2+（n﹣﹣1+ ）2=2（n﹣1）2，∵A（﹣2，3）．B（3，﹣2），∴AB2=50，∵AB=PQ，∴50=2（n﹣1）2，∴n=﹣4或6，∴Q（﹣4. ）或（6，﹣1）【解析】【分析】（1）先利用待定系数法求出反比例函数解析式，进而求出点B的坐标，再用待定系数法求出直线解析式；（2）先判断出AB=PQ，AB∥PQ，设出点Q的坐标，进而得出点P的坐标，即可求出PQ，最后用PQ=AB建立方程即可得出结论．2．如图，点P（x，y1）与Q（x，y2）分别是两个函数图象C1与C2上的任一点．当a≤x≤b 时，有﹣1≤y1﹣y2≤1成立，则称这两个函数在a≤x≤b上是“相邻函数”，否则称它们在a≤x≤b 上是“非相邻函数”．例如，点P（x，y1）与Q （x，y2）分别是两个函数y=3x+1与y=2x﹣1图象上的任一点，当﹣3≤x≤﹣1时，y1﹣y2=（3x+1）﹣（2x﹣1）=x+2，通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质，得到该函数值的范围是﹣1≤y≤1，所以﹣1≤y1﹣y2≤1成立，因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”．（1）判断函数y=3x+2与y=2x+1在﹣2≤x≤0上是否为“相邻函数”，并说明理由；（2）若函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”，求a的取值范围；（3）若函数y= 与y=﹣2x+4在1≤x≤2上是“相邻函数”，直接写出a的最大值与最小值．【答案】（1）解：是“相邻函数”，理由如下：y1﹣y2=（3x+2）﹣（2x+1）=x+1，构造函数y=x+1，∵y=x+1在﹣2≤x≤0，是随着x的增大而增大，∴当x=0时，函数有最大值1，当x=﹣2时，函数有最小值﹣1，即﹣1≤y≤1，∴﹣1≤y1﹣y2≤1，即函数y=3x+2与y=2x+1在﹣2≤x≤0上是“相邻函数”（2）解：y1﹣y2=（x2﹣x）﹣（x﹣a）=x2﹣2x+a，构造函数y=x2﹣2x+a，∵y=x2﹣2x+a=（x﹣1）2+（a﹣1），∴顶点坐标为：（1，a﹣1），又∵抛物线y=x2﹣2x+a的开口向上，∴当x=1时，函数有最小值a﹣1，当x=0或x=2时，函数有最大值a，即a﹣1≤y≤a，∵函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”，∴﹣1≤y1﹣y2≤1，即，∴0≤a≤1（3）解：y1﹣y2= ﹣（﹣2x+4）= +2x﹣4，构造函数y= +2x﹣4，∵y= +2x﹣4∴当x=1时，函数有最小值a﹣2，当x=2时，函数有最大值，即a﹣2≤y≤ ，∵函数y= 与y=﹣2x+4在1≤x≤2上是“相邻函数”，∴﹣1≤y1﹣y2≤1，即，∴1≤a≤2；∴a的最大值是2，a的最小值1【解析】【分析】（1）y1﹣y2=（3x+2）﹣（2x+1）=x+1，构造函数y=x+1，因为y=x+1在﹣2≤x≤0，是随着x的增大而增大，所以当x=0时，函数有最大值1，当x=﹣2时，函数有最小值﹣1，即﹣1≤y≤1，所以﹣1≤y1﹣y2≤1，即函数y=3x+2与y=2x+1在﹣2≤x≤0上是“相邻函数”；（2）y1﹣y2=（x2﹣x）﹣（x﹣a）=x2﹣2x+a，构造函数y=x2﹣2x+a，因为y=x2﹣2x+a=（x﹣1）2+（a﹣1），所以顶点坐标为：（1，a﹣1），又抛物线y=x2﹣2x+a的开口向上，所以当x=1时，函数有最小值a﹣1，当x=0或x=2时，函数有最大值a，即a﹣1≤y≤a，因为函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”，所以﹣1≤y1﹣y2≤1，即0≤a≤1；（3）当x=1时，函数有最小值a﹣2，当x=2时，函数有最大值，因为函数y=与y=﹣2x+4在1≤x≤2上是“相邻函数”，﹣1≤y1﹣y2≤1，即1≤a≤2，所以a的最大值是2，a 的最小值1.3．如图，一次函数y=kx+b的图象交反比例函数y= （x＞0）的图象于A（4，-8）、B （m，-2）两点，交x轴于点C．（1）求反比例函数与一次函数的关系式；（2）根据图象回答：当x为何值时，一次函数的值大于反比例函数的值？（3）以O、A、B、P为顶点作平行四边形，请直接写出点P的坐标．【答案】（1）解：∵反比例函数y= （x＞0）的图象于A（4，-8），∴k=4×（-8）=-32．∵双曲线y= 过点B（m，-2），∴m=16．由直线y=kx+b过点A，B得：，解得，，∴反比例函数关系式为，一次函数关系式为（2）解：观察图象可知，当0＜x＜4或x＞16时，一次函数的值大于反比例函数的值（3）解：∵O（0，0），A（4，-8）、B（16，-2），分三种情况：①若OB∥AP，OA∥BP，∵O（0，0），A（4，-8），∴由平移规律，点B（16，-2）向右平移4个单位，向下平移8个单位得到P点坐标为（20，-10）；②若OP∥AB，OA∥BP，∵A（4，-8），B（16，-2），∴由平移规律，点O（0，0）向右平移12个单位，向上平移6个单位得到P点坐标为（12，6）；③若OB∥AP，OP∥AB，∵B（16，-2），A（4，-8），∴由平移规律，点O（0，0）向左平移12个单位，向下平移6个单位得到P点坐标为（-12，-6）；∴以O，A，B，P为顶点作平行四边形，第四个顶点P的坐标为（12，6）或（-12，-6）或（20，-10）【解析】【分析】（1）将点A（4，-8），B（m，-2）代入反比例函数y= （x＞0）中，可求k、a；再将点A（4，-8），B（m，-2）代入y=kx+b中，列方程组求k、b即可；（2）根据两函数图象的交点，图象的位置可确定一次函数的值大于反比例函数的值时x的范围；（3）根据平行四边形的性质，即可直接写出．4．如图，过原点O的直线与双曲线交于上A（m，n）、B，过点A的直线交x轴正半轴于点D，交y轴负半轴于点E，交双曲线于点P.（1）当m＝2时，求n的值；（2）当OD：OE＝1：2，且m＝3时，求点P的坐标；（3）若AD＝DE，连接BE，BP，求△PBE的面积.【答案】（1）解：∵点A（m，n）在双曲线y＝上，∴mn＝6，∵m＝2，∴n＝3；（2）解：由（1）知，mn＝6，∵m＝3，∴n＝2，∴A（3，2），∵OD：OE＝1：2，设OD＝a，则OE＝2a，∵点D在x轴坐标轴上，点E在y轴负半轴上，∴D（a，0），E（0，﹣2a），∴直线DE的解析式为y＝2x﹣2a，∵点A（3，2）在直线y＝2x﹣2a上，∴6﹣2a＝2，∴a＝2，∴直线DE的解析式为y＝2x﹣4①，∵双曲线的解析式为y＝②，联立①②解得，（点A的横纵坐标，所以舍去）或，∴P（﹣2，﹣3）；（3）解：∵AD＝DE，点D在x轴坐标轴上，点E在y轴负半轴上，A（m，n），∴E（0，﹣n），D（ m，0），∴直线DE的解析式为y＝ x﹣n，∵mn＝6，∴m＝，∴y＝ x﹣n③，∵双曲线的解析式为y＝④，联立③④解得，∴（点A的横纵坐标，所以舍去）或，∴P（﹣2m，﹣2n），∵A（m，n），∴直线AB的解析式为y＝x⑤.联立④⑤解得，（点A的横纵坐标，所以舍去）或∴B（﹣m，﹣n），∵E（0，﹣n），∴BE∥x轴，∴S△PBE＝ BE×|y E﹣y P|＝ ×m×|﹣n﹣（﹣2n）|＝ mn＝3.【解析】【分析】（1）把A（2，n）代入解析式即可求出n；（2）先求出A点坐标，设OD＝a，则OE＝2a，得D（a，0），E（0，﹣2a），直线DE的解析式为y＝2x﹣2a，把点A（3，2）代入求出a，再联立两函数即可求出交点P；（3）由AD＝DE，点D在x轴坐标轴上，点E在y轴负半轴上，故A（m，n），E（0，﹣n），D（ m，0），求得直线DE的解析式为y＝ x﹣n，又mn＝6，得y＝ x﹣n，与y＝联立得，即为P点坐标，由直线AB的解析式为y＝ x与双曲线联立解得B （﹣m，﹣n），再根据S△PBE＝ BE×|y E﹣y P|＝ ×m×|﹣n﹣（﹣2n）|求出等于3.5．如图，在平面直角坐标系中，直线与双曲线相交于点A（，6）和点B（-3，），直线AB与轴交于点C．（1）求直线AB的表达式；（2）求的值．【答案】（1）解：∵点A（，6）和点B（-3，）在双曲线，∴m=1，n=-2，∴点A（1，6），点B（-3，-2），将点A、B代入直线，得，解得，∴直线AB的表达式为：（2）解：分别过点A、B作AM⊥y轴，BN⊥y轴，垂足分别为点M、N，则∠AMO＝∠BNO＝90°，AM=1，BN=3，∴AM//BN，∴△ACM∽△BCN，∴【解析】【分析】根据反比例函数的解析式可得m和n的值，利用待定系数法求一次函数的表达式；作辅助线，构建平行线，根据平行线分线段成比例定理可得结论．6．在平面直角坐标系xOy中，反比例函数的图象经过点A（1，4），B（m，n）．（1）求反比例函数的解析式；（2）若二次函数的图象经过点B，求代数式的值；（3）若反比例函数的图象与二次函数的图象只有一个交点，且该交点在直线y＝x的下方，结合函数图象，求a的取值范围．【答案】（1）解：将A（1，4）代入函数y＝得：k=4反比例函数y＝的解析式是（2）解：∵B（m，n）在反比例函数y＝上，∴mn=4，又二次函数y＝（x－1）2的图象经过点 B（m，n），∴即n-1=m2-2m∴（3）解：由反比例函数的解析式为，令y＝x，可得x2＝4，解得x＝±2．∴反比例函数的图象与直线y＝x交于点（2，2），（－2，－2）．如图，当二次函数y＝a（x－1）2的图象经过点（2，2）时，可得a＝2；当二次函数y＝a（x－1）2的图象经过点（－2，－2）时，可得a＝－ .∵二次函数y＝a（x－1）2图象的顶点为（1，0），∴由图象可知，符合题意的a的取值范围是0＜a＜2或a＜－ .【解析】【分析】（1）只需将点A的坐标代入反比例函数的解析式就可得出答案。

长春备战中考数学培优专题复习反比例函数练习题一、反比例函数1．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y 随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？【答案】（1）解：设线段AB所在的直线的解析式为y1=k1x+20，把B（10，40）代入得，k1=2，∴y1=2x+20．设C、D所在双曲线的解析式为y2= ，把C（25，40）代入得，k2=1000，∴当x1=5时，y1=2×5+20=30，当，∴y1＜y2∴第30分钟注意力更集中．（2）解：令y1=36，∴36=2x+20，∴x1=8令y2=36，∴，∴∵27.8﹣8=19.8＞19，∴经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目．【解析】【分析】（1）根据一次函数和反比例函数的应用，用待定系数法求出线段AB所在的直线的解析式，和C、D所在双曲线的解析式；把x1=5时和进行比较得到y1＜y2，得出第30分钟注意力更集中；（2）当y1=36时，得到x1=8，当y2=36，得到，由27.8﹣8=19.8＞19，所以经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目.2．在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为梦之点，例如，点（1，1），（﹣ 2，﹣ 2），（，），…，都是梦之点，显然梦之点有无数个．（1）若点P（2，b）是反比例函数 (n为常数，n≠0)的图象上的梦之点，求这个反比例函数解析式；（2）⊙O的半径是，①求出⊙O上的所有梦之点的坐标；②已知点M（m，3），点Q是（1）中反比例函数图象上异于点P的梦之点，过点Q的直线l与y轴交于点A，∠OAQ＝45°．若在⊙O上存在一点N，使得直线MN∥l或MN⊥l，求出m的取值范围．【答案】（1）解：∵P（2，b）是梦之点，∴b=2∴P（2，2）将P（2，2）代入中得n=4∴反比例函数解析式是（2）解：①设⊙O上梦之点坐标是（，）∴∴=1或 =-1∴⊙O上所有梦之点坐标是（1，1）或（-1，-1）②由（1）知，异于点P的梦之点Q的坐标为（-2，-2）由已知MN∥l或MN⊥l∴直线MN为y=-x+b或y=x+b当MN为y=-x+b时，m=b-3由图可知，当直线MN平移至与⊙O相切时，且切点在第四象限时，b取得最小值，此时MN记为，其中为切点，为直线与y轴的交点∵△O 为等要直角三角形，∴O =∴O =2∴b的最小值是-2，∴m的最小值是-5当直线MN平移至与⊙O相切时，且切点在第二象限时，b取得最大值，此时MN记为，其中为切点，为直线与y轴的交点。

中考数学一轮复习《反比例函数》专项练习题-附带参考答案学校:___________班级：___________姓名：___________考号：___________一、选择题1．若反比例函数y=k−1x的图象经过点(−1，−2)，则k的值是（）A．−1B．1C．−3D．32．已知反比例函数kyx=(0k≠)的图象经过点(3，2-)，则该函数的图象还经过点（）A．(3,2)B．(3-,2-)C．(32,4-)D．(32-,4-)3．在同一平面直角坐标系中，反比例函数y=kx与一次函数y=kx−k（k为常数，且k≠0）的图象可能是（）A．B．C．D．4．若点A(−1，y1)，B(1，y2)，C(3，y3)在反比例函数y=9x的图像上，则y1，y2，y3的大小关系是（）A．y1<y2<y3B．y1<y3<y2C．y2<y3<y1D．y3<y2<y15．关于函数y=−1x的图像，下列说法错误的是（）A．该函数图象是双曲线B．经过点(1，1)C．在第二象限内，y随x的增大而增大D．是中心对称图，且对称中心是坐标原点6．如图，点A是反比例函数4yx=-图象上的一个动点，过点A作AB⊥x轴，AC⊥y轴，垂足分别为B，C，则矩形ABOC的面积为（）A．-4 B．2 C．4 D．87．如图，在平面直角坐标系中，函数y=8x (x>0)与y=x−2的图象交于点P(a，b)，则代数式1a−1b的值为（）A．−12B．12C．−14D．148．如图，直线y=ax+b与x轴相交于点A(1，0)，与函数y=kx的图象交于点B、C，点B的横坐标是4，点C的横坐标是−3，则不等式组0<ax+b<kx的解是（）A．−3<x<1B．−3<x<4C．−3<x<0D．0<x<1二、填空题9．已知函数y＝（m+3）x|m|﹣4是反比例函数，则m＝．10．已知反比例函数y=k−1x的图象经过点(2，−4)，则k的值为．11．点A（2，1）在反比例函数y=kx的图象上，当1＜x＜4时，y的取值范围是．12．如图，点P(x，y)在双曲线y=kx的图象上，PA⊥x轴，垂足为A，若S△AOP=4，则该反比例函数的表达式为．13．如图，点B在反比例函数y=kx(k>0，x>0)的图象上，点A在x轴上，过点A作AC//OB交y轴负半轴于点C ，若OC =OB =AB ，AC =4，则k 的值为 .三、解答题14．如图，一次函数y ＝x ＋m 的图象与反比例函数y ＝ 的图象交于A ，B 两点，且与x 轴交于点C ，点A 的坐标为(2，1)．（1）求m 及k 的值；（2）求点C 的坐标，并结合图象写出不等式组0＜x ＋m ≤的解集． 15．在工程实施过程中，某工程队接受一项开挖水渠的工程，所需天数y(天)与每天完成工程量x(米)是反比例函数关系，图象如图所示：（1）求y 与x 之间的函数关系式（2）若该工程队有4台挖掘机，每台挖掘机每天能够开挖水渠30米，问该工程队需要用多少天才能完成此项任务?16．如图，在平面直角坐标系xOy 中，已知正比例函数y 1＝﹣2x 的图象与反比例函数y 2＝ 的图象交于A （﹣1，n ），B 两点.kxkxkx（1）求出反比例函数的解析式及点B的坐标；（2）观察图象，请直接写出满足y≤2的取值范围；（3）点P是第四象限内反比例函数的图象上一点，若△POB的面积为1，请直接写出点P的横坐标.17．为了做好校园疫情防控工作，学校后勤每天对全校办公室和教室进行药物喷洒消毒，完成．．1．间教室的．．．．药物喷洒要．．．．．5min．．．．，药物喷洒时教室内空气中的药物浓度y（单位：）与时间x（单位：min）的函数关系式为，其图象为图中线段OA，药物喷洒完成后y与x成反比例函数关系，两个函数图象的交点为.（1）点A的坐标为；（2）当教室空气中的药物浓度不高于时，对人体健康无危害.如果后勤人员依次对一班至十班教室（共10间）进行药物喷洒消毒，当最后一间教室药物喷洒完成后，一班是否能让人进入教室?请通过计算说明.18．如图，点A(1，m)和点B是反比例函数y1=kx(k>0，x>0)图象上的两点，一次函数y2=ax+2(a≠0)的图象经过点A，与y轴交于点C，过点B作BD⊥x轴，垂足为D，连接OA，OB.已知ΔOAC与ΔOBD的面积满足SΔOAC ：SΔOBD=2：3.（1）求ΔOAC的面积和k的值；（2）求直线AC的表达式；（3）过点B的直线MN分别交x轴和y轴于M，N两点NB=2MB，若点P为∠MON的平分线上一点，且满足OP2=OM·ON，请求出点P的坐标.参考答案 1．D 2．C 3．B 4．B 5．B 6．C 7．C 8．C 9．3 10．-7 11．12＜y ＜2 12．y =−8x13．√314．（1）解：由题意可得：点A （2，1）在函数y=x+m 的图象上，∴2+m=1即m=﹣1 ∵A （2， 1）在反比例函数y= 的图象上，∴k12∴k=2；（2）解：∵一次函数解析式为y=x ﹣1，令y=0，得x=1，∴点C 的坐标是（1，0）由图象可知不等式组0＜x+m ≤ 的解集为1＜x ≤2．15．（1）解：设 y =kx ∵点(24，50)在其图象上 ∴所求函数关系式为 y =1200x.（2）解：由题意知，4台挖掘机每天能够开挖水渠30×4=120(米)，当x=120时 y =1200120=10.答：该工程队需要用10天才能完成此项任务. 16．（1）解：把A （﹣1，n ）代入y ＝﹣2x ，可得n ＝2 ∴A （﹣1，2）k x kx把A （﹣1，2）代入y ＝，可得k ＝﹣2 ∴反比例函数的表达式为y ＝﹣∵点B 与点A 关于原点对称 ∴B （1，﹣2）. （2）解：∵A （﹣1，2）∴y ≤2的取值范围是x ＜﹣1或x ＞0； （3）解：作BM ⊥x 轴于M ，PN ⊥x 轴于N∵S 梯形MBPN ＝S △POB ＝1 设P （m ，﹣2m），则 （2+ ）（m ﹣1）＝1或 （2+ ）（1﹣m ）＝1整理得，m 2﹣m ﹣1＝0或m 2+m+1＝0 解得m ＝51+ .或m ＝51- . ∴P 点的横坐标为51± . 17．（1）（5，10）（2）解：设药物喷洒完成后y 与x 的反比例函数关系为把代入可得：所以药物喷洒完成后y 与x 的反比例函数关系为而10间教室喷洒完成需要（分钟）kx2x122m 122m当时所以当最后一间教室药物喷洒完成后，一班能让人进入教室. 18．（1）解：∵一次函数y2 = ax + 2与y轴交于C∴C(0，2)∴OC= 2∴S△OAC=12×2×2×1=1∵SΔOAC ：SΔOBD=2：3∴S△OBD=32∵点B在反比例函数y1=kx上∴k=2×32=3；（2）解：∵点A (1，m)在反比例函数y1=3x上∴m= 3∴ A(1，3)将A (1，3)代入一次函数y2 = ax+ 2得a+2=3∴a=1∴一次函数y2=x+2（3）解：设B(a，b)当点N在y轴正半轴上时，作BH⊥y轴于H∴BH∥OM∴△NBH∽△NMO∴BHOM =BNMN=NHNO∵NB=2MB∴BNMN =23∴OM=32a，ON=3b ∵OP2=OM·ON∴OP=√OM×ON=√32a×3b=3√62∵点P为∠MON的平分线上一点∴∠MON=90°∴点P到x轴和y轴的距离相等为3√32∴P(3√32，3√32)当点N在y轴负半轴上时，如图同理可得OM=12BH=12a，ON=OH=b∴OP=√OM×ON=√12a×b=√62∵点P为∠MON的平分线上一点∴∠MON=90°∴点P到x轴和y轴的距离相等为√32∴P(√32，−√32)综上所述，P(3√32，3√32)或(√32，−√32) .。