旋转同步练习

面的旋转同步练习一、填空题。

1、点动成（），线动成（），面动成（）。

2、长方形绕一条边旋转形成（），直角三角形绕一条边旋转形成（）。

3、圆柱的两个圆面叫做（），周围的曲面叫做（），圆柱两个底面之间的距离叫做（）。

4、圆锥有（）个顶点，（）个底面。

二、判断题。

1、圆柱和圆锥分别是由长方形和直角三角形绕一条边旋转形成的。

（）2、圆柱有无数条高，每条高都相等。

（）3、圆锥有两个底面，他们是两个相同的圆。

（）4、从圆锥的顶点到底面圆心的距离叫做圆锥的高。

（）三、选择题。

1、下列物品的形状属于圆柱的是（）。

A、B、C、D、2、下列物体中，由正方形绕一条边旋转形成的物体是（）。

A、B、C、D、3、一个圆锥有（）条高；一个圆柱有（）条高，并且圆柱的每条高都相等。

A、1B、2C、3D、无数4、下列关于圆柱和圆锥的高，说法错误的个数有（）个。

①圆柱两个底面之间的距离叫做圆柱的高。

②从圆柱的顶点到底面圆心的距离叫做圆柱的高。

③圆锥有无数条高。

A、0B、1C、2D、3四、连一连。

参考答案一、填空题。

1、答案：线；面；体解析：连续的点连接成线，线在平面内转动形成面，面经过旋转成体。

2、答案：圆柱；圆锥3、答案：底面；侧面；高4、答案：1；1二、判断题。

1、答案：√解析：长方形绕一条边旋转形成圆柱，，直角三角形绕一条边旋转形成圆锥。

2、答案：√3、答案：×解析：圆柱有两个底面，他们是两个相同的圆；圆锥只有一个底面。

4、答案：√解析：圆锥高的定义：从圆锥的顶点到底面圆心的距离叫做圆锥的高。

三、选择题。

1、答案：D解析：A是圆锥；B是正方体；C是球体；D是圆柱。

2、答案：C解析：回答此类问题，可以通过观察旋转后图形的一半得到答案。

A选项的一半是半圆，故是由半圆旋转而得；B选项的一半是长方形，故是由长方形旋转而得；C选项的一半是正方形，故由正方形旋转而得；D选项的一半是直角三角形，故由直角三角形旋转而得。

四、连一连。

学校： 班级： 姓名： 考号： ………………………………密…………………………………………封………………………………线………………………………罗平轻松学习辅导中心13年初中生周末辅导班同步专题第二十三章旋转-第一节图形的旋转一、单选题 （选择一个正确的选项） 1 、如图，将三角尺ABC （其中∠B=60°，∠C=90°，AB=6）绕点B 按顺时针转动一个角度到A 1BC 1的位置，使得点A 、B 、C 1在同一条直线上，点A 所经过的路程是（ ）A 、2πB 、4πC 、8πD 、12π 2 、观察下列图案，其中旋转角最大的是（ ） A 、B 、C 、D 、3 、如图，△ABO ，经过旋转得到△CDO 则 下列结论不对的是（ ）A 、AB=CDB 、∠B=∠DC 、∠AOB=∠AOD D 、∠BOD=∠AOC 4 、如图，在直角梯形ABCD 中，AD ∥BC ，∠C=90°，AD=5，BC=9，以A 为中心将腰AB 顺时针旋转90°至AE ，连接DE ，则△ADE 的面积等于（ ）A 、10B 、11C 、12D 、135 、旋转不改变图形的（ ）A 、大小和形状B 、位置和形状C 、位置和大小D 、位置、大小和形状6 、如图，将边长为2cm 的两个正方形纸片完全重合，按住其中一个不动，另一个绕点B顺时针旋转一个角度，若使重叠部分的面积为3cm 2，则这个旋转角度为（ ）A 、30°B 、35°C 、45°D 、60° 7 、在平面上有一个角是60°的菱形绕它的中心旋转，使它与原来的菱形重合，那么旋转的角度至少是（ ） A 、90° B 、180° C 、270° D 、360° 8 、如图，∠AOB ＝90°，∠B ＝30°，△A′OB′可以看作是由△AOB 绕点O 顺时针旋转α角度得到的，若点A′在AB 上，则旋转角α的大小可以是（ ）A 、30°B 、45°C 、60°D 、90°9 、下列图形中，不能由图经过平移和旋转得到的图形是（ ）A 、B 、C 、D 、10 、将等腰三角形绕底边的中点旋转180°，所得的三角形与原三角形拼成的图形是（ ）A 、矩形B 、菱形C 、正方形D 、无法确定 11 、如图，△ABC 旋转180°得到△A′B′C′，则下列结论不成立的是（ ）A 、点A 与点A′是对应点B 、∠ACB=∠C′A′B′C 、AB=A′B′D 、BO=B′O 12 、如图所示的图形变换是（ ）A 、轴对称变换B 、旋转变换C 、平移变换D 、相似变换13 、如图，在Rt △ABC 中，AB=AC ，D 、E 是斜边BC 上两点，且∠DAE=45°，将△ADC 绕点A 顺时针旋转90°后，得到△AFB ，连接EF ，下列结论：学校： 班级： 姓名： 考号： ………………………………密…………………………………………封………………………………线………………………………①△AED ≌△AEF ；②AE ADBE CD；③△ABC 的面积等于四边形AFBD 的面积； ④BE 2+DC 2=DE 2⑤BE+DC=DE 其中正确的是（ ）A 、①②④B 、③④⑤C 、①③④D 、①③⑤14 、如图是一个旋转对称图形，要使它旋转后能与自身重合，至少应将它绕中心点旋转（ ）度．A 、30B 、60C 、120D 、18015 、如图，将等腰直角△ABC （∠ACB=90°，AC=BC ）绕C 点按逆时针方向旋转到△A'CB'的位置，若∠A'+∠A'CB=170°，则∠ACB'等于（ ）A 、35°B 、45°C 、55°D 、65°16 、如图所示，两个边长都为2的正方形ABCD 和OPQR ，如果O 点正好是正方形ABCD 的中心，而正方形OPQR 可以绕O 点旋转，那么它们重叠部分的面积为（ ）A 、4B 、2C 、1D 、1217 、已知正方形ABCD 的边长为5，E 在BC 边上运动，DE 的中点G ，EG 绕E 顺时针旋转90°得EF ，问CE 为多少时A 、C 、F 在一条直线上（ ）A 、35 B 、43 C 、53 D 、3418 、下面四个图案中，是轴对称图形但不是旋转对称图形的是（ ）A 、B 、C 、D 、19 、如图，点O 是等边△ABC 内一点，∠AOB=110°，∠BOC=145°．将△BOC 绕点C 按顺时针方向旋转60°得△ADC ，连接OD ．则∠AOD=（ ）A 、40°B 、45°C 、50°D 、55°20 、如图，若正六边形ABCDEF 绕着中心O 旋转角α得到的图形与原来的图形重合，则α最小值为（ ）A 、180°B 、120°C 、90°D 、60°学校： 班级： 姓名： 考号： ………………………………密…………………………………………封………………………………线………………………………罗平轻松学习辅导中心13年初中生周末辅导班同步专题第二节中心对称-课后同步练习-课后作业一、单选题 （选择一个正确的选项）1 、在下列图形中，为中心对称图形的是（ ）A 、等腰梯形B 、平行四边形C 、正五边形D 、等腰三角形 2 、点A （2，5）绕着原点O 逆时针旋转90°得到点A′，则A′的坐标是（ ） A 、（-2，5） B 、（-5，2） C 、（-2，-5） D 、（-5，-2） 3 、如图既是轴对称又是中心对称的是（ ） A 、B 、C 、D 、4 、对右图的对称性表述，正确的是（ ）A 、轴对称图形B 、中心对称图形C 、既是轴对称图形又是中心对称图形D 、既不是轴对称图形又不是中心对称图形5 、下列图形是中心对称图形的是（ ） A 、B 、C 、D 、6 、在等边三角形、平行四边形、矩形、菱形、正方形和等腰梯形中，既是轴对称图形又是中心对称图形的有（ ）A 、1种B 、2种C 、3种D 、4种7 、如果一个四边形ABCD 是中心对称图形，那么这个四边形一定是（ ） A 、等腰梯形 B 、矩形 C 、菱形 D 、平行四边形8 、以下图形既是轴对称图形，又是中心对称图形的是（ ） A 、等腰梯形 B 、平行四边形 C 、矩形 D 、等边三角形9 、以下是电脑显示的时间或日期，其中是轴对称图形，但不是中心对称图形的是（ ） A 、 B 、 C 、 D 、10 、点A （x ，y ）在第二象限内，且|x|=2，|y|=3，则点A 关于原点对称点的坐标为（ ） A 、（-2，3） B 、（2，-3） C 、（-3，2） D 、（3，-2） 11 、给出下列结论： ①有一个角是100°的两个等腰三角形相似． ②三角形的内切圆和外接圆是同心圆．③圆心到直线上一点的距离恰好等于圆的半径，则该直线是圆的切线． ④等腰梯形既是轴对称图形，又是中心对称图形． ⑤平分弦的直径垂直于弦，并且平分弦所对的两弧． ⑥过直线外一点有且只有一条直线平行于已知直线． 其中正确命题有（ ）个．A 、2个B 、3个C 、4个D 、5个12 、下列十字星，禁止符，头像，波形图形中，既不是轴对称图形又不是中心对称图形的是（ ） A 、B 、C 、D 、13 、下列各图中，是中心对称图形的是（ ） A 、B 、C 、D 、14 、下列图形中，不是中心对称图形的是（ ）A 、B 、C 、D 、15 、小伟自制了一个小孔成像演示仪，如图所示，在一个圆纸筒的两端分别用半透明纸和黑纸封住，并用针在黑纸的中心刺出一个小孔．小伟将有黑纸的一端正对着竖直放置的“F”形状的光源，则他在半透明纸上观察到的像的形是（ ）A 、B 、C 、D 、16 、下列是中心对称图形的有（ ） （1）线段；（2）角；（3）等边三角形；（4）正方形；（5）平行四边形；（6）矩形；（7）等腰梯形．A 、2个B 、3个C 、4个D 、5个17 、如图是一个中心对称图形，A 为对称中心，若∠C=90°，∠B=30°，BB′的长为（ ）A 、B 、C 、D 、18 、下列图形中，是中心对称图形，但不是轴对称图形的是（ ） A 、正方形 B 、矩形 C 、菱形 D 、平行四边形19 、下列图形既是轴对称图形又是中心对称图形的有（ ） ①平行四边形；②正方形；③等腰梯形；④菱形；⑤正六边形． A 、1个 B 、2个 C 、3个 D 、4个20 、在以下几何图形中，既是轴对称图形又是中心对称图形的是（ ） A 、等边三角形 B 、等腰梯形 C 、平行四边形 D 、圆学校： 班级： 姓名： 考号： ………………………………密…………………………………………封………………………………线………………………………23．3课题学习（图案设计）1、下列交通标志中既是中心对称图形，又是轴对称图形的是（ ）2、在下图右侧的四个三角形中，不能由△ABC 经过旋转或平移得到的是（ ）3、如图的方格纸中，左边图形到右边图形的变换是（）A 、向右平移7格B 、绕AB 的中点旋转1800，再以AB为对称轴作轴对称 C 、以AB 的垂直平分线为对称轴作轴对称，再以AB 为对称轴作轴对称D 、以AB 为对称轴作轴对称，再向右平移7格4、如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，ABC △的顶点均在格点上，点C 的坐标为(41)-，． (1)把ABC △向上平移5个单位后得到对应的111A B C △，画出111A B C △，并写出1C 的坐标； (2)以原点O 为对称中心，再画出与111A B C △关于原点O 对称的222A B C △，并写出点2C 的坐标．◆典例分析在如图的方格纸中，每个小方格都是边长为1个单位的正方形，ABC △的三个顶点都在格点上（每个小方格的顶点叫格点）．（1）画出ABC △向下平移4个单位后的111A B C △； （2）画出ABC △绕点O 顺时针旋转90后的222A B C △，并求点A 旋转到2A 所经过的路线长．◆课下作业1、起重机将重物垂直提起，这可以看作为数学上的（ ） A 、轴对称 B 、平移 C 、旋转 D 、变形2、国旗上的四个小五角星，通过怎样的移动可以相互得到（ ） A 、轴对称 B 、平移 C 、旋转 D 、平移和旋转3、如图，上面的图案由三个叶片组成，绕点O 旋转1200后可以和自身重合，若每个叶片的面积为4cm 2,∠AOB 为1200，则图中阴影部分的面积之和=_______cm 2.4、如图是某汽车的标志，它可以看作是由什么“基本图案”通过怎样旋转得到的？每次旋转了多少度？5、在等腰直角△ABC 中，∠C=90°，BC=2cm ，如果以AC 的中点O 为旋 转中心，将这个三角形旋转180°，点B 落在点B ′处，作出点B ′并求 BB ′的长度. w w w .x k b 1.c o m●体验中考 1、判断下列两个结论：①正三角形是轴对称图形；②正三角形是中心对称图形，结果（ ） A 、①②都正确 B 、①②都错误 C 、①正确，②错误 D 、①错误，②正确 2、下列图形中既是轴对称图形，又是中心对称图形的是（ ）3、已知ABC △在平面直角坐标系中的位置如图所示． （1）分别写出图中点A C 和点的坐标；（2）画出ABC △绕点C 按顺时针方向旋转90A B C '''°后的△； （3）求点A 旋转到点A '所经过的路线长（结果保留π）．A B C A B C D Ａ Ｂ Ｃ Ｄ B。

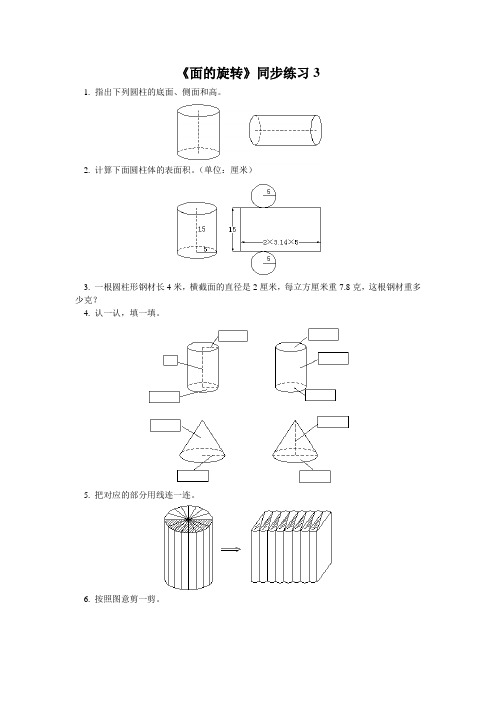
《面的旋转》同步练习3
1. 指出下列圆柱的底面、侧面和高。

2. 计算下面圆柱体的表面积。（单位：厘米）

3. 一根圆柱形钢材长4米，横截面的直径是2厘米，每立方厘米重7.8克，这根钢材重多
少克？
4. 认一认，填一填。

5. 把对应的部分用线连一连。
6. 按照图意剪一剪。
7. 仔细观察，研究圆柱和圆锥的关系。（单位：cm）
a. 按要求填表。
圆柱体 与圆柱体等底等高的圆锥体
图形序号 S h V 图形序号
S h V

b. 把这些圆柱、圆锥按照体积之间的关系分成两类。（把序号填入圈内）

c. 上面8个图形中还有哪几个图形需要单独计算体积，请算一下。

FB'C'23.1.1图形的旋转1、下列说法正确的是（ ）A 、平移不改变图形的形状和大小，而旋转则改变图形的形状和大小B 、平移和旋转的共同点是改变图形的位置C 、图形可以向某方向平移一定距离，也可以向某方向旋转一定距离D 、在平移和旋转图形中，对应角相等，对应线段相等且平行2、将一图形绕着点O 顺时针方向旋转700后，再绕着点O 逆时针方向旋转1200，这时如果要使图形回到原来的位置，需要将图形绕着点O 什么方向旋转多少度？（ ）A 、顺时针方向，500B 、逆时针方向，500C 、顺时针方向，1900D 、逆时针方向，19003、如图，图形旋转一定角度后能与自身重合，则旋转的角度可能是A 、300B 、600C 、900D 、1204、如图，在正方形ABCD 中，E 为DC 边上的点，连结BE ，将△BCE 绕点C顺时针方向旋转900得到△DCF，连结EF ，若∠BEC=600，则∠EFD 的度数为（ ）A 、100B 、150C 、200D 、2505、等边三角形至少旋转__________度才能与自身重合。

6、如图，△ABC 以点A 为旋转中心，按逆时针方向旋转600，得△AB＇C ＇则△ABB＇是__________三角形。

7、如图，△ABC 绕点B 逆时针方向旋转到△EBD 的位置，若∠A=150，∠C=100，E ，B ，C 在同一直线上，则∠ABC=________，旋转角度是__________。

【拓展探究】8、四边形ABCD 是正方形，△ADF 旋转一定角度后得到△ABE ，如图所示，如果AF=4，AB=7， 求：（1）指出旋转中心和旋转角度（2）求DE 的长度（3）BE 与DF 的位置关系如何？【答案】1、 B ；2、 A ；3、C；4、B；5、120；6、等边；7、155°，25°；8、（1）旋转中心：点A，旋转角度：90°；（2）DE=3；（3）垂直关系.23.2.2中心对称图形基础训练1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）． A ．角 B ．等边三角形 C ．线段 D ．平行四边形2. 下列说法：（1）中心对称与中心对称图形是两个不同的概念，它们既有区别，又有联系；（2）中心对称图形是指两个图形之间的一种对称关系；（3）中心对称和中心对称图形有一个共同的特点是它们都有且只有一个对称中心；（4）任何一条经过对称中心的直线都将一个中心对称图形分成两个全等的图形，其中说法正确的序号是（ ）A ．（1）（2）B ．（1）（2）（3）C ．（2）（3）（4）D ．（1）（3）（4） 3．国旗上的每个五角星（ ）A ．是中心对称图形而不是轴对称图形B ．是轴对称图形而不是中心对称图形C ．既是中心对称图形又是轴对称图形D ．既不是中心对称图形，又不是轴对称图形4. 下列图形是中心对称图形的是（ ）5 ） 初中数学资源网能力提升1.如图所示，△ABC 中，点O 是AC 的中点，画出△ABC 关于点O 中心对称的图形△CAD ，其中点B 与点D 是对称点，观察四边形ABCD 的形状，你能说出它的名称吗？2.如图是正六边形ABCDEF ，请找出它的对称中心.3.分别画出下列图形关于点O 对称的图形. （1） （2）4.如下的两个图形是关于某点中心对称的图形吗？如果不是，请说明理由；如果是，找出它们的对称中心，并指出点A 和点B 的对称点.发展创新 1.如图（a ），A B C D的面积被过其对称中心的直线l 直线，使其将图（b ）、（c ）分成面积相等的两部分.23.2中心对称 23.2.1中心对称 23.2.2中心对称图形 基础训练 1.C 2.D 3.B 4.C 5.B能力提升 1.图略，四边形ABCD 是平行四边形. 2.画两条对角线的交点. 3.图略.4.是关于某点D C FAODCBA(c)(b)(a)O CB ABA中心对称的图形.图略.发展创新23.2.3关于原点对称的点的坐标知识网络：在平面直角坐标系中，两个点关于原点对称时，它们的坐标符号相反，即点P（,x y）关于原点的对称点为P′（,x y--）.基础训练1．点A（2，-3）关于原点对称的点的坐标是.点B（-5，0）关于原点对称的点的坐标是.2．如图，⊿DEF是由⊿ABC经过某种变换后得到的图形，观察各顶点的坐标，可知点A和点D 的坐标分别是；点B和点E的坐标分别是；点C和点F的坐标分别是，如果⊿ABC边上任意一点M的坐标为（,x y），则它对应于⊿DEF上点的坐标是.能力提升1.如图，四边形ABCD各顶点坐标分别为A（-5，0），B（-5，2），C（-3，3），D（-1，1），作出与四边形ABCD关于原点O对称的图形。

2023-2024学年三年级数学下册第2单元 2.3平移和旋转同步练习北师大版一、填一填1．动车在笔直平坦的铁轨上行驶，动车的运动是现象。

钟表上秒针在表盘上的运动是现象。

（填“平移”或“旋转”）2．“神舟七号”飞船升向天空时，属于现象，当它进入预定的轨道，绕地球飞行时，属于现象。

（填“旋转”或“平移”）3．炎热的夏天，妈妈回家便打开了风扇，此时，扇叶的运动属于现象。

妈妈走进厨房，打开冰箱门，拉开冰箱抽屉取出一个柠檬泡水喝，此时，冰箱抽屉的运动属于现象。

4．在做平移运动的物体后而面“△"，在做旋转运动的物体后面画"○"。

方向盘米老鼠拖的蛋糕5．（如图）平行四边形ABCD由两块七巧板拼组而成．②号三角板不动，将①号三角板向平移格，可与②号三角板重新拼成一个正方形．6．看图，填一填。

松树向平移了格；小船向平移了6格。

7．下面的图形通过平移互相重合的有，通过旋转互相重合的有。

二、选一选8．下面物体的运动属于旋转的是（）A．B．C．D．9．下面（）组图形经过平移能够完全重合。

A．B．C．D．10．下列的运动现象中，是“平移”现象的共有（）种。

①学校升国旗时国旗的运动②风车转动时所做的运动③钟面上分针的运动④直上直下的电梯所做的运动A．1B．2C．3D．411．如图，要想正好铺满最下面两层，图①需要进行怎样的平移？下列说法正确的是（）A．先向右平移2格，再向下平移2格B．先向右平移2格，再向下平移3格C．先向右平移2格，再向下平移4格D．先向右平移2格，再向下平移5格12．把图甲平移到上，使两图完全重合，会拼成（）图形。

A．B．C．D．三、涂一涂，画一画13．下面哪些鱼可以通过平移与红色小鱼重合，把它们涂上颜色14．把小船向右移动10格答案解析部分1．【答案】平移；旋转【知识点】平移与平移现象；旋转与旋转现象【解析】【解答】解：动车的运动是平移现象；钟表上秒针在表盘上的运动是旋转现象。

一、平移、旋转和轴对称第1课时一、填空题。

1、时针从9：00到12：00，旋转了（）°。

从3时到3时15分，分针旋转了（）°。

2、体育课上，老师口令是“立正，向左转”时，你的身体（）旋转了（）°，口令是“立正，向后转”时，你的身体（）旋转了（）°。

3、我们戴的红领巾是一个（）形，它又是一个（）图形。

4、（1）图形1绕点0顺时针旋转90°到图形（）所在的位置。

（2）图形4绕点0（）时针旋转90°到图形3所在的位置。

（3）图形3绕点0逆时针旋转（）度到图形1所在的位置。

5、①②③图①先向（）移动（）格到图②的位置，再向（）移动（）格可以与图③重合，或者先向（）移动（）格，再向（）移动（）格也可以与图③重合。

二、判断题。

1、所有的三角形都不是轴对称图形。

（）X k B 1 . c o m2、收费站转杆打开，旋转了180度。

（）3、拉抽屉时抽屉的运动时平移。

（）4、直升飞机在天上飞时只有平移没有旋转。

（）5、芳芳晚上10点睡觉，早晨闹钟4点准时响起，则时针在这段时间旋转了60°。

（）三、连一连。

荡秋千缆车的运动平移拉抽屉摩天轮的运动旋转翻课本升国旗时国旗的运动四、实践与操作。

1、（1）将先向下平移5格，再向右平移13格。

（2）将平行四边形沿A点顺时针方向旋转90°。

第2课时一、填空题。

1、与时针旋转方向相同的是（）旋转，相反的是（）旋转。

对折后两边能（）的图形是轴结称图形，折痕所在的直线叫作轴对称图形的（）。

2、行驶中的自行车车轮的运动是（）现象，电梯的上下移动是（）现象。

3、在字母A.B.C.D.E.F.G.H.I.J.K中可以看作轴对称图形的是（）。

4、从中午12：00到下午3：00，时针旋转了（）度；从中午12：00到12：15，分针旋转了（）度。

5、等腰梯形有（）条对称轴。

二、选择题。

1、圆有（）条对称轴。

A、1B、4C、无数2、下面的图形中对称轴最多的是（）。

人教版2021年九年级上册：23.1图形的旋转同步练习第2课时旋转作图一、选择题1.下列图形绕某个点旋转72°后能与自身重合的是()2.如图是几种汽车轮轴的图案,图案绕中心旋转90°后能与原来的图案重合的是()3.下列选项中可以看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是 ()4.[芜湖期中]正三角形绕其中心旋转一定角度后,与自身重合,旋转角至少为()A.30°B.60°C.120°D.180°5.在平面直角坐标系中,将点A(1,2)绕点P(－1,1)顺时针旋转90°到点A'处,则点A'的坐标为()A.(－2,3)B.(－3,0)C.(1,0)D.(0,－1)6.如图,将线段AB绕点C(4,0)顺时针旋转90°得到线段A'B',那么点A(2,5)的对应点A'的坐标是()A.(9,2)B.(7,2)C.(9,4)D.(7,4)7.(2020·赤峰)下列图形绕某一点旋转一定角度都能与原图形重合，其中旋转角度最小的是()8.(2020·青岛)如图，将△ABC 先向上平移1个单位长度，再绕点P 按逆时针方向旋转90°，得到△A ′B ′C ′，则点A 的对应点A ′的坐标是( )A ．(0，4)B ．(2，－2)C ．(3，－2)D ．(－1，4)9.(2020·枣庄)如图，平面直角坐标系中，点B 在第一象限，点A 在x 轴的正半轴上，∠AOB ＝∠B ＝30°，OA ＝2.将△AOB 绕点O 逆时针旋转90°，点B 的对应点B ′的坐标是( )A.()－3，3B.()－3，3C.()－3，2＋3D.()1，2＋3二、填空题10.旋转作图的步骤和方法：(1)确定旋转中心、____________及____________； (2)作出图形的关键点经过旋转后的__________； (3)按一定的顺序连接对应点．11.把一个图案进行旋转变换，选择不同的旋转中心、不同的旋转方向、不同的_____________，会有不同的效果．12.正八边形绕它的中心旋转一定角度后能与自身完全重合,则其旋转的角度至少为 . 三、解答题13.如图,在平面直角坐标系中,等边△OAB 的边长为2,y 轴的正半轴恰好是△OAB 的角平分线,先将△OAB 绕点O 按顺时针方向旋转120°,再关于y 轴对称后得到△A 1B 1O ,求点A 1的坐标..14.在图中作出“三角旗”绕点O 逆时针旋转90°后的图案.15.如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.求DP的长及点D的坐标.16.(2020·鄂尔多斯)(1)【操作发现】如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．①请按要求画图：将△ABC绕点A顺时针方向旋转90°，点B的对应点为点B′，点C的对应点为点C′.连接BB′.②在①中所画图形中，∠AB′B＝________°.(2)【问题解决】如图②，在Rt△ABC中，BC＝1，∠C＝90°，延长CA到点D，使CD＝1，将斜边AB绕点A顺时针旋转90°到AE，连接DE，求∠ADE的度数．17.如图,边长为3的正方形纸片ABCD的相邻边AB,AD分别在x轴、y轴的正半轴上,点E在纸片上,点E的坐标是(1,2),将正方形纸片绕其右下角的顶点按顺时针方向旋转90°至图①位置,此时点E的对应点为E1,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,此时点E1的对应点为E2,以此类推,这样连续旋转2020次,求点E2020的坐标.18.[安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中,给出以格点(网格线的交点)为端点的线段AB,线段MN在网格线上.(1)画出线段AB关于线段MN所在直线对称的线段A1B1;(A1,B1分别为点A,B的对应点)(2)将线段B1A1绕点B1顺时针旋转90°得到线段B1A2,画出线段B1A2.参考答案一、选择题1.下列图形绕某个点旋转72°后能与自身重合的是(B)2.如图是几种汽车轮轴的图案,图案绕中心旋转90°后能与原来的图案重合的是(B)3.下列选项中可以看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是 (B)4.[芜湖期中]正三角形绕其中心旋转一定角度后,与自身重合,旋转角至少为(C)A.30°B.60°C.120°D.180°5.在平面直角坐标系中,将点A(1,2)绕点P(－1,1)顺时针旋转90°到点A'处,则点A'的坐标为(D)A.(－2,3)B.(－3,0)C.(1,0)D.(0,－1)6.如图,将线段AB绕点C(4,0)顺时针旋转90°得到线段A'B',那么点A(2,5)的对应点A'的坐标是(A)A.(9,2)B.(7,2)C.(9,4)D.(7,4)7.(2020·赤峰)下列图形绕某一点旋转一定角度都能与原图形重合，其中旋转角度最小的是(C)8.(2020·青岛)如图，将△ABC先向上平移1个单位长度，再绕点P按逆时针方向旋转90°，得到△A′B′C′，则点A的对应点A′的坐标是(D)A ．(0，4)B ．(2，－2)C ．(3，－2)D ．(－1，4)9.(2020·枣庄)如图，平面直角坐标系中，点B 在第一象限，点A 在x 轴的正半轴上，∠AOB ＝∠B ＝30°，OA ＝2.将△AOB 绕点O 逆时针旋转90°，点B 的对应点B ′的坐标是( )A.()－3，3B.()－3，3C.()－3，2＋3D.()1，2＋3【点拨】如图，过点B ′作B ′H ⊥y 轴于点H . ∵∠AOB ＝∠B ＝30°，∴AB ＝OA ＝2.∵将△AOB 绕点O 逆时针旋转90°得到△A ′OB ′， ∴A ′B ′＝AB ＝2，OA ′＝OA ＝2，∠A ′OB ′＝∠A ′B ′O ＝30°. ∴∠B ′A ′H ＝60°. ∴∠A ′B ′H ＝30°. ∴A ′H ＝12A ′B ′＝1.∴B ′H ＝A ′B ′2－A ′H 2＝3，OH ＝OA ′＋A ′H ＝3. ∴点B ′的坐标是(－3，3)．【答案】A 二、填空题10.旋转作图的步骤和方法：(1)确定旋转中心、____________及____________；(2)作出图形的关键点经过旋转后的__________；(3)按一定的顺序连接对应点．【答案】旋转角度旋转方向对应点11.把一个图案进行旋转变换，选择不同的旋转中心、不同的旋转方向、不同的_____________，会有不同的效果．【答案】旋转角度12.正八边形绕它的中心旋转一定角度后能与自身完全重合,则其旋转的角度至少为45°.三、解答题13.如图,在平面直角坐标系中,等边△OAB的边长为2,y轴的正半轴恰好是△OAB的角平分线,先将△OAB绕点O按顺时针方向旋转120°,再关于y轴对称后得到△A1B1O,求点A1的坐标..解:先将△OAB绕点O按顺时针方向旋转120°,点A的对应点在x轴的正半轴上,且坐标为(2,0),再关于y轴对称后得点A1的坐标为(－2,0).14.在图中作出“三角旗”绕点O逆时针旋转90°后的图案.解:如图.15.如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.求DP的长及点D的坐标.解:∵△AOB是等边三角形,∴∠OAB=60°.由旋转得∠OAB=∠PAD=60°,AD=AP.∵OA=3,AP平分∠OAB,∴∠OAP=30°,∴AP=2OP.∵OP2+32=(2OP)2,∴OP=√3,AP=2√3,∴AD=AP=2√3.∵∠OAP=30°,∠PAD=60°,∴∠OAD=30°+60°=90°,∴点D的坐标为(2√3,3).16.(2020·鄂尔多斯)(1)【操作发现】如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．①请按要求画图：将△ABC绕点A顺时针方向旋转90°，点B的对应点为点B′，点C的对应点为点C′.连接BB′.解：如图①，△AB′C′即为所求．②在①中所画图形中，∠AB′B＝________°.【答案】45(2)【问题解决】如图②，在Rt△ABC中，BC＝1，∠C＝90°，延长CA到点D，使CD＝1，将斜边AB绕点A顺时针旋转90°到AE，连接DE，求∠ADE的度数．解：如图②，过点E作EH⊥CD，交CD的延长线于点H.∵∠C＝∠BAE＝∠H＝90°，∴∠B＋∠CAB＝90°，∠CAB＋∠EAH＝90°.∴∠B＝∠EAH.又∵AB＝AE，∴△ABC≌△EAH(AAS)．∴BC＝AH，EH＝AC.∵BC＝CD，∴CD＝AH.∴DH＝AC＝EH.∴∠EDH＝45°.∴∠ADE＝135°.17.如图,边长为3的正方形纸片ABCD的相邻边AB,AD分别在x轴、y轴的正半轴上,点E在纸片上,点E的坐标是(1,2),将正方形纸片绕其右下角的顶点按顺时针方向旋转90°至图①位置,此时点E的对应点为E1,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,此时点E1的对应点为E2,以此类推,这样连续旋转2020次,求点E2020的坐标.解:∵正方形的边长为3,∴OB=3,∵点E的坐标是(1,2),将正方形纸片绕其右下角的顶点按顺时针方向旋转90°至图①位置,∴E1(5,2),以此类推,E2(8,1),E3(10,1),E4(13,2),…,观察可知:纵坐标的变化规律是四次一个循环(2,1,1,2),2020÷4=505,∴点E2020的纵坐标与点E4相同,纵坐标为2,横坐标为3×2020+1=6061,∴点E2020的坐标为(6061,2).18.[安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中,给出以格点(网格线的交点)为端点的线段AB,线段MN在网格线上.(1)画出线段AB关于线段MN所在直线对称的线段A1B1;(A1,B1分别为点A,B的对应点)(2)将线段B1A1绕点B1顺时针旋转90°得到线段B1A2,画出线段B1A2.解:(1)如图所示,线段A1B1即为所求.(2)如图所示,线段B1A2即为所求.。

苏教版四年级下册《图形的旋转》小学数学-有答案-同步练习卷一、看图填空．1.图1绕________点________时针旋转________度得到现在的图形。

图2绕________点________时针旋转________度得到现在的图形。

2. 从6:00到9:00，时针旋转了（）A.30∘B.60∘C.90∘D.180∘3. （1）图形1绕A点________旋转90∘到图形2． 3.（2）图形2绕A点________旋转90∘到图形3．3.（3）图形4绕A点顺时针旋转________到图形2．3.（4）图形3绕A点顺时针旋转________到图形1．4. 如图中，指针逆时针旋转90∘，从指向A旋转到指向________；指针顺时针旋转90∘，从指向D旋转到指向________．5. (1)把三角形绕点A顺时针旋转90∘．(2)把四边形绕点B逆时针旋转90∘．参考答案与试题解析苏教版四年级下册《图形的旋转》小学数学-有答案-同步练习卷一、看图填空．1.【答案】B,顺,90,B,逆,180【考点】旋转【解析】把一个图形绕着某一点转动一个角度的图形变换叫做旋转，旋转时图形位置发生变化，大小不变，形状不变。

【解答】解：图1绕B点顺时针旋转90度得到现在的图形。

图2绕B点逆时针旋转180度得到现在的图形。

故答案为：B，顺，90；B，逆，180．2.【答案】C【考点】时、分、秒及其关系、单位换算与计算角的度量【解析】先求出时钟上的时针一小时匀速旋转的度数为30∘，再求从“6”绕中心点旋转到“9”经过几个小时，从而计算出时针旋转的度数。

【解答】因为时钟上的时针匀速旋转一周的度数为360∘，时钟上的时针匀速旋转一周需要12小时，则时钟上的时针一小时匀速旋转的度数为：360÷12＝30∘，那么从“6”绕中心点旋转到“9”经过了9−6＝3小时，时针旋转了3×30∘＝90∘．3.【答案】逆时针逆时针180∘180∘【考点】旋转【解析】本题的基本图形为椭圆形，（1）（2）是依次逆时针旋转；（3）（4）顺时针旋转180∘、180∘可得出如图所示的图形。

4.2.3《旋转与角》题型练习 重点梳理 1.角的大小 2.认识锐角、直角、钝角、平角、周角 3.角可以通过旋转得到 题型练习 （一）填空

（1）写出下面各角的名称。

（2）一条射线以（ ）为中心，在平面上旋转（ ）所成的角是周角。 （3）从5时整到6时整，分针旋转所成的角是（ ）角。 （4）用剪刀分别剪出一个直角三角形和一个梯形纸片。 ①把直角三角形的各个角撕下来拼在一起，三角形的三个角合起来是（ ）角。 ②把梯形的各个角撕下来拼在一起，梯形的四个角合在一起是（ ）角。 （5）比直角小的角是( );比( )大、比( )小的角是钝角。 （6）1个平角= ( )个直角，1个周角= ( )个平角= ( )个直角。 （7）比一比，填一填。

把上面的角按从小到大的顺序排列起来 ( )＜( )＜( )＜( )＜( )＜( ) 比较角的大小时要注意: 角的( )越大，角越大，角的大小与边的长短( )。 （二）判断 （1）平面就是一条射线。 （ ） （2）周角是一条直线。 （ ）

（3）7时15分，时针与分针所成的角是钝角。 （ ） （三）选择题 (1)下列说法正确的是( ) A.平角是一条直线 B.周角是一条射线 C.钟面上3 时 30 分,时针与分针所成的较小角是锐角 D.钟面上9时 30 分,时针与分针所成的较小角是锐角 (2)把平角分成两个角,其中一个角是钝角,则另一个角是( ) A.锐角 B.直角 C.钝角 D.周角 (3)(探究题)动手撕一撕,拼一拼。三角形上的三个角撕下来拼在一起可以组成一个( ),长方形四个角撕下来拼在一起可以组成一个( )。 A.锐角 B.直角 C.平角 D.周角 （四）画图题 （1）在下面的点子图上分别画一个锐角和一个平角。

（2）在钟面上，时针和分针形成了一个角。随着指针的转动，角的大小也会发生改变。请你拨一拨，观察一下，几时整，时针和分针会形成下面的角，并把它们画下来. （五）综合题

人教版2021年九年级上册：23.1图形的旋转同步练习第1课时图形的旋转及性质一、选择题1.下列运动形式属于旋转的是()A.放飞的风筝B.飞奔的高铁动车C.时钟上分针的运动D.鱼在水中游动2.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是()A.∠AOCB.∠AODC.∠AOBD.∠BOC第2题图第3题图第4题图3.如图,在4×4的正方形网格中,△PMN绕某点旋转一定的角度,得到△P1M1N1,其旋转中心是()A.点AB.点BC.点CD.点D4.如图所示的每个小三角形是全等的等边三角形,其中的菱形AEFG可以看成是菱形ABCD以点A 为中心()A.顺时针旋转60°所得到的B.逆时针旋转60°所得到的C.顺时针旋转120°所得到的D.逆时针旋转120°所得到的5.如图,将△ABC绕点C逆时针旋转60°得到△A'B'C,点A在边B'C上.若∠B＝30°,则∠A'的大小是( )A.30°B.60°C.90°D.120°第5题图第6题图第7题图6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当点B,C,A'在一条直线上时,三角板ABC的旋转角度为()A.150°B.120°C.60°D.30°7.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,使得点B的对应点D恰好落在BC 边上.若AB＝1,∠B＝60°,则CD的长为()A.0.5B.1.5C.√2D.18.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数()A.20°B.25°C.30°D.35°9.如图,在矩形ABCD中,AD＝4,DC＝3,将△ADC绕点A逆时针旋转一定角度得到△AEF(点A,B,E 在同一条直线上),连接CF,则CF的长为()A.5B.3√2C.4√2D.5√2第8题图第9题图第10题图10.如图,在Rt△ABC中,∠ACB＝90°,线段BC绕点B逆时针旋转α(0°<α<180°)得到线段BD,过点A作AE⊥射线CD于点E,则∠CAE的度数是()A.90°－αB.αC.90°－α2D.α211.(2020·天津)如图，在△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转得到△DEC，使点B的对应点E恰好落在边AC上，点A的对应点为D，延长DE交AB于点F，则下列结论一定正确的是()A．AC＝DE B．BC＝EFC．∠AEF＝∠D D．AB⊥DF12.(2020·大连)如图，在△ABC中，∠ACB＝90°，∠ABC＝40°.将△ABC绕点B逆时针旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠CAA′的度数是()A．50° B．70° C．110° D．120°13.(2020·苏州)如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上，且AB′＝CB′，则∠C′的度数为()A．18° B．20° C．24° D．28°14.(2020·海南)如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝1 cm，将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′，使点C′落在AB边上，连接BB′，则BB′的长度是()A．1 cm B．2 cmC. 3 cm D．2 3 cm二、填空题15.如图,△ABC是等腰直角三角形,D是AB边上一点,△CBD经旋转后到达△CAE的位置,则旋转中心是;旋转角度是;点B的对应点是;点D的对应点是;线段CB的对应线段是;∠B的对应角是.16.如图,F是等边△ABC内一点,将△ABF绕点B顺时针旋转60°得△CBG,连接FG,则△BFG的形状是.17.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一条直线上,且有一个公共顶点A.若正五边形ABCDE绕点A旋转x度恰好与正五边形AFGHM的一条边重合,则x的最小值为.18.如图,正方形ABCD的边长为5,O是AB边的中点,E是正方形内的一个动点,OE＝2,将线段CE绕点C逆时针旋转90°得到CF,连接OF,则线段OF的最小值为.三、解答题19.如图,在△ABC中,AB＝AC,∠BAC＝100°,将△ABC绕点A逆时针旋转40°得到△ADE,BC与AD,DE分别交于点G,F.(1)求∠AGC的度数;(2)求证:四边形ABFE是菱形.20.如图,在Rt△ABC中,∠ACB＝90°,点D,E分别在AB,AC上,EC＝BC,连接CD,将线段CD绕点C顺时针旋转90°得到线段CF,连接EF.(1)补全图形;(2)若EF∥CD,求证:∠BDC＝90°.21.如图,E是正方形ABCD的边BC上一点,连接AE,将线段AE绕点E顺时针旋转一定的角度得到EF,点C在EF上,连接AF交边CD于点G.(1)若AB＝4,BF＝8,求CE的长;(2)求证:AE＝BE＋DG.22.(中考·宁波)如图，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点(点D与A，B不重合)，连接CD，将线段CD绕点C按逆时针方向旋转90°得到线段CE，连接DE交BC于点F，连接BE.(1)求证：△ACD≌△BCE；(2)当AD＝BF时，求∠BEF的度数；(3)求证：DE2＝BD2＋AD2.23.(2019·荆州)如图①，等腰直角三角形OEF的直角顶点O为正方形ABCD的中心，点C，D分别在OE和OF上，现将△OEF绕点O逆时针旋转α角(0°<α<90°)，连接AF，DE(如图②)．(1)在图②中，∠AOF＝________(用含α的式子表示)；(2)在图②中猜想AF与DE的数量关系，并证明你的结论．24.【探索新知】如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.(1)一个角的平分线这个角的“巧分线”;(填“是”或“不是”)(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=.(用含α的代数式表示出所有可能的结果)【深入研究】如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.(3)当t为何值时,射线PM是∠QPN的“巧分线”?(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ 是∠MPN的“巧分线”时t的值.参考答案一、选择题1.下列运动形式属于旋转的是(C)A.放飞的风筝B.飞奔的高铁动车C.时钟上分针的运动D.鱼在水中游动2.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是(A)A.∠AOCB.∠AODC.∠AOBD.∠BOC第2题图第3题图第4题图3.如图,在4×4的正方形网格中,△PMN绕某点旋转一定的角度,得到△P1M1N1,其旋转中心是(B)A.点AB.点BC.点CD.点D4.如图所示的每个小三角形是全等的等边三角形,其中的菱形AEFG可以看成是菱形ABCD以点A 为中心(D)A.顺时针旋转60°所得到的B.逆时针旋转60°所得到的C.顺时针旋转120°所得到的D.逆时针旋转120°所得到的5.如图,将△ABC绕点C逆时针旋转60°得到△A'B'C,点A在边B'C上.若∠B＝30°,则∠A'的大小是(C)A.30°B.60°C.90°D.120°第5题图第6题图第7题图6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当点B,C,A'在一条直线上时,三角板ABC的旋转角度为(A)A.150°B.120°C.60°D.30°7.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,使得点B的对应点D恰好落在BC 边上.若AB＝1,∠B＝60°,则CD的长为(D)A.0.5B.1.5C.√2D.18.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数(B)A.20°B.25°C.30°D.35°9.如图,在矩形ABCD中,AD＝4,DC＝3,将△ADC绕点A逆时针旋转一定角度得到△AEF(点A,B,E 在同一条直线上),连接CF,则CF的长为(D)A.5B.3√2C.4√2D.5√2第8题图第9题图第10题图10.如图,在Rt△ABC中,∠ACB＝90°,线段BC绕点B逆时针旋转α(0°<α<180°)得到线段BD,过点A作AE⊥射线CD于点E,则∠CAE的度数是(C)A.90°－αB.αC.90°－α2D.α211.(2020·天津)如图，在△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转得到△DEC，使点B的对应点E恰好落在边AC上，点A的对应点为D，延长DE交AB于点F，则下列结论一定正确的是(D)A．AC＝DE B．BC＝EFC．∠AEF＝∠D D．AB⊥DF12.(2020·大连)如图，在△ABC中，∠ACB＝90°，∠ABC＝40°.将△ABC绕点B逆时针旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠CAA′的度数是(D)A．50° B．70° C．110° D．120°13.(2020·苏州)如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上，且AB′＝CB′，则∠C′的度数为(C)A．18° B．20° C．24° D．28°14.(2020·海南)如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝1 cm，将Rt△ABC绕点A 逆时针旋转得到Rt△AB′C′，使点C′落在AB边上，连接BB′，则BB′的长度是(B)A．1 cm B．2 cmC. 3 cm D．2 3 cm二、填空题15.如图,△ABC是等腰直角三角形,D是AB边上一点,△CBD经旋转后到达△CAE的位置,则旋转中心是点C;旋转角度是90°;点B的对应点是A;点D的对应点是E;线段CB的对应线段是CA;∠B的对应角是∠CAE.16.如图,F是等边△ABC内一点,将△ABF绕点B顺时针旋转60°得△CBG,连接FG,则△BFG的形状是等边三角形.17.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一条直线上,且有一个公共顶点A.若正五边形ABCDE绕点A旋转x度恰好与正五边形AFGHM的一条边重合,则x的最小值为36.18.如图,正方形ABCD的边长为5,O是AB边的中点,E是正方形内的一个动点,OE＝2,将线段CE绕点C逆时针旋转90°得到CF,连接OF,则线段OF的最小值为5√102－2.提示:如图,连接CO,将线段CO绕点C逆时针旋转90°得到CM,连接FM,OM,∴∠ECF＝∠OCM ＝90°,∴∠ECO＝∠FCM.∵CE＝CF,CO＝CM,∴△ECO≌△FCM(SAS),∴FM＝OE＝2.∵正方形ABCD中,AB＝5,O是AB边的中点,∴OB＝2.5,∴OC＝√52＋(52)2＝5√52,∴OM＝√2OC＝5√10 2.∵OF＋MF≥OM,∴OF≥5√102－2,∴线段OF的最小值为5√102－2.三、解答题19.如图,在△ABC中,AB＝AC,∠BAC＝100°,将△ABC绕点A逆时针旋转40°得到△ADE,BC与AD,DE分别交于点G,F.(1)求∠AGC的度数;(2)求证:四边形ABFE是菱形.解:(1)∵AB＝AC,∠BAC＝100°,∴∠B＝∠C＝40°.由旋转的性质可知∠BAD＝40°,∴∠AGC＝∠B＋∠BAD＝80°.(2)由旋转的性质可知∠D＝∠B＝∠BAD＝40°,∠DAE＝100°,∴AB∥DE.由(1)知∠AGC＝80°,∴∠DAE＋∠AGC＝180°,∴AE∥BF,∴四边形ABFE是平行四边形.又∵AB＝AC＝AE,∴四边形ABFE是菱形.20.如图,在Rt△ABC中,∠ACB＝90°,点D,E分别在AB,AC上,EC＝BC,连接CD,将线段CD绕点C顺时针旋转90°得到线段CF,连接EF.(1)补全图形;(2)若EF∥CD,求证:∠BDC＝90°.解:(1)补全图形,如图所示.(2)由旋转的性质可知∠DCF ＝∠DCE ＋∠ECF ＝90°,CD ＝CF.∵∠ACB ＝∠DCE ＋∠BCD ＝90°,∴∠ECF ＝∠BCD.∵EF ∥CD ,∴∠EFC ＋∠DCF ＝180°,∴∠EFC ＝90°.在△BDC 和△EFC 中,{CD ＝CF,∠BCD ＝∠ECF,BC ＝EC,∴△BDC ≌△EFC (SAS),∴∠BDC ＝∠EFC ＝90°.21.如图,E 是正方形ABCD 的边BC 上一点,连接AE ,将线段AE 绕点E 顺时针旋转一定的角度得到EF ,点C 在EF 上,连接AF 交边CD 于点G.(1)若AB ＝4,BF ＝8,求CE 的长;(2)求证:AE ＝BE ＋DG.解:(1)∵四边形ABCD 为正方形,∴AB ＝BC ＝4,∠ABC ＝90°.∵BF ＝8,∴CF ＝BF －BC ＝4.由旋转的性质知,EF ＝AE ,∴BE ＝BF －EF ＝BF －AE ＝8－AE ,在Rt △ABE 中,AB 2＋BE 2＝AE 2,即42＋(8－AE )2＝AE 2,解得AE ＝5,∴CE ＝EF －CF ＝AE －CF ＝5－4＝1.(2)延长EB 到点H ,使得BH ＝DG ,易证△ADG ≌△ABH (AAS),∴∠BAH ＝∠DAG ,∴∠HAF ＝∠BAD ＝90°.∵AE ＝EF ,∴∠EAF ＝∠F.∵∠EAH ＋∠EAF ＝90°,∠F ＋∠H ＝90°,∴∠H ＝∠EAH ,∴EA ＝EH.∵EH ＝BE ＋BH ＝BE ＋DG ,∴AE ＝BE ＋BG.22.(中考·宁波)如图，在△ABC 中，∠ACB ＝90°，AC ＝BC ，D 是AB 边上一点(点D 与A ，B 不重合)，连接CD ，将线段CD 绕点C 按逆时针方向旋转90°得到线段CE ，连接DE 交BC 于点F ，连接BE .(1)求证：△ACD ≌△BCE ；证明：由题意可知CD ＝CE ，∠DCE ＝90°.∵∠ACB ＝90°，∴∠DCE ＝∠ACB .∵∠ACD ＝∠ACB －∠DCB ，∠BCE ＝∠DCE －∠DCB ，∴∠ACD ＝∠BCE .在△ACD 和△BCE 中，⎩⎨⎧AC ＝BC ，∠ACD ＝∠BCE ，CD ＝CE ，∴△ACD ≌△BCE (SAS)．(2)当AD ＝BF 时，求∠BEF 的度数；解：∵∠ACB ＝90°，AC ＝BC ，∴∠A ＝45°.由(1)知△ACD ≌△BCE ，∴∠A ＝∠CBE ＝45°，AD ＝BE .∵AD ＝BF ，∴BE ＝BF .∴∠BEF ＝180°－45°2＝67.5°. (3)求证：DE 2＝BD 2＋AD 2.证明：由(1)知△ACD ≌△BCE ，∴∠A ＝∠CBE ，AD ＝BE .∵∠ACB ＝90°，∴∠A ＋∠CBA ＝90°.∴∠CBE ＋∠CBA ＝90°.∴∠EBD ＝90°.∴DE 2＝BD 2＋BE 2.∴DE 2＝BD 2＋AD 2.23.(2019·荆州)如图①，等腰直角三角形OEF 的直角顶点O 为正方形ABCD 的中心，点C ，D 分别在OE 和OF 上，现将△OEF 绕点O 逆时针旋转α角(0°<α<90°)，连接AF ，DE (如图②)．(1)在图②中，∠AOF ＝________(用含α的式子表示)；【思路点拨】如图②，利用旋转的性质得到∠DOF ＝∠COE ＝α，再根据正方形的性质得到∠AOD ＝90°，从而得到∠AOF ＝90°－α；(2)在图②中猜想AF 与DE 的数量关系，并证明你的结论．【思路点拨】如图②，利用正方形的性质得到∠AOD ＝∠COD ＝90°，OA ＝OD ，再利用△OEF 为等腰直角三角形得到OF ＝OE ，利用(1)的结论得到∠AOF ＝∠DOE ，则可证明△AOF ≌△DOE ，从而得到AF ＝DE .解：AF ＝DE .证明如下：∵四边形ABCD 为正方形，∴∠AOD ＝∠COD ＝90°，OA ＝OD .∵∠DOF ＝∠COE ＝α.∴∠AOF ＝∠DOE .∵△OEF 为等腰直角三角形，∴OF ＝OE .在△AOF 和△DOE 中，⎩⎨⎧AO ＝DO ，∠AOF ＝∠DOE ，OF ＝OE ，∴△AOF ≌△DOE (SAS)．∴AF ＝DE .24.【探索新知】如图1,射线OC 在∠AOB 的内部,图中共有3个角:∠AOB ,∠AOC 和∠BOC ,若其中有一个角的度数是另一个角度数的两倍,则称射线OC 是∠AOB 的“巧分线”.(1)一个角的平分线 是 这个角的“巧分线”;(填“是”或“不是”)(2)如图2,若∠MPN=α,且射线PQ 是∠MPN 的“巧分线”,则∠MPQ= 12α或13α或23α .(用含α的代数式表示出所有可能的结果)【深入研究】如图2,若∠MPN=60°,且射线PQ 绕点P 从PN 位置开始,以每秒10°的速度逆时针旋转,当PQ 与PN 成180°时停止旋转,旋转的时间为t 秒.(3)当t 为何值时,射线PM 是∠QPN 的“巧分线”?(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ 是∠MPN的“巧分线”时t的值.×60,解得t=9;解:(3)依题意有①10t=60+12②10t=2×60,解得t=12;③10t=60+2×60,解得t=18.故当t为9或12或18时,射线PM是∠QPN的“巧分线”.(4)当t为2.4或4或6时,射线PQ是∠MPN的“巧分线”.提示:依题意有①10t=1(5t+60),解得t=2.4;3②10t=1(5t+60),解得t=4;2③10t=2(5t+60),解得t=6.3。