高等流体力学讲义课件-第二章流体力学基本方程PPT

p z z hp g
hp p g
§2-3 重力场中流体的平衡
几何意义
在重力作用下，静止的 不可压缩流体的静水头 线和计示静水头线均为 水平线

§2-3 重力场中流体的平衡
帕斯卡原理
p p z z h 0 g g
p p0 gh
——静力学基本方程形式之二。
§2-2 流体平衡微分方程式
一、方程式的建立 它是流体在平衡条件下，质量力与表面力所满足的关系式。
l 根据流体平衡的充要条件，静止流体受的所有力在各个坐标轴 方向的投影和都为零，可建立方程。
fi 0
l
方法：微元分析法。在流场中取微小六面体，其边长为 dx、dy、dz，然后进行受力分析，列平衡方程。
1、 流体静压强：静止流体作用在单位面积上的力。
设微小面积上的总压力为
P
平均静压强：
，则
P p A
ΔP
点静压强：
p lim
A0
P A
ΔA
即流体单位面积上所受的垂直于该表面上的力。单位：N/m2 (Pa) 1、 ( 牛) 2、总压力：作用于某一面上的总的静压力。P 单位：N
3、流体静压强单位：
2
n
略去二阶以上无穷小量，得到A1、A2处的压强分别为：
p dx p1 p x 2
则表面力在x方向的合力为：
p dx p 2 p＋ x 2
p dx p dx p p1 p2 dy dz p p dy dz dx dy dz x 2 x 2 x
代入Ⅱ式得
dp dU
所以
p U C
令 p＝p0时，U＝U0 ， 则 C＝p0－ρU0

第二章 流体静力学
本章学习要求:
流体静力学主要研究流体平衡时，其内部的压强分布规律 及流体与其他物体间的相互作用力。它以压强为中心，主要 阐述流体静压强的特性、静压强的分布规律、欧拉平衡微分 方程，作用在平面上或曲面上静水总压力的计算方法，潜体 与浮体的稳定性，并在此基础上解决一些工程实际问题。
无论是静止的流体还是相对静止的流体，流体之间没有相 对运动，因而粘性作用表现不出来，故切应力为零。
• 2.3.3 静止液体中的等压面 • 由于等压面与质量力正交，在静止液体中只有重
力存在，因此，在静止液体中等压面必为水平面。
• 对于不连续的液体或者一个水平面穿过了两种不 同介质连续液体，则位于同一水平面上各点压强 并不一定相同，即水平面不一定是等压面。
2.3 流体静力学的基本方程
2.3.4 绝对压强、相对压强、真空度
(z A (g p A )W ) (z B (g p B )W ) (( (g g ) ) H W g2 1 ) h 1 2 .6 h
2.4 压强单位和测压仪器
2、U形水银测压计
p1=p+ρ1gh1 p2=pa+ρ2gh2 所以 ： p+ρ1gh1=pa+ρ2gh2
M点的绝对压强为： p=pa+ρ2gh2-ρ1gh1
具有的压强势能，简称压能（压强水头）。
测压管水头（ z+p/g）：单位重量流体的总势能。
物理意义： 1. 仅受重力作用处于静止状态的流体中，任意点对同一基准面 的单位势能为一常数，即各点测压管水头相等，位头增高，压 头减小。
2. 在均质（g=常数）、连通的液体中，水平面（z1 = z2=常数）
必然是等压面（p1 = p2 =常数）。

z4
p z C g
pa 4 3 真空 1
p2 g
p=0
z1
z3
2
z=0
p 为压强水头 g
z 为位置水头
2.3 重力场中的平衡流体 重要结论
p p0 gh
(1) 在重力作用下的静止液体中，静压强随深度按线性 规律变化，即随深度的增加，静压强值成正比增大。 (2)在静止液体中，任意一点的静压强由两部分组成： 一部分是自由液面上的压强P0；另一部分是该点到自由 液面的单位面积上的液柱重量ρgh。 (3)在静止液体中，位于同一深度(h＝常数)的各点的静 压强相等，即任一水平面都是等压面。
2.2 流体平衡微分方程 一、欧拉平衡方程
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
2 3
2
3
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
dA dA n
dF pdAn
F pdAn
A
流体静压力：作用在某一面积上的总压力； （矢量） 流体静压强：作用在某一面积上的平均压强或某一点的 （标量） 没有方向性 压强。
2.1 平衡流体上的作用力 证明：
z A
pn px
微元四面体受力分析
py
dx C x
dz O dy B y
y
p x p y p z pn
C x
pz
f
↑
z
表 面 力 质 量 力
1 d yd z 2 1 Py p y d zd x 2 1 P p d yd x z z 2 P n pn d A P x px

证明
质量力 表面力
1 f x dxdydz 6
1 p 0 0 p A cos( n , x ） x dydz n n 2
导出关系式 得出结论
F 0
x
px pn
第一节 平衡流体中的应力特征
第二节 流体平衡微分方程
压强在流体运动、流体与固体相互作用中扮演重要角色，如 机翼升力、高尔夫球及汽车的尾流阻力，龙卷风产生强大的 负压强作用，液压泵和压缩机推动流体做功等都与压强有关。 然而，压强在静止流体、相对静止流体及粘性运动流体中的 分布规律将明显不同。
如图所示的密闭容器中，液面压强 问题1： p0＝9.8kPa，A点压强为49kPa， 则B点压强为多少 ,在液面下的深度为多少? 答案 39.2kPa;
3m
问题2： 露天水池水深5m处的相对压强为：
答案
49kPa
图示容器内 A、B 两点同在一水 问题3：平面上，其压强分别为 pA 及 pB。 因 h1 h 2，所以 pA pB。 答案
• 点压强的定义及特性 • 微元体法推导出流体平衡微分方程 即流体平衡的规律 • 重力作用下流体的平衡
p p ( U U ) 0 0
pp gh 0
等压– 绝对压强p‘ 绝对压强不可为负 – 相对压强（表压强）p 相对压强可正可负 – 真空压强（真空值）pv 真空压强恒为正值
自由面上 p 0 所以 AB 上各点的压强均为 0
[例]试标出如图所示盛液容器内A、B、C三点的位置水头、 测压管高度、测压管水头。以图示0-0为基准面。
pC g pB g
A
pA g
Z
Z
c
ZB
C 因为 ，所以，以A点的测压管水头为依据， g 可以确定B点的位置水头为2m和测压管高度为6m ；C点的 位置水头6m，测压管高度为2m.

2.2 描述流体运动的一些基本概念
2.2.1定常流与非定常流
流场中所有的运动 要素不随时间变化
u u(x, y, z)
(x, y, z)
p p(x, y, z)
u 0 t p 0 t
0
t
流场中有运动 要素随时间变化
u u(x, y, z,t)
(x, y, z,t)
p p(x, y, z,t)
p p(x, y, z,t) (x, y, z,t)
x, y, z ,t--欧拉变量，其中x，y，z与时间t有关。
欧拉法是常用的方法。
5
16 October 2021
欧拉法中的加速度 -- 质点速度矢量对时间的变化率。
a
u t
ux
u x
uy
u y
uz
u z
三个分量：
ax
ux t
ux
ux x
拉格朗日法 从流体质点的运动着手，描述每一个流体质点自始至 终的运动过程。如果知道了所有流体质点的运动规律，那么整个流 体的运动规律也就清楚了。是质点--时间描述法。
质点运动的轨迹
x x(a,b,c,t)
y y(a,b,c,t)
z z(a,b,c,t)
a, b, c --- t = t0 时刻质点所在的空间位置坐标， 称为拉格朗日变量，用来指定质点。
ln x t ln y t ln c
(x t)(y t) c
将 t = 0，x = -1，y = -1 代入，得瞬时流线 xy = 1, 流线是双曲线。
y x
12
16 October 2021
2. 求迹线
将已知速度分布代入式(2.2.1)可得
dx x t, dy ( y t), dz 0

如果垂直液缸活塞上没负 载，则在略去活塞重量及 其它阻力时，不论怎样推 动水平液压缸活塞，不能 在液体中形成压力。
.Hale Waihona Puke 四、绝对压力、相对压力和真空度
压力有两种表示方法：以绝对零压力作为基准所表示的压力， 称为绝对压力。
以当地大气压力为基准所表示的压力，称为相对压力。相对压 力也称表压力。
相对压力为负数时，工程上称为真空度。真空度的大小以此负 数的绝对值表示。
运动黏度。
单位：m2/s，（米2/秒）或 mm2/s 。1 m2/s=106 mm2/s
液体的运动黏度没有明确的物理意义，但它在工程 实际中经常用到。
我国液压油的牌号就是用它在温度为40℃时的运动 黏度平均值来表示的。例如N32号液压油，就是指这种油 在40℃时的运动黏度平均值为32 mm2/s。
h1=0.1m,h2=0.2m,汞的密度为 1.3 6130kg /m3
油液的密度为90k0g/m3。试计算A
点的绝对压力和真空度。
M
M
.
例5 如图所示，如图所示U形管测压计，已知汞的
密度是 g1.3613 0kg /，m 油3的密度
.
5. 油液的机械稳定性 指液体在长时间的高压作用（主要是挤压作用）下，
保持其原有的物理性质的能力。 液压油应具有良好的机械稳定性。
6. 油液的化学安定性 指液体抗氧化的能力。 液压油应具有良好的化学稳定性，并且不含杂质。
.
二、液压油的分类
.
.
三、液压油的选择
1、液压油的使用要求
➢ 粘温特性好 ➢ 有良好的润滑性 ➢ 成分要纯净 ➢ 对热、氧化水解都有良好的化学稳定性，使用寿命长 ➢ 比热和传热系数大，体积膨胀系数小，闪点和燃点高，流

流体速度v、压力p、密度ρ和温度T等的对应表达式为：
流动空间中的流动诸参
因此流动参数构成了场（矢量与标量），就可使用场论这
一有力的数学工具。
欧拉法质点加速度表达式为：
在直角坐标系中：
*
加速度矢量式：
*
用欧拉法描述流体的运动时，加速度由两部分组成：
拉格朗日法和欧拉法的比较
*
欧拉法中a=dv/dt为一阶导数，相应的运动方程是一阶偏微分方程；拉格朗日法中a=∂2r/ ∂ t2为二阶导数，相应的运动方程是二阶偏微分方程。 [例2-1]见书P12-13
欧拉法得到流场，拉格朗日法得不到流场；
*
第二节 流体运动的基本概念
PART ONE
一.定常流动和非定常流动
*
流体运动过程中，若各空间点上对应的物理量不随时间而变化，则称此流动为定常流动，反之为非定常流动。
在定常流动中，流场内物理量不随时间而变化，仅是空间点的函数。
二.均匀流动和非均匀流动
*
流体在运动过程中，若所有物理量皆不依赖于空间坐标，只是时间t的函数，则称此流动为均匀流动，反之为非均匀流动。
三.一维、二维、三维流动
积分以上微分方程，消去时间t，即得迹线方程。
M2
M1
M3
M4
V1
V2
V3
V4
（二）流线 流线是某固定时刻流场中的瞬时曲线，是流场的几何表示，是在同一瞬时形成的曲线，曲线上每一点的切线都与速度矢量相重合。与欧拉法相对应。
给出流场V(x,y,z,t)后，对x,y,z积分上式，即可得到流线方程。
t = 0 时过 M(-1,-1)点的流线：
举 例
t = 0 时过 M(-1,-1)： C1 = C2 = 0

T
单位 阵
23
e2
x2
24
4
ij 的置换特性：
A ijik A kj
例 2: 将实体式写为指标式
坐标变 换矩阵
ij 符号相当于单位矩阵，与任意指标量作用时， ij 自身消失，同时改变作用指标量的符号. 规则是若 有一指标与作用指标量的某一指标相同，则用 ij另一 指标置换作用指标量的相同指标, 同时自身消失。
剪应力

du U dy h
变形(速 度梯度) 问题3？
无滑移条件 y h
u(0) = 0 u(h) = U
U

y o
du dy
2. 粘性的度量 —— 粘性系数(viscosity
牛顿内摩擦定律只能 用于平行直线流动 粘性是流体的固有特性
1

u(y)
h
x
-h 牛顿平板试验
0.2 粘性的概念
Poiseuille 流动
2
0.2 粘性的概念
气体分子动量输运
流体的变形(deformation) 若流体质点间的距离发生了改变，则表明流 体产生了变形。
如何判断变形？ 答：根据微元形状的变化
A
uA

B
uB 问题1？
角变形 线变形


0.2 粘性的概念
du dy
0.2 粘性的概念
3
4
粘性的度量—— 粘性系数
20
e1
e2
x2
x1
A A 21
A
31
19
A 11
A 12 A A
22 32
这是老坐标系
1.1 张量表示法
A A
A 13 A ij 23 A ij 33

二、解析法 求解作用在任意平面上的液体总压力
二、解析法 求解作用在任意平面上的液体总压力 作用在dA面积上的液体总压力为 作用在 面积上的液体总压力为 作用在整个受压平面面积为A上的液体总压力为 作用在整个受压平面面积为 上的液体总压力为
作用在任意形状平面上的液体总压力大小， 作用在任意形状平面上的液体总压力大小，等于该平面的淹没 面积与其形心处静压强的乘积， 面积与其形心处静压强的乘积，而形心处的静压强就是整个受 压平面上的平均压强。 压平面上的平均压强。 总压力的方向垂直于平面，并指向平面。 总压力的方向垂直于平面，并指向平面。
ω
旋转
等压面方程
自由表面方程
第五节 一、图解法
作用在平面上的液体总压力来自液体总压力的方向垂直于矩形平面，并指向平面， 液体总压力的方向垂直于矩形平面，并指向平面，液体总压力的 作用线通过静压强分布图体积的重心。 作用线通过静压强分布图体积的重心。液体总压力作用线与矩形 平面相交的作用点D称为压力中心 称为压力中心。 平面相交的作用点 称为压力中心。
三、流体静力学基本方程的物理意义和几何意义 1. 流体静力学基本方程的物理意义
Z：单位重量流体从某一基准面算起所 ： 具有的位能，因为是对单位重量而言， 具有的位能，因为是对单位重量而言， 所以称单位位能。 所以称单位位能。
：单位重量流体所具有的压能，称 单位重量流体所具有的压能， 单位压能。 单位压能。
等压面方程
三、等压面 帕斯卡定 律 等压面方程 当流体质点沿等压面移动距离ds时 质量力所作的微功为零。 当流体质点沿等压面移动距离ds时，质量力所作的微功为零。 ds 因为质量力和位移ds都不为零，所以等压面和质量力正交。 ds都不为零 因为质量力和位移ds都不为零，所以等压面和质量力正交。 这是等压面的一个重要特性。 这是等压面的一个重要特性。

du 试验结果写成表达式： A T dy
T du 单位面积上内摩擦力（切应力）： A dy
y U U+du u 0 x
பைடு நூலகம்
h dy y
式中： —动力黏滞系数（动力黏度） 单位：pa·s
du —流速在流层法线方向的变化率，称流速梯度。 dy
当u和h较小情况下，该值为常数。
即流速呈线性分布
H O s 1000 0.92 920 kg / m3） （
2
动力黏度为
920 5.6 104 0.5152 Pa s) （
由牛顿内摩擦定律
du F A dy
F A u 0 1 0.5152 3.14 0.2 1 103 107.8 Dd 206 200 2 2
上式两边分别乘以dx、dy、dz，然后相加得：
5、流体力学的工程应用
由于空气动力学的发展，人类研制出3倍声速的战斗机。
由于空气动力学的发展，人类研制出3倍声速的战斗机。
使重量超过3百吨，面积达半个足球场的大型民航客机， 靠空气的支托象鸟一样飞行成为可能，创造了人类技术 史上的奇迹。
时速达200公里的新型地效艇等，它们的设计都建立在 水动力学，船舶流体力学的基础之上。
用翼栅及高温，化学，多相流动理论设计制造成功大型 气轮机，水轮机，涡喷发动机等动力机械，为人类提供 单机达百万千瓦的强大动力。
大型水利枢纽工程，超高层建筑，大跨度桥梁等的设 计和建造离不开水力学和风工程。
环境工程
灾害预报与控制；
发展更快更安全更舒适的交通工具；
流体力学需要与其他学科交叉，如工程学，地学，天 文学，物理学，材料科学，生命科学等，在学科交叉 中开拓新领域，建立新理论，创造新方法。

ρQv
ρ v2A
∫ 1ρ dQ u 2 = α 1 ρ Q v 2
A2
2
α
=
∫
1 2
ρ
dQ u 2
=
∫
1 2
ρ
u
3 dAΒιβλιοθήκη 1 ρ Qv21 ρ v3A
2
2
16
江苏大学
Jiangsu University
第三节 连续性方程
∑ 质量守恒方程 Q厂 = Q用户
一、三维连续性方程
vx
−
∂vx ∂x
dx 2
vx
速度。
加速度=当地加速度+迁移加速度
5
江苏大学
Jiangsu University
用欧拉法求其它物理量N对时间的变化率时
dN = ∂N + (vv ⋅ ∇)N dt ∂t
∇ = iv
∂
+ vj
∂
+
v k
∂
∂x ∂y ∂z
全导数=当地导数+迁移导数 ∇ ：微分算子
四、系统与控制体
6
江苏大学
Jiangsu University
其中a、b、c、t为拉格朗日变量。
vv = ∂ rv ∂t
av = ∂ 2rv ∂t2
2
江苏大学
Jiangsu University
二、欧拉法 欧拉法研究的是各空间上流体运动参数随时间的变化，把全部空间点上的 流动情况综合起来，就得到整个流场的运动情况。
场：如果在空间中的每一点，都对应着某个物理量的一个确定值，这个空 间就称为这个物理量的场。如：数量场（温度场、密度场、电位场）、矢 量场（力场、速度场）。
21

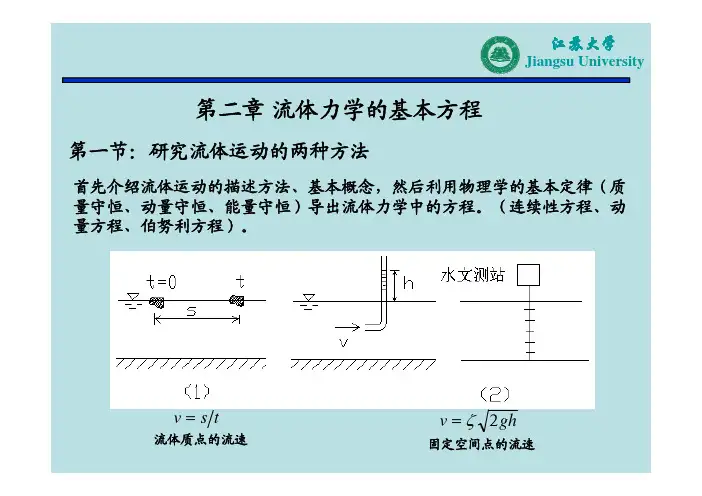
第二章流体力学的基本方程2.1 连续方程2.1 连续方程2.2 动量方程2.2 动量方程2.3 能量方程2.3 能量方程2.4 牛顿流体的基本方程组2.4 牛顿流体的基本方程组2.5 边界条件2.5 边界条件2.1 连续方程质量守恒质量守恒系统质量在运动过程中不变()0t ==⎰ττρd Dt DDt Dm 应用雷诺输运定理0S =⋅+∂∂⎰⎰dS n u d t ρτρτ积分形式连续方程()0=⎥⎦⎤⎢⎣⎡⋅∇+∂∂=⎪⎭⎫ ⎝⎛⋅∇+=⎰⎰⎰ττττρρτρρτρd u t d u Dt D d Dt D 由初始时刻系统与控制体重合假定被积函数连续，且体积是任取的，当积分恒等于零时可知被积函数必须恒等于零0=∂∂+kk x u Dt D ρρ()0=⋅∇+∂∂u tρρ微分形式连续方程0=⋅∇+u DtD ρρ()0=∂∂+∂∂k k x u tρρ相对密度变化率等于负的相对体积变化率单位控制体内流体质量的变化率与净流出控制体的流体质量流量之和为零xzyρuδxδzδy x 方向净流出控制体的质量流量()z y x xu δδδρ∂∂对微元控制体应用质量守恒定律()2x x u u δρρ∂∂+()2x x u u δρρ∂∂-通过单位面积的质量流量y 、z 方向净流出控制体的质量流量()z y x yv δδδρ∂∂()z y x zw δδδρ∂∂控制体内流体质量随时间的变化率z y x tδδδρ∂∂微分形式连续方程微分形式连续方程()()()0=∂∂+∂∂+∂∂+∂∂zw y v x u t ρρρρ()0=⋅∇+∂∂u tρρ()0=⋅∇u ρ定常流动=∂∂t ρ()0=∂∂kk x u ρ定常流动净流出单位控制体的质量流量为零0=⋅∇u 不可压缩流动0=Dt D ρ0=∂∂kkx u 不可压缩流动净流出单位控制体的体积流量为零不可压缩流动连续方程导出无需定常假设Ma < 0.3可视为不可压缩流动A 2A 122,ρu 11,ρu 流管内的流动和一维流动引入平均速度和密度，则定常流动222111A u A u ρρ=const=uA ρ☞定常流动时，通过流管任意过流断面的质量流量保持不变不可压缩流动2211A u A u =const=uA ☞不可压缩流动，通过流管任意过流断面的体积流量保持不变ρ =ρ1 ρ =ρ2=Dt D ρ流体质点运动过程中密度不变，但密度场不均匀0,0≠∂∂≠∂∂yx ρρ由空气温度变化引起大气中的分层流动由于水的含盐量变化引起海洋中的分层流动流体质点沿ρ= ρ1或ρ= ρ2线运动时，密度保持为常数ρ1和ρ2但密度的分层流动不可压缩均质流动设流体不可压缩且均质=Dt D ρ0=∇ρ由物质导数定义()ρρρ∇⋅+∂∂=u tDt D 0=∂∂tρconst=ρ绝大多数情况下，单质流体可以看作不可压缩的，流体密度就等于常数连续方程例题1例：试对柱坐标形式的微元六面体推导连续方程例：试对柱坐标形式的微元六面体推导连续方程xzθδθδzδRR质量守恒：控制体内质量的增加率+ 净流出控制体的质量流率= 0δt 时间内控制体质量的变化()⎥⎦⎤⎢⎣⎡∂∂+t t z R R z R R δδδθδρδδθδρ()ttz R R z R R δδδθδρδδθδρ∂∂=-控制体内质量的变化率z R R tδδθδρ∂∂δt 时间沿R 方向净流出控制体的质量xzθδθδzδRR()t z R R R u R u R R δδθδδρρ⎥⎦⎤⎢⎣⎡∂∂+2()t z R R R u R u R R δδθδδρρ⎥⎦⎤⎢⎣⎡∂∂--2()tz R RR u R δδθδδρ∂∂=沿R 方向净流出控制体的质量流率()zR RR u R δθδδρ∂∂δt 时间沿θ方向净流出控制体的质量xzθδθδzδRR()t z R u u δδδδθθρρθθ⎥⎦⎤⎢⎣⎡∂∂+2()t z R u u δδδδθθρρθθ⎥⎦⎤⎢⎣⎡∂∂--2()t z R u δδθδδθρθ∂∂=沿θ方向净流出控制体的质量流率()zR u δθδδθρθ∂∂δt 时间沿z 方向净流出控制体的质量xzθδθδzδRR()t R R z z u u z z δδθδδρρ⎥⎦⎤⎢⎣⎡∂∂+2()t R R z z u u z z δδθδδρρ⎥⎦⎤⎢⎣⎡∂∂--2()t z R R zu z δδδθδρ∂∂=沿z 方向净流出控制体的质量流率()z R R zu z δδθδρ∂∂()()()0=∂∂+∂∂+∂∂+∂∂z R R zu z R u zR R R u z R R tz R δδθδρδθδδθρδθδδρδδθδρθ连续方程：控制体内质量的变化率+ 净流出控制体的质量流量= 0()()()011=∂∂+∂∂+∂∂+∂∂z u u R RR u R t z R ρθρρρθ2.2 动量方程⎰⎰⎰+=S n ds p d f d u Dt Dτττρτρ初始时刻系统与控制体重合⎰⎰⎰⎰⋅+∂∂=+S S n dSn u u d u t ds p d f ρτρτρττ系统中流体动量的变化率等于作用在该系统上的质量力和表面力之和质量力表面力系统动量变化率动量定理动量定理积分形式动量方程⎰∂∂ττρd u t ⎰⋅SdSn u u ρ控制体中流体的动量对时间的变化率，定常该项为零流出控制体的流体动量的净流率作用在控制体上的外力之和⎰⎰+Sn dsp d f ττρ⎰⎰⎰⎰⋅+∂∂=+S S n dS n u u d u t ds p d f ρτρτρττ⎰⎰=τττρτρd Dtu D d u Dt D由()()⎰⎰⎰∑⋅∇=∑⋅=ττd ds n ds p SSn由高斯公式()⎰⎰⎰∑⋅∇+=τττττρτρd d f d Dt uD ∑⋅∇+=f Dtu D ρρ由于体积是任取的，所以积分相等时被积函数必然相等微分形式动量方程∑⋅==n p n n jij niσσ()∑⋅∇+=∇⋅+∂∂f u u tu ρρρ 作用在单位体积流体上的质量力单位体积流体的动量随时间的变化率t u ∂∂ ρ密度（单位体积流体的质量）与当地加速度乘积，由速度的非定常性引起当地加速度()uu ∇⋅ρ密度与对流加速度项乘积，由流体质点运动及速度分布的不均匀性引起。

17世纪中叶——18世纪中叶：1687年牛顿的黏性流体 内摩擦定律 1738年伯努利<<水动力学>>,基本概念 1755年欧拉<<流体运动的一般原理>>,理流方程 第三阶段：沿着古典流体力学和水力学两条道路发展 （18世纪中叶——19世纪末）
古典流体力学： 欧拉提出 理想流体 1826年 纳维提出黏性流体运动微分方程 水力学： 达西与魏斯巴赫 沿程水头损失公式 第四阶段：发展成为近代流体力学阶段（19世纪末至今） 理论与实验密切结合： 雷诺于1882年提出相似原理加速理论与实验的结 合、理论与生产实践密切联系： 1904年普朗特提出光辉的边界层理论
P
N N τ
2、特性二：静压强的大小与作用面方向无关，或说作 用于同一点上各方向的静压强大小相等。 证明： z C dz △py A x △pn △px dy B y
（1）作用力 ① 表面力：
0 dx
△pz
1 p x p x SOBC p x dydz 2 1 p y p y SOAC p y dxdz 2 1 p z p z SOAB p Z dxdy 2 p n p S ABC
pN d‘
N O’ d c‘ dx
1 p 0 化简得： X x
同理：
a
1 p Y 0 y
1 p Z 0 z
z dz
b‘
M
b pM dy
c y
0
x
上式用向量表示： f
1

p 0
该方程表明：静止流体中各点单位质量流体 所受质量力和表面力平衡。 2、平衡微分方程的全微分式：
b‘
b p M
c y

如果流体是不可压缩的，则流出的流体质量必 然等于流入的流体质量。
一、拉格朗日观点下的连续方程
d ( m) 0
dt
d ( )
dt
1 d 1 d ( ) 0 dt dt d V 0
dt
(2.1.1) (2.1.2) (2.1.3) (2.1.4)
V 称为速度散度，表示体膨涨速度。 V 0表示流体微团在运动过程中发生体积
沿变深度矩形截面河道水面上有波动运动，求 此波动应满足的连续方程
解：设x轴取在河道方向静止水面上
自静止水面起的深度为H(x)，自由表面离静 止 水面为(x,t) ,河截面水流速度为 u(x,t) ， 河宽b不变，水密度为常数 。
取一长为δx的控制体，体积为 (H )b x
单位时间流入质量：(H )bu
在 δt 时间内沿x方向净流出控制体（流出质量 减去流入质量）的质量为
(2.1.7)
按质量守恒定律，在 时间内沿三个方向净流 出控制体的总质量应等于控制体内减少的质量：
(2.1.8)
取极限后可得
即：
(V ) 0
t
(2.1.9) (2.1.10)
( 2.1.10)式为欧拉形式的连续性方程。
单位时间流出质量：
(H
)bu
x
( H
)bux
净流出质量为：
(H )bux
x
单位时间控制体质量减少为： (H )b x
由质量守恒：
t
b (H ) x b (H )u x
t
x
(H )u 0
t x
(2.1.16)
§2. 作用于流体的力、应力张量
一、质量力和表面力： 1. 质量力 质量力为穿越空间作用在所有流体元上的非 接触力，如重力、万有引力、电磁力等。

6
流体的研究意义
流体的输送：根据生产要求，往往要将流体按照生产程序 从一个设备输送到另一个设备，从而完成流体输送的任务， 实现生产的连续化。
压强、流速和流量的测量：以便更好的掌握生产状况。
为强化设备提供适宜的流动条件：为了降低传递阻力，减 小设备尺寸，材料生产中的传热、传质过程以及化学反应大 都是在流体流动下进行的。流体流动状态对这些操作有较大 影响。
➢静压头：
式中的第二项 p/ρg 称为静压头，又称为单位重量流体 的静压能。
29
静压头的意义：
，
ห้องสมุดไป่ตู้
如图所示：密闭容器，内盛 有液体，液面上方压力为p。
图 静压能的意义 说明Z1处的液体对于大气压力来说，具有上升一定高度的能力。
30
Z+ p 常数
g
位压头＋静压头＝常数
也可将上述方程各项均乘以g，可得
gZ p 常数
上式为单位质量流体的静力学基本方程式
31
3 流体静力学基本方程式的应用
一、压强测量
1 U型管液柱压差计 指示液密度 ρ0，被测流体密度
为ρ，图中 a、b两点的压力是相
等的，因为这两点都在同一种静 止液体（指示液）的同一水平面 上。通过这个关系，便可求出p1
－p2的值。
注：指示剂的选择
Ar1% (均为体积%)。试求干空气在压力为
9.81×104Pa、温度为100℃时的密度。
18
解： 首先将摄氏度换算成开尔文：
100℃＝273+100=373K
1)求干空气的平均分子量：
Mm = M１y1 + M2y2 + … + Mnyn
=32 × 0.21+28 ×0.78+39.9 × 0.01

由此可知
⎧1 ⎪1 − x ⎪ u ( x, t ) = ⎨ ⎪1− t ⎪ ⎩0
参见图 1
x≤t t < x ≤1 x >1
u
t=1/2
t=1
5
即t → 1时
⎧1, x < 1 u ( x, t ) |t →1 = ⎨ ⎩0, x > 1
可见,对于非线性问题,即使初始值是连续的,其解仍然可能出现间断。 对于 Euler 方程， 其解的结构中可能出现激波或接触间断，此时，不存在古典意义下的解（古典解要求解是充 分光滑的） 。为此，必须拓展双曲型守恒律解的概念。 定义（广义解或弱解） ： 设 U( x , t )是分片连续可微的函数，在 t ≥ 0 的半平面，如果对于与 U( x , t )的间断线 只有有限个交点的任意分段光滑的闭曲线 Γ ，都有:
S = const
4. 广义解(弱解)
考虑 Bergers 方程
ut + uu x = 0
G x ∈ R, t > 0
(26)
u ( x, 0) = u0 ( xx) = ⎨1 − x ⎪0 ⎩
当存在连续解时,
x≤0 0 < x ≤1 x >1
u ( x, t ) = u ( x − ut , 0) = u0 ( x − ut )
特征相容关系为
Dp Du ± ρa = 0， Dt Dt dx =u±a dt
（24）
4
DS =0， Dt
dx =u dt
（25）
其中 S = C v ln
p
ργ
为熵。对于均熵流动， （24）式可以积分出：
R ± = const ，沿 dx =u±a dt
其中 R ± = u ±