当前位置：文档之家 › 72粘性流体力学PPT课件

72粘性流体力学PPT课件

  • 格式：ppt
  • 大小：11.10 MB
  • 文档页数：46

下载文档原格式

  / 46

合集下载

粘性流体力学第一章

粘性流体力学第一章

4、湍流理论发展概况
致力于湍流大尺度分量的描述
大尺度分量与流动的边界条件和外力性质有关， 如湍流中动量和热量的交换，对于工程问题很重要。 在这方面对于管流、渠道、自由湍流和边界层做了很 多试验，在试验基础上产生了湍流的半经验理论。 这个理论主要包括20－30年代产生的Prandtl的混和 长度理论，Taylor的涡量传输理论和Karman的相似性 理论。这些半经验理论基于湍流微团运动和分子运动 的类比。
第二节 两种基本流态——层流、 湍流和雷诺数
1、层流和湍流
粘性流动存在两种流态——层流和湍流
Reynolds在1883年的著名试验研究了这一现象。 试验装置如图1－1所示。当大容器T中的流体处 于某一温度之下，阀门 K 开度很小时，玻璃管 G 内流 体以极低速度流动；此时，如让另一种与容器T内流 体比较相近似的有颜色的流体自小容器 B通过细管和 尖针流入玻璃管G，可以看出此股有颜色流体的流束 与周围的流体不发生混杂。此时流体做层状流动， 这种流体分层的流动状态叫做层流。流体层间只有 分子级的动量交换，而看不出流体间的混掺。
B
图1－1 雷诺试验
G T
K
如果试管内流速逐渐提高，可以看出颜色流束逐渐波动， 但还与周围流体没发生混杂。随着流速的进一步提高，颜色流 束开始断开，发生了局部混杂。当到某一流速Vcr＇（上临界流 速）时，颜色流体在尖针出口即与周围流体发生混杂，整个玻 璃管呈淡的颜色流。可以认为此时层流流态已完全破坏，流体 微团间发生强烈的动量交换，液流呈不规律的湍乱状态，称为 湍流。
构造湍流模式总须引进封闭假设和待定常数。促使 人们考虑直接从Navier-Stokes方程出发模拟湍流，这 就是湍流的直接数值模拟(DNS),也称完全湍流数值模拟 （FTS）和大涡模拟（LES）。

粘性流体力学.ppt

粘性流体力学.ppt

e

2
dVv

Vv F VdVv
V
Vv
dVv
Vv kT dVv Vv qdVv
(e)
同样，由于流场中各种物理量分布都是连续的，体
积Vv可以任选，故得

D Dt
e

V2 2


F
V


V

+



V


V

=
F
-p
+




V

+


2


对上式等号两边取旋度，得
t
+



V
=

F
-



1
p

+


1



V

+


1


2



又因 + V = V - V+ V - V

e

V2 2
dVv


Vv



D Dt
e

V2 2


1 dVv
e

V2 2

D Dt
dVv



dVv
(b)

Vv

D Dt
e

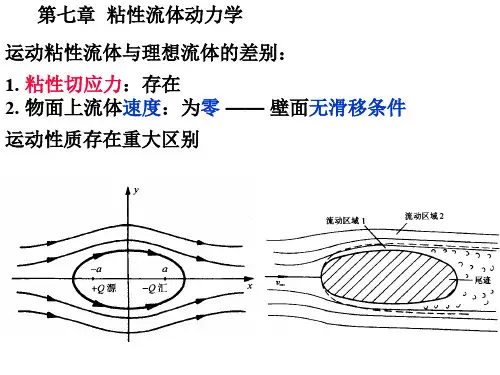
《工程流体力学》第七章 粘性流体动力学

《工程流体力学》第七章 粘性流体动力学

x方向 ： 1)表面力：作用在左右两面上力的合力：
作用在上下两面上力的合力：
作用在前后两面上力的合力：
作用在整个六面体上表面力沿x轴方向的合力：
2) x方向质量力 ： 单位质量流体受到的质量力分量：X;
六面体受到的质量力： Xrdxdydz
牛顿第二定律：
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式：
应力：各向同性
运动粘性流体：存在法向、切向表面力 应力：各向异性
流体中：任一点c ：绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz：定义c上的应力
需要2个下标表示：9个应力分量
第1个下标i：应力作用方向 第2个下标j：作用面方向
第七章 粘性流体动力学
运动粘性流体与理想流体的差别： 1. 粘性切应力：存在 2. 物面上流体速度：为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力： 1.质量力：与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法：和理想流体相同
2. 表面力： 静止和运动理想流体：仅存在指向作用面法向表面力
由于外部无粘流：受到分离流的排挤 明显改变：其中压强分布 实际计算：用实测物面压力分布计算分离点前附面层流动 附面层分离：使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生：是工程上一个重要问 题
边界层分离后：形成尾涡区 尾涡区压强：基本上等于分离点压强 压强：上下对称 若将压强在圆柱面上积分：则得压差阻力
流体在y+l层时均速度：

粘性流体运动及其阻力计算 ppt课件

粘性流体运动及其阻力计算 ppt课件
二、流体运动与流动阻力的两种形式
PPT课件
6
4.2 流体运动的两种状态
一、雷诺实验
实验装置
颜料
细管 水箱
玻璃管
阀门
PPT课件
7
4.2 流体运动的两种状态
一、雷诺实验(续)
实验现象
层流：整个流场呈一簇互相平行的流线。 着色流束为一条明晰细小的直线。
过渡状态：流体质点的运动处于不稳定 状态。着色流束开始振荡。
2、临界流速
vcr ——下临界流速
vcr ——上临界流速
PPT课件
层 流： v vcr
不稳定流： vcr v vcr
紊 流： v vcr
10
4.2 流体运动的两种状态
二、两种流动状态的判定（续）
3、临界雷诺数
Re cr 2320
雷诺数 Re vd
——下临界雷诺数
Recr 13800 ——上临界雷诺数
h
l
g
h
h
两边同除 r2dl得
p 2 1 hg sin 0
l r
由于sin h 得，
l
h
r (p g h)
2 l
l
p
mg
h
g
h

r r0
x r r0
p+(p/l)dl dl p mg
r d ( p gh)
工程上常用的圆管临界雷诺数
层 流： Re Re cr 不稳定流： Re cr Re Recr 紊 流： Re Recr
Re cr 2000
层 流： Re 2000
紊 流： Re 2000
PPT课件

《工程流体力学》第七章 粘性流体动力学

《工程流体力学》第七章 粘性流体动力学
附面层厚度d：从外边界到物面的垂直距离
2.附面层位移厚度d*: 设物面P点附面层厚度d ，在垂直于纸面方向取单位宽度，
则该处通过附面层的质量流量：
通过同一面积理想流体流量：
ro, Vo —— 附面层外边界处理想
流体的密度和速度
以d*高度作一条线平行于物面，
使两块阴影处面积相同：
即在流量相等条件下将理想流体流动区从物面向外移动了
流体绕物体流动，整个流场分为三个区域：
1)附面层： 流速：由壁面上零值急剧增加到自由来流速度同数量级值 沿物面法线方向：速度梯度很大
即使流体粘性系数小：粘性应力仍可达到一定数值
由于速度梯度很大： 使得通过附面层物体 涡旋强度很大，流体 是有旋的
2)尾迹流： 附面层内流体：离开物体流入下游，在物体后形成尾迹流
各物理量都是统计平均值， \ 瞬时物理量＝平均物理量＋脉动物理量， 对整个方程进行时间平均的运算。
一、常用时均运算关系式：
时均运算规律：
推论：脉动量对空间坐标各阶导数的时均值=0。
二、连续方程：对二维流动，瞬态运动连续方程 进行时均运算：
\ 可压缩紊流运动连续方程：
进行时均运算： 上两式相减：
\ 附加法向应力
法向应力： l： 比例系数，与体积变化率有关
三个法向应力平均值的负值：为粘性流体在该点压强
最后得表面应力与变形率之间的关系：
第二节 粘性流体运动的基本方程
一、连续方程：
粘性流体运动：服从质量守恒定律 连续方程：不涉及力的作用 仍能得出与理想流体相同形式的方程
二、运动微分方程： 粘性流体中：微元六面体 微元六面体中心：c
三、雷诺方程： 二维不可压缩粘性流，不考虑质量力，N-S为：
对上式进行时均运算：

高等流体力学(粘性流体力学部分)课件

高等流体力学(粘性流体力学部分)课件
及变形率的关系式代入公式，
uy ux x y ux uz xz z x uz uy yz y z
2 C 将 12 3
2 ux uy uz ux 2 3 x x y z 2 ux uy uz uy yy 2 3 y x y z 2 ux uy uz uz zz 2
zz C12 xx C12 yy C11 zz C37
xy (C11 C12 ) xy
xz (C11 C12 ) xz
yz (C11 C12 ) yz
5个系数是C11,C12,C17,C27,C37。 根据第三个前提。当变形率等于零时， xx yy zz 则，C17 C27 C37 剩下两个系数C11和C12待定。
x l 1 x m1y n 1z y l 2 x m 2y n 2 z z l 3 x m 3y n 3 z
流速分量u′，v′，w′可以表示为
ux ' l1ux m1uy n1uz
ux ' l2ux m2uy n2uz
本例题说明,已知流速场、 和p以后，从本构方程即可得任一点处 的各个应力分量。
§3-2 粘性流体的运动方程 在实际液体中分离出一个微分平行六面体，各边 长为dx、dy、dz，其质量为ρdxdydz。作用在六 面体上的表面力每面有三个：一个法向正应力， 两个切应力。法向力都是沿内法线方向。
x'x' xxl12 yy m12 zz n12 2 xyl1m1 2 yz m1n1 2 xzl1n1

粘性流体-PPT

粘性流体-PPT

现在,我们将考虑定常流。例如,若讨论绕固体得流动(为 确定起见,下面我们将讨论这种情况),则来流速度应为常数。 此外还假设流体就是不可压缩得。
在流体动力学方程组(纳维-斯托克斯方程组)里,就表征流
体本身特性得参数而言,只出现运动粘性系数
。还有,求
解这个方程组所必须确定得未知函数就是速度 和 ,这里
类似得,我们可以写出流体中得压力分布公式。为此, 我们必须由参数 和 作出某个量纲为压力除以密度得 量,比如,这个量可以就是 。于就是, 就是无量纲变 量 和无量纲参数R得函数,所以
最后,类似得考虑也可适用于这样一些量:她们描写流
动得特性,但不就是坐标得函数。例如作用在物体上得阻力
F就就是这样一个量。我们可以说,阻力F与用
不难写出周围流体作用于固体表面得力得表达式。 一个面元上所受得作用力恰等于通过这个面元得动量通 量。通过面元 得动量通量就是
把 写成
得形式,这里 就是沿法线得单位
矢量,并考虑到在固体表面上
,我们得到作用在单位
面积上得力 为
其中等式右边第一项就是普通得流体压力,而第二项就是由 于粘性引起得作用在固体表面上得摩擦力。式中 就是单 位矢量,她沿流体界面得外法线,即沿固体表面得内法线。
组成得并具有力得量纲得某个量之比必定只就是雷诺数得
函数。比如,
组合成力得量纲可以就是
。
因而
若重力对流动有重要作用,则流动不就是由三个参数确
定,而就是由
和重力加速度 这四个参数确定。由
这四个参数可构成两个独立得无量纲量,而不就是一个。比
如,这两个量可以就是雷诺数和弗劳德数,弗劳德数为
最后,提一下非定常流。要描述一个确定类型得非定常
第四节 两个旋转圆柱面之间得流动

8-非牛顿流体流动-72

8-非牛顿流体流动-72

幂律关系式同样也可以用于描述胀塑性非牛顿流体，只要选择不同的稠 度系数和流动指数。胀塑性非牛顿流体的流动指数总是大于1。不规则形状 固体颗粒悬浮于液体的稠流体就属于这种流体，其胀塑性随浓度迅速变化， 浓度低时可能呈现拟塑性流动特性，浓度高时其可能呈现胀塑性非牛顿流体 流动特性。
2.粘塑性非牛顿流体
宾汉塑性流体是指在剪切速率超过一有限值后才流动，并且随后其应 力应变关系呈现线性关系的一类非牛顿流体。石蜡、沥青、某些钻井液、 漂浮在空中的灰尘悬浮液和下水道中排放的污液都属于宾汉流体。宾汉流 体的本构方程为:
第八章
非牛顿流体流动
§1 非牛顿流体的流变特性 §2 拟塑性流体在圆管中的层流运动 §3 宾汉流体在圆管中的层流运动 §4 粘弹性流体在圆管中的不稳定层流运动 §5 拟塑性流体在环空中的层流运动 §6 非牛顿流体在圆管中的湍流运动
《高等流体力学》
汪志明教授
1/72
§1 非牛顿流体的流变特性
任何流动问题的数学描述都建立在力学的一般性原理基础上。这些 原理都可以用平衡方程来描述。流体对机械作用的响应不仅依据于这些 守恒律，而且取决于该种流体的特性，这种响应称之为物质的应力应变 关系（或以流变曲线的形式给出），而这种应力应变关系称之为流体的 本构方程或流变模式。尽管物质系统都遵守质量守恒方程、动量守恒方 程和能量守恒方程，但现实的问题是守恒方程的数目常少于未知数数目。 严格意义上，一种特定的本构方程只适用于一种假设的模型化的流 体。因此本构关系的建立相当于定义一种假设的流体模型，即用一种近 似的方法描述某一特定流体的流变行为。
增大，那么我们称之为振凝性流体。最常见的实例就是鸡 蛋白。尽管振凝性流体作为压裂液是有用的，但与触变性 流体相比，振凝性流体不太常见。

第一章 流体力学基础ppt课件(共105张PPT)

第一章 流体力学基础ppt课件(共105张PPT)

原
力〔垂直于作用面，记为 ii〕和两个切向 应力〔又称为剪应力，平行于作用面，记为
理
ij，i j），例如图中与z轴垂直的面上受
到的应力为 zz〔法向）、 zx和 zy〔切
电 向），它们的矢量和为：
子
课
件 τ zzix zjy zkz
返回
前页
后页
主题
西
1.1 概述
安
交 • 3 作用在流体上的力
大 化
子 课 件
返回
前页
后页
主题
西
1.2.3 静力学原理在压力和压力差测量上的应用
安
交
大 思索：若U形压差计安装在倾斜管路中，此时读数 R反
化 映了什么？
工 原
理 p1p2
p2
p1 z2
电 子
(0)gR(z2z1)g z1
课
R
件
A A’
返回
前页
后页
主题
西 1.2.3 静力学原理在压力和压力差测量上的应用
安
交 大
•
2．压差计
化 • （2〕双液柱压差计
p1
p2
工•
原•
理
电•
子•
课
件
又称微差压差计适用于压差较小的场合。
z1
1
z1
密度接近但不互溶的两种指示
液1和2 ， 1略小于 2 ；
R
扩p 大1 室p 内2 径与2 U 管1 内g 径之R 比应大于10 。 2
图 1-8 双 液 柱 压 差 计
返回
安
交 大
•
1．压力计
化 • （2〕U形压力计
pa
工 • 设U形管中指示液液面高度差为RA，1 指• 示液

粘性流体力学 课件

粘性流体力学 课件

N是与阿佛伽得罗常数(Avogadro，6.03×1023)同量级的正整数。 解这样庞大数目的方程组，连同初始条件给定的困难，不难想象。 这条路子是根本无法走通的。
2. 连续介质假设
2.2 解决办法
• 分子动力学是用质点力学和统计学相结合的方法来研究物 质宏观力学和热力学性质的科学。

这一理论确实取得了很大的成就，但是，它目前也只能应用于某 些简单的气体，远不能解决范围十分宽广的流体力学和固体力学 中的大量问题。

1. 物质结构
1.2 物质的微观性质
• 固、液、气的微观性质比较
固体 d0 强 <<1 有序 弱 量子统计 液体 d0 中等 ~1 部分有序 强 量子统计+经典 统计 气体 10 d0 弱 >>1 无序 强 经典统计
分子间距 分子间作用力 分子随机热运动振幅 与d0的比值 分子排列 可运动性(mobility) 需用的统计类型
Repulsion
d0
d
Attraction
• 对于简单分子组成的物质，常温常压下，分子间距的量级

气相分子，d~10d0 液相和固相分子， d~d0
1. 物质结构
1.2 物质的微观性质
• 气体

当d>>d0，分子力为弱相互作用，此时，只要分子的平均动能足够 大，单个分子就能克服邻近分子的吸引力而处于一种自由运动状 态，也就是说分子在邻近分子力场中具有的势能远小于分子本身 具有的动能，势能可以被忽略。 在偶尔的场合下，高能量分子也可能在运动过程中与其他分子十 分靠近，出现分子间短暂的强相互作用，通常，这种偶然出现的 强相互作用过程被称为碰撞 对于分子热运动平均能量高的物质，在分子碰撞以外的绝大部分 时间，分子都处于自由状态，大量分子的自由运动就呈现出高度 混乱的情景，这种宏观状态称作气体

粘性流体动力学基础.ppt

粘性流体动力学基础.ppt

体质量受到的力，如重力、离心力、电磁力等等。表面力是由
于控制面上应力的作用而产生的力，这些应力包括压强p和流体
运动而产生的粘性应力 ij,其中压强的作用方向垂直指向控制面。
p xx yx
zx
ij
xy p yy zy
（10.6）
xz yx p zz
ij表示在与i轴垂直的面上j方向的应力。
t
(
V)dxdydz
（10.2）
动量流量发生在六个面上，三个流入三个流出.
F=[
t
( V)＋x ( VxV)＋x ( VyV)+
x
(
VzV)]
dxdydz（10.3）
上式为矢量方程，右边中括号内可以改写成
t
(
V)＋x
(
VxV)＋
x
(
VyV)+
x
(
VzV)
=V[
t
+
(
V)]+
(
V t
Vx
式(10.31) 和式(10.36) 又可以写成用温度表示的能量方程
cv
dT dt
p( V ) k2T
q
(10.38)
cp
dT dt
dp dt
k2T
q
(10.39)
10.3 初始条件和边界条件
通过上边的推导，我们得出了描述牛顿流体运动的微分方程
组，共5个方程，包括连续方程（1个），动量方程（3个），
式中V0 (x, y, z) ，p0 (x, y, z) ，0(x, y, z) ，T0 (x, y, z) 均为时刻的
已知函数。
（二）边界条件
在运动流体的边界上，方程组的解所应满足的条件称为边界 条件。边界条件随具体问题而定，一般来讲可能有以下几种 情况：固体壁面（包括可渗透壁面）上的边界条件；不同流 体的分界面（包括自由液面、气液界面、液液界面）上的边 界条件；无限远或管道进出口处的边界条件等。

粘性流体力学第一章

粘性流体力学第一章
6年研究了网后均匀各向同性湍流的衰减 规律。同时在统计理论方面对湍流的封闭性做了很多工 作，主要有准正则近似理论、Kraichnan的直接相互近 似（DIA）和应用非平衡统计力学方法解决湍流的封闭 性问题。 湍流的拟序结构。70年代以来湍流的拟序结构成为 了研究湍流结构的新的起点。湍流的特征是间歇有序性， 即拟序结构的触发是不规律的，但一旦触发，它以近乎 确定的规律发展。这方面的研究包括发现和证实拟序结 构，如边界层中的猝发现象、混合层中的大涡；利用现 代信息处理技术（条件采样，模式识别）检测和分析拟 序结构；定量描述和了解拟序结构的生成和发展，应用 它控制湍流，和构造湍流模式。
第二节 两种基本流态——层流、 湍流和雷诺数
1、层流和湍流
粘性流动存在两种流态——层流和湍流
Reynolds在1883年的著名试验研究了这一现象。 试验装置如图1－1所示。当大容器T中的流体处 于某一温度之下，阀门 K 开度很小时，玻璃管 G 内流 体以极低速度流动；此时，如让另一种与容器T内流 体比较相近似的有颜色的流体自小容器 B通过细管和 尖针流入玻璃管G，可以看出此股有颜色流体的流束 与周围的流体不发生混杂。此时流体做层状流动， 这种流体分层的流动状态叫做层流。流体层间只有 分子级的动量交换，而看不出流体间的混掺。
2、粘性的影响
均匀流动流过一个二维圆柱（半径为R）的理想流 动的解是一个均匀流U∞与一个偶极子叠加而得到的势 y 流解。
B R r C
U P
A
R2 ur U cos (1 2 ) r x R2 u U sin (1 2 ) r
p p

2
2 U (1 4sin 2 )
1904年普朗特（Ludwig Prandtl）提出了边界层理 论，才把实验与理论分析结合起来。以后粘性流体力 学主要在边界层理论和湍流理论两个方面发展起来。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12
减小流动阻力：鲨鱼皮泳衣
据验证，穿着“鲨鱼皮”在比 赛中可比着普通泳衣减少7．5 ％的水阻力，可将一般选手的 平均成绩提高3％左右。
13
游泳运动的CFD模拟
14
游泳运动员手臂的CFD计算
15
游泳运动员手的CFD计算
16
泳镜的CFD计算
17
减小流动阻力：仿鱼皮及其在航空航天中的 应用
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
讲师：XXXXXX
XX年XX月XX日
23
2
粘性流体力学——从北航的荷花池说起吧
想像在一个美好的夏天，我们一起逛逛北航的荷 花池—— 首先，一只蜻蜓翩翩飞来； 然后，一只蜜蜂嗡嗡光临； 然后，一只小鸟飘然而至； 接着，看到一条小鱼悠闲自得、游来游去； 还有，当然是荷花和荷叶； 最后，一池碧水，水波涟漪;
3
蜻蜓：粘性非定常流动、翅膀机理涡运动
4
蜜蜂：粘性非定常流动、人类飞行的希望
5
科学研究：尚没有答案
6
科学家一直在探索
7
科学家一直在探索:飞机尾涡？
8
鸟：可靠安全和高效的飞行、粘性流 体力学的专家、羽毛的奥妙？
9
昆虫飞行的CFD模拟
10
鱼类：粘性流体力学的专家、鱼鳞的秘密？
11
仿生：机器鱼、降噪及其军事意义如潜艇 （粘性流动中涡结构的运动导致噪声）
克的科学堡垒！
21
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
22
结束语
感谢聆听
《粘性流体力学》
1
阎超简介
江苏徐州人，清华大学毕业，后在法国留学。博士学位，教 授、博士导师
专业：空气动力学、流体力学 研究方向：计算流体动力学（CFD）、导弹飞船等航天飞行
器总体布局及气动仿真、CFD软件系统开发及其应用 、 复杂流动的数值模拟研究 电话：010－82317019（o） E-mail: chyan@ 办公室：国家CFD实验室320房间 业余爱好:爬山、郊游、运动（羽毛球、乒乓球、高尔夫、 游泳）、桥牌。
18
减小流动阻力：仿鱼皮及其在航空航天中 的应用
19
荷花和荷叶——出污泥而不染： 为什么始终能自己保持清洁？
20
水波似的东西，为什么？
最光滑的物体上流动阻力最小吗？ 人类能够像小鸟、昆虫一样安全、自如的飞行吗？ 人类能够像鱼儿一样游泳吗？ 这些都同粘性流体力学有关，可又都是人类还没有攻