2019高考数学文科总复习第11单元【等差数列与等比数列】测试A卷及答案解析
- 格式:pdf
- 大小:159.61 KB
- 文档页数:8
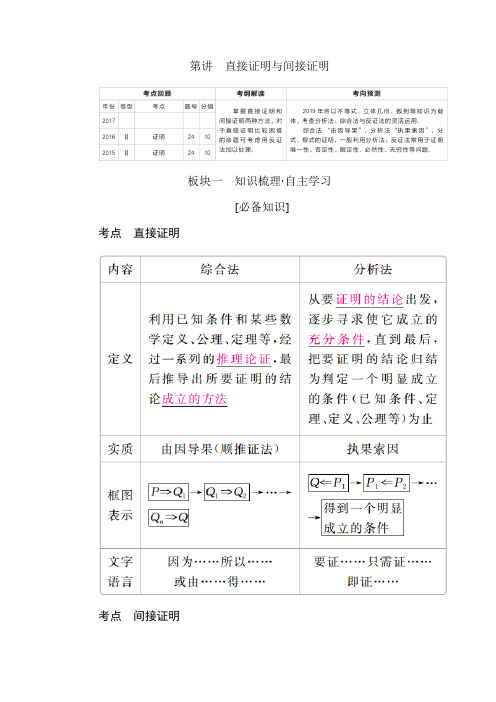
第讲直接证明与间接证明
板块一知识梳理·自主学习
[必备知识]
考点直接证明
考点间接证明
.反证法的定义
假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立的证明方法.
.利用反证法证题的步骤
()假设命题的结论不成立,即假设结论的反面成立;
()由假设出发进行正确的推理,直到推出矛盾为止;
()由矛盾断言假设不成立,从而肯定原命题的结论成立.简言之,否定→归谬→断言.
[必会结论]
分析法与综合法相辅相成,对较复杂的问题,常常先从结论进行分析,寻求结论与条件、基础知识之间的关系,找到解决问题的思路,再运用综合法证明,或者在证明时将两种方法交叉使用.
[考点自测]
.判断下列结论的正误.(正确的打“√”,错误的打“×”) ()综合法是直接证明,分析法是间接证明.()
()分析法是从要证明的结论出发,逐步寻找使结论成立的充要条件.()
()用反证法证明结论“>”时,应假设“<”.()
()反证法是指将结论和条件同时否定,推出矛盾.()
()在解决问题时,常常用分析法寻找解题的思路与方法,再用综合法展现解决问题的过程.()
答案()×()×()×()×()√
.要证明+<,可选择的方法有以下几种,其中最合理的是()
.综合法.分析法。


高考数学精品复习资料2019.5专题二十九 等差数列【高频考点解读】 1.理解等差数列的概念.2.掌握等差数列的通项公式与前n 项和公式.3.能在具体的问题情境中识别数列的等差关系,并能用有关知识解决相应的问题.4.了解等差数列与一次函数的关系. 【热点题型】题型一 等差数列的定义通项公式及前n 项和公式例1、已知{a n }为等差数列,其前n 项和为S n ,若a 3=6,S 3=12,则公差d 等于( ) A .1 B.53C .2D .3【提分秘籍】1.概念中的“同一个常数”十分重要.如果一个数列,从第2项起,每一项与它的前一项的差,尽管等于常数,但不是同一个常数,那么这个数列就不是等差数列.2.由等差数列通项公式的变形可知,已知等差数列中的任意两项就可以确定等差数列中的任何一项.3.等差数列的两个求和公式分析两个公式可得,它们的共同点是需要知道a 1和n ,不同点是公式S n =n a 1+a n2还需要知道a n ,公式S n =na 1+n n -2d 还需要知道d ,解题时需根据已知条件决定选用哪个公式:当已知首项、末项和项数时,用前一个公式较为简便;当已知首项、公差和项数时,用后一个公式较好.【举一反三】等差数列{a n }的前7项和等于前2项和,若a 1=1,a k +a 4=0,则k =________.【热点题型】题型二 等差数列的性质例2、已知等差数列{a n }的前n 项和为S n ,若a 4+3a 8+a 12=120,则2a 11-a 14+S 15=( ) A .384 B .382 C .380D .352【提分秘籍】1.等差数列{a n }中,若m =p +q ,则a m =a p +a q ,不一定成立,只有当a 1=d 时才成立. 2.运算性质求解基本运算,可减少运算量、但要注意判断项数之间的关系.3.利用等差数列的性质解决基本量的运算体现了整体求值思想的应用,应用时常将a m +a n =2a m +n 2与a m +a n =a p +a q 相结合考查.【举一反三】已知等差数列 {a n }满足a 2=3,S n -S n -3=51(n >3),S n =100,则n 的值为( ) A .8B .9C .10D .11【热点题型】题型三 等差数列的判定例3、已知数列{a n }的前n 项和为S n ,且满足a 1=12,a n =-2S n S n -1(n ≥2).(1)求证:数列⎩⎨⎧⎭⎬⎫1S n 是等差数列;(2)求S n 和a n .【提分秘籍】等差数列的判定方法(1)定义法:对于n≥2的任意自然数,验证a n-a n-1为同一常数;(2)等差中项法:验证2a n-1=a n+a n-2(n≥3,n∈N*)成立;(3)通项公式法:验证a n=pn+q;(4)前n项和公式法:验证S n=An2+Bn.注意:在解答题中常应用定义法和等差中项法,而通项公式法和前n项和公式法主要适用于选择题、填空题中的简单判断.【举一反三】已知数列{a n}的通项公式a n=pn2+qn(p、q∈R,且p、q为常数).(1)当p和q满足什么条件时,数列{a n}是等差数列;(2)求证:对任意实数p和q,数列{a n+1-a n}是等差数列.∴{a n+1-a n}是等差数列.【热点题型】题型四等差数列的基本运算例4、(1)设等差数列{a n}的前n项和为S n,若S m-1=-2,S m=0,S m+1=3,则m=() A.3B.4C.5D.6(2)在等差数列{a n}中,a2=2,a3=4,则a10=()A.12 B.14C.16 D.18【提分秘籍】1.等差数列的通项公式a n =a 1+(n -1)d 及前n 项和公式S n =n a 1+a n2 =na 1+n n -2d ,共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了用方程的思想解决问题.2.数列的通项公式和前n 项和公式在解题中起到变量代换作用,而a 1和d 是等差数列的两个基本量,用它们表示已知和未知是常用方法.【举一反三】在数列{a n }中,若a 1=-2,且对任意的n ∈N *有2a n +1=1+2a n ,则数列{a n }前10项的和为( )A .5B .10 C.52D.54【热点题型】题型五 等差数列的前n 项和最值问题例5、已知数列{a n }是等差数列,a 1+a 3+a 5=105,a 2+a 4+a 6=99,{a n }的前n 项和为S n ,则使得S n 达到最大的n 是( )A .18B .19C .20D .21【提分秘籍】与等差数列前n 项和有关的最值问题是命题的热点;主要命题角度有:(1)前n 项和的最大值;(2)前n 项和的最小值;(3)与前n 项和有关的最值问题.1.解决等差数列前n 项和最大值的方法 (1)将S n 表示为n 的二次函数,注意n ∈N *.(2)利用通项不等式组S n 最大⇔⎩⎪⎨⎪⎧a n ≥0,a n +1≤0.2.等差数列前n 项和最小值⇔⎩⎪⎨⎪⎧a n ≤0,a n +1≥0.【举一反三】在首项为负数的等差数列{a n }中,若a 10+a 11+a 12=0,则当前n 项和S n 取最小值时,n 等于( )A .10B .10或11C .11D .9或10【高考风向标】1.(20xx·重庆卷)在等差数列{a n }中,a 1=2,a 3+a 5=10,则a 7=( )A .5B .8C .10D .142.(20xx·天津卷)设{a n }是首项为a 1,公差为-1的等差数列,S n 为其前n 项和.若S 1,S 2,S 4成等比数列,则a 1=( )A .2B .-2 C.12 D .-123.(20xx·北京卷)已知{a n }是等差数列,满足a 1=3,a 4=12,数列{b n }满足b 1=4,b 4=20,且{b n -a n }为等比数列.(1)求数列{a n }和{b n }的通项公式;(2)求数列{b n}的前n项和.4.(20xx·福建卷)在等比数列{a n}中,a2=3,a5=81.(1)求a n;(2)设b n=log3a n,求数列{b n}的前n项和S n.5.(20xx·湖北卷)已知等差数列{a n}满足:a1=2,且a1,a2,a5成等比数列.(1)求数列{a n}的通项公式.(2)记S n为数列{a n}的前n项和,是否存在正整数n,使得S n>60n+800?若存在,求n 的最小值;若不存在,说明理由.6.(20xx·湖南卷)已知数列{a n }的前n 项和S n =n 2+n2,n ∈N *.(1)求数列{a n }的通项公式;(2)设b n =2a n +(-1)n a n ,求数列{b n }的前2n 项和.7.(20xx·江西卷)在等差数列{a n }中,a 1=7,公差为d ,前n 项和为S n ,当且仅当n =8时S n 取得最大值,则d 的取值范围为________.【答案】⎝⎛⎭⎫-1,-78 【解析】 由题可知a 8>0且a 9<0,即7+7d >0且7+8d <0,所以-1<d <-78.8.(20xx·辽宁卷)设等差数列{a n }的公差为d ,若数列{2a 1a n }为递减数列,则( ) A .d >0 B .d <0 C .a 1d >0 D .a 1d <09.(20xx·全国卷)数列{a n }满足a 1=1,a 2=2,a n +2=2a n +1-a n +2. (1)设b n =a n +1-a n ,证明{b n }是等差数列; (2)求{a n }的通项公式.10.(20xx·新课标全国卷Ⅱ] 等差数列{a n }的公差为2,若a 2,a 4,a 8成等比数列,则{a n }的前n 项和S n =( )A .n (n +1)B .n (n -1) C.n (n +1)2 D.n (n -1)211.(20xx·全国新课标卷Ⅰ] 已知{a n }是递增的等差数列,a 2,a 4是方程x 2-5x +6=0的根.(1)求{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n 的前n 项和.12.(20xx·山东卷)在等差数列{a n }中,已知公差d =2,a 2是a 1与a 4的等比中项. (1)求数列{a n }的通项公式;(2)设b n =a n (n +1)2,记T m =-b 1+b 2-b 3+b 4-…+(-1)n b n ,求T n .13.(20xx·陕西卷)△ABC的内角A,B,C所对的边分别为a,b,c.(1)若a,b,c成等差数列,证明:sin A+sin C=2sin(A+C);(2)若a,b,c成等比数列,且c=2a,求cos B的值.14.(20xx·四川卷)设等差数列{a n }的公差为d ,点(a n ,b n )在函数f (x )=2x 的图像上(n ∈N *).(1)证明:数列{b n }为等比数列;(2)若a 1=1,函数f (x )的图像在点(a 2,b 2)处的切线在x 轴上的截距为2-1ln 2,求数列{a n b 2n }的前n 项和S n .所以,S n =(3n -1)4n +1+49.15.(20xx·浙江卷)已知等差数列{a n }的公差d >0.设{a n }的前n 项和为S n ,a 1=1,S 2·S 3=36.(1)求d 及S n ;(2)求m ,k (m ,k ∈N *)的值,使得a m +a m +1+a m +2+…+a m +k =65.16.(20xx·重庆卷)已知{a n }是首项为1,公差为2的等差数列,S n 表示{a n }的前n 项和. (1)求a n 及S n ;(2)设{b n }是首项为2的等比数列,公比q 满足q 2-(a 4+1)q +S 4=0,求{b n }的通项公式及其前n 项和T n .17.(20xx·安徽卷)设数列{a n }满足a 1=2,a 2+a 4=8,且对任意n ∈N *,函数f(x)=(a n-a n +1+a n +2)x +a n +1cos x -a n +2sin x 满足f′⎝⎛⎭⎫π2=0.(1)求数列{a n }的通项公式;(2)若b n =2⎝⎛⎭⎫a n +12a n,求数列{b n }的前n 项和S n .18.(20xx·安徽卷)设S n为等差数列{a n}的前n项和,S8=4a3,a7=-2,则a9=() A.-6 B.-4 C.-2 D.219.(20xx·北京卷)给定数列a1,a2,…,a n,对i=1,2,…,n-1,该数列前i项的最大值记为A i,后n-i项a i+1,a i+2,…,a n的最小值记为B i,d i=A i-B i.(1)设数列{a n}为3,4,7,1,写出d1,d2,d3的值;(2)设a1,a2,…,a n(n≥4)是公比大于1的等比数列,且a1>0.证明:d1,d2,…,d n-1是等比数列;(3)设d1,d2,…,d n-1是公差大于0的等差数列,且d1>0,证明:a1,a2,…,a n-1是等差数列.20.(20xx·全国卷)等差数列{a n}中,a7=4,a19=2a9.(1)求{a n}的通项公式;(2)设b n=1na n,求数列{b n}的前n项和S n.21.(20xx·福建卷)已知等差数列{a n}的公差d=1,前n项和为S n.(1)若1,a1,a3成等比数列,求a1;(2)若S5>a1a9,求a1的取值范围.22.(20xx·新课标全国卷Ⅱ] 已知等差数列{a n }的公差不为零,a 1=25,且a 1,a 11,a 13成等比数列.(1)求{a n }的通项公式; (2)求a 1+a 4+a 7+…+a 3n -2.23.(20xx·山东卷)设等差数列{a n }的前n 项和为S n ,且S 4=4S 2,a 2n =2a n +1. (1)求数列{a n }的通项公式;(2)若数列{b n }满足b 1a 1+b 2a 2+…+b n a n =1-12n ,n ∈N *,求{b n }的前n 项和T n .24.(20xx·陕西卷)设S n表示数列{}a n的前n项和.(1)若{}a n是等差数列,推导S n的计算公式;(2)若a1=1,q≠0,且对所有正整数n,有S n=1-q n1-q.判断{}a n是否为等比数列,并证明你的结论.25.(20xx·四川卷)在等比数列{a n}中,a2-a1=2,且2a2为3a1和a3的等差中项,求数列{a n}的首项、公比及前n项和.26.(20xx·新课标全国卷Ⅰ] 已知等差数列{a n }的前n 项和S n 满足S 3=0,S 5=-5. (1)求{a n }的通项公式; (2)求数列⎩⎨⎧⎭⎬⎫1a 2n -1a 2n +1的前n 项和.27.(20xx·浙江卷)在公差为d 的等差数列{a n }中,已知a 1=10,且a 1,2a 2+2,5a 3成等比数列.(1)求d ,a n ;(2)若d<0,求|a 1|+|a 2|+|a 3|+…+|a n |.28.(20xx·重庆卷)设数列{a n }满足:a 1=1,a n +1=3a n ,n ∈N +. (1)求{a n }的通项公式及前n 项和S n ;(2)已知{b n }是等差数列,T n 为其前n 项和,且b 1=a 2,b 3=a 1+a 2+a 3,求T 20.29.(20xx·重庆卷)若2,a ,b ,c ,9成等差数列,则c -a =________. 【答案】72 【解析】 设公差为d ,则d =9-25-1=74,所以c -a =2d =72.【随堂巩固】1.若数列{a n }的首项a 1=1,且a n =a n -1+2(n ≥2),则a 7=( ) A .13 B .14 C .15 D .172.已知等差数列{a n }的前n 项和为S n ,a 4=15,S 5=55,则数列{a n }的公差是( )A.14B .4C .-4D .-33. S n 为等差数列{a n }的前n 项和,a 2+a 8=6,则S 9=( ) A.272B .27C .54D .1084.已知{a n }为等差数列,其公差为-2,且a 7是a 3与a 9的等比中项,S n 为{a n }的前n 项和,n ∈N *,则S 10的值为( )A .-110B .-90C .90D .110答案:D5.一个首项为23,公差为整数的等差数列,如果前6项均为正数,第7项起为负数,则它的公差为( )A .-2B .-3C .-4D .-66.把70个面包分五份给5个人,使每人所得成等差数列,且使较大的三份之和的16是较小的两份之和,则最小的一份为( )A .2B .8C .14D .207.等差数列{a n }中,a 1,a 2,a 3分别是下表第一、二、三行中的某一个数,且a 1,a 2,a 3中的任何两个数不在下表的同一列.则a 4的值为( ) A .18 B .15 C .12 D .208.在6月11日成功发射了“神舟十号”,假设运载火箭在点火第一秒钟通过的路程为2 km ,以后每秒钟通过的路程都增加2 km ,在到达离地面240 km 的高度时,火箭与飞船分离,则这一过程需要的时间大约是( )A .10秒钟B .13秒钟C .15秒钟D .20秒钟9.一个等差数列的前20项和为420,前20项中偶数项的和与奇数项的和之比为11∶10,则此数列的公差为________.10.已知等差数列{a n}的前n项和为S n,若a3+a4+a5=12,则S7的值为________.11.等差数列{a n}前9项的和等于前4项的和.若a1=1,a k+a4=0,则k=________.12.已知数列{a n}是等差数列,且a3+a9=5,b n=2a n,则b5+2b7的最小值为________.13.已知等差数列{a n}中,a5=12,a20=-18.(1)求数列{a n}的通项公式;(2)求数列{|a n|}的前n项和S n.14.已知a 2、a 5是方程x 2-12x +27=0的两根,数列{a n }是公差为正数的等差数列,数列{b n }的前n 项和为T n ,且T n =1-12b n (n ∈N *).(1)求数列{a n }、{b n }的通项公式; (2)记c n =a n b n ,求数列{c n }的前n 项和S n .。

2019年高中数学单元测试试题 数列专题(含答案)学校:__________ 姓名:__________ 班级:__________ 考号:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.已知数列{a n }的前n 项和S n =3a n -2,那么下面结论正确的是 A.此数列为等差数列 B.此数列为等比数列C.此数列从第二项起是等比数列D.此数列从第二项起是等差数列2.某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入a 元定期储蓄,若年利率为p 且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将 所有的存款及利息全部取回,则可取回的钱的总数(元)为 ( )A .7(1)a p +B .8(1)a p +C .7[(1)(1)]ap p p+-+ D .()()811ap p p +-+⎡⎤⎣⎦3.已知数列{an }满足a1=3,an+1 - an + 1=0 (n ∈N* ), 则数列{an }的通项公式为 A. an= n 2 +2 B. an= n +2 C. an=4-n D. an= 2 n +14.已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于( ) A .64B .100C .110D .120(2008陕西理)第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题5.(5分)(2011•山东)设函数f (x )=(x >0),观察:f 1(x )=f (x )=,f 2(x )=f (f 1(x ))=, f 3(x )=f (f 2(x ))=, f 4(x )=f (f 3(x ))=,…根据以上事实,由归纳推理可得:当n ∈N *且n ≥2时,f n (x )=f (f n ﹣1(x ))= .6.1 .(2013年高考广东卷(文))设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++=________7.2 .(2013年高考重庆卷(文))若2、a 、b 、c 、9成等差数列,则c a -=____________.8.在数列}{n a 中,若11=a ,212=a ,)(112*21N n a a a n n n ∈+=++,则该数列的通项为 .9.一个正方形被分成九个相等的小正方形,将中间的一个正方形挖去;再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖去;如此继续下去……,试问第n 个图共挖 去 个正方形.10.在等差数列{}n a 中,465a a +=,前5项和510S =,则其公差d 的值为 ▲ . 11.设等差数列{}n a 的首项及公差均是正整数,前n 项和为n S ,且11a >,46a >,312S ≤,则2010a = .12.等差数列{}n a 中,45a =,1213a =,则8a = ▲ .13.设}{n a 是公比为q 的等比数列,n S 是它的前n 项和,}{n S 是等差数列,则公比q =_____14.已知数列}{n a 的通项公式n a n 373-=,其前n 项和n S 达到最大值时n 的值是_____15. 已知数列{}n a 满足112a =,()1111n n a n a +=-≥,则6a = .16.等差数列{a n }中,若a 1+a 2=5,a 3+a 4=17,则a 5+a 6= .17.设函数)10(2log log )(2<<-=x x x f x ,数列{}n a 满足)(2)2(*N n n f n a∈=⑴ 求数列{}n a 的通项公式; ⑵ 判断数列{}n a 的单调性.18.对大于1的自然数m 的三次幂,可用奇数进行以下方式的拆分: 23=3+5 33=7+9+11 43=13+15+17+19 …若159在m 3的拆分中,则m 的值为 .19.如图,△OA 1A 2是等腰直角三角形,OA 1=A 1A 2=1,以OA 2为直角边作等腰直角△OA 2A 3,再以OA 3为直角边作等腰直角△OA 3A 4,如此继续下去得到等腰直角△OA 4A 5,…….则△OA 9A 10的面积为____________.三、解答题20.(本小题满分16分)已知数列{a n }的前n 项和为S n ,满足a n ≠ 0,11112n n n n n n n a S a S a a -+++-=,*n ∈N . (1)求证:12n n n S a -=; (2)设1nn n a b a +=,求数列{b n }的前n 项和T n . 21.设等差数列{}n a 的前n 项和为n S ,公差0d ≠,已知5346S a =+,且1a ,3a ,9a 成等比数列.(1)求数列{}n a 的通项公式; (2)求数列1{}nS 的前n 项和n T .(本小题满分10 分)22.(本题满分16分)平面直角坐标系xoy 中,已知点),(111y x A ,),(222y x A , ),,(,n n n y x A 是直线b kx y +=上的点(k 、b 均为非零常数).(1)若数列{}n x 是等差数列,求证:数列{}n y 也是等差数列; (2)若点P 是直线l 上一点,且2211OA a a +=,求21a a +的值;(3)已知点P 满足n n OA a OA a a +++= 2211(*N n ∈),其中102311=a ,n a a a ,,,21 成等比数列,公比为2.若点P 在直线l 上,求n 的值.23.已知数列{}n a 是各项均不为0的等差数列,公差为d ,n S 为其前 n 项和,且满足221n n a S -=,n *N ∈.数列{}n b 满足11n n n b a a +=⋅,n T 为数列{}n b 的前n 项和.(1)求数列{}n a 的通项公式n a 和数列{}n b 的前n 项和n T ;(2)若对任意的n *N ∈,不等式8(1)n n T n λ<+⋅-恒成立,求实数λ的取值范围; (3)是否存在正整数,m n (1)m n <<,使得1,,m n T T T 成等比数列?若存在,求出所有,m n 的值;若不存在,请说明理由.24. (本小题满分16分)下列数阵称为“森德拉姆筛”,记为S .其特点是每行每列都是等差数列,第i 行第j 列的数记为ij A1 4 7 10 13 … 4 8 12 16 20 … 7 12 17 22 27 … 10 16 22 28 34 … … … … … …⑴证明:存在常数C ,对任意正整数i 、j ,ij A +C 总是合数;⑵设S 中主对角线上的数1,8,17,28,…组成数列{}n b ,是否存在正整数k 和m ()1k m <<,使得1b ,k b ,m b 成等比数列,说明理由;⑶对于⑵中的数列{}n b ,是否存在正整数p 和r ()1150r p <<<,使得1b ,r b ,p b 成等差数列?若存在,写出p ,r 的一组解;若不存在,请说明理由.25.在等比数列{}n a 中,已知,831,215-==S q 则=3a ▲ .26.已知各项均为正数的数列{}n a 中,n S a ,11=是数列{}n a 的前n 项和,对任意*∈N n ,有 )(222R p p pa pa S n n n ∈-+=(1)求常数p 的值;(2)求数列{}n a 的通项公式; (3)记n nn n S b 234⋅+=,求数列{}n b 的前n 项和n T 。

2019高考数学文一轮复习含答案解析:选C 依题意,结合题中的程序框图,注意到sinv 3,分层演练•直击高考1 •执行如图所示的程序框图,若输出i 的值为2,则输入x 的最大值是()A • 5B • 6C . 11D • 22x>8,解得f 即8<x w 22,所以输入x 的最大值是22 •22,2・(2018新疆第二次适应性检测)阅读如图所示的程序框图,运行相应的程序,则输出 的n 的值为()[学生用书P284(单独成册)]一、选择题 基础达标A • 3C . 5B • 4D • 6解析:选D •执行该程序可知S-0〔结東〕H=F>+1¥+ sin 瞥|+ 3>3,因此输出的n 的值为5,选C .3. (2018太原模拟)执行如图所示的程序框图, 已知输出的s € [0 ,4].若输入的t € [0 , m],则实数m 的最大值为()C . 3D . 43t , t V 1解析:选D .由程序框图得s =*2,图象如图所示.由图象得,若输入的t € [0 ,4t - t 2, t > 1m],输出的s € [0 , 4],贝U m 的最大值为4,故选D .4「…厂\3 2 1 • 1 !/NA.. -1 -2 Q 123 i 5由T)\4. (2017高考天津卷)阅读如图所示的程序框图,则输出N 的值为(n - 2 n - sin 6+sin 訂sin运行相应的程序,若输入N 的值为19,/输出S / 〔结虫〕B . 1C. 264,A . i>6 C . i>8解析:选D .要使输出的点恰有B . i>7 D . i>95次落在直线y = x 上,贝U i = 2, 3, 4,…,9都不满足判断框内的条件,i = 10满足判断框内的条件,则判断框内可填写的条件是 i>9,故选D .6. (2018郑州第一次质量预测)我们可以用随机模拟的方法估计 图表示其基本步骤(函数RAND 是产生随机数的函数,它能随机产生n 的值,下面的程序框(0, 1)内的任何一个数).若输出的结果为781,则由此可估计n 的近似值为( )A . 3. 119B . 3. 124C . 3. 132151解析:选B .根据题意,本题可以转化为在平面直角坐标系中,在{(x, y)|0<x<1, 0<y<1}中随机产生1 000个点,其中满足{(x , y )|x 2 + y 2<1}的点有781 个.根据几何概型概率计算1 24^ nX 12 公式可得卫81 =- ,由此可估计n 的近似值为3. 124 .故选B .1 000 17.秦九韶是我国南宋时期的数学家,普州 (现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法, 至今仍是比较先进的算法.如图所示的程序框图给解析:选C .由程序框图可知,N 的取值依次为19, 18, 6, 2,故输出N 的值为2. 5•运行如图所示的程序框图,若输出的点恰有 5次落在直线y =x 上,则判断框中可填写的条件是()出了利用秦九韶算法求某多项式值的一个实例,若输入n, x的值分别为3, 2,则输出v的值为()/输人d at /I已一】------- ; - 1i=i-l/ 输L B V/朿)A. 35B20C. 18D9解析:选C.根据程序框图有:n= 3,x= 2, v = 1, i=2> 0,所以v= 1 X 2+ 2= 4,=1》0,所以v= 4 X 2 + 1 = 9, i = 0》0,所以v = 9X 2 + 0 = 18, i = —1<0,不满足条件,跳出循环,输出v= 18.& (2018东北四市教研联合体模拟)庄子说:“一尺之锤,日取其半,万世不竭”.这句话描述的是一个数列问题.现用程序框图描述,如图所示,若输入某个正整数n后,输出A. 7C. 5解析:选C .由程序框图,可知:S= + 2^2+召+…+的S€15,H,则输入的n的值为(金Qi隔出刃—I因为15 c6364,C . i >50, n = n +2D . i < 50, n = n + 2即4<n<6.又n € Z ,所以n = 5.故选C .9. (2018 •州综合质量检测)执行如图所示的程序框图,若输入的 m = 168, n = 112,则输出的k ,m 的值分别为()解析:选C .对第一个当型循环结构,第一次循环:k = 1, m = 84, n = 56, m , n 均为 偶数;第二次循环:k = 2, m = 42, n = 28, m , n 均为偶数;第三次循环:k = 3, m = 21, n=14,因为m 不是偶数,所以结束第一个循环.又 m z n ,所以执行第二个当型循环结构 , 第一次循环:d = |21 — 14|= 7, m = 14, n = 7, m z n ;第二次循环:d = |14— 7|= 7, m = 7, n =7,因为m = n ,所以结束循环,输出k = 3, m = 7,故选C .1 1 110.如图,给出的是计算+;+…+ 而的值的一个程序框图,则图中判断框内 ⑴处和执行框中的(2)处应填的语句是(A . 4,7 C . 3, 7D . 3, 56A . i > 100, n = n + 1B . i > 100, n = n + 2 所以挣1-rw4, 56据观察S中最后一项的分母与i的关系是分母—2(i - 1),令2(i- 1)= 100,解得i= 51,即需要i —51时输出.故图中判断框内(1)处和执行框中的⑵处应填的语句分别是i> 50, n=n + 2.11. (2018福州五校联考)定义[x]为不超过x的最大整数,例如[1 . 3] —1.执行如图所示的程序框图,当输入的x为4. 7时,输出的y值为()A . 7B . 8. 6C. 10. 2 D . 11. 8解析:选C.当输入的x为4. 7时,执行程序框图可知,4. 7- [4 . 7] —0. 7,即4. 7 -[4 . 7]不等于0,因而可得y= 7+ ([4 . 7 —3] + 1)X 1 . 6—10 . 2,输出的值为10 . 2,故选C .12 . (2018湖南五市十校联考)执行如图所示的程序框图,则输出的a值为()解析:选C •经第一次循环得到的结果是经第二次循环得到的结果是s— 1+1S— 2 十n—6,i —经第三次循环得到的结果是s_ 1 +丄+1S—2十4十n= 8,i —4./输出丁/4A . —3B . ~31 C.—2 D ・21解析:选D •第1次循环,a=—3, i = 2;第2次循环,a=—勺,i = 3;第3次循环,a1 =3, i = 4;第4次循环,a = 2, i = 5;…所以周期为4,故最后输出的a的值为2.3二、填空题13 •执行如图所示的程序框图,则输出的s的值为_________ .解析:由程序框图可知k= 1, s= 2; k = 2, s= -; k= 3, s=5.此时k v3不成立,故2 3输出s= 5.答案:5314.下列程序执行后输出的结果是 ___________i = 11S= 1DOS= S*ii = i —1LOOP UNTIL i<9解析:程序反映出的算法过程i= 11? S= 11X 1, i = 10; i= 10? S= 11X 10, i = 9;i= 9? S= 11X 10X 9, i = 8;i= 8<9退出循环,执行“PRINT S”,故S= 990.答案:99015.下面左图是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为A1, A?,…,A16,右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,则该算法流程图输出的结果是__________________ .解析:由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图可知:数学成绩大于等于90的人数为10,因此输出的结果为10.答案:1016•输入x= 5,运行如图所示的程序之后得到的y等于_________ .解析:由题意,得y= f(x) =* 2(x—1) , x> 0,所以f(5) = (5 —1)2= 16.答案:16。

2019年全国统一高考数学试卷(文科)(新课标Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)设z=,则|z|=()A.2B.C.D.12.(5分)已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩∁U A=()A.{1,6}B.{1,7}C.{6,7}D.{1,6,7} 3.(5分)已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a4.(5分)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是()A.165cm B.175cm C.185cm D.190cm5.(5分)函数f(x)=在[﹣π,π]的图象大致为()A.B.C.D.6.(5分)某学校为了解1000名新生的身体素质,将这些学生编号1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是()A.8号学生B.200号学生C.616号学生D.815号学生7.(5分)tan255°=()A.﹣2﹣B.﹣2+C.2﹣D.2+8.(5分)已知非零向量,满足||=2||,且(﹣)⊥,则与的夹角为()A.B.C.D.9.(5分)如图是求的程序框图,图中空白框中应填入()A.A=B.A=2+C.A=D.A=1+10.(5分)双曲线C:﹣=1(a>0,b>0)的一条渐近线的倾斜角为130°,则C 的离心率为()A.2sin40°B.2cos40°C.D.11.(5分)△ABC的内角A,B,C的对边分别为a,b,c.已知a sin A﹣b sin B=4c sin C,cos A =﹣,则=()A.6B.5C.4D.312.(5分)已知椭圆C的焦点为F1(﹣1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为()A.+y2=1B.+=1C.+=1D.+=1二、填空题:本题共4小题,每小题5分,共20分。
等差数列与等比数列【2019年高考考纲解读】1.等差、等比数列基本量和性质的考查是高考热点,经常以小题形式出现.2.数列求和及数列与函数、不等式的综合问题是高考考查的重点,考查分析问题、解决问题的综合能力.【重点、难点剖析】一、等差数列、等比数列的运算1.通项公式等差数列:a n =a 1+(n -1)d ;等比数列:a n =a 1·qn -1. 2.求和公式 等差数列:S n =n a 1+a n 2=na 1+n n -2d ;等比数列:S n =a 11-q n 1-q =a 1-a n q 1-q(q ≠1). 3.性质若m +n =p +q ,在等差数列中a m +a n =a p +a q ;在等比数列中a m ·a n =a p ·a q .二 等差数列、等比数列的判定与证明证明数列{a n }是等差数列或等比数列的证明方法(1)证明数列{a n }是等差数列的两种基本方法:①利用定义,证明a n +1-a n (n ∈N *)为一常数;②利用等差中项,即证明2a n =a n -1+a n +1(n ≥2,n ∈N *).(2)证明数列{a n }是等比数列的两种基本方法: ①利用定义,证明a n +1a n(n ∈N *)为一常数; ②利用等比中项,即证明a 2n =a n -1a n +1(n ≥2,n ∈N *).三、等差数列、等比数列的综合问题解决等差数列、等比数列的综合问题,要从两个数列的特征入手,理清它们的关系;数列与不等式、函数、方程的交汇问题,可以结合数列的单调性、最值求解.【高考题型示例】题型一、等差数列、等比数列的运算例1、(2018·北京)设{a n }是等差数列,且a 1=3,a 2+a 5=36,则{a n }的通项公式为______.答案 a n =6n -3(n ∈N *)解析 方法一 设公差为d .∵a 2+a 5=36,∴(a 1+d )+(a 1+4d )=36,∴2a 1+5d =36.∵a 1=3,∴d =6,∴通项公式a n =a 1+(n -1)d =6n -3(n ∈N *).方法二 设公差为d ,∵a 2+a 5=a 1+a 6=36,a 1=3,∴a 6=33,∴d =a 6-a 15=6.∵a 1=3,∴通项公式a n =6n -3(n ∈N *). 【变式探究】(2018·全国Ⅲ)等比数列{a n }中,a 1=1,a 5=4a 3.①求{a n }的通项公式;②记S n 为{a n }的前n 项和,若S m =63,求m .【变式探究】(2017·全国Ⅰ)记S n 为等差数列{a n }的前n 项和.若a 4+a 5=24,S 6=48,则{a n }的公差为________.答案 4解析 设{a n }的公差为d ,由⎩⎪⎨⎪⎧ a 4+a 5=24,S 6=48,得⎩⎪⎨⎪⎧ a 1+3d +a 1+4d =24,6a 1+6×52d =48,解得d =4. 【感悟提升】在进行等差(比)数列项与和的运算时,若条件和结论间的联系不明显,则均可化成关于a 1和d (q )的方程组求解,但要注意消元法及整体计算,以减少计算量.【变式探究】设公比为q (q >0)的等比数列{a n }的前n 项和为S n ,若S 2=3a 2+2,S 4=3a 4+2,则a 1等于( )A .-2B .-1 C.12 D.23答案 B解析 S 4-S 2=a 3+a 4=3a 4-3a 2,即3a 2+a 3-2a 4=0,即3a 2+a 2q -2a 2q 2=0,即2q 2-q -3=0,解得q =-1(舍)或q =32, 当q =32时,代入S 2=3a 2+2, 得a 1+a 1q =3a 1q +2,解得a 1=-1.【变式探究】设等比数列{a n }的前n 项和为S n ,若a 3a 11=2a 25,且S 4+S 12=λS 8,则λ=________.答案 83解析 ∵a 3a 11=2a 25,∴a 27=2a 25,∴q 4=2,∵S 4+S 12=λS 8,∴a 11-q 41-q +a 11-q 121-q =λa 11-q 81-q , 1-q 4+1-q 12=λ(1-q 8),将q 4=2代入计算可得λ=83. 题型二 等差数列、等比数列的判定与证明例2、已知数列{a n },{b n },其中a 1=3,b 1=-1,且满足a n =12(3a n -1-b n -1),b n =-12(a n -1-3b n -1),n ∈N *,n ≥2.(1)求证:数列{a n -b n }为等比数列;(2)求数列⎩⎨⎧⎭⎬⎫2na n a n +1的前n 项和T n . (1)证明 a n -b n =12(3a n -1-b n -1)-⎝ ⎛⎭⎪⎫-12(a n -1-3b n -1)=2(a n -1-b n -1), 又a 1-b 1=3-(-1)=4,所以{a n -b n }是首项为4,公比为2的等比数列.(2)解 由(1)知,a n -b n =2n +1,①又a n +b n =12(3a n -1-b n -1)+⎝ ⎛⎭⎪⎫-12(a n -1-3b n -1)=a n -1+b n -1, 又a 1+b 1=3+(-1)=2,所以{a n +b n }为常数数列,a n +b n =2,②联立①②得,a n =2n+1,2n a n a n +1=2n 2n +n +1+=12n +1-12n +1+1, 所以T n =⎝⎛⎭⎪⎫121+1-122+1+⎝ ⎛⎭⎪⎫122+1-123+1+…+⎝ ⎛⎭⎪⎫12n +1-12n +1+1 =121+1-12n +1+1=13-12n +1+1(n ∈N *). 【感悟提升】(1)判断一个数列是等差(比)数列,也可以利用通项公式及前n 项和公式,但不能作为证明方法.(2)a 2n =a n -1a n +1(n ≥2)是数列{a n }为等比数列的必要不充分条件,判断时还要看各项是否为零.【变式探究】已知{a n }是各项都为正数的数列,其前n 项和为S n ,且S n 为a n 与1a n的等差中项. (1)求证:数列{S 2n }为等差数列;(2)求数列{a n }的通项公式;(3)设b n =-n a n ,求{b n }的前n 项和T n .(2)解 由(1)可得S 2n =1+n -1=n ,∵数列{a n }的各项都为正数,∴S n =n ,∴当n ≥2时,a n =S n -S n -1=n -n -1,又a 1=S 1=1满足上式,∴a n =n -n -1(n ∈N *).(3)解 由(2)得b n =-n a n =-n n -n -1 =(-1)n (n +n -1),当n 为奇数时,T n =-1+(2+1)-(3+2)+…+(n -1+n -2)-(n +n -1)=-n ,当n 为偶数时,T n =-1+(2+1)-(3+2)+…-(n -1+n -2)+(n +n -1)=n ,∴数列{b n }的前n 项和T n =(-1)n n (n ∈N *).题型三 等差数列、等比数列的综合问题例3、已知等差数列{a n }的公差为-1,且a 2+a 7+a 12=-6.(1)求数列{a n }的通项公式a n 与其前n 项和S n ;(2)将数列{a n }的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{b n }的前3项,记{b n }的前n 项和为T n ,若存在m ∈N *,使得对任意n ∈N *,总有S n <T m +λ恒成立,求实数λ的取值范围.解 (1)由a 2+a 7+a 12=-6,得a 7=-2,∴a 1=4,∴a n =5-n ,从而S n =n 9-n 2(n ∈N *). (2)由题意知b 1=4,b 2=2,b 3=1,设等比数列{b n }的公比为q ,则q =b 2b 1=12, ∴T m =4⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12m 1-12=8⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12m , ∵⎝ ⎛⎭⎪⎫12m 随m 的增加而减少, ∴{T m }为递增数列,得4≤T m <8.又S n =n 9-n 2=-12(n 2-9n ) =-12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫n -922-814, 故(S n )max =S 4=S 5=10,若存在m ∈N *,使得对任意n ∈N *,总有S n <T m +λ,则10<8+λ,得λ>2.即实数λ的取值范围为(2,+∞).【感悟提升】(1)等差数列与等比数列交汇的问题,常用“基本量法”求解,但有时灵活地运用性质,可使运算简便.(2)数列的项或前n 项和可以看作关于n 的函数,然后利用函数的性质求解数列问题.(3)数列中的恒成立问题可以通过分离参数,通过求数列的值域求解.【变式探究】已知数列{a n }的前n 项和为S n ,且S n -1=3(a n -1),n ∈N *.(1)求数列{a n }的通项公式; (2)设数列{b n }满足a n +1=32n n a b ⋅⎛⎫ ⎪⎝⎭,若b n ≤t 对于任意正整数n 都成立,求实数t 的取值范围.(2)由a n +1=32n n a b ⋅⎛⎫ ⎪⎝⎭,得b n =1a n 312log n a +=⎝ ⎛⎭⎪⎫23n -1323log 2n ⎛⎫ ⎪⎝⎭ =n ·⎝ ⎛⎭⎪⎫23n -1, 所以b n +1-b n =(n +1)·⎝ ⎛⎭⎪⎫23n -n ·⎝ ⎛⎭⎪⎫23n -1 =2n -13n (2-n ), 所以(b n )max =b 2=b 3=43,所以t ≥43. 即t 的取值范围为⎣⎢⎡⎭⎪⎫43,+∞.。
全国100所名校单元测试示范卷·高三·数学卷(十一)第十一单元数列综合测试(120分钟150分)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知数列{a n}为等比数列,且a3a9=2a52,a2=2,则a1等于A.±√2B.√2C.-√2D.2解析:a3a9=a62=2a52,q=a6a5=±√2,故a1=a2q=±√2.答案:A2.在等差数列{a n}中,a1=0,公差d≠0,若a n=a2+a3+a6+a8,则n等于A.15B.16C.17D.18解析:a n=a2+a3+a6+a8=4a1+15d=a1+15d,故a n为等差数列{a n}的第16项,∴n=16.故选B.答案:B3.若等差数列{a n}满足递推关系a n+1=-a n+n,则a5等于A.92B.94C.114D.134解析:令n=4,则a5+a4=4,令n=5,则a6+a5=5,两式相加2a5+a4+a6=9,∴a5=9 4 .答案:B4.设S n为等比数列{a n}的前n项和,已知3S2013=a2014-2012,3S2012=a2013-2012,则公比q等于A.4B.3C.2D.8解析:由3S2013=a2014-2012,3S2012=a2013-2012得3a2013=a2014-a2013,∴q=a2014a2013=4.答案:A5.已知数列{a n}的通项公式是a n=-n2+bn+c,若a n+1<a n对n∈N+恒成立,则实数b的取值范围是A.b>0B.b≥-1C.b≤3D.b<3解析:∵a n+1<a n恒成立,∴a n+1-a n=b-(2n+1)<0,即b<2n+1恒成立,∴b<3.答案:D6.已知函数f(x)是R 上的单调增函数且为奇函数,数列{a n }是等差数列,a 11>0,则f(a 9)+f(a 11)+f(a 13)的值A.恒为正数B.恒为负数C.恒为0D.可正可负解析:因为f(a 11)>f(0)=0,a 9+a 13=2a 11>0,a 9>-a 13, 所以有f(a 9)>f(-a 13)=-f(a 13),f(a 9)+f(a 13)>0,故选A. 答案:A 7.已知等差数列{a n }的前n 项和为S n ,若m>1,2a m-1+2a m+1-a m 2-4=0,S 2m-1=38,则m等于A.7B.8C.9D.10解析:∵a m-1+a m+1=2a m ,∴2a m-1+2a m+1-a m 2-4=4a m -a m 2-4=0,∴a m =2.故S 2m-1=(a 1+a 2m -1)(2m -1)2=2a m (2m -1)2=2(2m-1)=38.∴m=10. 答案:D8.若数列{a n }满足a 1=12,a n+1=1+an 1-a n(n ∈N +),则该数列的前2014项的乘积a 1·a 2·a 3·…·a 2014等于A.3B.1C.32D.23解析:易求得a 1=12,a 2=3,a 3=-2,a 4=-13,a 5=12,…,这是一个周期为4的周期数列, 且每相邻四项a 1·a 2·a 3·a 4=1,故原式=12×3=32. 答案:C9.已知数列{a n }的通项公式a n =n 2+n,若数列{1a n}的前n 项和为S n ,则S n 的取值范围为A.[0,1]B.(2,1)C.[12,1) D.[12,1]解析:依题意1a n =1n(n+1)=1n -1n+1,∴S n =1a 1+1a 2+…+1a n =1-12+12-13+…+1n -1n+1=1-1n+1<1,∴当n=1时,S n 取最小值12,∴S n 值范围为[12,1).答案:C10.在数列{a n }中,对于任意的n ∈N +,都有a n+2-a n+1a n+1-a n=k(k为常数),则称{a n }为“等差比数列”.下面对“等差比数列”的判断:①等差数列一定是“等差比数列”;②等比数列一定是“等差比数列”;③通项公式为a n =a ·b n +c(a ≠0,b ≠0,1)的数列一定是“等差比数列”.其中正确的个数是A.0B.1C.2D.3解析:①②错误,对于①②只要举常数列即可验证它是错的;③正确,对于③,其中k=b.答案:B11.已知数列{a n }满足a 1=1,na n =(n+1)a n-1(n ≥2,且n ∈N +),则a n 2+14n取最小值的n 值为A.2B.3C.4D.5解析:∵na n =(n+1)a n-1,∴a n a n -1=n+1n ,∴a 2a 1·a 3a 2·…·a n a n -1=21·32·…·n+1n=n+1,即a n =n+1(n ≥2),∴a n 2+14n =n+15n +2,令f(x)=x+15x+2,∵f(x)在(0,√15)上单调递减,在(√15,+∞)上单调递增.故当n=3或4时,a n 2+14n取最小值, ∵a 32+143=3+153+2=10,a 42+144=4+154+2=394,故当n=4时取最小值,故选C. 答案:C12.对任意x ∈R ,函数f(x)满足f(x+1)=√2f(x)-[f(x)]2+1,设a n =[f(n)]2-2f(n),数列{a n }的前2013项的和为-1003,则f(2013)等于A.4B.3C.2D.1解析:因为[f(x+1)-1]2=[f(x+1)]2-2f(x+1)+1=2f(x)-[f(x)]2,所以有a n+1+a n =-1. 前2013项和S 2013=1006·(-1)+a 2013=-1003,由此可得a 2013=3,a 2012=-4. 因而f(2013)=√-a 2012+1=3,故选B. 答案:B第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.等差数列{a n }的前n 项和为S n ,且S 3=6,a 3=4,则公差d= . 解析:由题意知{a 1+2d =4,3a 1+3×22×d =6,解得d=2. 答案:214.设S n 是等差数列{a n }的前n 项和,若a 3+a 9=17S 7,且a 4,a 6为等比数列{b n }相邻的两项,则等比数列{b n }的公比q= .解析:∵a 3+a 9=17S 7,∴2a 6=17×7(a 1+a 7)2=a 4,∴q=12或2. 答案:12或215.数列{a n }中,a 1=1,a n+1=2a n +1,则通项a n = .解析:由题可得a n+1+1=2(a n +1),∴a n+1+1a n +1=2,数列{a n +1}为等比数列,∴a n +1=2n-1(a 1+1)=2n ,故a n =2n -1.答案:2n -116.数列{a n }中,对任意的m,n,p ∈N +,当m+n=p 时,都有a m ·a n =a p ,若a 1=12,则a 10的值为 .解析:∵a m ·a n =a p ,∴a 12=a 2,a 1·a 2=a 3, a 1·a 3=a 4, …… a 1·a 9=a 10,累乘得a 110=a 10=(12)10=11024. 答案:11024三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.17.(本小题满分10分)设{a n }是一个公差为d(d ≠0)的等差数列,它的前10项和S 10=110且a 1,a 2,a 4成等比数列,求数列{a n }的通项公式.解析:因a 1,a 2,a 4成等比数列,故a 22=a 1a 4,而{a n }是等差数列,有a 2=a 1+d,a 4=a 1+3d,于是(a 1+d)2=a 1(a 1+3d),即a 12+2a 1d+d 2=a 12+3a 1d,化简得a 1=d.5分∵S 10=10a 1+10×92d=110,∴10a 1+45d=110. 又∵a 1=d,∴55d=110,∴d=2,∴a n =a 1+(n-1)d=2n.10分18.(本小题满分12分)已知幂函数f(x)图象过点(-12,-2),数列{a n },{b n }满足a 1=1,b 1=1,且对任意n ∈N +,均有a n+1=a nf(a n )f(an )+3,b n+1-b n =1a n .(1)求函数f(x)的解析式; (2)试求数列{a n },{b n }的通项公式.解析:(1)由题意可知(-12)a =-2,所以a=-1,故f(x)=1x(x ≠0).4分 (2)由(1)可得a n+1=11a n +3=a n 3a n +1,所以有1a n+1=1a n +3,故a n =13n -2. b n =(b n -b n-1)+(b n-1-b n-2)+…+(b 2-b 1)+b 1=3[(n-1)+(n-2)+…+2+1]-2(n-1)+1=3·n -1+12(n-1)-2n+2+1=3n 2-7n+62.12分19.(本小题满分12分)设S n 是正项数列{a n }的前n 项和,且S n =13a n 2+12a n .(1)求a n ; (2)设√b n =34an +3(n ∈N +),且数列{b n }的前n 项和为T n ,试比较T n 与14的大小.解析:(1)由已知可得a 1=13a 12+12a 1,a 1>0,所以a 1=32. 当n ≥2时,有a n =S n -S n-1=13a n 2+12a n -(13a n -12+12a n-1) =13(a n 2-a n -12)+12(a n -a n-1),∴(a n +a n-1)(a n -a n-1-32)=0, 又a n >0,所以有a n -a n-1=32,数列{a n }为等差数列. 所以a n =32n.6分 (2)由(1)可知b n =1(2n+1)2=14n 2+4n+1<14n 2+4n <14(1n -1n+1), 所以有T n =b 1+b 2+…+b n <14[(11-12)+(12-13)+…+(1n -1n+1)]=14(1-1n+1)<14.12分 20.(本小题满分12分)已知{a n }是各项均为正数的等比数列,且a 1+a 2=2(1a 1+1a 2),a 3+a 4+a 5=64(1a 3+1a 4+1a 5).(1)求{a n }的通项公式;(2)设b n =(a n +1a n)2,求数列{b n }的前n 项和T n .解析:(1)设公比为q,则a n =a 1q n-1,易知q ≠1.由已知得{a 1+a 1q =2(1a 1+1a 1q ),a 1q 2+a 1q 3+a 1q 4=64(1a 1q 2+1a 1q3+1a 1q4), 化简得{a 12q =2,a 12q 6=64.又a 1>0,故q=2,a 1=1,∴a n =2n-1.6分(2)由(1)知b n =(a n +1a n )2=a n 2+1a n2+2=4n-1+14n -1+2,∴T n =b 1+b 2+b 3+…+b n =(1+4+…+4n-1)+(1+14+…+14n -1)+2n=4n -14-1+1-14n 1-14+2n=13(4n -41-n )+2n+1.12分21.(本小题满分12分)已知f(x)是定义在R 上不恒为零的函数,对于任意的x,y ∈R ,都有f(x ·y)=xf(y)+yf(x)成立.数列{a n }满足a n =f(2n )(n ∈N +),且a 1=2. (1) 试求数列{a n }的通项公式a n . (2)若b n =a nn(n+1)2,求数列{b n }的最小项.解析: (1)因为a 1=f(2)=2,令x=2n-1,y=2,则有f(2n )=2n-1f(2)+2f(2n-1) =2n +2[2n-2f(2)+2f(2n-2)]=2·2n +22f(2n-2)=2·2n +22[2n-3f(2)+2f(2n-3)]=3·2n +23f(2n-3)=…=(n-2)·2n +2n-2[2n-(n-1)f(2)+2f(2n-(n-1))]=n ·2n ,7分 即a n =n ·2n . (2)由(1)可知b n =2n (n+1)2,令b n+1b n =2·[n+1n+2]2>1得n 2>2,n>√2, 即当n ≥2,n ∈N ,都有b 2<b 3<…<b n ,而b 1=12>b 2=49,故(b n )min =b 2=49.12分22.(本小题满分12分)已知数列{a n }的前n(n ∈N +)项和为S n ,a 1=t,a 2=-1,点P n (a n ,S n ),若点P n (n=2,3,4,…)都在斜率为13的同一条直线上.(1)当t 为何值时,数列{a n }是等比数列?(2)在满足(1)的条件下,设b n =λa n -n 2,若数列{b n }中,有b 1>b 2,b 3>b 4,…,b 2n-1>b 2n ,…成立,求实数λ的取值范围.解析:(1)∵点P n ,P n+1(n=2,3,4,…)都在斜率为13的直线上, ∴S n+1-S n a n+1-a n =13. 又∵S n+1-S n =a n+1, ∴a n+1=13(a n+1-a n ),整理得a n+1a n =-12(n ≥2). 又∵当n ∈N +时,数列{a n }是等比数列, ∴只需要a 2a 1=-1t=-12, ∴t=2.6分(2)由(1)得a n =2·(-12)n-1, ∵b n =λa n -n 2, ∴b n =2λ(-12)n-1-n 2,由b 2n-1>b 2n 得,2λ(-12)2n-2-(2n-1)2>b 2n =2λ(-12)2n-1-(2n)2, 即2λ(-12)2n-2[1-(-12)]>(2n-1)2-(2n)2,∴λ>-(4n -1)·4n12, ∵-(4n -1)·4n 12单调递减, ∴当n=1时,-(4n -1)·4n12取最大值为-1, ∴λ>-1.12分。
2019高考数学文一轮复习: 数列综合复习一、选择题:1.已知数列{a n }满足a 1=1,a n +1=a 2n -2a n +1(n ∈N *),则a 2 018=( ) A.1 B.0 C.2 018 D.-2 018 2.设数列{a n }的前n 项和为S n ,且S n =2(a n -1),则a n = ( ) A.2n B.2n -1 C.2nD.2n-1 3.已知数列{a n }满足a 1=1,a n +1a n =2n(n ∈N *),则a 10=( ) A.64 B.32 C.16 D.8 4.设等差数列{a n }的前n 项和为S n ,且a 2+a 7+a 12=24,则S 13=( ) A.52 B.78 C.104 D.208 5.若等差数列{a n }的前5项和S 5=25,且a 2=3,则a 7=( ) A.12 B.13 C.14 D.156.设等差数列{a n }的前n 项和为S n ,则“a 6+a 7>0”是“S 9≥S 3”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充要也不必要条件7.设S n 为等比数列{a n }的前n 项和,已知3S 3=a 4-2,3S 2=a 3-2,则公比q=( ) A.3 B.4 C.5 D.68.在等比数列{a n }中,已知a 3=6,a 3+a 5+a 7=78,则a 5=( ) A.12 B.18 C.36 D.249.已知等比数列{a n }的各项都为正数,且a 3,12a 5,a 4成等差数列,则a 3+a 5a 4+a 6的值是( )A.5-12 B.5+12 C.3-52 D.3+5210.在递增的等比数列{a n }中,已知a 1+a n =34,a 3·a n -2=64,且前n 项和S n =42,则n 等于( ) A.3 B.4 C.5 D.6 11.S n =12+12+38+…+n2n 等于( )A.2n-n 2n B.2n +1-n -22n C.2n -n +12n +1D.2n +1-n +22n12.数列{a n }的通项公式是a n =1n +n +1,若前n 项和为10,则项数n 为( )A.120B.99C.11D.121二、填空题:13.已知数列{a n },{b n },若b 1=0,a n =1n (n +1),当n ≥2时,有b n =b n -1+a n -1,则b 10=________.14.在等差数列{a n }中,a 3+a 9=27-a 6,S n 表示数列{a n }的前n 项和,则S 11=________. 15.设等差数列{a n }的前n 项和为S n ,S m -1=-2,S m =0,S m +1=3,则正整数m 的值为________. 16.已知数列{a n }是递增的等比数列,a 1+a 4=9,a 2a 3=8,则数列{a n }的前n 项和S n =________. 17.设等比数列{a n }的前n 项和为S n ,若27a 3-a 6=0,则S 6S 3=________.18.设函数f(x)=12+log 2x 1-x ,定义S n =f ⎝ ⎛⎭⎪⎫1n +f ⎝ ⎛⎭⎪⎫2n +…+f ⎝ ⎛⎭⎪⎫n -1n ,其中n ∈N *,且n ≥2,则S n=________.三、解答题:19.已知数列{a n }中,a 1=1,前n 项和S n =n +23a n .(1)求a 2,a 3; (2)求{a n }的通项公式.20.已知等差数列{a n }前三项的和为-3,前三项的积为8. (1)求数列{a n }的通项公式;(2)若a 2,a 3,a 1成等比数列,求数列{|a n |}的前n 项和S n .21.已知公差大于零的等差数列{a n}的前n项和为S n,且满足a3·a4=117,a2+a5=22.(1)求数列{a n}的通项公式;(2)若数列{b n}满足b n=S nn+c,是否存在非零实数c使得{b n}为等差数列?若存在,求出c的值;若不存在,请说明理由.22.已知{a n}是等差数列,满足a1=3,a4=12,数列{b n}满足b1=4,b4=20,且{b n-a n}为等比数列.(1)求数列{a n}和{b n}的通项公式;(2)求数列{b n}的前n项和.23.设数列{a n}的前n项和为S n,已知a1+2a2+3a3+…+na n=(n-1)S n+2n(n∈N*).(1)求a2,a3的值;(2)求证:数列{S n+2}是等比数列.24.已知等比数列{a n}的前n项和为S n,且6S n=3n+1+a(n∈N*).(1)求a的值及数列{a n}的通项公式;(2)若b n=(1-an)log3(a2n·a n+1),求数列{1b n}的前n项和T n.25.已知数列{a n }的前n 项和为S n ,且S n =2a n -2. (1)求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫n +1a n 的前n 项和T n .26.已知S n 为数列{a n }的前n 项和.已知a n >0,a 2n +2a n =4S n +3. (1)求{a n }的通项公式;(2)设b n =1a n a n +1,求数列{b n }的前n 项和.参考答案解析1.解析:选B.因为a 1=1,所以a 2=(a 1-1)2=0,a 3=(a 2-1)2=1,a 4=(a 3-1)2=0,…,可知数列{a n }是以2为周期的数列,所以a 2 018=a 2=0.2.解析:选C.当n=1时,a 1=S 1=2(a 1-1),可得a 1=2,当n ≥2时,a n =S n -S n -1=2a n -2a n -1,所以a n =2a n -1,所以数列{a n }为等比数列,公比为2,首项为2,所以a n =2n. 3.解析:选B.因为a n +1a n =2n,所以a n +2a n +1=2n +1,两式相除得a n +2a n=2.又a 1a 2=2,a 1=1,所以a 2=2.法一:a 10a 8·a 8a 6·a 6a 4·a 4a 2=24,即a 10=25=32.法二:数列{a 2n }是首项为2,公比为2的等比数列,所以a 10=2×24=32. 4.解析:选C.依题意得3a 7=24,a 7=8,S 13=13(a 1+a 13)2=13a 7=104,选C.5.解析:选B.设{a n }的公差为d ,由S 5=5(a 2+a 4)2⇒25=5(3+a 4)2⇒a 4=7,所以7=3+2d ⇒d=2,所以a 7=a 4+3d=7+3×2=13.6.解析:选A.法一:将它们等价转化为a 1和d 的关系式.a 6+a 7>0⇒a 1+5d +a 1+6d>0⇒2a 1+11d>0;S 9≥S 3⇒9a 1+9×8×d 2≥3a 1+3×2×d2⇒2a 1+11d ≥0.法二:a 6+a 7>0⇒a 1+a 12>0,S 9≥S 3⇒a 4+a 5+…+a 9≥0⇒3(a 1+a 12)≥0.7.解析:选B.由题意知,q ≠1,则⎩⎪⎨⎪⎧3a 1(1-q 3)1-q =a 1q 3-23a 1(1-q 2)1-q=a 1q 2-2,两式相减可得-3(q 3-q 2)1-q =q 3-q 2, 即-31-q=1,所以q=4. 8.解析:a 3+a 5+a 7=a 3(1+q 2+q 4)=6(1+q 2+q 4)=78⇒1+q 2+q 4=13⇒q 2=3,所以a 5=a 3q 2=6×3=18.故选B. 9.解析:选A.设等比数列{a n }的公比为q ,由a 3,12a 5,a 4成等差数列可得a 5=a 3+a 4,即a 3q 2=a 3+a 3q ,故q 2-q -1=0,解得q=1+52或q=1-52(舍去),由a 3+a 5a 4+a 6=a 3+a 3q 2a 4+a 4q 2=a 3(1+q 2)a 4(1+q 2)=1q =25+1=2(5-1)(5+1)(5-1)=5-12,故选A. 10.解析:选A.因为{a n }为等比数列,所以a 3·a n -2=a 1·a n =64.又a 1+a n =34,所以a 1,a n 是方程x 2-34x +64=0的两根,解得⎩⎪⎨⎪⎧a 1=2,a n =32或⎩⎪⎨⎪⎧a 1=32,a n =2. 又因为{a n }是递增数列,所以⎩⎪⎨⎪⎧a 1=2,a n=32.由S n =a 1-a n q 1-q =2-32q1-q =42,解得q=4.由a n =a 1qn -1=2×4n -1=32,解得n=3.故选A.11.解析:选B.由S n =12+222+323+…+n 2n ,①得12S n =122+223+…+n -12n +n2n +1,②①-②得,12S n =12+122+123+…+12n -n 2n +1,所以S n =2n +1-n -22n. 12.解析:选A.a n =1n +n +1=n +1-n(n +1+n )(n +1-n )=n +1-n ,所以a 1+a 2+…+a n =(2-1)+(3-2)+…+(n +1-n)=n +1-1=10. 即n +1=11,所以n +1=121,n=120.13.解析:由b n =b n -1+a n -1得b n -b n -1=a n -1,所以b 2-b 1=a 1,b 3-b 2=a 2,…,b n -b n -1=a n -1,所以b 2-b 1+b 3-b 2+…+b n -b n -1=a 1+a 2+…+a n -1=11×2+12×3+…+1(n -1)×n ,即b n -b 1=a 1+a 2+…+a n -1=11×2+12×3+…+1(n -1)×n =11-12+12-13+…+1n -1-1n=1-1n =n -1n ,又b 1=0,所以b n =n -1n ,所以b 10=910.答案:91014.解析:因为a 3+a 9=27-a 6,2a 6=a 3+a 9,所以3a 6=27,所以a 6=9,所以S 11=112(a 1+a 11)=11a 6=99.答案:9915.解析:因为等差数列{a n }的前n 项和为S n ,S m -1=-2,S m =0,S m +1=3,所以a m =S m -S m -1=2,a m +1=S m +1-S m =3,数列的公差d=1,a m +a m +1=S m +1-S m -1=5,即2a 1+2m -1=5,所以a 1=3-m.由S m =(3-m)m +m (m -1)2×1=0,解得正整数m 的值为5.答案:516.解析:设等比数列的公比为q ,则有⎩⎪⎨⎪⎧a 1+a 1q 3=9,a 21q 3=8,解得⎩⎪⎨⎪⎧a 1=1,q =2或⎩⎪⎨⎪⎧a 1=8,q =12.又{a n }为递增数列,所以⎩⎪⎨⎪⎧a 1=1,q =2,所以S n =1-2n1-2=2n -1.答案:2n-117.解析:由题可知{a n }为等比数列,设首项为a 1,公比为q ,所以a 3=a 1q 2,a 6=a 1q 5,所以27a 1q 2=a 1q 5,所以q=3,由S n =a 1(1-q n)1-q ,得S 6=a 1(1-36)1-3,S 3=a 1(1-33)1-3,所以S 6S 3=a 1(1-36)1-3·1-3a 1(1-33)=28.答案:28 18.解析:因为f(x)+f(1-x)=12+log 2 x 1-x +12+log 2 1-xx=1+log 21=1,所以2S n =⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫1n +f ⎝ ⎛⎭⎪⎫n -1n +[f ⎝ ⎛⎭⎪⎫2n +f ⎝ ⎛⎭⎪⎫n -2n ]+…+⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫n -1n +f ⎝ ⎛⎭⎪⎫1n =n -1.所以S n=n -12.答案:n -1219.解:(1)由S 2=43a 2得3(a 1+a 2)=4a 2,解得a 2=3a 1=3.由S 3=53a 3得3(a 1+a 2+a 3)=5a 3,解得a 3=32(a 1+a 2)=6.(2)由题设知a 1=1.当n ≥2时,有a n =S n -S n -1=n +23a n -n +13a n -1,整理得a n =n +1n -1a n -1.于是a 1=1,a 2=31a 1,a 3=42a 2,…a n -1=n n -2a n -2,a n =n +1n -1a n -1.将以上n 个等式两端分别相乘,整理得a n =n (n +1)2.显然,当n=1时也满足上式.综上可知,{a n }的通项公式a n =n (n +1)2.20.解:(1)设等差数列{a n }的公差为d ,则a 2=a 1+d ,a 3=a 1+2d.由题意得⎩⎪⎨⎪⎧3a 1+3d =-3,a 1(a 1+d )(a 1+2d )=8,解得⎩⎪⎨⎪⎧a 1=2,d =-3,或⎩⎪⎨⎪⎧a 1=-4,d =3.所以由等差数列通项公式可得a n =2-3(n -1)=-3n +5或a n =-4+3(n -1)=3n -7.故a n =-3n +5或a n =3n -7.(2)当a n =-3n +5时,a 2,a 3,a 1分别为-1,-4,2,不成等比数列; 当a n =3n -7时,a 2,a 3,a 1分别为-1,2,-4,成等比数列,满足条件.故|a n |=|3n -7|=⎩⎪⎨⎪⎧-3n +7,n =1,2,3n -7,n ≥3.记数列{|a n |}的前n 项和为S n .当n=1时,S 1=|a 1|=4;当n=2时,S 2=|a 1|+|a 2|=5;当n ≥3时,S n =S 2+|a 3|+|a 4|+…+|a n |=5+(3×3-7)+(3×4-7)+…+(3n -7) =5+(n -2)[2+(3n -7)]2=32n 2-112n +10.当n=2时,满足此式,当n=1时,不满足此式.综上,S n =⎩⎪⎨⎪⎧4,n =1,32n 2-112n +10,n ≥2.21.解:(1)因为数列{a n }为等差数列,所以a 3+a 4=a 2+a 5=22.又a 3·a 4=117,所以a 3,a 4是方程x 2-22x +117=0的两实根,又公差d>0,所以a 3<a 4,所以a 3=9,a 4=13,所以⎩⎪⎨⎪⎧a 1+2d =9,a 1+3d =13,解得⎩⎪⎨⎪⎧a 1=1,d =4.所以数列{a n }的通项公式为a n =4n -3.(2)由(1)知a 1=1,d=4,所以S n =na 1+n (n -1)2×d=2n 2-n ,所以b n =S n n +c =2n 2-n n +c ,所以b 1=11+c ,b 2=62+c ,b 3=153+c,其中c ≠0.因为数列{b n }是等差数列,所以2b 2=b 1+b 3,即62+c ×2=11+c +153+c ,所以2c 2+c=0,所以c=-12或c=0(舍去),故c=-12.即存在一个非零实数c=-12,使数列{b n }为等差数列.22.解:(1)设等差数列{a n }的公差为d ,由题意得d=a 4-a 13=12-33=3,所以a n =a 1+(n -1)d=3n(n=1,2,…).设等比数列{b n -a n }的公比为q ,由题意得q 3=b 4-a 4b 1-a 1=20-124-3=8,解得q=2.所以b n -a n =(b 1-a 1)q n -1=2n -1.从而b n =3n +2n -1(n=1,2,…).(2)由(1)知b n =3n +2n -1(n=1,2,…).数列{3n}的前n 项和为32n(n +1),数列{2n -1}的前n 项和为1-2n1-2=2n -1.所以,数列{b n }的前n 项和为32n(n +1)+2n-1.23.解:(1)因为a 1+2a 2+3a 3+…+na n =(n -1)S n +2n(n ∈N *),所以当n=1时,a 1=2×1=2; 当n=2时,a 1+2a 2=(a 1+a 2)+4,所以a 2=4;当n=3时,a 1+2a 2+3a 3=2(a 1+a 2+a 3)+6,所以a 3=8.综上,a 2=4,a 3=8.(2)证明:因为a 1+2a 2+3a 3+…+na n =(n -1)S n +2n(n ∈N *).①所以当n ≥2时,a 1+2a 2+3a 3+…+(n -1)a n -1=(n -2)S n -1+2(n -1).②①-②,得na n =(n -1)S n -(n -2)S n -1+2=n(S n -S n -1)-S n +2S n -1+2=na n -S n +2S n -1+2. 所以-S n +2S n -1+2=0,即S n =2S n -1+2,所以S n +2=2(S n -1+2). 因为S 1+2=4≠0,所以S n -1+2≠0,所以S n +2S n -1+2=2,故{S n +2}是以4为首项,2为公比的等比数列.24.解:(1)因为6S n =3n +1+a(n ∈N *),所以当n=1时,6S 1=6a 1=9+a ,当n ≥2时,6a n =6(S n -S n -1)=2×3n ,即a n =3n -1,所以{a n }是等比数列,所以a 1=1,则9+a=6,得a=-3,所以数列{a n }的通项公式为a n =3n -1(n ∈N *).(2)由(1)得b n =(1-an)log 3(a 2n ·a n +1)=(3n -2)(3n +1), 所以T n =1b 1+1b 2+…+1b n =11×4+14×7+…+1(3n -2)(3n +1)=13(1-14+14-17+…+13n -2-13n +1)=n3n +1. 25.解:(1)当n=1时,a 1=2.当n ≥2时,S n -1=2a n -1-2, 所以a n =S n -S n -1=2a n -2-(2a n -1-2),即a n a n -1=2(n ≥2,n ∈N *), 所以数列{a n }是首项为2,公比为2的等比数列,故a n =2n(n ∈N *). (2)令b n =n +1a n =n +12n ,则T n =221+322+423+…+n +12n ,①①×12,得12T n =222+323+424+…+n 2n +n +12n +1,②①-②,得12T n =32-n +32n +1,整理得T n =3-n +32n .26.解:(1)由a 2n +2a n =4S n +3,①可知a 2n +1+2a n +1=4S n +1+3.② ②-①,得a 2n +1-a 2n +2(a n +1-a n )=4a n +1,即2(a n +1+a n )=a 2n +1-a 2n =(a n +1+a n )(a n +1-a n ).由a n >0,得a n +1-a n =2.又a 21+2a 1=4a 1+3,解得a 1=-1(舍去)或a 1=3. 所以{a n }是首项为3,公差为2的等差数列,通项公式为a n =2n +1. (2)由a n =2n +1可知b n =1a n a n +1=1(2n +1)(2n +3)=12⎝ ⎛⎭⎪⎫12n +1-12n +3.设数列{b n }的前n 项和为T n ,则T n =b 1+b 2+…+b n =12[⎝ ⎛⎭⎪⎫13-15+⎝ ⎛⎭⎪⎫15-17+…+⎝ ⎛⎭⎪⎫12n +1-12n +3]=n 3(2n +3).。