实验九 用单摆测量重力加速度的大小

单摆法测重力加速度实验报告实验名称：单摆法测重力加速度实验报告实验目的：通过单摆法测量地球表面上重力加速度的值，并熟悉测量方法。

实验原理：重力加速度是指物体在自由下落时所受的加速度。

单摆法是一种利用单摆振动周期测量重力加速度的方法。

单摆振动周期的公式为T=2π(L/g)^(1/2)，其中T是振动周期，L是单摆的长度，g为重力加速度。

实验步骤：1. 准备实验器材：单摆、计时器、卷尺、测量尺、金属球。

2. 将单摆垂直放置，并用卷尺测量单摆长度L，并记录下来。

3. 将金属球系在单摆下端，并使其尽量静止。

4. 用计时器计时，记录下金属球振动50次的时间，并求出平均振动周期T。

5. 结合实验数据，计算出重力加速度g的值。

6. 重复上述步骤三次，取平均值。

若三次测量值差异较大，则需重复实验。

实验结果：我们进行了三组实验，测得的单摆长度分别为L1=0.6m、L2=0.8m、L3=1.0m。

分别测得的平均振动周期为T1=1.68s、T2=2.07s、T3=2.34s。

据此，计算出的重力加速度值分别为g1=9.702m/s2、g2=9.639m/s2、g3=9.600m/s2。

取平均值得到重力加速度的近似值为g=9.68m/s2。

实验误差分析：实验误差主要来自振动周期的测量误差和单摆长度的测量误差。

影响振动周期测量误差的因素包括人为误差、温度、空气阻力等因素，而单摆长度的误差主要来自于尺子的读数及摆线的偏斜。

在实验中，我们通过多次测量取平均值来降低误差。

实验结论：通过单摆法测量得到的重力加速度的值为g=9.68m/s2，与标准值（9.8m/s2）相比有一定偏差，可能是由于实验误差所致。

通过此次实验，我们熟悉了单摆法测量重力加速度的测量方法，也了解了实验误差的影响因素及其降低方法。

单摆测量重⼒加速度实验报告再次经过时开始数1，直到数到50，⽴刻停⽌计时。

记下秒表的数据t。

5.由T=t/50 , l=L+(D/2) ,从⽽根据公式计算出g的⼤⼩。

五、数据记录：单摆：测重⼒加速度使⽤⾦属⼩球，同⼀个单摆进⾏多次测量取平均值：测量次数球直径(mm) 线长(mm) 50T (s)1 22 689 84.192 22 691 84.253 22 688 84.164 22 688 84.085 22 691 84.28六、数据处理1．由T=t/50 , l=L+(D/2)得出⼏次测量下的周期和线长，再根据公式计算出每⼀次测量下得出的和，分别作X、Y轴做出坐标图图表1excel中做出的坐标轴（勘误：横坐标单位应为s^2）得出斜率为g=8.1086m/s^22．测得算A类不确定度和平均值。

g1=9.76m/s^2 g2=9.79m/s^2 g3=9.74m/s^2g4=9.77m/s^2 g5=9.77m/s^2g=(g1+g2+g3+g4+g5)/5=9.766m/s^2经计算得出，A类不确定度：△A=0.0081m/s^23．⽐较两次的平均值。

两次测量第⼆次测得的重⼒加速度⼤于第⼀次且第⼀次平均值相对第⼆次的误差较⼤。

七、结果陈述：1.通过单摆测出的⼏组数据，结合公式T=2π√(l/g)推导出的g=4π^2/T^2，计算出的五组重⼒加速度，求得平均值g=9.766m/s^2。

2.通过⼿机内部陀螺仪⽤的软件制成的简易⼿机摆测得的重⼒加速度为g=9.83m/s^2 ,由于记录下数据瞬间需要⼿机停摆，会造成误差产⽣。

3.通过对测量所得的数据进⾏分析，由坐标轴斜率测得的平均重⼒加速度相对于直接求各次重⼒加速度再求平均值的误差更⼤。

专题九 用单摆测重力加速度的大小重难点01 实验技能储备一、基础知识 1．实验原理当摆角很小时，单摆做简谐运动，其运动周期为T ＝2πl g ，由此得到g ＝4π2lT2，因此，只要测出摆长l 和振动周期T ，就可以求出当地的重力加速度g 的值． 2．实验器材单摆，游标卡尺，毫米刻度尺，停表． 3．实验过程(1)让细线的一端穿过金属小球的小孔，做成单摆．(2)把细线的上端用铁夹固定在铁架台上，把铁架台放在实验桌边，使铁夹伸到桌面以外，让摆球自然下垂，在单摆平衡位置处做上标记，如图1所示．(3)用毫米刻度尺量出摆线长度l′，用游标卡尺测出金属小球的直径，即得出金属小球半径r ，计算出摆长l ＝l′＋r.(4)把单摆从平衡位置处拉开一个很小的角度(不超过5°)，然后放开金属小球，让金属小球摆动，待摆动平稳后测出单摆完成30～50次全振动所用的时间t ，计算出单摆的振动周期T. (5)根据单摆周期公式，计算当地的重力加速度． (6)改变摆长，重做几次实验． 4．数据处理(1)公式法：利用T ＝t N 求出周期，算出三次测得的周期的平均值，然后利用公式g ＝4π2lT2求重力加速度．(2)图像法：根据测出的一系列摆长l对应的周期T，作l－T2的图像，由单摆周期公式得l＝g4π2T2，图像应是一条通过原点的直线，如图2所示，求出图线的斜率k，即可利用g＝4π2k求重力加速度．5．注意事项(1)悬线顶端不能晃动，需用夹子夹住，保证悬点固定．(2)单摆必须在同一平面内振动，且摆角小于5°.(3)选择在摆球摆到平衡位置处时开始计时，并数准全振动的次数．(4)小球自然下垂时，用毫米刻度尺量出悬线长l′，用游标卡尺测量小球的直径，然后算出摆球的半径r，则摆长l＝l′＋r.(5)一般选用一米左右的细线．例1.在“用单摆测量重力加速度”的实验中：(1)摆动时偏角满足的条件是偏角小于5°，为了减小测量周期的误差，计时开始时，摆球应是经过最________(填“高”或“低”)点的位置，且用停表测量单摆完成多次全振动所用的时间，求出周期。

第八章机械振动和机械波实验九用单摆测量重力加速度的大小随着新高考的实施，选择性必修一的内容在高考中的占比有所增加，因此用单摆测量重力加速度的实验地位也随之提升，其中在2023年新课标卷T23、2020年海南卷T14中均对该实验进行了考查，该实验的考查方向主要是测量仪器的读数、实验原理以及实验数据的处理.预计2025年高考对该实验的考查力度会有所加大.1.实验原理在偏角很小时单摆做简谐运动，其固有周期为T＝2π√lg ，由此可得g＝[1]4π2lT2，据此，只要测出摆长l和周期T，即可计算出当地的重力加速度.2.实验器材铁架台及铁夹、中心有小孔的金属小球、约1m长的细线、停表、刻度尺、游标卡尺.3.实验步骤（1）制作单摆：如图所示.（2）测量摆长：用刻度尺测出摆线长L，用游标卡尺测出小球直径d，然后计算出悬点到球心的距离l＝L＋d2.（3）测量周期：把单摆从平衡位置拉开一个很小的角度（小于[2]5°），然后放开小球让它摆动，用停表测出单摆完成30～50次全振动的时间，计算出完成一次全振动的时间，这个时间就是单摆的振动周期.（4）重复实验：改变摆长，重做几次实验.4.数据处理（1）平均值法：根据单摆的周期公式，计算出每次实验的重力加速度，求出几次实验得到的重力加速度的平均值，即本地的重力加速度的值.（2）图像法：由T＝2π√lg 得T2＝4π2gl，以T2为纵轴，以l为横轴，作出T2－l图像如图所示，其斜率为k＝4π2g，由图像的斜率即可求出重力加速度g.5.注意事项制作单摆①选择材料时应选择细、轻又不易伸长的线，长度一般在1m 左右，小球应选用密度较大、直径较小的金属球②单摆悬线的上端不可随意卷在铁架台的杆上，应用铁夹夹紧，以免摆球摆动时摆线滑动，引起摆长改变 单摆摆动①注意摆动时控制摆线偏离竖直方向的偏角小于5°，可通过估算振幅的办法加以控制②摆球摆动时，要使之保持在同一个竖直平面内，不要形成圆锥摆测量摆长摆长应是悬点到球心的距离，等于摆线长加上小球的半径.测摆长时，应将摆球悬挂好后再测，不能错误地认为摆线长就是摆长测量周期①应从摆球通过平衡位置时开始计时，并且采用倒数到0开始计时的方法，即“4、3、2、1、0、1、2、3、…”，在数“0”的同时按下停表开始计时计数②应测量多次全振动的时间后计算出振动周期误差分析单摆的振动不符合简谐运动的要求引起的系统误差①单摆不在同一竖直平面内振动，成为圆锥摆，测得的g 值偏大（圆锥摆周期T ＝2π√lcosθg）；②振幅过大，摆角超过5°，摆角越大，摆球的实际周期T 也越大，测得的g ＝4π2l T 2值偏小测定摆长l 时引起的误差①在未悬挂摆球前测定摆长或漏加摆球半径d 2，测得的摆长l 测＝l 0＜l ，则g 测＜g ；②测摆长时摆线拉得过紧或以摆球的直径与摆线长之和作为摆长，测得的摆长l 测＞l ，则g 测＞g ；③悬点未固定好，摆球摆动时出现松动，测得的摆长l 测＜l ，则g 测＜g测定周期时引起的误差①开始计时时，停表过迟按下，会使所测时间t 偏小，g 值偏大；②计算单摆的全振动次数时，不从摆球通过最低点时开始计时，容易产生误差命题点1 教材基础实验1.[2023新课标]一学生小组做“用单摆测量重力加速度的大小”实验.（1）用实验室提供的螺旋测微器测量摆球直径.首先，调节螺旋测微器，拧动微调旋钮使测微螺杆和测砧相触时，发现固定刻度的横线与可动刻度上的零刻度线未对齐，如图（a）所示，该示数为0.008（0.007～0.009均可）mm；螺旋测微器在夹有摆球时示数如图（b）所示，该示数为20.035（20.034～20.036均可）mm，则摆球的直径为20.027（20.025～20.029均可）mm.（2）单摆实验的装置示意图如图（c）所示，其中角度盘需要固定在杆上的确定点O处，摆线在角度盘上所指的示数为摆角的大小.若将角度盘固定在O点上方，则摆线在角度盘上所指的示数为5°时，实际摆角大于5°（填“大于”或“小于”）.（3）某次实验所用单摆的摆线长度为81.50cm，则摆长为82.5cm.实验中观测到从摆球第1次经过最低点到第61次经过最低点的时间间隔为54.60s，则此单摆周期为 1.82s，该小组测得的重力加速度大小为9.83m/s2.（结果均保留3位有效数字，π2取9.870）解析（1）题图（a）中，螺旋测微器固定刻度读数为0.0mm，可动刻度部分读数为0.8×0.01mm＝0.008mm，所以读数为0.008mm；题图（b）中，螺旋测微器固定刻度读数为20.0mm，可动刻度部分读数为3.5×0.01mm＝0.035mm，所以读数为20.035mm；摆球的直径d＝20.035mm－0.008mm＝20.027mm.（2）角度盘固定在O点时，摆线在角度盘上所指角度为摆角大小，若将角度盘固定在O 点上方，由几何知识可知，摆线在角度盘上所指的示数为5°时，实际摆角大于5°.（3）单摆的摆长L等于摆线长l与摆球半径之和，即L＝l＋d2＝82.5cm；从摆球第1次经过最低点到第61次经过最低点，单摆完成30次全振动，故单摆的周期T＝54.630s＝1.82s；由单摆的周期公式T＝2π√Lg 可得g＝4π2LT2，代入相关数据解得g＝9.83m/s2.命题点2创新设计实验2.[实验器材创新]在探究单摆运动的实验中：（1）图（a）是用力传感器对单摆运动过程进行测量的装置图，图（b）是与力传感器连接的计算机屏幕所显示的F－t图像，根据图（b）的信息可得，从t＝0时刻开始摆球第一次摆到最低点的时刻为0.5s，摆长为0.64m（取π2＝10，重力加速度大小g＝10m/s2）.（2）单摆运动的回复力是B.A.摆球所受的重力B.摆球重力在垂直摆线方向上的分力C.摆线对摆球的拉力D.摆球所受重力和摆线对摆球拉力的合力（3）某同学的操作步骤如下，其中正确的是AC.A.取一根细线，下端系住直径为d的金属小球，上端固定在铁架台上B.用米尺量得细线长度l，即摆长为lC.在摆线偏离竖直方向5°位置由静止释放小球D.让小球在水平面内做圆周运动，测得周期，再根据公式计算重力加速度解析（1）摆球摆到最低点时力传感器显示的力最大，根据题图（b）的信息可得，所对应的时刻为t＝0.5s.根据题图（b）的信息可得，单摆周期T＝1.6s，由单摆周期公式T＝2π√lg，解得摆长为l＝0.64m.（2）单摆运动的回复力是摆球重力在垂直摆线方向上的分力，而摆球所受重力和摆线对摆球拉力的合力在径向上的分力提供向心力，B正确.（3）测得摆长应为l＋d2，B错误；若让小球在水平面内做圆周运动，则为圆锥摆运动，测得的摆动周期不是单摆的周期，D错误；A、C说法正确.1.实验小组的同学们用如图甲所示的装置做“用单摆测量重力加速度的大小”的实验.图甲（1）测出悬点到小球球心的距离（摆长）l及单摆完成n次全振动所用的时间t，则重力加速度g＝4π2n2lt2（用l、n、t表示）.（2）实验时除用到停表、刻度尺外，还应该用到下列器材中的AC（填选项前的字母）.A.长约1m的细线B.长约1m的橡皮绳C.直径约1cm的均匀铁球D.直径约10cm的均匀木球（3）选择好器材，将符合实验要求的单摆悬挂在铁架台上，应采用图丙中所示的固定方式.（4）某实验小组组装单摆时，在摆线上端的悬点处，用一块开有狭缝的橡皮夹牢摆线，再用铁架台的铁夹将橡皮夹紧，如图丁所示，这样做的目的是AC（填选项前的字母）.图丁A.保持摆动过程中摆长不变B.可使周期测量得更加准确C.需要改变摆长时便于调节D.保证摆球在同一竖直平面内摆动（5）他们组装好单摆后在摆球自然悬垂的情况下，用毫米刻度尺测得从悬点到摆球的最低端的长度L＝0.9990m，再用游标卡尺测量摆球直径，结果如图戊所示，则该摆球的直径为12.0mm.图戊（6）将单摆正确悬挂后进行如下操作，其中正确的是BC（填选项前的字母）.A.测出摆线长作为单摆的摆长B.把单摆从平衡位置拉开一个很小的角度释放，使之做简谐运动C.在摆球经过平衡位置时开始计时D.用停表测量摆球完成一次全振动所用的时间并作为单摆的周期（7）甲同学多次改变单摆的摆长并测得相应的周期，他根据测量数据作出了如图己所示的图像，但忘记在图中标明横轴表示的物理量.你认为横轴表示的物理量是√l（选填“l2”“l”或“√l”）；若图线斜率为k，则重力加速度g＝4π2k2（用k表示）.图己（8）乙同学测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是CD（填选项前的字母）.A.开始摆动时振幅较小B.开始计时时，过早按下停表C.测量周期时，误将摆球（n－1）次全振动的时间记为n次全振动的时间D.测量摆长时，以悬点到小球最低端的距离为摆长解析（1）单摆的周期T＝tn ，由单摆周期公式T＝2π√lg得重力加速度g＝4π2lT2＝4π2n2lt2.（2）为了便于测量周期和减小空气阻力，摆线选择较细且结实、无弹性的线，故选A；为了减小空气阻力的影响，摆球选择质量大、体积小的，故选C.（3）为了避免摆动过程中摆长发生变化，悬点要固定，不能松动，则选图丙所示的固定方式.（4）这样做的目的是便于调节摆长，把摆线夹得更紧一些，使摆动过程中摆长不变，故选A、C.（5）摆球的直径为d＝12.0mm.（6）摆长等于摆线的长度加上摆球的半径，A错误；用停表测量摆球完成一次全振动所用的时间并作为单摆的周期，误差较大，应采用累积法测量周期，D错误；B、C正确.（7）根据单摆周期公式T＝2π√lg ＝√g√l，可知T－√l图像为过原点的直线，故横轴表示的物理量是√l，斜率k＝√g ，解得g＝4π2k2.（8）由单摆周期公式T＝2π√lg ，得g＝4π2lT2，g与单摆振幅大小无关；开始计时时，过早按下停表，测得的周期偏大，则g的测量值比实际值偏小；测量周期时，误将摆球（n－1）次全振动的时间记为n次全振动的时间，测得的周期偏小，则g的测量值比实际值偏大；摆长等于摆线的长度加上摆球的半径，若测量摆长时以悬点到小球最低端的距离为摆长，测得的摆长偏大，则g的测量值比实际值偏大.故选C、D.2.[2024浙江名校联考]在“用单摆测定重力加速度”的实验中：（1）先用游标卡尺测小球的直径D，如图1所示，则小球的直径D＝19.00mm.图1图2（2）调节好装置，用毫米刻度尺测得摆线长为l，拉开一个小角度（小于5°）释放小球开始摆动，记小球某次经过最低点为“1”并按下停表开始计时，再次经过最低点记为“2”，一直数到“n”时停止计时，停表记录时间为t，请写出重力加速度的字母表达式g＝π2（n－1）2（l＋D2）t2（用D、l、n、t表示）.（3）为了提高实验的准确度，在实验中可改变几次摆长L并测出相应的周期T，从而得出几组对应的L和T的数值，以L为横坐标、T2为纵坐标作出T2－L图线，但同学们不小心每次都把小球直径当作半径来计算摆长，由此得到的T2－L图像是图2中的a（选填“a”“b”或“c”）.解析（1）根据游标卡尺的读数规则可知，该小球的直径为D＝19mm＋0.05mm×0＝19.00mm.（2）设单摆的周期为T，根据计时过程有t＝（n－1）T2，摆长为L＝l＋D2，根据单摆周期公式T＝2π√Lg ，解得g＝π2（n－1）2（l＋D2）t2.（3）由于把小球直径当作半径来计算摆长，则实际摆长为L－D2，则有T＝2π√L－D2g，解得T2＝4π2g L－2π2Dg，可知图像的纵截距为负值，则由此得到的T2－L图像是图2中的a.3.某同学在“用单摆测量重力加速度的大小”的实验中进行了如下的操作：（1）用游标尺为10分度（测量值可精确到0.1mm）的游标卡尺测量摆球直径d，游标卡尺的示数如图甲所示，则摆球直径为 2.06cm.把摆球用细线悬挂在铁架台上，测量摆线长为l0，通过计算得到摆长L.图甲图乙（2）用停表测量单摆的周期.当单摆摆动稳定且到达最低点时开始计时并计数为0，单摆每经过最低点一次计数一次，当数到n＝60时按下停表，停表的示数如图乙所示，该单摆的周期T＝ 2.25s（结果保留3位有效数字）.（3）①测量出多组周期T、摆长L的数值后，作出T2－L图像如图丙，造成图线不过坐标原点的原因可能是B（填选项前的字母）.图丙A.摆球的振幅过小B.将l0计为摆长LC.将（l0＋d）计为摆长LD.摆球质量过大②根据图丙得出的g的测量值不受影响（选填“偏大”或“不受影响”）.（4）在测量过程中，下列操作合理的是C（填选项前的字母）.A.先测量好摆长，再将单摆悬挂到铁架台上B.释放单摆时，摆角尽量大些，以便观察C.单摆摆动稳定后，摆球经过平衡位置时开始计时D.单摆摆动过程中，若逐渐形成了圆锥摆，可以继续测量，不影响单摆的周期（5）甲同学通过实验测得：悬点O到小球球心的距离L；计时开始后，从小球第一次通过平衡位置到第n次通过平衡位置所用的时间t，则重力加速度g＝π2（n－1）2t2L（用L、n、t表示）.（6）该小组的另一位同学没有使用游标卡尺也测出了重力加速度.他采用的方法是：先测出一摆线较长的单摆的振动周期T1，然后把摆线缩短适当的长度Δl，再测出其振动周期T2，则该同学测出的重力加速度的表达式为g＝4π2ΔlT12－T22（用所测得的物理量符号表示）.（7）本实验测得的重力加速度一般略微偏小，这是由以下哪些误差造成的？CD（填选项前的字母）.A.小球经过平衡位置时计时，看不准平衡位置造成周期测量的系统误差B.小球球心位置较难确定，使摆长测量存在系统误差C.由于存在空气阻力，会减慢单摆的速度，使周期测量值比理论值偏大D.单摆摆动过程中，摆线会稍微伸长，造成摆长的测量值比实际值偏小解析（1）主尺上的读数为2.0cm，游标尺读数为6×0.1mm＝0.6mm＝0.06cm，所以摆球直径为2.0cm＋0.06cm＝2.06cm.（2）单摆做全振动的次数为n2＝30，停表读数为t＝67.5s，得该单摆的周期T＝2.25s.（3）①由T＝2π√Lg 可得T2＝4π2gL，即周期与摆球的质量和振幅都无关.由图丙可知，当L＝0时，T2＞0，所以T2－L图线不过原点的原因是测得的摆长偏小，可能是将l0计为摆长L，B正确.②根据以上分析可知，T2－L图像的斜率不受影响，则g的测量值不受影响.（4）先测好摆长，再将单摆悬挂到铁架台上，这样测得的摆长误差较大，故A不合理；摆角小于5°时单摆的运动才可以看成简谐运动，故B不合理；单摆摆动稳定后，摆球经过平衡位置时开始计时误差比较小，故C合理；单摆摆动过程中，若逐渐形成了圆锥摆，会使单摆周期的测量值偏小，不可以继续测量，故D不合理.故选C.（5）由题意可得单摆的周期为T＝tn－12＝2tn－1，可得g＝4π2T2L＝π2（n－1）2t2L.（6）摆线较长的单摆的振动周期T1＝2π√l1g，把摆线缩短适当的长度Δl，其振动周期T2＝2π√l1－Δlg ，联立解得g＝4π2ΔlT12－T22.（7）小球经过平衡位置时计时，看不准平衡位置造成周期测量的偶然误差，这样测得的重力加速度可能偏大，也可能偏小，故A不符合题意；小球球心位置较难确定，使摆长测量存在偶然误差，这样测得的重力加速度可能偏大，也可能偏小，故B不符合题意；由于存在空气阻力，单摆的速度会减慢，使周期测量值比理论值偏大，根据T＝2π√Lg可知，重力加速度的测量值偏小，故C符合题意；单摆摆动过程中，摆线会稍微伸长，造成摆长的测量值比实际值偏小，根据T＝2π√Lg可知，重力加速度的测量值偏小，故D符合题意.故选C、D.4.某实验小组用单摆测量重力加速度.所用实验器材有摆球、长度可调的轻质摆线、刻度尺、50分度的游标卡尺、摄像装置等.图甲图乙（1）用游标卡尺测量摆球直径d.当量爪并拢时，游标尺和主尺的零刻度线对齐.放置摆球后游标卡尺示数如图甲所示，则摆球的直径d为19.20mm.（2）用摆线和摆球组成单摆，如图乙所示.当摆线长度l＝990.1mm时，记录并分析单摆的振动视频，得到单摆的振动周期T＝2.00s，由此算得重力加速度g为9.86m/s2（保留3位有效数字）.（3）改变摆线长度l，记录并分析单摆的振动视频，得到相应的振动周期.他们发现，分别用l和l＋d2作为摆长，这两种计算方法得到的重力加速度数值的差异大小Δg随摆线长度l 的变化曲线如图丙所示.由图可知，该实验中，随着摆线长度l的增加，Δg的变化特点是逐渐减小并趋于稳定，原因是摆线长度越大，小球半径相对摆线的长度就越小，小球半径对重力加速度测量的影响就越小.图丙解析（1）由于该游标卡尺为50分度的游标卡尺，所以其分度值为0.02mm，则d＝19mm＋10×0.02mm＝19.20mm.（2）根据单摆的周期公式有T＝2π√l＋d 2g，代入数据解得g＝9.86m/s2.（3）根据题图丙可知，随着l的增大，Δg逐渐减小并趋于稳定，原因是摆线长度越大，小球半径相对摆线的长度就越小，小球半径对重力加速度测量的影响就越小.。

一、实验目的利用单摆来测量重力加速度二、实验原理单摆在摆角小于10°时的振动是简谐运动，其固有周期为T=2π ，由此可得g= 。

据此，只要测出摆长l和周期T，即可计算出当地的重力加速度值。

由此通过测量周期T,摆长l求重力加速度三、实验设备及工具铁架台（带铁夹），中心有孔的金属小球，约1m长的细线，米尺，游标卡尺（选用），秒表等。

四、实验内容及原始数据（一）实验内容1．在细线的一端打一个比小球上的孔径稍大些的结，将细线穿过球上的小孔，制成一个单摆。

2．将铁夹固定在铁架台的上端，铁架台放在实验桌边，使铁夹伸到桌面以外，把做好的单摆固定在铁夹上，使摆球自由下垂。

3．测量单摆的摆长l：用游标卡尺测出摆球直径2r，再用米尺测出从悬点至小球上端的悬线长l'，则摆长l=l'+r。

4．把单摆从平衡位置拉开一个小角度（不大于10°），使单摆在竖直平面内摆动，用秒表测量单摆完成全振动30至50次所用的时间，求出完成一次全振动所用的平均时间，这就是单摆的周期T。

5．将测出的摆长l和周期T代入公式g= 求出重力加速度g的值。

（二）原始数据1．用游标卡尺测量钢球直径2rn 1 2 3 4 5 6直径2r(cm) 1.712 1.712 1.692 1.692 1.712 1.7222．用米尺测量悬线长l'n 1 2 3 4 5 6悬线长l' (cm) 91.90 91.90 91.91 91.90 91.88 91.903．用秒表测量摆动50个周期用时为1’34’’84=94.84’’五、实验数据处理及结果（数据表格、现象等）1．钢球直径平均值2r=(1.712+1.712+1.692+1.692+1.712+1.722)÷6=1.707(cm)2．悬线长平均值l'=(91.90+91.90+91.91+91.90+91.88+91.90)÷6=91.898(cm)3．摆长l=l'+r=91.898+1.707=93.605(cm)4．求出完成一次全振动所用的平均时间，即单摆的周期TT=94.84÷50=1.8968(s)5．计算g将测出的摆长l和周期T代入公式g= =10.27六、实验结果分析（实验现象分析、实验中存在问题的讨论）误差分析：为什么所得g=10.27大于标准值？1．振动次数：可能是振动次数的有问题2．摆长测量：可能是摆长测量偏大3．秒表使用：可能是开表晚了。

实验九用单摆测量重力加速度的大小实验目的和器材实验原理实验目的1.练习使用秒表、刻度尺和游标卡尺。

2.探究影响单摆运动周期的因素。

3.学会用单摆测定当地重力加速度。

当摆角很小时,单摆做简谐运动,其运动周期为T=2πlg,由此得到g=4π2lT2,因此,只要测出摆长l和振动周期T,就可以求出当地的重力加速度g的值。

实验器材中心带有孔的小钢球、细线(长约1 m)、游标卡尺、毫米刻度尺、停表。

1．让细线的一端穿过金属小球的小孔，做成单摆。

2．把细线的上端用铁夹固定在铁架台上，把铁架台放在实验桌边，使铁夹伸到桌面以外，让摆球自然下垂，在单摆平衡位置处做上标记，如图所示。

3．用毫米刻度尺量出摆线长度l′，用游标卡尺测出金属小球的直径，即得出金属小球半径r，计算出摆长l＝l′＋r。

4．把单摆从平衡位置处拉开一个很小的角度(不超过5°)，然后放开金属小球，让金属小球摆动，待摆动平稳后测出单摆完成30～50次全振动所用的时间t，计算出单摆的振动周期T。

5．根据单摆周期公式，计算当地的重力加速度。

6．改变摆长，重做几次实验。

方法一：公式法。

根据公式T＝2πlg，g＝4π2lT2。

将测得的几组周期T和摆长l分别代入公式g＝4π2lT2中算出多组重力加速度g的值，再求出g的平均值，即为当地重力加速度的值。

方法二：图像法。

由单摆的周期公式T ＝2πl g 可得l ＝g4π2 T 2，因此以摆长l 为纵轴，以T 2为横轴描点作图，作出的l ­T 2图像理论上是一条过原点的倾斜直线，如图所示，求出图像的斜率k ，即可求出g 值。

g ＝4π2k ，k ＝2l T ＝2l T ∆∆。

1．本实验的系统误差主要来源于单摆模型本身是否符合要求，单摆应满足以下条件：悬点固定，小球质量大、体积小，细线轻质且伸缩不明显，振动是在同一竖直平面内的振动。

2．本实验的偶然误差主要来自时间的测量和摆线长度的测量，因此，要从摆球通过平衡位置时开始计时，不能多计或漏计摆球全振动次数。

实验九用单摆测量重力加速度的大小1．实验目的(1)练习使用秒表和刻度尺。

(2)学会用单摆测定当地重力加速度。

2．实验原理当偏角很小时，单摆做简谐运动，其运动周期为T＝2πlg，它与偏角的大小及摆球的质量无关，由此得到g＝4π2lT2。

因此，只要测出摆长l和振动周期T，就可以求出当地的重力加速度g的值。

3．实验器材中心带有孔的小钢球、细线(长约1 m)、毫米刻度尺、游标卡尺、秒表、铁架台等。

4．实验步骤(1)做单摆将细线穿过中心带有孔的小钢球，并打一个比小孔大一些的结，然后把线的另一端用铁夹固定在铁架上，让摆球自然下垂。

如图1所示。

图1(2)测摆长用毫米刻度尺量出摆线长l′，用游标卡尺测出摆球直径D，则单摆的摆长l＝l′＋D 2。

(3)测周期将单摆从平衡位置拉开一个角度(小于5°)，然后释放小球，记下单摆摆动30～50次全振动的总时间，算出一次全振动的时间，即为单摆的振动周期。

(4)改变摆长，重做几次实验。

5.数据处理(1)公式法：g ＝4π2lT2，算出重力加速度g的值，再算出g的平均值。

(2)图像法：图2根据测出的一系列摆长l对应的周期T，作l－T2的图像，由单摆周期公式得l＝g4π2T2，图像应是一条通过原点的直线，如图2所示，求出图线的斜率k，即可利用g＝4π2k求重力加速度。

6．误差分析产生原因减小方法偶然误差测量时间(单摆周期)及摆长时产生误差①多次测量求平均值②计时从摆球经过平衡位置时开始系统误差主要来源于单摆模型本身①摆球要选体积小，密度大的②最大摆角要小于5°7.注意事项(1)摆线要选1 m左右，不要过长或过短。

(2)悬线长要待悬挂好球后再测，计算摆长时要将悬线长加上摆球半径。

(3)单摆要在竖直平面内摆动，不要形成圆锥摆。

(4)要从平衡位置开始计时，并数准全振动的次数。

命题点一教材原型实验【真题示例1[2020·浙江7月选考]某同学用单摆测量重力加速度，(1)为了减少测量误差，下列做法正确的是________(多选)；A．摆的振幅越大越好B．摆球质量大些、体积小些C．摆线尽量细些、长些、伸缩性小些D．计时的起、止位置选在摆球达到的最高点处(2)改变摆长，多次测量，得到周期平方与摆长的关系图像如图3所示，所得结果与当地重力加速度值相符，但发现其延长线没有过原点，其原因可能是________。

单摆测量重力加速度实验报告单摆测量重力加速度实验报告引言重力加速度是物理学中一个重要的概念，它描述了物体在自由下落过程中速度的增加情况。

为了准确测量重力加速度，我们进行了单摆实验。

本实验通过测量单摆的周期，利用公式计算出重力加速度的数值。

本实验的目的是通过实际操作，加深对重力加速度的理解，并掌握实验测量的方法。

实验器材和方法实验器材：单摆装置、计时器、尺子、质量砝码、直尺。

实验方法：1. 将单摆装置固定在一个稳定的支架上，保证其能够自由摆动。

2. 在单摆上方固定一个质量为m的砝码，使单摆摆动时具有一定的质量。

3. 用尺子测量单摆的长度L，并记录下来。

4. 将单摆摆动到一定幅度，然后释放，开始计时。

5. 使用计时器记录单摆的摆动周期T，重复多次测量，取平均值。

实验结果通过多次测量，我们得到了如下数据：单摆长度L：0.5m摆动周期T1：1.98s摆动周期T2：1.96s摆动周期T3：1.97s实验数据处理根据实验数据，我们可以计算出单摆的平均周期T_avg：T_avg = (T1 + T2 + T3) / 3 = (1.98 + 1.96 + 1.97) / 3 = 1.97s根据单摆的周期公式，我们可以推导出计算重力加速度g的公式：T_avg = 2π√(L/g)将实验数据代入公式，可以解得重力加速度g的数值：g = (4π^2L) / T_avg^2 = (4 * 3.14^2 * 0.5) / 1.97^2 = 9.76m/s^2讨论与分析通过实验测量，我们得到了重力加速度的数值为9.76m/s^2。

与理论值9.8m/s^2相比，实验结果存在一定的误差。

可能的误差来源包括实验操作中的不确定性、测量仪器的精度等。

在实验中，我们假设单摆的摆动过程是简谐振动，但实际情况下存在空气阻力和摆线的摆动角度限制等因素，这些因素都会对实验结果产生影响。

此外，实验中使用的计时器的精度也会对测量结果造成一定的误差。

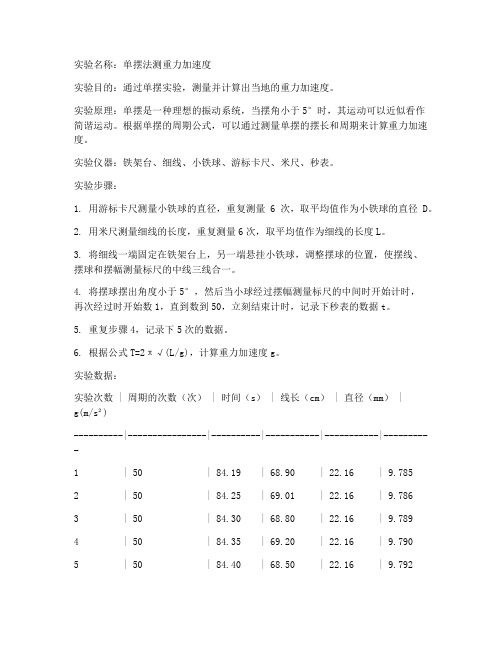
实验名称：单摆法测重力加速度实验目的：通过单摆实验，测量并计算出当地的重力加速度。

实验原理：单摆是一种理想的振动系统，当摆角小于5°时，其运动可以近似看作简谐运动。

根据单摆的周期公式，可以通过测量单摆的摆长和周期来计算重力加速度。

实验仪器：铁架台、细线、小铁球、游标卡尺、米尺、秒表。

实验步骤：1. 用游标卡尺测量小铁球的直径，重复测量6次，取平均值作为小铁球的直径D。

2. 用米尺测量细线的长度，重复测量6次，取平均值作为细线的长度L。

3. 将细线一端固定在铁架台上，另一端悬挂小铁球，调整摆球的位置，使摆线、摆球和摆幅测量标尺的中线三线合一。

4. 将摆球摆出角度小于5°，然后当小球经过摆幅测量标尺的中间时开始计时，再次经过时开始数1，直到数到50，立刻结束计时，记录下秒表的数据t。

5. 重复步骤4，记录下5次的数据。

6. 根据公式T=2π√(L/g)，计算重力加速度g。

实验数据：实验次数 | 周期的次数（次） | 时间（s） | 线长（cm） | 直径（mm） |g(m/s²)----------|----------------|----------|-----------|-----------|----------1 | 50 | 84.19 | 68.90 | 22.16 | 9.7852 | 50 | 84.25 | 69.01 | 22.16 | 9.7863 | 50 | 84.30 | 68.80 | 22.16 | 9.7894 | 50 | 84.35 | 69.20 | 22.16 | 9.7905 | 50 | 84.40 | 68.50 | 22.16 | 9.792数据处理：1. 计算单摆的周期T，T=2t/n，其中t为每次实验的时间，n为周期的次数。

2. 计算重力加速度g，g=4π²L/T²。

实验结果：根据实验数据，计算得到的重力加速度g的平均值为9.788m/s²。

高考回归复习—力学实验之用单摆测量重力加速度的大小1．小雷在做“利用单摆测重力加速度”实验中，先测得摆线长为97.20cm；用20分度的游标卡尺测得小球直径如图所示，然后用秒表记录了单摆全振动50次所用的时间。

则：(1)小球直径为____cm；(2)他以摆长（L）为横坐标、周期的二次方（T2）为纵坐标作出了T2－L图线，由图像测得的图线的斜率为k，则测得的重力加速度g=___；（用题目中给定的字母表示）(3)小俊根据实验数据作出的图像如图所示，造成图像不过坐标原点的原因可能是___。

2．某实验小组在实验室中用如图甲所示的装置完成“用单摆测定重力加速度”的实验。

(1)下表是该实验小组记录的3组实验数据，并做了部分计算处理。

组次123摆长L/cm80.0090.00100.0050次全振动所用的时间t/s90.095.5100.5振动周期T/s 1.80 1.91重力加速度g/（m·s-2）9.749.73m/s；（保留三位有效数字）请计算出第3组实验中的T=________s，g=___________2(2)若实验测出的加速度与真实值相比偏大，则可能的原因是_______________（至少写出一条）；(3)某同学在家里测重力加速度。

他找到细线和铁锁，制成一个单摆，如图乙所示。

由于家里只有一根量程为40cm的刻度尺，于是他在细线上的A点做了一个标记，使得悬点O到A点间的细线长度小于刻度尺量程。

保持该标记以下的细线长度不变，通过改变O、A间细线长度以改变摆长。

实验中，当O、A间细线的长度分别为l1和l2时，测得相应单摆的周期为T1、T2，由此可得重力加速度g=__________（用l1、l2、T1、T2表示）。

3．根据单摆周期公式T ，可以通过实验测当地的重力加速度。

如图甲所示，将细线的上端固定在铁架台上，下端系一小钢球，就做成了单摆：(1)为尽量减少误差，用秒表测时间时应从钢球通过____（选填“最高点”或“最低点”）时开始计时；(2)某同学在实验中测出多组摆长L和振动周期T，作出T2—L图像如图乙所示。

第3讲实验：用单摆测量重力加速度的大小A组基础巩固1. 利用单摆测量当地重力加速度的实验中，利用游标卡尺测得金属小球直径如图所示，小球直径d= ____ cm。

答案 2.26解析①主尺读数为22 cm;游标尺读数为:6 X 0.1 mm=0.6 mm=0.06 cm,故小球直径为2.2cm+0.06 cm=2.26 cm;2. （2018海淀期中）在用如图所示“用单摆测量重力加速度的大小”的实验中，某同学的操作步骤如下：a. 取一根细线，下端系住直径为d的金属小球，上端固定在铁架台上；b. 用米尺测量细线长度为1,1与小球半径之和记为摆长；c. 缓慢拉动小球，使细线偏离竖直方向约5°位置由静止释放小球；d. 用秒表记录小球完成n次全振动所用的总时间t,计算单摆周期T=;e. 用公式g=—计算当地重力加速度；f. 改变细线长度，重复b、c、d、e步骤,进行多次测量。

⑵ 该同学为了减少误差，利用上述未改正错误测量中的多组实验数据做出了 I-T 2图像, 该图像对应图中的 ______ 图 1: k_UIA fl 0 0 C 7■- D(3)(多选)在“用单摆测定重力加速度的大小”的正确实验中，下列做法有利于减小实 验误差的是 __________ 。

A. 适当加长摆线B. 质量相同，体积不同的摆球，应选用体积较大的C. 单摆偏离平衡位置的角度不能太大D. 当单摆经过平衡位置时开始计时，经过一次全振动后停止计时，用此时间间隔作为单 摆振动的周期 ⑷ 北京时间2005年5月22日上午10点05分,中国女子登山队首次登上珠穆朗玛峰 顶峰,五星红旗再一次在珠峰峰顶飘扬。

若登山队员利用单摆来确定珠峰的高度 ，测得该单 摆在海平面处的周期是T o ,在峰顶的周期是T,则珠峰峰顶的海拔高度h= _________ 。

(地球可看 作质量均匀分布的半径为R 的球体)答案(1)e 用公式g= 计算当地重力加速度 ⑵C (3)AC解析（1）摆线长度与摆球半径之和是单摆的摆长，由实验步骤可知，步骤e 错误,单摆摆 长:L=l+ ,由单摆周期公式T=2n 可知,重力加速度g= ；⑴ 在上述步骤中，错误的是 _____ (写出该步骤的字母)；改正后正确的应该⑵单摆摆长L=l+，由单摆周期公式T=2n 可知,1= —T2-,把摆线长度l作为摆长,当T=0时,1二,l-T 2图像在横轴上有截距,由图示图像可知,C正确,故选C。