常用函数傅里叶变换

常用信号的傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的数学工具。

对于任意一个周期信号，傅里叶变换可以将其表示成一系列正弦波的叠加形式，从而更好地理解和处理信号。

在实际应用中，有很多信号都需要进行傅里叶变换。

下面介绍一些常用信号的傅里叶变换。

1. 正弦信号正弦信号是一种最基本的周期信号，其函数形式为y=sin(wt)，其中w为角频率。

通过傅里叶变换，可以将正弦信号表示为一组频率为w的正弦波的叠加形式，即：y(t) = A1*sin(wt) + A2*sin(2wt) + A3*sin(3wt) + …其中，An为振幅，表示第n个正弦波的幅度。

2. 方波信号方波信号是一种由周期为T的矩形波形组成的信号，其函数形式为：y(t) = sgn(sin(wt))其中，sgn表示符号函数，即当sin(wt)>0时，sgn(sin(wt))=1，否则sgn(sin(wt))=-1。

通过傅里叶变换，可以将方波信号表示为一组频率为w的正弦波的叠加形式，即：y(t) = (4/pi)*[sin(wt) + (1/3)*sin(3wt) + (1/5)*sin(5wt) + …]3. 带限信号带限信号是指信号的频率范围有限，通常是指截止频率为一定值的信号。

通过傅里叶变换，可以将带限信号表示为一组频率在一定范围内的正弦波的叠加形式，即：y(t) = (1/2*pi)*Int[-w0,w0]{F(w)*e^(jwt)dw}其中，F(w)为信号的频谱，w0为信号的截止频率，Int表示积分运算。

以上三种信号只是常用信号中的一部分，实际应用中还有很多其他类型的信号需要进行傅里叶变换。

傅里叶变换不仅可以分析信号的频域特性，还可以用于信号的滤波、压缩、编码等方面，具有广泛的应用价值。

傅里叶全部公式
傅里叶变换是一种将函数从时域（时间域）转换到频域的数学工具。

它通过将时域函数表示为不同频率的正弦和余弦函数的叠加来实现。

傅里叶变换和逆变换的公式如下：
傅里叶变换公式：F(ω) = ∫[−∞,+∞] f(t) e^−jωt dt
逆傅里叶变换公式：f(t) = (1 / 2π) ∫[−∞,+∞] F(ω) e^jωt dω
其中，f(t)是时域函数，F(ω)是频域函数，e是自然常数，j 是虚数单位√(-1)，ω是频率，t是时间。

此外，傅里叶级数展开公式也是傅里叶变换的一种形式，它用来将周期函数分解成一系列振幅和相位不同的正弦和余弦函数的和。

傅里叶级数展开公式：f(t) = a0/2 + ∑[n=1,∞] (an cos(nωt) + bn sin(nωt))
其中，a0、an、bn是常数系数，表示不同频率分量的振幅，ω是基本频率。

这些公式是傅里叶变换和级数展开的基础公式，用于将函数在时域和频域之间进行转换，并在信号处理、图像处理、通信等领域有广泛应用。

需要注意的是，傅里叶变换和级数展开还有一些特定的性质和变体公式，这些公式可以根据具体的应用场景进行扩展和变换。

常用函数的傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的方法，常用于信号处理、通信、图像处理等领域。

在实际应用中，有很多常用的函数需要进行傅里叶变换，本文将介绍一些常用函数的傅里叶变换公式。

1. 正弦函数和余弦函数正弦函数和余弦函数是最基本的周期函数，它们的傅里叶变换公式如下：$$begin{aligned}mathcal{F}(sin(omega_0t)) &= frac{j}{2}[delta(omega-omega_0)-delta(omega+omega_0)]mathcal{F}(cos(omega_0t)) &= frac{1}{2}[delta(omega-omega_0)+delta(omega+omega_0)]end{aligned}$$其中，$omega_0$表示正弦函数和余弦函数的基频，$delta(omega)$表示狄拉克脉冲函数，$j$表示虚数单位。

2. 矩形函数矩形函数是一个限制在有限区间的常数函数，它的傅里叶变换公式如下：$$mathcal{F}(mathrm{rect}(t/T)) = Tmathrm{sinc}(omega T) $$其中，$mathrm{sinc}(x)=frac{sin(pi x)}{pi x}$为正弦积分函数。

3. 三角函数三角函数包括正弦函数、余弦函数、正切函数等，它们的傅里叶变换公式如下：$$begin{aligned}mathcal{F}(sin^2(omega_0t)) &= frac{j}{4}[delta(omega-2omega_0)-delta(omega)-delta(omega+2omega_0)]mathcal{F}(cos^2(omega_0t)) &= frac{1}{4}[delta(omega-2omega_0)+2delta(omega)+delta(omega+2omega_0)]mathcal{F}(tan(omega_0t)) &= -jfrac{pi}{2}mathrm{sgn}(omega-omega_0)-jfrac{pi}{2}mathrm{sgn}(omega+omega_0)end{aligned}$$其中，$mathrm{sgn}(x)$为符号函数。

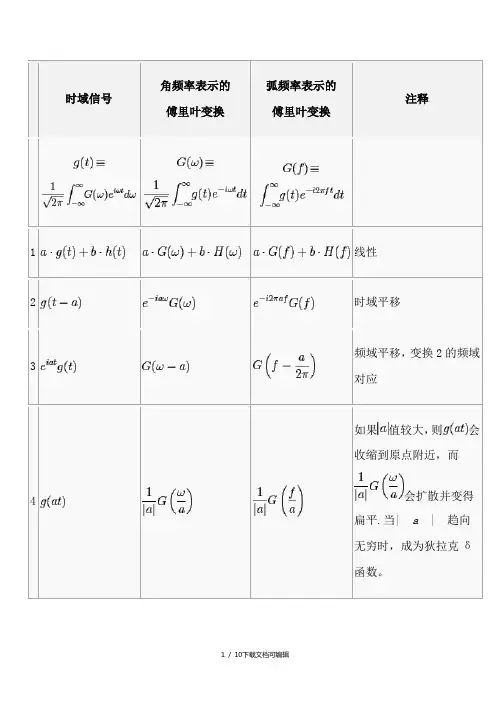
时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释1线性2时域平移3频域平移，变换2的频域对应4如果值较大，则会收缩到原点附近，而会扩散并变得扁平.当| a| 趋向无穷时，成为狄拉克δ函数。

5傅里叶变换的二元性性质。

通过交换时域变量和频域变量得到.6傅里叶变换的微分性质7变换6的频域对应8表示和的卷积—这就是卷积定理9变换8的频域对应。

[编辑]平方可积函数时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释1 0矩形脉冲和归一化的sinc函数1 1变换10的频域对应。

矩形函数是理想的低通滤波器，sinc函数是这类滤波器对反因果冲击的响应。

1 2tri是三角形函数1 3变换12的频域对应1 4高斯函数exp( − αt2)的傅里叶变换是他本身.只有当Re(α) > 0时，这是可积的。

1 5光学领域应用较多161718a>01变换本身就是9一个公式2 0J0(t)是0阶第一类贝塞尔函数。

2 1上一个变换的推广形式; T n(t)是第一类切比雪夫多项式。

2 2U n(t)是第二类切比雪夫多项式。

[编辑]分布时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释23δ(ω)代表狄拉克δ函数分布.这个变换展示了狄拉克δ函数的重要性：该函数是常函数的傅立叶变换24变换23的频域对应25由变换3和24得到.26由变换1和25得到，应用了欧拉公式: cos(at) = (e iat+ e−iat)/ 2.27由变换1和25得到28这里, n是一个自然数.δ(n)(ω)是狄拉克δ函数分布的n阶微分。

这个变换是根据变换7和24得到的。

将此变换与1结合使用，我们可以变换所有多項式。

29此处sgn(ω)为符号函数；注意此变换与变换7和24是一致的.30变换29的推广. 31变换29的频域对应.32此处u(t)是单位阶跃函数;此变换根据变换1和31得到.33u(t)是单位阶跃函数，且a> 0.34狄拉克梳状函数——有助于解释或理解从连续到离散时间的转变.[编辑]二元函数时域信号角频弧频率表示的傅里叶变换注释率表示的傅里叶变换两个函数都是高斯函数，而且可能都没有单位体积.此圆有单位半径，如果把circ(t)认作阶梯函数u(1-t); Airy分布用J1(1阶第一类贝塞尔函数)表达; f r是频率矢量的量值{f x,f y}.三元函数角频率时域信号弧频率表示的注释表示的傅里叶傅里叶变换变换此球有单位半径；f r是频率矢量的量值{f x,f y,f z}.（学习的目的是增长知识，提高能力，相信一分耕耘一分收获，努力就一定可以获得应有的回报）。

常用傅里叶变换公式大全傅里叶变换是一种重要的数学工具，它可以将时域信号转换为频域信号，从而更好地理解信号的特性。

下面就是常用的傅里叶变换公式大全：1、傅里叶变换：$$F(u)=\int_{-\infty}^{\infty}f(x)e^{-2\pi iux}dx$$2、傅里叶反变换：$$f(x)=\int_{-\infty}^{\infty}F(u)e^{2\pi iux}du$$3、离散傅里叶变换：$$F(u)=\sum_{n=-\infty}^{\infty}f(n)e^{-2\pi iun}$$4、离散傅里叶反变换：$$f(n)=\frac{1}{N}\sum_{u=-\infty}^{\infty}F(u)e^{2\pi iun}$$5、快速傅里叶变换：$$F(u)=\sum_{n=0}^{N-1}f(n)W_N^{nu}$$6、快速傅里叶反变换：$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)W_N^{-nu}$$7、离散余弦变换：$$F(u)=\sum_{n=0}^{N-1}f(n)\cos\frac{(2n+1)u\pi}{2N}$$8、离散余弦反变换：$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\cos\frac{(2n+1)u\pi}{2N}$$9、离散正弦变换：$$F(u)=\sum_{n=0}^{N-1}f(n)\sin\frac{(2n+1)u\pi}{2N}$$10、离散正弦反变换：$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\sin\frac{(2n+1)u\pi}{2N}$$以上就是常用的傅里叶变换公式大全，它们可以帮助我们更好地理解信号的特性，并且可以用来解决许多实际问题。

因此，傅里叶变换在科学研究和工程应用中都有着重要的作用。

信号与系统的基本思想：把复杂的信号用简单的信号表示，再进行研究。

怎么样来分解信号？任何信号可以用Delta 函数的移位加权和表示。

只有系统是线性时不变系统，才可以用单位冲激函数处理，主要讨论各个单位冲激函数移位加权的响应的叠加能得到总的响应。

线性系统（齐次性，叠加定理）时不变系统对一个系统输入单位冲激函数，得到的响应为h(t).表征线性时不变系统的非常重要的东西，只要知道了系统对单位冲击函数的响应，就知道了它对任何信号的响应，因为任何信号都可以表示为单位冲激函数的移位加权和。

例如：d(t)__h(t) 那么a*d(t-t0)__a*h(t-t0)-()=()(t-)d f t f τδττ∝∝⎰ 的响应为-y()=()(-)t f h t d τττ∝∝⎰ 记为y(t)=f(t)*h(t),称为f(t)和h(t)的卷积总结为两点：对于现行时不变系统，任何信号可以用单位冲激信号的移位加权和表示，任何信号的响应可以用输入函数和单位冲激函数响应的卷积来表示连续时间信号和系统的频域分析时域分析的重点是把信号分解为单位冲激函数的移位加权和，只讨论系统对单位冲激函数的响应。

而频域的分析是把信号分解为各种不同频率的正弦函数的加权和，只讨论系统对sinwt 的响应。

都是把信号分解为大量单一信号的组合。

周期函数可以展开为傅里叶级数，将矩形脉冲展开成傅里叶级数，得到傅里叶级数的系数n A sin F =T x x τ 其中0=2nw x τ。

取样函数sin ()=x S a x 。

产生一种震荡，0点的值最大，然后渐渐衰减直至0 第一：对于傅里叶级数的系数，n 是离散的，所以频谱也是离散状的每条谱线都出现在基波频率的整数倍上，其包络是取样函数。

第二：谱线的间距是0w .。

零点是0=2nw x τ，02w =Tπ是谱的基波频率。

如果τ不变，T 增大，那么0w 减小，当T 非常大的时候，0w 非常小，谱线近似连续，越来越密，幅度越来越小。

常用函数的傅里叶变换汇总
傅里叶变换是一种在信号处理和通信领域中广泛使用的数学工具。

MATLAB是一种常用的数学软件，提供了许多傅里叶变换的函数，可以进行各种类型的信号处理。

n连续函数的傅里叶变换是指将一个包含无限个采样点的函数，通过离散傅里叶变换（DFT）方法，将其离散化，转化为一系列离散的频域信号。

在MATLAB中，可以使用fft函数来进行傅里叶变换，该函数可以对输入的n连续函数进行fft变换，将其转化为对应的频域信号。

使用fft函数的步骤如下： 1. 定义输入信号，使用linspace函数生成一系列均匀分布的采样点。

2. 对采样点进行傅里叶变换，使用fft函数实现。

3. 将傅里叶变换得到的频域信号转换为幅度谱和相位谱，使用abs和angle函数实现。

4. 可以通过ifft函数将得到的傅里叶变换结果转换回原始的n连续函数。

在MATLAB中，还可以使用其他函数来实现不同类型的傅里叶变换，例如fft2可以用于二维离散傅里叶变换，fftshift可以将频域信号进行中心化等。

总之，MATLAB提供了丰富的傅里叶变换函数，可以对不同类型的信号进行处理，为信号处理和通信领域的研究提供了有力的工具。