当前位置：文档之家 › 线性系统的时域分析习题答案

线性系统的时域分析习题答案

  • 格式：doc
  • 大小：1.04 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

吴大正《信号与线性系统分析》笔记及习题(离散系统的时域分析)【圣才出品】

吴大正《信号与线性系统分析》笔记及习题(离散系统的时域分析)【圣才出品】

第3章离散系统的时域分析3.1 复习笔记一、基本概念1．前向差分与后向差分一阶前向差分一阶后向差分2．差分方程包含未知序列及其各阶差分的方程式称为差分方程。

将差分展开为移位序列，得一般形式二、离散系统的时域分析与连续系统的时域分析类似，离散系统的时域分析也是分析求解系统响应的过程，全部在时间域里进行。

不同的是离散系统的数学模型是借助差分方程，求解系统响应常用两种方法：时域经典法与时域卷积和法。

1．经典解法与微分方程经典解类似，全解y（k）＝齐次解y h（k）＋特解y p（k）。

（1）齐次解y h（k）齐次解由齐次方程解出。

设差分方程的n个特征根为。

齐次解的形式取决于特征根，y h（k）又称自由响应。

①当特征根λ为单根时，齐次解y h（k）形式为：②当特征根λ为r重根时，齐次解y h（k）形式为：③有一对共轭复根，齐次解y h（k）形式为：，其中（2）特解y p（k）特解y p（k）的求解过程类同连续系统时求y p（t）的过程。

差分方程的齐次解又称为系统的自由响应，特解又称强迫响应。

2．卷积和法全响应y（k）＝零输入响应y zi（k）＋零状态响应y zs（k）其求解过程如下：①建立系统的差分方程；②特征值→求零输入响应y zi（k）；③单位样值响应→利用卷积和求零状态响应y zs（k）＝h（k）*f（k）；④全响应y（k）＝y zi（k）＋y zs（k）。

三、零输入响应和零状态响应1．零输入响应y zi（k）激励为零时，仅由系统的初始状态引起的响应，若特征根为单根时，则零状态响应为起始条件代入上式求出。

2．零状态响应y zs（k）当系统的初始状态为零，仅由激励所产生的响应，若特征根为单根时，则零状态响应为y p（k）求法同经典解法一样。

由零状态条件用递推法导出，再代入上式求出。

系统的全响应既可以分解为自由响应和强迫响应，又可以分解为零输入响应和零状态响应。

四、单位序列响应和阶跃响应1．单位序列响应由单位序列δ（k）所引起的零状态响应，称为单位序列响应或单位样值响应或单位取样响应，或简称单位响应，记为h（k），即。

《自动控制原理》第三章 3-5 稳态误差计算

《自动控制原理》第三章 3-5 稳态误差计算

R(s) E(s)
k
C(s)
--
s(s 2)
（参考答案：
kt s
k 355.6, kt 0.094; k 44.4, kt 0.055;）
能源与动力学院 第三章 线性系统的时域分析法
26
二、系统的闭环特征方程为， s33 s22sk0
试确定使系统稳定的k值范围以及系统产生等幅振荡的 频率。
能源与动力学院 第三章 线性系统的时域分析法
21
渐进稳定：若线性控制系统在初始扰动的影响下， 其动态过程随时间的推移逐渐衰减并趋于零(原平衡 工作点)。 不稳定：若在初始扰动影响下，系统的动态过程随 时间的推移而发散。
临界稳定：若系统的响应随时间的推移而趋于常值 或等幅正弦振荡
能源与动力学院 第三章 线性系统的时域分析法
第三章 线性系统的时域分析法
25
一、系统结构如图
（1）当kt 0，k9 且r(t)1(t) ，求系统的调节时 t s
间 和超调量% (;n 3 , 1 /3 ,ts 3 .5 ,% 3 .9 2 % 3
（2）若要求阶跃响应的峰值时t间p 0.5 秒，单位斜
坡响应的稳态误差ess 0.1 ，求k，k t 。
N(s)
C(s)
G2 (s)
H (s)
输出端误差定义
E'n
(s)
Cn(s)
G2(s)
1G1(s)G2(s)H(s)
N(s)
输入端误差定义
En(s)
Cn(s)H(s)
G2(s)H(S) 1G1(s)G2(s)H(s)
N(s)
能源与动力学院 第三章 线性系统的时域分析法
15
4. 扰动作用下稳态误差…

线性系统分析_习题答案

线性系统分析_习题答案

线性系统分析_(吴大正_第四版)习题答案(总184页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除专业课习题解析课程西安电子科技大学844信号与系统2专业课习题解析课程第1讲第一章信号与系统（一）3专业课习题解析课程第2讲第一章信号与系统（二）451-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=6（4）)(sin )(t t f ε=（5）)(sin )(t r t f =7（7）)(2)(k t f k ε=（10）)(])1(1[)(k k f k ε-+=81-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε9（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε10（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ11（12）)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。

线性系统的时域分析与校正习题及答案

线性系统的时域分析与校正习题及答案

当
h(t ) = 0.9 = 1 −
T − τ −t 2 / T ; e T T − τ −t1 / T ; e T
t2 = T [ln(
T−τ ) − ln 0.1] T T−τ ) − ln 0. 9] T
当
h(t ) = 0.1 = 1 −
t1 = T [ln(
则
t r = t2 − t1 = T ln
T1 = 4， T2
3-7
⎛ ts ⎞ ∴ ts = ⎜ ⎜T ⎟ ⎟ T1 = 3.3T1 = 3.3 。 ⎝ 1⎠
设角速度指示随动系统结构图如图 3-48 所示。若要求系统单位阶跃响应无超调，
且调节时间尽可能短，问开环增益 K 应取何值，调节时间 t s 是多少？ 解 依题意应取
ξ =1 ， 这 时 可 设 闭 环 极 点 为
10 101
h(T ) = 0.632
（b）系统达到稳态温度值的 63.2%需要 0.099 个单位时间。
（2）对（a）系统：
Gn (s) =
C ( s) =1 N (s)
n(t ) = 0.1 时，该扰动影响将一直保持。
对（b）系统：
Φ n ( s) =
C ( s) = N (s)
1 10s + 1 = 100 10s + 101 1+ 10s + 1
（1） 若 ξ = 0.5 对应最佳响应，问起博器增益 K 应取多大？ （2） 若期望心速为 60 次/min，并突然接通起博器，问 1s 钟后实际心速为多少？瞬时最大 心速多大？ 解 依题，系统传递函数为
K 2 ωn 0.05 Φ( s) = = 2 2 K 1 s + 2ξω n s + ω n s2 + s+ 0.05 0.05

第三章 线性系统的时域分析法(第三四五讲)

第三章 线性系统的时域分析法(第三四五讲)
若变号系统不稳定!
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为：
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e

1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0＜ξ＜1 s1, 2 n jjn 1 2 ξ＝0 0＜ξ＜1
0
h( t ) 1 ξ＝0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示，试在同一平面画出3个系统闭环 极点的相对位置，并说明理由。

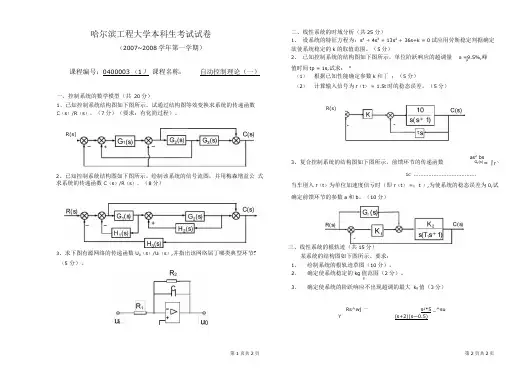
哈尔滨工程大学答案自动控制原理A卷试题答案及平分标准-07A

哈尔滨工程大学答案自动控制原理A卷试题答案及平分标准-07A

哈尔滨工程大学本科生考试试卷（2007~2008学年第一学期）课程编号：0400003 （1）课程名称：自动控制理论（一）二、线性系统的时域分析（共25分）1、设系统的特征方程为：s4+ 4s3+ 13s2+ 36s+k = 0试应用劳斯稳定判据确定欲使系统稳定的k的取值范围。

（5分）2、已知控制系统的结构图如下图所示，单位阶跃响应的超调量 a =9.5%,峰p值时间tp = 1s,试求：p（1）根据已知性能确定参数k和丁；（5分）2、已知控制系统结构图如下图所示。

绘制该系统的信号流图，并用梅森增益公式求系统的传递函数C（s）/R（s）。

（8分）1c ......................................当车刖入r（t）为单位加速度信亏时（即r（t） =；t ）,为使系统的稳态误差为0,试确定前馈环节的参数a和b。

（10分）三、线性系统的根轨迹（共15分）某系统的结构图如下图所示。

要求：1、绘制系统的根轨迹草图（10分）。

2、确定使系统稳定的kg值范围（2分）。

g3、确定使系统的阶跃响应不出现超调的最大k g值（3分）一、控制系统的数学模型（共20分）1、已知控制系统结构图如下图所示。

试通过结构图等效变换求系统的传递函数C（s）/R（s）。

（7分）（要求：有化简过程）。

R(s)（2）计算输入信号为r（t） = 1.5t时的稳态误差。

（5分）R(s)3、复合控制系统的结构图如下图所示，前馈环节的传递函数as2 bsG r(s)=『r ‘Rs^wj 一s2*5 _^suY (s+2)(s—0.5)3、求下图有源网络的传递函数U0（s）/U i（s）,并指出该网络届丁哪类典型环节?（5 分）。

第1页共2页第2页共2页第3页共4页 第4页 共4页四、线性系统的频域分析（共10分）1、已知最小相位系统的 Bode 图如下图所示。

求该系统的传递函数 G （s ）。

（5分）L()A 10 一 0__ 1六、非线性控制系统分析（共15分）非线性控制系统如下图所示。

第3章 线性系统的时域分析第九节_3

第3章 线性系统的时域分析第九节_3

（3）根轨迹起始于开环极点，终止于开环零点
说明 当根轨迹增益K1从0变化到∞时，在s平面就会画 出一条一条的根轨迹，每条根轨迹都有起点和终 点，对应于K1 =0的s点叫根轨迹的起点，对应于 K1 →∞的s点叫根轨迹的终点。 由幅值条件
可见 当s=pj时， K1 =0 ；根轨迹起始于开环极点； 当s=zi时， K1 →∞ ；终止于开环零点； 当|s|→∞且n≥m时， K1 →∞。如果开环零点个 数m少于开环极点个数n，则有(n-m)条根轨迹终 止于无穷远处。
（5）两条根轨迹的交点方程为
其中sd为交点。
说明： 交点sd是指两支根轨迹会合后分离的点， 该点为闭环特征方程的重根
假设闭环特征方程有2个重根，则可将其 改写为
例3-6 单位负反馈系统开环传递函数为
试画出系统实轴上的根轨迹并求出系统根轨迹 的交点。
解： 由规则1），系统有3条根轨迹； 由规则3），3条根轨迹的起点为
（4）实轴上的根轨迹 实轴上的某一区域，若其右边开环实数零、 极点个数之和为奇数，则该区域必是根轨迹。 （如红线所示）
红色部分 为根轨迹
说明：以实轴上的s0点为例，根据相角条 件，分三个方面说明这个法则。
G ( s ) H ( s )
m n
(s z ) (s p )
解 系统有3条根轨迹分支，且3条根轨迹都趋 于无穷远处。 实轴上的根轨迹： ,2 1,0 渐近线：
根轨迹的交点满足以下方程
交点必须在根轨迹上，所以交点取
根轨迹与虚轴的交点及临界增益。
令s=iω
令实部及虚部分别为0
解得
第一组解为根迹的起点,第二组得根迹和虚轴的 交点 ,临界根轨迹增益为6
K s ( s 1)( s 2） K 1 s ( s 1)( s 2）

自动控制原理第3章练习题

自动控制原理第3章练习题

第三章 线性系统的时域分析习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。

解： Φ()()./(.)s L k t s ==+001251253-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ∙∙+=+()()()()τ近似描述，其中，1)(0<-<τT 。

试证系统的动态性能指标为t T r =22.T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解： 设单位阶跃输入ss R 1)(=当初始条件为0时有：11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 求t r （即)(t c 从1.0到9.0所需时间)当 Tt e TT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt e TT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ...2) 求 t sTt s s e TT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [lnTT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。

要求系统闭环增益2=ΦK ，调节时间4.0≤s t s ，试确定参数21,K K 的值。

解： 由结构图写出闭环系统传递函数111)(212211211+=+=+=ΦK K sK K K s K s K K s K s令闭环增益212==ΦK K ， 得：5.02=K 令调节时间4.03321≤==K K T t s ，得：151≥K 。

3-4在许多化学过程中，反应槽内的温度要保持恒定， 图3-46（a ）和（b ）分别为开环和闭环温度控制系统结构图，两种系统正常的K 值为1。

自动控制原理胡寿松第五版第三章答案

自动控制原理胡寿松第五版第三章答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t 25.1e 0125.0)t (k -=，试求系统闭环传递函数)s (Φ。

解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 设某高阶系统可用下列一阶微分方程)t (r )t (r )t (c )t (c T +τ=+∙∙近似描述，其中，1)T (0<τ-<。

试求系统的调节时间s t 。

解 设单位阶跃输入ss R 1)(=当初始条件为0时有：1T s 1s )s (R )s (C ++τ= 1Ts T s 1s 11Ts 1s )s (C +τ--=⋅++τ=∴ T/t e T T 1)t (h )t (c -τ--== T )0(h τ=，1)(h =∞，20T T )]0(h )(h [05.0τ-=-∞=∆求 s tT/t s s e TT 1)0(h )]0(h )(h [95.0)t (h -τ--=+-∞= 3T 05.ln0T t s ==∴3-2 一阶系统结构如图所示。

要求单位阶跃输入时调节时间4.0t s ≤s （误差带为5%），稳态 输出为2，试确定参数21k ,k 的值。

解 由结构图写出闭环系统传递函数1k k sk 1k k s k sk k 1s k )s (212211211+=+=+=Φ闭环增益2k 1k 2==Φ， 得：5.0k 2= 令调节时间4.0k k 3T 3t 21s ≤==，得：15k 1≥。

3-4 在许多化学过程中，反应槽内的温度要保持恒定， 下图（a ）和（b ）分别为开环和闭环温度控制系统结构图，两种系统正常的K 值为1。

解 （1）对（a ）系统： 1s 1011s 10K )s (G a +=+=， 时间常数 10T =632.0)T (h = （a ）系统达到稳态温度值的63.2%需要10秒；对（b ）系统：1s 10110101100101s 10100)s (b+=+=Φ， 时间常数 10110T = 632.0)T (h = （b ）系统达到稳态温度值的63.2%需要0.099秒。

信号与线性系统-白恩健书答案

信号与线性系统-白恩健书答案

第1章基本概念K第1章习题k1.1解：（1）x(t)为周期信号，周期为T=10。

（2）x(t)为非周期信号。

（3）x[n]为非周期信号。

（4）x[n]为周期信号，周期为N=2。

（5）x(t)为非周期信号。

（6）x[n]为周期信号，周期为N=2。

1.2解：（1）x(t)为功率信号。

（2）x(t)既不是能量信号也不是功率信号。

（3）x[n]为能量信号。

（4）x(t)为能量信号。

（5）x(t)为能量信号。

（6）x[n]为能量信号。

1.3略。

1.4略。

1.5（原题有误）一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。

用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统，即x[n−k]=S−k(x[n])。

写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。

解：提示：可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。

1.6解：（1）因果、无记忆、非线性、时不变、BIBO稳定系统。

（2）因果、无记忆、线性、时变和BIBO稳定系统。

（3）因果、无记忆、线性、时变和非稳定系统。

（4）因果、记忆、线性、时不变和BIBO稳定系统。

（5）因果、无记忆、线性、时变和BIBO稳定系统。

（6）因果、记忆、时不变、非稳定系统。

–2/48–第1章基本概念（7）因果、无记忆、线性、时不变和BIBO稳定系统。

（8）非因果系统、无记忆、线性、时不变、BIBO稳定系统。

1.7证明略。

1.8解：（1）x[n]的响应为{1,1,−1,2,n=0,1,2,3}。

（2）x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。

（3）x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。

1.9证明提示：根据微积分的极限定义证明。

1.10解：（1）x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。

（2）x(t)的响应为[2(t+e−t)−2]u(t)。

第三章 线性系统的时域分析

第三章 线性系统的时域分析
前 页 后 页
（3）欠阻尼即0＜ξ＜1时二阶系统的单位阶跃响应动态性能分析 设r(t)=1，即R（S）=1/S 则二阶系统在时的单位阶跃响应式为： C(S) =ф(s)·R(S)=
ωn2
s2+2ξωns +ωn2
1 · S
=
1 S+2ξωn － S （s+ξωn）2 +ωn2（1- ξ2 ）
令： ξωn = σ （衰减系数） ωn√1- ξ2 = ω d （阻尼振荡频率）
前 页 后 页
峰值时间 tp ：指响应从0到达第一次峰值（稳态值）时所需要的时间；
调节时间 ts ：即过渡过程时间。指响应到达并保持在终值±5%（△=0.05） 或±2%（△=0.02）内所需要的最短时间。
超调量 Mp ：指阶跃响应的最大值超出其稳态值的部分。 Mp =
c (tp)－c (∞)
c (∞) Mp——平稳性；
当 1时，
c(t ) 1 e s1t 1 e
( n n 2 1 ) t
图3-15 过阻尼二阶系统单位 阶跃响应
当 1.25 时，系统的过渡过程时间可近 1 似为 t s (3 ~ 4)
s1
系统的超调量 M p 0
(5) 当阻尼比ζ=1时，系统的特征根为两相
t
② ξ = 1时，（临界阻尼） S1 ，S2 为一对相等的负实数根。
③ 0＜ξ＜1时，（欠阻尼） S1 ，S2 为一对具有负实部的共轭复根。
前 页 后 页
④ 当ξ=0时，（无阻尼，零阻尼） S1 ，S2 为一对幅值相等的虚根。
⑤ 当ξ＜0时，（负阻尼） S1 ，S2 为一对不等的负实数根。
小结： ⅰ） 二阶系统正常工作的基本条件是 ξ＞0 ；而ξ＜0系统不稳定； ⅱ） 当ξ ≥1时，其阶跃响应曲线是单调上升的（即非周期性的）； ⅲ） 当0＜ξ＜1时，其阶跃响应曲线是振荡衰减的（即具周期性）。

线性时不变系统--习题

线性时不变系统--习题

dt
dt
dt
et t et t
t t t
t
方法二没有注意利用冲激函数的性质，求解过
程较繁。另外，对冲激偶信号的性质
f t t f 0 t f 0 t
往往被错误写成
f t t f 0 t
从而得出错误结论。
(2) f t t e3 δτ d τ
1 O t 3 1
t
t 3 1
t
3
1
即2 t 4
g(t) 1 1(t )d t 2 t 2
t3 2
42
T4
1 f1
f2 t
t
1 O
1 t3
t-31
即t 4
gt 0
卷积结果
f1t
1
1 O 1 t
f2 t
3
2
O
3t
t2 t 1
g(t
)
4 t
t
2
2
4
x(t t0 ) h(t) x(t) h(t t0 ) y(t t0 )
例1 粗略绘出下列各函数式的波形图
(1) f1t u t2 1
(2)
f2 t
d dt
et cos tut
描绘信号波形是本课程的一项基本训练，在绘 图时应注意信号的基本特征，对所绘出的波形，应标 出信号的初值、终值及一些关键的值，如极大值和极 小值等，同时应注意阶跃、冲激信号的特点。
设x3(t) ax1 t bx2 t x3 t y3 t x32 t ax1 t bx2 t 2 a2 x12 t b2 x22 t 2abx1 t x2 t
a2 y1 t b2 y2 t 2abx1 t x2 t ay1 t by2 t

自动控制原理-胡寿松-第二版-答案全解参考word

自动控制原理-胡寿松-第二版-答案全解参考word

第二章控制系统的数学模型习题及参考答案自动控制原理胡寿松第二版课后答案2-2 由牛顿第二运动定律，在不计重力时，可得整理得将上式拉氏变换，并注意到运动由静止开始，即初始条件全部为零，可得于是传递函数为②其上半部弹簧与阻尼器之间，取辅助点A，并设A点位移为x，方向朝下；而在其下半部工。

引出点处取为辅助点B。

则由弹簧力与阻尼力平衡的原则，从A和B两点可以分别列出如下原始方程：消去中间变量x，可得系统微分方程对上式取拉氏变换，并计及初始条件为零，得系统传递函数为③以引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：移项整理得系统微分方程对上式进行拉氏变换，并注意到运动由静止开始，即则系统传递函数为2-3(b)以k1和f1之间取辅助点A，并设A点位移为x，方向朝下；根据力的平衡原则，可列出如下原始方程：所以2-6解：2-7 解：2-8 解：2-9解：2-10解：系统的结构图如下：系统的传递函数为：2-11 解：(a)(b)(c)(d)(e)(f)2-12 解：第三章线性系统的时域分析习题及参考答案自动控制原理胡寿松第二版课后答案3-1解：3-2 解：3-3 解：3-4 解：3-5 解：3-6 解：3-7 解：3-8 解：3-9 解：列劳斯表如下：系统不稳定3-10 解：（略）3-11 解：系统的特征方程为：化简得;列劳斯表如下：0<k<1.73-12 解：系统的开环传递函数为：特征方程为：列劳斯表如下：所以τ>03-13 解：（1）、（2）（3）3-14 解：（1）（2）（3）3-15 解：（1）系统的开环传递函数为：而（2）系统的开环传递函数为：而（3）系统的开环传递函数为：而同时作用下的系统误差为：第四章线性系统的根轨迹法习题及参考答案自动控制原理胡寿松第二版课后答案4-1 解：系统的开环传递函数为根轨迹如图所示4-2 解：4-3 解：（1）系统的开环传递函数为概略的根轨迹如下图所示：（2）系统的开环传递函数为根轨迹如下图所示4-4 解：（1）系统的开环传递函数为（2）系统的开环传递函数为有三个极点一个零点：（-20，j0）。

哈尔滨工程大学答案自动控制原理(A卷)试题答案及平分标准-07A

哈尔滨工程大学答案自动控制原理(A卷)试题答案及平分标准-07A
3、求下图有源网络的传递函数 ，并指出该网络属于哪类典型环节？（5分）。
二、线性系统的时域分析（共25分）
1、设系统的特征方程为： 试应用劳斯稳定判据确定欲使系统稳定的 的取值范围。（5分）
2、已知控制系统的结构图如下图所示，单位阶跃响应的超调量 ，峰值时间 s分）
2、确定使系统稳定的 值范围（2分）。
3、确定使系统的阶跃响应不出现超调的最大 值（3分）。
四、线性系统的频域分析（共10分）
1、已知最小相位系统的Bode图如下图所示。求该系统的传递函数 。（5分）
2、已知某系统当开环增益 时的开环频率特性Nyquist图如下图所示。该系统在右半平面的极点数 ，试分析当开环增益 变化时其取值对闭环稳定性的影响。（5分）
3、阐述消除自持振荡的方法。
（注：非线性控制系统的描述函数为： ）
（2）计算输入信号为 时的稳态误差。（5分）
3、复合控制系统的结构图如下图所示，前馈环节的传递函数 ，当输入 为单位加速度信号时（即 ），为使系统的稳态误差为0，试确定前馈环节的参数 和 。（10分）
三、线性系统的根轨迹（共15分）
某系统的结构图如下图所示。要求：
1、绘制系统的根轨迹草图（10分）。
哈尔滨工程大学本科生考试试卷
（2007~2008学年第一学期）
课程编号：0400003（1）课程名称：自动控制理论（一）
一、控制系统的数学模型（共20分）
1、已知控制系统结构图如下图所示。试通过结构图等效变换求系统的传递函数 。（7分）（要求：有化简过程）。
2、已知控制系统结构图如下图所示。绘制该系统的信号流图，并用梅森增益公式求系统的传递函数 。（8分）
五、线性系统的校正（共15分）
设单位反馈系统的开环传递函数为 ，试采用滞后-超前校正装置进行串联校正，要求：

信号与系统王明泉第二章习题解答

信号与系统王明泉第二章习题解答
分析：响应中 不含齐次解 ，所以答案(a)(b)(c)都不是
题2、两线性时不变系统分别为S1和S2，初始状态均为零。将激励信号 先通过S1再通过S2，得到响应 ；将激励信号 先通过S2再通过S1，得到响应 。则 与 的关系为_________________。
答案：
分析：该题是考查级联系统的交换率：两级联系统交换保持不变
特征方程为 ，
特征根为 ，
所以
代入初始条件 ， ，解得 ，
所以，
（2）求零状态响应
（3）
2.6 已知某线性时不变系统的方程式为
试求系统的冲激响应h(t)。
解：方程右端的冲激函数项最高阶数为 ，设
，
则有： ，将其代入原系方程，得
2.7若描述系统的微分方程为
试求系统的阶跃响应。
解：由题可知：
阶跃响应：
2.8已知某线性时不变(LTI)系统如题图2.8所示。已知图中 ， ， ,试求该系统的冲激响应 。
（7）理解卷积运算在信号与系统中的物理意义和运算规律，会计算信号的卷积。；
2.2 本章重点
（1）系统（电子、机械）数学模型（微分方程）的建立；
（2）用时域经典法求系统的响应；
（3）系统的单位冲激响应及其求解；
（4）卷积的定义、性质及运算，特别是 函数形式与其它信号的卷积；
（5）利用零输入线性与零状态线性，求解系统的响应。
2.4.4系统的零输入响应与零状态响应
（1）零输入响应
系统的零输入响应是当系统没有外加激励信号时的响应。
零输入响应 是满足
及起始状态 的解,它是齐次解的一部分
由于没有外界激励作用，因而系统的状态不会发生跳变， ，所以 中的常数 可由 确定。
（2）零状态响应

信号与系统 第二章 线性时不变系统的时域分析

信号与系统 第二章 线性时不变系统的时域分析
r
外加信号 常数A
特解 常数B
r 1i k t i r 1 i 1
tr
sin t或cos t
eλt
k1 cost k2 sin t keλt， λ不是方程的特征根 kteλt， λ是方程的特征根
k t
i 1 i
r 1
r 1i t
e ， λ是方程的r阶特征重根
一、微差分方程的建立以及经典解法
'' 1
di1 (t ) 1 t L i2 ( )d R2i2 (t ) f (t ) dt C
一、微差分方程的建立以及经典解法
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
(1)

t

i ( )d
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
例题，已知线性时不变系统方程如下： y˝(t)+6y΄(t)+8y(t)= f(t), t>0. 初始条件y(0)=1， y΄(0)=2，输入信号f(t)=e-tu(t) , Q求系统的完全响应y(t)。
解：1）求方程的齐次解 特征方程为：m2+6m+8=0 显然特征根为：m1=-2，m2=-4
故原方程的齐次解为：yn(t)= Ae-2t+Be-4t

管致中《信号与线性系统》(第5版)(课后习题 连续时间系统的时域分析)

管致中《信号与线性系统》(第5版)(课后习题 连续时间系统的时域分析)
故系统零输入响应为： 系统的自然频率为 0，－1 和－2。
8 / 43
圣才电子书

十万种考研考证电子书、题库视频学习平 台
2.6 已知电路如图 2-5 所示，电路未加激励的初始条件为：
（1） i10 2A,i'1 0 1A s ；（2） i10 1A,i'2 0 2A 。 求上述两种情况下电流 i1t及 i2t的零输入响应。
由②式可得：
③
由①式可得：
④
将式③代入式④可得：
用微分算子表示为： 即 （2）同理，将式①代入式③可得：
整理得： 用微分算子表示为：
1 / 43
圣才电子书

即
十万种考研考证电子书、题库视频学习平
台
。
2.2 H（p）。
写出图 2-2 中输入 e t 和输出 i1 t 之间关系的线性微分方程，并求转移算子
圣才电子书
十万种考研考证电子书、题库视频学习平

台
第 2 章 连续时间系统的时域分析
2.1 写出图 2-1 中输入 it 和输出 u1t 及 u2 t 之间关系的线性微分方程，并求转移
算子。
图 2-1 答：（1）利用节点法来分析电路，可得
对于节点 1：
①
对于节点 2：
②
（1）
d3 dt 3
r(t)
2
d2 dt 2
r(t)
d dt
r(t)
3
d dt
e(t)
e(t) ，
r0
r0
0,r0
1；
（2）
d3 dt 3
r(t)
3
d2 dt 2
r(t)
2
d dt
r(t)

《信号与系统》考研试题解答第二章连续系统的时域分析

《信号与系统》考研试题解答第二章连续系统的时域分析

第二章 连续系统的时域分析一、单项选择题X2.1（东南大学2002年考研题）一线性时不变连续时间系统，其在某激励信号作用下的自由响应为(e -3t +e -t )ε(t )，强迫响应为(1-e -2t )ε(t )，则下面的说法正确的是 。

（A ）该系统一定是二阶系统 （B ）该系统一定是稳定系统（C ）零输入响应中一定包含(e -3t +e -t )ε(t ) （D ）零状态响应中一定包含(1-e -2t )ε(t )X2.2（西安电子科技大学2005年考研题）信号f 1(t )和 f 2(t ) 如图X2.2所示，f =f 1(t )* f 2(t )，则 f (-1)等于 。

（A ）1 （B ）-1 （C ）1.5 （D ）-0.5图X2.2X2.3（西安电子科技大学2005年考研题）下列等式不成立的是 。

[])()(*)()()()(*)()()(*)()(*)()()(*)()(*)()(2121210201t f t t f D t f t t f C t f dt d t f dt d t f t f dt d B t f t f t t f t t f A ='='⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==+-δδ答案：X2.1[D]，X2.2[C]，X2.3[B]二、判断与填空题T2.1（北京航空航天大学2001年考研题）判断下列说法是否正确，正确的打“√”，错误的打“×”。

（1）若)(*)()(t h t f t y =，则)2(*)2(2)2(t h t f t y =。

[ ] （2）如果x (t )和y (t )均为奇函数，则x (t )*y (t )为偶函数。

[ ] （3）卷积的方法只适用于线性时不变系统的分析。

[ ] （4）若)(*)()(t h t f t y =，则)(*)()(t h t f t y --=-。

[ ]（5）两个LTI 系统级联，其总的输入输出关系与它们在级联中的次序没有关系。

线性系统时域分析

线性系统时域分析

线性系统时域分析您的姓名： [填空题] *_________________________________班级： [填空题] *_________________________________学号： [填空题] *_________________________________系统的瞬态性能通常以系统在零初始条件下，对单位阶跃输入信号的响应来衡量。

[判断题] *对(正确答案)错答案解析：系统的动态(瞬态)性能分析是基于输入(激励)-输出(响应)的关系的。

输入信号和系统特性共同决定系统的输出响应信号。

为了方便进行不同系统的性能比较，约定用单位阶跃响应作为系统性能定量指标的计算依据。

在零初始条件下，当系统的输入信号为原来的输入信号的导数时，系统的输出为原来输出的导数。

[判断题] *对(正确答案)错答案解析：正确。

这是由系统和信号的关系决定的。

注意上述关系只适用于线性定常系统。

如果要求系统的快速性好，则闭环极点应距离虚轴越远越好。

( ) [单选题] *对(正确答案)错答案解析：正确。

根据系统模态的形式：，稳定的系统极点距离虚轴越远，则动态过程衰减越快，快速性越好。

一阶系统的时间常数为系统响应达到稳态值的73.2% 所需时间。

或，若系统响应曲线以初始速度增加，达到稳定值所需时间。

[判断题] *对错(正确答案)答案解析：从响应曲线看，一阶系统在阶跃信号作用下，其响应达到稳态值63.2%所用的时间是。

且系统时间常数是系统本身的结构决定的，不是动态时间值。

第二句的错误在于：不谈输入讨论系统响应没有意义。

对于一阶系统，单位阶跃响应是单调变化的，达到稳态值时间会趋于无穷。

一阶系统的时间常数越大，系统的阶跃输出响应达到稳定值的时间越长。

[判断题] *对(正确答案)错答案解析：一阶系统的阶跃响应动态参数均与系统时间常数成正比关系。

越大，延迟时间、上升时间和调节时间均会同比增大。

从物理意义上看，时间常数大，说明一阶惯性环节的惯性比较大，调节过程比较缓慢在对二阶系统阶跃响应进行讨论时，通常将、0＜＜1、和＞1称为无阻尼、临界阻尼、欠阻尼和过阻尼。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第3章 线性系统的时域分析学习要点1控制系统时域响应的基本概念，典型输入信号及意义； 2控制系统稳定性的概念、代数稳定判据及应用；3控制系统的时域指标，一阶二阶系统的阶跃响应特性与时域指标计算； 4高阶系统时域分析中主导极点和主导极点法；5 控制系统稳态误差概念、计算方法与误差系数，减小稳态误差的方法。

思考与习题祥解题 思考与总结下述问题。

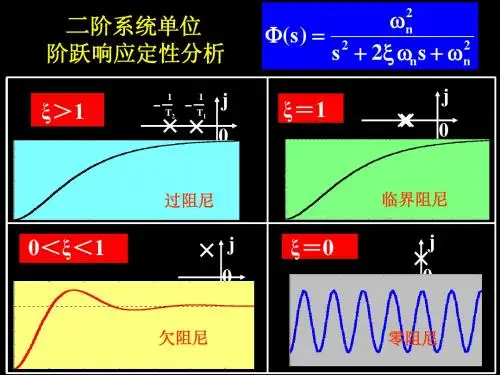
（1）画出二阶系统特征根在复平面上分布的几种情况，归纳ξ值对二阶系统特征根的影响规律。

（2）总结ξ和n ω对二阶系统阶跃响应特性的影响规律。

（3）总结增加一个零点对二阶系统阶跃响应特性的影响规律。

（4）分析增加一个极点可能对二阶系统阶跃响应特性有何影响（5）系统误差与哪些因素有关试归纳减小或消除系统稳态误差的措施与方法。

（6）为减小或消除系统扰动误差，可采取在系统开环传递函数中增加积分环节的措施。

请问，该积分环节应在系统结构图中如何配置，抗扰效果是否与扰动点相关答：（1）二阶系统特征根在复平面上分布情况如图所示。

图 二阶系统特征根在复平面上的分布当0ξ=，二阶系统特征根是一对共轭纯虚根，如图中情况①。

当01ξ<<，二阶系统特征根是一对具有负实部的共轭复数根，变化轨迹是以n ω为半径的圆弧，如图中情况②。

当1ξ=，二阶系统特征根是一对相同的负实根，如图中情况③。

当1ξ>，二阶系统特征根是一对不等的负实根，如图中情况④。

（2）ξ和n ω是二阶系统的两个特征参量。

ξ是系统阻尼比，描述了系统的平稳性。

当0ξ=，二阶系统特征根是一对共轭纯虚根，二阶系统阶跃响应为等幅振荡特性，系统临界稳定。

当01ξ<<，二阶系统特征根是一对具有负实部的共轭复数根，二阶系统阶跃响应为衰减振荡特性，系统稳定。

ξ越小，二阶系统振荡性越强，平稳性越差；ξ越大，二阶系统振荡性越弱，平稳性越好。

因此，二阶系统的时域性能指标超调量由ξ值唯一确定，即001_100%2⨯=-πξξσe。

在工程设计中，对于恒值控制系统，一般取 ξ＝～；对于随动控制系统ξ＝～。

n ω是系统无阻尼自然振荡频率，反映系统的快速性。

当ξ一定，二阶系统的时域性能指标调节时间与n ω值成反比，即34s nt ξω≈:。

（3）二阶系统增加一个零点后，增加了系统的振荡性，将使系统阶跃响应的超调量增大，上升时间和峰值时间减小。

所增加的零点越靠近虚轴，则上述影响就越大；反之，若零点距离虚轴越远，则其影响越小。

（4）二阶系统增加一个极点后，减弱了系统的振荡性，将使系统阶跃响应的超调量减小，上升时间和峰值时间减小； 所增加的极点越靠近虚轴，则上述影响就越大；反之，若极点距离虚轴越远，则其影响越小。

（5）系统误差与系统的误差度（开环传递函数所含纯积分环节的个数或系统型别）、开环放大系数，以及作用于系统的外部输入信号有关。

如果是扰动误差还与扰动作用点有关。

因此，减小或消除系统稳态误差的措施与方法有：增大开环放大系数，增加系统开环传递函数中的积分环节，引入按给定或按扰动补偿的复合控制结构。

无论采用何种措施与方法减小或消除系统稳态误差，都要注意系统须满足稳定的条件。

（6）采取在系统开环传递函数中增加积分环节的措施来减小或消除系统扰动误差时，所增加的积分环节须加在扰动作用点之前。

若所增加的积分环节加在扰动作用点之后，则该积分环节无改善抗扰效果作用。

这一点可以通过误差表达式分析得到。

题系统特征方程如下，试判断其稳定性。

（a ）0203.002.023=+++s s s ； （b ）014844122345=+++++s s s s s ； （c ）025266.225.11.0234=++++s s s s解：（a ）稳定； （b ）稳定； （c ）不稳定。

题 系统结构如题图所示。

控制器)11()(sT K s G i p c +=，为使该系统稳定，控制器参数p K 、i T 应满足什么关系题图解：闭环系统特征方程为：025.0)25.01(152=+++p p i i K s K T s T 所以系统稳定的条件是⎩⎨⎧>>00p i K T ； ⎩⎨⎧<<-<040p i K T题 设单位反馈系统的开环传递函数为()(10.2)(10.1)KG s s s s =++，要求闭环特征根的实部均小于-1，求K 值应取的范围。

解：系统特征方程为0)1.01)(2.0.1(=++K s s s要使系统特征根实部小于1-，可以把原虚轴向左平移一个单位，令1+=s w ，即 1-=w s ，代入原特征方程并整理得072.046.024.002.023=-+++K w w w 运用劳斯判据，最后得24.672.0<<K题 设单位反馈系统的开环传递函数为12 )1()(23++++=s s s s K s G α若系统以2rad/s 频率持续振荡，试确定相应的K 和α值解：可以利用Routh 判据或其它方法解答。

系统的闭环传递函数()32(1)()2(1)K s s s as K s K +Φ=+++++ 闭环特征方程()322(1)0s as K s K +++++=利用Routh 判据。

作Routh 表如下： 3s 1 K +22s a K +1 1s[(2)1]/a K K a +--0s K +1 系统持续振荡的条件是1[(2)1]/02Ka K K a a K++--=→=+ 210410as K a K ++=→-++=所以2=K ， 75.0=α题 单位反馈系统的开环传递函数)5(4)(+=s s s G ，求单位阶跃响应()c t 和调节时间t s 。

解：依题，系统闭环传递函数)1)(1(4)4)(1(4454)(212T s T s s s s s s ++=++=++=Φ其中 121,0.25T T ==。

41)4)(1(4)()()(210++++=++=Φ=s C s C s C s s s s R s s C1)4)(1(4lim)()(lim 000=++=Φ=→→s s s R s s C s s 34)4(4lim)()()1(lim 011-=+=Φ+=→-→s s s R s s C s s 31)1(4lim)()()4(lim 042=+=Φ+=→-→s s s R s s C s s 单位阶跃响应441()133t t c t e e --=-+Θ 421=T T， ∴3.33.3111==⎪⎪⎭⎫ ⎝⎛=T T T t t s s 。

题机器人控制系统结构如题图所示。

试确定参数21,K K 值，使系统阶跃响应的峰值时间5.0=p t s ，超调量%2%=σ。

题图解：依题，系统闭环传递函数为222121212112)1()1()1(1)1()(n n n s s K K s K K s K s s s K K s s K s ωξωωΦΦ++=+++=++++= 由 ⎪⎩⎪⎨⎧=-=≤=--5.0102.0212n p oo t e ωξπσξπξ 联立求解得 ⎩⎨⎧==1078.0n ωξ比较)(s Φ分母系数得⎪⎩⎪⎨⎧=-===146.0121001221K K K n n ξωω题 系统结构如题图所示。

（1） 当025,0f K K ==时，求系统的动态性能指标%σ和s t ；（2） 若使系统0.5ξ=，单位速度误差0.1ss e =时，试确定0K 和f K 值。

题图解：按题思路合方法，可解得（1）%25.4%1.75ts σ==（2）0100,6f K K ==题 已知质量-弹簧-阻尼器系统如题 (a) 图所示，其中质量为m 公斤，弹簧系数为k 牛顿/米，阻尼器系数为μ牛顿秒/米，当物体受F = 10牛顿的恒力作用时，其位移y (t )的的变化如图(b)所示。

求m 、k 和μ的值。

F)t图(a) 图(b)题图解：系统的微分方程为 ：()()()()m y t y t ky t F t μ++=g gg系统的传递函数为 ：221()1()()Y s m G s k F s ms s k s s m mμμ===++++ 因此 221110(()()m G Y s F s k ms s k s s s m mμμ==⨯++++利用拉普拉斯终值定理及图上的稳态值可得：2110()lim ()lim 0.06s s m y sY s sk ss s mmμ→→∞==⨯=++所以 10/ k = ，从而求得k = N/m由系统得响应曲线可知，系统得超调量为0.02/0.0633.3%σ==，由二阶系统性能指标的计算公式100%33.3%e ξπσ-== 解得 0.33ξ=由响应曲线得，峰值时间为3s ，所以由3p t ==解得 1.109/n rad s ω= 由系统特征方城22220n n ks s s s mmμξωω++=++= 可知2n mμξω=2nk mω= 所以22166.7135.51.109n km kg ω=== 220.33 1.109135.599.2/(/)n m N m s μξω==⨯⨯⨯=题 已知一控制系统的结构如题图，1）确定该系统在输入信号()1()r t t =下的时域性能指标：超调量%σ，调节时间st 和峰值时间p t ； 2）当()21(),()4sin3r t t n t t =⋅=时，求系统的稳态误差。

题图解：1）系统的开环传递函数为：288()(4)(2)68G s s s s s ==++++系统的闭环传递函数为28()616G s s s =++比较 二阶系统的标准形式222()2nn n G s s s ωξωω=++，可得 4n ω=而26n ξω=，所以0.75ξ=1.795p t s ==100% 2.8%eξπσ-==31(5%)s nt s ξω==∆= 2）由题意知，该系统是个线性系统，满足叠加原理，故可以分别求取，()21()r t t =⋅和()4sin 3n t t =分别作用于系统时的稳态误差1ess 和2ess ，系统的稳态误差就等于12ess ess ess =+。

A ） ()21()r t t =⋅单独作用时，由系统的开环传递函数知，系统的开环增益1k K =，所以系统对()21()r t t =⋅的稳态误差1ess 为：11211kess K =⨯=+ B ） ()4sin 3n t t =单独作用时，系统的方块图为图。

图 题用图 系统的闭环传递函数为：28(4)()616e s W s s s +=++频率特性为：28(4)()616e j W j j ωωωω+=+-当系统作用为()4sin 3n t t =时，3ω=，所以28(34)3224(3) 2.0763163718e j jW j j j++===⨯+-+2418(3)arctan arctan -0.5564327e W j ∠=-=系统的输出为：24(3)sin(3(3))8.56sin(30.5564)e e ess W j t W j t =⨯+∠=-所以系统的误差为：18.56sin(30.5564)ess t =+-题 已知一个n 阶闭环系统的微分方程为r b r b y a ya y a y a y a n n n n 0101)2(2)1(1)(+=+++++--&&Λ 其中r 为输入，y 为输出，所有系数均大于零。