北师大版九年级数学第六章《反比例函数》单元复习练习题(含答案)

第六章单元测试卷(时间：100分钟 满分：120分)一、选择题(本大题10小题，每小题3分，共30分) 1. 下列函数中，y 是x 的反比例函数的是(D )A ．x(y －1)＝1B ．y ＝1x ＋1C ．y ＝1x 2D ．y ＝3x 2. 图象经过点(2，1)的反比例函数是(B )A ．y ＝－2xB ．y ＝2xC ．y ＝－12xD ．y ＝2x3. 在反比例函数y ＝m －7x 的图象的每一支上，y 随x 的增大而减小，则m 的取值范围是(A )A ．m>7B ．m<7C ．m ＝7D ．m ≠74. 已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为I ＝UR ，当电压为定值时，I 关于R 的函数图象是(C )5. 一司机驾驶汽车从甲地去乙地，他以平均80千米/小时的速度用了4个小时到达乙地，当他按原路匀速返回时，汽车的速度v 千米/小时与时间t 小时的函数关系式是(B )A ．v ＝320tB ．v ＝320t C ．v ＝20t D ．v ＝20t6. 对于反比例函数y ＝－3x，下列说法不正确的是(D )A ．图象经过点(1，－3)B ．图象分布在第二、四象限C ．当x ＞0时，y 随x 的增大而增大D ．点A(x 1，y 1)，B(x 2，y 2)都在反比例函数y ＝－3x的图象上，若x 1＜x 2，则y 1＜y 27. 一次函数y ＝ax ＋b 与反比例函数y ＝a －bx ，其中ab<0，a ，b 为常数，它们在同一坐标系中的图象可以是(C )8. 如图，菱形OABC 的顶点C 的坐标为(3，4)，顶点A 在x 轴的正半轴上．反比例函数y ＝kx (x>0)的图象经过顶点B ，则k 的值为(D )A ．12B ．20C ．24D ．32,第8题图) ,第9题图),第10题图)9. 一次函数y 1＝kx ＋b 和反比例函数y 2＝mx的图象如图，则使y 1＞y 2的x 范围是(B )A ．x ＜－2或x ＞3B ．－2＜x ＜0或x ＞3C ．x ＜－2或0＜x ＜3D ．－2＜x ＜310. 如图，在直角坐标系中，点A 在函数y ＝4x (x>0)的图象上，AB ⊥x 轴于点B ，AB 的垂直平分线与y 轴交于点C ，与函数y ＝4x (x>0)的图象交于点D ，连接AC ，CB ，BD ，DA ，则四边形ACBD 的面积等于(C )A ．2B ．23C ．4D ．4 3二、填空题(本大题6小题，每小题4分，共24分)11. 若反例函数y ＝kx 的图象经过点(－1，2)，则k 的值是－2.12. 已知反比例函数y ＝2x，当x<－1时，y 的取值范围为－2<y<0.13. 已知正比例函数y ＝－2x 与反比例函数y ＝kx 的图象的一个交点坐标为(－1，2)，则另一个交点的坐标为(1，－2)．14. 如图，反比例函数y ＝2x 的图象经过矩形OABC 的边AB 的中点D ，则矩形OABC 的面积为4.,第14题图) ,第15题图),第16题图)15. 如图，直线x ＝2与反比例函数y ＝2x ，y ＝－1x的图象分别交于A ，B 两点，若点P是y 轴上任意一点，则△PAB 的面积是32.16. 某校举行田径运动会，学校准备了某种气球，这些气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P(kPa )是气体体积V(m 3)的反比例函数，其图象如图所示．当气球内的气压大于150 kPa 时，气球会将爆炸，为了安全起见，气体的体积应不小于0.4m 3.三、解答题(一)(本大题3小题，每小题6分，共18分)17. 已知反比例函数的图象与直线y ＝2x 相交于点A(1，a)，求这个反比例函数的表达式．解：将点A(1，a)代入直线y ＝2x 得a ＝2×1＝2.点A 的坐标为(1，2)，代入y ＝kx 得k＝2，∴反比例函数的表达式为y ＝2x18. 已知反比例函数的图象过点A(－2，3)． (1)求这个反比例函数的表达式；(2)这个函数的图象分布在哪些象限？y 随x 的增大如何变化？解：(1)y ＝－6x (2)分布在第二、四象限，在每个象限内y 随x 的增大而增大19. 如图，一辆汽车从甲地到乙地的行驶时间t(h )与行驶速度v(km /h )的函数关系如图所示，根据图象提供的信息，求：(1)t 与v 之间的函数关系式；(2)若要在3 h 内到达乙地，则汽车的速度应不低于多少？解：(1)t ＝300v (2)当t ＝3 h 时，v ＝100(km /h )．∵t 随v 地增大而减小，∴v ≥100，即汽车的速度应不低于100 km /h四、解答题(二)(本大题3小题，每小题7分，共21分)20. 如图，一次函数y ＝2x －4的图象与反比例函数y ＝kx 的图象交于A ，B 两点，且点A的横坐标为3.(1)求反比例函数的表达式； (2)求点B 的坐标．解：(1)把x ＝3代入y ＝2x －4得y ＝6－4＝2，则A 的坐标是(3，2)．把(3，2)代入y ＝k x 得k ＝6，则反比例函数的表达式是y ＝6x (2)根据题意得2x －4＝6x ，解得x ＝3或x ＝－1，把x ＝－1代入y ＝2x －4得y ＝－6，则B 的坐标是(－1，－6)21. 已知反比例函数y ＝kx (k≠0)的图象经过点B(3，2)，点B 与点C 关于原点O 对称，BA ⊥x 轴于点A ，CD ⊥x 轴于点D.(1)求这个反比函数的表达式； (2)求△ACD 的面积．解：(1)将B 点坐标代入函数表达式，得k 3＝2，解得k ＝6，反比例函数的表达式为y ＝6x(2)由B(3，2)，点B 与点C 关于原点O 对称，得C(－3，－2)．由BA⊥x 轴于点A ，CD ⊥x 轴于点D ，得A(3，0)，D(－3，0)．S △ACD ＝12AD·CD＝12[3－(－3)]×|－2|＝622. 如图，一次函数y ＝kx ＋b 的图象与坐标轴分别交于A ，B 两点，与反比例函数y ＝nx的图象在第一象限的交点为C ，CD ⊥x 轴，垂足为D ，若OB ＝3，OD ＝6，△AOB 的面积为3. (1)求一次函数与反比例函数的表达式； (2)直接写出当x>0时，kx ＋b －nx<0的解集．解：(1)∵S AOB ＝3，OB ＝3，∴OA ＝2，∴B(3，0)，A(0，－2)，代入y ＝kx ＋b 得⎩⎪⎨⎪⎧0＝3k ＋b ，－2＝b ，解得k ＝23，b ＝－2，∴一次函数的表达式为y ＝23x －2，∵OD ＝6，∴D(6，0)，CD ⊥x 轴，当x ＝6时，y ＝23×6－2＝2，∴C(6，2)，∴n ＝6×2＝12，∴反比例函数的表达式是y ＝12x(2)当x>0时，kx ＋b －nx<0的解集是0<x<6五、解答题(三)(本大题3小题，每小题9分，共27分) 23. 保护生态环境，建设绿色社会已经从理念变为人们的行动，某化工厂1月的利润为200万元．设1月为第1个月，第x 个月的利润为y 万元．由于排污超标，该厂决定从1月底起适当限产，并投入资金进行治污改造，导致月利润明显下降，从1月到5月，y 与x 成反比例，到5月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加20万元(如图)．(1)分别求该化工厂治污期间及治污改造工程完工后，y 与x 之间的函数关系式； (2)治污改造工程顺利完工后经过几个月，该厂月利润才能达到200万元？(3)当月利润少于100万元时，为该厂资金紧张期，问该厂资金紧张期共有几个月？解：(1)①当1≤x≤5时，y ＝200x ；②当x>5时，y ＝20x －60 (2)当y ＝200时，20x－60＝200，解得x ＝13，13－5＝8，所以治污改造工程顺利完工后经过8个月后，该厂利润达到200万元 (3)对于y ＝200x ，当y ＝100时，x ＝2；对于y ＝20x －60，当y ＝100时，x ＝8，所以资金紧张的时间为8－2－1＝5(个月)24. 如图，正方形OABC 的面积为9，点O 为坐标原点，点B 在函数y ＝kx (k ＞0，x ＞0)的图象上点P(m ，n)是函数图象上任意一点，过点P 分别作x 轴y 轴的垂线，垂足分别为E ，F.并设矩形OEPF 和正方形OABC 不重合的部分的面积为S.(1)求k 的值；(2)当S ＝92时，求点P 的坐标；(3)写出S 关于m 的关系式．解：(1)k ＝9 (2)分两种情况：①当点P 在点B 的左侧时，∵P(m ，n)在函数y ＝kx 上，∴mn ＝9，∴S ＝m(n －3)＝mn －3m ＝92，解得m ＝32，∴n ＝6，∴点P 的坐标是P(32，6)；②当点P 在点B 的右侧时，∵P(m ，n)在函数y ＝k x 上，∴mn ＝9，∴S ＝n(m －3)＝mn －3n ＝92，解得n ＝32，∴m ＝6，∴点P 的坐标是P(6，32)，综上所述：P 点坐标为(6，32)或(32，6) (3)当0＜m ＜3时，点P 在点B 的左边，此时S ＝9－3m ，当m≥3时，点P 在点B 的右边，此时S ＝9－3n ＝9－27m25. 如图，一次函数y ＝kx ＋b 的图象与反比例函数y ＝mx (x ＞0)的图象交于点P(n ，2)，与x 轴交于点A(－4，0)，与y 轴交于点C ，PB ⊥x 轴于点B ，点A 与点B 关于y 轴对称．(1)求一次函数，反比例函数的表达式； (2)求证：点C 为线段AP 的中点；(3)反比例函数图象上是否存在点D ，使四边形BCPD 为菱形？如果存在，说明理由并求出点D 的坐标；如果不存在，说明理由．解：(1)反比例函数表达式为y ＝8x ，一次函数表达式为y ＝14x ＋1 (2)∵点A 与点B 关于y 轴对称，∴OA ＝OB ，∵PB ⊥x 轴于点B ，∴∠PBA ＝∠COA＝90°，∴PB ∥CO ，∴OA OB ＝ACPC ＝1，即AC ＝PC ，∴点C 为线段AP 的中点 (3)存在点D ，使四边形BCPD 为菱形．理由：∵点C 为线段AP 的中点，∴BC ＝12AP ＝PC ，∴BC 和PC 是菱形的两条边，由y ＝14x ＋1可得C(0，1)，过点C 作CD∥x 轴，交PB 于点E ，交反比例函数图象于点D ，分别连接PD ，BD ，∴D(8，1)，且PB⊥CD，∴PE ＝BE ＝1，CE ＝DE ＝4，∴PB 与CD 互相垂直平分，即四边形BCPD 为菱形，∴存在满足条件的点D ，其坐标为(8，1)。

一、选择题经过第二、四象限，则直线y=2x+k−1经过的象限是( )1.若双曲线y=k−1xA．第一、二、三象限B．第一、二、四象限C．第一、三、四象限D．第二、三、四象限(k≠0)与y=kx+k(k≠0)的图象大致为( )2.在同一直角坐标系中，函数y=kxA．B．C．D．3.如图，一次函数与反比例函数的图象相交于A，B两点，则图中使反比例函数的值大于一次函数的值的x的取值范围是( )A．x<−1B．x>2C．−1<x<0或x>2D．x<−1或0<x<24.如图，矩形ABCD的对角线BD过原点O，各边分别平行于坐标轴，点C在反比例函数y=3k+1x的图象上，若点A的坐标是(−2,−2)，则k的值是( )A．−1B．0C．1D．45.如图，双曲线y=kx 与直线y=−12x交于A，B两点，且A(−2,m)，则点B的坐标是( )A．(2,−1)B．(1,−2)C．(12,−1)D．(−1,12)6.已知点A(x1,2)，B(x2,4)，C(x3,−1)都在反比例函数y=kx(k<0)的图象上，则x1，x2，x3的大小关系是( )A．x3<x1<x2B．x2<x1<x3C．x1<x3<x2D．x1<x2<x37.对于反比例函数y=k2x（k为常数，k≠0），有下列说法：①它的图象分布在第一、三象限；②点(k,k)在它的图象上；③它的图象是中心对称图形；④ y随x的增大而增大．正确的说法是( )A．①③④B．②③④C．①②④D．①②③8.如图，一次函数y=x+1和y=2x与反比例函数y=2x的交点分别为点A，B和C，下列结论中，正确的个数是( )①点A与点B关于原点对称；② OA=OC；③点A的坐标是(1,2)；④ △ABC是直角三角形．A．1B．2C．3D．49.如图，点A，B为反比例函数y=kx在第一象限上的两点，AC⊥y轴于点C，BD⊥x轴于点D，若B点的横坐标是A点横坐标的一半，且图中阴影部分的面积为k−2，则k的值为( )A．43B．83C．143D．16310.下列说法正确的是( )A．圆面积公式S=πr2中，S与r成正比例关系B．三角形面积公式S=12aℎ中，当S是常量时，a与ℎ成反比例关系C．y=1x+1中，y与x成反比例关系D．y=x−12中，y与x成正比例关系二、填空题11.过双曲线y=kx(k>0)的动点A作AB⊥x轴于点B，P是直线AB上的点，且满足AP= 2AB，过点P作x轴的平行线交此双曲线于点C．如果△APC的面积为8，则k的值是．12.在平面直角坐标系xOy中，已知直线y=mx(m>0)与双曲线y=4x交于A，C两点（点A在第一象限），直线y=nx(n<0)与双曲线y=−1x交于B，D两点．当这两条直线互相垂直，且四边形ABCD的周长为10√2时，点A的坐标为．13.山西拉面，又叫甩面、扯面、抻面，是西北城乡独具地方风味的面食名吃，为山西四大面食之一，将一定体积的面团做成拉面，面条的总长度y（cm）与粗细（横截面面积）x（cm2）之间的关系如图所示（双曲线的一支），如果将这个面团做成粗为0.16cm2的拉面，则做出来的面条的长度为．14.如图，点M，N是反比例函数y=kx(x<0)图象上的两点，过点M，N分别作MA⊥x轴于点A，NB⊥x轴于点B，连接BM，ON，已知点B(−2,0)，AM=2，S△ABM=3，则S△BON=．15.如图，在平面直角坐标系中，点M为x轴正半轴上一点，过点M的直线l∥y轴，且直线l分别与反比例函数y=8x (x>0)和y=kx(x>0)的图象交于P，Q两点，若S△POQ=12，则k的值为．16.如图，已知函数y=2x和函数y=kx(k≠0)的图象交于A，B两点，过点A作AE⊥x轴于点E．若△AOE的面积为4，P是坐标平面上的点，且以点B，O，E，P为顶点的四边形是平行四边形，则满足条件的P点坐标是．的图象经过平行四边形ABCD对角线的交点P，已知点A，C，D在17.如图，反比例函数y=kx坐标轴上，BD⊥DC，平行四边形ABCD的面积为6，则k=．三、解答题(m≠0)的图象交于点18.如图，在平面直角坐标系中，一次函数y=kx+b与反比例函数y=mxA(3,1)，且过点B(0,−2)(1) 求反比例函数和一次函数的表达式(2) 如果点P是x轴上一点，且△ABP的面积是3，求点P的坐标．(x>0)的图象上有一点A(m,4)，过点A作19.如图，在平面直角坐标系中，反比例函数y=kxAB⊥x轴于点B，将点B向右平移2个单位长度得到点C，过点C作y轴的平行线交反比．例函数的图象于点D，CD=43(1) 点D的横坐标为．(用含m的式子表示);(2) 求反比例函数的解析式．(x>0)的20.如图，一次函数y1=kx+2的图象与x轴交于点B(−2,0)，与反比例函数y2=mx 图象交于点A(1,a)．(1) 求m的值．(2) 点C为x轴上一动点．若△ABC的面积是6，请直接写出点C的坐标．21.如图，已知反比例函数y=mx(x>0)的图象经过点A(4,2)，过A作AC⊥y轴于点C．点B 为反比例函数图象上的一动点，过点B作BD⊥x轴于点D，连接AD．直线BC与x轴的负半轴交于点E．(1) 若BD=3OC，求△BDE的面积；(2) 是否存在点B，使得四边形ACED为平行四边形？若存在，请求出点B的坐标；若不存在，请说明理由．22.一个长方形的宽为x cm，长为y cm，面积为24cm2．(1) 求y与x之间的函数关系式．(2) 当x=8时，长方形的长为多少cm．23.如图，反比例函数y1=kx 的图象与一次函数y2=14x的图象交于点A，B，点B的横坐标实数4，点P(1,m)在反比例函数y1=kx的图象上．(1) 求反比例函数的表达式；(2) 观察图象回答：当为何范围时，y1>y2；(3) 求△PAB的面积．24.在平面直角坐标系xOy中，直线y=x+2与双曲线y=k相交于点A(m,3)．x(1) 求反比例函数的表达式；(2) 画出直线和双曲线的示意图；(3) 若P是坐标轴上一点，当OA=PA时．直接写出点P的坐标．25.已知A=2(−a2+5+4ab)+(5ab−4+2a2)．(1) 化简A；的图象上，求A的值．(2) 若点(a,b)在反比例函数y=3x答案一、选择题1. 【答案】C【解析】∵双曲线y=k−1x经过第二、四象限，∴k−1<0，则直线y=2x+k−1一定经过一、三、四象限．【知识点】k,b对一次函数图象及性质的影响、k对反比例函数的图象及性质的影响2. 【答案】C【知识点】k对反比例函数的图象及性质的影响3. 【答案】C【解析】∵点A的坐标为(−1,2)，点B的坐标为(2,−1)，∴当−1<x<0或x>2时，反比例函数图象在一次函数图象上方，∴图中使反比例函数的值大于一次函数的值的x的取值范围是−1<x<0或x>2．故选：C．【知识点】反比例函数与方程、不等式4. 【答案】C【解析】∵矩形ABCD的对角线BD过原点O，BO为四边形BGOE的对角线，OD为四边形OHDF的对角线，∴S△BEO=S△BGO，S△OFD=S△OHD，S△CBD=S△ADB，∴S△CBD−S△BGO−S△OHD=S△ADB−S△BEO−S△OFD，∴S四边形CHOG =S四边形AEOF=2×2=4，∴3k+1=4，即k=1．【知识点】反比例函数系数k的几何意义、矩形的性质、反比例函数的解析式5. 【答案】A【解析】当x=−2时，y=−12×(−2)=1，即A(−2,1)，将A点坐标代入y=kx，得k=−2×1=−2，反比例函数的解析式为y=−2x，联立双曲线、直线，得{y=−2x,y=−12x,解得 {x 1=−2,y 1=1, {x 2=2,y 2=−1,B (2,−1)．【知识点】反比例函数与方程、不等式、反比例函数的解析式6. 【答案】D【解析】 ∵ 反比例函数 y =kx (k <0)，如图，∴ 反比例函数图象位于第二、四象限，且在每一个象限 y 随 x 的增大而增大， ∵ 点 A (x 1,2)，B (x 2,4)，C (x 3,−1) 都在反比例函数 y =kx (k <0) 的图象上， ∴x 1<x 2<x 3．【知识点】k 对反比例函数的图象及性质的影响7. 【答案】D【解析】 ∵k 2>0，∴ ①它的图象分布在第一、三象限，正确； ② x =k 时，y =k 2k=k ，∴ 点 (k,k ) 在它的图象上，正确； ③它的图象是中心对称图形，正确；④应为：在每一个象限内，y 随 x 的增大而增大，错误． ∴ ①②③正确． 故选：D ．【知识点】反比例函数的增减性、k 对反比例函数的图象及性质的影响、反比例函数的对称性8. 【答案】D【知识点】勾股逆定理、反比例函数与方程、不等式、一次函数与二元一次方程（组）的关系9. 【答案】B【解析】设 B (t,kt)．∵AC ⊥y 轴于点 C ，BD ⊥x 轴于点 D ，B 点的横坐标是 A 点横坐标的一半， ∴AC =2CE =2t ， ∴A (2t,k2t )，∴BD=2OC=2BE，在△OCM和△BEM中，{∠OCM=∠MEB,∠CMO=∠EMB, OC=BE,∴△OCM≌△BEM，∴CM=EM=12t，同理可证：△ODN≌△AEN，∴EN=DN=k4t，∴阴影部分的面积=12ME×BE+12NE×AE=12×t2×k2t+12×t×k4t=k−2.解得：k=83．【知识点】反比例函数的解析式10. 【答案】B【知识点】反比例函数的概念二、填空题11. 【答案】12或4【解析】（1）如图：设点A的坐标为：(a,ka )，则点P的坐标为：(a,3ka)，点C的纵坐标为：3ka ，代入反比例函数y=kx(k>0)，点C的横坐标为：a3，S△APC=12(3ka−ka)×(a−a3)=8，解得：k=12．（2）如图：设点A的坐标为：(a,ka )，则点P的坐标为：(a,−ka)，点C的纵坐标为：AC∩AE=A，代入反比例函数y=kx(k>0)，点C的横坐标为：−a，S△APC=12×2ka×2a=8，解得：k=4．【知识点】反比例函数的解析式12. 【答案】(√2,2√2)或(2√2,√2)【知识点】反比例函数与方程、不等式、一次函数图象的垂直问题13. 【答案】800cm【解析】设y与x的函数关系式为y=kx(k≠0)，将(0.04,3200)代入得k=xy=0.04×3200=128，∴y=128x(x>0)，当x=0.16时，y=1280.16=800．【知识点】反比例函数的应用14. 【答案】5【解析】∵MA⊥x轴于点A，AM=2，∴S△ABM=12AB⋅AM=3，即AB=3．∵B(−2,0)，即OB=2，∴OA=OB+AB=2+3=5，∴M(−5,2)，代入反比例解析式得：k=−5×2=−10，即y=−10x ，则S△BON=12∣k∣=5．【知识点】反比例函数系数k的几何意义、反比例函数的图象与性质15. 【答案】−16【解析】∵S△POQ=S△OMQ+S△OMP，∴12∣k∣+12×∣8∣=12，∴∣k∣=16，而k<0，∴k=−16．【知识点】反比例函数系数k的几何意义16. 【答案】(0,−4)或(−4,−4)或(4,4)【解析】∵AE⊥x轴于点E，△AOE的面积为4，∴k=8，∴函数y=2x和函数y=8x的图象交于A，B两点，令2x=8x，解得x=±2，当x=2时，y=4，当x=−2时，y=−4，∴A(2,4)，B(−2,−4)，∴E(2,0)．如图，以点B，O，E，P为顶点的平行四边形共有3个，满足条件的P点坐标分别为P1(0,−4)，P2(−4,−4)，P3(4,4)．【知识点】平行四边形及其性质、反比例函数与方程、不等式、反比例函数系数k的几何意义17. 【答案】−3【解析】过点P作PE⊥y轴于点E，∵四边形ABCD为平行四边形，∴AB=CD，又∵BD⊥x轴，∴ABDO为矩形，∴AB=DO，∴S矩ABDO =S平行四边形ABCD=6，∵P为对角线交点，PE⊥y轴，∴四边形PDOE为矩形，面积为3，即DO⋅EO=3，∴设P点坐标为(x,y)，∴k=xy=−3．【知识点】反比例函数系数k 的几何意义、平行四边形及其性质、矩形的判定三、解答题 18. 【答案】(1) 因为反比例函数 y =m x(m ≠0) 的图象过点 A (3,1)，所以 1=m3，所以 m =3．所以反比例函数的表达式为 y =3x ．因为一次函数 y =kx +b 的图象过点 A (3,1) 和 B (0,−2)． 所以 {3k +b =1,b =−2.解得 {k =1,b =−2.所以一次函数的表达式为 y =x −2． (2) 令 y =0，所以 x −2=0，x =2，所以一次函数 y =x −2 的图象与 x 轴的交点 C 的坐标为 (2,0)． 因为 S △ABP =3，12PC ⋅1+12PC ⋅2=3． 所以 PC =2，所以点 P 的坐标为 (0,0) 或 (4,0)．【知识点】反比例函数的解析式、一次函数的解析式、三角形的面积19. 【答案】(1) m +2 (2) 因为 CD =43 ,所以点 D 的坐标为 (m +2,43)．因为点 A (m,4)，点 D (m +2,43) 在函数 y =kx 的图象上， 所以 4m =43(m +2)，所以m=1，所以k=4m=4×1=4，所以反比例函数的解析式为y=4x．【知识点】反比例函数的解析式、坐标平面内图形的平移变换20. 【答案】(1) ∵一次函数y1=kx+2的图象与x轴交于点B(−2,0)，∴−2k+2=0，∴k=1，∴y1=x+2，∵一次函数y1=kx+2的图象与反比例函数y2=mx(x>0)的图象交于点A(1,a)，∴a=1+2=3．把A(1,3)代入y2=mx，得m=3．(2) (2,0)或(−6,0)．【解析】(2) 设C点坐标为(t,0)，∵B点坐标为(−2,0)，∴BC=∣t+2∣，∴S△ABC=12BC⋅∣y A∣=12∣t+2∣×3=6，∴∣t+2∣=4，∴t=2或t=−6，∴C点坐标为(2,0)或(−6,0)．【知识点】反比例函数的解析式、坐标平面内图形的面积21. 【答案】(1) ∵反比例函数y=mx(x>0)的图象经过点A(4,2)，∴m=8，∴反比例函数y=8x(x>0)．∵AC⊥y轴，A(4,2)，∴OC=2，∵BD=3OC，∴BD=6，∵BD⊥x轴，∴B(43,6)，∵C(0,2)，设直线BC的解析式为y=kx+b，则有{b=2,43k+b=6,解得{k=3,b=2,∴直线BC的解析式为y=3x+2，∴E(−23,0)，∴DE=23+43=2，∴S△BED=12×DE×BD=6．(2) 存在．如图，设BD交AC于F．设B(a,8a)，∵A(4,2)，∴AC=4．∵四边形ACED是平行四边形，∴DE=AC=4，且CF∥DE，∴△BCF∽△BED，∴CFDE =BFBD，即a4=8a−28a，解得a=2，∴B(2,4)．【知识点】反比例函数的解析式、两角分别相等、反比例函数与四边形综合22. 【答案】(1) 由题意可知：y=24x(x>0)．(2) 当x=8时，y=248=3．【知识点】反比例函数的应用、简单的代数式求值23. 【答案】(1) 将x=4代入y2=14x得：y=1，所以B(4,1)．所以k=xy=4×1=4，所以反比例函数的表达式为y=4x．(2) 由正比例函数和反比例函数的对称性可知点A的横坐标为−4．所以反比例函数图象位于正比例函数图象上方， 所以 x <−4 或 0<x <4．(3) 过点 A 作 AR ⊥y 轴于 R ，过点 P 作 PS ⊥y 轴于 S ，连接 PO ，设 AP 与 y 轴交于点 C ，如图，因为点 A 与点 B 关于原点对称， 所以 OA =OB ， 所以 S △MOP =S △BOP ， 所以 S △PAB =2S △AOP ．y 1=4x 中，当 x =1 时，y =4，所以 P (1,4)．设直线 AP 的函数关系式为 y =mx +n ， 把点 A (−4,−1)，P (1,4) 代入 y =mx +n ， 则 {−4m +n =−1,m +n =4,解得 m =1，n =3．故直线 AP 的函数关系式为 y =x +3， 则点 C 的坐标 (0,3)，OC =3，所以 S △AOP =S △AOC +S △POC =12OC ⋅AR +12OC ⋅PS =12×3×4+12×3×1=152，所以 S △PAB =2S △AOP =15．【知识点】反比例函数与一次函数综合、反比例函数与三角形综合、反比例函数与方程、不等式24. 【答案】(1) ∵ 直线 y =x +2 与双曲线 y =kx 相交于点 A (m,3)． ∴3=m +2，解得 m =1． ∴A (1,3)．把 A (1,3) 代入 y =kx 解得 k =3， ∴y =3x ．(2) 如图．(3) P (0,6) 或 P (2,0)．【知识点】k 对反比例函数的图象及性质的影响、反比例函数的解析式、勾股定理25. 【答案】(1) 原式=−2a 2+10+8ab +5ab −4+2a 2=13ab +6； (2) ∵ 点 (a,b ) 在反比例函数 y =3x ，∴A=13ab+6=13×3+6=45．【知识点】反比例函数的解析式、整式的加减运算。

第六章反比例函数单元测试北师大版2024—2025学年秋季九年级上册秋季考生注意：本试卷共三道大题，23道小题，满分120分，时量120分钟注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。

笞卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答第I卷时，选出每小题答案后，把答案填写在答题卡上对应题目的位置，填空题填写在答题卡相应的位置写在本试卷上无效。

3.回答第II卷时，将答案写在第II卷答题卡上。

4.考试结束后，将本试卷和答题卡一并交回。

第I卷一、选择题（每题只有一个正确选项，每小题3分，满分36分）1．反比例函数y＝﹣的图象一定经过的点是（）A．（1，10）B．（﹣2，5）C．（2，5）D．（2，8）2．关于反比例函数y＝﹣的图象，下列说法正确的是（）A．y随着x的增大而减小B．图象分布在一、三象限C．当x＞﹣2时，y＞3D．若（﹣a，b）在该图象上，则（a，﹣b）也在该图象上3．若点A（1，a），B（﹣2，b），C（2，c）在反比例函数的图象上，则a，b，c的大小关系是（）A．c＞b＞a B．b＞a＞c C．a＞c＞b D．b＞c＞a4．如图，反比例函数的图象过矩形OABC的顶点B，OA，OC分别在x 轴，y轴的正半轴上，若点A（2，0），点C（0，4），则k的值为（）A．8B．6C．﹣8D．﹣65．已知正比例函数y1＝﹣2x与反比例函数．对于实数m，当x＝m时，y1＞y2；当x＝m+1时，y1＜y2，则m的取值范围为（）A．m＜﹣2或0＜m＜2B．﹣2＜m＜2C．﹣3＜m＜﹣2或1＜m＜2D．﹣2＜m＜0或m＞26．如图，点A是反比例函数在第二象限内图象上一点，点B是反比例函数在第一象限内图象上一点，直线AB与y轴交于点C，且AC＝BC，连接OA、OB，则△AOB的面积是（）A．2B．2.5C．3D．3.5 7．如图，点P（﹣2a，a）是反比例函数y＝的图象与⊙O的一个交点，图中阴影部分的面积为10π，则该反比例函数的表达式为（）A．y＝﹣B．y＝﹣C．y＝﹣D．y＝﹣8．两个反比例函数C1：和C2：在第一象限内的图象如图所示，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，则四边形P AOB的面积为（）A．1B．2C．3D．49．在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标（0，2），顶点B恰好落在第一象限的双曲线上，则该反比例函数的解析式为（）A．B．C．D．10．如图，A是反比例函数y＝图象上一点，且A点的横坐标为a（a ＞0）．P是y轴负半轴上一点，且P点的纵坐标为b．连结AP，延长AP至点B，使得BP＝AP，且点B恰好落在反比例函数y＝（k＞0，x＜0）的图象上．已知ab＝﹣2，则k的值为（）A．2B．4C．6D．8二．填空题（6小题，每题3分，共18分）11．若y＝（m﹣3）x|m|﹣4是反比例函数，则m的值是．12．如图所示，由反比例函数的对称性可知，点P关于原点的对称点Q也在图象y＝上．作P A⊥x轴于点A，QC⊥P A交延长线于点C，则△PQC的面积为．（用含k的式子表示）13．若反比例函数的图象的一个分支在第二象限，则m的取值范围是．14．若反比例函数y1＝，y2＝﹣，当1≤x≤3时，函数y1的最大值是a，函数y2的最大值是b，则a b＝．15．如图，反比例函数y＝（x＜0）的图象经过平行四边形ABCO的顶点A，OC在x轴上，若点B（﹣1，3），S▱ABCO＝3，则实数k的值为．16．如图，矩形OABC顶点A、C分别在x、y轴上，双曲线分别交BC、AB 于点D、E，连接DE并延长交x轴于点F，连接AC．下列结论：①DE∥CA；②S四边形ACDF＝k；③若BD＝2CD，则AE＝2BE；④若点E为DF的中点，且S△AEF＝3，则k＝12；其中正确的有．（填写所有正确结论的序号）第II卷第六章反比例函数单元测试北师大版2024—2025学年秋季九年级上册秋季姓名：____________ 学号：____________准考证号：___________一、选择题12345678910题号答案二、填空题11、_______ 12、______13、_______ 14、______15、_______ 16、______三、解答题（17—22题每题10分，23题10分，共计72分，解答题要有必要的文字说明）17.已知y＝y1+y2，其中y1与x2成正比例，y2与x成反比例，并且当x＝时y＝5，当x＝1时y＝﹣1，求y与x之间的函数关系式．18.如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A（﹣3，n），B（2，3）．（1）求反比例函数与一次函数的函数表达式；（2）请结合图象直接写出不等式kx+b≥的解集；（3）若点P为x轴上一点，△ABP的面积为10，直接写出点P的坐标．19.平面直角坐标系中，A（x1，y1），B（x2，y2），C（x3，y3）是反比例函数图象上的三点，且x1+x2＝0．（1）若x1y2＝﹣2，求k的值；（2）若x1＝y3，求证：x3+y2＝0．20.在平面直角坐标系中，已知A（t，0），B（0，﹣t），C（t，2t）三点，其中t＞0，双曲线y＝分别与线段BC，AC交于点D，E．（1）当t＝1时，求点D的坐标；（2）当S△ABE＝时，求△ADE的面积；（3）若S△DAB﹣S△BDE＝，求t的值．21.如图，A为反比例函数y＝（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA，AB，且OA＝AB＝2．（1）求k的值；（2）过点B作BC⊥OB，交反比例函数y＝（其中x＞0）的图象于点C，连接OC交AB于点D，求的值．22.如图，一次函数y＝﹣x+的图象与反比例函数y＝（k＞0）的图象交于A，B两点，过点A作x轴的垂线，垂足为M，△AOM面积为1．（1）求反比例函数的解析式；（2）在x轴上求一点P，使|P A﹣PB|的值最大，并求出其最大值和P点坐标．23.如图，点M、N是反比例函数的图象上的两个动点，过点M作MP⊥y轴、过点N作NQ⊥x轴，分别交反比例函数的图象于点P、Q，连接PN、QM．设点M的横坐标为m（m＞0），点N的横坐标为n（n＜0）．（1）若m＝3，求MP的长；（2）若MP＝NQ，求mn的值；（3）①求△MNP的面积（用含m、n的代数式表示）；②点P、Q到直线MN的距离是否相等？并说明理由．。

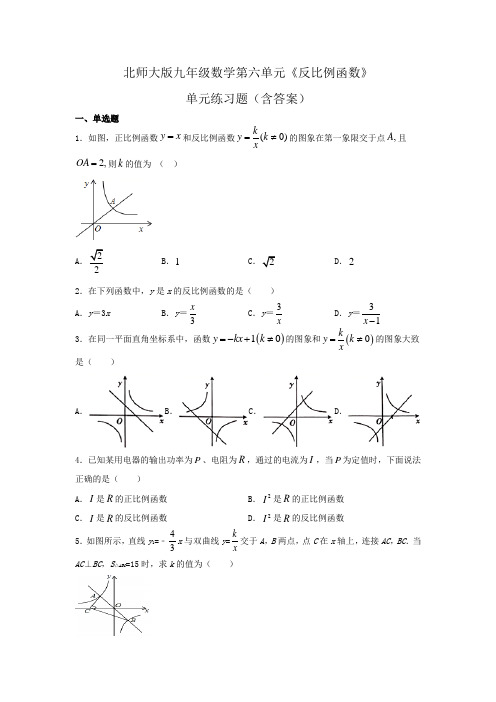
北师大版九年级数学第六单元《反比例函数》单元练习题（含答案）一、单选题1．如图，正比例函数y x =和反比例函数(0)k y k x =≠的图象在第一象限交于点,A 且2,OA =则k 的值为 （ ）A ．22B ．1C ．2D ．22．在下列函数中，y 是x 的反比例函数的是（ ）A ．y ＝3xB ．y ＝3xC ．y ＝3xD ．y ＝31x - 3．在同一平面直角坐标系中，函数()10y kx k =-+≠的图象和()0k y k x=≠的图象大致是（ ） A ．B ．C ． D ．4．已知某用电器的输出功率为P 、电阻为R ，通过的电流为I ，当P 为定值时，下面说法正确的是（ ）A ．I 是R 的正比例函数B ．2I 是R 的正比例函数C ．I 是R 的反比例函数D ．2I 是R 的反比例函数 5．如图所示，直线y 1=﹣43x 与双曲线y =k x交于A ，B 两点，点C 在x 轴上，连接AC ，BC ．当AC ⊥BC ，S △ABC =15时，求k 的值为（ ）A ．﹣10B ．﹣9C ．6D ．46．若点1(3,)A y -，2(2,)B y -，3(1,)C y 都在反比例函数12y x =-的图象上，则1y ，2y ，3y 的大小关系是（ ） A ．213y y y << B ．312y y y << C ．123y y y << D ．321y y y <<7．如图，A 为反比例函数y ＝k x图象上一点，AB ⊥x 轴与点B ，若S △AOB ＝2，则k 为（ ）A ．4B ．2C ．1D ．无法确定8．在同一平面直角坐标系中，函数y=kx （k>0）与k y x=（k>0）的图象可能是（ ） A ． B ． C ． D ．9．关于函数2y x=，下列判断正确的是（ ） A ．当x 增大时，y 减小； B ．该函数的图象在第二、四象限C ．该函数的图象是抛物线D ．若点()a b ，在该函数的图象上，则点()b a ，也在该函数的图象上10．如图，Rt AOB ∆中，90OAB ∠=︒，6OA =，OA 在x 轴的正半轴，OB ，AB 分别与双曲线1k y x =()10k ≠，21k y x=()20k ≠相交于点C 和点D ，且:1:2BC CO =，若//CD OA ，则点E 的横坐标为（ ）A ．4B ．3C ．83D ．2611．如图，直线y=﹣x+2与x 轴交于点A ，与y 轴交于点B ，与反比例函数(x<0)的图象交于点C ，点D(3，a)在直线y=﹣x+2上，连接OD ，OC ，若∠COD=135°，则k 的值为( )A ．﹣2B ．﹣4C ．﹣6D ．﹣812．已知一个反比例函数的图像经过点A （3，﹣4），那么不在这个函数图像上的点是（ ）A ．（﹣3，﹣4）B ．（﹣3，4）C ．（2，﹣6）D ．（22，﹣122）二、填空题13．如图，矩形OABC 的对角线OB ，CA 交于点D ，OA ＝1，∠ODA ＝60°．双曲线y ＝经过点B ，则k ＝_____．14．直线y ＝ax(a ＞0)与双曲线y ＝3x交于A(x 1，y 1)，B(x 2，y 2)两点．则4x 1y 2－3x 2y 1＝____． 15．如图，已知点A 在反比例函数(0)k y k x =≠的图象上，过点A 作AB y ⊥轴于点B ，OAB 的面积是2．则k 的值是_________．16．如果反比例函数kyx=（k是常数，k≠0）的图象经过点（-1，2），那么这个反比例函数的图象在第______象限．17．如图，点A，B是双曲线上的点，分别过点A，B作轴和轴的垂线段，若图中阴影部分的面积为2，则两个空白矩形面积的和为____________．18．如图，点A是反比例函数y=-2的图象第二象限分支上的动点，连结AO并延长交另一支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第三象限，AC与x轴交于点D，连结BD．当BD平分∠ABC时，点C的坐标是___．19．如图，反比例函数3(0)y xx=>的图像与矩形ABCO的边AB交于点G，与边BC交于点D，过点A，D作DE//AF，交直线y = kx (k < 0)于点E，F，若OE=OF，BG=3GA，则四边形ADEF 的面积为_____；20．如图，点P 在反比例函数图象上，PA 垂直y 轴于点A ，点B 为x 轴上任意一点，且PAB 的面积为2，则这个反比例函数的解析式为______．三、解答题21．如图，在平面直角坐标系中，一次函数1y k x b =+的图像与反比例函数2k y x=的图像交与A （4，-2），B （-2，n ）两点，与x 轴交与点C ．（1）求2k ，n 的值；（2）请直接写出不等式21k k x b x+＜的解集； （3）点A 关于x 轴对称得到点A ’，连接A ’B ，A ’C ，求△A ’BC 的面积．22．如图，一次函数y=kx+b 与反比例函数y k x'=（x>0)的图象交于点A(a ，3)和B(3，1）． （1）求一次函数的解析式．（2）观察图象，写出反比例函数值小于一次函数值时x的取值范围．（3）点P是线段AB上一点，过点P作PD⊥x轴于点D，交反比例函数图象于点Q，连接OP、OQ，若△POQ的面积为12，求P点的坐标。

可编辑修改精选全文完整版九年级数学上册第六章《反比例函数》测试卷-北师大版（含答案）（满分 120 分）一、选择题（每题3分，共30分） 1.下列函数中，是反比例函数的是（ ）A. y = -2xB. y =-12xC. y =11x- D. y =21x2.已知点 P （-1，4）在反比例函数y = kx（k =0）的图象上，则K 值是（ ） A. -14B.14 C. 4 D. -4 3.下列各点中，在函数y = -6x图象上的是（ ）A. （-2，-4）B.（2，3）C.（-1，6）D.（-12，3）4.反比例函数y =5m x-的图象在第二、四象限内，那么m 的取值范围是（ ） A. m <0B. m >0C.m >5D. m <55. 函数4y=-x，当x >0时的图象为下图中的（ ）6.已知点（1，y 1），B （2，y 2），C （-3，y 3）都在反比例函数y =6x 的图象上，则y 1，y 2 ，y 3；的大小关系是（ ） A. y 3<y 1 <y 2； B. y 1<y 2<y 3； C. y 2，y 1，y 3； D. y 3<y 2<y 1；7.关于反比例函数y = 4x的图象，下列说法正确的是（ ） A.必经过点（1，1）B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.两个分支关于原点成中心对称8.三角形的面积为4 c m²，底边上的高y（c m）与底边x（c m）之间的函数关系图象大致应为（）9. 函数y= ax与y=αx-a（a≠0）在同一坐标系中的大致图象是（）10.如图，函数y1=x-1和函数y2=-2x的图象相交于点M（2，m），N（-1，n），若y1<y2，则x的取值范围是（）A.x<-1或0<x<2B.x<-1或x>2C.-1<x<0或0<x<2D．-1<x<0或x>2二、填空题（每题4分，共28分）11.反比例函数y=- 1x的图象在第__________象限，在每个象限内，y随x的增大而________ .12. 反比例函数y= kx过A（-1，4）和B（2，m）两点，则m= ___________________.13．对于函数y= 3x，当x>0时y__________0，这部分图象在第_____________象限.14.完成某项任务可获得500 元报酬，考虑由x人完成这项任务，试写出人均报酬y（元）与人数x（人）之间的函数关系式_________________________________.15.若点P（1，m），P，（2，n）在反比例函数y=kx（k<0）的图象上，则m_____n（填">""<"或"="）.16.如图，已知点A在反比例函数图象上，A M⊥x轴于点M，且⊥AO M的面积为1，则反比例函数的解析式为______________________.17.如图，一次函数y= kx＋b与反比例函数y=mx的图象交于A（2，1），B（-1，n）两点.连接OA，OB，则三角形OAB 的面积为____________.三、解答题（一）（每题6分，共18 分）18.某打印店要完成一批电脑打字任务，如果每天完成100 页，需8天完成任务.（1）每天完成的页数y与所需天数x之间是什么函数关系?（2）要求4天完成，每天应完成几页?19.已知反比例函数y =kx（k为常数，k≠0）的图象经过A（2，3）.（1）求这个函数的解析式；（2）判断点B（-1，6）是否在这个函数的图象上，并说明理由.20.如图，反比例函数y =kx（k为常数，且k≠0）经过点A（1，3）.（1）求反比例函数的解析式；（2）在x轴正半轴上有一点B，若⊥AOB 的面积为6，求直线AB的解析式.四、解答题（二）（每题8 分，共24 分）21.码头工人以每天30 吨的速度往一艘轮船上装载货物，装载完毕恰好用了8 天时间.（1）轮船到达目的地后开始卸货，卸货速度ν（单位：吨/天）与卸货时间t（单位：天）之间有怎样的函数关系?（2）由于遇到紧急情况，船上的货物必须在不超过5天内卸载完毕，那么平均每天至少要卸多少吨货物?22.如图，已知A （-4，2），B （n ，-4）是一次函数y =kx +b 的图象与反比例函数y =mx的图象的两个交点. （1）求此反比例函数和一次函数的解析式；（2）根据图象写出使一次函数的值小于反比例函数的值的x 的取值范围.23．如图，已知在平面直角坐标系x O y 中，0是坐标原点，点A （2，5）在反比例函数y =kx的图象上，过点A 的直线y =x +b 交x 轴于点 B. （1）求k 和b 的值； （2）求⊥OAB 的面积；（3）当-3≤x ≤-1时，反比例函数值的范围为_________________.五、解答题（三）（每题10 分，共 20 分） 24.一次函数y =k 1x ＋b 与反比例函数y =2k x（x <0）的图象相交于A ，B 两点，且与坐标轴的交点为（-6，0），（0，6），点B 的横坐标为-4.（1）试确定反比例函数的解析式； （2）求⊥AOB 的面积； （3）直接写出不等式后k 1x +b>2k x的解.25.对教室进行"薰药消毒".已知药物在燃烧释放过程中，室内空气中每立方米含药量y （毫克）与燃烧时间x （分钟）之间的关系如图所示（即图中线段 OA 和双曲线在 A 点及其右侧的部分），根据图象所示信息，解答下列问题： （1）写出从药物释放开始，y 与x 之间的函数关系式及自变量的取值范围； （2）据测定，当空气中每立方米的含药量低于 2 毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室?参考答案一、1.B 2.D 3.C 4.D 5.B 6.D 7.D 8.B 9.A 10. A 二、11.二、四 增大 12. -2 13. > 一 14.500y x= 15. <16. y =-2x 17. 32三、18.解：(1)800y x=，反比例函数 (2)当x =4，800y x== 200(页) 19.解：(1) 6y x= (2)不在，理由如下： 当x = -1，61y =-= -6≠6 ⊥点B(-1，6)不在y =6x 的图象上。

第六章 反比例函数6．1 反比例函数基础题知识点1 反比例函数的概念1．下列函数是反比例函数的是( )A ．y ＝xB ．y ＝kx －1C ．y ＝－8xD ．y ＝8x22．反比例函数y ＝－25x 中，k 的值是( )A ．2B ．－2C ．－25D ．－523．若函数y ＝x 2m ＋1为反比例函数，则m 的值是( )A ．1B ．0 C.12D ．－14．在函数y ＝1x －1中，自变量x 的取值范围是( )A ．x ≠1B ．x ≠0C ．x<1D ．一切实数5．若y ＝m （m －3）x是反比例函数，则满足的条件是( )A ．m ≠0B ．m ＝3C ．m ＝0或m ＝3D ．m ≠0且m≠3知识点2 判断反比例函数关系6．如果直角三角形的面积一定，那么下列关于这个直角三角形边的关系中，正确的是( ) A ．两条直角边成正比例 B ．两条直角边成反比例C ．一条直角边与斜边成正比例D ．一条直角边与斜边成反比例7．用电器的输出功率P 与通过的电流I 、用电器的电阻R 之间的关系是P ＝I 2R ，下面说法正确的是( ) A ．P 为定值，I 与R 成反比例B ．P 为定值，I 2与R 成反比例 C ．P 为定值，I 与R 成正比例D ．P 为定值，I 2与R 成正比例8．下列问题中，两个变量间的函数关系式是反比例函数的是( ) A ．小颖每分钟可以制作2朵花，x 分钟可以制作y 朵花B ．体积为10 cm 3的长方体，高为h cm ，底面积为S cm 2C ．用一根长50 cm 的铁丝弯成一个矩形，一边长为x cm ，面积为S cm 2D ．汽车油箱中共有油50升，设平均每天用油5升，x 天后油箱中剩下的油量为y 升知识点3 建立反比例函数模型9．小华以每分钟x 个字的速度书写，y 分钟写了300个字，则y 与x 的函数关系式为( ) A ．y ＝x 300 B ．y ＝300xC ．y ＝300－xD ．y ＝300－xx10．近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜镜片的焦距为0.25 m ，则y 与x 的函数关系式为( )A ．y ＝400xB ．y ＝14xC ．y ＝100xD ．y ＝1400x11．若y 与x 成反比例，且x ＝3时，y ＝7，则y 与x 的函数关系式为________．12．计划修建铁路1 200 km ，试写出铺轨天数y(d)与每天铺轨量x(km/d)之间的函数关系式，并判断该函数是否是反比例函数．中档题13．已知y 与x 成正比例，z 与y 成反比例，那么z 与x 之间的关系是( ) A ．成正比例 B ．成反比例C ．有可能成正比例，也有可能成反比例D ．无法确定14．已知函数y ＝(n ＋2)xn 2＋n －3(n 是常数)，当n ＝________时，此函数是反比例函数． 15．列出下列问题中的函数关系式，并判断它们是否为反比例函数．(1)某农场的粮食总产量为1 500 t ，则该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式；(2)在加油站，加油机显示器上显示的某一种油的单价为每升4.75元，总价从0元开始随着加油量的变化而变化，则总价y(元)与加油量x(L)的函数关系式；(3)小明完成100 m 赛跑时，时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式．16．已知函数y 与x ＋1成反比例，且当x ＝－3时，y ＝2. (1)求y 与x 的函数关系式；(2)当x ＝3时，求y 的值．17．已知函数y＝(5m－3)x2－n＋(n＋m)．(1)当m，n为何值时，为一次函数？(2)当m，n为何值时，为正比例函数？(3)当m，n为何值时，为反比例函数？综合题18．(丽水中考)如图，科技小组准备用材料围建一个面积为60 m2的矩形科技园ABCD，其中一边AB靠墙，墙长为12 m．设AD的长为x m，DC的长为y m.(1)求y与x之间的函数关系式；(2)若围成矩形科技园ABCD的三边材料总长不超过26 m，材料AD和DC的长都是整米数，求出满足条件的所有围建方案．参考答案1．C 2.C 3.D 4.A 5.D 6.B 7.B 8.B 9.B 10.C 11.y ＝21x 12.∵铺轨天数＝铁路长÷每天铺轨量，∴y＝1 200x .∴y 是x 的反比例函数． 13.B 14.1 15.(1)y ＝1 500x，是反比例函数．(2)y ＝4.75x ，不是反比例函数．(3)t ＝100v ，是反比例函数． 16.(1)由题意，设y 与x ＋1的函数关系式为y ＝k x ＋1(k≠0)，将x ＝－3，y ＝2代入，得k －3＋1＝2.解得k ＝－4.所以y 与x 的函数关系式为y ＝－4x ＋1.(2)将x ＝3代入，得y ＝－43＋1＝－1. 17.(1)由题意，得2－n ＝1，且5m －3≠0，解得n ＝1且m≠35.(2)由题意，得2－n ＝1，5m －3≠0，且m ＋n ＝0，解得n ＝1，m ＝－1.(3)由题意，得2－n ＝－1，5m －3≠0，且m ＋n ＝0，解得n ＝3，m ＝－3. 18.(1)由题意，得S矩形ABCD＝AD·DC＝xy ，故y ＝60x .(2)由y ＝60x ，且x ，y 都是正整数，可得x 可取1，2，3，4，5，6，10，12，15，20，30，60.∵2x ＋y≤26，0＜y≤12，∴符合条件的围建方案为AD ＝5 m ，DC ＝12 m 或AD ＝6 m ，DC ＝10 m 或AD ＝10 m ，DC＝6 m.第2课时 反比例函数的性质基础题知识点1 反比例函数图象的增减性1．反比例函数y ＝1x(x ＞0)的图象如图所示，随着x 值的增大，y 值( )A ．减小B ．增大C ．不变D ．先减小，后不变2．(随州中考)关于反比例函数y ＝2x 的图象，下列说法正确的是( )A ．图象经过点(1，1)B ．两个分支分布在第二、四象限C ．两个分支关于x 轴成轴对称D ．当x ＜0时，y 随x 的增大而减小3．(宁夏中考)已知两点P 1(x 1，y 1)，P 2(x 2，y 2)在函数y ＝5x 的图象上，当x 1＞x 2＞0时，下列结论正确的是( )A ．0＜y 1＜y 2B ．0＜y 2＜y 1C ．y 1＜y 2＜0D ．y 2＜y 1＜04．(永州中考)已知点A(1，y 1)，B(－2，y 2)在反比例函数y ＝kx (k ＞0)的图象上，则y 1_______y 2.(填“＞”“＜”或“＝”)5．(上海中考)已知反比例函数y ＝kx (k 是常数，k ≠0)，在其图象所在的每一个象限内，y 的值随着x 的值的增大而增大，那么这个反比例函数的表达式是________________(只需写一个)．6．已知下列反比例函数：①y＝1x ；②y＝－1x ；③y＝12x ；④y ＝1－2x ；⑤y＝k 2＋1x ，在其图象所在的每个象限内，y 随x 的值的增大而增大的函数有______________(填序号)． 7．反比例函数y ＝(2m －1)xm 2－2，当x ＞0时，y 随x 的增大而增大，求m 的值．知识点2 反比例函数中k 的几何意义8．(宜昌中考)如图，点B 在反比例函数y ＝2x (x>0)的图象上，横坐标为1，过B 分别向x 轴，y 轴作垂线，垂足分别为A ，C ，则矩形OABC 的面积为( ) A ．1 B ．2 C ．3 D ．49．如图，正方形ABOC 的边长为2，反比例函数y ＝kx 的图象经过点A ，则k 的值是( )A ．2B ．－2C ．4D ．－4中档题10．已知反比例函数y ＝－5x ，下列结论中不正确的是( )A ．图象必经过点(1，－5)B ．y 随x 的增大而增大C ．图象在第二、四象限内D ．若x ＞1，则－5＜y ＜011．(贵州中考)如果点A(－2，y 1)，B(－1，y 2)，C(2，y 3)都在反比例函数y ＝kx (k>0)的图象上，那么y 1，y 2，y 3的大小关系是( )A ．y 1＜y 3＜y 2B ．y 2＜y 1＜y 3C ．y 1＜y 2＜y 3D ．y 3＜y 2＜y 112．(黔东南中考)如图，正比例函数y ＝x 与反比例函数y ＝1x 的图象相交于A ，B 两点，BC ⊥x 轴于点C ，则△ABC的面积为( )A ．1B ．2 C.32 D.5213．已知反比例函数y ＝2k ＋1x (k 为常数，k ≠－12)．(1)若在这个函数图象的每一分支上，y 随x 的增大而增大，求k 的取值范围；14．(柳州中考)如图，函数y ＝kx 的图象过点A(1，2)．(1)求该函数的表达式；(2)过点A 分别向x 轴和y 轴作垂线，垂足为B 和C ，求四边形ABOC 的面积；(3)求证：过此函数图象上任意一点分别向x 轴和y 轴作垂线，这两条垂线与两坐标轴所围成矩形的面积为定值．综合题15．(苏州中考)如图，已知函数y ＝kx (x ＞0)的图象经过点A ，B ，点A 的坐标为(1，2)，过点A 作AC∥y 轴，AC ＝1(点C 位于点A 的下方)，过点C 作CD∥x 轴，与函数的图象交于点D ，过点B 作BE⊥CD，垂足E 在线段CD 上，连接OC ，OD.(1)求△OCD 的面积；(2)当BE ＝12AC 时，求CE 的长．参考答案1．A 2.D 3.A 4.＞ 5.y ＝－1x (不唯一，只要k ＜0即可) 6.②④ 7.根据题意，得m 2－2＝－1，解得m ＝±1.∵当x ＞0时，y 随x 的值的增大而增大，∴2m －1＜0.解得m ＜12.∴m ＝－1. 8.B 9.D 10.B 11.B 12.A 13.(1)∵在这个函数图象的每一分支上，y 随x 的增大而增大，∴2k ＋1<0.解得k<－12.(2)点M(3，－3)在这个函数的图象上．理由：∵当k ＝－5时，2k ＋1＝－9，∴反比例函数的表达式为y ＝－9x .当x ＝3时，y ＝－3，∴点M(3，－3)在这个函数的图象上． 14.(1)∵函数y ＝k x 的图象过点A(1，2)，∴将点A 的坐标代入反比例函数表达式，得2＝k1.解得k ＝2.∴反比例函数的表达式为y ＝2x .(2)∵点A 是反比例函数上一点，∴矩形ABOC 的面积S ＝AC·AB＝|xy|＝|k|＝2.(3)证明：设图象上任一点的坐标为(x ，y)．∴过这点分别向x 轴和y 轴作垂线，矩形面积为|xy|＝|k|＝2.∴矩形的面积为定值． 15.(1)∵y＝kx (x ＞0)的图象经过点A(1，2)，∴k ＝2.∵AC∥y 轴，AC ＝1，∴点C 的坐标为(1，1)．∵CD ∥x 轴，点D 在函数图象上，∴点D 的坐标为(2，1)．∴S △OCD ＝12×1×1＝12.(2)∵BE＝12AC ，∴BE ＝12.∵BE ⊥CD ，∴点B 的横坐标是43，纵坐标是32.∴CE ＝43－1＝13.6.3 反比例函数的应用基础题知识点1 反比例函数的实际应用1．(临沂中考)已知甲、乙两地相距20千米，汽车从甲地匀速行驶到乙地，则汽车行驶时间t(单位：小时)关于行驶速度v(单位：千米/小时)的函数关系式是( ) A ．t ＝20v B ．t ＝20v C ．t ＝v 20 D ．t ＝10v2．(河北中考)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系，当x ＝2时，y ＝20，则y 与x 的函数图象大致是( )3．某蓄水池的排水管每时排水8 m 3，6 h 可将满池水全部排空．如果增加排水管，使每时的排水量达到Q(m 3)，那么将满池水排空所需的时间为t(h)．写出t 与Q 之间的关系：________. 知识点2 反比例函数跨学科应用4．(台州中考)在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也随之改变．密度ρ(单位：kg/m 3)与体积V(单位：m 3)满足函数关系式ρ＝k V (k 为常数，k ≠0)，其图象如图所示，则k 的值为( )A ．9B ．－9C ．4D ．－45．水平地面上重1 500 N 的物体，与地面的接触面积为x m 2，那么该物体对地面的压强y(单位：N/m 2)与地面的接触面积x(m 2)之间的函数关系可以表示为________．6．蓄电池的电压为定值．使用此电源时，电流I(A)是电阻R(Ω)的反比例函数，其图象如图所示． (1)求这个反比例函数的表达式；(2)当R ＝10 Ω时，电流能是4 A 吗？为什么？知识点3 反比例函数与一次函数的综合应用7．(广安中考)如图，一次函数y 1＝k 1x ＋b(k 1，b 为常数，且k 1≠0)的图象与反比例函数y 2＝k 2x (k 2为常数，且k 2≠0)的图象都经过点A(2，3)．则当x ＞2时，y 1与y 2的大小关系为( ) A ．y 1＞y 2 B ．y 1＝y 2C ．y 1＜y 2D ．以上说法都不对8．(枣庄中考)已知正比例函数y ＝－2x 与反比例函数y ＝kx 的图象的一个交点坐标为(－1，2)，则另一个交点的坐标为________．9．(黔南中考)如图，正比例函数y 1＝k 1x 与反比例函数y 2＝k 2x 的图象交于A ，B 两点，根据图象可直接写出当y 1＞y 2时，x 的取值范围是____________．中档题10．某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压p(kPa)是气球体积V 的反比例函数，其图象如图所示，当气球内的气压大于120 kPa 时，气球将爆炸，为了安全，气球的体积应该( ) A ．不大于54 m 3 B ．小于54 m 3C ．不小于45 m 3D ．小于45m 311．随着私家车的增加，城市的交通也越来越拥挤，通常情况下，某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示，当x≥10时，y 与x 成反比例函数关系，当车速度低于20千米/时，交通就会拥堵，为避免出现交通拥堵，高架桥上每百米拥有车的数量x 应该满足的范围是________．12．(益阳中考)我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种．图是某天恒温系统从开启到关闭及关闭后，大棚内温度y(℃)随时间x(小时)变化的函数图象，其中BC 段是双曲线y ＝kx 的一部分．请根据图中信息解答下列问题：(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时？(2)求k 的值；(3)当x ＝16时，大棚内的温度约为多少度？综合题13．(玉林中考)工匠制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料烧到800 ℃，然后停止煅烧进行锻造操作，经过8 min 时，材料温度降为600 ℃.煅烧时，温度y(℃)与时间x(min)成一次函数关系；锻造时，温度y(℃)与时间x(min)成反比例函数关系(如图)．已知该材料初始温度是32 ℃. (1)分别求出材料煅烧和锻造时y 与x 的函数关系式，并且写出自变量x 的取值范围；(2)根据工艺要求，当材料温度低于480 ℃时，须停止操作．那么锻造的操作时间有多长？参考答案1．B 2.C 3.t ＝48Q 4.A 5.y ＝1 500x 6.(1)设I ＝k R (k≠0)，把(4，9)代入，得k ＝4×9＝36，∴I ＝36R .(2)当R＝10 Ω时，I ＝3.6 A ≠4 A ，∴电流不可能是4 A ． 7.A 8.(1，－2) 9.－1＜x ＜0或x ＞1 10.C 11.0＜x≤40 12.(1)恒温系统在这天保持大棚温度18 ℃的时间为10小时．(2)∵点B(12，18)在双曲线y ＝k x 上，∴18＝k12.解得k ＝216.(3)当x ＝16时，y ＝21616＝13.5，所以当x ＝16时，大棚内的温度约为13.5 ℃. 13.(1)停止加热时，设y＝k x (k≠0)，由题意得600＝k 8.解得k ＝4 800.当y ＝800时，4 800x ＝800，解得x ＝6.∴点B 的坐标为(6，800)．材料加热时，设y ＝ax ＋32(a≠0)，由题意得800＝6a ＋32，解得a ＝128.∴材料加热时，y 与x 的函数关系式为y ＝128x ＋32(0≤x≤6)；停止加热进行操作时，y 与x 的函数关系式为y ＝4 800x (6＜x≤150)．(2)把y ＝480代入y ＝4 800x ，得x ＝10，故锻造的操作时间为10－6＝4(分钟)．专题训练 反比例函数中k 的几何意义1．如图，在平面直角坐标系中，点A 是双曲线y ＝3x (x ＞0)上的一个动点，过点A 作x 轴的垂线，交x 轴于点B ，点A 运动过程中△AOB 的面积将会( ) A ．逐渐增大 B ．逐渐减小 C ．先增大后减小 D ．不变2．如图，过反比例函数y ＝2x (x ＞0)图象上任意两点A ，B 分别作x 轴的垂线，垂足分别为C ，D ，连接OA ，OB ，设AC 与OB 的交点为E ，△AOE 与梯形ECDB 的面积分别为S 1，S 2，比较它们的大小，可得( ) A ．S 1＞S 2 B ．S 1＜S 2 C ．S 1＝S 2D ．S 1、S 2的大小关系不能确定3．(鄂州中考)点A 为双曲线y ＝kx (k ≠0)上一点，B 为x 轴上一点，且△AOB 为等边三角形，△AOB 的边长为2，则k 的值为( )A ．2 3B ．±2 3 C. 3 D ．± 34．设P 是函数y ＝2x 在第一象限的图象上的任意一点，点P 关于原点的对称点为点P ′，过点P 作PA 平行于y 轴，过点P ′作P ′A 平行于x 轴，PA 与P ′A 交于A 点，则△PAP ′的面积( ) A ．随P 点的变化而变化 B ．等于1 C ．等于2 D ．等于45．如图，点A 是反比例函数y ＝kx 图象上的一点，过点A 作AB ⊥x 轴，垂足为点B ，点C 为y 轴上的一点，连接AC ，BC.若△ABC 的面积为3，则k 的值是( ) A ．3 B ．－3 C ．6 D ．－66．(黔西南中考)如图，点A 是反比例函数y ＝kx 图象上的一个动点，过点A 作AB ⊥x 轴，AC ⊥y 轴，垂足点分别为B 、C ，矩形ABOC 的面积为4，则k ＝________．7．(陕西中考)如图，在平面直角坐标系中，过点M(－3，2)分别作x 轴，y 轴的垂线与反比例函数y ＝4x 的图象交于A ，B 两点，则四边形MAOB 的面积为________．8．(临沂中考)如图，反比例函数y ＝4x 的图象经过直角△OAB 的顶点A ，D 为斜边OA 的中点，则过点D 的反比例函数的表达式为________．9．如图，矩形ABCD 的边AB 与y 轴平行，顶点A 的坐标为(1，2)，点B 与点D 在反比例函数y ＝6x (x ＞0)的图象上，则点C 的坐标为________．10．(铁岭中考)如图，点P 是正比例函数y ＝x 与反比例函数y ＝kx 在第一象限内的交点，PA ⊥OP 交x 轴于点A ，△POA的面积为2，则k 的值是________．11．(资阳中考)如图，在平面直角坐标系中，点M 为x 轴正半轴上一点，过点M 的直线l ∥y 轴，且直线l 分别与反比例函数y ＝8x (x ＞0)和y ＝kx(x ＞0)的图象交于P 、Q 两点，若S △POQ ＝14，则k 的值为________．12．如图，已知反比例函数y ＝kx (k ＜0)的图象经过点A(－3，m)，过点A 作AB ⊥x 轴于点B ，且△AOB 的面积为 3.求k 和m 的值．13．反比例函数y ＝1x 和y ＝k x (k ≠0)在第一象限内的图象如图所示，点P 在y ＝kx 的图象上，PC ⊥x 轴，垂足为C ，交y ＝1x 的图象于点A ，PD ⊥y 轴，垂足为D ，交y ＝1x 的图象于点B.已知点A(m ，1)为线段PC 的中点． (1)求m 和k 的值；(2)求四边形OAPB 的面积．参考答案1．D 2.C 3.D 4.D 5.D 6.－4 7.10 8.y ＝1x 9.(3，6) 10.2 11.－20 12.设点A 的坐标为(x ，y)．∵△AOB 的面积为3，∴12|x|·|y|＝12|k|＝ 3.解得|k|＝2 3.又∵k ＜0，∴k ＝－2 3.∴反比例函数表达式为y ＝－23x .∵反比例函数图象经过点A(－3，m)，∴m ＝－23－3.解得m ＝2.综上可知：k ＝－23，m ＝2. 13.(1)把A(m ，1)代入y ＝1x ，得m ＝1，∴A 点坐标为(1，1)．∵点A(1，1)为线段PC 的中点，∴点P 坐标为(1，2)．把(1，2)代入y ＝k x ，得k ＝1×2＝2.(2)∵点P 坐标为(1，2)，∴四边形OCPD 的面积为1×2＝2.又∵△ODB 的面积为12，△OAC 的面积为12，∴四边形O APB 的面积为2－12－12＝1.专题训练 反比例函数与一次函数综合1．(益阳中考)正比例函数y ＝6x 的图象与反比例函数y ＝6x 的图象的交点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第一、三象限2．若在同一坐标系中，直线y ＝k 1x(k 1≠0)与双曲线y ＝k 2x 无交点，则有( )A ．k 1＋k 2＞0B ．k 1＋k 2＜0C ．k 1k 2＞0D ．k 1k 2＜03．(怀化中考)已知一次函数y ＝kx ＋b 的图象如图，那么正比例函数y ＝kx 和反比例函数y ＝kx 在同一坐标系中的图象大致是( )4．(菏泽中考)如图，在平面直角坐标系xOy 中，已知一次函数y ＝kx ＋b 的图象经过点A(1，0)，与反比例函数y ＝mx (x>0)的图象相交于点B(2，1)． (1)求m 的值和一次函数的表达式；(2)结合图象直接写出：当x>0时，不等式kx ＋b>mx 的解集．5．(宜昌中考)下表中，y 是x 的一次函数．x －2 1 2 5(2)已知该函数图象上一点M(1，－3)也在反比例函数y ＝mx 图象上，求这两个函数图象的另一交点N 的坐标．6．(成都中考)如图，一次函数y ＝kx ＋5(k 为常数，且k≠0)的图象与反比例函数y ＝－8x 的函数交于A(－2，b)，B 两点．(1)求一次函数的表达式；(2)若将直线AB 向下平移m(m ＞0)个单位长度后与反比例函数的图象有且只有一个公共点，求m 的值．7．(自贡中考)如图，一次函数y ＝kx ＋b 与反比例函数y ＝6x (x ＞0)的图象交于A(m ，6)，B(3，n)两点．(1)求一次函数的表达式；(2)根据图象直接写出kx ＋b －6x ＜0的x 的取值范围；参考答案1．D 2.D 3.B 4.(1)反比例函数y ＝mx (x>0)的图象经过点B(2，1)，则m ＝1×2＝2.∵一次函数y ＝kx ＋b 的图象经过点A(1，0)，B(2，1)两点，∴一次函数的表达式为y ＝x －1.(2)x>2. 5.(1)4 －6 设该一次函数为y ＝kx ＋b(k≠0)．∵当x ＝－2时，y ＝6，当x ＝1时，y ＝－3，∴⎩⎪⎨⎪⎧－2k ＋b ＝6，k ＋b ＝－3.解得⎩⎪⎨⎪⎧k ＝－3，b ＝0.∴一次函数的表达式为y ＝－3x.当x ＝2时，y ＝－6；当y ＝－12时，x ＝4.(2)∵点M(1，－3)在反比例函数y ＝m x (m≠0)上，∴－3＝m1.∴m ＝－3.∴反比例函数表达式为y ＝－3x .∵⎩⎪⎨⎪⎧y ＝－3x ，y ＝－3x .解得⎩⎪⎨⎪⎧x ＝1，y ＝－3或⎩⎪⎨⎪⎧x ＝－1，y ＝3.∴另一交点坐标为(－1，3)． 6.(1)把A(－2，b)代入y ＝－8x ，得b ＝4.∴A 点坐标为(－2，4)．把A(－2，4)代入y ＝kx ＋5，得－2k ＋5＝4.解得k ＝12.∴一次函数表达式为y ＝12x ＋5.(2)将直线AB 向下平移m(m ＞0)个单位长度得直线表达式为y ＝12x＋5－m.根据题意方程组⎩⎪⎨⎪⎧y ＝－8x ，y ＝12x ＋5－m只有一组解，消去y 得－8x ＝12x ＋5－m ，整理得12x 2－(m －5)x ＋8＝0.Δ＝(m－5)2－4×12×8＝0.解得m 1＝9，m 2＝1，即m 的值为1或9. 7.(1)∵A(m，6)，B(3，n)两点在反比例函数y ＝6x(x＞0)图象上．∴m＝1，n ＝2，即A(1，6)，B(3，2)．又∵A(1，6)，B(3，2)在一次函数y ＝kx ＋b 图象上，∴⎩⎪⎨⎪⎧6＝k ＋b ，2＝3k ＋b.解得⎩⎪⎨⎪⎧k ＝－2，b ＝8.∴一次函数表达式为y ＝－2x ＋8.(2)根据图象可知kx ＋b －6x <0的x 的取值范围是0＜x ＜1或x ＞3.(3)分别过A ，B 点作AE⊥x 轴，BC ⊥x 轴，垂足分别为E ，C 点，直线AB 交x 轴于D 点．令y ＝－2x ＋8＝0，得x ＝4，即D(4，0)．∵A(1，6)，B(3，2)，∴AE ＝6，BC ＝2.∴S △AOB ＝S △AOD －S △DOB ＝12×4×6－12×4×2＝8.单元测试 反比例函数(满分：150分，考试用时120分钟)一、选择题(本大题共15个小题，每小题3分，共45分) 1.下列函数中，变量y 是x 的反比例函数的是( ) A ．y ＝1x 2 B ．y ＝x －1C ．y ＝2x ＋3D ．y ＝1x－12．已知y ＝8x n －2，当n ＝________时，y 是x 的反比例函数( )A ．1B ．－1C ．1或－1D ．0 3．下列各点中，在反比例函数y ＝3x 图象上的是( )A ．(3，1)B ．(－3，1)C ．(3，13)D ．(13，3)4．若反比例函数y ＝k －1x 的图象位于第二、四象限，则k 的取值可以是( )A ．0B ．1C ．2D ．以上都不是5．对于反比例函数y ＝2x，下列说法正确的是( )A ．点(－2，1)在它的图象上B ．它的图象经过原点C ．它的图象在第一、三象限D ．当x>0时，y 随x 的增大而增大6．已知三角形的面积一定，则它底边a 上的高h 与底边a 之间的函数关系的图象大致是( )7．下面关于反比例函数y ＝－3x 与y ＝3x的说法，不正确的是( )A ．其中一个函数的图象可由另一个函数的图象沿x 轴或y 轴翻折“复印”得到B ．它们的图象都是轴对称图形C ．它们的图象都是中心对称图形D ．当x>0时，两个函数的函数值都随自变量的增大而增大 8．反比例函数y ＝kx 的图象如图所示，则k 的值可能是( )A ．－1 B.12C ．1D ．29．已知反比例函数y ＝10x ，当1＜x ＜2时，y 的取值范围是( )A ．0＜y ＜5B ．1＜y ＜2C ．5＜y ＜10D ．y ＞1010．如图，M 为反比例函数y ＝kx 的图象上的一点，MA 垂直于y 轴，垂足为点A ，△MAO 的面积为2，则k 的值为( )A ．－4B ．4C ．－2D ．211．已知直线y ＝mx 与双曲线y ＝kx 的一个交点坐标为(3，4)，则它们的另一个交点坐标为( )A ．(－3，4)B ．(－4，－3)C ．(－3，－4)D ．(4，3) 12．若y 与1x 成反比例，x 与1z 成正比例，则y 是z 的( )A ．正比例函数B ．反比例函数C ．一次函数D ．以上均不对13．若A(x 1，y 1)，B(x 2，y 2)，C(x 3，y 3)是反比例函数y ＝3x 图象上的点，且x 1＜x 2＜0＜x 3，则y 1、y 2、y 3的大小关系正确的是( )A ．y 3＞y 1＞y 2B ．y 1＞y 2＞y 3C ．y 2＞y 1＞y 3D ．y 3＞y 2＞y 114．在同一直角坐标系中，函数y ＝kx ＋1与y ＝－kx(k ≠0)的图象大致是( )15．如图，A ，B 两点在双曲线y ＝4x上，分别经过A ，B 两点向轴作垂线段，已知S 阴影＝1，则S 1＋S 2＝( )A ．3B ．4C ．5D ．6二、填空题(本大题共5小题，每小题5分，共25分)16．若反比例函数y ＝kx的图象经过点(－1，2)，则k 的值是________．17．小玲将一篇8 000字的社会调查报告录入电脑，那么完成录入的时间t(秒)与录入文字的速度v(字/秒)的函数关系式是________．18．已知y 是x 的反比例函数，当x>0时，y 随x 的增大而减小．请写出一个满足以上条件的函数表达式：________________________．19．如图，已知函数y ＝kx 的图象经过点A(2，2)，结合图象，请直接写出函数值y≥－2时，自变量x 的取值范围是____________．20．如图，反比例函数y ＝kx (k ＞0)的图象与矩形ABCO 的两边相交于E ，F 两点，若E 是AB 的中点，S △BEF ＝2，则k的值为________．三、解答题(本大题共7个小题，各题分值见题号后，共80分)21．(8分)已知反比例函数的图象与直线y ＝2x 相交于点A(1，a)，求这个反比例函数的表达式．22．(8分)反比例函数y ＝kx ，当x 的值由4增加到6时，y 的值减少3，求这个反比例函数的表达式．23．(10分)已知反比例函数y ＝k －1x(k 为常数，k ≠1)．(1)若在这个函数图象的每一分支上，y 随x 的增大而减小，求k 的取值范围；(2)若k ＝13，试判断点C(2，5)是否在这个函数的图象上，并说明理由．24．(12分)如图，在平面直角坐标系中，点O 为原点，反比例函数y ＝kx 的图象经过点(1，4)，菱形OABC 的顶点A在函数的图象上，对角线OB 在x 轴上．(1)求反比例函数的表达式； (2)直接写出菱形OABC 的面积．25．(12分)如图，已知反比例函数y ＝kx (k ＞0)的图象经过点A(1，m)，过点A 作AB⊥y 轴于点B ，且△AOB 的面积为1.(1)求m ，k 的值；(2)若一次函数y ＝nx ＋2(n≠0)的图象与反比例函数y ＝kx 的图象有两个不同的公共点，求实数n 的取值范围．26．(14分)一辆汽车匀速通过某段公路，所需时间t(h)与行驶速度v(km/h)满足函数关系：t ＝kv ，其图象为如图所示的一段曲线，且端点为A(40，1)和B(m ，0.5)．(1)求k 和m 的值；(2)若行驶速度不得超过60 km/h ，则汽车通过该路段最少需要多少时间？27．(16分)已知：如图，反比例函数y ＝kx 的图象与一次函数y ＝x ＋b 的图象交于点A(1，4)、点B(－4，n)．(1)求一次函数和反比例函数的表达式；(2)求△OAB 的面积；(3)直接写出一次函数值大于反比例函数值的自变量x 的取值范围．参考答案1．B 2.A 3.A 4.A 5.C 6.D 7.D 8.B 9.C 10.B 11.C 12.B 13.A 14.D 15.D 16.－2 17.t ＝8 000v 18.答案不唯一，只要k>0即可，如：y ＝2x 19.x≤－2或x ＞0 20.8 21.设反比例函数表达式为y ＝kx .将点A(1，a)代入直线y ＝2x ，得a ＝2×1＝2.∴点A 的坐标为(1，2)，代入y ＝kx ，得k ＝2.∴反比例函数的表达式为y ＝2x . 22.当x ＝4时，y ＝k 4；当x ＝6时，y ＝k 6.∵当x 的值由4增加到6时，y 的值减少3，∴k 4－k6＝3.解得k＝36.∴这个反比例函数的表达式为y ＝36x . 23.(1)∵这个函数图象的每一分支上，y 随x 的增大而减小，∴k －1＞0.解得k ＞1.(2)点C(2，5)不在这个函数的图象上．理由：∵当k ＝13时，k －1＝12，∴反比例函数的表达式为y ＝12x .当x ＝2时，y ＝6≠5，∴点C(2，5)不在这个函数的图象上． 24.(1)∵反比例函数y ＝kx 的图象经过点(1，4)，∴4＝k 1.即k ＝4.∴反比例函数的表达式为y ＝4x .(2)8. 25.(1)由已知，得S △AOB ＝12×1×m ＝1，解得m ＝2.把A(1，2)代入反比例函数表达式，得k ＝2.(2)由(1)知反比例函数表达式是y ＝2x ，由题意知2x ＝nx ＋2有两个不同的解，方程去分母，得nx 2＋2x －2＝0，则Δ＝4＋8n ＞0，解得n ＞－12且n≠0. 26.(1)将(40，1)代入t ＝k v ，得1＝k 40，解得k ＝40.∴该函数的表达式为t ＝40v .当t ＝0.5时，0.5＝40m，解得m ＝80.所以k ＝40，m ＝80.(2)令v ＝60，得t ＝4060＝23.结合函数图象可知，汽车通过该路段最少需要23小时． 27.(1)把A 点(1，4)分别代入反比例函数y ＝k x ，一次函数y ＝x ＋b ，得k ＝1×4，1＋b ＝4，解得k ＝4，b ＝3.反比例函数的表达式是y ＝4x ，一次函数表达式是y ＝x ＋3.(2)设AB 与x 轴交于点C.当x ＝－4时，y ＝－1，∴B(－4，－1)．当y ＝0时，x ＋3＝0，x ＝－3，∴C(－3，0)．∴S △AOB ＝S △AOC ＋S △BOC ＝12×3×4＋12×3×1＝152.(3)∵B(－4，－1)，A(1，4)，∴根据图象可知：当x ＞1或－4＜x ＜0时，一次函数值大于反比例函数值．。

北师大版九年级数学上册第六章 反比例函数 单元测试题一、选择题（每小题3分，共24分）1．已知反比例函数的表达式为y ＝|a|－2x，则a 的取值范围是( )A ．a ≠2B ．a ≠－2C ．a ≠±2D ．a ＝±22．如果点(3，－4)在反比例函数y ＝kx的图象上，那么下列各点中，在此图象上的是( )A ．(3，4)B ．(－2，－6)C ．(－2，6)D ．(－3，－4)3．对于反比例函数y ＝－2x，下列说法不正确的是( )A ．图象分布在第二、四象限B ．当x>0时，y 随x 的增大而增大C ．图象经过点(1，－2)D ．若点A(x 1，y 1)，B(x 2，y 2)都在图象上，且x 1<x 2，则y 1<y 24．如图，在△AOB 中，AO ＝AB ，点A 在第一象限，点B 在x 轴上，△AOB 的面积为4，反比例函数y ＝kx (x ＞0)的图象经过点A ，则k 的值等于( )A ．1B.2C ．4D ．85．已知A ，B 两点分别在反比例函数y ＝3m x (m ≠0)和y ＝2m －5x (m ≠52)的图象上．若点A 与点B 关于x 轴对称，则m的值为( )A ．4B.2 C ．1D ．36．码头工人往一艘轮船上装载货物，装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y ＝kx的一支)．如果以5 t/min 的速度卸货，那么卸完货物需要的时间是( )min.A ．120B.125C ．130D ．1357.已知反比例函数y ＝kx(k≠0)，当－2≤x≤－1时，y 的最大值是3，则当x≥6时，y 有( )A ．最大值－12B ．最大值－1C ．最小值－12D ．最小值－18．在平面直角坐标系中，点A 在反比例函数y 1＝kx (x ＞0)的图象上，点A ′与点A 关于点O 对称，直线AA ′的表达式为y 2＝mx ，将直线AA ′绕点A ′顺时针旋转，与反比例函数图象交于点B ，直线A ′B 的表达式为y 3＝m2x ＋n.若△AA ′B 的面积为3，则k 的值为( )．A ．±25B.±4 C ．±3D ．±2二、填空题（每小题3分，共21分） 9．已知函数y ＝(m －2)xm2－10是反比例函数，且当x ＜0时，y 随x 的增大而减小，则m 的值是________．10．如图，一次函数y 1＝ax ＋b 和反比例函数y 2＝kx 的图象相交于A ，B 两点，则使y 1＞y 2成立的x 的取值范围是________．11．正比例函数y ＝x 的图象与反比例函数y ＝4x 的图象在第一象限内交于点B ，点C 是反比例函数y ＝4x 在第一象限图象上的一个动点．当△OBC 的面积为3时，点C 的横坐标是________．12．在平面直角坐标系中，对于点P(x ，y)和Q(x ，y ′)，给出如下定义：如果当x ≥0时，y ′＝y ；当x ＜0时，y ′＝－y ，那么称点Q 为点P 的“关联点”．例如：点(－5，6)的“关联点”为(－5，－6)．若点N(t ，t －1)在反比例函数y ＝2x的图象上，且点N 是点M 的“关联点”，则点M 的坐标为________．13．如图，将反比例函数y ＝kx (k ＞0)的图象向左平移2个单位长度后记为图象c ，c 与y 轴相交于点A ，点P 为x轴上一点，点A 关于点P 的对称点B 在图象c 上，以线段AB 为边作等边△ABC ，顶点C 恰好在反比例函数y ＝－kx (x＞0)的图象上，则k ＝________．14．如图，已知直线AB 交x 轴于点A ，分别与函数y ＝a x (x ＞0，a ＞0)和y ＝bx (x ＞0，b ＞a ＞0)的图象相交于点B ，C ，过点B 作BD ∥x 轴，交函数y ＝b x 的图象于点D ，过点C 作CE ∥x 轴，交函数y ＝ax 的图象于点E ，连接AD ，BE.若BC AB ＝12，S △ABD ＝2，则S △BCE ＝________．15．如图，将双曲线y ＝kx (k ＜0)在第四象限的一支沿直线y ＝－x 方向向上平移到点E 处，交该双曲线在第二象限的一支于A ，B 两点，连接AB 并延长交x 轴于点C.双曲线y ＝mx (m ＞0)与直线y ＝x 在第三象限的交点为D ，将双曲线y ＝mx 在第三象限的一支沿射线OE 方向平移，D 点刚好可以与C 点重合，此时该曲线与前两支曲线围成一条“鱼”(如图中阴影部分)．若C 点坐标为(－5，0)，AB ＝32，则mk 的值为________三、解答题（共55分）16．如图，已知反比例函数y ＝kx的图象经过点A(4，m)，AB ⊥x 轴，且△AOB 的面积为4.(1)k ＝_____，m ＝_____；(2)若点C(x ，y)也在反比例函数y ＝kx的图象上，当y ≤2(y ≠0)时，求自变量x 的取值范围．17．如图，在平面直角坐标系xOy 中，正比例函数y ＝kx 的图象与反比例函数y ＝mx的图象都经过点A(2，－2)．(1)分别求这两个函数的表达式；(2)将直线OA 向上平移3个单位长度后与y 轴交于点B ，与反比例函数图象在第四象限内的交点为C ，连接AB ，AC ，求点C 的坐标及△ABC 的面积．18．如图，在平面直角坐标系xOy 中，已知正比例函数y ＝12x 的图象与反比例函数y ＝kx 的图象交于A(a ，－2)，B两点．(1)求反比例函数的表达式和点B 的坐标；(2)P 是第一象限内反比例函数图象上一点，过点P 作y 轴的平行线，交直线AB 于点C ，连接PO.若△POC 的面积为3，求点P 的坐标．19．如图，已知一次函数y 1＝kx ＋b 与反比例函数y 2＝mx (x ＞0)的图象分别交于点A(2，4)和点B(4，n)，与坐标轴分别交于点C 和点D.(1)求反比例函数和一次函数的表达式； (2)求y 1＜y 2时，自变量x 的取值范围；(3)若点P 是x 轴上一动点，当△ABP 为直角三角形时，求点P 的坐标．20．如图，菱形OABC 的一边OA 在x 轴负半轴上，O 是坐标原点，点A(－13，0)，对角线AC 与OB 相交于点D ，且AC ·OB ＝130.若反比例函数y ＝kx(x ＜0)的图象经过点D ，并与BC 的延长线交于点E.(1)求双曲线y ＝kx 的表达式；(2)求S △AOB ∶S △OCE 的值．21．如图，在平面直角坐标系中，直线l 1：y ＝－12x 与反比例函数y ＝kx 的图象交于A ，B 两点(点A 在点B 左侧)，已知A 点的纵坐标是2.(1)求反比例函数的表达式；(2)根据图象直接写出－12x ＜kx的解集；(3)将直线l 1：y ＝－12x 沿y 向上平移后的直线l 2与反比例函数y ＝kx 在第二象限内交于点C ，如果△ABC 的面积为30，求平移后的直线l 2与y 轴的交点坐标．22．小明根据学习函数的经验，对函数y ＝x ＋1x的图象与性质进行了探究．下面是小明的探究过程，请补充完整：(1)函数y ＝x ＋1x的自变量x 的取值范围是_____；(2)下表列出了y 与x 的几组对应值，请写出m ，n 的值：m ＝_____，n ＝_____；(3)如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；(4)结合函数图象，请完成： ①当y ＝－174时，x ＝_____；②写出该函数的一条性质_____；③若方程x ＋x1＝t 有两个不相等的实数根，则t 的取值范围是_____．23．如图，一次函数y ＝kx ＋b 的图象交反比例函数y ＝ax (x ＞0)的图象于A(4，－8)，B(m ，－2)两点，交x 轴于点C ，P 是x 轴上一个动点．(1)求反比例函数与一次函数的表达式；(2)根据图象回答：当x 为何值时，一次函数的值大于反比例函数的值？(3)若△BCP 与△OAC 相似，请直接写出点P 的坐标．参考答案1、C2、C3、D4、C5、C6、A7、C8、D9、3 10、x ＜－2或0＜x ＜4 11、1或4 12、(2，1)或(－1，2) 13、2 3 14、2315、－2516、(1)k ＝8，m ＝2 （2）解：当y ≤2(y ≠0)时，x ＜0或x ≥4. 17、解：(1)将点A(2，－2)代入y ＝kx ，得－2＝2k ， 解得k ＝－1.∴正比例函数的表达式为y ＝－x. 将点A(2，－2)代入y ＝mx ，得－2＝m2，解得m ＝－4.∴反比例函数的表达式为y ＝－4x.(2)直线OA ：y ＝－x 向上平移3个单位长度后的表达式为y ＝－x ＋3， 则点B 的坐标为(0，3)．联立⎩⎨⎧y ＝－x ＋3，y ＝－4x ，解得{x ＝－1，y ＝4或{x ＝4，y ＝－1.∴第四象限内的交点C 的坐标为(4，－1)． 连接OC ，∵OA ∥BC ，∴S △ABC ＝S △OBC ＝12BO ·x C ＝12×3×4＝6.18、解：(1)把A(a ，－2)代入y ＝12x ，可得a ＝－4，∴A(－4，－2)．把A(－4，－2)代入y ＝kx ，得k ＝8，∴反比例函数的表达式为y ＝8x .∵点B 与点A 关于原点对称， ∴B(4，2)．(2)过点P 作PE ⊥x 轴于点E ，交AB 于点C ， 设P(m ，8m )，则C(m ，12m)．∵△POC 的面积为3，∴12m ·|12m －8m |＝3，解得m ＝27或2(负值舍去)． ∴P(27，477)或(2，4)．19、解：(1)把A(2，4)代入y 2＝mx ，得m ＝2×4＝8，∴反比例的表达式为y 2＝8x.把B(4，n)代入y 2＝8x ，得4n ＝8，解得n ＝2.∴B(4，2)．把A(2，4)和B(4，2)代入y 1＝kx ＋b ，得{2k ＋b ＝4，4k ＋b ＝2，解得{k ＝－1，b ＝6.∴一次函数的表达式为y 1＝－x ＋6. (2)当0＜x ＜2或x ＞4时，y 1＜y 2. (3)设P(t ，0)，∵A(2，4)，B(4，2)，∴PA 2＝(t －2)2＋42＝t 2－4t ＋20，PB 2＝(t －4)2＋22＝t 2－8t ＋20，AB 2＝(4－2)2＋(2－4)2＝8.①当∠PAB ＝90°时，PA 2＋AB 2＝PB 2，即t 2－4t ＋20＋8＝t 2－8t ＋20，解得t ＝－2，此时P 点坐标为(－2，0)； ②当∠PBA ＝90°时，PB 2＋AB 2＝PA 2，即t 2－8t ＋20＋8＝t 2－4t ＋20，解得t ＝2，此时P 点坐标为(2，0)； ③当∠APB ＝90°时，PA 2＋PB 2＝AB 2，即t 2－4t ＋20＋t 2－8t ＋20＝8，整理，得t 2－6t ＋16＝0，方程没有实数解．综上所述，P 点坐标为(－2，0)或(2，0)． 20、解：(1)过点C 作CG ⊥AO 于点G ， ∵AC ·OB ＝130， ∴S 菱形OABC ＝12AC ·OB ＝65.∴S △OAC ＝12S 菱形OABC ＝652，即12AO ·CG ＝652. ∵A(－13，0)，∴OA ＝13. ∴CG ＝5.在Rt △OGC 中，∵OC ＝OA ＝13， ∴OG ＝12.∴C(－12，－5)． ∵D 为AC 的中点， ∴D(－252，－52)．∵点D 在反比例函数的图象上， ∴k ＝－252×(－52)＝1254.∴反比例函数的表达式为y ＝1254x .(2)∵D 为OB 的中点，∴B(－25，－5)． 当y ＝－5时，x ＝－254，∴E(－254，－5)．∴CE ＝234.∴S △OCE ＝12CE ·CG ＝12×234×5＝1158，S △AOB ＝12S 菱形OABC ＝652.∴S △AOB ∶S △OCE ＝52∶23.21、解：(1)在y ＝－12x 中，当y ＝2时，－12x ＝2，解得x ＝－4，则A(－4，2)．把A(－4，2)代入y ＝k x，得 k ＝－4×2＝－8，∴反比例函数的表达式为y ＝－8x. (2)－4＜x ＜0或x ＞4.(3)设直线l 2交x 轴于点D ，连接AD ，BD.∵AB ∥CD ，∴S △ADB ＝S △ACB ＝30，即12×OD ×2＋12×OD ×2＝30，解得OD ＝15. ∴D(15，0)．设直线l 2的表达式为y ＝－12x ＋b ， 把D(15，0)代入，得－12×15＋b ＝0，解得b ＝152， ∴直线l 2的表达式为y ＝－12x ＋152. 当x ＝0时，y ＝－12x ＋152＝152， ∴平移后的直线l 2与y 轴的交点坐标为(0，152)．22、（1）x ≠0 （2）m ＝103，n ＝103（3）如图(4)结合函数图象，请完成：①当y ＝－174时，x ＝－4或－14； ②写出该函数的一条性质答案不唯一，如：图象在第一、三象限且关于原点对称；当－1≤x<0或0<x ≤1时，y 随x 增大而减小；当x<－1或x>1时，y 随x 的增大而增大；③若方程x ＋x1＝t 有两个不相等的实数根，则t 的取值范围是t>2或t<－2． 23、解：(1)∵反比例函数y ＝a x(x ＞0)的图象过点A(4，－8)， ∴a ＝4×(－8)＝－32.∴反比例函数的表达式为y ＝－32x. ∵双曲线y ＝－32x过点B(m ，－2)， ∴－2m ＝－32.∴m ＝16.∴B(16，－2)．∵直线y ＝kx ＋b 过点A ，B ，∴{4k ＋b ＝－8，16k ＋b ＝－2，解得⎩⎨⎧k ＝12，b ＝－10. ∴一次函数的表达式为y ＝12x －10. (2)观察图象可知，当0＜x ＜4或x ＞16时，一次函数的值大于反比例函数的值．(3)在直线y ＝12x －10中，令y ＝0，则x ＝20， ∴C(20，0)．∴OC ＝20，AC ＝（20－4）2＋82＝85，BC ＝（20－16）2＋22＝2 5.设P(n ，0)，则PC ＝20－n.当△BCP ∽△ACO 时，则PC OC ＝BC AC ，即20－n 20＝2585，∴n ＝15.此时P(15，0)；当△BCP ∽△OCA 时，则PC AC ＝BCOC ，即20－n 85＝2520，∴n ＝16.此时P(16，0)．综上，点P 的坐标为(15，0)或(16，0)．。

北师大版九年级数学上册《第六章反比例函数》单元测试卷及答案学校:___________班级：___________姓名：___________考号：___________考试时间：90分钟；总分：100第I 卷（选择题）一、单选题（每小题3分，共30分）1．下列y 关于x 的函数中，y 是x 的反比例函数的是（ ） A ．12y x=-B ．xy k =C ．11y x =+ D ．21y x =2．若反比例函数2k y x-=的图象经过点()3,2-，则下列各点在该函数图象上的是（ ） A ．()2,3 B ．()1,6- C ．()6,1 D ．()2,3--3．若反比例函数21k y x+=的图象经过第一、三象限，则k 的取值范围是（ ） A ．12k <-B ．12k >-C ．12k =-D ．0k >4．已知反比例函数6y x=，则下列描述不正确的是（ ） A ．图象位于第一、三象限 B ．图象必经过点3,42⎛⎫⎪⎝⎭C ．图象不可能与坐标轴相交D ．y 随x 的增大而减小5．在同一平面直角坐标系中，一次函数2y kx =-与反比例函数k y x=（其中0k ≠）的大致图象可能是（ ）A ．B ．C ．D ．6．如图，直线y ax b =+与x 轴相交于点A ()2,0，与函数k y x=的图象交于点B ，C ，点B 的横坐标是8，点C 的横坐标是6-，则不等式组0kax b x<+<的解集是（ ）A ．62x -<<B ．60x -<<C ．68x -<<D ．02x <<7．已知函数21k y x+=-的图象经过点()111P x y ，，()222P x y ，如果210x x <<，那么（ ） A ．210y y <<B ．120y y >>C ．210y y <<D ．120y y <<8．如图，A 是反比例函数k y x= 图像上一点，过点A 作x 轴的平行线交反比例函数3y x=-的图像于点B ，点C 在x 轴上，且2ABCS=，则k 的值为（ ）A ．7B ．7-C ．5-D ．59．已知反比例函数52y x=-，直线24y x =-+交于(),P a m 、(),Q b n 两点，则代数式1010b a m n+--的值是（ ）A ．5B ．5-C ．10D ．10-10．在平面直角坐标系xOy 中，将一块含有45︒角的直角三角板如图放置，直角顶点C 的坐标为()1,0，顶点A 的坐标()0,2，顶点B 恰好落在第一象限的双曲线上，则该双曲线的解析式为（ ）A ．3y x = B ．3y x=-C ．2y x=D ．2y x=-二、填空题（每小题3分，共15分）11．反比例函数1k y x-=的图象分布情况如图所示，则k 的值可以是 ．（写出一个符合条件的k 值即可）12．科技小组为了验证某电路的电压U （V ）、电流I （A ）、电阻()R Ω三者之间的关系：UI =，测得数据如下： ()R Ω 100 200 220 400()I A 2.2 1.11 0.55那么，当电阻55R =Ω时，电流I = A ．13．在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强P （kPa ）与汽缸内气体的体积V （mL ）成反比例，P关于V 的函数图象如图所示．若压强由75kPa 加压到100kPa ，则气体体积压缩了mL ．14．如图，在平面直角坐标中，菱形OABC 的顶点A 在y 轴的正半轴上，点B 在函数ky x=的图象上，若60ABC ∠=︒，且菱形OABC 的面积为6，则k 的值为 ．15．已知函数1y x =与函数21y x =的部分图像如图所示，有以下结论：①当0x <时，12,y y 都随x 的增大而增大； ②当1x <-时 12y y >；③12,y y 的图像的两个交点之间的距离是2； ④函数12y y y =+的最小值为2； 则所有正确的结论是 ．三、解答题16．（6分）反比例函数k y x=的图象经过点A (2，3)． (1)求这个函数的解析式；(2)请判断点B (1，6)是否在这个反比例函数的图象上，并说明理由．17．（7分）如图，在平面直角坐标系中，一次函数1y mx n =+的图象与反比例函数2ky x=的图绳交于第二、四象限内的A 、B 两点，与y 轴交于点C ，过点A 作AM x ⊥轴，垂足为M ，AM=3，OM=1，点B 的纵坐标为1-．(1)求反比例函数表达式和一次函数的解析式； (2)直接写出当12y y >时，自变量的取值范围； (3)连接OA 、OB ，求AOB 的面积； (4)已知点P 为图中双曲线上的一点，而且ABPABOS S=，请直接写出点P 的坐标．18．（8分）小明新买了一盏亮度可调节的台灯（如图1所示），他发现调节的原理是当电压一定时，通过调节电阻控制电流的变化从而改变灯光的明暗，台灯的电流I （单位：A ）与电阻R （单位：Ω）满足反比例函数关系，其图象如图2所示．图1 图2 (1)求I 关于R 的函数解析式； (2)当1375ΩR =时，求I 的值；(3)若该台灯工作的最小电流为0.1A ，最大电流为0.25A ，求该台灯的电阻R 的取值范围．19．（8分）如图，反比例函数()0k y x x=>和()60y x x=>的图象如图所示，点(),0C a 是x 轴正半轴上一动点，过点C 作x 轴的垂线，分别与()0ky x x=>和()60y x x=>的图象交于点A ，B ．(1)当2a =时，线段92AB =，求A ，B 两点的坐标及k 值．(2)小明同学提出了一个猜想：“当k 值一定时，OAB △的面积随a 值的增大而减小．”你认为他的猜想对吗？请说明理由．20．（8分）喝茶前需要烧水和泡茶两个工序，电热水壶将水烧到100℃，然后继续加热1分钟后断电，烧水时水温y （℃）与时间()min x 成一次函数关系；断电后，水壶中水的温度（℃）与时间()min x 近似于反比例函数关系（如图）．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．(1)分别求出图中AB 段和CD 段所对应的函数关系式；(2)从水壶中的水烧开（100℃）降到80℃就可以进行泡茶，问从水烧开到泡茶需要等待多长时间？21．（8分）如图，点(,4)A m 在反比例函数(0)ky x x =>的图象上，点B 在y 轴上，OB=2，将线段AB 向右下方平移，得到线段CD ，此时点C 落在反比例函数的图象上，点D 落在x 轴正半轴上，且1OD =．(1)点B 的坐标为__________，点D 的坐标为__________，点C 的坐标为__________（用含m 的式子表示）；(2)求k 的值和直线AC 的表达式．22．（10分）已知函数()()()31{31131x xy x x x x≤-=-≥＜＜ （1）画出函数图象； 列表：x ．．． ．．． y ．．． ．．． 描点，连线得到函数图象：（2）该函数是否有最大或最小值？若有，求出其值，若没有，简述理由； （3）设1122(,),(,)x y x y 是函数图象上的点，若120x x +=，证明：120y y +=．参考答案题号 1 2 3 4 5 6 7 8 9 10 答案 ABBDA BDBCA1．A【分析】根据反比例函数的定义“(0)ky k x=≠”即可求解．【详解】解：A 12y x=-符合反比函数定义，是反比例函数，符合题意； B xy k =不符合反比函数定义，不是反比例函数，不符合题意；C 11y x =+不符合反比函数定义，不是反比例函数，不符合题意； D 21y x =不符合反比函数定义，不是反比例函数，不符合题意； 故选：A ．【点睛】本题主要考查反比例函数定义的理解，掌握其定义，表达式的形式是解题的关键． 2．B【分析】将点代入反比例函数中，求出反比例函数，观察反比例函数的特征，排除法选出选项． 【详解】解：2k yx图像经过()3,2- ∴将点()3,2-代入反比例函数得：223k 4k ∴=-∴反比例函数为：6y x=-通过观察反比例函数可知反比例函数中x 和y 值为一正一负，排除选项A 、D 和C 故选B【点睛】本题考查的是通过待定系数求反比例函数．解题时需要观察x 和y 的正负性，排除法是解这道题的技巧． 3．B【分析】本题考查反比例函数的性质：反比例函数的图象在一、三象限，比例系数大于0．让反比例函数的比例系数大于0列式求解即可． 【详解】解：∵反比例函数21k y x+=的图象分布在第一、三象限 ∵210k +> 解得12k >-． 故选：B ． 4．D【分析】本题考查了反比例函数的图象及性质，根据0k >可判断A ；当32x =时4y =，可判断B ；根据0x ≠可判断C ；当0x <或0x >时，y 随x 的增大而减小可判断D ，熟练掌握反比例函数的图象及性质是解题的关键．【详解】解：A 、0k > ∴图象位于第一、三象限，则正确，故不符合题意； B 、当32x =时6432y ==，∴图象必经过点3,42⎛⎫⎪⎝⎭，则正确，故不符合题意；C 、0x ≠ ∴图象不可能与坐标轴相交，则正确，故不符合题意；D 、当0x <或0x >时，y 随x 的增大而减小，则错误，故符合题意； 故选D ． 5．A【分析】根据一次函数与反比例函数的性质，判断图象经过的象限即可得出结果． 【详解】解：0k >时，一次函数2y kx =-的图象经过第一、三、四象限，反比例函数k y x=的两个分支分别位于第一、三象限，无选项符合题意；0k <时，一次函数2y kx =-的图象经过第二、三、四象限，反比例函数ky x=的两个分支分别位于第二、四象限，选项A 符合题意． 故选：A ．【点睛】题目主要考查一次函数与反比例函数的图象判断，熟练掌握一次函数与反比例函数的基本性质是解题关键． 6．B【分析】利用数形结合的思想，直接得出关于x 的不等式0kax b x<+<的解集． 【详解】解：观察图象可得当60x -<<时，直线y ax b =+位于x 轴的上方、函数ky x=图象的下方 ∴不等式组0kax b x<+<的解是60x -<<． 故选：B ．【点睛】本题主要考查了一次函数与反比例函数的交点问题，利用数形结合思想解答是解题关键． 7．D【分析】先判断()210k -+<进而得到反比例函数21k y x+=-的图象经过第二、四象限，由此即可得到答案． 【详解】解：∵210k +>∵()210k -+<∵反比例函数21k y x+=-的图象经过第二、四象限∵210x x << ∵120y y << 故选D ．【点睛】本题主要考查了比较反比例函数函数值的大小，正确判断出反比例函数图象经过的象限是解题的关键． 8．B【分析】本题考查反比例函数系数k 的几何意义，根据反比例函数系数k 的几何意义得出2AOMBOMABCSSS-==是正确解答的关键．根据反比例函数系数k 的几何意义可得13322BOMS =⨯-=，12AOMS k =根据平行线的性质和三角形的面积公式可得2OABCABSS==，根据2AOMBOMS S-=，求出k 的值即可．【详解】解：如图，连接OA 、OB ，延长AB 交y 轴于M ，则13322BOMS=⨯-= 12AOMS k =AB x ∥轴2OABCABSS∴== 即2AOMBOMS S-=13222k ∴-= 0k <7k ∴=-故选：B ．9．C【分析】本题主要考查了反比例函数与一次函数的综合，联立两直线解析式求出交点坐标，然后代入式子即可得出答案． 【详解】解：联立反比例函数52y x=-与直线24y x =-+． 5224y x y x ⎧=-⎪⎨⎪=-+⎩①②把①代入②得：5242x x-=-+ 整理得：24850x x -++=()()2288445481448122382b b ac -±--⨯-±--±-±-±====-- 解得：1215,22x x =-=把1215,22x x =-=代入 ②式得125,1==-y y故12a =- 52b = 5m = 1n =-故()10105121022101022b a m n ⎛⎫+--=+----=-+= ⎪⎝⎭故选：C ． 10．A【分析】过点B 作BD∵x 轴于点D ，易证∵ACO∵∵CBD （AAS ），从而可求出B 的坐标，进而可求出反比例函数的解析式．【详解】解：如图所示，过点B 做BD ⊥x 轴交x 轴于D ∵∠ACO+∠BCD=90°，∠ACO+∠CAO=90° ∴∠CAO=∠BCD 又∵AC=CB∴∵ACO∵∵CBD （AAS ） ∵AO=CD=2，OC=BD=1 ∵B 点坐标为（3,1）设反比例函数的解析式为：k y x= 将B （3,1）代入ky x=得：k=3 ∴双曲线的解析式为：3y x=． 故选： A ．【点睛】本题考查反比例函数的综合问题，涉及全等三角形的性质与判定，反比例函数的解析式，综合程度较高． 11．0（答案不唯一）【分析】本题主要考查了反比例函数图象的性质，对于反比例函数()0ky k x=≠，当0k >时，图象在一、三象限；当0k <时，图象在二、四象限，据此可得10k -<，即1k <，由此可得答案．【详解】解：由反比例函数1k y x-=的图象位于第二，四象限可知10k -< 1k ∴<k ∴的值可以是0故答案为：0（答案不唯一）． 12．4【分析】由表格数据得到定值220U =V ，代入电阻值即可求解； 【详解】解：∵100 2.2200 1.122014000.55220⨯=⨯=⨯=⨯= ∵220U =V∵当电阻55R =Ω时220455I ==A 故答案为：4．【点睛】本题主要考查变量间的关系，根据表格得到电压的值是解题的关键． 13．20【分析】由图象易得P 关于V 的函数解析式为6000P V=，然后问题可求解． 【详解】解：设P 关于V 的函数解析式为kP V=，由图象可把点()100,60代入得：6000k =∵P 关于V 的函数解析式为6000P V= ∵当75kPa P =时，则60008075V == 当100kPa P =时，则600060100V == ∵压强由75kPa 加压到100kPa ，则气体体积压缩了806020mL -=； 故答案为20．【点睛】本题主要考查反比例函数的应用，熟练掌握反比例函数的应用是解题的关键． 14．-9【详解】试题解析：作BC OA ⊥于D ，∵四边形OABC 是菱形，∵60AB ∠=︒ ∵30ABD ∠=︒ 设AD x =，则2AB x = 3BD x = 236S OA BD x x =⋅==菱 解得：23x = 因为点B 在k y x=()32x x x k ⋅+= 2339k x == ∵9k =-． 15．②③④【分析】先补充完整两个函数的图象，再根据函数图象的增减性、对称性、交点问题可判断结论①②③，然后根据完全平方公式、偶次方的非负性可判断结论④． 【详解】当0x >时1y x = 21=y x当0x <时1y x =- 21y x=-画出两个函数的图象如下所示：则当0x <时，1y 随x 的增大而减小；2y 随x 的增大而增大，结论①错误 当1x <-时，函数1y 的图象位于函数2y 的图象的上方，则12y y >，结论②正确 当1x =时121y y ==即12,y y 的图象位于第一象限的交点坐标为(1,1)由对称性可知，12,y y 的图象位于第二象限的交点坐标为(1,1)- 因此，12,y y 的图象的两个交点之间的距离是1(1)2--=，结论③正确 1210y y y x x=+=+> 22211()2y x x x x∴=+=++又22211()20x x x x -=+-≥，当且仅当10x x-=，即1x =±时，等号成立 2212x x ∴+≥ 2212222y x x ∴=+++= 即函数12y y y =+的最小值为2，结论④正确 综上，所有正确的结论是②③④ 故答案为：②③④．【点睛】本题考查了正比例函数与反比例函数的综合、完全平方公式、偶次方的非负性等知识点，熟练掌握正比例函数与反比例函数的图象与性质是解题关键． 16．（1）y=6x- （2）点B(1,6)在这个反比例函数的图象上【分析】（1）设反比例函数的解析式是y=kx，只需把已知点的坐标代入，即可求得函数解析式；（2）根据反比例函数图象上点的坐标特征进行判断． 【详解】()1设反比例函数的解析式是k y x= 则32k -=得6k =-．则这个函数的表达式是6y x=-；()2因为1666⨯=≠-所以B 点不在函数图象上．【点睛】本题考查了待定系数法求反比例函数解析式：设出含有待定系数的反比例函数解析式y=kx（k 为常数，k≠0）；把已知条件（自变量与函数的对应值）代入解析式，得到待定系数的方程；解方程，求出待定系数；写出解析式．也考查了反比例函数图象上点的坐标特征． 17．(1)反比例函数的解析式为23y x-=；一次函数的解析式为12y x =-+ (2)当12y y >时，自变量的取值范围为1x <-或03x << (3)4(4)点P 的坐标为3,3或(3,3或()27,27或(27,27【分析】本题考查了反比例函数与一次函数的交点问题，熟练掌握以上知识点并灵活运用，采用数形结合的思想是解此题的关键．（1）运用待定系数法求出反比例函数解析式，即可得出点B 的坐标，再根据待定系数法求解即可得出一次函数的解析式； （2）根据函数图象即可得解；（3）先求出()0,2C 得到2OC =，再根据AOB AOC BOC S S S =+△△△计算即可得解；（4）分两种情况：过点O 作AB 的平行线交反比例函数于P ，则直线OP 的解析式为y x =-，联立3y xy x =-⎧⎪-⎨=⎪⎩，求解即可；②在y 轴上取点N ，使2CN CO ==，过N 作NH AB ⊥于H ，过点O 作OG AB ⊥于G ，过N 点作AB 的平行线交反比例函数于P 可求出直线NP 的解析式为4y x =-+，联立43y x y x =-+⎧⎪-⎨=⎪⎩，求解即可． 【详解】（1）解：∵AM x ⊥轴，垂足为M ，AM=3，OM=1 ∵()1,3A -把()1,3A -代入反比例函数2ky x =，可得31k =- 解得：3k =-∵反比例函数的解析式为23y x-=； 令1y =-，则3x = ∵()3,1B -把()1,3A -，()3,1B -代入一次函数1y mx n =+可得313k bk b =-+⎧⎨-=+⎩解得：12k b =-⎧⎨=⎩ ∵一次函数的解析式为12y x =-+；（2）解：由图象可得：当12y y >时，自变量的取值范围为1x <-或03x <<； （3）解：在12y x =-+中，令0x =，则12y =，即()0,2C ∵2OC = ∵11212313422AOBAOC BOCSSS=+=⨯⨯+⨯⨯=+=； （4）解：①如图，过点O 作AB 的平行线交反比例函数于P ，则ABPABOS S=，故直线OP 的解析式为y x =-联立3y xy x =-⎧⎪-⎨=⎪⎩解得：33x y ⎧=⎪⎨=⎪⎩33x y ⎧=-⎪⎨=⎪⎩∵点P 的坐标为(3,3-或(3,3-；②在y 轴上取点N ，使2CN CO ==，过N 作NH AB ⊥于H ，过点O 作OG AB ⊥于G ，过N 点作AB 的平行线交反比例函数于P则90NHC OGC ∠=∠=︒ 又HCN OCG ∠=∠ ∵HCN OCG ≌ ∵HN OG = ∵ABPABOSS=∵2CN CO == ∵4ON = ∵()0,4N∵直线NP 的解析式为4y x =-+ 联立43y x y x =-+⎧⎪-⎨=⎪⎩解得：2727x y ⎧=⎪⎨=⎪⎩2727x y ⎧=⎪⎨=⎪⎩∵点P 的坐标为(27,27或(27,27 综上，点P 的坐标为3,3或(3,3-或(27,27或(27,27．18．(1)220I R= (2)0.16A(3)8802200R Ω≤≤Ω【分析】本题考查反比例函数的实际应用． （1）待定系数法求出函数解析式；（2）将1375ΩR =，代入解析式，求出I 的值，即可；（3）求出最小电流和最大电流对应的电阻R 的阻值，根据增减性即可得出结果．正确的求出函数解析式，掌握反比例函数的性质，是解题的关键． 【详解】（1）解：设kI R=，由图象可知 当1100R =Ω时0.2A I = ∵0.21100220k =⨯= ∵220I R=； （2）当1375ΩR =时2200.16A 1375I ==； （3）当0.1A I = 22022000.1R ==Ω 当0.25A I = 2208800.25R ==Ω ∵该台灯的电阻R 的取值范围为8802200R Ω≤≤Ω． 19．(1)点A 为3(2,)2-，点B 为(2,3)，k 的值为3-．(2)小明猜想不正确，理由见解析【分析】本题考查了反比例函数k 的几何意义，三角形面积，一次函数的性质等知识点，其中理解反比例函数k 的几何意义是解题的关键．（1）由过点C 作x 轴的垂线叫解析式为A 、B 两点可知：当点C 为(,0)a ，则点B 坐标为6(,)a a ，点A 坐标为(,)ka a -，再将2a =，92AB =代入计算即可求解．（2）根据题意列出AB 的关系式，再根据公式12OABSAB OC =⋅代入化简即可得出结论． 【详解】（1）由题意可知：点C 为(,0)a ，则点B 坐标为6(,)a a ，点A 坐标为(,)ka a -．当2a =时，则点A 为(2,)2k-，点B 为(2,3)3BC ∴=．92AB =． 32AC AB BC ∴=-=． 322k ∴-=． 3k ∴=-．∴点A 为3(2,)2-，点B 为(2,3)，k 的值为3-．（2）由题意可知：66k k AB a a a-=-= OC a =． 11611(6)32222OABk SAB OC a k k a -∴=⋅=⋅⋅=-=-+． k 值一定OAB ∴△的面积一定 ∴小明猜想不正确．20．(1)y ＝100(8＜x ≤9)；y ＝900x(9＜x ≤45)； (2)134分钟 【分析】（1）将D 点的坐标代入反比例函数的一般形式，利用待定系数法确定反比例函数的解析式；再求得点C 和点B 的坐标，继而用待定系数法确定一次函数的解析式； （2）将y ＝80代入反比例函数的解析式，从而求得答案． 【详解】（1）解：停止加热时，设k y x= 由题意得：50＝18k 解得：k ＝900 ∵y ＝900x当y ＝100时，解得：x ＝9 ∵C 点坐标为(9，100) ∵B 点坐标为(8，100) 当加热烧水时，设y ＝ax +20 由题意得：100＝8a +20 解得：a ＝10∵当加热烧水，函数关系式为y ＝10x +20(0≤x ≤8)；当停止加热，得y 与x 的函数关系式为y ＝100(8＜x ≤9)；y ＝900x(9＜x ≤45)； （2）把y ＝80代入y ＝900x ，得454x =因此从烧水开到泡茶需要等待9013884-=分钟． 【点睛】本题考查了求一次函数解析，求反比例函数的解析式，反比例函数的实际应用，解题的关键是从实际问题中整理出反比例函数和一次函数模型，解题时注意根据图象确定对应函数的取值范围．21．(1)（0，2），（1，0），（m ＋1，2）(2)4；y ＝-2x ＋6【分析】（1）根据OB ＝2可得点B 的坐标，根据OD ＝1可得点D 的坐标为（1，0），由平移规律可得点C 的坐标；（2）根据点C 和D 的坐标列方程可得m 的值，从而得k 的值，再利用待定系数法可得直线AC 的解析式．【详解】（1）∵点B 在y 轴上 2OB =∵B （0，2）∵点D 落在x 轴正半轴上，且1OD =∵D （1，0）∵线段AB 向下平移2个单位，再向右平移1个单位，得到线段CD∵点A （m ，4）∵C （m ＋1，2）故答案为：（0，2），（1，0），（m ＋1，2）；（2）∵点A 和点C 在反比例函数(0)k y x x=>的图象上∵k ＝4m ＝2（m ＋1）∵m ＝1∵A （1，4），C （2，2）∵k ＝1×4＝4设直线AC 的表达式为：y sx t =+ ∵422s t s t +=⎧⎨+=⎩解得26s t =-⎧⎨=⎩ ∵直线AC 的表达式为：y ＝-2x ＋6．【点睛】此题主要考查了一次函数和反比例函数的综合应用以及平移的性质，根据OB 和OD 的长得出平移的规律是解题关键．22．（1）见解析；（2）有，当1x =时，最大值为3；当1x =-时，函数有最小值3-；（3）见解析【分析】（1）选取特殊值，代入函数解析式，求出y 值，列表，在图像中描点，画出图像即可；（2）观察图像可得函数的最大值；（3）根据120x x +=，得到1x 和2x 互为相反数，再分111x -<< 11x ≤- 11x ≥分别验证120y y +=．【详解】解：（1）列表如下： x ．．． -3 -2-1 0 1 2 3 4 ．．． y ．．． -1 32- -3 0 3 32 1 34．．． 函数图像如图所示：（2）根据图像可知：当x =1时，函数有最大值3；当1x =-时，函数有最小值3-；（3）∵1122(,),(,)x y x y 是函数图象上的点120x x +=∵1x 和2x 互为相反数当111x -<<时211x -<<∵113y x = 223y x =∵()1212123330y y x x x x +=+=+=；当11x ≤-时21x ≥则()121212123330x x y y x x x x ++=+==； 同理：当11x ≥时21x ≤-()121212123330x x y y x x x x ++=+== 综上：120y y +=．【点睛】本题主要考查正比例函数，反比例函数的图像和性质，描点法画函数图像，准确画出图像，理解120x x +=是解题的关键．。

第六单元反比例函数测试卷(时间:100分钟 满分:120分)一、选择题(每小题3分，共30分，下列各小题均有四个答案，其中只有一个是正确的)1.下列函数中，y 是x 的反比例函数的是 ( )A. x(y-1)=1B.y =1x +1 C.y =1x2 D.y =13x 2.已知甲、乙两地相距s( km)，汽车从甲地匀速行驶到乙地，则汽车行驶的时间t(h)与行驶速度 v( km/h)的函数关系图象大致是 ( )3.已知反比例函数 y =kx(k ≠0)的图象经过点(2，3)，若点(1，n)在反比例函数的图象上，则n 等于( )A.(-2,3)B.(-2,-3)C.(2,3)D.(3,2)5.已知反比例函数 y =−3x,则下列描述不正确的是 ( )A.图象位于第二、第四象限B.图象必经过点(-3,1)C.图象不可能与坐标轴相交D. y 随x 的增大而增大6.如果等腰三角形的面积为10，底边长为x ，底边上的高y ，则y 与x 的函数关系式为( ）A.y =10xB.y =5xC.y =20xD.y =x 207.如图，在同一平面直角坐标系中，直线y =k ₁x (k ₁≠0)与双曲线y =k 2x(k 2≠0)相交于A ，B 两点，已知点 A 的坐标为(1,2),则点B 的坐标为 ( )A.(-1,-2) B.(-2,-1) C.(-1,-1) D.(-2,-2)8.如图所示，A ，B 是函数 y =1x的图象上关于原点O 的任意一对对称点,AC 平行于y 轴,BC平行于x 轴,△ABC 的面积为S ，则 ( )A. S=1 B. S=2 C.1<S<2 D. S>29.在同一直角坐标系中，函数y= kx-k 与 y =kx (k ≠0)的图象大致是 ( )10.如图，在第一象限内，A 是反比例函数y= k1x (k 1⟩0)图象上的任意一点，AB 平行于 y 轴交反比例函数 y =k 2x(k 2<0)的图象于点 B ，作以 AB 为边的平行四边形 ABCD,其顶点 C,D在 y 轴上,若 S ABCD =7,则这两个反比例函数可能是 ( )A.y =2x 和y =−3x B.y =3x 和y =−4x C.y =4x 和y =−5x D.y =5x和y =−6x 二、填空题(本大题共5小题，每小题3分，共15分)11.反比例函数 y =(m +2)x m 2−10的图象分布在第二、四象限内,则m 的值为 .12.若A(-2,y ₁),B(--1,y ₂),C(1,y ₃)三点都在函数 y =kx(k<0)的图象上,则 y ₁,y ₂,y ₃的大小关系是 (用“>”“<”或“=”连接)。

第6章反比例函数一．选择题（共10小题）1．下列函数中，是反比例函数的是（）A．y＝B．y＝C．y＝x﹣1D．y＝2．今年，某公司推出一款新手机深受消费者推崇，但价格不菲．为此，某电子商城推出分期付款购买手机的活动，一部售价为9688元的新手机，前期付款3000元，后期每个月分别付相同的数额，则每个月付款额y（元）与付款月数x（x为正整数）之间的函数关系式是（）A．B．C．D．3．函数y＝﹣ax+a与y＝（a≠0）在同一坐标系中的图象可能是（）A．B．C．D．4．对于反比例函数y＝，下列说法错误的是（）A．函数图象位于第一、三象限B．函数值y随x的增大而减小C．若A（﹣1，y1）、B（1，y2）、C（2，y3）是图象上三个点，则y1＜y3＜y2D．P为图象上任意一点，过P作PQ⊥y轴于Q，则△OPQ的面积是定值5．如图，菱形ABCD的两个顶点B，D在反比例函数y＝的图象上，对角线AC与BD的交点恰好是坐标原点O，已知点A（﹣2，2），∠ABC＝60°，则k的值是（）A．4 B．6 C．4D．126．如图，正方形ABCD的边长为5，点A的坐标为（0，3），点D在x轴的正半轴上．若反比例函数y＝（k≠0）的图象经过点B，则k的值是（）A．3 B．4 C．5 D．67．如图，在平面直角坐标系中，Rt△ABC的顶点A，B分别在y轴、x轴上，OA＝2，OB＝1，斜边AC∥x轴．若反比例函数y＝（k＞0，x＞0）的图象经过AC的中点D，则k的值为（）A．4 B．5 C．6 D．88．如图，在正方形ABCD中，点C（8，5），AB边不动，将正方形向左下方推动变形，使点D落在y轴的点D′处，点C落在点C′处，则经过点C′的反比例函数解析式是（）A．y＝B．y＝C．y＝D．y＝9．设双曲线y＝（k＞0）与直线y＝x交于A\B两点（点A在第三象限），将双曲线在第一象限的一支沿射线BA的方向平移，使其经过点A，将双曲线在第三象限的一支沿射线AB的方向平移，使其经过点B，平移后的两条曲线相交于P、Q两点，此时我们称平移后的两条曲线所围部分（如图中阴影部分）为双曲线的“眸”，PQ为双曲线的“眸径“，当双曲线y＝（k＞0）的眸径为6时，k的值为（）A．B．2 C．D．310．如图，为某公园“水上滑梯”的侧面图，其中BC段可看成是一段双曲线，建立如图的坐标系后，其中，矩形AOEB为向上攀爬的梯子，OA＝5米，进口AB∥OD，且AB＝2米，出口C点距水面的距离CD为1米，则B、C之间的水平距离DE的长度为（）A．5米B．6米C．7米D．8米二．填空题（共7小题）11．已知反比例函数y＝（k﹣1）x，那么k的值是．12．如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点B的坐标为（3，6），反比例函数y＝（k＞0）的图象分别交边BC、AB于点D、F，连结DF，△DEF与△DBF关于直线DF对称，当点E正好落在边OC上时，则k的值为．13．如图，点A为函数y＝（x＞0）图象上一点，连结OA，交函数y＝（x＞0）的图象于点B，点C是x轴上一点，且AO＝AC，则△ABC的面积为．14．若反比例函数y＝﹣，当y≤，且y≠0时自变量x的取值范围．15．如图，是反比例函数y＝和y＝（k1＞k2）在第一象限的图象，直线AB∥x轴，并分别交两条曲线于A、B两点，若S△AOB＝4，则k1﹣k2的值是．16．如图，△ABC在第一象限内，∠C＝90°，BC∥x轴，点C（2，2），AB所在直线的函数关系式是y＝x+6．当反比例函数y＝﹣的图象与△ABC有交点时，k的取值范围是．17．如图，Rt△AOB中，∠OAB＝90°，∠OBA＝30°，顶点A在反比例函数y＝图象上，若Rt△AOB的面积恰好被y轴平分，则进过点B的反比例函数的解析式为．三．解答题（共5小题）18．如图，直线y＝2x﹣4分别交坐标轴于A、B两点，交双曲线y＝（x＞0）于C点，且sin∠COB＝；（1）求双曲线的解析式；（2）若过点B的直线y＝ax+b（a＞0）交y轴于D点，交双曲线于点E，且OD：AD＝1：2，求E点横坐标．19．如图，一次函数y＝x+b与反比例函数y＝的图象交于A（m，3），B（﹣3，n）两点．过点B作BC⊥x轴，垂足为点C，且S△ABC＝5．（1）求一次函数与反比例函数的表达式；（2）根据所给条件，请直接写出不等式x+b的解集；（3）若P（p，y1），Q（﹣2，y2）是反比例函数y＝图象上的两点，且y1≥y2，求实数P的取值范围．20．如图，在所给的直角坐标系（O是坐标原点）中，每个小方格都是边长为1的正方形，直线y＝mx+n与反比例函数y＝的图象的交点A，B均在格点上．（1）请直接写出点A，B的坐标为：；当mx+n≥时，x的取值范围是；（2）将直线AB向右平移3个单位，再向上平移5个单位，在图中画出平移后的直线A′B′，并求出直线A′B′的解析式；（3）若点C在函数y＝的图象上，且△ABC是以AB为底的等腰三角形，请直接写出点C的坐标．21．如图，在平面直角坐标系中，Rt△OAB的直角顶点A在x轴上，OB＝5，OA＝4，动点M 从点A出发，以每秒1个单位长度的速度，沿AO向终点O运动，同时点N从点O出发，以每秒2个单位长度的速度，沿OB向终点B移动，当两个动点运动了x（0＜x＜2.5）秒时，解答下列问题：（1）若点B在反比例函数y＝（x＞0）的图象上，求出该函数的解析式；（2）在两个动点运动过程中，当x为何值时，使得以O，M，N为顶点的三角形与△OAB 相似？22．冬天即将到来，龙泉某中学的初三学生到某蔬菜生产基地作数学实验．在气温较低时，蔬菜生产基地用装有恒温系统的大棚栽培蔬菜，经收集数据，该班同学将大棚内温度和时间的关系拟合为一个分段函数，如图是某天恒温系统从开启到关闭后，大棚内的温度y（℃）与时间x（h）之间的函数关系，其中线段AB，BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段．请根据图中信息解答下列问题：（1）求这天的温度y与时间x（0≤x≤24）的函数关系式；（2）若大棚栽种某种蔬菜，温度低于10℃时会受到伤害．问若栽种这种蔬菜，恒温系统最多可以关闭多少小时就必须再次启动，才能使蔬菜避免受到伤害？参考答案与试题解析一．选择题（共10小题）1．下列函数中，是反比例函数的是（）A．y＝B．y＝C．y＝x﹣1D．y＝【分析】根据反比例函数的一般形式即可作出判断．【解答】解：A、该函数是常函数，故本选项不符合题意．B、该函数是y与（1﹣x）成反比例函数关系，故本选项不符合题意．C、该函数是反比例函数，故本选项符合题意．D、该函数不是反比例函数，故本选项不符合题意．故选：C．2．今年，某公司推出一款新手机深受消费者推崇，但价格不菲．为此，某电子商城推出分期付款购买手机的活动，一部售价为9688元的新手机，前期付款3000元，后期每个月分别付相同的数额，则每个月付款额y（元）与付款月数x（x为正整数）之间的函数关系式是（）A．B．C．D．【分析】直接利用后期每个月分别付相同的数额，进而得出y与x的函数关系式．【解答】解：由题意得y＝，即y＝，故选：D．3．函数y＝﹣ax+a与y＝（a≠0）在同一坐标系中的图象可能是（）A．B．C．D．【分析】根据反比例函数与一次函数的图象特点解答即可．【解答】解：a＞0时，﹣a＜0，y＝﹣ax+a在一、二、四象限，y＝在一、三象限，无选项符合．a＜0时，﹣a＞0，y＝﹣ax+a在一、三、四象限，y＝（a≠0）在二、四象限，只有D 符合；故选：D．4．对于反比例函数y＝，下列说法错误的是（）A．函数图象位于第一、三象限B．函数值y随x的增大而减小C．若A（﹣1，y1）、B（1，y2）、C（2，y3）是图象上三个点，则y1＜y3＜y2D．P为图象上任意一点，过P作PQ⊥y轴于Q，则△OPQ的面积是定值【分析】先判断出k2+1的符号，再根据反比例函数的性质即可得出结论．【解答】解：A、∵k2+1＞0，∴它的图象分布在第一、三象限，故本选项正确；B、∵它的图象分布在第一、三象限，∴在每一象限内y随x的增大而减小，故本选项错误；C、∵它的图象分布在第一、三象限，在每一象限内y随x的增大而减小，∵x1＝﹣1＜0，∴y1＜0，∵x2＝1＞0，x3＝2＞0，∴y2＞y3，∴y1＜y3＜y2故本选项正确；D、∵P为图象上任意一点，过P作PQ⊥y轴于Q，∴△OPQ的面积＝（k2+1）是定值，故本选项正确．故选：B．5．如图，菱形ABCD的两个顶点B，D在反比例函数y＝的图象上，对角线AC与BD的交点恰好是坐标原点O，已知点A（﹣2，2），∠ABC＝60°，则k的值是（）A．4 B．6 C．4D．12【分析】根据题意可以求得点B的坐标，从而可以求得k的值．【解答】解：∵四边形ABCD是菱形，∴BA＝BC，AC⊥BD，∵∠ABC＝60°，∴△ABC是等边三角形，∵点A（﹣2，2），∴OA＝2，∴BO＝＝，∵直线AC的解析式为y＝﹣x，∴直线BD的解析式为y＝x，∴点B的坐标为（2，2），∵点B在反比例函数y＝的图象上，∴，解得，k＝12，故选：D．6．如图，正方形ABCD的边长为5，点A的坐标为（0，3），点D在x轴的正半轴上．若反比例函数y＝（k≠0）的图象经过点B，则k的值是（）A．3 B．4 C．5 D．6【分析】作BE⊥y轴于E，根据勾股定理求得OD＝4，然后证明△ABE≌△DAO，可得BE ＝AO＝3，AE＝OD＝4，所以点B坐标为（﹣3，﹣1），把点B代入双曲线y＝可得k的值．【解答】解：作BE⊥y轴于E，∵正方形ABCD的边长为5，点A的坐标为（0，3），∴AD＝5，OA＝3，∴OD＝＝＝4，∵四边形ABCD为正方形，∴∠BAD＝90°，AB＝AD，∴∠BAE＝90°﹣∠DAO＝∠ADO，∵∠AEB＝∠AOD＝90°，∴△ABE≌△DAO（AAS），∴BE＝AO＝3，AE＝OD＝4，∴OE＝AE﹣OA＝1，∴B（﹣3，﹣1），∵反比例函数y＝（k≠0）的图象经过点B，∴k＝﹣3×（﹣1）＝3，故选：A．7．如图，在平面直角坐标系中，Rt△ABC的顶点A，B分别在y轴、x轴上，OA＝2，OB＝1，斜边AC∥x轴．若反比例函数y＝（k＞0，x＞0）的图象经过AC的中点D，则k的值为（）A．4 B．5 C．6 D．8【分析】根据平行于x轴的直线上任意两点纵坐标相同，可设C（x，2）．则D（x，4），由勾股定理得出AB2+BC2＝AC2，列出方程22+12+（x﹣1）2+22＝x2，求出x，得到D点坐标，代入y＝，利用待定系数法求出k．【解答】解：∵AC∥x轴，OA＝2，OB＝1，∴A（0，2），∴C、A两点纵坐标相同，都为2，∴可设C（x，2）．∵D为AC中点．∴D（x，2）．∵∠ABC＝90°，∴AB2+BC2＝AC2，∴12+22+（x﹣1）2+22＝x2，解得x＝5，∴D（，2）．∵反比例函数y＝（k＞0，x＞0）的图象经过点D，∴k＝×2＝5．故选：B．8．如图，在正方形ABCD中，点C（8，5），AB边不动，将正方形向左下方推动变形，使点D落在y轴的点D′处，点C落在点C′处，则经过点C′的反比例函数解析式是（）A．y＝B．y＝C．y＝D．y＝【分析】由点C（8，5）可知A（3，0），OD'＝4，过点C'作C'M⊥OB，可证△AOD'≌△BMC'（HL），可求C'（5，4），即可求反比例函数解析式；【解答】解：∵正方形ABCD中，点C（8，5），∴A（3，0），AB＝5，∵AD'＝5，∴OD'＝4，过点C'作C'M⊥OB，∵BC'＝AD'，C'M＝OD'，∴△AOD'≌△BMC'（HL），∴MB＝OA＝3，∴C'（5，4），∴y＝；故选：A．9．设双曲线y＝（k＞0）与直线y＝x交于A\B两点（点A在第三象限），将双曲线在第一象限的一支沿射线BA的方向平移，使其经过点A，将双曲线在第三象限的一支沿射线AB的方向平移，使其经过点B，平移后的两条曲线相交于P、Q两点，此时我们称平移后的两条曲线所围部分（如图中阴影部分）为双曲线的“眸”，PQ为双曲线的“眸径“，当双曲线y＝（k＞0）的眸径为6时，k的值为（）A．B．2 C．D．3【分析】以PQ为边，作矩形PQQ′P′交双曲线于点P′、Q′，联立直线AB及双曲线解析式成方程组，通过解方程组可求出点A、B的坐标，由PQ的长度可得出点P的坐标（点P在直线y＝﹣x上找出点P的坐标），由图形的对称性结合点A、B和P的坐标可得出点P′的坐标，再利用反比例函数图象上点的坐标特征即可得出关于k的一元一次方程，解之即可得出结论．【解答】解：以PQ为边，作矩形PQQ′P′交双曲线于点P′、Q′，如图所示．联立直线AB及双曲线解析式成方程组，，解得：，，∴点A的坐标为（﹣，﹣），点B的坐标为（，）．∵PQ＝6，∴OP＝3，点P的坐标为（﹣，）．根据图形的对称性可知：PP′＝AB＝QQ′，∴点P′的坐标为（﹣+2，+2）．又∵点P′在双曲线y＝上，∴（﹣+2）•（+2）＝k，解得：k＝．故选：A．10．如图，为某公园“水上滑梯”的侧面图，其中BC段可看成是一段双曲线，建立如图的坐标系后，其中，矩形AOEB为向上攀爬的梯子，OA＝5米，进口AB∥OD，且AB＝2米，出口C点距水面的距离CD为1米，则B、C之间的水平距离DE的长度为（）A．5米B．6米C．7米D．8米【分析】根据矩形的性质得到BE＝OA＝5，AB＝2，求得B（2，5），设双曲线BC的解析式为y＝，得到k＝10，于是得到结论．【解答】解：∵四边形AOEB是矩形，∴BE＝OA＝5，AB＝2，∴B（2，5），设双曲线BC的解析式为y＝，∴k＝10，∴y＝，∵CD为1∴当y＝1时，x＝10，∴DE的长＝10﹣2＝8m，故选：D．二．填空题（共7小题）11．已知反比例函数y＝（k﹣1）x，那么k的值是±2 ．【分析】根据反比例函数的定义解答．【解答】解：依题意得：k2﹣5＝﹣1且k﹣1≠0．解得k＝±2．故答案是：±2．12．如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点B的坐标为（3，6），反比例函数y＝（k＞0）的图象分别交边BC、AB于点D、F，连结DF，△DEF与△DBF关于直线DF对称，当点E正好落在边OC上时，则k的值为．【分析】过点F作FG⊥OC，垂足为G．由于四边形OABC是矩形，△DEF与△DBF关于直线DF对称，当点E正好落在边OC上，可得△DGF∽△FAE，然后把D、F两点的坐标用含k的代数式表示出来，再由相似三角形对应边成比例求出CE的长，然后利用勾股定理求出k．【解答】解：过点F作FG⊥OC，垂足为G，如图所示．由题意知D（，6），F（3，），FG＝3．又∵△DEF与△DBF关于直线DF对称，点E在边OC上，∴DE＝DB，∠B＝∠DEF＝90°，∴∠DEC+∠GEF＝90°，∵∠EGF＝∠DCE＝90°，∠GEF+∠EFG＝90°，∴∠DEC＝∠EFG，∴△EGF∽△DCE，∴＝，即＝，解得：CE＝，∵DE2＝DC2+CE2，即（3﹣）2＝（）2+（）2，解得：k＝．故答案为：．13．如图，点A为函数y＝（x＞0）图象上一点，连结OA，交函数y＝（x＞0）的图象于点B，点C是x轴上一点，且AO＝AC，则△ABC的面积为 6 ．【分析】根据题意可以分别设出点A、点B的坐标，根据点O、A、B在同一条直线上可以得到A、B的坐标之间的关系，由AO＝AC可知点C的横坐标是点A的横坐标的2倍，从而可以得到△ABC的面积．【解答】解：方法一：设点A的坐标为（a，），点B的坐标为（b，），∵点C是x轴上一点，且AO＝AC，∴点C的坐标是（2a，0），设过点O（0，0），A（a，）的直线的解析式为：y＝kx，∴，解得，k＝，又∵点B（b，）在y＝上，∴，解得，或（舍去），∴S△ABC＝S△AOC﹣S△OBC＝＝，故答案为：6．方法二：作BD⊥x轴于点D，作AE⊥x轴于点E，∵点A在为函数y＝（x＞0）图象上一点，AO＝AC，∴△AOC的面积是9，∵点A为函数y＝（x＞0）图象上一点，连结OA，交函数y＝（x＞0）的图象于点B，∴＝，∴，∴，∴S△ABC＝6，故答案为：6．14．若反比例函数y＝﹣，当y≤，且y≠0时自变量x的取值范围x≤﹣9或x＞0 ．【分析】首先画出图形，进而利用函数图象得出x的取值范围．【解答】解：如图所示：∵反比例函数y＝﹣，当y≤，∴y＝时，则x＝﹣9，故y≤时，x≤﹣9或x＞0．故答案为：x≤﹣9或x＞0．15．如图，是反比例函数y＝和y＝（k1＞k2）在第一象限的图象，直线AB∥x轴，并分别交两条曲线于A、B两点，若S△AOB＝4，则k1﹣k2的值是8 ．【分析】设A（a，b），B（c，d），代入双曲线得到k1＝ab，k2＝cd，根据三角形的面积公式求出ab﹣cd＝8，即可得出答案．【解答】解：设A（a，b），B（c，d），代入得：k1＝ab，k2＝cd，∵S△AOB＝4，∴ab﹣cd＝4，∴ab﹣cd＝8，∴k1﹣k2＝8，故答案为：8．16．如图，△ABC在第一象限内，∠C＝90°，BC∥x轴，点C（2，2），AB所在直线的函数关系式是y＝x+6．当反比例函数y＝﹣的图象与△ABC有交点时，k的取值范围是4≤k≤．【分析】先求出点A、B的坐标，根据反比例函数图象上点的坐标特征可知，当反比例函数图象与△ABC相交于点C时k的取值最小，当与线段AB相交时，k能取到最大值，根据直线y＝x+6，设交点为（x，﹣x+6）时k值最大，然后列式利用二次函数的最值问题解答即可得解．【解答】解：∵△ABC在第一象限内，∠C＝90°，BC∥x轴，点C（2，2），∴把x＝2代入y＝x+6得，y＝﹣×2+6＝，把y＝2代入y＝x+6得，﹣x+6＝2，解得x＝6，∴点A、B的坐标分别为A（2，），B（6，2），根据反比例函数系数的几何意义，当反比例函数与点C相交时，k＝2×2＝4最小，设反比例函数与线段AB相交于点（x，﹣x+6）时k值最大，则k＝x（﹣x+6）＝﹣x2+6x＝﹣（x﹣）2+，∵2≤x≤6，∴当x＝时，k值最大，此时交点坐标为（，3），因此，k的取值范围是4≤k≤．故答案为：4≤k≤．17．如图，Rt△AOB中，∠OAB＝90°，∠OBA＝30°，顶点A在反比例函数y＝图象上，若Rt△AOB的面积恰好被y轴平分，则进过点B的反比例函数的解析式为10 ．【分析】分别过A、B作AE⊥x轴于E，BD⊥y轴交AE于F．设A（a，b），则ab＝﹣4．根据两角对应相等的两三角形相似，得出△OAE∽△ABF，由相似三角形的对应边成比例，则BD、OD都可用含a、b的代数式表示，从而求出B的坐标，进而得出结果．【解答】解：分别过A、B作AE⊥x轴于E，BD⊥y轴交AE于F．设A（a，b）．∵顶点A在反比例函数y＝图象上，∴ab＝﹣4．∵∠OAB＝90°，∠OAE＝90°﹣∠BAF＝∠ABF，∠OEA＝∠BFA＝90°，∴△OAE∽△ABF，∴OA：AB＝OE：AF＝AE：BF，在Rt△AOB中，∠AOAB＝90°，∠OBA＝30°，∴OA：AB＝1：，∴﹣a：AF＝b：BF＝1：，∴AF＝﹣，BF＝b，∵Rt△AOB的面积恰好被y轴平分，∴AC＝BC，∴BD＝DF＝BF＝﹣a，OD＝AE+AF＝b﹣a，∴b＝﹣a，∴A（﹣b，b），B（b，b﹣）∴﹣b•b＝﹣4，∴b2＝，∴k＝b（b﹣）＝b2﹣ab＝10，故答案为：10．三．解答题（共5小题）18．如图，直线y＝2x﹣4分别交坐标轴于A、B两点，交双曲线y＝（x＞0）于C点，且sin∠COB＝；（1）求双曲线的解析式；（2）若过点B的直线y＝ax+b（a＞0）交y轴于D点，交双曲线于点E，且OD：AD＝1：2，求E点横坐标．【分析】（1）根据题意设出点C的坐标，由sin∠COB＝可以求得点C的坐标，进而可以求得双曲线的解析式；（2）根据y＝2x﹣4求得A、B的坐标，OD：AD＝1：2，可知D的坐标，根据待定系数法求得BD的解析式，联立解析式即可求出E横坐标．【解答】解：（1）设点C的坐标是（a，2a﹣4），∵sin∠COB＝，∴tan∠COB＝＝，解得，a＝6，∴点C为（6，8），∵点C在双曲线y＝（x＞0）上，∴k＝6×8＝48，即双曲线的解析式为：y＝；（2）∵直线y＝ax+b（a＞0）交y轴于D点，∴点D的坐标是（0，b），∵直线y＝2x﹣4分别交坐标轴于A、B两点，∴点A的坐标是（0，﹣4），B（2，0），∵OD：AD＝1：2，∴OD＝，∴D（0，﹣），把B（2，0），D（0，﹣）代入y＝ax+b得，解得，∴y＝x﹣，解x﹣＝得x＝1+，x＝1﹣（舍去），∴E的横坐标为1+．19．如图，一次函数y＝x+b与反比例函数y＝的图象交于A（m，3），B（﹣3，n）两点．过点B作BC⊥x轴，垂足为点C，且S△ABC＝5．（1）求一次函数与反比例函数的表达式；（2）根据所给条件，请直接写出不等式x+b的解集；（3）若P（p，y1），Q（﹣2，y2）是反比例函数y＝图象上的两点，且y1≥y2，求实数P的取值范围．【分析】（1）把A、B的坐标代入反比例函数解析式求出m＝﹣n，即可得出A（m，3），B （﹣3，﹣m），根据三角形面积求得m、n的值，得到A、B的坐标，代入反比例函数和一次函数的解析式，即可求出答案；（2）根据A、B的横坐标，结合图象即可得出答案；（3）分为两种情况：当点P在第一象限时和当点P在第三象限时，根据坐标和图象即可得出答案．【解答】解：（1）把A（m，3），B（﹣3，n）代入反比例函数y＝得：k＝3m＝﹣3n，即m＝﹣n，则B（﹣3，﹣m），∵A（m，3），B（﹣3，﹣m），S△ABC＝•BC•（x A﹣x B）∴×m×（m+3）＝5，解得：m＝2或m＝﹣5（舍去），∴n＝﹣2，即A（2，3），B（﹣3，﹣2），把A（2，3）代入y＝得：k＝6，即反比例函数的解析式是y＝；把A（2，3）代入y＝x+b得：3＝2+b，解得：b＝1，即一次函数的解析式是y＝x+1；（2）∵A（2，3），B（﹣3，﹣2），∴不等式x+b的解集是x≤﹣3或0＜x≤2；（3）∵P（p，y1），Q（﹣2，y2）是反比例函数y＝图象上，则点Q（﹣2，y2）在第三象限，∴当点P在第一象限时，总有y1＞y2，此时p＞0；当点P在第三象限时，要使y1≥y2，实数p的取值范围是P≤﹣2，即P的取值范围是p≤﹣2或p＞0．20．如图，在所给的直角坐标系（O是坐标原点）中，每个小方格都是边长为1的正方形，直线y＝mx+n与反比例函数y＝的图象的交点A，B均在格点上．（1）请直接写出点A，B的坐标为：点A（﹣1，﹣4），点B（﹣4，﹣1）；当mx+n ≥时，x的取值范围是x＞﹣4或﹣1＜x＜0 ；（2）将直线AB向右平移3个单位，再向上平移5个单位，在图中画出平移后的直线A′B′，并求出直线A′B′的解析式；（3）若点C在函数y＝的图象上，且△ABC是以AB为底的等腰三角形，请直接写出点C的坐标．【分析】（1）观察图象，可求解；（2）由题意画出图象，由待定系数法可求直线解析式；（3）由待定系数法可求反比例函数解析式，设点C（a，），由等腰三角形的性质和两点距离公式可求a的值，即可求点C坐标．【解答】解：（1）由图象可知：点A（﹣1，﹣4），点B（﹣4，﹣1），当mx+n≥时，x的取值范围是x＞﹣4或﹣1＜x＜0，故答案为：点A（﹣1，﹣4），点B（﹣4，﹣1），x＞﹣4或﹣1＜x＜0；（2）图象如图：∵点A（﹣1，﹣4），点B（﹣4，﹣1），且直线AB向右平移3个单位，再向上平移5个单位，∴点A'（2，1），点B'（﹣1，4）设直线A'B'解析式为：y＝kx+b，∴解得：∴直线A′B′的解析式为：y＝﹣x+3；（3）∵反比例函数y＝的图象过点A（﹣1，﹣4），∴k＝﹣1×（﹣4）＝4，∴反比例函数的解析式为：y＝，设点C（a，），∵△ABC是以AB为底的等腰三角形，∴CA＝CB，∴（a+1）2+（+4）2＝（a+4）2+（+1）2，∴a＝±2，∴点C（﹣2，﹣2）或（2，2）21．如图，在平面直角坐标系中，Rt△OAB的直角顶点A在x轴上，OB＝5，OA＝4，动点M 从点A出发，以每秒1个单位长度的速度，沿AO向终点O运动，同时点N从点O出发，以每秒2个单位长度的速度，沿OB向终点B移动，当两个动点运动了x（0＜x＜2.5）秒时，解答下列问题：（1）若点B在反比例函数y＝（x＞0）的图象上，求出该函数的解析式；（2）在两个动点运动过程中，当x为何值时，使得以O，M，N为顶点的三角形与△OAB 相似？【分析】（1）由勾股定理可求点B坐标（4，3），代入解析式可求k的值，即可求函数的解析式；（2）分两种情况讨论，由相似三角形的性质可求解．【解答】解：（1）∵△ABC是直角三角形，且BA⊥x轴于A，OA＝4，OB＝5，∴∴B（4，3），∴将B（4，3）代入得k＝12，∴函数的解析式为：；（2）在两个动点运动过程中，分两种情况：①若∠OMN＝90°，如图1所示，则MN∥AB，此时OM＝4﹣x，ON＝2x，∵∠OMN＝∠OAB，∠NOM＝∠BOA，∴△MON∽△AOB，∴，即：∴；②若∠ONM＝90°，如图2所示，则∠ONM＝∠OAB，此时OM＝4﹣x，ON＝2x，∵∠ONM＝∠OAB，∠MON＝∠BOA，∴△OMN～△OBA，∴即：，∴，综上所述，当或秒时，使得以O，M，N为顶点的三角形与△OAB相似．22．冬天即将到来，龙泉某中学的初三学生到某蔬菜生产基地作数学实验．在气温较低时，蔬菜生产基地用装有恒温系统的大棚栽培蔬菜，经收集数据，该班同学将大棚内温度和时间的关系拟合为一个分段函数，如图是某天恒温系统从开启到关闭后，大棚内的温度y（℃）与时间x（h）之间的函数关系，其中线段AB，BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段．请根据图中信息解答下列问题：（1）求这天的温度y与时间x（0≤x≤24）的函数关系式；（2）若大棚栽种某种蔬菜，温度低于10℃时会受到伤害．问若栽种这种蔬菜，恒温系统最多可以关闭多少小时就必须再次启动，才能使蔬菜避免受到伤害？【分析】（1）应用待定系数法分段求函数解析式；（2）代入临界值y＝10即可．【解答】解：（1）设线段AB解析式为y＝k1x+b（k≠0）∵线段AB过点（0，10），（2，14）代入得，得，AB解析式为：y＝2x+10（0≤x＜5）∵B在线段AB上当x＝5时，y＝20∴B坐标为（5，20）∴线段BC的解析式为：y＝20（5≤x＜10）设双曲线CD解析式为：y＝（k2≠0）∵C（10，20）∴k2＝200∴双曲线CD解析式为：y＝（10≤x≤24）∴y关于x的函数解析式为：y＝（2）把y＝10代入y＝中，解得，x＝20∴20﹣10＝10答：恒温系统最多关闭10小时，蔬菜才能避免受到伤害．。