初一数学期末复习综合卷 2011

2011学年第二学期七年级期末考试数学试题一、选择题（本大题共有4个小题，每题3分，满分18分）10、3.14159、3、723、2π、0.1010010001…、31.0 中，是无理数的个数为( ) （A ）1个； （B ）2个； （C ）3个； （D ）4个． 2. 下列四个式子中，正确的是（ ）（A ）981±=； （B ）662=--）（； （C ）41621=； （D ）5322=+）（. 3.若点)1,(-a a P 在x 轴上，则点)1,2(+-a a Q 在第（ ）象限.（A ）一； （B ）二； （C ）三； （D ）四.4、等边三角形是轴对称图形，它的对称轴共有 （ ） （A ）1条； （B ）2条； （C ）3条； （D ）无数条.5.已知两条直线被第三条直线所截，下列四个说法中正确的个数是（ ） （1）同位角的平分线互相平行； （2）内错角的平分线互相平行； （3）同旁内角的平分线互相垂直； （4）邻补角的平分线互相垂直. （A ）4个； （B ）3个； （C ）2个； （D ）1个.6.如图，在△ABC 中，已知点D 、E 分别在AB 、AC 上，BE 与CD 相交于点O ，依据下列各个选项中所列举的条件，不能说明AC AB =的是（ ）（A ）CD BE =，DCB EBC ∠=∠；（B ）AE AD =，CD BE =；（C ）OE OD =，ACD ABE ∠=∠； （D ）CD BE =，CE BD =.二、填空题（本大题共有12题，每题3分，满分36分） 7．计算：4= ___________. 8.计算：328= .9．近似数290.0的有效数字有_______________个.10．在△ABC 中,如果30B ∠=︒,45C ∠=︒,那么按角分类,△ABC 是_________三角形． 11．经过点(2,1)P 且垂直于x 轴的直线可以表示为直线 ．12.对于同一平面内的三条不同直线a 、b 、c ，若a ∥b ，b ∥c,则直线a 、c 的位置关系是____________.13.如果等腰三角形的两边分别是2和3，那么这个三角形的周长为 . 14.在平面直角坐标系中，点M （-3，2）关于x 轴对称的点的坐标是____________． 15.在平面直角坐标系中，点A （－1，5）,A B ∥Y 轴，AB=4，则B 点的坐标是 ．A BE D O（第6题图）B16.直线AB 与CD 相交于点O ，∠AOC: ∠BOC=1:5，直线AB 与CD 夹角的度数是 度17.如图，AD ∥BC ，请写出图中面积相等的三角形： . 18.在直角坐标系中，已知点A （2，0），B （1，3），以AB 为边在第一象限内作正方形ABCD,则C 点坐标为 ，D 点坐标为 。

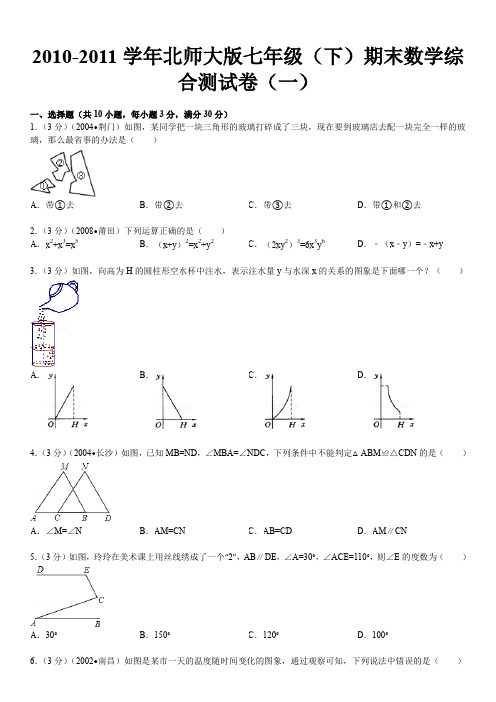
2010-2011学年北师大版七年级（下）期末数学综合测试卷（一）一、选择题（共10小题，每小题3分，满分30分）1．（3分）（2004•荆门）如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）3．（3分）如图，向高为H的圆柱形空水杯中注水，表示注水量y与水深x的关系的图象是下面哪一个？（）．C D．4．（3分）（2004•长沙）如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（）5．（3分）如图，玲玲在美术课上用丝线绣成了一个“2”，AB∥DE，∠A=30°，∠ACE=110°，则∠E的度数为（）6．（3分）（2002•南昌）如图是某市一天的温度随时间变化的图象，通过观察可知，下列说法中错误的是（）二、填空题（共10小题，每小题3分，满分30分）11．（3分）计算：x2•x3=_________；4a2b÷2ab=_________．12．（3分）（2005•扬州）若整式4x2+Q+1是完全平方式，请你写一个满足条件的单项式Q是_________．13．（3分）（2006•伊春）如图，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为_________度．14．（3分）（2006•无锡）温家宝总理在十届全国人大四次会议上谈到解决关于“三农”问题时说，2006年中央财政用于“三农”的支出将达到33 970 000万元，这个数据用科学记数法可表示为_________万元．15．（3分）（2005•南平）用6个球（除颜色外没有区别）设计满足以下条件的游戏：摸到白球的概率为，摸到红球的概率为，摸到黄球的概率为．则应设_________个白球，_________个红球，_________个黄球．16．（3分）等腰三角形一边长是10cm，一边长是6cm，则它的周长是_________cm或_________cm．17．（3分）（2005•海南）如图所示，A、B、C、D在同一直线上，AB=CD，DE∥AF，若要使△ACF≌△DBE，则还需要补充一个条件：_________．18．（3分）现在规定两种新的运算“﹡”和“◎”：a﹡b=a2+b2；a◎b=2ab，如（2﹡3）（2◎3）=（22+32）（2×2×3）=156，则[2﹡（﹣1）][2◎（﹣1）]=_________．19．（3分）某商贩购进一批苹果到集贸市场出售，已知卖出的苹果数量x与售价y的关系如下表：写出用含x代数式表示y：_________．20．（3分）某公路急转弯处设立了一面大镜子，从镜子中看到汽车的车辆的号码如图所示，则该汽车的号码是_________．三、解答题（共9小题，满分60分）21．（5分）（2008•双柏县）先化简，再求值：（a2b﹣2ab2﹣b3）÷b﹣（a+b）（a﹣b），其中a=，b=﹣1．22．（5分）在“五•四”青年节中，全校举办了文艺汇演活动．小丽和小芳都想当节目主持人，但现在只有一个名额．小丽想出了一个办法，她将一个转盘（均质的）均分成6份，如图所示．游戏规定：随意转动转盘，若指针指到3，则小丽去；若指针指到2，则小芳去．若你是小芳，会同意这个办法吗？为什么？23．（6分）如图，斜折一页书的一角，使点A落在同一书页的A′处，DE为折痕，作DF平分∠A′DB，试猜想∠FDE 等于多少度，并说明理由．24．（6分）如图，如果AD∥BC，∠B=∠C，那么AD是∠EAC的平分线吗？请说明你判别的理由．25．（6分）下面是我县某养鸡场2001～2006年的养鸡统计图：（1）从图中你能得到什么信息？（2）各年养鸡多少万只？（3）所得（2）的数据都是准确数吗？（4）这张图与条形统计图比较，有什么优点？26．（8分）两个全等的三角形，可以拼出各种不同的图形，如图所示中已画出其中一个三角形，请你分别补画出另一个与其全等的三角形，使每个图形分别成为不同的轴对称图形（所画三角形可与原三角形有重叠的部分），你最多可以设计出几种（至少设计四种）．27．（8分）某种产品的商标如图所示，O是线段AC、BD的交点，并且AC=BD，AB=CD．小明认为图中的两个三角形全等，他的思考过程是：在△ABO和△DCO中你认为小明的思考过程正确吗？如果正确，他用的是判定三角形全等的哪个条件？如果不正确，请你增加一个条件，并说明你的思考过程．28．（8分）（2002•吉林）一位农民带上若干千克自产的土豆进城出售．为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图，结合图象回答下列问题：（1）农民自带的零钱是多少？（2）求出降价前每千克的土豆价格是多少？（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，试问他一共带了多少千克土豆？29．（8分）乘法公式的探究及应用（1）如图1，可以求出阴影部分的面积是_________（写成两数平方差的形式）；（2）如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是_________，长是_________，面积是_________（写成多项式乘法的形式）；（3）比较图1、图2阴影部分的面积，可以得到公式_________；（4）运用你所得到的公式，计算下列各题：①10.2×9.8，②（2m+n﹣p）（2m﹣n+p）．2010-2011学年北师大版七年级（下）期末数学综合测试卷（一）参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）（2004•荆门）如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）3．（3分）如图，向高为H的圆柱形空水杯中注水，表示注水量y与水深x的关系的图象是下面哪一个？（）．C D．4．（3分）（2004•长沙）如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（）5．（3分）如图，玲玲在美术课上用丝线绣成了一个“2”，AB∥DE，∠A=30°，∠ACE=110°，则∠E的度数为（）6．（3分）（2002•南昌）如图是某市一天的温度随时间变化的图象，通过观察可知，下列说法中错误的是（）二、填空题（共10小题，每小题3分，满分30分）11．（3分）计算：x2•x3=x5；4a2b÷2ab=2a．12．（3分）（2005•扬州）若整式4x2+Q+1是完全平方式，请你写一个满足条件的单项式Q是±4x、4x4、﹣4x2、﹣1．13．（3分）（2006•伊春）如图，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为48度．14．（3分）（2006•无锡）温家宝总理在十届全国人大四次会议上谈到解决关于“三农”问题时说，2006年中央财政用于“三农”的支出将达到33 970 000万元，这个数据用科学记数法可表示为 3.397×107万元．15．（3分）（2005•南平）用6个球（除颜色外没有区别）设计满足以下条件的游戏：摸到白球的概率为，摸到红球的概率为，摸到黄球的概率为．则应设3个白球，2个红球，1个黄球．，××=2×=1．16．（3分）等腰三角形一边长是10cm，一边长是6cm，则它的周长是26cm或22cm．17．（3分）（2005•海南）如图所示，A、B、C、D在同一直线上，AB=CD，DE∥AF，若要使△ACF≌△DBE，则还需要补充一个条件：∠E=∠F．18．（3分）现在规定两种新的运算“﹡”和“◎”：a﹡b=a2+b2；a◎b=2ab，如（2﹡3）（2◎3）=（22+32）（2×2×3）=156，则[2﹡（﹣1）][2◎（﹣1）]=﹣20．19．（3分）某商贩购进一批苹果到集贸市场出售，已知卖出的苹果数量x与售价y的关系如下表：写出用含x代数式表示y：y=2.1x．20．（3分）某公路急转弯处设立了一面大镜子，从镜子中看到汽车的车辆的号码如图所示，则该汽车的号码是B6395．三、解答题（共9小题，满分60分）21．（5分）（2008•双柏县）先化简，再求值：（a2b﹣2ab2﹣b3）÷b﹣（a+b）（a﹣b），其中a=，b=﹣1．，×22．（5分）在“五•四”青年节中，全校举办了文艺汇演活动．小丽和小芳都想当节目主持人，但现在只有一个名额．小丽想出了一个办法，她将一个转盘（均质的）均分成6份，如图所示．游戏规定：随意转动转盘，若指针指到3，则小丽去；若指针指到2，则小芳去．若你是小芳，会同意这个办法吗？为什么？这说明小丽去的可能性是而小丽去的可能性是23．（6分）如图，斜折一页书的一角，使点A落在同一书页的A′处，DE为折痕，作DF平分∠A′DB，试猜想∠FDE 等于多少度，并说明理由．24．（6分）如图，如果AD∥BC，∠B=∠C，那么AD是∠EAC的平分线吗？请说明你判别的理由．25．（6分）下面是我县某养鸡场2001～2006年的养鸡统计图：（1）从图中你能得到什么信息？（2）各年养鸡多少万只？（3）所得（2）的数据都是准确数吗？（4）这张图与条形统计图比较，有什么优点？26．（8分）两个全等的三角形，可以拼出各种不同的图形，如图所示中已画出其中一个三角形，请你分别补画出另一个与其全等的三角形，使每个图形分别成为不同的轴对称图形（所画三角形可与原三角形有重叠的部分），你最多可以设计出几种（至少设计四种）．27．（8分）某种产品的商标如图所示，O是线段AC、BD的交点，并且AC=BD，AB=CD．小明认为图中的两个三角形全等，他的思考过程是：在△ABO和△DCO中你认为小明的思考过程正确吗？如果正确，他用的是判定三角形全等的哪个条件？如果不正确，请你增加一个条件，并说明你的思考过程．28．（8分）（2002•吉林）一位农民带上若干千克自产的土豆进城出售．为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图，结合图象回答下列问题：（1）农民自带的零钱是多少？（2）求出降价前每千克的土豆价格是多少？（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，试问他一共带了多少千克土豆？29．（8分）乘法公式的探究及应用（1）如图1，可以求出阴影部分的面积是a2﹣b2（写成两数平方差的形式）；（2）如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是a﹣b，长是a+b，面积是（a+b）（a ﹣b）（写成多项式乘法的形式）；（3）比较图1、图2阴影部分的面积，可以得到公式（a+b）（a﹣b）=a2﹣b2；（4）运用你所得到的公式，计算下列各题：①10.2×9.8，②（2m+n﹣p）（2m﹣n+p）．。

2011学年第二学期新思源初一期末数学试卷一、选择题（每小题2分、共20分） 1、下列各式是分式的是（ ）A 、B 、C 、D 、2、下列计算正确的是（ ） A 、＝ B 、＋2＝C 、＝D 、3、方程组⎩⎨⎧=+=-13432y x y x 的解是………………………………………………………（ ） （A ）⎩⎨⎧-==11y x（B ）⎩⎨⎧-=-=11y x（C ）⎩⎨⎧==12y x（D ）⎩⎨⎧-=-=72y x4、下列长度的三条木棒能制作成三角形的是（ ）A 、25．48．80B 、3．4．5C 、15．47．62D 、1．2．3 5、下列多项中，能因式分解的是（ ） A 、B 、C 、D 、6、下列事件中，可能性最大的是（ ）A 、从标有1～5共5个号码的5张纸片中，任取两张，它们的和恰好为10；B 、任意选择电视的频道，正好播放动画片；C 、早晨太阳从东方升起；D 、100件产品中有2件次品，从中任意取一件，取到次品。

7、若分式中的a 、b 都有扩大到原来的2倍，则分式的值（ ）A 、扩大到原来的2倍B 、扩大到原来的4倍C 、缩小到原来的D 、不变8、如图，在△ABC 中，AD ⊥BC 于D 点，BD=CD ，若BC=6，AD=5，则图中阴影部分的面积为……………………（ ）（A ）30 （B ）15 （C ）7.5 （D ）69、从1、2、3、4四个数中任意取两个求和，其结果最有可能是…………………（ ）（A ）3 （B ）4 （C ）5 （D）D BC610、如图所示，△ABC ≌△AEF ，AB ＝AE ，∠B ＝∠E ，在下列结论中，不正确的是（ ）A 、∠EAB ＝∠FAC B 、BC ＝EF C 、∠BAC ＝∠CAFD 、∠AFE ＝∠ACB二、填空题（每小题2分，共20分）11、据查阅有关资料，我国因环境污染造成的巨大经济损失，每年高达680000000元，这个数据用科学记数法表示为 元； 12、当x =时，分式293--x x 的值为零；13、如图：△ABD 与△CDB ，其中AB=CD ，则需要加 上条件 ，就可达到△ABD ≌△CDB ； 14、分解因式：=-22916b a；15、如图，往正方形地面任意抛掷一个小球，则此球 的着地点落在阴影部分的概率是 ； 16、如果是一个完全平方式，则k= ； 17、当x=2时，分式没有意义，则x=3时，分式的值等于 ；18、已知商品的买入价为a ，售出价为b ，则毛利率计算公式为p ＝，（p ≠-1），请用p 、b 的代数式表示a ＝ ； 19、如图，在△ABC 中，AI 和CI 分别平分∠BAC 和 ∠BCA ，如果∠B=X °，那么∠AIC= ； 20、如图，ABD ∆≌ACE ∆，点B 和点C 是对应顶点，8AB cm =，7BD cm =，3AD cm =，则=DC㎝.三、解答题（21，22，每小题4分共20分，23、24每小题6分共12分，25题8分，26、27每题10分共20分） 21、解方程（组） 〔1〕 x ＝y 6x －5y ＝3 〔2〕＝2x －5y ＝7 〔3〕 －＝1EDCB A22、计算：〔1〕＋〔2〕÷23、先化简再求值：(x＋1－)÷，其中x ＝24、如下图，由小正方形组成的L形图中，请你用三种方法分别在图中添画一个小正方形，使它成为轴对称图形：方法一方法二方法三25、一个口袋中放有20个球，其中红球6个，白球和黑球各若干个，每个球除了颜色以外没有任何区别。

2011-2012学年第二学期期末学业水平测试试卷（解析版）一、精心选一选，慧眼识金！1．下列图形中，是中心对称图形但不是轴对称图形的是（A）考点：中心对称图形；轴对称图形；生活中的旋转现象．分析：根据轴对称图形与中心对称图形的概念求解．解答：解：A、不是轴对称图形，是中心对称图形，符合题意；B、是轴对称图形，不是中心对称图形，不符合题意；C、是轴对称图形，也是中心对称图形，不符合题意；D、是轴对称图形，不是中心对称图形，不符合题意．故选A．点评：掌握中心对称图形与轴对称图形的概念．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．2、为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调查．那么最终买什么水果，下面的调查数据中最值得关注的是（ C ）A．中位数B．平均数 C．众数 D．加权平均数考点：统计量的选择．分析：根据平均数、中位数、众数的意义进行分析选择．解答：解：平均数、中位数、众数是描述一组数据集中程度的统计量．既然是为筹备班级的初中毕业联欢会做准备，那么买的水果肯定是大多数人爱吃的才行，故最值得关注的是众数．故选C．点评：此题主要考查统计的有关知识，主要包括平均数、中位数、众数的意义．反映数据集中程度的平均数、中位数、众数各有局限性，因此要对统计量进行合理的选择和恰当的运用．3、矩形不一定具有的特征是（C）A、对角线相等B、四个角是直角C、对角线互相垂直D、对边分别相等考点：矩形的性质．分析：矩形对角线的性质：平分、相等，但不垂直． 解答：解：A 、矩形的对角线平分、相等，故A 具有； B 、矩形的四个角都是直角，故B 具有；； C 、矩形的对角线平分、相等，故C 不具有； D 、矩形的对边相等，故D 具有；故选C ．点评：本题考查矩形的性质：对边平行且相等，矩形的对角线平分、相等，四个角都是直角．4．不等式组2130x x ≤⎧⎨+≥⎩的解集在数轴上可以表示为（ A ）ACD 5、关于x 的方程a x 4125=+的解都是负数，则x 的取值范围是（ A ） A 、<3a Ｂ、<3a - Ｃ、>3a Ｄ、>3a - 考点：一元一次方程的解；解一元一次不等式．分析：本题首先要解这个关于x 的方程，求出方程的解，根据解是负数，可以得到一个关于a 的不等式，就可以求出a 的范围． 解答：解：解关于x 的方程得到：x=4-125a ，根据题意得：4-125a ＜0，解得a ＜3．故选A点评：本题是一个方程与不等式的综合题目．解关于x 的不等式是本题的一个难点． 6．若25kx 9x2++是完全平方式，则k=（ D ）A 、30 Ｂ、30- Ｃ、15± Ｄ、30± 考点：完全平方式． 分析：由于25kx 9x2++是完全平方式，根据完全平方公式得到25kx 9x2++=2(35)x ±，然后把2(35)x ±展开得2930+25x x ±，即可得到k 的值． 解答：解：∵25kx 9x2++是完全平方式，∴25kx 9x 2++=2(35)x ±， 而2(35)x ±=2930+25x x ±， ∴k=30±． 故答案为30±．点评：本题考查了完全平方公式：2222+=()a ab b a b ±± 二、耐心填一填，一锤定音！7．要使正方形旋转后与自身重合，至少将它绕中心顺时针旋转 90° 考点：旋转对称图形．分析：正方形可以被其对角线平分成4个全等的部分，则旋转的角度即可确定．解答：解：要使正方形旋转后，与其自身重合，至少应将它绕中心逆时针方向旋转的度数是 360°÷4 =90°．点评：本题考查旋转对称图形，解答此题的关键是要明确“至少应将它绕中心顺时针旋转的度数”为其中心角的度数，然后根据正方形中心角的求法解答．8、已知一个多边形的内角和是它的外角和的2倍，则这个多边形的边数为 六 ． 考点：多边形内角与外角．分析：多边形的外角和是360°，内角和是它的外角和的2倍，则内角和是2×360=720度．n 边形的内角和可以表示成（n-2）•180°，设这个多边形的边数是n ，就得到方程，从而求出边数解答：解：设这个多边形的边数为n ，∵n 边形的内角和为（n-2）•180°，多边形的外角和为360°， ∴（n-2）•180°=360°×2， 解得n=6．∴此多边形的边数为六．点评：本题主要考查了多边形的内角和定理以及多边形的外角和定理，注意多边形的外角和不随边数的变化而变化．9. 若一组数据6,9,9,x,12，6的众数是9，则x 的值是 9 考点：众数．分析：众数又是指一组数据中出现次数最多的数据，根据定义就可以求出． 解答：解：因为一组数据6,9,9,x,12，6的众数是9，根据众数的定义，9出现的次数最多，因为6已经出现了2次，所以9必出现3次． 所以x 是9．点评：本题比较容易，考查众数的知识．解题的关键是此题的众数是唯一的． 10. 菱形的对两条对角线长分别是10cm 和24cm ，则这菱形的面积为2120cm 11.2ab a 分解因式的结果是a(b+1)(b-1)12. 如图，△ABC 以点A 旋转中心，按逆时针方向旋转60°，△AB ′C ′，则△ABB ′是等边 三角形。

七年级第二学期期末考试数学试卷（满分100分，考试时间90分钟） 2011.6题号 一 二 三四 总分 得分一、选择题：（本大题共6题，每题3分，满分18分） 1. 下列四个实数中，一定是无理数的是（ ）（A ）22-； （B ）327-； （C ）1415926.3； （D ）13133.0……. 2. 下列四个式子中，正确的是（ ）（A ）981±=； （B ）662=--）（； （C ）41621=； （D ）5322=+）（. 3. 某网站2011年4月28日报道：国务院第六次全国人口普查登记发现，中国总人口已经达到7.13 亿.这里的近似数“7.13亿”精确到（ ）（A ）亿位； （B ）千万位； （C ）百万位； （D ）十分位. 4. 下列说法中，正确的是（ ）（A ）两条直线被第三条直线所截，同位角相等；（B ）联结直线外一点到直线上各点的所有线段中，垂线最短； （C ）经过一点，有且只有一条直线与已知直线平行；（D ）在平面内经过直线上或直线外的一点作已知直线的垂线可以作一条，并且只可以作一条. 5. 下列条件中，不能说明ABC △为等边三角形的是（ ）.（A ）︒=∠=∠60B A ； （B ）︒=∠+∠120C B ； （C ）︒=∠60B ，AC AB =； （D ）︒=∠60A ，AC AB =. 6. 等腰三角形的顶角为α，那么这个等腰三角形一条腰上的高与底边的夹角为（ ）（A ）α； （B ）α-︒90； （C ）α21； （D ）α2． 二、填空题（本大题共12题，每题2分，满分24分） 7. 化简：=-23 . 8. 如果814=y ，那么=y .9. 计算：=-222425 . 10.把433写成幂的形式：________． 11.比较大小：3- 10-（填“>”，“=”，“<” ）．12.已知直线a 、b 、c ，满足a ∥b ，a ∥c ，那么直线b 、c 的位置关系是 . 13.如图1.已知︒=∠100DEF ，请增加一个条件使得AB //CD ，这个条件可以是 .ABC北东（图2）14.经过点)3,1(-Q 且垂直于y 轴的直线可以表示为直线 . 15.如果点),(b a P 在第三象限，那么点P 到x 轴的距离是 ．16.在直角坐标平面内，将点），32(A 向右平移4个单位长度所对应的点的坐标是 . 17.等腰三角形的周长是50,一边长为10，则其余两边长为 . 18.如图2.在一次夏令营活动中，某同学从营地A 点出发，先沿北偏东︒70 方向到达B 地，再沿北偏西︒15方向去目的地C ,则ABC ∠的度数是 . 三、简答题（本大题共4题，每题8分，满分32分）19.计算：232131033276205)13(⨯-⨯-⨯+--.20.试卷上的一个等腰三角形被墨汁污染了，现在只有它的底边AB 和B ∠还清楚可见（如图3）.请用直尺与圆规画出一个与原来形状一样的等腰三角形（不写画法，保留画图痕迹，写出最后答案）.21. 如图4.在ABC △中，点D 是边BC 上的一点，点E 在边AC 上.（1）如果B CAD ∠=∠，那么BAC ∠与ADC ∠相等吗？为什么？ （2）如果C ADE ∠=∠，那么ADB ∠与CED ∠相等吗？为什么？ （3）已知C ADE ∠=∠，试说明ADC AED ∠=∠的理由. 解：（1）（在括号内填写依据）在ABC △中，︒=∠+∠+∠180C B BAC ，在ADC △中，︒=∠+∠+∠180C CAD ADC （ ）. 所以=∠+∠+∠C B BAC C CAD ADC ∠+∠+∠（等量代换）. 因为B CAD ∠=∠（已知）， ABDE （图4）AC（图3）（2）（在括号内填写依据）因为C CED BDE ∠+∠=∠（ ）， 即=∠+∠ADE ADB C CED ∠+∠.又C ADE ∠=∠（已知），所以=∠ADB CED ∠（等式性质）. （3）22.如图5.在ABC △中，点D 、E 分别在边AB 、AC 上，且满足CD BE =，21∠=∠.试说明ABC △是等腰三角形的理由.四、解答题（本大题共3题，满分26分）23.（本题满分8分）在直角坐标平面内，点A 的坐标为（2，0），点B 与点A 关于原点对称；点C 的坐标为（2，3），点D 与点C 关于x 轴对称.（1）分别写出点B 、点D 的坐标，在图6所示的直角坐标平面内画出BCD △，并求其面积；（2）已知点B 与点D 的距离为5，试求点C 到直线BD 的距离. （图6）ABCED 1 2（图5）24.（本题满分9分）已知等边ABC △，点D 在射线CA 上，点E 在射线AB 上，且BE AD =. （1）如图7.当点D 、E 分别在ABC △的边CA 、AB 上，求BPE ∠的度数； （2）如图8.若点D 、E 分别在ABC △的边CA 、AB 的延长线上， ① 直线BD 与直线CE 的夹角是多少度？简述理由.②（供民办学校的同学选做．．．．．．．．．．）过点B 作BF ∥EC ，交AC 于点F ，试判断ABD ∠与CBF ∠的大小，在图8的基础上画出图形并简述说理过程.解： ABC D EP（图7）AB CDE P（图8）25.（本题满分9分）已知ABC △中，AC AB =，︒=∠45BAC .绕点C 顺时针旋转ABC △，使点B 落在AB 边上，得C B A 11△（如图9），联结1AA .（1）说明AB ∥C A 1的理由；（2）11AB A △与A CB 1△全等吗？为什么？（3）绕点C 顺时针旋转ABC △，使点B 落在AC 边上，得C B A 22△（如图10），联结2AA . 求22A AB ∠的度数. 解：AB C1B1A（图9）BAC2B2A（图10）参考答案（若答案有误，请自行更正）一、选择题：（本大题共6题，每题3分，满分18分） 1、A ；2、C ；3、B ；4、D ；5、B ；6、C.二、填空题（本大题共12题，每题2分，满分24分）7、32-；8、3±；9、7；10、433；11、>；12、b ∥c ；13、︒=∠100AFE （方法不唯一）；14、3-=y ；15、b -；16、（6,3）；17、20,20；18、︒95. 三、简答题（本大题共4题，每题8分，满分32分）19.解：原式=23213333161001+-⨯-+…………………………………………4分23316101-⨯-+=………………………………………………………3分 =092101=--+.…………………………………………………………1分 20.解：评分标准：（1）体现截取AB B A =11的痕迹，……1分；（2）体现出作线段11B A 的垂直平分线的痕迹，……1分； （3）体现出作B C B A ∠=∠111的痕迹，…………1分； （4）确定出交点C ，画出所要求的等腰三角形，……4分； （5）写出答案，指明所求作的三角形，…………1分.CA B（第20题图）1A1B1CABC △全等.21.解：（1）在ABC △中，︒=∠+∠+∠180C B BAC ，在ABC △中，︒=∠+∠+∠180C CAD ADC （三角形的内角和等于︒180 ）.……2分 所以=∠+∠+∠C B BAC C CAD ADC ∠+∠+∠（等量代换）. 因为B CAD ∠=∠（已知）， 所以=∠BAC ADC ∠（等式性质）.（2）因为C CED BDE ∠+∠=∠（三角形的一个外角等于与它不相邻的两个内角的和），…2分即=∠+∠ADE ADB C CED ∠+∠.又C ADE ∠=∠（已知），所以=∠ADB CED ∠（等式性质）. （3）这里提供两种方法，供参考.方法1：使用第（1）小题的方法；方法2：在第（2）小题的基础上，使用“等角的补角相等”说理. 无论使用哪种方法说理，只要正确，皆可得4分.22.解：因为︒=∠+∠1801ADC ，︒=∠+∠1802AEC （邻补角的意义），……………1分21∠=∠(已知)，所以 AEC ADC ∠=∠（等角的补角相等）.……………1分 在ABE △和在ACD △中，⎪⎩⎪⎨⎧=∠=∠∠=∠,,CD BE A A ADC AEB （公共角），所以ABE △≌ACD △（A.A.S ）.………………………4分 所以AC AB =（全等三角形的对应边相等）.………………1分 所以 ABC △是等腰三角形.…………1分 备注：其他方法请参照评分标注评分. 四、解答题（本大题共3题，满分26分） 23.解：（1）)0,2(-B ，)3,2(-D .……1分； 画出 BCD △，…………2分；633=--=CD ，422=--=）（BA ，……1分1ABCED 1 2（第22题图）.. ..CADB HABCDE （图4）124621=⨯⨯=…………1分 （2）过点C 作BD CH ⊥，垂足为点H .……1分； 因为 CH BD S BCD ⋅⋅=∆21，12=∆BCD S ， 所以1221=⋅⋅CH BD . 因为5=BD ，所以12521=⨯CH .解得 524=CH .所以点C 到BD 的距离为524.…………………………2分.24.解：（1）因为ABC △是等边三角形（已知），所以BC AB =，EBC A ∠=∠（等边三角形的性质）.……1分 在ABD △和BCE △中，⎪⎩⎪⎨⎧=∠∠=∠=,,,BE AD EBC A BC AB 所以ABD △≌BCE △（S.A.S ）. ……1分所以 BCE ABD ∠=∠（全等三角形的对应角相等）. ……1分所以︒=∠=∠+∠=∠+∠=∠60ABC CBD ABD CBD BCE EPB .……1分 （2）①因为ABC △是等边三角形（已知），所以︒=∠=∠60ABC BAC ，BC AB =（等边三角形的性质）. 所以︒=∠-︒=∠120180BAC BAD ，︒=∠-︒=∠120180ABC CBE .所以CBE BAD ∠=∠.……1分 在ABD △和BCE △中，⎪⎩⎪⎨⎧==∠=∠,,,BE AD BC AB CBE BAD 所以ABD △≌BCE △（A.S.A ）.所以 E D ∠=∠（全等三角形的对应角相等）.……公办学校2分，民办学校1分 所以 ︒=∠=∠+∠=∠+∠=∠60BAC ABP D EBP E DPC . 故直线BD 与CE 的夹角等于︒60.……公办学校2分，民办学校1分. ② CBF ABD ∠=∠.…………1分 A BCD EP（第24题图①）AB CDE P（图8）由①可知，︒=∠=∠60BAC DPC ， 所以 ︒=∠=∠60DPC DBF .所以 ABF CBF ABF ABD ∠+∠=∠+∠. 所以CBF ABD ∠=∠.…………1分25.解：（1）方法1：因为AC AB =，所以 ACB B ∠=∠.因为C B BC 1=，所以B C BB ∠=∠1.因为 ︒=∠+∠18021B BCB ，︒=∠+∠1802B BAC ， 所以︒=∠=∠451BAC BCB .………………1分 因为 111ACB ACB CA A ∠=∠+∠，ACB ACB BCB ∠=∠+∠11， ACB CB A ∠=∠11，所以︒=∠=∠4511BCB CA A .…………1分所以 AB ∥C A 1（内错角相等，两直线平行）.………………1分 方法2：︒=∠=∠5.671B C BB ，︒=︒⨯-︒=∠455.6721801BCB . 以下类同方法1的说明过程.（2）因为AB ∥C A 1，所以︒=∠=∠451111C A B A AB . 所以︒=∠=∠45111CAB A B A .……………………1分 因为AB B A =11,AC AB =，所以AC B A =11.…………1分在11AB A △与A CB 1△中，⎪⎩⎪⎨⎧=∠=∠=,,,1111111A B AB CAB A B A CA B A 所以11AB A △≌A CB 1△（S.A.S ）……………………1分 （3） ︒=∠=∠5.6722ACB CB A .因为AC C A =2，所以AC A C AA 22∠=∠. 所以 ︒=︒-︒=∠-︒=∠25.56)5.67180(1)180(122CA A C AA . …………………1分 ABC1B1A（图10）又因为︒=∠=∠4522BAC B CA ，所以 ︒=︒-︒=∠25.114525.5622A AB .………1分。

2011 第二学期期末考试七年级数学试卷三题号一二总分1718 19 20 21 22 23得分一、选择题（每题 3 分，共 30 分）1．实数 1、 3 、3.14 、 25 中，无理数有············（）3A ．1 个B．2 个个个2. 已知 a b, 则以下不等式建立的是· ················( ) A. a c b cB.a cbcC. ac bcD.a bcc3. 以下计算错误的选项是·······························（）A. x 3 x 4 x 7B. (x 2 )3x 6 C. x 3 x 3 x D. ( 2xy 2 )4 16x 4 y 84．化简a b 的结果是·························（）a ba bA. a 2 b 2B.(a b)2C.a 2b 2 D.a 2b 2a 2b 2a 2b 2a 2b 2( a b)25. 以下各式中，与 ( a 1) 2 相等的是···················（ ）A. a 2 1B ． a 21 C. a 22a 1 D.a 2 2a 16. 把 a 3 ab 2 分解因式，正确结果是···················（ ）A. (a 2b)(a 2b)B.a(a 2 b 2 ) C. a(ab)(a b) D.a(a b) 27．不论 x 为任何实数，以下分式都存心义的是· ··········（ ）A.1B.1C.1D.1x 23x3 x 2 1x8. 剖析以下说法，选出你以为正确的一项· ············（）A. 两个形状和大小都同样的图形能够当作此中一个是另一个平移获得的B. 由平移获得的两个图形的形状和大小同样C. 边长相等的两个正方形必定可当作是由平移获得的D. 图形平移后对应线段不行能在同向来线上9. 如图，已知 OC AB ，OD 均分AOC ，D 、O 、E 、三点在同一条直线上，那么 AOE 等于·························（）A. 45B. 50C. 135D.C155D10. 现装置 30 台机器，在装置好 6 台此后，因为采纳了新的技术，每日的工作效率提 AB高了一倍，结果共用了3 天达成任务，求OE本来每日装置机器的台数。

2011年七年级数学期末试卷第一学期班级_________ 姓名________ 学号_________一、填空（每小题2分，共20分）1、-181的倒数是 。

2、如果x= -3，那么x 的相反数是 。

3、计算-2-5= 。

4、比较-54和-65的大小，结果是：-54 -65 5、据统计，到2005年底，某州总人口约为391万，如果用科学记数法来表示，可以表示成 人。

6、木工师傅要把一根14m 长的木头锯成七段，锯一段要用5分钟，一共需要 分钟。

7、1.45度= 分= 秒。

8、2700秒= 分 度。

9、当x= 时，代数式513-x —1等于零。

10、将圆分成三个扇形，其三个扇形的面积比为2：3：4，则最小那个扇形的圆心角为 度二、选择（每小题3分，共30分）11、下列说法中，不正确的是（ ）A 有最小正整数，没有最小的负整数B 若一个数是整数，则它一定是有理数C 0既不是正有理数，也不是负有理数D 正有理数和负有理数组成有理数12、三峡大坝坝顶从2005年7月到9月共92天对游客开放，每天限接待1000人，在整个开放期间最多能接待游客的总人数用科学记数法表示为（ ）A 92×103人 B.9.2×104人 C.9.2×103人 D.9.2×105人13、下列各数中,不相等的组数有( )①(-3)2与-32 ②(-3)2与32 ③(-2)3与-23 ④2-3与32- ⑤(-2)3与2-3 A.0组 B.1组 C.2组 D.3组14、计算23()a a b--的结果是（）Ａ．3a b--Ｂ．3a b-Ｃ．3a b+Ｄ．3a b-+15、汽车以72千米/时的速度在公路上行驶，开向寂静的山谷，驾驶员揿一下喇叭，4秒后听到回响，这时汽车离山谷多远？已知空气中声音的传播速度约为340米/秒．设听到回响时，汽车离山谷x米，根据题意，列出方程为（）Ａ．24204340x+⨯=⨯Ｂ．24724340x-⨯=⨯Ｃ．24724340x+⨯=⨯Ｄ．24204340x-⨯=⨯16、有一个商店把某件商品按进价加20%作为定价，可是总卖不出去；后来老板按定价降价20%以96元出售，很快就卖掉了.则这次生意的赢亏情况为（）A．亏4元 B.亏24元 C.赚6元 D.不亏不赚.17、两个角大小的比为7﹕3，它们的差是72°，则这两个角的数量关系是（）A. 相等B. 互补C. 互余D. 无法确定18、图表示从上面看一个由相同小立方块搭成的几何体得到的平面图形，小正方形中的数字表示该位置上小立方块的个数，则该从正面看该几何体得到的平面图形为（）19、下列调查中不适合抽样调查的是( )A.调查某景区一年内的客流量;B.了解全国食盐加碘情况;C.调查某小麦新品种的发芽率; C.调查某班学生骑自行车上学情况;20、如图是某学校七年级学生跳绳成绩的条形统计图（共三等），则下面回答正确的是（）A. C等人最少，只有40人B. 该学校七年级共有120人C. A等人占总人数的30%D. B等人最多，占总人数的2 3第14题A．B．Ｃ．Ｄ．三、计算题（共18分）21．计算（每题5分，共10分）（1）41)4(2)2(3÷-⨯-- （2）]2)31()4[(10223⨯---+-23.化简求值：5(3a 2b －ab 2) －(ab 2+3a 2b), 其中a=21，b=31。

2011学年第一学期七年级数学期末试卷参考答案、评分意见一、选择题（每题3分，共30分）二、填空题（每空2分，共20分）11.__-1 _4 12.a+1 13、2011；14. 2.5 ；15.7.5 ；17.55 18. 10 ；19. 2.5或8 (一个值1分) 三、解答题 20、(1)原式=12133344+-- （2分） (2)原式=2(1)2(2)⨯-+⨯- （2分） =0 （3分） = -6 ( 3分) （3）原式=103.460.6︒-︒ （1分）=62.8︒ （3分） 21.(1) 2354t t -=+ (2分) (2).3(31)62(1)x x -+=+ ( 1分)9-=t （4分） 71x =- (3分)17x =- （4分） 22.(1) 原式=3122161x y x y --++ （2分） 41x y =++ （3分）12,41)124x y =-=-⨯+=-当时原式=-2+4(- （5分）23.（1）有4种作图法,只要作出其中一个,给3分(1) (2)(3) (4) （2）(每个图形有一种关系,对应图形作答)相等 (4分) 相等 (4分)∵OC ⊥OA,OD ⊥OB ∵OC ⊥OA,OD ⊥OB∴∠COD+∠AOD=90° ∴∠COD+∠BOC=90° ∠AOB+∠AOD=90° ∠AOB+∠BOC=90°∴∠AOB=∠COD （6分） ∴∠AOB=∠COD （6分）互补 （4分） 互补 （4分）∵OC ⊥OA,OD ⊥OB ∵OC ⊥OA,OD ⊥OB ∴∠AOC=∠BOD=90 ∴∠AOC=∠BOD=90 ∵∠AOC+∠BOD+∠AOB+∠COD=180° ∴∠AOB+∠COD =∴∠AOB+∠COD=180° (6分) ∠AOC+∠BOD= 180° (6分)24.(1) 400，（1分） 280 （2分） (2)赞成10%（3分），反对70% （4分）(3)表示家长“赞成”的圆心角：36010%36︒⨯=︒ （6分） （4）120070%840⨯= （8分） 25解：（1）设这列地铁有x 节车厢 （2）设这些乘客中有x 成人200x+150=230(x-1)+20 （2分） 5x+3(500-x)=2300 (5分) x=12 （3分） x=400 （6分） 答:这列地铁有12节车厢 答：这些乘客中有400成人,100个儿童 26.解：（1）40 º （1分） （2α）º （2分）∠BOE =2∠COF (4分) （2）成立 (5分)设∠AOC=β，则∠AOF=290β-︒,所以∠C OF=45°+2β=21(90°+β) (6分)∠BOE=180°﹣∠AOE=180°﹣(90°﹣β)=90°+β所以∠BOE=2∠C OF(8分)。

2010—2011学年度第二学期期末考试七年级数学试卷本试卷分选择题和非选择题两部分，共三大题23小题，共4页，满分100分．考试时间90分钟 一、选择题(本大题共10小题，每小题2分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．)1．已知二元一次方程3x －y =1，当x =2时，y 等于（ ） A ．5 B ．－3 C ．－7 D ．7 2．不等式组⎩⎨⎧-≥-≥23x x 的解集在数轴上表示正确的是（ ）Ox2-3-A Ox2-3-B Ox2-3-C Ox2-3-D3．下列调查，比较容易用普查方式的是( )A 、了解某市居民年人均收入B 、了解某市初中生数学的中考成绩C 、了解某市中小学生视力情况D 、了解某一天离开该市的人口流量 4．如图，直线AB 与直线CD 相交于点O ，OE ⊥AB ，垂足为O ，∠EOD=21∠AOC ，则∠BOC=（ ） A ．150° B ．140° C ．130° D ．120°O EDCBAEDCBAHF GDCBA第4题图 第8题图 第12题图5．以下各组线段为边，可组成三角形的是（ ）A ．a =15cm ，b =30cm ，c = 45cmB ．a =30cm ，b =30cm ，c = 45cmC ．a =30cm ，b = 45cm ，c = 75cmD ．a =30cm ，b =45cm ，c = 90cm 6．在平面直角坐标系中，线段AB 两端点的坐标分别为A （1，0），B （3，2）. 将线段AB 平移后，A 、B 的对应点的坐标可以是（ ） A ．（1，－1），（－1，－3） B ．（1，1），（3，3） C ．（－1，3），（3，1） D ．（3，2），（1，4）7．一个多边形的内角和比它的外角和的3倍少180°，则这个多边形的边数为（ ） A ．5 B ．6 C ．7 D ．88．如图，下列条件中，不能判断直线AB ∥CD 的是（ ）A ．∠HEG =∠EGFB ．∠EHF +∠CFH =180°C ．∠AEG =∠DGED ．∠EHF =∠CFH 9．如图，周长为34cm 的长方形ABCD 被分成7个形状大小完全相同的小长方形，则长方形ABCD 的面积为（ ） A ．49cm 2 B ．68cm 2 C ．70cm 2 D ．74cm 210．某种商品的进价为80元，出售时标价为120元，后来由于该商品积压，商店准备打折出售，但要保证利润率不低于5%，则至多可打（ ）A ．六折B ．七折C ．八折D ．九折 二、填空题(本大题共6小题，每小题3分，共18分．)11、小明在计算一个多边形的内角和时，由于粗心少计算了一个内角，结果得1345°，则未计算的内角的大小为_____12、若方程组234,3223x y x y m +=⎧⎨+=-⎩的解满足x+y=15，则m=______．13．调查某种家用电器的使用寿命，合适的调查方法是___________调查（填“抽样”或“全面”）.14．如图，已知AB 、CD 、EF 互相平行，且∠ABE =70°，∠ECD = 150°，则∠BEC =________.15．点P （3a + 6，3－a ）在x 轴上，则a 的值为___________.16．把m 个练习本分给n 个学生，如果每人分3本，那么余80本；如果每人分5本，那么最后一个同学有练习本但不足5本，n 的值为___________. 三、解答题（共7小题，共72分） 17．（本题10分）解方程组（1）⎩⎨⎧=-=+351143y x y x . （2）18．（本题10分）解下列不等式（组）（1） 3273248x x +--> （2） （2）273(1),4231.33x x x x -<-⎧⎪⎨+≤-⎪⎩19．（本题8分）在平面直角坐标系中，四边形ABCD 的顶点坐标分别为A （1，0），B （5，0），C （3，3），D （2，4）.（1）求四边形ABCD 的面积.（2）把原来ABCD 各个顶点纵坐标保持不变，横坐标增加3，所得的四边形面积又是多少？Oy x543214321DCB AFE D CB A20、（本题满12分，每小题6分）（1）已知AE 平分∠BAC ，CE 平分∠ACD ，且∠1+∠2=90°，试说明AB//CD ．（2）如图，在△ABC 中，AD 是高线，点M 在AD 上，且∠BAD =∠DCM ，求证：CM ⊥AB .DCBMA21．（本题10分）某中学新建了一栋4层的教学大楼，每层楼有8间教室，进出这栋大楼共有4道门，其中两道正门大小相同，两道侧门大小也相同．安全检查中，对4道门进行了测试：当同时开启一道正门和两道侧门时，2分钟内可以通过560名学生；当同时开启一道正门和一道侧门时，4分钟内可以通过800名学生．（1）求平均每分钟一道正门和一道侧门各可以通过多少名学生？（2）检查中发现，紧急情况时因学生拥挤，出门的效率将降低20%，安全检查规定，在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离．假设这栋教学大楼每门教室最多有45名学生，问：建造的这4道门是否符合安全规定？请说明理由．22、（本题10分）某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机的进货量的一半．电视机与洗衣机的进价和售价如下表：类别电视机洗衣机进价（元/台）1800 1500售价（元/台）2000 1600计划购进电视机和洗衣机共100台，商店最多可筹集资金161 800元．（1）请你帮助商店算一算有多少种进货方案？（不考虑除进价之外的其它费用）（2）哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多？并求出最多利润．（利润＝售价－进价）23、（本题10分）某学校为了学生的身体健康，每天开展体育活动一小时，开设排球、然球、羽毛球、体操课。

2011年下学期七年级期末考试试卷数 学（时量：120分钟 满分：120分）一、精心选一选，旗开得胜 (每小题3分, 满分30分，请将正确答A. 2011B. -2011C.12011 D. -120112．第六次全国人口普查数据显示，中国大陆31个省、自治区、直辖市和现役军人的人口共约13.4亿人，大陆总人口这个数据用科学记数法表示为A. 1.34⨯105人B. 1.34⨯108人C. 1.34⨯109人D. 1.34⨯1010人 3．表示“x 与4-的和的3倍”的代数式为A ．3)4(⨯-+xB ．3)4(⨯--xC ．)4(3+xD ．)]4([3-+x 4．化简[][])()(y x y x +-----可得A ．x 2B ．y 2C ．y x 22+D ．y x 22- 5．站在笔直的公路中间，往公路的远处望，所看到的公路是A ．远处宽，近处窄B ．远处窄，近处宽C ．远近一样宽D ．以上都不对6. 下列方程: (1)132=+y x , (2)63=-m , (3)13221=+x , (4) 212=+x , (5) 4213=-x , 其中一元一次方程的个数是A ．1个B ．2个C ．3个D ．4个7．不等式54≤-x 的解集是 A ．45-≤x B ．54-≤x C ．54-≥x D ．45-≥x 8. 不等式12-4x ≥13的正整数解的个数是A ．0个B ．1个C ．2个D ．3个9. 电脑公司为了宣传某种品牌电脑近几年的销售价格在逐年降低，你认为公司用来表示这些数据最恰当的统计图是．A ．条形统计图B ．折线统计图C ．扇形统计图D ．统计表10. 在一次100米竞赛中，6名学生所用时间(秒)是：14，16，16，17，18，19，其中正确的说法是A. 中位数是16B.平均数是16C.众数是16D. 以上都不是。

二、细心填一填，一锤定音 (每小题3分, 满分24分)11. 2-的绝对值是______________.12. 已知珠穆朗玛峰海拔8848米， 吐鲁番盆地海拔-155米， 珠穆朗玛峰比吐鲁番盆地海拔高 米． 13. 若单项式n y x 25与32y x m -的和仍为单项式，则)(n m +的值为 .14. 已知代数式x+2y 的值是3，则代数式3x+6y+1的值为 . 15. 一个正方体有8个顶点、12条棱、_________个面． 16. 三个连续奇数的和是6033，则这三个奇数分别是______ ________.17. 请写出一个一元一次不等式，使它的解集在数轴上表示如图1所示，该不等式为 . 图118. 已知一组数据23,25,20,15,x ,15，若它们的中位数是21，那么x 的值为___________.三、耐心做一做，慧眼识金 (每小题6分, 满分18分)19.计算：])1(3[]31)24([)1()2()3(232--÷⨯----⨯-⨯- .20．已知3-=x 是方程106+=-a ax 的解，求a 的值．得分得分21. 当x 在什么范围内取值时，代数式312-x 的值不大于代数式22+x 的值.四、用心画一画，马到成功(每小题4分，满分8分)22．有两根竹竿AB ，CD 在同一个平面上直立着，如图2，竹竿AB 在太阳光下的影子BE 与AB一样长，请你在图2中画出这时木棒CD 在太阳光下的影子．图223．七巧板游戏是我国古代人民创造的益智游戏，用七巧板可以拼出许多图形，利用如图3所示的七巧板分别拼出了如图4所示的狐狸和小桥，请你在图4中拼成狐狸和小桥的各部分中分别标出七巧板中的第3块和第5块．七巧板图3 狐狸 图4 小桥得分五、综合用一用，再接再厉(每小题8分，满分24分)24．有15名同学的期末考试成绩如下：685，678，682，679，686，685，678，676，677，689，684，679，678，688，686（1）如果要你用简便方法算出这15名同学的平均成绩,你应定多少分为标准,超出的记为正,不足的记为负,并把他们的成绩用正负表示出来；(2)用以上的简便方法算出这15 名同学期末考试的平均成绩.25.小明带了35元钱去菜市场买东西，已经买了每千克价格为4元的饺子皮2千克，还需买每千克价格为36元的肉馅，要使所带的钱够用，你认为小明买肉馅的质量应控制在什么范围以内？26.如图5所示是冷水江实验中学七年级（5）班同学参加课外研究性学习小组的情况统计图，(1)从这个扇形统计图中可知参加哪个小组的人数最多？(2)若这个班共有50人，则参加“科技”小组的同学有多少人？（3）扇形统计图中，表示参加“生物”小组人数的扇形的圆心角的度数为多少度？（4）从扇形统计图中可知，同学们对参加哪个组（学科）的学习兴趣有待加强？图5六、探究试一试，超越自我(每小题8分，满分16分)得分27.如下图6，用火柴棒按以下方式搭小鱼，搭1条小鱼用8根火柴棒，搭2条小鱼用14根火柴棒……,请探究：图6(1)、搭10条小鱼需要用多少根火柴棒？你是怎样得出的？(2)、搭m条小鱼需要用多少根火柴棒？28．某开发公司要生产若干件新产品，需要精加工后，才能投放市场，现有红星和巨星两个加工厂都想加工这批产品，已知红星厂单独加工比巨星厂单独加工这批产品多用20天，红星厂每天可加工16件产品，巨星厂每天可加工24件产品，公司需付红星厂每天加工费80元，巨星厂每天加工费120元.（1）这个公司要加工多少件新产品？（2）在加工过程中，公司需另派一名工程师每天到厂家进行指导，并负责每天5元的午餐补助费，公司制定产品加工方案如下：可由一个厂单独加工完成，也可以由两厂合作完成，请你帮助公司从所有可供选择的方案中，选择一种既省钱又省时的加工方案.。