河北省衡水中学高2020届高2017级高三数学二轮复习课件配套课件讲义第1部分 专题2 第1讲

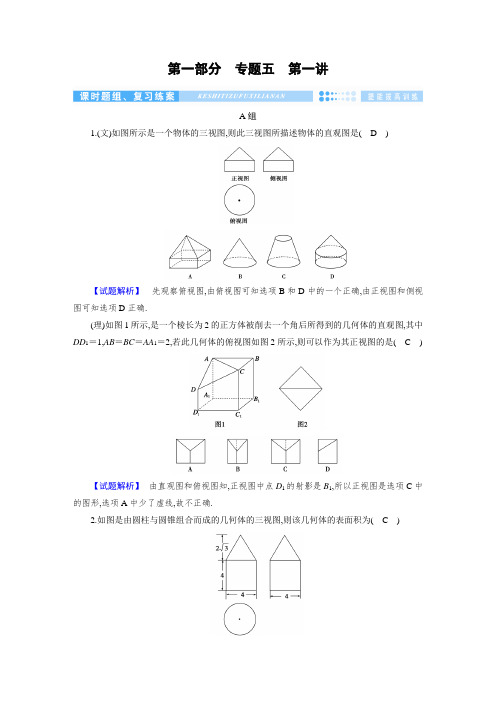
第一部分专题五第一讲A组1.(文)如图所示是一个物体的三视图,则此三视图所描述物体的直观图是(D)【试题解析】先观察俯视图,由俯视图可知选项B和D中的一个正确,由正视图和侧视图可知选项D正确.(理)如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中DD1＝1,AB＝BC＝AA1＝2,若此几何体的俯视图如图2所示,则可以作为其正视图的是(C)【试题解析】由直观图和俯视图知,正视图中点D1的射影是B1,所以正视图是选项C中的图形,选项A中少了虚线,故不正确.2.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(C)A.20πB.24πC.28πD.32π【试题解析】 该几何体是圆锥与圆柱的组合体,由三视图可知圆柱底面圆的半径r ＝2,底面圆的周长c ＝2πr ＝4π,圆锥的母线长l ＝22＋(23)2＝4,圆柱的高h ＝4,所以该几何体的表面积S 表＝πr 2＋ch ＋12cl ＝4π＋16π＋8π＝28π,故选C.3.设一个球形西瓜,切下一刀后所得切面圆的半径为4,球心到切面圆心的距离为3,则该西瓜的体积为( D )A.100πB.2563π C.4003π D.5003π 【试题解析】 因为切面圆的半径r ＝4,球心到切面的距离d ＝3,所以球的半径R ＝r 2＋d 2＝42＋32＝5,故球的体积V ＝43πR 3＝43π×53＝5003π,即该西瓜的体积为5003π.4.某几何体的三视图如图所示,则该几何体的表面积为( B )A.18＋2πB.20＋πC.20＋π2D.16＋π【试题解析】 由三视图可知,这个几何体是一个边长为2的正方体割去了相对边对应的两个半径为1、高为1的14圆柱体,其表面积相当于正方体五个面的面积与两个14圆柱的侧面积的和,即该几何体的表面积S ＝4×5＋2×2π×1×1×14＝20＋π.故选B.5.《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.已知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的侧面积为( C )A.2B.4＋2 2C.4＋4 2D.4＋6 2【试题解析】 由三视图知,该几何体是直三棱柱ABC －A 1B 1C 1,其直观图如图所示,其中AB ＝AA 1＝2,BC ＝AC ＝2,∠C ＝90°,侧面为三个矩形,故该“堑堵”的侧面积S ＝(2＋22)×2＝4＋4 2.6.如图,正方体ABCD －A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1－EDF 的体积为__16__.【试题解析】 利用三棱锥的体积公式直接求解.VD 1－EDF ＝VF －DD 1E ＝13SD 1DE ·AB ＝13×12×1×1×1＝16.7.已知E ,F 分别是矩形ABCD 的边BC 与AD 的中点,且BC ＝2AB ＝2,现沿EF 将平面ABEF 折起,使平面ABEF ⊥平面EFDC ,则三棱锥A －FEC 外接球的体积为__32π__. 【试题解析】 如图,平面ABEF ⊥平面EFDC ,AF ⊥EF ,所以AF ⊥平面ECDF ,将三棱锥A －FEC 补成正方体ABC ′D ′－FECD . 依题意,其棱长为1,外接球的半径R ＝32,所以外接球的体积V ＝43πR 3＝43π·(32)3＝32π.8.(2017·江苏卷)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切,记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是__32__.【试题解析】 设球O 的半径为R ,∵球O 与圆柱O 1O 2的上、下底面及母线均相切, ∴圆柱O 1O 2的高为2R ,底面半径为R . ∴V 1V 2＝πR 2·2R 43πR 3＝32. 9.下图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,EC ∥PD ,且PD ＝AD ＝2EC ＝2.(1)请画出该几何体的三视图； (2)求四棱锥B －CEPD 的体积.【试题解析】 (1)该组合体的三视图如图所示.(2)∵PD ⊥平面ABCD , PD ⊂平面PDCE ,∴平面PDCE ⊥平面ABCD . ∵四边形ABCD 为正方形,∴BC ⊥CD ,且BC ＝DC ＝AD ＝2. 又∵平面PDCE ∩平面ABCD ＝CD , BC ⊂平面ABCD . ∴BC ⊥平面PDCE .∵PD ⊥平面ABCD ,DC ⊂平面ABCD , ∴PD ⊥DC .又∵EC ∥PD ,PD ＝2,EC ＝1,∴四边形PDCE 为一个直角梯形,其面积： S 梯形PDCE ＝12(PD ＋EC )·DC ＝12×3×2＝3.∴四棱锥B －CEPD 的体积V B －CEPD ＝13S 梯形PDCE ·PD ＝13×3×2＝2.10.(文)如图,三棱柱ABC －A 1B 1C 1中,CA ＝CB ,AB ＝AA 1,∠BAA 1＝60°.(1)证明：AB ⊥A 1C .(2)若AB ＝CB ＝2,A 1C ＝6,求三棱柱ABC －A 1B 1C 1的体积. 【试题解析】 (1)取AB 的中点O ,连接OC ,OA 1,A 1B . 因为CA ＝CB ,所以OC ⊥AB .由于AB ＝AA 1,∠BAA 1＝60°,故△AA 1B 为等边三角形,所以OA 1⊥AB . 因为OC ∩OA 1＝O ,所以AB ⊥平面OA 1C . 又A 1C ⊂平面OA 1C ,故AB ⊥A 1C .(2)由题设知△ABC 与△AA 1B 都是边长为2的等边三角形,所以OC ＝OA 1＝ 3. 又A 1C ＝6,则A 1C 2＝OC 2＋OA 21,故OA 1⊥OC .因为OC ∩AB ＝O ,所以OA 1⊥平面ABC ,OA 1为三棱柱ABC －A 1B 1C 1的高. 又△ABC 的面积S △ABC ＝ 3.故三棱柱ABC －A 1B 1C 1的体积V ＝S △ABC ×OA 1＝3. (理)如图,四棱锥P －ABCD 中,侧面P AD 为等边三角形且垂直于底面ABCD ,AB ＝BC ＝12AD ,∠BAD ＝∠ABC ＝90°.(1)证明：直线BC ∥平面P AD ；(2)若△PCD 的面积为27,求四棱锥P －ABCD 的体积.【试题解析】 (1)证明：在平面ABCD 内,因为∠BAD ＝∠ABC ＝90°,所以BC ∥AD . 又BC ⊄平面P AD ,AD ⊂平面P AD , 故BC ∥平面P AD .(2)如图,取AD 的中点M ,连接PM ,CM .由AB ＝BC ＝12AD 及BC ∥AD ,∠ABC ＝90°得四边形ABCM 为正方形,则CM ⊥AD .因为侧面P AD 为等边三角形且垂直于底面ABCD , 平面P AD ∩平面ABCD ＝AD , 所以PM ⊥AD ,PM ⊥底面ABCD . 因为CM ⊂底面ABCD ,所以PM ⊥CM .设BC ＝x ,则CM ＝x ,CD ＝2x ,PM ＝3x ,PC ＝PD ＝2x . 如图,取CD 的中点N ,连接PN ,则PN ⊥CD , 所以PN ＝142x . 因为△PCD 的面积为27,所以12×2x ×142x ＝27,解得x ＝－2(舍去)或x ＝2.于是AB ＝BC ＝2,AD ＝4,PM ＝2 3.所以四棱锥P －ABCD 的体积V ＝13×2(2＋4)2×23＝4 3.B 组1.(文)某三棱锥的三视图如图所示,则该三棱锥的体积为( D )A.60B.30C.20D.10【试题解析】 由三视图画出如图所示的三棱锥P －ACD ,过点P 作PB ⊥平面ACD 于点B ,连接BA ,BD ,BC ,根据三视图可知底面ABCD 是矩形,AD ＝5,CD ＝3,PB ＝4,所以V 三棱锥P －ACD＝13×12×3×5×4＝10.故选D.(理)已知某几何体的三视图如图所示,根据图中标出的尺寸(单位：cm),可得这个几何体的体积是( B )A.43 cm 3 B.83 cm 3 C.2 cm 3D.4 cm 3【试题解析】 由三视图可知,该几何体为底面是正方形,且边长为2 cm,高为2 cm 的四棱锥,如图,故V ＝13×22×2＝83(cm 3).2.三棱锥A －BCD 内接于半径为2的球O ,BC 过球心O ,当三棱锥A －BCD 体积取得最大值时,三棱锥A －BCD 的表面积为( D )A.6＋4 3B.8＋2 3C.4＋6 3D.8＋4 3【试题解析】 由题意,BC 为直径,△BCD 的最大面积为12×4×2＝4,三棱锥A －BCD 体积最大时,AO ⊥平面BCD ,三棱锥的高为2, 所以三棱锥A －BCD 的表面积为4×2＋2×12×22×6＝8＋4 3.3.三棱锥P －ABC 中,P A ⊥平面ABC 且P A ＝2,△ABC 是边长为3的等边三角形,则该三棱锥外接球的表面积为( C )A.4π3B.4πC.8πD.20π【试题解析】 由题意得,此三棱锥外接球即为以△ABC 为底面、以P A 为高的正三棱柱的外接球,因为△ABC 的外接圆半径r ＝32×3×23＝1,外接球球心到△ABC 的外接圆圆心的距离d ＝1,所以外接球的半径R ＝r 2＋d 2＝2,所以三棱锥外接球的表面积S ＝4πR 2＝8π.故选C.4.某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( B )A.2 2B.2 3C.4D.2 6【试题解析】 如图,四面体的直观图是棱长为2的正方体ABCD －MNPQ 中的三棱锥Q －BCN ,且QB ＝22＋(22)2＝23,NC ＝QN ＝QC ＝22,四面体Q －BCN 各面的面积分别为S△QBN＝S △QBC ＝12×2×22＝22,S △BCN ＝12×2×2＝2,S △QCN ＝34×(22)2＝23,面积最大为2 3.5.(2019·昆明摸底)古人采取“用臼舂米”的方法脱去稻谷的外壳,获得可供食用的大米,用于舂米的“臼”多用石头或木头制成.一个“臼”的三视图如图所示,则凿去部分(看成一个简单的组合体)的体积为( A )A.63πB.72πC.79πD.99π【试题解析】 由三视图得凿去部分是圆柱与半球的组合体,其中圆柱的高为5,底面圆的半径为3,半球的半径为3,所以组合体的体积为π×32×5＋12×43π×33＝63π.6.已知在直角梯形ABCD 中,AB ⊥AD ,CD ⊥AD ,AB ＝2AD ＝2CD ＝2,将直角梯形ABCD 沿AC 折叠成三棱锥D －ABC ,当三棱锥D －ABC 的体积取最大值时,其外接球的体积为__43π__.【试题解析】 当平面DAC ⊥平面ABC 时,三棱锥D －ABC 的体积取最大值.此时易知BC ⊥平面DAC ,∴BC ⊥AD ,又AD ⊥DC ,∴AD ⊥平面BCD ,∴AD ⊥BD ,取AB 的中点O ,易得OA ＝OB ＝OC ＝OD ＝1,故O 为所求外接球的球心,故半径r ＝1,体积V ＝43πr 3＝43π.7.如图,半径为4的球O 中有一内接圆柱,则圆柱的侧面积最大值是__32π__.【试题解析】 设圆柱的上底面半径为r ,球的半径与上底面夹角为α,则r ＝4cos α,圆柱的高为8sin α.所以圆柱的侧面积为32πsin2α.当且仅当α＝π4时,sin2α＝1,圆柱的侧面积最大,所以圆柱的侧面积的最大值为32π.8.(2019·惠州二调)如图,某几何体的三视图是三个全等的等腰直角三角形,且直角边长都等于1,则该几何体的外接球的体积为__32π__.【试题解析】还原几何体为如图所示的三棱锥A－BCD,将其放入棱长为1的正方体中,如图所示,则三棱锥A－BCD外接球的半径R＝32,该几何体的外接球的体积V＝43πR3＝32π.9.(文)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明：平面AEC⊥平面BED.(2)若∠ABC＝120°,AE⊥EC,三棱锥E－ACD的体积为63,求该三棱锥的侧面积.【试题解析】(1)证明：因为四边形ABCD为菱形, 所以AC⊥BD.因为BE⊥平面ABCD,AC⊂平面ABCD,所以AC⊥BE. 又BD⊂平面BED,BE⊂平面BED,BD∩BE＝B,故AC⊥平面BED.又AC⊂平面AEC,所以平面AEC⊥平面BED.(2)设AB＝x,在菱形ABCD中,由∠ABC＝120°,可得AG＝GC＝3 2x,GB＝GD＝x2. 因为AE⊥EC,所以在Rt△AEC中,可得EG＝3 2x.由BE⊥平面ABCD,知△EBG为直角三角形,可得BE＝2 2x.由已知得,三棱锥E－ACD的体积V E－ACD＝13×12AC·GD·BE＝624x3＝63.故x＝2.从而可得AE＝EC＝ED＝ 6.所以△EAC的面积为3,△EAD的面积与△ECD的面积均为 5.故三棱锥E－ACD的侧面积为3＋2 5.(理)如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF＝3,G和H分别是CE和CF的中点.(1)求证：AC⊥平面BDEF；(2)求证：平面BDGH//平面AEF；(3)求多面体ABCDEF的体积.【试题解析】(1)证明：因为四边形ABCD是正方形,所以AC⊥BD.又因为平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD＝BD,且AC⊂平面ABCD,所以AC⊥平面BDEF.(2)证明：在△CEF中,因为G,H分别是CE,CF的中点,所以GH∥EF,又因为GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面AEF.设AC∩BD＝O,连接OH,在△ACF中,因为OA＝OC,CH＝HF,所以OH∥AF,又因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF.又因为OH∩GH＝H,OH,GH⊂平面BDGH,所以平面BDGH ∥平面AEF .(3)解：由(1),得AC ⊥平面BDEF , 又因为AO ＝2,四边形BDEF 的面积S BDEF ＝3×22＝62,所以四棱锥A －BDEF 的体积V 1＝13×AO ×S BDEF ＝4. 同理,四棱锥C －BDEF 的体积V 2＝4. 所以多面体ABCDEF 的体积V ＝V 1＋V 2＝8.。

第一部分 专题八 第一讲A 组1．在直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝3－32t ，y ＝12t .(t 为参数)，以O 为极点，x 轴的正半轴为极轴(长度单位与直角坐标系xOy 中相同)的极坐标系中，曲线C 的方程为ρ＝2a cos θ(a >0)，l 与C 相切于点P .(1)求C 的直角坐标方程； (2)求切点P 的极坐标．[解析] (1)l 表示过点(3,0)倾斜角为150°的直线，曲线C 表示以C ′(a,0)为圆心，a 为半径的圆．∵l 与C 相切，∴a ＝12(3－a )，⇒a ＝1．于是曲线C 的方程为ρ＝2cos θ，∴ρ2＝2ρcos θ， 于是x 2＋y 2＝2x ，故所求C 的直角坐标方程为x 2＋y 2－2x ＝0. (2)∵∠POC ′＝∠OPC ′＝30°，∴OP ＝ 3. ∴切点P 的极坐标为(3，π6)．2．(2019·贵阳摸底考试)曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ(φ为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρcos(θ＋π4)＝ 2.(1)写出C 的普通方程，并用⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(α为直线的倾斜角，t 为参数)的形式写出直线l 的一个参数方程；(2)l 与C 是否相交？若相交，求出两交点的距离，若不相交，请说明理由． [解析] (1)C 的普通方程为x 24＋y 2＝1，由ρcos(θ＋π4)＝2得x －y －2＝0，则直线l 的倾斜角为π4，又直线l 过点(2,0)，得直线l 的一个参数方程为⎩⎨⎧x ＝2＋22t ，y ＝22t(t 为参数) .(2)将l 的参数方程代入C 的普通方程得 5t 2＋42t ＝0，解得t 1＝0，t 2＝－425，显然l 与C 有两个交点，分别记为A ，B ，且|AB |＝|t 1－t 2|＝425.3．在平面直角坐标系xOy 中，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1，C 2的极坐标方程分别为ρ＝2sin θ，ρcos(θ－π4)＝ 2.(1)求C 1和C 2交点的极坐标；(2)直线l 的参数方程为：⎩⎨⎧x ＝－3＋32t ，y ＝12t(t 为参数)，直线l 与x 轴的交点为P ，且与C 1交于A ，B 两点，求|P A |＋|PB |.[解析] (1)C 1，C 2极坐标方程分别为ρ＝2sin θ，ρcos(θ－π4)＝2，化为直角坐标方程分别为x 2＋(y －1)2＝1，x ＋y －2＝0. 得交点坐标为(0,2)，(1,1)．即C 1和C 2交点的极坐标分别为(2，π2)，(2，π4)．(2)把直线l 的参数方程⎩⎨⎧x ＝－3＋32t ，y ＝12t(t 为参数)代入x 2＋(y －1)2＝1，得(－3＋32t )2＋(12t －1)2＝1， 即t 2－4t ＋3＝0，t 1＋t 2＝4，t 1t 2＝3， 所以|P A |＋|PB |＝4.B 组1．(2017·全国卷Ⅲ，22)在直角坐标系xOy 中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝m k (m 为参数)．设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为l 3与C 的交点，求M 的极径．[解析] (1)消去参数t 得l 1的普通方程l 1：y ＝k (x －2)； 消去参数m 得l 2的普通方程l 2：y ＝1k (x ＋2)．设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝k (x －2)，y ＝1k (x ＋2)，消去k 得x 2－y 2＝4(y ≠0)，所以C 的普通方程为x 2－y 2＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0<θ<2π，θ≠π)，联立⎩⎨⎧ρ2(cos 2θ－sin 2θ)＝4，ρ(cos θ＋sin θ)－2＝0，得cos θ－sin θ＝2(cos θ＋sin θ)．故tan θ＝－13，从而cos 2θ＝910，sin 2θ＝110.代入ρ2(cos 2θ－sin 2θ)＝4得ρ2＝5， 所以点M 的极径为 5.2．(2018·全国卷Ⅲ，22)在平面直角坐标系xOy 中，⊙O 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ (θ为参数)，过点()0，－2且倾斜角为α的直线l 与⊙O 交于A ，B 两点．(1)求α的取值范围；(2)求AB 中点P 的轨迹的参数方程．[解析] (1)⊙O 的直角坐标方程为x 2＋y 2＝1． 当α＝π2时，l 与⊙O 交于两点．当α≠π2时，记tan α＝k ，则l 的方程为y ＝kx － 2.l 与⊙O 交于两点当且仅当⎪⎪⎪⎪⎪⎪21＋k 2<1，解得k <－1或k >1，即α∈⎝⎛⎭⎫π4，π2或α∈⎝⎛⎭⎫π2，3π4. 综上，α的取值范围是⎝⎛⎭⎫π4，3π4.(2)l 的参数方程为⎩⎨⎧x ＝t cos α，y ＝－2＋t sin α，(t 为参数，π4<α<3π4)．设A ，B ，P 对应的参数分别为t A ，t B ，t P ，则t P ＝t A ＋t B2，且t A ，t B 满足t 2－22t sin α＋1＝0.于是t A ＋t B ＝22sin α，t P ＝2sin α.又点P 的坐标(x ，y )满足⎩⎨⎧x ＝t P cos α，y ＝－2＋t P sin α.所以点P 的轨迹的参数方程是⎩⎨⎧x ＝22sin2α，y ＝－22－22cos2α(α为参数，π4<α<3π4)．3．极坐标系与直角坐标系xOy 有相同的长度单位，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．已知曲线C 1的极坐标方程为ρ＝4cos θ，曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝m ＋t cos α，y ＝t sin α(t 为参数，0≤α<π)，射线θ＝φ，θ＝φ＋π4，θ＝φ－π4与曲线C 1交于(不包括极点O )三点A ，B ，C .(1)求证：|OB |＋|OC |＝2|OA |；(2)当φ＝π12时，B ，C 两点在曲线C 2上，求m 与α的值．[解析] (1)证明：设点A ，B ，C 的极坐标分别为(ρ1，φ)，(ρ2，φ＋π4)，(ρ3，φ－π4)，因为点A ，B ，C 在曲线C 1上，所以ρ1＝4cos φ，ρ2＝4cos(φ＋π4)，ρ3＝4cos(φ－π4)，所以|OB |＋|OC |＝ρ2＋ρ3＝4cos(φ＋π4)＋4cos(φ－π4)＝42cos φ＝2ρ1，故|OB |＋|OC |＝2|OA |.(2)由曲线C 2的方程知曲线C 2是经过定点(m,0)且倾斜角为α的直线． 当φ＝π12时，B ，C 两点的极坐标分别为(2，π3)，(23，－π6)，化为直角坐标为B (1，3)，C (3，－3)， 所以tan α＝－3－33－1＝－3，又0≤α<π，所以α＝2π3.故曲线C 2的方程为y ＝－3(x －2)，易知曲线C 2恒过点(2,0)，即m ＝2.4．(2019·邵阳三模)在直角坐标系xOy 中，直线的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos αy ＝t sin α(t 为参数)，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ＝22cos(θ＋π4)． (1)求曲线C 的直角坐标方程，并指出其表示何种曲线．(2)设直线l 与曲线C 交于A ，B 两点，若点P 的直角坐标为(1,0)，试求当α＝π4时，|P A |＋|PB |的值．[解析] (1)曲线C ：ρ＝22cos(θ＋π4)，可以化为ρ2＝22ρcos(θ＋π4)，ρ2＝2ρcos θ－2ρsin θ，因此，曲线C 的直角坐标方程为x 2＋y 2－2x ＋2y ＝0. 它表示以(1，－1)为圆心，2为半径的圆． (2)当α＝π4时，直线的参数方程为⎩⎨⎧x ＝1＋22t ，y ＝22t(t 为参数)．点P (1,0)在直线上，且在圆C 内，把⎩⎨⎧x ＝1＋22t ，y ＝22t ，代入x 2＋y 2－2x ＋2y ＝0中得t 2＋2t －1＝0.设两个实数根为t 1，t 2，则A ，B 两点所对应的参数为t 1，t 2， 则t 1＋t 2＝－2，t 1t 2＝－1． 所以|P A |＋|PB |＝|t 1－t 2| ＝(t 1＋t 2)2－4t 1t 2＝ 6.。

第一部分 专题七 第三讲A 组1.小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N 中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是( C )A.815 B.18 C.115D.130【试题解析】 根据题意可以知道,所输入密码所有可能发生的情况如下：M1,M2,M3,M4,M5,I1,I2,I3,I4,I5,N1,N2,N3,N4,N5共15种情况,而正确的情况只有其中一种,所以输入一次密码能够成功开机的概率是115.2.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( A )A.0.8B.0.75C.0.6D.0.45【试题解析】 本题考查条件概率的求法.设A ＝“某一天的空气质量为优良”,B ＝“随后一天的空气质量为优良”,则 P (B |A )＝P (A ∩B )P (A )＝0.60.75＝0.8,故选A. 3.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( A )A.0.648B.0.432C.0.36D.0.312【试题解析】 3次投篮投中2次的概率为P (k ＝2)＝C 23×0.62×(1－0.6),投中3次的概率为P (k ＝3)＝0.63,所以通过测试的概率为P (k ＝2)＋P (k ＝3)＝C 23×0.62×(1－0.6)＋0.63＝0.648.4.(2017·浙江卷,8)已知随机变量ξi 满足P (ξi ＝1)＝p i ,P (ξi ＝0)＝1－p i ,(i ＝1,2).若0<p 1<p 2<12,则( A )A.E (ξ1)<E (ξ2),D (ξ1)<D (ξ2)B.E (ξ1)<E (ξ2),D (ξ1)>D (ξ2)C.E (ξ1)>E (ξ2),D (ξ1)<D (ξ2)D.E (ξ1)>E (ξ2),D (ξ1)>D (ξ2)【试题解析】 由题意可知ξi (i ＝1,2)服从两点分布, ∴E (ξ1)＝p 1,E (ξ2)＝p 2,D (ξ1)＝p 1(1－p 1), D (ξ2)＝p 2(1－p 2).又∵0<p 1<p 2<12,∴E (ξ1)<E (ξ2).把方差看作函数y ＝x (1－x ),根据0<ξ1<ξ2<12知,D (ξ1)<D (ξ2).故选A.5.随机变量ξ的取值为0,1,2.若P (ξ＝0)＝15,E (ξ)＝1,则D (ξ)＝__25__.【试题解析】 设P (ξ＝1)＝p ,则P (ξ＝2)＝45－p ,从而由E (ξ)＝0×15＋1×p ＋2×(45－p )＝1,得p ＝35.故D (ξ)＝(0－1)2×15＋(1－1)2×35＋(2－1)2×15＝25.6.(2019·河南信阳二模)如图所示,A ,B 两点由5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为ξ,则P (ξ≥8)＝__45__.【试题解析】 解法一(直接法)：由已知得,ξ的可能取值为7,8,9,10,∵P (ξ＝7)＝C 22C 12C 35＝15,P (ξ＝8)＝C 22C 11＋C 22C 12C 35＝310,P (ξ＝9)＝C 12C 12C 11C 35＝25,P (ξ＝10)＝C 22·C 11C 35＝110,∴ξ的概率分布列为：ξ 7 8 9 10 P1531025110∴P (ξ≥8)＝P (ξ＝8)＋P (ξ＝9)＋P (ξ＝10)＝310＋25＋110＝45.解法二(间接法)：由已知得,ξ的可能取值为7,8,9,10,故P (ξ≥8)与P (ξ＝7)是对立事件,所以P (ξ≥8)＝1－P (ξ＝7)＝1－C 22C 12C 35＝45.7.(2018·天津卷,16)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人？(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.①用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X 的分布列与数学期望； ②设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率.【试题解析】 (1)由已知,甲、乙、丙三个部门的员工人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(2)①随机变量X 的所有可能取值为0,1,2,3.P (X ＝k )＝C k 4·C 3－k3C 37(k ＝0,1,2,3).所以随机变量X 的分布列为随机变量X 的数学期望E (X )＝0×135＋1×1235＋2×1835＋3×435＝127.②设事件B 为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”；事件C 为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,则A ＝B ∪C ,且B 与C 互斥,由(i)知,P (B )＝P (X ＝2)＝1835,P (C )＝P (X ＝1)＝1235,故P (A )＝P (B ∪C )＝P (X ＝2)＋P (X ＝1)＝67.所以,事件A 发生的概率为67.8.甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分；如果只有一个人猜对,则“星队”得1分；如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是34,乙每轮猜对的概率是23；每轮活动中甲、乙猜对与否互不影响,各轮结果亦互不影响.假设“星队”参加两轮活动,求：(1)“星队”至少猜对3个成语的概率；(2)“星队”两轮得分之和X 的分布列和数学期望EX .【试题解析】 (1)记事件A ：“甲第一轮猜对”,记事件B ：“乙第一轮猜对”, 记事件C ：“甲第二轮猜对”,记事件D ：“乙第二轮猜对”, 记事件E ：“‘星队’至少猜对3个成语”.由题意,E ＝ABCD ＋A －BCD ＋A B －CD ＋AB C －D ＋ABC D －. 由事件的独立性与互斥性,得P (E )＝P (ABCD )＋P (A －BCD )＋P (A B －CD )＋P (AB C －D )＋P (ABC D －)＝P (A )P (B )P (C )P (D )＋P (A －)P (B )P (C )P (D )＋P (A )P (B －)P (C )P (D )＋P (A )P (B )P (C －)P (D )＋P (A )P (B )P (C )P (D －)＝34×23×34×23＋2×(14×23×34×23＋34×13×34×23)＝23. 所以“星队”至少猜对2个成语的概率为23.(2)由题意,随机变量X 可能的取值为0,1,2,3,4,6. 由事件的独立性与互斥性,得 P (X ＝0)＝14×13×14×13＝1144,P (X ＝1)＝2×(34×13×14×13＋14×23×14×13)＝10144＝572,P (X ＝2)＝34×13×34×13＋34×13×14×23＋14×23×34×13＋14×23×14×23＝25144,P (X ＝3)＝34×23×14×13＋14×13×34×23＝12144＝112,P (X ＝4)＝2×(34×23×34×13＋34×23×14×23)＝60144＝512,P (X ＝6)＝34×23×34×23＝36144＝14.可得随机变量X 的分布列为所以数学期望EX ＝0×1144＋1×572＋2×25144＋3×112＋4×512＋6×14＝236. B 组1.(2018·全国卷Ⅰ,20)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品,检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为p ()0<p <1,且各件产品是否为不合格品相互独立.(1)记20件产品中恰有2件不合格品的概率为f ()p ,求f ()p 的最大值点p 0.(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p 0作为p 的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.①若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X ,求E (X )； ②以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验？【试题解析】 (1)20件产品中恰有2件不合格品的概率为f (p )＝C 220p 2(1－p )18. 因此f ′(p )＝C 220[2p (1－p )18－18p 2(1－p )17]＝2C 220p (1－p )17(1－10p )(0<p <1).令f ′(p )＝0,得p ＝0.1.当p ∈(0,0.1)时,f ′(p )＞0； 当p ∈(0.1,1)时,f ′(p )＜0. 所以f (p )的最大值点为p 0＝0.1. (2)由(1)知,p ＝0.1.①令Y 表示余下的180件产品中的不合格品件数,依题意知Y ～B (180,0.1),X ＝20×2＋25Y ,即X ＝40＋25Y .所以E (X )＝E (40＋25Y )＝40＋25E (Y )＝490.②如果对余下的产品作检验,则这一箱产品所需要的检验费为400元.由于E (X )＞400,故应该对余下的产品作检验.2.(2019·长春质检)某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在[100,150),[150,200),[200,250),[250,300),[300,350),[350,400](单位：克)中,经统计得频率分布直方图如图所示.(1)现按分层抽样的方法,从质量为[250,300),[300,350)的芒果中随机抽取9个,再从这9个中随机抽取3个,记随机变量X 表示质量在[300,350)内的芒果个数,求X 的分布列及数学期望E (X )；(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有10 000个,经销商提出如下两种收购方案：A ：所有芒果以10元/千克收购；B ：对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购. 通过计算确定种植园选择哪种方案获利更多？【试题解析】 (1)由频率分布直方图可得,随机抽取的9个芒果中,质量在[250,300)和[300,350)内的分别有6个和3个.则X 的可能取值为0,1,2,3.P (X ＝0)＝C 36C 39＝2084,P (X ＝1)＝C 26C 13C 39＝4584,P (X ＝2)＝C 16C 23C 39＝1884,P (X ＝3)＝C 33C 39＝184.所以X 的分布列为∴E (X )＝0×2084＋1×4584＋2×1884＋3×184＝1.(2)方案A ：(125×0.002＋175×0.002＋225×0.003＋275×0.008＋325×0.004＋375×0.001)×50×10 000×10×0.001＝25 750(元)方案B ：低于250克：(0.002＋0.002＋0.003)×50×10 000×2＝7 000(元) 高于或等于250克：(0.008＋0.004＋0.001)×50×10 000×3＝19 500(元) 总计：7 000＋19 500＝26 500(元)由25 750<26 500,故B 方案获利更多,应选B 方案.3.已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.(1)求第一次检测出的是次品且第二次检测出的是正品的概率；(2)已知每检测一件产品需要费用100元,设X 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位：元),求X 的分布列和均值(数学期望).【试题解析】 (1)记“第一次检测出的是次品且第二次检测出的是正品”为事件A .P (A )＝A 12A 13A 25＝310.(2)X 的可能取值为200,300,400.P (X ＝200)＝A 22A 25＝110.P (X ＝300)＝A 33＋C 12C 13A 22A 35＝310. P (X ＝400)＝1－P (X ＝200)－P (X ＝300)＝1－110－310＝610.故X 的分布列为EX ＝200×110＋300×310＋400×610＝350.4.某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图：以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.(1)求X的分布列.(2)若要求P(X≤n)≥0.5,确定n的最小值.(3)以购买易损零件所需费用的期望值为决策依据,在n＝19与n＝20之中选其一,应选用哪个？【试题解析】(1)每台机器更换的易损零件数为8,9,10,11,记事件A i为第一台机器3年内换掉i＋7个零件(i＝1,2,3,4)记事件B i为第二台机器3年内换掉i＋7个零件(i＝1,2,3,4)由题知P(A1)＝P(A3)＝P(A4)＝P(B1)＝P(B3)＝P(B4)＝0.2,P(A2)＝P(B2)＝0.4.设2台机器共需更换的易损零件数的随机变量为X,则X的可能的取值为16,17,18,19,20,21,22,P(X＝16)＝P(A1)P(B1)＝0.2×0.2＝0.04,P(X＝17)＝P(A1)P(B2)＋P(A2)P(B1)＝0.2×0.4＋0.4×0.2＝0.16,P(X＝18)＝P(A1)P(B3)＋P(A2)P(B2)＋P(A3)P(B1)＝0.2×0.2＋0.4×0.4＋0.2×0.2＝0.24, P(X＝19)＝P(A1)P(B4)＋P(A2)P(B3)＋P(A3)P(B2)＋P(A4)P(B1)＝0.2×0.2＋0.4×0.2＋0.2×0.4＋0.2×0.2＝0.24,P(X＝20)＝P(A2)P(B4)＋P(A3)P(B3)＋P(A4)P(B2)＝0.4×0.2＋0.2×0.2＋0.2×0.4＝0.2, P(X＝21)＝P(A3)P(B4)＋P(A4)P(B3)＝0.2×0.2＋0.2×0.2＝0.08,P(X＝22)＝P(A4)P(B4)＝0.2×0.2＝0.04.所以X的分布列为X 16171819202122P 0.040.160.240.240.20.080.04(2)要令∵0.04＋0.16＋0.24<0.5,0.04＋0.16＋0.24＋0.24≥0.5,则n的最小值为19.(3)购买零件所需费用含两部分,一部分为购买机器时购买零件的费用,另一部分为备件不足时额外购买的费用,当n＝19时,费用的期望为19×200＋500×0.2＋1 000×0.08＋1 500×0.04＝4 040, 当n＝20时,费用的期望为20×200＋500×0.08＋1 000×0.04＝4 080.所以应选用n＝19.。

第一部分 专题二 第四讲A 组1.函数f (x )＝ax 3＋bx 2＋cx ＋d 的图象如图所示,则下列结论成立的是( A )A.a >0,b <0,c >0,d >0B.a >0,b <0,c <0,d >0C.a <0,b <0,c >0,d >0D.a >0,b >0,c >0,d <0【试题解析】 由图象知f (0)＝d >0,因为f ′(x )＝3ax 2＋2bx ＋c ＝0有两个不相等的正实根,所以a >0,－2b 6a ＝－b3a>0,所以b <0,又f ′(0)＝c >0,所以a >0,b <0,c >0,d >0.2.若存在正数x 使2x (x －a )<1成立,则a 的取值范围是( D ) A.(－∞,＋∞) B.(－2,＋∞) C.(0,＋∞)D.(－1,＋∞)【试题解析】 ∵2x (x －a )<1,∴a >x －12x .令f (x )＝x －12x ,∴f ′(x )＝1＋2－x ln2>0. ∴f (x )>f (0)＝0－1＝－1,∴a 的取值范围为(－1,＋∞),故选D.3.(文)(2019·昆明市高三摸底调研测试)若函数f (x )＝2x －x 2－1,对于任意的x ∈Z 且x ∈(－∞,a ),都有f (x )≤0恒成立,则实数a 的取值范围为( D )A.(－∞,1]B.(－∞,0]C.(－∞,4]D.(－∞,5]【试题解析】 对任意的x ∈Z 且x ∈(－∞,a ),都有f (x )≤0恒成立,可转化为对任意的x ∈Z 且x ∈(－∞,a ),2x ≤x 2＋1恒成立. 令g (x )＝2x ,h (x )＝x 2＋1, 当x <0时,g (x )<h (x ), 当x ＝0或1时,g (x )＝h (x ), 当x ＝2或3或4时,g (x )<h (x ), 当x ≥5时,g (x )>h (x ).综上,实数a 的取值范围为(－∞,5],故选D.(理)已知函数y ＝f (x )是R 上的可导函数,当x ≠0时,有f ′(x )＋f (x )x >0,则函数F (x )＝xf (x )＋1x的零点个数是( B ) A.0 B.1 C.2D.3【试题解析】 由F (x )＝xf (x )＋1x ＝0,得xf (x )＝－1x ,设g (x )＝xf (x ),则g ′(x )＝f (x )＋xf ′(x ), 因为x ≠0时,有f ′(x )＋f (x )x >0,所以x ≠0时,f (x )＋xf ′(x )x>0,即当x >0时,g ′(x )＝f (x )＋xf ′(x )>0,此时函数g (x )单调递增,此时g (x )>g (0)＝0,当x <0时,g ′(x )＝f (x )＋xf ′(x )<0,此时函数g (x )单调递减,此时g (x )>g (0)＝0,作出函数g (x )和函数y ＝－1x 的图象,(直线只代表单调性和取值范围),由图象可知函数F (x )＝xf (x )＋1x的零点个数为1个.4.(文)已知x ＝1是函数f (x )＝ax 3－bx －ln x (a >0,b ∈R )的一个极值点,则ln a 与b －1的大小关系是( B )A.ln a >b －1B.ln a <b －1C.ln a ＝b －1D.以上都不对【试题解析】 f ′(x )＝3ax 2－b －1x ,∵x ＝1是函数f (x )的极值点, ∴f ′(1)＝3a －b －1＝0,即3a －1＝b . 令g (a )＝ln a －(b －1)＝ln a －3a ＋2(a >0), 则g ′(a )＝1a －3＝1－3a a,∴g (a )在(0,13)上递增,在(13,＋∞)上递减,故g (a )max ＝g (13)＝1－ln3<0.故ln a <b －1.(理)已知函数f (x )＝ln(e x ＋e －x )＋x 2,则使得f (2x )>f (x ＋3)成立的x 的取值范围是( D ) A.(－1,3) B.(－∞,－3)∪(3,＋∞) C.(－3,3)D.(－∞,－1)∪(3,＋∞)【试题解析】 ∵函数f (x )＝ln(e x ＋e －x )＋x 2, ∴f ′(x )＝e x －e －xe x ＋e －x ＋2x ,当x >0时,f ′(x )>0,f (x )单调递增, 当x <0时,f ′(x )<0,f (x )单调递减, 当x ＝0时,f ′(x )＝0,f (x )取最小值,∵f (x )＝ln(e x ＋e －x )＋x 2是偶函数,且在(0,＋∞)上单调递增, ∴f (2x )>f (x ＋3)等价于|2x |>|x ＋3|, 整理,得x 2－2x －3>0, 解得x >3或x <－1,∴使得f (2x )>f (x ＋3)成立的x 的取值范围是(－∞,－1)∪(3,＋∞),故选D.5.设f (x ),g (x )分别是定义在R 上的奇函数和偶函数,且g (x )≠0,当x <0时,f ′(x )g (x )>f (x )g ′(x ),且f (－3)＝0,则不等式f (x )g (x )<0的解集是____(－∞,－3)∪(0,3)__.【试题解析】 因为f (x )和g (x )(g (x )≠0)分别是定义在R 上的奇函数和偶函数, 所以f (－x )＝－f (x ),g (－x )＝g (x ). 因为当x <0时,f ′(x )g (x )－f (x )g ′(x )>0, 当x <0时,[f (x )g (x )]′＝f ′(x )g (x )－f (x )g ′(x )g 2(x )>0,令h (x )＝f (x )g (x ),则h (x )在(－∞,0)上单调递增. 因为h (－x )＝f (－x )g (－x )＝－f (x )g (x )＝－h (x ),所以h (x )为奇函数,根据奇函数的性质可得函数h (x )在(0,＋∞)上单调递增, 因为f (－3)＝－f (3)＝0, 所以h (－3)＝－h (3)＝0.h (x )<0的解集为(－∞,－3)∪(0,3).6.已知函数f (x )＝x 2＋mx －1,若对于任意x ∈[m ,m ＋1],都有f (x )<0成立,则实数m 的取值范围是____⎝⎛⎭⎫－2，0__. 【试题解析】 ⎩⎪⎨⎪⎧f (m )＝m 2＋m 2－1<0，f (m ＋1)＝(m ＋1)2＋m (m ＋1)－1<0，解得－22<m <0. 7.定义1：若函数f (x )在区间D 上可导,即f ′(x )存在,且导函数f ′(x )在区间D 上也可导,则称函数f (x )在区间D 上存在二阶导数,记作f ″(x ),即f ″(x )＝[f ′(x )]′.定义2：若函数f (x )在区间D 上的二阶导数恒为正,即f ″(x )>0恒成立,则称函数f (x )在区间D 上为凹函数.已知函数f (x )＝x 3－32x 2＋1在区间D 上为凹函数,则x 的取值范围是____(12,＋∞)__.【试题解析】 ∵f (x )＝x 3－32x 2＋1,∴f ′(x )＝3x 2－3x ,∴f ″(x )＝6x －3.令f ″(x )>0,即6x －3>0,解得x >12.∴x 的取值范围是(12,＋∞).8.已知f (x )＝ln x ＋ax ,a ∈R . (1)讨论函数f (x )的单调性.(2)若函数f (x )的两个零点为x 1,x 2,且x 2x 1≥e 2,求证：(x 1－x 2)f ′(x 1＋x 2)>65.【试题解析】 (1)函数f (x )＝ln x ＋ax 的定义域为{x |x >0}, 所以f ′(x )＝1x＋a .①若a ≥0,则f ′(x )>0,∴f (x )在(0,＋∞)内单调递增. ②若a <0,则f ′(x )＝1x ＋a ,由f ′(x )>0,得0<x <－1a ,∴f (x )在(0,－1a )内单调递增；由f ′(x )＝1x ＋a <0,得x >－1a ,∴f (x )在(－1a ,＋∞)内单调递减.(2)证明：∵ln x 1＋ax 1＝0,ln x 2＋ax 2＝0,∴ln x 2－ln x 1＝a (x 1－x 2). (x 1－x 2)f ′(x 1＋x 2)＝(x 1－x 2)(1x 1＋x 2＋a )＝x 1－x 2x 1＋x 2＋ a (x 1－x 2)＝x 1－x 2x 1＋x 2＋ln x 2x 1＝1－x 2x 11＋x 2x 1＋ln x 2x 1.令x 2x 1＝t ≥e 2,令φ(t )＝1－t 1＋t ＋ln t , 则φ′(t )＝t 2＋1(1＋t )2t >0,∴φ(t )在[e 2,＋∞)内单调递增, φ(t )≥φ(e 2)＝1＋2e 2＋1>1＋232＋1＝65.∴(x 1－x 2)f ′(x 1＋x 2)>65.9.某造船公司年最大造船量是20艘,已知造船x 艘的产值函数为R (x )＝3 700x ＋45x 2－10x 3(单位：万元),成本函数为C (x )＝460x ＋5 000(单位：万元),又在经济学中,函数f (x )的边际函数Mf (x )定义为Mf (x )＝f (x ＋1)－f (x ).(1)求利润函数P (x )及边际利润函数MP (x ).(提示：利润＝产值－成本) (2)问：年造船量安排多少艘时,可使公司造船的年利润最大？(3)求边际利润函数MP (x )的单调递减区间,并说明单调递减在本题中的实际意义是什么. 【试题解析】 (1)P (x )＝R (x )－C (x )＝－10x 3＋45x 2＋3 240x －5 000(x ∈N *,且1≤x ≤20)； MP (x )＝P (x ＋1)－P (x )＝－30x 2＋60x ＋3 275(x ∈N *,且1≤x ≤19). (2)P ′(x )＝－30x 2＋90x ＋3 240 ＝－30(x －12)(x ＋9),因为x >0,所以P ′(x )＝0时,x ＝12, 当0<x <12时,P ′(x )>0,当x >12时,P ′(x )<0, 所以x ＝12时,P (x )有极大值,也是最大值.即年造船量安排12艘时,可使公司造船的年利润最大. (3)MP (x )＝－30x 2＋60x ＋3 275 ＝－30(x －1)2＋3 305.所以,当x ≥1时,MP (x )单调递减.所以单调减区间为[1,19].MP (x )是减函数的实际意义是：随着产量的增加,每艘利润与前一艘比较,利润在减少.B 组1.对于R 上可导的任意函数f (x ),若满足1－x f ′(x )≤0,则必有( A )A.f (0)＋f (2)>2f (1)B.f (0)＋f (2)≤2f (1)C.f (0)＋f (2)<2f (1)D.f (0)＋f (2)≥2f (1)【试题解析】 当x <1时,f ′(x )<0,此时函数f (x )递减；当x >1时,f ′(x )>0,此时函数f (x )递增,即当x ＝1时,函数f (x )取得极小值同时也取得最小值f (1),所以f (0)>f (1),f (2)>f (1),则f (0)＋f (2)>2f (1).故选A.2.已知函数f (x )＝x (ln x －ax )有两个极值点,则实数a 的取值范围是( B ) A.(－∞,0) B.(0,12)C.(0,1)D.(0,＋∞)【试题解析】 ∵f (x )＝x (ln x －ax ),∴f ′(x )＝ln x －2ax ＋1,故f ′(x )在(0,＋∞)上有两个不同的零点,令f ′(x )＝0,则2a ＝ln x ＋1x ,设g (x )＝ln x ＋1x ,则g ′(x )＝－ln x x2,∴g (x )在(0,1)上单调递增,在(1,＋∞)上单调递减.又∵当x →0时,g (x )→－∞,当x →＋∞时,g (x )→0,而g (x )max ＝g (1)＝1,∴只需0<2a <1⇒0<a <12.3.(文)已知函数f (x )＝ax 2＋bx －ln x (a >0,b ∈R ),若对任意x >0,f (x )≥f (1),则( A ) A.ln a <－2b B.ln a ≤－2b C.ln a >－2bD.ln a ≥－2b【试题解析】 f ′(x )＝2ax ＋b －1x ,由题意可知f ′(1)＝0,即2a ＋b ＝1,由选项可知,只需比较ln a ＋2b 与0的大小,而b ＝1－2a ,所以只需判断ln a ＋2－4a 的符号.构造一个新函数g (x )＝2－4x ＋ln x ,则g ′(x )＝1x －4,令g ′(x )＝0,得x ＝14,当x <14时,g (x )为增函数；当x >14时,g (x )为减函数,所以对任意x >0有g (x )≤g (14)＝1－ln4<0,所以有g (a )＝2－4a ＋ln a ＝2b ＋ln a <0⇒ln a <－2b .故选A.(理)已知函数f (x )＝x 3＋ax 2＋bx ＋c 有两个极值点x 1,x 2.若f (x 1)＝x 1<x 2,则关于x 的方程3(f (x ))2＋2af (x )＋b ＝0的不同实根个数为( A )A.3B.4C.5D.6【试题解析】 f ′(x )＝3x 2＋2ax ＋b ,原题等价于方程3x 2＋2ax ＋b ＝0有两个不等实数根x 1,x 2,且x 1<x 2,x ∈(－∞,x 1)时,f ′(x )>0,f (x )单调递增；x ∈(x 1,x 2)时,f ′(x )<0,f (x )单调递减；x ∈(x 2,＋∞)时,f ′(x )>0,f (x )单调递增.∴x 1为极大值点,x 2为极小值点.∴方程3(f (x ))2＋2af (x )＋b ＝0有两个不等实根, f (x )＝x 1或f (x )＝x 2.∵f (x 1)＝x 1,∴由图知f (x )＝x 1有两个不同的解,f (x )＝x 2仅有一个解.故选A.4.已知函数f (x )＝2ax 3－3ax 2＋1,g (x )＝－a 4x ＋32,若任意给定的x 0∈[0,2],总存在两个不同的x i (i ＝1,2)∈[0,2],使得f (x i )＝g (x 0)成立,则实数a 的取值范围是( A )A.(－∞,－1)B.(1,＋∞)C.(－∞,－1)∪(1,＋∞)D.[－1,1]【试题解析】 当a ＝0时,显然不成立,故排除D ；当a >0时,注意到f ′(x )＝6ax 2－6ax ＝6ax (x －1),即f (x )在[0,1]上是减函数,在[1,2]上是增函数,又f (0)＝1<32＝g (0),当x 0＝0时,结论不可能成立；进一步,可知a <0,此时g (x )在[0,2]上是增函数,且取值范围是[32,－a 2＋32],同时f (x )在0≤x ≤1时,函数值从1增大到1－a , 在1≤x ≤2时,函数值从1－a 减少到1＋4a ,所以“任意给定的x 0∈[0,2],总存在两个不同的x i (i ＝1,2)∈[0,2],使得f (x i )＝g (x 0)成立”,当且仅当⎩⎪⎨⎪⎧f (x )的最大值>g (x )的最大值，f (x )的最小值<g (x )的最小值，即⎩⎨⎧1－a >－a 2＋32，1＋4a <32，解得a <－1.5.已知y ＝f (x )为R 上的连续可导函数,且xf ′(x )＋f (x )>0,则函数g (x )＝xf (x )＋1(x >0)的零点个数为____0__.【试题解析】 因为g (x )＝xf (x )＋1(x >0),g ′(x )＝xf ′(x )＋f (x )>0,所以g (x )在(0,＋∞)上单调递增.又g (0)＝1,y ＝f (x )为R 上的连续可导函数,所以g (x )为(0,＋∞)上的连续可导函数,所以g (x )>g (0)＝1,所以g (x )在(0,＋∞)上无零点.6.已知函数f (x )＝e xx ,g (x )＝－(x －1)2＋a 2,若当x >0时,存在x 1,x 2∈R ,使得f (x 2)≤g (x 1)成立,则实数a 的取值范围是____(－∞,－e]∪[e,＋∞)__.【试题解析】 由题意得存在x 1,x 2∈R ,使得f (x 2)≤g (x 1)成立,等价于f (x )min ≤g (x )max . 因为g (x )＝－(x －1)2＋a 2,x >0, 所以当x ＝1时,g (x )max ＝a 2.因为f (x )＝e xx,x >0,所以f ′(x )＝e x ·x －e x x 2＝e x (x －1)x 2.所以f (x )在(0,1)上单调递减,在(1,＋∞)上单调递增,所以f (x )min ＝f (1)＝e. 又g (x )max ＝a 2,所以a 2≥e ⇔a ≤－e 或a ≥ e.故实数a 的取值范围是(－∞,－e]∪[e,＋∞).7.(2019·武汉市武昌区调研考试)已知函数f (x )＝ln x ＋ax ,a ∈R .(1)讨论函数f (x )的单调性； (2)当a >0时,证明f (x )≥2a －1a.【试题解析】 (1)f ′(x )＝1x －a x 2＝x －ax 2(a >0).当a ≤0时,f ′(x )>0,f (x )在(0,＋∞)上单调递增.当a >0时,若x >a ,则f ′(x )>0,函数f (x )在(a ,＋∞)上单调递增； 若0<x <a ,则f ′(x )<0,函数f (x )在(0,a )上单调递减. (2)证明：由(1)知,当a >0时,f (x )min ＝f (a )＝ln a ＋1. 要证f (x )≥2a －1a ,只需证ln a ＋1≥2a －1a ,即证ln a ＋1a －1≥0.令函数g (a )＝ln a ＋1a －1,则g ′(a )＝1a －1a 2＝a －1a2(a >0),当0<a <1时,g ′(a )<0,当a >1时,g ′(a )>0,所以g (a )在(0,1)上单调递减,在(1,＋∞)上单调递增. 所以g (a )min ＝g (1)＝0. 所以ln a ＋1a －1≥0恒成立,所以f (x )≥2a －1a.8.(文)设函数f (x )＝(1－x 2)e x . (1)讨论f (x )的单调性；(2)当x ≥0时,f (x )≤ax ＋1,求a 的取值范围. 【试题解析】 (1)f ′(x )＝(1－2x －x 2)e x .令f ′(x )＝0得x ＝－1－2或x ＝－1＋ 2. 当x ∈(－∞,－1－2)时,f ′(x )<0； 当x ∈(－1－2,－1＋2)时,f ′(x )>0； 当x ∈(－1＋2,＋∞)时,f ′(x )<0.所以f (x ) 在(－∞,－1－2),(－1＋2,＋∞)上单调递减,在(－1－2,－1＋2)上单调递增.(2)f (x )＝(1＋x )(1－x )e x .当a ≥1时,设函数h (x )＝(1－x )e x , 则h ′(x )＝－x e x <0(x >0), 因此h (x )在[0,＋∞)上单调递减. 而h (0)＝1,故h (x )≤1所以f (x )＝(x ＋1)h (x )≤x ＋1≤ax ＋1. 当0<a <1时,设函数g (x )＝e x －x －1, 则g ′(x )＝e x －1>0(x >0), 所以g (x )在[0,＋∞)上单调递增. 而g (0)＝0,故e x ≥x ＋1.当0<x <1时,f (x )>(1－x )(1＋x )2,(1－x )(1＋x )2－ax －1＝x (1－a －x －x 2), 取x 0＝5－4a －12, 则x 0∈(0,1),(1－x 0)(1＋x 0)2－ax 0－1＝0, 故f (x 0)>ax 0＋1. 当a ≤0时,取x 0＝5－12,则x 0∈(0,1),f (x 0)>(1－x 0)(1＋x 0)2＝1≥ax 0＋1. 综上,a 的取值范围是[1,＋∞).(理)已知函数f (x )＝ax 2－ax －x ln x ,且f (x )≥0. (1)求a ；(2)证明：f (x )存在唯一的极大值点x 0,且e －2<f (x 0)<2－2. 【试题解析】 (1)f (x )的定义域为(0,＋∞). 设g (x )＝ax －a －ln x ,则f (x )＝xg (x ),f (x )≥0等价于g (x )≥0. 因为g (1)＝0,g (x )≥0,故g ′(1)＝0, 而g ′(x )＝a －1x ,g ′(1)＝a －1,得a ＝1.若a ＝1,则g ′(x )＝1－1x.当0<x <1时,g ′(x )<0,g (x )单调递减； 当x >1时,g ′(x )>0,g (x )单调递增.所以x ＝1是g (x )的极小值点,故g (x )≥g (1)＝0. 综上,a ＝1.(2)证明：由(1)知f (x )＝x 2－x －x ln x , f ′(x )＝2x －2－ln x .设h (x )＝2x －2－ln x ,则h ′(x )＝2－1x .当x ∈(0,12)时,h ′(x )<0；当x ∈(12,＋∞)时,h ′(x )>0.所以h (x )在(0,12)上单调递减,在(12,＋∞)上单调递增.又h (e －2)>0,h (12)<0,h (1)＝0,所以h (x )在(0,12)上有唯一零点x 0,在[12,＋∞)上有唯一零点1,且当x ∈(0,x 0)时,h (x )>0；当x ∈(x 0,1)时,h (x )<0；当x ∈(1,＋∞)时,h (x )>0. 因为f ′(x )＝h (x ),所以x ＝x 0是f (x )的唯一极大值点. 由f ′(x 0)＝0,得ln x 0＝2(x 0－1),故f (x 0)＝x 0(1－x 0). 由x 0∈(0,12)得f (x 0)<14.因为x ＝x 0是f (x )在(0,1)上的最大值点, 由e －1∈(0,1),f ′(e －1)≠0得f (x 0)>f (e －1)＝e －2. 所以e －2<f (x 0)<2－2.。

第一部分 专题六 第一讲A 组1.(文)“ab ＝4”是“直线2x ＋ay －1＝0与直线bx ＋2y －2＝0平行”的( C ) A.充要条件 B.充分不必要条件 C.必要不充分条件D.既不充分也不必要条件【试题解析】 因为两直线平行,所以斜率相等,即－2a ＝－b2,可得ab ＝4,又当a ＝1,b ＝4时,满足ab ＝4,但是两直线重合,故选C.(理)若直线l 1：x ＋ay ＋6＝0与l 2：(a －2)x ＋3y ＋2a ＝0平行,则l 1与l 2间的距离为( B ) A.2 B.823C.3D.833【试题解析】 由l 1∥l 2知3＝a (a －2)且2a ≠6(a －2), 2a 2≠18,求得a ＝－1,∴l 1：x －y ＋6＝0,l 2：x －y ＋23＝0,两条平行直线l 1与l 2间的距离为d ＝|6－23|12＋(－1)2＝823.故选B.2.已知直线l 1过点(－2,0)且倾斜角为30°,直线l 2过点(2,0)且与直线l 1垂直,则直线l 1与直线l 2的交点坐标为( C )A.(3,3)B.(2,3)C.(1,3)D.(1,32) 【试题解析】 直线l 1的斜率k 1＝tan30°＝33,因为直线l 2与直线l 1垂直,所以直线l 2的斜率k 2＝－1k 1＝－3,所以直线l 1的方程为y ＝33(x ＋2),直线l 2的方程为y ＝－3(x －2),联立⎩⎪⎨⎪⎧y ＝33(x ＋2)，y ＝－3(x －2)，解得⎩⎨⎧x ＝1，y ＝3，即直线l 1与直线l 2的交点坐标为(1,3). 3.(文)直线x ＋y ＋2＝0截圆x 2＋y 2＝4所得劣弧所对圆心角为( C ) A.π6 B.π3 C.2π3D.5π6【试题解析】 弦心距d ＝|2|2＝1,半径r ＝2, 所以劣弧所对的圆心角为2π3.故选C.(理)⊙C 1：(x －1)2＋y 2＝4与⊙C 2：(x ＋1)2＋(y －3)2＝9相交弦所在直线为l ,则l 被⊙O ：x 2＋y 2＝4截得弦长为( D )A.13B.4C.43913D.83913【试题解析】 由⊙C 1与⊙C 2的方程相减得l ：2x －3y ＋2＝0. 圆心O (0,0)到l 的距离d ＝21313,⊙O 的半径R ＝2,所以截得弦长为2R 2－d 2＝24－413＝83913.4.过圆x 2＋y 2＝4外一点P (4,2)作圆的两条切线,切点分别为A 、B ,则△ABP 的外接圆的方程是( D )A.(x －4)2＋(y －2)2＝1B.x 2＋(y －2)2＝4C.(x ＋2)2＋(y ＋1)2＝5D.(x －2)2＋(y －1)2＝5【试题解析】 ∵P A ⊥OA ,PB ⊥OB ,∴以OP 为直径的圆过A 、B 两点,故△ABP 的外接圆就是以OP 为直径的圆,从而圆心为(2,1),半径r ＝5,圆的方程为(x －2)2＋(y －1)2＝5.5.(文)与直线x －y －4＝0和圆x 2＋y 2＋2x －2y ＝0都相切的半径最小的圆的方程是( A )A.(x －1)2＋(y ＋1)2＝2B.(x －1)2＋(y ＋1)2＝4C.(x ＋1)2＋(y ＋1)2＝2D.(x ＋1)2＋(y ＋1)2＝4【试题解析】 如图当两圆圆心的连线与已知直线垂直时,所求圆的半径最小,易知所求圆C 的圆心在直线y ＝－x 上,故设其坐标为C (c ,－c ),又圆A 的方程为(x ＋1)2＋(y －1)2＝2,∴A (－1,1),则点A 到直线x －y －4＝0的距离d ＝|－1－1－4|2＝3 2.设圆C 的半径为r ,则2r ＝32－2＝22,∴r ＝ 2.即点C (c ,－c )到直线x －y －4＝0的距离等于 2.故有|2c －4|2＝2,∴c ＝3或c ＝1.结合图形知当c ＝3时,圆C 在直线x －y －4＝0下方,不合题意,故所求圆的方程为(x －1)2＋(y ＋1)2＝2.(理)在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线2x ＋y －4＝0相切,则圆C 面积的最小值为( A )A.45π B.34π C.(6－25)πD.54π【试题解析】 由题意易知AB 为直径的圆C 过原点O ,圆心C 为AB 的中点,设D 为切点,要使圆C 的面积最小,只需圆的半径最短,也只需OC ＋CD 最小,其最小值为OE (过原点O 作直线2x ＋y －4＝0的垂线,垂足为E )的长度.由点到直线的距离公式得OE ＝45. ∴圆C 面积的最小值为π(25)2＝45π.故选A.6.已知直线l ：x ＋my －3＝0与圆C ：x 2＋y 2＝4相切,则m ＝__±52__.【试题解析】 因为圆C ：x 2＋y 2＝4的圆心为(0,0),半径为2,直线l ：x ＋my －3＝0与圆C ：x 2＋y 2＝4相切,所以2＝31＋m 2,解得m ＝±52.7.若直线3x －4y ＋5＝0与圆x 2＋y 2＝r 2(r >0)相交于A ,B 两点,且∠AOB ＝120°(O 为坐标原点),则r ＝__2__.【试题解析】 直线3x －4y ＋5＝0与圆x 2＋y 2＝r 2(r ＞0)交于A ,B 两点,O 为坐标原点,且∠AOB ＝120°,则圆心(0,0)到直线3x －4y ＋5＝0的距离为12r ,即532＋42＝12r ,∴r ＝2.8.一个圆经过椭圆x 216＋y 24＝1的三个顶点,且圆心在x 轴的正半轴上,则该圆的标准方程为__(x －32)2＋y 2＝254__.【试题解析】 设圆心为(a,0),则圆的方程为(x －a )2＋y 2＝r 2,依题意得a 2＋22＝(4－a )2,解得a ＝32, r 2＝254,所以圆的方程为(x －32)2＋y 2＝254.9.已知圆(x －1)2＋y 2＝25,直线ax －y ＋5＝0与圆相交于不同的两点A ,B . (1)求实数a 的取值范围；(2)若弦AB 的垂直平分线l 过点P (－2,4),求实数a 的值. 【试题解析】 (1)把直线ax －y ＋5＝0代入圆的方程, 消去y 整理,得(a 2＋1)x 2＋2(5a －1)x ＋1＝0, 由于直线ax －y ＋5＝0交圆于A ,B 两点, 故Δ＝4(5a －1)2－4(a 2＋1)>0, 即12a 2－5a >0,解得a >512或a <0,所以实数a 的取值范围是(－∞,0)∪(512,＋∞).(2)由于直线l 为弦AB 的垂直平分线,且直线AB 的斜率为a ,则直线l 的斜率为－1a ,所以直线l 的方程为y ＝－1a (x ＋2)＋4,即x ＋ay ＋2－4a ＝0,由于l 垂直平分弦AB , 故圆心M (1,0)必在l 上,所以1＋0＋2－4a ＝0. 解得a ＝34,由于34∈(512,＋∞),所以a ＝34.10.已知点P (0,5)及圆C ：x 2＋y 2＋4x －12y ＋24＝0.(1)若直线l 过点P 且被圆C 截得的线段为43,求l 的方程； (2)求过P 点的圆C 的弦的中点的轨迹方程.【试题解析】 (1)如图所示,|AB |＝43,将圆C 方程化为标准方程为(x ＋2)2＋(y －6)2＝16,所以圆C 的圆心坐标为(－2,6),半径r ＝4.设D 是线段AB 的中点,则CD ⊥AB , 所以|AD |＝23,|AC |＝4. C 点坐标为(－2,6).在Rt △ACD 中,可得|CD |＝2.若直线l 的斜率存在,设为k ,则直线l 的方程为y －5＝kx ,即kx －y ＋5＝0. 由点C 到直线AB 的距离公式：|－2k －6＋5|k 2＋(－1)2＝2,得k ＝34.故直线l 的方程为3x －4y ＋20＝0.直线l 的斜率不存在时,也满足题意,此时方程为x ＝0. 所以所求直线l 的方程为x ＝0或3x －4y ＋20＝0. (2)设过点P 的圆C 的弦的中点为E (x ,y ),则EC ⊥PE , 所以CE →·PE →＝0,即(x ＋2,y －6)·(x ,y －5)＝0, 化简得所求轨迹方程为x 2＋y 2＋2x －11y ＋30＝0.B 组1.已知圆M ：x 2＋y 2－2ay ＝0(a >0)截直线x ＋y ＝0所得线段的长度是22,则圆M 与圆N ：(x －1)2＋(y －1)2＝1的位置关系是( B )A.内切B.相交C.外切D.相离【试题解析】 圆M ：x 2＋y 2－2ay ＝0(a >0)可化为x 2＋(y －a )2＝a 2,由题意,M (0,a )到直线x ＋y ＝0的距离d ＝a 2,所以a 2＝a 22＋2,解得a ＝2.所以圆M ：x 2＋(y －2)2＝4,所以两圆的圆心距为2,半径和为3,半径差为1,故两圆相交.2.(2018·全国卷Ⅲ,6)直线x ＋y ＋2＝0分别与x 轴,y 轴交于A ,B 两点,点P 在圆(x －2)2＋y 2＝2上,则△ABP 面积的取值范围是( A )A.[2,6]B.[4,8]C.[2,32]D.[22,32]【试题解析】 由A (－2,0),B (0,－2),则三角形ABP 的底边|AB |＝22,圆心(2,0)到直线x ＋y ＋2＝0的距离为d ＝|2＋0＋2|2＝22,又因为半径为r ＝2,所以点P 到直线x ＋y ＋2＝0的距离的最大值为22＋2＝32,最小值为22－2＝2,则三角形ABP 的面积的最大值为S max ＝12×22×32＝6,最小值为S min ＝12×22×2＝2,故△ABP 面积的取值范围为[2,6].3.(文)设直线x －y －a ＝0与圆x 2＋y 2＝4相交于A ,B 两点,O 为坐标原点,若△AOB 为等边三角形,则实数a 的值为( B )A.±3B.±6C.±3D.±9【试题解析】 由题意知,圆心坐标为(0,0),半径为2,则△AOB 的边长为2,所以△AOB 的高为3,即圆心到直线x －y －a ＝0的距离为3,所以|－a |12＋(－1)2＝3,解得a ＝±6.(理)直线y ＝kx ＋3被圆(x －2)2＋(y －3)2＝4截得的弦长为23,则直线的倾斜角为( A ) A.π6或5π6 B.－π3或π3C.－π6或π6D.π6【试题解析】 圆(x －2)2＋(y －3)2＝4的圆心为(2,3),半径r ＝2,圆心(2,3)到直线y ＝kx ＋3的距离d ＝|2k |k 2＋1,因为直线y ＝kx ＋3被圆(x －2)2＋(y －3)2＝4截得的弦长为23,所以由勾股定理得r 2＝d 2＋(232)2,即4＝4k 2k 2＋1＋3,解得k ＝±33,故直线的倾斜角为π6或5π6.4.已知点A (－2,0),B (0,2),若点C 是圆x 2－2ax ＋y 2＋a 2－1＝0上的动点,△ABC 面积的最小值为3－2,则a 的值为( C )A.1B.－5C.1或－5D.5【试题解析】 解法一：圆的标准方程为(x －a )2＋y 2＝1,圆心M (a,0)到直线AB ：x －y ＋2＝0的距离为d ＝|a ＋2|2,可知圆上的点到直线AB 的最短距离为d －1＝|a ＋2|2－1,(S △ABC )min ＝12×22×|a ＋2|－22＝3－2,解得a ＝1或－5.解法二：圆的标准方程为(x －a )2＋y 2＝1,设C 的坐标为(a ＋cos θ,sin θ),C 点到直线AB ：x －y ＋2＝0的距离为 d ＝|a ＋cos θ－sin θ＋2|2＝|－2sin (θ－π4)＋a ＋2|2.△ABC 的面积为S △ABC ＝12×22×|－2sin (θ－π4)＋a ＋2|2＝|－2sin(θ－π4)＋a ＋2|,当a ≥0时,a ＋2－2＝3－2,解得a ＝1； 当－2≤a <0时,|a ＋2－2|＝3－2,无解； 当a <－2时,|a ＋2＋2|＝3－2,解得a ＝－5.解法三：设与AB 平行且与圆相切的直线l ′的方程为x －y ＋m ＝0(m ≠2),圆心M (a,0)到直线l ′的距离d ＝1,即|a ＋m |2＝1, 解得m ＝±2－a ,两平行线l ,l ′之间的距离就是圆上的点到直线AB 的最短距离, 即|m －2|2＝|±2－a －2|2, (S △ABC )min ＝12×22×|±2－a －2|2＝|±2－a －2|.当a ≥0时,|±2－a －2|＝3－2,解得a ＝1. 当a <0时,|±2－a －2|＝3－2,解得a ＝－5. 故a ＝1或－5.5.在平面直角坐标系中,O 为坐标原点,直线x －ky ＋1＝0与圆C ：x 2＋y 2＝4相交于A ,B 两点,OM →＝OA →＋OB →,若点M 在圆C 上,则实数k 的值为( C )A.－2B.－1C.0D.1【试题解析】 方法一：设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧x －ky ＋1＝0，x 2＋y 2＝4得(k 2＋1)y 2－2ky －3＝0,则Δ＝4k 2＋12(k 2＋1)>0,y 1＋y 2＝2k k 2＋1,x 1＋x 2＝k (y 1＋y 2)－2＝－2k 2＋1,因为OM →＝OA →＋OB →,故M (－2k 2＋1,2k k 2＋1),又点M 在圆C 上,故4(k 2＋1)2＋4k 2(k 2＋1)2＝4,解得k ＝0.方法二：由直线与圆相交于A ,B 两点,OM →＝OA →＋OB →,且点M 在圆C 上,得圆心C (0,0)到直线x －ky ＋1＝0的距离为半径的一半,为1,即d ＝11＋k 2＝1,解得k ＝0. 6.过点C (3,4)作圆x 2＋y 2＝5的两条切线,切点分别为A ,B ,则点C 到直线AB 的距离为__4__. 【试题解析】 以OC 为直径的圆的方程为(x －32)2＋(y －2)2＝(52)2,AB 为圆C 与圆O ：x 2＋y 2＝5的公共弦,所以AB 的方程为x 2＋y 2－[(x －32)2＋(y －2)2]＝5－254,化简得3x ＋4y －5＝0,所以C 到直线AB 的距离d ＝|3×3＋4×4－5|32＋42＝4.7.(文)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若sin 2A ＋sin 2B ＝12sin 2C ,则直线ax －by ＋c＝0被圆x 2＋y 2＝9所截得弦长为【试题解析】 由正弦定理得a 2＋b 2＝12c 2,∴圆心到直线距离d ＝|c |a 2＋b 2＝c12c 2＝2, ∴弦长l ＝2r 2－d 2＝29－2＝27.(理)(2019·贵阳适应性考试)已知直线l ：ax －3y －12＝0与圆M ：x 2＋y 2－4y ＝0相交于A ,B 两点,且∠AMB ＝π3,则实数a ＝__±3__.【试题解析】 直线l 的方程可变形为y ＝13ax ＋4,所以直线l 过定点(0,4),且该点在圆M上.圆的方程可变形为x 2＋(y －2)2＝4,所以圆心为M (0,2),半径为2.如图,因为∠AMB ＝π3,所以△AMB 是等边三角形,且边长为2,高为3,即圆心M 到直线l 的距离为3,所以|－6＋12|a 2＋9＝3,解得a ＝±3.8.过点P (－1,1)作圆C ：(x －t )2＋(y －t ＋2)2＝1(t ∈R )的切线,切点分别为A ,B ,则P A →·PB →的最小值为__214__.【试题解析】 圆C ：(x －t )2＋(y －t ＋2)2＝1的圆心坐标为(t ,t －2),半径为1, 所以PC ＝(t ＋1)2＋(t －3)2 ＝2(t －1)2＋8≥8,P A ＝PB ＝PC 2－1,cos ∠APC ＝AP PC, 所以cos ∠APB ＝2⎝⎛⎭⎫AP PC 2－1＝1－2PC 2, 所以P A →·PB →＝(PC 2－1)(1－2PC 2)＝－3＋PC 2＋2PC 2≥－3＋8＋14＝214,所以P A →·PB →的最小值为214.9.(2018·全国卷Ⅱ,19)设抛物线C ：y 2＝4x 的焦点为F ,过F 且斜率为k (k >0)的直线l 与C 交于A ,B 两点,|AB |＝8.(1)求l 的方程.(2)求过点A ,B 且与C 的准线相切的圆的方程.【试题解析】 (1)由题意得F (1,0),l 的方程为y ＝k (x －1)(k ＞0).设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y ＝k (x －1)，y 2＝4x ，得k 2x 2－(2k 2＋4)x ＋k 2＝0.Δ＝16k 2＋16＞0,故x 1＋x 2＝2k 2＋4k2.所以|AB |＝|AF |＋|BF |＝(x 1＋1)＋(x 2＋1)＝4k 2＋4k 2.由题设知4k 2＋4k 2＝8,解得k ＝－1(舍去),k ＝1.因此l 的方程为y ＝x －1. (2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为y －2＝－(x －3), 即y ＝－x ＋5.设所求圆的圆心坐标为(x 0,y 0),则⎩⎪⎨⎪⎧y 0＝－x 0＋5，(x 0＋1)2＝(y 0－x 0＋1)22＋16，解得⎩⎪⎨⎪⎧ x 0＝3，y 0＝2，或⎩⎪⎨⎪⎧x 0＝11，y 0＝－6. 因此所求圆的方程为(x －3)2＋(y －2)2＝16或(x －11)2＋(y ＋6)2＝144.10.(2017·全国卷Ⅲ,20)在直角坐标系xOy 中,曲线y ＝x 2＋mx －2与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题：(1)能否出现AC ⊥BC 的情况？说明理由.(2)证明：过A ,B ,C 三点的圆在y 轴上截得的弦长为定值. 【试题解析】 (1)不能出现AC ⊥BC 的情况.理由如下： 设A (x 1,0),B (x 2,0),则x 1,x 2满足x 2＋mx －2＝0, 所以x 1x 2＝－2. 又点C 的坐标为(0,1),故AC 的斜率与BC 的斜率之积为－1x 1·－1x 2＝－12,所以不能出现AC ⊥BC 的情况.(2)证明：BC 的中点坐标为(x 22,12),可得BC 的中垂线方程为y －12＝x 2(x －x 22).由(1)可得x 1＋x 2＝－m ,所以AB 的中垂线方程为x ＝－m2.联立⎩⎨⎧x ＝－m 2，y －12＝x 2(x －x22)，又x 22＋mx 2－2＝0,可得⎩⎨⎧x ＝－m 2，y ＝－12.所以过A ,B ,C 三点的圆的圆心坐标为(－m 2,－12),半径r ＝m 2＋92.故圆在y 轴上截得的弦长为2r 2－(m2)2＝3,即过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.。

第一部分 专题四 第一讲A 组1.(文)(2019·陕西商洛模拟)在等差数列{a n }中,a 5＝9,且2a 3＝a 2＋6,则公差d ＝( C ) A.－3 B.－2 C.3D.2【试题解析】 因为2a 3＝a 2＋6,所以a 2＋a 4＝a 2＋6,所以a 4＝6,故d ＝a 5－a 4＝9－6＝3. (理)(2019·黄石模拟)已知数列{a n }的前n 项和为S n ,且2,S n ,a n 成等差数列,则S 17＝( B ) A.0 B.2 C.－2D.34【试题解析】 由题意可知：2S n ＝a n ＋2,① ∴2S n －1＝a n －1＋2(n ≥2),② ①－②,得2a n ＝a n －a n －1, ∴a na n －1＝－1(n ≥2). 又∵2a 1＝a 1＋2,∴a 1＝2,∴{a n }为以2为首项,－1为公比的等比数列. ∴S 17＝2[1－(－1)17]1＋1＝2.故选B.2.(2019·株洲模拟)若等差数列{a n }的公差为2,且a 5是a 2与a 6的等比中项,则该数列的前n 项和S n 取最小值时,n 的值等于( B )A.7B.6C.5D.4【试题解析】 设数列{a n }的首项为a 1,则数列{a n }的通项a n ＝a 1＋(n －1)×2,∴a 5＝a 1＋8,a 2＝a 1＋2,a 6＝a 1＋10,a 5是a 2与a 6的等比中项,即a 25＝a 2·a 6,即(a 1＋8)2＝(a 1＋2)·(a 1＋10),解得a 1＝－11,所以a n ＝2n －13,a 6<0,a 7>0,∴前6项的和最小,故n ＝6.故选B.3.等差数列{a n }的前n 项和为S n ,若S 11＝22,则a 3＋a 7＋a 8＝( D ) A.18 B.12 C.9D.6【试题解析】 本题主要考查等差数列的通项公式及前n 项和公式.由题意得S 11＝11(a 1＋a 11)2＝11(2a 1＋10d )2＝22,即a 1＋5d ＝2,所以a 3＋a 7＋a 8＝a 1＋2d ＋a 1＋6d ＋a 1＋7d ＝3(a 1＋5d )＝6,故选D.4.设等比数列{a n }的前n 项和为S n .若S 2＝3,S 4＝15,则S 6＝( C ) A.31B.32C.63D.64【试题解析】 方法一：由条件知,a n >0,且⎩⎪⎨⎪⎧ a 1＋a 2＝3，a 1＋a 2＋a 3＋a 4＝15，∴⎩⎪⎨⎪⎧a 1(1＋q )＝3，a 1(1＋q ＋q 2＋q 3)＝15，∴q ＝2.∴a 1＝1,∴S 6＝1－261－2＝63.方法二：由题意知,S 2,S 4－S 2,S 6－S 4成等比数列,即(S 4－S 2)2＝S 2(S 6－S 4),即122＝3(S 6－15),∴S 6＝63.5.正项等比数列{a n }满足：a 3＝a 2＋2a 1,若存在a m ,a n ,使得a m ·a n ＝16a 21,m ,n ∈N *,则1m ＋9n 的最小值为( C )A.2B.16C.114D.32【试题解析】 设数列{a n }的公比为q ,a 3＝a 2＋2a 1⇒q 2＝q ＋2⇒q ＝－1(舍)或q ＝2,∴a n＝a 1·2n －1,a m ·a n ＝16a 21⇒a 21·2m＋n －2＝16a 21⇒m ＋n ＝6.∵m ,n ∈N *,∴(m ,n )可取的数值组合为(1,5),(2,4),(3,3),(4,2),(5,1),计算可得,当m ＝2,n ＝4时,1m ＋9n 取最小值114.6.已知{a n }是等差数列,公差d 不为零,若a 2,a 3,a 7成等比数列,且2a 1＋a 2＝1,则a 1＝__23__,d＝__－1__.【试题解析】 由题可得(a 1＋2d )2＝(a 1＋d )(a 1＋6d ),故有3a 1＋2d ＝0,又因为2a 1＋a 2＝1,即3a 1＋d ＝1,联立可得d ＝－1,a 1＝23.7.已知数列{a n }中,a 1＝1,a 2＝2,设S n 为数列{a n }的前n 项和,对于任意的n >1,n ∈N ,S n ＋1＋S n－1＝2(S n ＋1)都成立,则S 10＝__91__.【试题解析】 因为任意的n >1,n ∈N ,S n ＋1＋S n －1＝2(S n ＋1)都成立,所以S n ＋1－S n ＝S n －S n－1＋2,所以a n ＋1＝a n ＋2,因为a 3＝a 2＋2＝4,所以a n ＝a 2＋(n －2)×2＝2＋(n －2)×2＝2n －2,n ≥2,所以S 10＝a 1＋a 2＋a 3…＋a 10＝1＋2＋4＋…＋18＝1＋2×9＋9×82×2＝91.8.设S n 是数列{a n }的前n 项和,且a 1＝－1,a n ＋1＝12S n ＋1S n ,则数列{S n }的通项公式为__－2n ＋1__.【试题解析】 由已知得a n ＋1＝S n ＋1－S n ＝12S n ＋1S n ,所以1S n ＋1－1S n＝－12.所以{1S n }是以－1为首项,－12为公差的等差数列,所以1S n ＝－1－12(n －1)＝－12n －12.故S n ＝－2n ＋1.9.(文)已知数列{a n }的前n 项和为S n ,且S n ＝2a n －3n (n ∈N *). (1)求a 1,a 2,a 3的值；(2)设b n ＝a n ＋3,证明数列{b n }为等比数列,并求通项公式a n .【试题解析】 (1)因为数列{a n }的前n 项和为S n ,且S n ＝2a n －3n (n ∈N *). 所以n ＝1时,由a 1＝S 1＝2a 1－3×1,解得a 1＝3, n ＝2时,由S 2＝2a 2－3×2,得a 2＝9, n ＝3时,由S 3＝2a 3－3×3,得a 3＝21. (2)因为S n ＝2a n －3n , 所以S n ＋1＝2a n ＋1－3(n ＋1), 两式相减,得a n ＋1＝2a n ＋3,①把b n ＝a n ＋3及b n ＋1＝a n ＋1＋3,代入①式, 得b n ＋1＝2b n (n ∈N *),且b 1＝6,所以数列{b n }是以6为首项,2为公比的等比数列, 所以b n ＝6×2n －1,所以a n ＝b n －3＝6×2n －1－3＝3(2n －1).(理)设数列{a n }的前n 项和为S n ,且S n ＝4a n －p (n ∈N *),其中p 是不为零的常数. (1)证明：数列{a n }是等比数列.(2)当p ＝3时,若数列{b n }满足b n ＋1＝a n ＋b n (n ∈N *),b 1＝2,求数列{b n }的通项公式. 【试题解析】 (1)证明：因为S n ＝4a n －p (n ∈N *), 则S n －1＝4a n －1－p (n ∈N *,n ≥2),所以当n ≥2时,a n ＝S n －S n －1＝4a n －4a n －1, 整理得a n ＝43a n －1.由S n ＝4a n －p ,令n ＝1,得a 1＝4a 1－p ,解得a 1＝p3.所以{a n }是首项为p 3,公比为43的等比数列.(2)因为a 1＝1,则a n ＝(43)n －1,由b n ＋1＝a n ＋b n (n ＝1,2,…),得b n ＋1－b n ＝(43)n －1,当n ≥2时,由累加法得b n ＝b 1＋(b 2－b 1)＋(b 3－b 2)＋…＋(b n －b n －1) ＝2＋1－(43)n －11－43＝3·(43)n －1－1,当n ＝1时,上式也成立.∴b n ＝3·(43)n －1－1.10.(文)已知数列{a n }是等比数列,S n 为数列{a n }的前n 项和,且a 3＝3,S 3＝9. (1)求数列{a n }的通项公式.(2)设b n ＝log 23a 2n ＋3,且{b n }为递增数列,若c n ＝4b n ·b n ＋1,求证：c 1＋c 2＋c 3＋…＋c n <1.【试题解析】 (1)设该等比数列的公比为q , 则根据题意有3·(1＋1q ＋1q 2)＝9,从而2q 2－q －1＝0, 解得q ＝1或q ＝－12.当q ＝1时,a n ＝3； 当q ＝－12时,a n ＝3·(－12)n －3.(2)证明：若a n ＝3,则b n ＝0,与题意不符, 故a n ＝3(－12)n －3,此时a 2n ＋3＝3·(－12)2n ,∴b n ＝2n ,符合题意. ∴c n ＝42n ·(2n ＋2)＝1n ·(n ＋1)＝1n －1n ＋1, 从而c 1＋c 2＋c 3＋…＋c n ＝1－1n ＋1<1.(理)已知正数数列{a n }的前n 项和为S n ,满足a 2n ＝S n ＋S n －1(n ≥2),a 1＝1.(1)求数列{a n }的通项公式.(2)设b n ＝(1－a n )2－a (1－a n ),若b n ＋1>b n 对任意n ∈N *恒成立,求实数a 的取值范围. 【试题解析】 (1)因为a 2n ＝S n ＋S n －1(n ≥2), 所以a 2n ＋1＝S n ＋1＋S n .两式相减,得a 2n ＋1－a 2n ＝a n ＋1＋a n .因为a n >0,所以a n ＋1－a n ＝1.又a 1＝1,所以{a n }是首项为1,公差为1的等差数列. 所以a n ＝n .(2)因为b n ＝(1－a n )2－a (1－a n ),且由(1)得a n ＝n , 所以b n ＝(1－n )2－a (1－n )＝n 2＋(a －2)n ＋1－a , 所以b n ＋1＝(n ＋1)2＋(a －2)(n ＋1)＋1－a ＝n 2＋an . 因为b n ＋1>b n 恒成立,所以n 2＋an >n 2＋(a －2)n ＋1－a , 解得a >1－2n ,所以a >－1. 则实数a 的取值范围为(－1,＋∞).B 组1.已知S n 为等差数列{a n }的前n 项和,若S 1＝1,S 4S 2＝4,则S 6S 4的值为( A )A.94 B.32 C.53D.4【试题解析】 由等差数列的性质可知S 2,S 4－S 2,S 6－S 4成等差数列,由S 4S 2＝4得S 4－S 2S 2＝3,则S 6－S 4＝5S 2,所以S 4＝4S 2,S 6＝9S 2,S 6S 4＝94.2.(文)设S n 为等比数列{a n }的前n 项和,且4a 3－a 6＝0,则S 6S 3＝( D )A.－5B.－3C.3D.5【试题解析】 ∵4a 3－a 6＝0,∴4a 1q 2＝a 1q 5.∵a 1≠0,q ≠0, ∴q 3＝4,∴S 6S 3＝a 1(1－q 6)1－q a 1(1－q 3)1－q＝1－q 61－q 3＝1＋q 3＝5.(理)等比数列{a n }的前n 项和为S n ,已知S 3＝a 2＋10a 1,a 5＝9,则a 1＝( C )A.13B.－13C.19D.－19【试题解析】 ∵S 3＝a 2＋10a 1,∴a 1＋a 2＋a 3＝a 2＋10a 1, a 3＝9a 1＝a 1q 2,∴q 2＝9,又∵a 5＝9,∴9＝a 3·q 2＝9a 3,∴a 3＝1, 又a 3＝9a 1,故a 1＝19.3.已知数列{a n }满足a n ＋2－a n ＋1＝a n ＋1－a n ,n ∈N *,且a 5＝π2,若函数f (x )＝sin2x ＋2cos 2x2,记y n＝f (a n ),则数列{y n }的前9项和为( C )A.0B.－9C.9D.1【试题解析】 由已知可得,数列{a n }为等差数列, f (x )＝sin2x ＋cos x ＋1, ∴f (π2)＝1.∵f (π－x )＝sin(2π－2x )＋cos(π－x )＋1 ＝－sin2x －cos x ＋1, ∴f (π－x )＋f (x )＝2,∵a 1＋a 9＝a 2＋a 8＝…＝2a 5＝π,∴f (a 1)＋…f (a 9)＝2×4＋1＝9,即数列{y n }的前9项和为9. 4.(2018·浙江卷,10)已知a 1,a 2,a 3,a 4成等比数列,且a 1＋a 2＋a 3＋a 4＝ln(a 1＋a 2＋a 3).若a 1>1,则( B )A.a 1<a 3,a 2<a 4B.a 1>a 3,a 2<a 4C.a 1<a 3,a 2>a 4D.a 1>a 3,a 2>a 4【试题解析】 由x >0,ln x ≤x －1,得a 1＋a 2＋a 3＋a 4＝ln(a 1＋a 2＋a 3)≤a 1＋a 2＋a 3－1,a 4≤－1,所以公比q <0,当q ≤－1时,a 1＋a 2＋a 3＋a 4＝a 1(1＋q )(1＋q 2)<0,此时a 1＋a 2＋a 3＝a 1(1＋q ＋q 2)≥a 1>1,ln(a 1＋a 2＋a 3)>0,矛盾,所以－1<q <0,所以a 1－a 3＝a 1(1－q 2)>0,a 2－a 4＝a 1q (1－q 2)<0.5.数列{a n }的前n 项和S n ＝2n 2－3n (n ∈N *),若p －q ＝5,则a p －a q ＝( D ) A.10 B.15 C.－5D.20【试题解析】 当n ≥2时,a n ＝S n －S n －1＝2n 2－3n －2(n －1)2＋3n －3＝4n －5,a 1＝S 1＝－1适合上式,所以a n ＝4n －5,所以a p －a q ＝4(p －q ),因为p －q ＝5,所以a p －a q ＝20.6.(文)数列{a n }中,a 1＝2,a 2＝3,a n ＋1＝a n －a n －1(n ≥2,n ∈N *),那么a 2 019＝( A ) A.1B.－2C.3D.－3【试题解析】 因为a n ＋1＝a n －a n －1(n ≥2),所以a n ＝a n －1－a n －2(n ≥3),所以a n ＋1＝a n －a n －1＝(a n －1－a n －2)－a n －1＝－a n －2(n ≥3).所以a n ＋3＝－a n (n ∈N *),所以a n ＋6＝－a n ＋3＝a n , 故{a n }是以6为周期的周期数列. 因为2 019＝336×6＋3,所以a 2 019＝a 3＝a 2－a 1＝3－2＝1.故选A.(理)(2019·西安八校联考)若等差数列{a n }的前n 项和为S n ,若S 6>S 7>S 5,则满足S n S n ＋1<0的正整数n 的值为( C )A.10B.11C.12D.13【试题解析】 由S 6>S 7>S 5,得S 7＝S 6＋a 7<S 6,S 7＝S 5＋a 6＋a 7>S 5,所以a 7<0,a 6＋a 7>0,所以S 13＝13(a 1＋a 13)2＝13a 7<0,S 12＝12(a 1＋a 12)2＝6(a 6＋a 7)>0,所以S 12S 13<0,即满足S n S n ＋1<0的正整数n 的值为12,故选C.7.设数列{a n }的前n 项和为S n ,且a 1＝1,a n ＋1＝2S n ＋3,则S 4＝__66__. 【试题解析】 本题主要考查数列的通项公式与求和.依题a n ＝2S n －1＋3(n ≥2),与原式作差得,a n ＋1－a n ＝2a n ,n ≥2,即a n ＋1＝3a n ,n ≥2,可见,数列{a n }从第二项起是公比为3的等比数列,a 2＝5,所以S 4＝1＋5×(1－33)1－3＝66.8.若等比数列{a n }的各项均为正数,且a 10a 11＋a 9a 12＝2e 5,则ln a 1＋ln a 2＋…＋ln a 20＝__50__.【试题解析】 ∵a 10a 11＋a 9a 12＝2e 5,∴a 1·a 20＝e 5. 又∵ln a 1＋ln a 2＋…＋ln a 20＝ln(a 1a 2…a 20) ＝ln[(a 1a 20)(a 2a 19)…(a 10a 11)] ＝ln(e 5)10＝lne 50＝50.注意等比数列性质：若m ＋n ＝p ＋q ,则a m ·a n ＝a p ·a q ,对数的性质log a m n ＝n log a m . 9.设数列{a n }(n ＝1,2,3,…)的前n 项和S n 满足S n ＝2a n －a 1,且a 1,a 2＋1,a 3成等差数列. (1)求数列{a n }的通项公式；(2)记数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为T n ,求使得|T n －1|<11 000成立的n 的最小值.【试题解析】 (1)由已知S n ＝2a n －a 1, 有a n ＝S n －S n －1＝2a n －2a n －1(n ≥2), 即a n ＝2a n －1(n ≥2). 从而a 2＝2a 1,a 3＝4a 1.又因为a 1,a 2＋1,a 3成等差数列,即a 1＋a 3＝2(a 2＋1), 所以a 1＋4a 1＝2(2a 1＋1),解得a 1＝2.所以数列{a n }是首项为2,公比为2的等比数列. 故a n ＝2n . (2)由(1)得1a n ＝12n .所以T n ＝12＋122＋123＋…＋12n ＝12⎣⎡⎦⎤1－⎝⎛⎭⎫12n 1－12＝1－12n .由|T n －1|<11 000得⎪⎪⎪⎪1－12n －1<11 000,即2n >1 000. 因为29＝512<1 000<1 024＝210, 所以n ≥10. 于是,使|T n －1|<11 000成立的n 的最小值为10. 10.已知数列{a n }的首项为1,S n 为数列{a n }的前n 项和,且满足S n ＋1＝qS n ＋1,其中q >0,n ∈N *,又2a 2,a 3,a 2＋2成等差数列.(1)求数列{a n }的通项公式；(2)记b n ＝2a n －λ(log 2a n ＋1)2,若数列{b n }为递增数列,求λ的取值范围. 【试题解析】 (1)由S n ＋1＝qS n ＋1,① 可得,当n ≥2时,S n ＝qS n －1＋1,② ①－②得a n ＋1＝qa n . 又S 2＝qS 1＋1且a 1＝1, 所以a 2＝q ＝q ·a 1,所以数列{a n }是以1为首项,q 为公比的等比数列. 又2a 2,a 3,a 2＋2成等差数列, 所以2a 3＝2a 2＋a 2＋2＝3a 2＋2, 即2q 2＝3q ＋2. 所以2q 2－3q －2＝0, 解得q ＝2或q ＝－12(舍去),所以数列{a n }的通项公式为：a n ＝2n －1(n ∈N *). (2)由题意得b n ＝2·2n －1－λ(log 22n )2＝2n －λn 2, 若数列{b n }为递增数列,则有b n ＋1－b n ＝2n ＋1－λ(n ＋1)2－2n＋λn 2＝2n－2nλ－λ>0,即λ<2n2n ＋1.因为2n ＋12n ＋32n 2n ＋1＝4n ＋22n ＋3>1,所以数列{2n2n ＋1}为递增数列.所以2n 2n ＋1≥23,所以λ<23.。