2018年中考数学总复习第四单元三角形专题13线段与角相交线与平行线试题

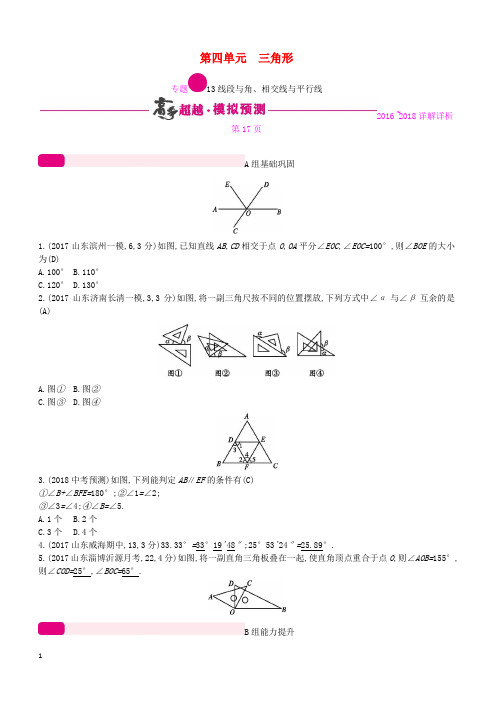
第四单元三角形专题13线段与角、相交线与平行线2016~2018详解详析第17页A组基础巩固1.(2017山东滨州一模,6,3分)如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为(D)A.100°B.110°C.120°D.130°2.(2017山东济南长清一模,3,3分)如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是(A)A.图①B.图②C.图③D.图④3.(2018中考预测)如图,下列能判定AB∥EF的条件有(C)①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.A.1个B.2个C.3个D.4个4.(2017山东威海期中,13,3分)33.33°=33°19'48″;25°53'24″=25.89°.5.(2017山东淄博沂源月考,22,4分)如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB=155°,则∠COD=25°,∠BOC=65°.B组能力提升1.(2017山东德州乐陵一模,12,3分)下列命题:①若a+b+c=0,则b2-4ac≥0;②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;③若b2-4ac>0,则二次函数的图象与坐标轴的公共点的个数是2或3.其中正确的是(D)A.①②B.①③C.②③D.①②③2.(2018中考预测)点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若BC=5,则AC=9或1.3.(2016浙江温州二中一模,17,6分)如图,在平面直角坐标系xOy中,点A(6,8),点B(6,0).(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):①点P到A,B两点的距离相等;②点P到∠xOy的两边的距离相等.(2)在(1)作出点P后,直接写出点P的坐标.解(1)如图,点P为所作.(2)P点坐标为(4,4).4.(2017重庆江津期中,27,9分)已知直线AB∥CD,E为AB,CD之间的一点,连接EA,EC.(1)如图①,若∠A=20°,∠C=40°,则∠AEC=°.(2)如图②,若∠A=x°,∠C=y°,则∠AEC=°.(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系,并简要说明.解(1)60(2)360-x-y(3)∠A=α,∠C=β,如图,过点E作EF∥AB,∵AB∥CD,∴AB∥CD∥EF.∴∠1+∠A=180°,∠2=∠C=β,∴∠1=180°-∠A=180°-α,∴∠AEC=∠1+∠2=180°-α+β.〚导学号92034057〛。

线段、角、相交线与平行线【命题趋势】在中考中.直线与线段主要以选择题和填空题形式考查；角及角平分线主要在选择题中考查；平行线常与角度结合考查.以选择题和填空题形式为主。

【中考考查重点】一、角的识别及余角、补角的计算二、平行线的判定三、平行线的性质求角度四、命题考点一：直线和线段 1．（2021春•自贡期末）在墙上要钉牢一根木条.至少要钉两颗钉子．能解释这一实际应用的数学知识是（ ）A ．两点之间线段最短B ．两点确定一条直线C ．直线比线段长D ．两条直线相交.只有一个交点2．（2021春•拱墅区月考）在同一平面内.不重合的三条直线的交点有（ ）个．A ．1或2B ．2或3C ．1或3D ．0或1或2或33．（2021春•白碱滩区期末）直线l 外有一点P .直线l 上有三点A 、B 、C .若P A ＝4cm .PB ＝2cm .PC ＝3cm .那么点P 到直线l 的距离（ ） 两个基本事实1. 线段的基本事实：两点确定一条直线2. 线段的基本事实：两点间线段最短 两点间的距离连接两点间的线段的长度 线段的和与差如图.在线段AC 上取一点B.则有AC=AB+BC ；AB=AC -BC; BC=AC -AB 线段的中点如图.M 是线段AB 的中点.即有AM=BM=AB 21A ．不小于2cmB ．大于2cmC ．不大于2cmD ．小于2cm4．如图.线段AB ＝12.点C 是它的中点．则AC 的长为（ ）A ．2B ．4C ．6D ．82.余角、补角、角平分线 5．（2021秋•洪山区期末）若一个角比它的余角大30°.则这个角等于（ ）A ．30°B ．60°C ．105°D ．120°6．（2021秋•盐池县期末）若∠α的补角是125°24′.则∠α的余角是（ ）A ．90°B ．54°36′C ．36°24′D ．35°24′7．（2021秋•龙江县期末）已知∠AOB ＝100°.过点O 作射线OC 、OM .使∠AOC ＝20°、OM 是∠BOC 的平分线.则∠BOM 的度数为（ ）A ．60°B ．60°或40°C ．120°或80°D ．40°8．（2021秋•江汉区期末）如图.在观测站O 发现客轮A 、货轮B 分别在它北偏西50°、西南方向.则∠AOB 的度数是（ ） 度分秒的换算1周角=360°.1平角=180°.1°=60′.1′=60″ 角的度分秒的进制是60 角的分类按大小分：周角（360°）＞平角（180°）＞直角（90°）＞锐角余角1. 概念：如若两个角之和=90°.那么这两个角互为余角；2. 性质：同角（等角）的余角相等 补角3. 1.概念：如若两个角之和=180°.那么这两个角互为补角；性质：同角（等角）的补角相等角平分线1. 性质：角平分线上的点到角两边的距离相等2. 逆定理：在角的内部.到角两边距离相等的点在角平分线上A ．80°B ．85°C ．90°D ．95°9．（2021秋•锦江区校级期末）如图.一副三角板（直角顶点重合）摆放在桌面上.若∠BOC ＝20°.则∠AOD 等于（ ）A ．160°B ．140°C ．130°D ．110°10．（2021秋•南岗区期末）下列四幅图中.∠1和∠2是对顶角的为（ ）A ．B ．图示对顶角性质：对顶角相等 如图.∠1与∠3.∠与∠4.∠5与∠7.∠6与∠8 邻补角性质：邻补角之和等于180° 如图.∠1与∠4.∠2与∠3.∠5与∠8.∠6与∠7 同位角如图。

A. 150°B. 130°如图，在△刃冏7中， 的度数为（）D. 50° ZACD=40° ,则匕万 A. 8 B. 6能说明命题“对于任何实数a, 例可以是（） C. 4 D. 2 a|> 一a"是假命题的一个反 A. a=—2 1 B. a=~O C. a=l 已知AD//BC, ABLAD,点E,点夕分别在射线AD, 若点万与点万关于力。

对称，点万与点夕关于匆对称, 射线此'上， m 与匆相交2018年初三数学中考专题复习：线段、角、相交线与平行线综合训练题1.如图，直线a//b,直线c 分别与a,力相交，匕1 = 50° ,则匕2 的度数为（）A. 40°B. 50°C. 60°D. 70°3. 如图，AB//CD,胪和6P 分别平分ZABC 和匕DCB,初过点只且与刃万垂直.若AD=8,则点户到此'的距离是（ ）A. 55°B. 60°C. 70°D. 75°6. 如图，费是ZAOC 的角平分线，况2是/COE 的角平分线.如果匕力阳= 40° ,匕COE=S 甘，则/BOD 的度数为（D. 70°7. 如图，直线a,力被直线c, d 所截，若Z1 = Z2, Z3 = 125° , 则匕4的度数为（8.如图，力〃是匕屈。

的平分线，AD//BC, 4=30° ,则/C=（ A. 30° B. 60° C. 80° D. 120°9. 已知命题“关于才的一元二次方程了+庭+1 = 0,当b<Q 时必有 实数解”，能说明这个命题是假命题的一个反例可以是（） 于点G 则 EA. b= —1B. b=2C. b=~2D. b=010.如图，AB VAC, ADLBC,垂足分别为A, D,则图中能表示点到直线距离的线段共有（ A. 2条11. 如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖 去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动 刀片时会形成如图2所示的匕1与匕2,则匕1与匕2的度数和是 度.12. 如图，点凡C, F,万在同一直线上，勿平分/ECB, FG//CD, 若/EG4为a 度，则/GFB 为 度（用关于。

相交线与平行线一、选择题1.如图，直线∥，直线与、都相交，如果∠1=50°，那么∠2的度数是（）A. 50°B. 100°C. 130°D. 150°【答案】C【解析】：∵a∥b，∠1=50°，∴∠1=∠3=50°，∵∠2+∠3=180°，∴∠2=180°-∠1=180°-50°=130°.故答案为：C.【分析】其中将∠2的邻补角记作∠3，利用平行线的性质与邻补角的意义即可求得∠2的度数.2.如图，AB∥CD，且∠DEC=100°，∠C=40°，则∠B的大小是（）A. 30°B. 40°C. 50°D. 60°【答案】B【解析】：∵∠DEC=100°，∠C=40°，∴∠D=40°，又∵AB∥CD，∴∠B=∠D=40°，故答案为：B．【分析】首先根据三角形的内角和得出∠D的度数，再根据二直线平行，内错角相等得出答案。

3.如图，若l1∥l2， l3∥l4，则图中与∠1互补的角有（）A. 1个B. 2个C. 3个 D. 4个【答案】D【解析】如图，∵l1∥l2， l3∥l4，∵∠2=∠4，∠1+∠2=180°，又∵∠2=∠3，∠4=∠5，∴与∠1互补的角有∠2、∠3、∠4、∠5共4个，故答案为：D.【分析】根据二直线平行同位角相等，同旁内角互补得出∠2=∠4，∠1+∠2=180°，再根据对顶角相等得出∠2=∠3，∠4=∠5，从而得出答案。

4.如图，直线，若，，则的度数为（）A. B.C.D.【答案】C【解析】：∵∠1=42°，∠BAC=78°，∴∠ABC=60°，又∵AD∥BC，∴∠2=∠ABC=60°，故答案为：C．【分析】首先根据三角形的内角和得出∠ABC的度数，再根据二直线平行内错角相等即可得出答案。

2018年初三数学中考专题复习：线段、角、订交线与平行线综合训练题含答案2018年初三数学中考专题复习：线段、角、订交线与平行线综合训练题1.如图，直线a∥b，直线c分别与a，b订交，∠1＝50°，则∠2的度数为()A．150°B．130°C．100°D．50°如图，在△ABC中，∠ACB＝90°，CD∥AB，∠ACD＝40°，则∠B的度数为()A．40°B．50°C．60°D．70°如图，AB∥CD，BP和CP分别均分∠ABC和∠DCB，AD 过点P，且与AB垂直．若AD＝8，则点P到BC的距离是()A．8B．6C．4D．24.能说明命题“对于任何实数a，|a|＞－a”是假命题的一个反例能够是()1C．a＝1D．a＝2已知AD∥BC，AB⊥AD，点E，点F分别在射线A．a＝－2B．a＝3AD，射线BC上，若点E与点B对于AC对称，点E与点F对于BD对称，AC与BD订交于点G.则()A．1＋tan∠ADB＝2B．2BC＝5CFC．∠AEB＋22°＝∠DEFD．4cos∠AGB＝61/4图，OB是∠AOC的角均分线，OD是∠COE的角均分线．假如∠AOB＝40°，∠COE＝60°，则∠BOD的度数为()A．50°B．60°C．65°D．70°如图，直线a，b被直线c，d所截，若∠1＝∠2，∠3＝125°，则∠4的度数为()A．55°B．60°C．70°D．75°8.如图，AD是∠EAC的均分线，AD∥BC，∠B＝30°，则∠C＝()A．30°B．60°C．80°D．120°已知命题“对于x的一元二次方程x2＋bx＋1＝0，当b＜0时必有实数解”，能说明这个命题是假命题的一个反例能够是()A．b＝－1B．b＝2C．b＝－2D．b＝0如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有()A．2条B．3条C．4条D．5条如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，此中刀片的两条边沿线可当作两条平行的线段，转动刀片刻会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是度．2/4如图，点A，C，F，B在同向来线上，CD均分∠ECB，FG∥CD，若∠ECA为α度，则∠GFB为度(用对于α的代数式表示)．12.如图折叠一张矩形纸片，已知∠1＝70°，则∠2的度数是_________．如图，已知直线AB，CD订交于点O，OE，OF为射线，∠AOE＝90°，OF均分∠AOC，∠AOF＋∠BOD＝51°，求∠EOD的度数．3/42018年初三数学中考专题复习：线段、角、订交线与平行线综合训练题含答案参照答案：1---10 BBCAA DAAADα 12.90－213. 55°14.解：∵∠AOC ＝∠BOD ，OF 均分∠AOC ，11∴∠AOF ＝2∠AOC ＝2∠BOD ．∵∠AOF ＋∠BOD ＝51°，∴∠AOF ＝17°，∠BOD ＝34°.∵∠AOE ＝90°，∴∠BOE ＝180°－∠AOE ＝90°，∴∠EOD ＝90°＋34°＝124°.4/4。

中考数学《相交线与平行线》专项复习综合练习题-附带答案一、单选题1．下列命题中，是假命题的是（）A．两点之间线段最短B．对顶角相等C．同旁内角互补D．直角的补角仍然是直角2．如图，直线a∥b，∠1=70°，那么∠2的度数是（）A．50°B．60°C．70°D．80°3．如图，下列四个条件中，能判断DF∥AC的是（）A．∠AED＝∠ACB B．∠EDC＝∠DCFC．∠FDC＝∠DCE D．∠ECF＝∠EDF4．如图，七年级（下）教材第4页给出了利用三角尺和直尺画平行线的一种方法能说明AB∥DE的条件是（）A．∠CAB=∠FDE B．∠ACB=∠DFE C．∠ABC=∠DEF D．∠BCD=∠EFG5．如图，把周长为10的△ABC沿BC方向平移1个单位得到△DFE，则四边形ABFD的周长为（）A．14 B．12 C．10 D．86．如图所示下列条件中，①∠1=∠4；②∠2=∠4；③∠1=∠3；④∠5=∠4 其中能判断直线l1∥l2的有（）A．1个B．2个C．3个D．4个7．轩轩准备参加马拉松比赛，得知一段跑道示意图（如图），其中AB∥DE 测得∠EDC=110°，∠ABC=130°则∠BCD的度数为（）A．120°B．100°C．240°D．90°8．将一直角三角板与两边平行的硬纸条如图所示放置，下列结论：（1）∠1＝∠2；（2）∠3＝∠4；（3）∠2+∠4＝90°；（4）∠4+∠5＝180°. 其中正确的个数是( )A．1 B．2 C．3 D．4二、填空题9．如图，已知AB∥CD ，∠1=130°，则∠2= .10．若∠α与∠β的两边分别平行，且∠α=(x+20)°∠β=(3x−40)°则∠α的度数为. 11．如图，AB∥CD 直线PQ分别交AB CD于点E F FG•是∠EFD的平分线交AB于点G ，若∠FEG=70°那么∠FGB等于．12．如图，DA是∠BDF的平分线∠3=∠4 若∠1=40°∠2=140°则∠CBD的度数为．13．如图，把一块三角板的60°角的顶点放在直尺的一边上若∠1=2∠2 则∠1= °．三、解答题14．已知：如图，AD⊥BC FG⊥BC．垂足分别为D G．且∠ADE=∠CFG．求证：DE∥AC．15．如图所示直线AB、CD、EF相交于点O ∠AOE＝40°∠BOC＝2∠AOC 求∠DOF.16．如图，AB⊥BF CD⊥BF∠1=∠2．求证：∠3=∠E．17．如图，直线AB与直线CD交于点C点P为直线AB、CD外一点根据下列语句画图并作答：（1）过点P画PQ//CD交AB于点Q；（2）过点P画PR⊥CD垂足为R；（3）点M为直线AB上一点连接PC连接PM.18．如图所示：（1）若DE//BC∠1=∠3∠CDF=90°求证：FG⊥AB .（2）若把（1）中的题设“DE//BC”与结论“FG⊥AB”对调所得命题是否是真命题？说明理由.参考答案1．C2．C3．C4．A5．B6．C7．A8．D9．50°10．70°或50°11．125º12．70°13．8014．证明：∵AD⊥BC FG⊥BC且∠ADE=∠CFG∴∠C+∠CFG=90°∠BDE+∠ADE=90°∴∠BDE=∠C∴DE∥AC．15．解：设∠AOC＝x°则∠BOC＝(2x)°.因为∠AOC与∠BOC是邻补角所以∠AOC+∠BOC＝180°所以x+2x＝180解得x＝60所以∠AOC＝60°.因为∠DOF与∠EOC是对顶角所以∠DOF＝∠EOC＝∠AOC－∠AOE＝60°－40°＝20°16．证明：如图所示：∵AB⊥BF CD⊥BF∴∠ABD=∠CDF=90°∴AB∥CD（同位角相等两直线平行）∴∠1=∠DGF∵∠1=∠2∴∠2=∠DGF（等量代换）∴CD∥EF（内错角相等两直线平行）∴∠3=∠E（两直线平行同位角相等）．17．（1）解：如图所示如图所示直线PQ即为所求；（2）解：如图所示垂线段PR即为所求；（3）解：如图所示线段PC、PM即为所求．18．（1）解：∵DE//BC（已知）∴∠1=∠2 .（两直线平行内错角相等）∵∠1=∠3（已知）∴∠2=∠3（等量代换）∴DC//FG .（同位角相等两直线平行）∴∠BFG=∠FDC=90° .（两直线平行同位角相等）∴FG⊥AB .（垂直的定义）；（2）解：是真命题理由如下：∵FG⊥AB（已知）∴∠BFG=90°=∠FDC∴DC//FG .（同位角相等两直线平行）∴∠2=∠3 .（两直线平行同位角相等）∵∠1=∠3（已知）∴∠1=∠2 .（等量代换）∴DE//BC .（内错角相等两直线平行）。

中考数学复习《角、相交线与平行线》经典题型及测试题（含答案）命题点分类集训命题点1 线段【命题规律】主要考查：①两点之间线段最短；②两点确定一条直线这两个基本事实．【命题预测】与图形的变换中立体图形的侧面展开结合，求两点之间的最短距离，另外也会与对称性结合，考查两线段和的最小值．1. 如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是( )A. 垂线段最短B. 经过一点有无数条直线C. 经过两点，有且仅有一条直线D. 两点之间，线段最短1. D第1题图第2题图2. 如图，AB⊥AC，AD⊥BC，垂足分别为A，D.则图中能表示点到直线距离的线段共有( )A. 2条B. 3条C. 4条D. 5条2. D【解析】AD是点A到直线BC的距离；BA是点B到直线AC的距离；BD是点B到直线AD的距离；CA是点C到直线AB的距离；CD是点C到直线AD的距离，共5条，故答案为D.命题点2 角、余角、补角及角平分线【命题规律】主要考查：①角度的计算(度分秒之间的互化)；②余角、补角的计算；③角平分线的性质．【命题预测】角、余角、补角及角平分线等基本概念是图形认识的基础，应给予重视．3. 下列各图中，∠1与∠2互为余角的是( )3. B4. 如图，OP为∠AOB的平分线，PC⊥OB于点C，且PC＝3，点P到OA的距离为________．4. 3【解析】如解图，过点P作PD⊥OA于点D，∵OP为∠AOB的平分线，PC⊥OB于点C，∴PD＝PC，∵PC＝3，∴PD＝3，即点P到点OA的距离为3.5. 1.45°＝________′.5. 87【解析】∵1°＝60′，∴0.45°＝27′，∴1.45°＝87′.6. 已知∠A＝100°，那么∠A的补角为________度．6. 80【解析】用180度减去已知角，就得这个角的补角．即∠A的补角为：180°－100°＝80°.命题点3 相交线与平行线【命题规律】考查形式：①三线八角中同位角、内错角、同旁内角的识别或计算，有时综合对顶角、邻补角求角度；②综合角平分线、垂线求角度；③综合三角形的相关知识求角度；④根据角的关系判断两直线的关系．【命题预测】平行线性质是认识图形的基础知识，也是全国命题的潮流和方向．7. 如图，直线a，b被直线c所截，∠1与∠2的位置关系是( )A. 同位角B. 内错角C. 同旁内角D. 对顶角7. B【解析】根据相交线的性质及角的定义可知∠1与∠2的位置关系为内错角，故选B.第7题图第8题图第9题图8. 如图，已知a、b、c、d四条直线，a∥b，c∥d，∠1＝110°，则∠2等于( )A. 50°B. 70°C. 90°D. 110°8. B【解析】如解图，∵a∥b，∴∠3＋∠4＝180°，∵c∥d，∴∠2＝∠4，∵∠1＝∠3，∴∠2＝180°－∠1＝70°，故本题选B.9. 如图，在下列条件中，不能．．判定直线a与b平行的是( )A. ∠1＝∠2B. ∠2＝∠3C. ∠3＝∠5D. ∠3＋∠4＝180°9. C【解析】逐项分析如下：选项逐项分析正误A∵∠1＝∠2，即同位角相等，两直线平行，∴a∥b √B∵∠2＝∠3，即内错角相等，两直线平行，∴a∥b √∵∠3、∠5既不是a与b被第三直线所截的同位角，也不是内错角，×C∴∠3＝∠5，不能够判定a与b平行D∵∠3＋∠4＝180°，即同旁内角互补，两直线平行，∴a∥b √10. 如图，将一块直角三角板的直角顶点放在直尺的一边上，如果∠1＝50°，那么∠2的度数是( )A. 30°B. 40°C. 50°D. 60°10. B 【解析】如解图，∠1＋∠3＝90°，∴∠3＝90°－∠1＝90°－50°＝40°，由平行线性质得∠2＝∠3＝40°.11. 如图所示，AB ∥CD ，EF ⊥BD ，垂足为E ，∠1＝50°，则∠2的度数为( )A . 50°B . 40°C . 45°D . 25°11. B 【解析】∵EF ⊥BD ，∠1＝50°，∴∠D ＝90°－50°＝40°，∵AB ∥CD ，∴∠2＝∠D ＝40°.第10题图 第11题图 第12题图 第13题图12. 如图，AB ∥CD ，直线EF 与AB ，CD 分别交于点M ，N ，过点N 的直线GH 与AB 交于点P ，则下列结论错误的是( )A . ∠EMB ＝∠END B . ∠BMN ＝∠MNC C . ∠CNH ＝∠BPGD . ∠DNG ＝∠AME12. D 【解析】A.两直线平行，同位角相等，∴∠EMB ＝∠END ；B.两直线平行，内错角相等，∴∠BMN ＝∠MNC ；C.两直线平行，同位角相等，∴∠CNH ＝∠APH ，又∠BPG ＝∠APH ，∴∠CNH ＝∠BPG ；D.∠DNG 和∠AME 无法推导数量关系，故不一定相等，答案为D.13. 如图，直线a∥b，∠1＝45°，∠2＝30°，则∠P＝________°.13. 75 【解析】如解图，过点P 作PH ∥a ∥b ，∴∠FPH ＝∠1，∠EPH ＝∠2，又∵∠1＝45°，∠2＝30°，∴∠EPF ＝∠EPH ＋∠HPF ＝30°＋45°＝75°.命题点4 命 题【命题概况】命题考查的知识点比较多，一般几个知识点结合考查，考查形式有：①下面说法错误(正确)的是；②写出命题…的逆命题；③能说明…是假命题的反例．【命题趋势】命题为新课标新增内容，考查知识比较综合，是全国命题点之一．14. (2016宁波)能说明命题“对于任何实数a ，|a|＞－a”是假命题的一个反例可以是( )A . a ＝－2B . a ＝13C . a ＝1D . a ＝ 214. A 【解析】由于一个正数的绝对值是它本身，它的相反数是一个负数，所以当a ＝13，1，2时，|a |>－a 总是成立，当a ＝－2时，|－2|＝2＝－(－2)，此时|a |＝－a ，故本题选A.15. 写出命题“如果a ＝b ，那么3a ＝3b”的逆命题．．．：________________________． 15. 如果3a ＝3b ，那么a ＝b 【解析】命题由条件和结论构成，则其逆命题只需将原来命题的条件和结论互换即可，即将结论作为条件，将条件作为结论. ∵命题“如果a ＝b ，那么3a ＝3b ，”中条件为“如果a ＝b ”，结论为“那么3a ＝3b ”，∴其逆命题为“如果3a ＝3b ，那么a ＝b ”．中考冲刺集训一、选择题1. 如图，AB∥CD，DA⊥AC，垂足为A，若∠ADC＝35°，则∠1的度数为( )A. 65°B. 55°C. 45°D. 35°第1题图第2题图第3题图2. 如图，AB∥CD，AE平分∠CAB交CD于点E.若∠C＝50°，则∠AED＝( )A. 65°B. 115°C. 125°D. 130°3. 如图，∠AOB的一边OA为平面镜，∠AOB＝37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是( )A．75°36′B．75°12′C．74°36′D．74°12′二、填空题4. 如图，平行线AB，CD被直线AE所截，∠1＝50°，则∠A＝________.第4题图第5题图第6题图5. 如图，直线CD∥EF，直线AB与CD、EF分别相交于点M、N，若∠1＝30°，则∠2＝________．6. 如图，AB∥CD，直线EF分别交AB，CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放．若∠EMB＝75°，则∠PNM等于________度．7. 如图，直线AB∥CD，BC平分∠ABD.若∠1＝54°，则∠2＝________°.第7题图第8题图第9题图8. 如图，AB∥CD∥EF，若∠A＝30°，∠AFC＝15°，则∠C＝________．9.如图，OP平分∠AOB，∠AOP＝15°，PC∥OA，PD⊥OA于点D，PC＝4，则PD＝________．答案与解析：1. B【解析】∵DA⊥AC，∠ADC＝35°，∴∠ACD＝90°－∠ADC＝90°－35°＝55°，∵AB∥CD，∴∠1＝∠ACD＝55°，故选B.2. B【解析】∵AB∥CD，∴∠C＋∠CAB＝180°，∵∠C＝50°，∴∠CAB＝130°，∵AE平分∠CAB，∴∠EAB＝12∠CAB＝65°.又∵AB∥CD，∴∠AED＋∠EAB＝180°，∴∠AED＝180°－∠EAB＝180°－65°＝115°.3. B【解析】根据平面镜反射原理可知，∠ADC＝∠ODE，∵DC∥OB，∴∠ADC＝∠AOE，∴∠ODE＝∠AOE＝37°36′，∴∠DEB＝∠ODE＋∠AOE＝37°36′＋37°36′＝75°12′，故选B.4. 50°5. 30°6. 307. 72【解析】∵CD∥AB，∴∠CBA＝∠1＝54°，∠ABD＋∠CDB＝180°，∵CB平分∠ABD，∴∠DBC＝∠CBA＝54°，∴∠CDB＝180°－54°－54°＝72°，∴∠2＝∠CDB＝72°.8. 15°【解析】由两直线平行，内错角相等，可得∠A＝∠AFE＝30°，∠C＝∠CFE，由∠AFC＝15°，可得∠CFE＝∠C＝∠AFE－∠AFC＝15°.第9题解图9. 2【解析】如解图，过点P作PE⊥OB于点E，∵OP平分∠AOB，∴PD＝PE，∠AOB＝2∠AOP＝30°，∵PC∥OA，∴∠ECP＝∠AOB＝30°，∴PE＝12PC＝2，∴PD＝PE＝2.。

2018年 初三数学中考专题复习： 线段、角、相交线与平行线综合训练题A. 1+ tan Z AD = , 2 C.Z AE 聊22°=ZDEFB . 2BC=5CF D . 4cos Z AG = 6AD = 8,则点P 到BC 的距离是（ ) R A/pc DA. 8B . 6C.4D . 24. 能说明命题“对于任何实数 a , |a | 〉—a ”是假命题的一个反例可以是()A. 1a = — 2 B . a = 33C.a = 1 D . a =/2 3. 5.已知AD// BC ABL AD 点E,点F 分别在射线AD 射线BC 上，若点E 与点B 关于AC 对称，点E 与点F 关于BD 对称，AC 与 BD 相交于点G 则（1. 如图，直线a // b,直线c 分别与a,b 相交，/ 1 = 50 ，则/2的度数为（A. 2. 150° B . 130° C .如图，在△ ABC 中, Z AC =90°,CD/ AB Z AC = 40，则/B 的度数为（40°B . 50°C . 60°D . 70°如图，AB// CD BP 和CP 分别平分Z ABC 和Z DCBAD 过点P,且与AB 垂直.A. b.506.如图，OB 是/ AOC 勺角平分线, / CO B 60°，则/ BOD 勺度数为(OD 是/ COE 的角平分线.如果/ )AO B= 40°, A. 50° B 7.如图，直线a , b 被直线c , 数为(A. 8. 55° 如图, d 所截，若/ 1 = Z 2, D. 75° ,则/ C=(B. 60° AD 是/ EAC 的平分线,D/ 3= 125°, .70°则/ 4的度 B . 60° C . 80° D . 120°30 已知命题“关于x 的一元二次方程x 2+bx + 1= 0,当b v 0时必有实数解”， 能说明这个命题是假命题的一个反例可以是 A. b =— 1 10.如图， 线段共有(A. 9.B . b = 2CAB 丄AC ADLBQ 垂足分别为 )( ) .b = — 2 D . b = 0A , D,则图中能表示点到直线距离的A. 2条 C . 4条 D . 5条11.如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小 半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的/ 1与/ 2,则/ 1与/ 2的度数和是 ___________ 度.12.如图，点A , C, F , B 在同一直线上，CD 平分/ ECB FGI CD 若/ ECA 为13.如图折叠一张矩形纸片，已知/ 1 = 70°，则/ 2的度数是14.如图，已知直线AB CD 相交于点Q OE OF 为射线，/ AO =90°, OF 平 分/AOC Z AOFb Z BO = 51°，求/ EOD 勺度数.Ca 度，则/ GFB 为 _______ 度（用关于a 的代数式表示）.参考答案：1---10 BBCAA DAAAD11. 90/ \a12. 90-*13. 55°14. 解：T/AO&Z BOD OF平分/ AOC1 1:丄 AO R-Z AO&-Z BOD.2 2vZ AO R-Z BO R 51 °,•••Z AO R 17°,Z BO R 34°.vZ AO R 90°,•Z BO R 180°-Z AOE R90°,•Z EO R90°+ 34°= 124°.。

天津市河西区普通中学2018届初三数学中考复习线段、角、相交线和平行线专项训练题1．把一条弯曲的公路改成直道，可以缩短路程．用几何知识解释其道理正确的是( C )A．两点确定一条直线B．垂线段最短C．两点之间线段最短D．三角形两边之和大于第三边2．如图，C，D是线段AB上两点，D是线段AC的中点，若AB＝10 cm，BC＝4 cm，则AD的长等于( B )A．2 cm B．3 cm C．4 cm D．6 cm3．如图，在△ABC中，∠C＝90°，点D，E分别在边AC，AB上．若∠B＝∠ADE，则下列结论正确的是( C )A．∠A和∠B互为补角B．∠B和∠ADE互为补角C．∠A和∠ADE互为余角D．∠AED和∠DEB互为余角4．如图，AB∥CD，FE⊥DB，垂足为E，∠1＝50°，则∠2的度数是( C )A．60° B．50° C．40° D．30°5．以下四种沿AB折叠的方法中，不一定能判定纸带两条边线a，b互相平行的是( C )A．如图①，展开后测得∠1＝∠2B．如图②，展开后测得∠1＝∠2且∠3＝∠4C．如图③，测得∠1＝∠2D．如图④，展开后再沿CD折叠，两条折痕的交点为O，测得OA＝OB，OC ＝OD6．图中是对顶角量角器，用它测量角的原理是__对顶角相等__．7．如图，∠1＝∠2，∠A＝60°，则∠ADC＝__120__度．8．如图，∠1＝∠2＝40°，MN平分∠EMB，则∠3＝__110°__．9．如图，已知矩形纸片的一条边经过直角三角形纸片的直角顶点，若矩形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1，∠2，则∠2－∠1＝__90°__．10．如图，AB∥CD，∠CDE＝119°，GF交∠DEB的平分线EF于点F，∠AGF＝130°，则∠F＝__9.5°__．11．如图，直线AB∥CD，BC平分∠ABD，∠1＝65°，求∠2的度数．解：∵AB∥CD，∴∠ABC＝∠1＝65°，∠ABD＋∠BDC＝180°，∵BC平分∠ABD，∴∠ABD＝2∠ABC＝130°，∴∠BDC＝180°－∠ABD＝50°，∴∠2＝∠BDC＝50°12．如图，已知，l1∥l2，C1在l1上，并且C1A⊥l2，A为垂足，C2，C3是l1上任意两点，点B在l2上．设△ABC1的面积为S1，△ABC2的面积为S2，△ABC3的面积为S 3，小颖认为S 1＝S 2＝S 3，请帮小颖说明理由．解：∵直线l 1∥l 2，∴△ABC 1，△ABC 2，△ABC 3的底边AB 上的高相等，∴△ABC 1，△ABC 2，△ABC 3这3个三角形同底，等高，∴△ABC 1，△ABC 2，△ABC 3这些三角形的面积相等．即S 1＝S 2＝S 313．如图，OM 是∠AOC 的平分线，ON 是∠BOC 的平分线．(1)如图①，当∠AOB 是直角，∠BOC ＝60°时，∠MON 的度数是多少？(2)如图②，当∠AOB＝α，∠BOC ＝60°时，猜想∠MON 与α的数量关系； (3)如图③，当∠AOB＝α，∠BOC ＝β时，猜想∠MON 与α，β有数量关系吗？如果有，指出结论并说明理由．解：(1)如图①，∵∠AOB ＝90°，∠BOC ＝60°，∴∠AOC ＝90°＋60°＝150°，∵OM 平分∠AOC，ON 平分∠BOC，∴∠MOC ＝12∠AOC＝75°，∠NOC ＝12∠BOC＝30°∴∠MON ＝∠MOC－∠NOC＝45°(2)如图②，∠MON ＝12α，理由是：∵∠AOB＝α，∠BOC ＝60°，∴∠AOC ＝α＋60°，∵OM 平分∠AOC，ON 平分∠BOC，∴∠MOC ＝12∠AOC＝12α＋30°，∠NOC＝12∠BOC＝30°∴∠MON ＝∠MOC－∠NOC＝(12α＋30°)－30°＝12α (3)如图③，∠MON ＝12α，与β的大小无关．理由：∵∠AOB＝α，∠BOC ＝β，∴∠AOC ＝α＋β. ∵OM 是∠AOC 的平分线，ON 是∠BOC 的平分线，∴∠MOC ＝12∠AOC＝12(α＋β)，∠NOC ＝12∠BOC＝12β，∴∠MON ＝∠MOC－∠NOC＝12(α＋β)－12β＝12α 即∠MON＝12α14．如图，B 是线段AD 上一动点，沿A→D→A 以2 cm/s 的速度往返运动1次，C 是线段BD 的中点，AD ＝10 cm ，设点B 运动时间为t 秒(0≤t≤10)．(1)当t ＝2时，①AB ＝__4__cm.②求线段CD 的长度； (2)用含t 的代数式表示运动过程中AB 的长； (3)在运动过程中，若AB 中点为E ，则EC 的长是否变化？若不变，求出EC 的长；若发生变化，请说明理由．解：(1)①∵B 是线段AD 上一动点，沿A→D→A 以2 cm/s 的速度往返运动，∴当t ＝2时，AB ＝2×2＝4 cm.故答案为：4②∵AD ＝10 cm ，AB ＝4 cm ，∴BD ＝10－4＝6 cm ，∵C 是线段BD 的中点，∴CD ＝12BD ＝12×6＝3 cm (2)∵B 是线段AD 上一动点，沿A→D→A 以2 cm/s 的速度往返运动，∴当0≤t≤5时，AB ＝2t ；当5＜t≤10时，AB ＝10－(2t －10)＝20－2t(3)不变．∵AB 中点为E ，C 是线段BD 的中点，∴EC ＝12(AB ＋BD)＝12AD ＝12×10＝5 cm。

中考数学试题分类汇总《线段、角、相交线与平行线》练习题（含答案）1．已知∠A＝10°，则∠A的余角等于80°．2．如图，点O是直线AB上一点，∠AOC＝50°，则∠BOC的度数为130°．【分析】根据补角的概念直接计算即可．【解答】解：∵∠AOC＝50°，∴∠BOC＝180°﹣∠AOC＝180°﹣50°＝130°，3．在△ABC中，已知∠A＝50°，∠B＝60°，则与∠C相邻的外角度数为110°．4．∠A＝50°，则∠A的余角等于40°．5．如图，点A，B，C在直线l上，PB⊥l，P A＝6，PB＝5，PC＝7，点P到直线l的距离是5．【分析】利用点到直线的距离的定义，判断即可．【解答】解：点到直线的距离就是点到直线的垂线段的长度，∵PB⊥l，PB＝5，∴点P到直线l的距离是5．平行线的性质6．（2022·佛山禅城区二模）一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB ＝90°，则∠DBC的度数为（）A．10°B．15°C．18°D．30°【分析】直接利用三角板的特点，结合平行线的性质得出∠ABD＝45°，进而得出答案．【解答】解：由题意可得：∠EDF＝45°，∠ABC＝30°，∵AB∥CF，∴∠ABD＝∠EDF＝45°，∴∠DBC＝45°﹣30°＝15°．7．一副三角板如图放置，两三角板的斜边互相平行，每个三角板的直角顶点都在另一个三角板的斜边上，图中∠α的度数为（）A．45°B．60°C．75°D．85°∵EF∥BC，∴∠FDC＝∠F＝30°，∴∠α＝∠FDC+∠C＝30°+45°＝75°，8．如图，直线AB∥CD，AB平分∠EAD．若∠1＝100°，则∠2的度数是（）A．30°B．40°C．50°D．60°【分析】根据邻补角的定义、角平分线的定义及平行线的性质求解即可．【解答】解：∵∠1＝100°，∴∠EAD＝180°﹣∠1＝80°，∵AB平分∠EAD，∴∠EAB＝∠BAD＝∠EAD＝40°，∵AB∥CD，∴∠2＝∠EAB＝40°，9．如图，直线AB∥CD，∠B＝40°，∠C＝50°，则∠E的度数是（）A．70°B．80°C．90°D．100°10．如图，将一副三角板如图叠放，且EF∥BC，则∠BFD＝15度．【分析】首先根据两直线平行，内错角相等得到∠BFE＝45°，再利用角的和差可得答案．【解答】解：由题意得，∠ABC＝45°，∠DFE＝30°，∵EF∥BC，∴∠BFE＝∠ABC＝45°，∴∠BFD＝45°﹣30°＝15°．11．如图，直线l与直线a，b相交，且a∥b，∠1＝110°，则∠2的度数是70°．【解答】解：∵直线a∥b，∠1＝100°，∴∠2＝180°﹣∠1＝70°．12．如图，若直线l1∥l2，l3是截线，∠1＝32°，则∠3的度数是32°．13．如图，∠1＝∠2＝58°，根据尺规作图痕迹，可得∠ADB的度数是（）A．58°B．60°C．61°D．122°【解答】解：根据作图过程可知：AD是∠BAC的平分线，∴∠BAD＝∠CAD，∵∠1＝∠2＝58°，∴AC∥BD，∴∠ADB＝∠CAD，∵∠1＝58°，∴∠BAC＝180°﹣58°＝122°，∴∠ADB＝∠CAD＝BAC＝61°，14．如图，AB∥CD，∠ABE＝120°，∠DCE＝110°，则∠BEC＝50°．【解答】解：延长AB到G，交EC与点F，∵AB∥CD，∴∠EFG＝∠DCE＝110°，又∵∠EBF＝180°﹣∠ABE＝180°﹣120°＝60°，∴∠BEC＝∠BEC﹣∠EBF＝110°﹣60°＝50°．15．四条线段a、b、c、d成比例，其中a＝1cm、b＝3cm、c＝3cm，则线段d＝9cm．【解答】解：∵a，b，c，d是成比例线段，∴ad＝cb，∵a＝1cm，b＝3cm、c＝3cm，∴d＝9，则d＝9cm．16．下列命题的逆命题中，是假命题的是（）A．对角线相等的四边形是矩形B．对角线互相平分的四边形是矩形C．对角线互相垂直的四边形是矩形D．有一个角是直角的四边形是矩形【分析】写出原命题的逆命题后判断正误即可．【解答】解：A、逆命题为矩形的对角线相等，正确，是真命题，不符合题意；B、逆命题为矩形的对角线互相平分，正确，是真命题，不符合题意；C、逆命题为矩形的对角线互相垂直，错误，是假命题，符合题意；D、逆命题为矩形有一个角是直角，正确，是真命题，不符合题意；故选：C．17．下列命题是真命题的是（）A．对角线相等的四边形是平行四边形B．对角线互相平分且相等的四边形是矩形C．对角线互相垂直的四边形是菱形D．对角线互相垂直平分的四边形是正方形【解答】解：A、对角线互相平分的四边形是平行四边形，对角线相等的四边形也可能是等腰梯形等四边形，故A不符合题意；B、对角线互相平分的四边形是平行四边形，若对角线再相等，则四边形是矩形，故B符合题意；C、对角线互相垂直的四边形不能判定是平行四边形，也就不能判定是菱形，故C不符合题意；D、对角线互相垂直平分的四边形是菱形，不能判断它的内角有直角，故D不符合题意；18．下列命题中，是真命题的是（）A．三角形的外心是三角形三个内角的角平分线的交点B．过一点有且只有一条直线与已知直线平行C．连接对角线相等的四边形各边中点所得四边形是矩形D．一组对边平行，一组对角相等的四边形是平行四边形【解答】解：A、三角形的外心是三角形的三边的垂直平分线的交点，故原命题错误，是假命题，不符合题意；B、过直线外一点有且只有一条直线与已知直线平行，故原命题错误，是假命题，不符合题意；C、连接对角线相等的四边形的各边中点所得四边形是菱形，故原命题错误，是假命题，不符合题意；D、一组对边平行，一组对角相等的四边形是平行四边形，正确，是真命题，符合题意．19．下列命题中，是假命题的是（）A．平行四边形的对角相等B．在同一个圆内，圆周角等于圆心角的一半C．反比例函数的图象与坐标轴没有交点D．0的立方根是0【解答】解：A、平行四边形的对角相等，正确，为真命题；B、在同圆或等圆中，同弧所对的圆周角等于圆心角的一半，故原命题为假命题；C、反比例函数的图象与坐标轴没有交点，正确，为真命题；D、0的立方根是0，正确，为真命题；20．下列命题中，假命题的是（）A．顺次连接对角线相等的四边形的四边中点所形成的图形是菱形B．各边对应成比例的两个多边形相似C．反比例函数的图象既是轴对称图形，也是中心对称图形D．已知二次函数y＝x²﹣1，当x＜0时，y随x的增大而减小【解答】解：A、顺次连接对角线相等的四边形的四边中点所形成的图形是菱形，本选项说法是真命题，不符合题意；B、各边对应成比例、各角相等的两个多边形相似，故本选项说法是假命题，符合题意；C、反比例函数的图象既是轴对称图形，也是中心对称图形，本选项说法是真命题，不符合题意；D、已知二次函数y＝x²﹣1，当x＜0时，y随x的增大而减小，本选项说法是真命题，不符合题意；21．下列命题是真命题的是（）A．平行四边形的对角互补B．对角线相等的四边形是矩形C．相似三角形的面积比等于对应高的比D．位似三角形是相似三角形【解答】解：A、平行四边形的对角相等，不一定互补，本选项说法是假命题，不符合题意；B、对角线相等的平行四边形是矩形，本选项说法是假命题，不符合题意；C、相似三角形的面积比等于对应高的比的平方，本选项说法是假命题，不符合题意；D、位似三角形是相似三角形，本选项说法是真命题，符合题意；22．下列命题：①有一个角等于100°的两个等腰三角形相似；②对角线互相垂直的四边形是菱形；③一个角为90°且一组邻边相等的四边形是正方形；④对角线相等的平行四边形是矩形．其中真命题的个数是（）A．1B．2C．3D．4【解答】解：①有一个角等于100°的两个等腰三角形相似，是真命题；②对角线互相垂直的平行四边形是菱形，故原说法是假命题；③一个角为90°且邻边相等的四边形是正方形，故原说法是假命题；④对角线相等的平行四边形是矩形，是真命题，故真命题有①④，共2个，23．下列命题中，是真命题的是（）A．三角形的外心是三角形三个内角角平分线的交点B．16的平方根是4C．对角线相等的四边形各边中点连线所得四边形是矩形D．五边形的内角和为540°【分析】根据平方根、矩形、多边形内角和、三角形的外心等知识进行判断即可．【解答】解：A、三角形的外心是三角形三边垂直平分线的交点，三角形三个内角角平分线的交点是三角形的内心，故为假命题；B、16的平方根是±4，算术平方根是4，故为假命题；C、对角线相等的四边形各边中点连线所得四边形是菱形，故为假命题；D、五边形的内角和为540°，为真命题．24．命题：已知△ABC，AB＝AC．求证：∠B＜90°．运用反证法证明这个命题时，第一步应假设（）成立．A．AB≠AC B．∠B＞90°C．∠B≥90°D．AB≠AC且∠B≥90°【分析】根据反证法的一般步骤判断即可．【解答】解：求证：∠B＜90°．运用反证法证明这个命题时，第一步应假设∠B≥90°，故选：C．。