安徽省舒城中学高二数学寒假作业第11天常用逻辑用语理

第一章常用逻辑用语一、命题1、定义：能够判断真假的陈说语句，分为真命题和假命题.2、一般形式：“ 若p则q” .二、四种命题原命题：若 p则 q p q抗命题：若 q则 p q p否命题：若p则 q p q逆否命题：若q则 p q p例：原：若一个数是负数，则它的平方是正数.(真)逆：若一个数的平方是正数，则这个数是负数.(假 )否：若一个数不是负数，则它的平方不是正数.(假 )逆否：若一个数的平方不是正数，则这个数不是负数.(真 )结论 :①互为逆否的命题同真，同假.②原命题与抗命题、原命题与否命题的真假没关.三、充足条件与必需条件1、若 p q , 称 p是 q的充足条件， q是 p的必需条件 .2、若 p q, 称 p不是 q的充足条件， q不是 p的必需条件 .3、若 p q并且 q p, 记作“ p q” , 称 p是q的充足必需条件，简称p是 q的充要条件 .注：能够借助会合关系来判断：p q p是 q的充足条件 .p q p是 q的充足不用要条件 .例：“ 福州人” “ 福建人” 会合“ 福州人”“ 福建人” 命题“福州人”是“福建人”的充足条件 .“福建人”是“福州人”的必需条件 .四、复合命题真假的表格.1、2、3、五、全称量词、存在量词1、全称命题 p :x M , P x2、特称命题 p : x0M , P x0它的否认 p :x M , P x0它的否认 p : x M , P x例：“ 四边形都有外接圆”P :四边形ABCD ,都有A、B、C、D共圆.全称命题P : 四边形 A1 B1C1D1此中A1 + C1 =200，此中 A、 B、 C、D不共圆 . 特称命题“存在 x0R，使 x02 +2x020 "P : x0R，使 x02 +2x020P : x R， x2 +2x 20。

第11天 常用逻辑用语【课标导航】1、了解四种命题及其关系；理解必要条件、充分条件与充要条件的意义.2、了解逻辑联结词“或”“且”“非”的含义.3、正确理解全称量词与存在量词意义. 一、选择题1．命题：“若12<x ，则11<<-x ”的逆否命题是（ ）A.若12≥x ，则11-≤≥x x ，或B.若11<<-x ，则12<xC.若11-<>x x ，或，则12>xD.若11-≤≥x x ，或，则12≥x 2．命题“所有能被2整除的整数都是偶数”的否定是（ ）A.所有不能被2整除的整数都是偶数B.所有能被2整除的整数都不是偶数C.存在一个不能被2整除的整数都是偶数D.存在一个能被2整除的整数都不是偶数3．下列四个命题中的假命题是（ ）A ．若方程x 2＋(a －3) x ＋a ＝0有一个正实根，一个负实根，则a ＜0B ．函数y =的图像既关于原点对称，又关于y 轴对称C ．函数f (x )的值域是[－2，2]，则函数f (x ＋1)的值域为[－3，1]D ．曲线y ＝|3－x 2|和直线y ＝a 的公共点个数是m ，则m 的值不可能是1 4．x ，y 是实数，且“xy>0”是“|x ＋y|＝|x|＋|y|”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 5．直线1l ，2l 互相平行的一个充分条件是（ ）A 、1l ，2l 都垂直于同一个平面B 、1l ，2l 与同一个平面所成的角相等C 、1l 平行于2l 所在的平面D 、1l ，2l 都平行于同一个平面6．已知 a b c R ∈、、,“240b ac -<”是“函数2()f x ax bx c =++的图像恒在x 轴上方”的 （ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件7．“0a <”是“函数()|(1)|f x x ax =+在区间(,0)-∞内单调递减”的 （ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要 8．下列命题正确的个数为 （ ）①“R x ∈∀都有02≥x ”的否定是“R x ∈∃0使得020≤x ”; ②“3≠x ”是“3≠x ”成立的充分条件; ③命题“若21≤m ，则方程0222=++x mx 有实数根”的否命题 A. 0 B. 1C. 2D. 3二、填空题9．命题“1>∃x ，使得22≥x ”的否定是 ．10．设p ：221a b b a -+-≤；q: 22113()()222a b -+-≤，则非p 是非q 的 条件．11．在一次跳伞训练中,甲.乙两位学员各跳一次,设命题p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为 12．下列结论：①若命题p ：∃x ∈R ，tan x ＝1；命题q ：∀x ∈R ，x 2－x ＋1＞0.则命题“p ∧ q ”是假命题；②已知直线l 1：ax ＋3y －1＝0，l 2：x ＋by ＋1＝0，则l 1⊥l 2的充要条件是a b＝－3； ③命题“若x 2－3x ＋2＝0，则x ＝1”的逆否命题为：“若x ≠1，则x 2－3x ＋2≠0”.其中正确结论的序号为 (把你认为正确结论的序号都填上). 三、解答题13．设:p x ∃∈5(1,)2使函数22()log (22)g x tx x =+-有意义，若p ⌝为假命题，求t 的取值范围．⌝14．已知命题p ：方程0222=-+ax x a 在[－1，1]上有解；命题q ：只有一个实数x 满足不等式2220x ax a ++≤，若命题“p 或q”是假命题，求实数a 的取值范围．15.命题p ：实数x 满足x 2－4ax ＋3a 2＜0，其中a ＜0，命题q ：实数x 满足x 2－x －6≤0或 x 2＋2x －8＞0，且 p ⌝是 q ⌝的必要不充分条件，求a 的取值范围.16．已知关于x 的方程04)2()1(2=-++-x a x a ,R a ∈。

高二数学集合与常用逻辑用语试题答案及解析1.已知集合M=｛1,｝，N＝｛1，3｝，M∩N＝｛1,3｝，则实数m的值为（）A．4B．－1C．4或－1D．1或6【答案】Ｂ【解析】略2.设集合A．B．C．D．【答案】C【解析】．【考点】集合运算．3.已知命题p：|x－1|≥2，命题q：x∈Z，若“p且q”与“非q”同时为假命题，则满足条件的x为（）A．{x|x≥3或x≤－1，x∈Z}B．{x|－1≤x≤3，x∈Z}C．{0,1,2}D．{－1,0,1,2,3}【答案】C【解析】由题意知q真，p假，∴|x－1|<2．∴－1<x<3且x∈Z．∴x＝0,1,2．选C．【考点】命题否定4.设四边形ABCD的两条对角线为AC，BD，则“四边形ABCD为菱形”是“”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【答案】A【解析】由“四边形ABCD为菱形”可得到“”，反之不成立，因此“四边形ABCD为菱形”是“”的充分不必要条件【考点】充分条件与必要条件5.设M、N是两个非空集合，定义M与N的差集为，则等于（）A．N B．M∩N C．M∪N D．M【答案】B【解析】根据题意是指图（1）中的阴影部分，同样是指图（2）中的阴影部分，即，故选择B【考点】韦恩图6.给出下列命题：①若“或”是假命题，则“且”是真命题；②若实系数关于的二次不等式，的解集为，则必有且；③；④．其中真命题的是（填写序号）。

【答案】①③【解析】①“或”是假命题，则两命题都是假命题，所以“且”是真命题；②不等式可能为一次不等式，满足解集为空集；③由不等式性质可知结论正确；④中可由，反之不成立【考点】1．复合命题；2．不等式性质7.若命题是（）A．B．C．D．【答案】D【解析】是对结论的否定，显然选D。

【考点】命题的否定8.不等式组的解集记为D，有下面四个命题：p1：∀（x，y）∈D，x＋2y≥－2，p2：∃（x，y）∈D，x＋2y≥2，p3：∀（x，y）∈D，x＋2y≤3，p4：∃（x，y）∈D，x＋2y≤－1．其中的真命题是（）A．p2，p3B．p1，p2C．p1，p4D．p1，p3【答案】B【解析】不等式组表示的平面区域如图所示区域。

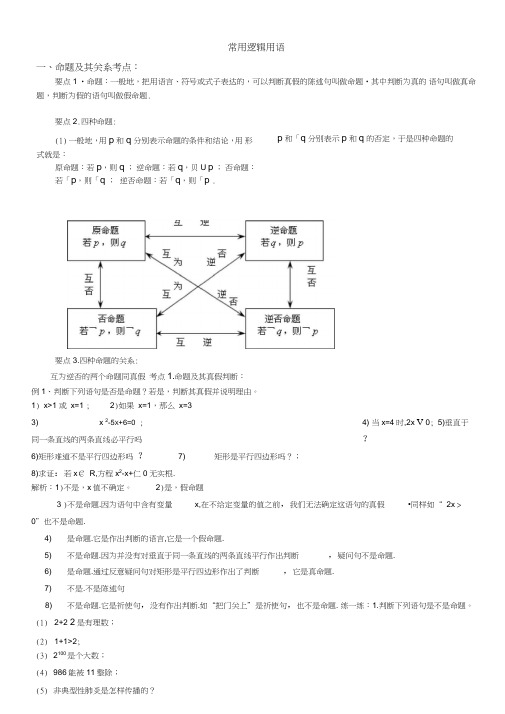
常用逻辑用语一、命题及其关系考点：要点1 •命题：一般地，把用语言、符号或式子表达的，可以判断真假的陈述句叫做命题•其中判断为真的语句叫做真命题，判断为假的语句叫做假命题.要点2.四种命题:p和「q分别表示p和q的否定，于是四种命题的(1)一般地，用p和q分别表示命题的条件和结论，用形式就是：原命题：若p，则q ；逆命题：若q，贝U p ；否命题：若「p，则「q ；逆否命题：若「q，则「p .要点3.四种命题的关系:互为逆否的两个命题同真假考点1.命题及其真假判断：例1、判断下列语句是否是命题？若是，判断其真假并说明理由。

1) x>1 或x=1 ; 2)如果x=1，那么x=33) x 2-5X+6=0 ; 4) 当x=4时,2x V 0; 5)垂直于同一条直线的两条直线必平行吗？6)矩形难道不是平行四边形吗？7) 矩形是平行四边形吗？；8)求证：若x€ R,方程x2-x+仁0无实根.解析：1)不是，x值不确定。

2)是，假命题3 )不是命题.因为语句中含有变量x,在不给定变量的值之前，我们无法确定这语句的真假•同样如“ 2x > 0”也不是命题.4) 是命题.它是作出判断的语言,它是一个假命题.5) 不是命题.因为并没有对垂直于同一条直线的两条直线平行作出判断，疑问句不是命题.6) 是命题.通过反意疑问句对矩形是平行四边形作出了判断，它是真命题.7) 不是.不是陈述句8) 不是命题.它是祈使句，没有作出判断.如“把门关上”是祈使句，也不是命题. 练一练：1.判断下列语句是不是命题。

(1)2+2 2是有理数；(2)1+1>2;(3)2100是个大数；(4)986能被11整除；(5)非典型性肺炎是怎样传播的？(6)( 6)x < 3。

2. 判断下列语句是不是命题。

(1 )矩形难道不是平行四边形吗？(2)垂直于同一条直线的两条直线平行吗？(3)一个数不是合数就是质数。

(4)大角所对的边大于小角所对的边；(5)y+x是有理数，则x、y也是有理数。

（数学选修1-1）第一章 常用逻辑用语[基础训练A 组]及答案一、选择题1．下列语句中是命题的是（ ）A ．周期函数的和是周期函数吗？B ．0sin 451=C ．2210x x +->D ．梯形是不是平面图形呢？2．在命题“若抛物线2y ax bx c =++的开口向下，则{}2|0x ax bx c φ++<≠”的 逆命题、否命题、逆否命题中结论成立的是（ ）A ．都真B ．都假C ．否命题真D ．逆否命题真3．有下述说法：①0a b >>是22a b >的充要条件. ②0a b >>是ba 11<的充要条件. ③0ab >>是33a b >的充要条件.则其中正确的说法有（ ）A ．0个B ．1个C ．2个D ．3个 4．下列说法中正确的是（ ）A ．一个命题的逆命题为真，则它的逆否命题一定为真B ．“a b >”与“ a c b c +>+”不等价C ．“220a b +=,则,a b 全为0”的逆否命题是“若,a b 全不为0, 则220a b +≠”D ．一个命题的否命题为真，则它的逆命题一定为真5．若:,1A a R a ∈<, :B x 的二次方程2(1)20x a x a +++-=的一个根大于零, 另一根小于零,则A 是B 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．已知条件:12p x +>，条件2:56q x x ->，则p ⌝是q ⌝的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件二、填空题1．命题：“若a b ⋅不为零，则,a b 都不为零”的逆否命题是 。

2．12:,A x x 是方程20(0)ax bx c a ++=≠的两实数根；12:b B x x a+=-, 则A 是B 的 条件。

第9天 常用逻辑用语【课标导航】1、了解四种命题及其关系；理解必要条件、充分条件与充要条件的意义.2、了解逻辑联结词“或”“且”“非”的含义.3、正确理解全称量词与存在量词意义. 一、选择题1.设m R ∈,命题“若0m >,则方程20x x m +-=有实根”的逆否命题是（ ）A.若方程20x x m +-=有实根，则0m > B.若方程20x x m +-=有实根，则0m ≤ C.若方程20x x m +-=没有实根，则0m > D.若方程20x x m +-=没有实根，则0m ≤ 2.设p:实数x ，y 满足1x >且1y >，q: 实数x ，y 满足2x y +>，则p 是q 的（ ）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.函数()f x 在0x x =处导数存在，若0:()0p f x =；0:q x x =是()f x 的极值点，则（ ）A ．p 是q 的充分必要条件 B. p 是q 的充分条件，但不是q 的必要条件C. p 是q 的必要条件，但不是q 的充分条件D. p 既不是q 的充分条件，也不是q 的必要条件4.设,,a b c 是非零向量，已知命题P ：若0a b ∙=，0b c ∙=，则0a c ∙=；命题q ：若//,//a b b c ，则//a c，则下列命题中真命题是（ ）A ．p q ∨B ．p q ∧C ．()()p q ⌝∧⌝D ．()p q ∨⌝ 5. 直线1l ，2l 互相平行的一个充分条件是（ ）A ．1l ，2l 都平行于同一个平面B ．1l ，2l 与同一个平面所成的角相等C ．1l 平行于2l 所在的平面D ．1l ，2l 都垂直于同一个平面6．设βα,为两个不同平面，m l ,为两条不同直线，且βα⊂⊂m l ,，有两个命题：①若α∥β，则l ∥m② 若l ⊥m，则α⊥β，那么（ ）A ．①真②假B ．②真①假C ．①②均为真D ．①②均为假7. 在ΔABC 中，条件甲：A<B ，条件乙：cos 2A> cos 2B,则甲是乙的（ ）A ．充分非必要条件B ．必要非充分条件C ．既非充分又非必要条件D ．充要条件 8. 下列说法正确的是 ( )A.函数y ＝2sin(2x －π6)的图象的一条对称轴是直线x ＝π12B.若命题p ：“存在x ∈R，x 2－x －1＞0”，则命题p 的否定为：“对任意x ∈R，x 2－x －1≤0”C.若x ≠0，则x ＋1x≥2D.“a ＝1”是“直线x －ay ＝0与直线x ＋ay ＝0互相垂直”的充要条件 二、填空题9. 命题“x ∀∈R ，20x >”的否定是10.设p ：514x ->；q:0132122≥+-++x x x x ，则非p 是非q 的 条件． 11.若“0,,tan 4x x m π⎡⎤∀∈≤⎢⎥⎣⎦”是真命题，则实数m 的最小值为 . 12.下列结论：①若命题p ：∃x ∈R，tan x ＝1；命题q ：∀x ∈R，x 2－x ＋1＞0.则命题“p ∧⌝q ”是假命题；②已知直线l 1：ax ＋3y －1＝0，l 2：x ＋by ＋1＝0，则l 1⊥l 2的充要条件是ab＝－3； ③命题“若x 2－3x ＋2＝0，则x ＝1”的逆否命题为：“若x ≠1，则x 2－3x ＋2≠0”.其中正确结论的序号为 (把你认为正确结论的序号都填上). 三、解答题13.设:p x ∃∈5(1,)2使函数22()log (22)g x tx x =+-有意义，若p ⌝为假命题，求t 的取值范围．⌝14．设函数()x f =ax ax --25lg的定义域为A.若命题p ：3∈A 和命题q ：5∈A，如果命题p 或q 为真命题，命题p 且q 为假命题，求实数a 的取值范围.15. 命题p ：实数x 满足x 2－4ax ＋3a 2＜0，其中a ＜0，命题q ：实数x 满足x 2－x －6≤0或x2＋2x －8＞0，且p ⌝是q ⌝的必要不充分条件，求a 的取值范围.16．已知关于x 的方程04)2()1(2=-++-x a x a ,R a ∈（Ⅰ）求方程有两个正根的充要条件；（Ⅱ）求方程至少有一个正根的充要条件。

高二数学常用逻辑用语试题答案及解析1.（本题满分12分）已知p:|1－|≤2, q:x2－2x+1－m2≤0(m>0)，若﹁p是﹁q的必要而不充分条件，求实数m的取值范围.【答案】由x2－2x+1－≤0得：1－m≤x≤1+m(m>0)所以：“﹁q”：A={x|x>1+m或x<1－m,m>0}………………………………4分由|1－|≤2得：－2≤x≤10,所以“﹁p”:B={x|x>10或x<－2}.………………………………8分由﹁p是﹁q的必要而不充分条件，知：A B,故m的取值范围为……………………………………………………….12分【解析】根据互为逆否命题的两个命题真假性相同，所以﹁p是﹁q的必要而不充分条件等价于p 是q是充分不必要条件，然后再分别求出p真q真对应的集合A，B，则,然后据此建立关于m的不等式解出m的取值范围.2.命题“有些负数满足不等式(1＋x)(1－9x)>0”用“∃”或“∀”可表述为___________．【答案】∃x0<0，使(1＋x)(1－9x)>0【解析】主要考查全称量词和全称命题的概念、存在量词和特称命题的概念以及两种命题的否定命题的写法与判断。

解：“有些”是存在量词。

3.已知a、b∈R，设p：|a|＋|b|>|a＋b|，q：函数y＝x2－x＋1在(0，＋∞)上是增函数，那么命题：p∨q、p∧q、p中的真命题是________．【答案】p【解析】主要考查简单的逻辑联结词的含义。

解：对于p，当a>0，b>0时，|a|＋|b|＝|a＋b|，故p假，p为真；对于q，抛物线y＝x2－x＋1的对称轴为x＝，故q假，所以p∨q假，p∧q假．这里p应理解成|a|＋|b|>|a＋b|不恒成立，而不是|a|＋|b|≤|a＋b|.4.命题p：若a，b∈R，则|a|＋|b|>1是|a＋b|>1的充分而不必要条件；命题q：函数y＝的定义域是(－∞，－1]∪[3，＋∞)，则()A．“p或q”为假B．“p且q”为真C．p真q假D．p假q真【答案】D【解析】主要考查简单的逻辑联结词的含义。

高二数学选修2-1第一章常用逻辑用语_知识点+习题+答案讲义
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高二数学选修2-1第一章常用逻辑用语_知识点+习题+答案讲义）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高二数学选修2-1第一章常用逻辑用语_知识点+习题+答案讲义的全部内容。

A B 16。