第三节 变量置换法与分部积分法

重积分换元法与分部积分法在高等数学领域，积分是一个重要的概念，通过对函数在一定区间上的“面积”进行求解，可以对函数的变化趋势和性质进行分析。

在积分中，重积分换元法和分部积分法是两种常用的积分方法，它们在求解复杂积分问题时发挥着重要的作用。

重积分换元法重积分换元法，也称为多重积分的换元法，是处理多重积分中变量替换的方法。

在进行多重积分时，往往需要通过变量代换的方式简化积分问题。

重积分换元法的基本思想是通过合适的变量替换，将原来的多重积分转化为一个简单的积分形式，从而更容易求解。

对于二重积分而言，重积分换元法的一般步骤如下： 1. 确定变量替换的形式，通常选择与坐标轴吻合的变换； 2. 计算变换后的积分区域，并变换原积分的被积函数； 3. 对新的积分进行求解。

通过重积分换元法，可以简化积分的计算过程，降低积分的难度，提高计算的效率。

分部积分法分部积分法是求解不定积分中的一种常用技巧，也可以应用于定积分的简化。

在定积分中，分部积分法是将积分号作用在两个函数的乘积上，通过对积分的展开和化简，将原积分转化成两个函数之积的形式。

分部积分法的基本思想是通过对被积函数进行拆分，选择一个函数进行求导，一个函数进行求不定积分，最终通过不断的交换角色，逐步简化和求解原积分。

对于定积分而言，分部积分法的一般步骤如下： 1. 选择一个函数进行求导，一个函数进行不定积分； 2. 对两个函数进行交替操作，最终将原积分问题转化为更容易求解的形式。

通过分部积分法，可以有效解决复杂积分问题，提高积分的求解速度和准确性。

综上所述，重积分换元法和分部积分法是高等数学中常用的积分方法，它们在不同的积分问题中发挥着重要的作用。

通过灵活运用这两种积分方法，可以更好地解决数学问题，提升问题的求解效率和准确性。

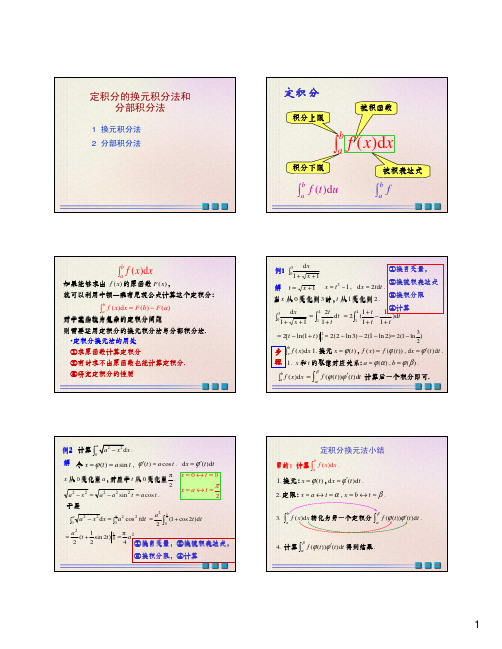
定积分的换元积分法和分部积分法1 换元积分法2 分部积分法∫ba xx f d )(定积分积分上限积分下限被积函数()d ba f t u∫ba f∫被积表达式∫ba xx f d )(，的原函数如果能够求出)()(x F x f 就可以利用牛顿就可以利用牛顿---------莱布尼茨公式计算这个定积分莱布尼茨公式计算这个定积分莱布尼茨公式计算这个定积分：：()d ()()ba f x x Fb F a =−∫对于某些较为复杂的定积分问题则需要运用定积分的换元积分法与分部积分法则需要运用定积分的换元积分法与分部积分法..•定积分换元法的用处定积分换元法的用处①求原函数计算定积分②有时求不出原函数也能计算定积分有时求不出原函数也能计算定积分..③研究定积分的性质例1解∫++311d x x 1+=x t .d 2d t t x =,12−=t x ∫++311d x x.2130变化到从，时变化到从当t x 412d 1t t t=+∫41112()d 11t t t t +=−++∫21)]1ln([2t t +−=)2ln 1(2)3ln 2(2−−−=)23ln 1(2−=步骤.d )(d ,))(()()(.1t t x t f x f t x ϕϕϕ′===，换元∫ba x x f d )(1.(),().x t a b ϕαϕβ==和的取值对应关系：∫ba x x f d )((())()d f t t t βαϕϕ′=∫计算后一个积分即可计算后一个积分即可..①换自变量换自变量，，②换被积表达式③换积分限④计算定积分换元法小结()d .b af x x ∫目的：计算3.()d (())()d .baf x x f t t t βαϕϕ′∫∫转化为另一个定积分.d )(d )(.1t t x t x ϕϕ′==，：换元.,.2βα=↔==↔=t b x t a x 定限定限：：4.(())()d .f t t t βαϕϕ′∫计算得到结果定理()[,]f x a b 假设在连续，()[,]([,]).x t ϕαββα=在或连续并且满足下列条件并且满足下列条件：：;)(,)()1(b a ==βϕαϕ(2)()[,]([,])t ϕαββα′在或连续；(3)[,]([,]),()[,].t t a b αββαϕ当在或变动时不超出∫′=∫βαϕϕtt t f x x f b a d )())((d )(则有（定积分的换元积分法定积分的换元积分法））(1),f 若为偶函数∫−+=∫−aa a xx f x f x x f 0d )]()([d )(∫=axx f 0d )(2()()f x f x −=则，于是∫−+=∫−a a a x x f x f x x f 0d )]()([d )((2),f 若为奇函数()()f x f x −=−则，于是d )]()([d )(0=∫−+=∫−aa a x x f x f x x f 例4(,),(0).f C T ∈−∞+∞>设周期等于,a 求证对于任意正数有∫=∫+TTa axx f x x f 0d )(d )(T Ta +a()d Tf x x∫()d a T af x x+∫直观解释例5解π20sin d .1cos x xI x x=+∫计算21I I +=∫+∫++=π2022π2πd cos 1sin d cos 1sin x x xx x x x x I ∫+=π222πd cos 1sin x xx x I tx−=π∫−+−=022π)d(cos 1sin )π(t ttt ∫+−=2π02d cos 1sin )π(t t t t ∫+−=2π02d cos 1sin )π(x xx x ∫+=2π02d cos 1sin πx x x ∫+−2π02d cos 1sin x xxx 例6解121sin cos d .1sin x xx x−++∫计算∫++∫+=∫++−−−112112112d sin 1cos d sin 1sin d sin 1cos sin x xx x x x x x x x 21I I +=这个积分是奇函数在对称区间上积分这个积分是奇函数在对称区间上积分,,1121sin d ,1sin xI x x−=+∫对于10.I =所以111122)arctan(sin d sin 1cos −−=∫+=x x xxI 另一方面另一方面,,利用牛顿利用牛顿——莱布尼茨公式得到莱布尼茨公式得到::.)1arctan(sin 2=例7解2202d ax ax x x −∫计算∫−a xx ax x 202d 2∫−+∫−−=aa xx ax a x x ax a x 202202d 2d 2)(对于其中前一个积分对于其中前一个积分, , , 令令x = a +t , , 用换元法得到用换元法得到用换元法得到::∫−−a x x ax a x 202d 2)(0d 22=−=∫−aa t t a t ∫−ax x ax 202d 22:02.D y ax x ≤≤−等于半圆的面积.π212a =∫−ax x ax 202d 2C a x a x a x ++−=)arcsin (21222∫−x x a d 221()t x t ϕ−=必须将变量还原成，第三个区别是第三个区别是：：求出不定积分以后以后，，C t t t a t t a ++=+∫)cos sin (2d 22cos 122进一步得到才能得到最终结果才能得到最终结果..另一方面另一方面，，220d a a x x −∫对于定积分，:sin :x a t =用换元将其转化为另一个定积分.d cos 2π022∫t t a 直接计算这个积分就可以了直接计算这个积分就可以了..注释2cos cos t t =−如果取，π3π(,).22t ∈也就是认为此时此时,,,sin t a x =.arcsin πax t −=xx a d 22∫−122)cos sin (2d )2cos 1(2C t t t a t t a +⋅+−=+−=∫12222)arcsin π(2C x a axa x a +−−−−=C x a axa x a +−+=)(arcsin 22222于是2 分部积分法∫′−=∫′ba ba ba x x v x u x v x u x x v x u d )()()]()([d )()()()()()())()((x u x v x v x u x v x u ′+′=′定理定理5.3.25.3.2(),()[,].u x v x a b 设在有连续导数则有证明函数乘积的导数公式函数乘积的导数公式::等式两端的函数进行积分等式两端的函数进行积分::xx v x u xx v x u xx v x u ba ba ba d )()(d )()(d ])()([∫′+′∫=′∫根据牛顿根据牛顿－－莱布尼茨公式得到莱布尼茨公式得到：：baba x v x u x x v x u )]()([d ])()([=′∫123将(3)(3)代入代入代入(2)(2)(2)，，就得到就得到(1)(1)(1)．．∫′−=∫′b a ba b a xx v x u x v x u x x v x u d )()()]()([d )()(注释也可以表示成下述形式也可以表示成下述形式：：∫∫−=bab a bax u x v x v x u x v x u )(d )()]()([)(d )(定积分的分部积分法∫−=∫b a ba b a uv uv v u d ][d 或者∫−=102102d e 21e 21x x xx uv 例8解1220e d .x x x ∫计算∫1022d e xx x∫−=∫b a ba b au v uv v u d ][d vd u ∫−=1021022d e e 21x x x x x uv uv d ∫−=1022d e e 21x x x 其中1∫102d e xx xu vd uv d 1022e 41e 21x −=)1e (41e 2122−−=将计算结果代入将计算结果代入(4)(4)(4)得到得到得到::∫1022d e x x x.)1e (412−=例9解120ln d .x x x ∫计算120ln d x x x ∫∫−=∫b a ba b au v uv v u d ][d v d u 3311111ln d 33ee x x x x x =−∫uv uv d 132011e d 33x x =−∫例91arctan d .x x ∫计算解11120arctand arctan d 1x x x x x x x =−+∫∫vd u uvuv d 2101ln(1)42x π=−+1ln 242π=−例11解π230e sin 2d x I x x−=∫计算3e ,d sin 2d ,x u v x x −==令1cos 2.2v x =−则∫=∫=−2π2π003d d2sin e v u x x I x ∫−=2π2π00)(d )()(x u x v uv 2π032cos e 21x x −−=∫−−2π03d 2cos e 23x x x ∫−+=−−2π03π23d 2cose 23)e 1(21x x x 5继续运用分部积分法继续运用分部积分法::∫−2π03d 2cos ex x x2π032sin e 21x x −=∫+−2π03d 2sin e 23x x x 例12解π2cos d .n n I x x =∫并计算ππ2200cos d sin d (N).n n x x x x n =∈∫∫求证运用定积分的分部积分法运用定积分的分部积分法::∫=2π0d cos x x I n n 2π01cos sin x x n −=∫−+−2π022d cos sin )1(xx x n n ∫=−2π01)d(sin cos x x n ∫−−=−2π022d cos )cos 1()1(x x x n n .)1()1(2n n I n I n −−−=−从而得到递推公式从而得到递推公式::21−−=n n I nn I ,2πd cos 2π000=∫=x x I 容易得到容易得到::.1d cos 2π01=∫=x x I 于是由递推公式得到于是由递推公式得到：：132231⋅−−−=L n n n n I n 当n 为奇数时为奇数时：：!!!)!1(n n −=2π21231L −−−=n n n n I n 当n 为偶数时为偶数时：：2π!!!)!1(n n −=ππ22cos d sin d (N).n n x x x x n =∈∫∫证明换元换元::.d d ,2πt x t x −=−=∫−−=∫002π2π)d )(2π(cos d cos t t x x n n ∫=2π0d sin t t n ∫=2π0d sin xx n 练习题∫−+10d )1ln(.1e x x ln 302.d x xe x −∫4203.sec d x x x π∫2ln 2304.d x x e x∫315.ln d ex x∫206.()(0)1,(2)3,(2) 5.()d f x f f f xf x x′′′′′===∫连续，计算11(2ln3)3−1(ln 4)4π−)3(2e −1ln 22−8例13证明()[π,π]f x −设在有二阶导数，.0)(>′′x f 求证求证：：.0d cos )(ππ<∫−x x x f 分部积分分部积分：：∫′−=∫−−−ππππππd sin )(sin )(d cos )(xx x f x x f x x x f ∫′−=−ππd sin )(xx x f ()0().f x f x ′′′>由推出单调增加使得∫′∫+′=∫′−−π00πππd sin )(d sin )(d sin )(xx x f x x x f x x x f 根据积分中值定理根据积分中值定理：：(π,0),(0,π),ξη∈−∈存在6.1d 222∫−−−x x x 计算例1，令t t x sec )(==ϕ.tan sec )(t t t =′ϕ解,]π43,π32[变化时在当t .]2,2[变化对应地在−−x ,23π2−==x t 时当.24π3−==x t ，时,0tan ]π43,π32[<∈t t ，时当.tan tan 2t t −=所以∫∫−=−−−4π33π2d )tan (sec tan sec 1d 222t t t t t x x x 于是∫−=4π33π2d t 12π−=。

第五章不定积分一、本章主要教学内容1．原函数与不定积分的概念、不定积分的性质、基本积分公式；2．直接积分法；第一换元积分法；分部积分法；查表法等。

二、教学目的1．理解原函数与不定积分的概念；2．掌握不定积分的性质，熟记基本积分公式；3．熟练掌握各种积分法。

三、教学重点、难点重点：直接积分法；第一换元积分法；第二换元积分法；分部积分法。

难点：第一换元积分法；第二换元积分法；分部积分法。

第一节、不定积分的概念与性质教学目标：理解原函数与不定积分的概念；掌握不定积分的性质，熟记基本积分公式。

教学重点：不定积分的定义与基本积分公式。

教学难点：不定积分的定义与基本积分公式。

教学手段：课堂讲解一、原函数的概念定义 已知)(x f 是一个定义在区间I 内的函数，如果存在着函数)(x F ， 使得对I 内任何一点x ，都有 )()('x f x F = 或 dx x f x dF )()(=，那么函数)(x F 就称为)(x f 在区间I 内的原函数。

例 F x x ()sin =是f x x ()cos =在区间I =-∞+∞(,)上的原函数。

原函数存在定理 如果函数)(x f 在区间I 内连续，那未在区间I 内它的原函数一定存在，即：存在)(x F ，对一切的x I ∈，均有'=F x f x ()()。

即：连续函数一定有原函数。

若)(x F 是)(x f 在区间I 内的一个原函数，即'=∀∈F x f x x I ()()，那么对于任意常数c ，由于 [()]()F x c f x +'=，于是，函数族c x F +)(中的任何一个函数也一定是)(x f 在区间I 内的原函数。

由此可知：如果)(x f 有原函数，那么原函数的个数为无限多个。

二、不定积分概念定义 在区间I 内，函数)(x f 的带有任意常数项的原函数称为)(x f 在区间I 内的不定积分，记作f x dx ()⎰ 其中：⎰称为积分号， )(x f 称为被积函数，f x dx ()称为被积表达式，x 称为积分变量。