下载文档原格式
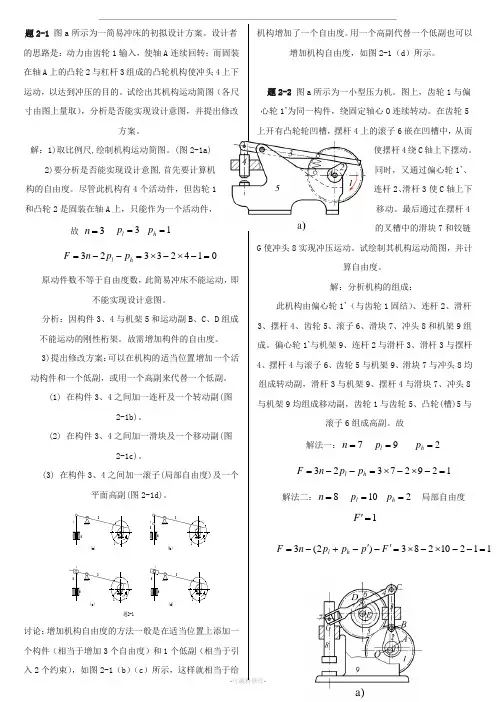
题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。
解：1)取比例尺,绘制机构运动简图。
(图2-1a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。
分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。
题2-2 图a 所示为一小型压力机。
图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。
同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
试绘制其机构运动简图，并计算自由度。
解：分析机构的组成：此机构由偏心轮1’（与齿轮1固结）、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。
机械原理第七版答案1. 引言《机械原理》是一门重要的工程学科，旨在研究机械系统中力学原理的应用。
本文将提供《机械原理第七版》的答案，帮助读者更好地理解和应用这一学科知识。
2. 答案以下是《机械原理第七版》部分章节的答案。
第一章简介与力学基础1.机械原理的定义：机械原理是研究力学系统中的力学原理及其应用的学科。
2.机械原理的基本思想：机械原理的基本思想是利用物理和数学原理来解释和预测物体的运动及其受力情况。
3.机械原理的应用领域：机械原理的应用范围广泛，包括机械工程、车辆工程、航空航天工程等领域。
4.计算力学和应用力学之间的关系：计算力学是机械原理的一部分，并且被广泛应用于机械系统的设计和分析中。
第二章静力学1.静力学的定义：静力学是研究静止系统中力学平衡的学科。
2.外力和内力的区别：外力是作用于系统外部的力，如重力、压力等；内力是作用于系统内部的力，如物体间的接触力。
3.刚体的定义：刚体是指其内部各点的相对位置不发生变化的物体。
4.力矩的计算公式：力矩等于力的大小与力臂的乘积。
5.平衡条件的描述：一个系统处于力学平衡的必要条件是合外力和合外力矩等于零。
第三章力的分析与计算1.力的三要素：大小、方向和作用点。
2.力的合成：将多个力的效果合成为一个力。
3.力的分解：将一个力分解为多个力的合力。
4.零力的定义：零力是指大小为零的力，不对物体产生任何作用。
5.夹角的计算方法：使用三角函数来计算夹角。
第四章平面结构分析1.结构的定义：结构是由构件组成的有机整体，在受到外力作用时始终保持平衡的系统。
2.静定结构与非静定结构的区别：静定结构是指其内部构件数目等于其内力数目的结构；非静定结构是指其内部构件数目大于其内力数目的结构。
3.阻力的作用：阻力是指对物体运动的阻碍力，常见的阻力有摩擦力和空气阻力。
4.结构分析方法的选择：选择合适的分析方法是分析结构的关键，常见的方法有力学平衡法、力法和位移法。
3. 总结本文提供了《机械原理第七版》部分章节的答案，包括机械原理的定义和基本思想、静力学、力的分析与计算以及平面结构分析等内容。
机械原理课后习题答案第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。
解：1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。
分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
11(c)题2-11(d)54364(a)5325215436426(b)321讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。
题2-12 图a 所示为一小型压力机。
图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。
同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
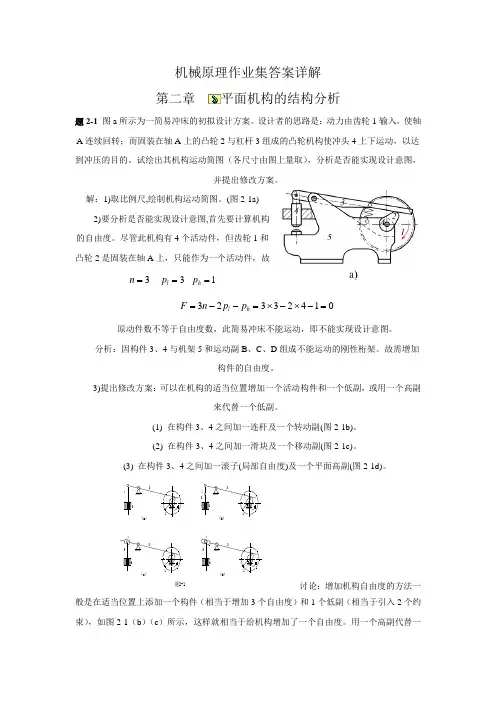
机械原理作业集答案详解 第二章平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。
解：1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。
分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
11(c)题2-1(d)54364(a)5325215436426(b)321讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。
题2-2 图a 所示为一小型压力机。
图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。
同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
机械原理课后全部习题解答文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]《机械原理》习题解答机械工程学院目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征机器通常由哪三部分组成各部分的功能是什么2）、机器与机构有什么异同点3）、什么叫构件什么叫零件什么叫通用零件和专用零件试各举二个实例。
4）、设计机器时应满足哪些基本要求试选取一台机器，分析设计时应满足的基本要求。
2、填空题1)、机器或机构，都是由组合而成的。
2）、机器或机构的之间，具有确定的相对运动。
3）、机器可以用来人的劳动，完成有用的。
4）、组成机构、并且相互间能作的物体，叫做构件。
5）、从运动的角度看，机构的主要功用在于运动或运动的形式。
6）、构件是机器的单元。
零件是机器的单元。
7）、机器的工作部分须完成机器的动作，且处于整个传动的。
8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。
3、判断题1)、构件都是可动的。
（）2）、机器的传动部分都是机构。
（）3）、互相之间能作相对运动的物件是构件。
（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。
（）5）、机构的作用，只是传递或转换运动的形式。
（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。
（）7）、机构中的主动件和被动件，都是构件。
（）2 填空题答案1）、构件 2）、构件 3）、代替机械功 4）、相对运动 5）、传递转换6）、运动制造 7）、预定终端 8）、中间环节 9）、确定有用构件3判断题答案1）、√ 2）、√ 3）、√ 4）、√ 5）、× 6）、√ 7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
机械原理习题选解武秀东2007年6月教材：普通高等教育“十五”国家级规划教材机械原理（第七版）西北工业大学机械原理及机械零件教研室编孙桓陈作模葛文杰主编高等教育出版社本教材第四版曾获全国第二届高等学校优秀教材优秀奖本教材第五版曾获教育部科技进步奖二等奖第二章 机构的结构分析2-11. 图示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案（要求用机构示意图表示出来）。
解⑴分析：绘制机构运动简图沿着运动传递的路线，根据各个活动构件参与构成运动副的情况（两构件组成的运动副的类型，取决于两构件之间的相对运动关系），确定表示各个构件的符号，再将各个构件符号连接起来，就得到机构运动简图（或机构示意图）。
构件2：与机架5构成转动副A ；与构件3构成凸轮高副。
所以构件2的符号为图a)。
构件3：与构件2构成凸轮高副；与机架5构成转动副；与机架4构成转动副。
所以构件3的符号为图b)。
构件4：与机架3构成转动副；与机架5构成移动副。
所以构件4的符号为图c)或图d)。
将这些构件符号依次连接起来，就得到机构运动简图，如题2-11答图a)或b)所示。
机构运动简图，如题2-11答图a)或b)所示。
⑵分析：是否能实现设计意图在机构的结构分析中判断该方案否能实现设计意图，应该从以下两点考虑：①机构自由度是否大于零；②机构原动件的数目是否等于机构自由度的数目。
因此，必须计算该机构的自由度F=3n-(2p L +p H )=3×3-(2×4+1)=0。
因为机构的自由度为 F=3n-(2p L +p H )=3×3-(2×4+1)=0 可知，该机构不能运动，不能实现设计意图。
题2-11图图a)图b)图c)题2-11答图a)b)⑶分析修改方案因为原动件的数目为1，所以修改的思路为：将机构的自由度由0变为1。
第七章 机械的运转及其速度波动的调节题7-7如图所示为一机床工作台的传动系统，设已知各齿轮的齿数，齿轮3的分度圆半径r 3，各齿轮的转动惯量J 1、J 2、J 2`、J 3，因为齿轮1直接装在电动机轴上，故J 1中包含了电动机转子的转动惯量，工作台和被加工零件的重量之和为G 。
当取齿轮1为等效构件时，试求该机械系统的等效转动惯量J e 。
解：根据等效转动惯量的等效原则，有∑=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ni i Si Si i e J v m J 122ωωω 2322123232213221222121⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+='''Z Z Z Z r g G Z Z Z Z J Z Z J Z Z J J J e 212133212221221⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=''ωωωωωωωv g G J J J J J e 题7-9已知某机械稳定运转时其主轴的角速度ωs =100rad/s ，机械的等效转动惯量J e =0.5Kg ·m 2，制动器的最大制动力矩M r =20N ·m （该制动器与机械主轴直接相联，并取主轴为等效构件）。
设要求制动时间不超过3s ，试检验该制动器是否能满足工作要求。
解：因此机械系统的等效转动惯量J e 及等效力矩M e 均为常数，故可利用力矩形式的机械运动方程式dtd J Me e ω= 其中：25.020m kg m N M M r e ⋅=⋅-=-= ωωωd d d M J dt r e 025.0205.0-=-=-= ()st S S 5.2025.0025.0==--=∴ωωω由于 s s t 35.2<= 所以该制动器满足工作要求。
题7-11 在图a 所示的刨床机构中，已知空程和工作行程中消耗于克服阻抗力的恒功率分别为P 1=367.7W 和P 2=3677W ，曲柄的平均转速n=100r/min ，空程中曲柄的转角φ1=120°。
机械原理课后习题答案第9章课后参考答案9-1 何谓凸轮机构传动中的刚性冲击和柔性冲击?试补全图示各段s 一δ、 v 一δ、α一δ曲线，并指出哪些地方有刚性冲击，哪些地方有柔性冲击？答 凸轮机构传动中的刚性冲击是指理论上无穷大的惯性力瞬问作用到构件上，使构件产生强烈的冲击；而柔性冲击是指理论上有限大的惯性力瞬间作用到构件上，使构件产生的冲击。
s-δ, v-δ, a-δ曲线见图。
在图9-1中B ，C 处有刚性冲击，在0，A ，D ，E 处有柔性冲击。
9—2何谓凸轮工作廓线的变尖现象和推杆运动的失真现象?它对凸轮机构的工作有何影响?如何加以避免?答 在用包络的方法确定凸轮的工作廓线时，凸轮的工作廓线出现尖点的现象称为变尖现象：凸轮的工作廓线使推杆不能实现预期的运动规律的现象件为失真现象。
变尖的工作廓线极易磨损，使推杆运动失真．使推杆运动规律达不到设计要求，因此应设法避免。
变尖和失真现象可通过增大凸轮的基圆半径．减小滚子半径以及修改推杆的运动规律等方法来避免。
9—3力封闭与几何封闭凸轮机构的许用压力角的确定是否一样?为什么?av sδδδ03/π3/2ππ3/4π3/5ππ2题9-1图答 力封闭与几何封闭凸轮机沟的许用压力角的确定是不一样的。
因为在回程阶段-对于力封闭的凸轮饥构，由于这时使推杆运动的不是凸轮对推杆的作用力F ，而是推杆所受的封闭力．其不存在自锁的同题，故允许采用较大的压力角。
但为使推秆与凸轮之间的作用力不致过大。
也需限定较大的许用压力角。
而对于几何形状封闭的凸轮机构，则需要考虑自锁的问题。
许用压力角相对就小一些。
9—4一滚子推杆盘形凸轮机构，在使用中发现推杆滚子的直径偏小，欲改用较大的滚子？问是否可行?为什么?答 不可行。
因为滚子半径增大后。
凸轮的理论廓线改变了．推杆的运动规律也势必发生变化。
9—5一对心直动推杆盘形凸轮机构，在使用中发现推程压力角稍偏大，拟采用推杆偏置的办法来改善，问是否可行?为什么?答 不可行。
因为推杆偏置的大小、方向的改变会直接影响推杆的运动规律．而原凸轮机构推杆的运动规律应该是不允许擅自改动的。
9-6 在图示机构中，哪个是正偏置?哪个是负偏置?根据式(9-24)说明偏置方向对凸轮机构压力角有何影响?答 由凸轮的回转中心作推杆轴线的垂线．得垂足点，若凸轮在垂足点的速度沿推杆的推程方向．刚凸轮机构为正偏置．反之为负偏置。
由此可知．在图 示机沟中，两个均为正偏置。
由220tan ()r e s α=-+ 可知．在其他条件不变的情况下。
若为正偏置(e 前取减号)．由于推程时(ds/dδ)为正．式中分子ds/d δ-e<ds/d δ, 故压力角α减小。
而回程时, 由于ds ／d δ为负, 式中分子为 |(ds ／d δ)-e|=| (ds ／d δ) |+ |e| >ds ／d δ。
故压力角增大。
负偏置时刚相反，即正偏置会使推程压力角减小，回程压力角增大；负偏置会使推程压力角增大，回程压力角减小。
9—7 试标出题9—6a 图在图示位置时凸轮机构的压力角，凸轮从图示位置转过90º后推杆的位移；并标出题9—6b 图推杆从图示位置升高位移s 时，凸轮的转角和凸轮机构的压力角。
解 如图 (a)所示，用直线连接圆盘凸轮圆心A 和滚子中心B ，则直线AB 与推杆导路之间所夹的锐角为图示位置时凸轮机构的压力角。
以A 为圆心, AB 为半径作圆, 得凸轮的理论廓线圆。
连接A与凸轮的转动中心O并延长，交于凸轮的理论廓线于C点。
以O为圆心．以OC为半径作圆得凸轮的基圆。
以O为圆心, 以O点到推杆导路的距离OD为半径作圆得推杆的偏距圆；。
延长推杆导路线交基圆于G-点，以直线连接OG。
过O点作OG的垂线，交基圆于E点。
过E 点在偏距圆的下侧作切线．切点为H点．交理论廓线于F点，则线段EF的长即为凸轮从图示位置转过90后推杆的位移s。
方法同前，在图(b)中分别作出凸轮的理论廓线、基圆、推杆的偏距圆。
延长推杆导路线交基圆于G点，以直线连接OG。
以O为圆心，以滚子中心升高s 后滚子的转动中心K到O点的距离OK为半径作圆弧，交理论廓线于F点。
过F点作偏距圆的切线，交基圆于E点，切点为H。
则∠GO E为推杆从图示位置升高位移s时-凸轮的转角，∠AFH为此时凸轮机构的压力角。
(a) (b)9—8在图示凸轮机构中，圆弧底摆动推杆与凸轮在B点接触。
当凸轮从图示位置逆时针转过90。
时，试用图解法标出：1)推杆在凸轮上的接触点；2)摆杆位移角的大小；3)凸轮机构的压力角。
解如图所示，以O为圆心，以O点到推杆转动中心A的距离AO为半径作圆，得推杆转动中心反转位置圆。
过O点怍OA的垂线，交推杆转动中心反转位置圆于D点。
以O`为圆心．以O`点到推杆圆弧圆心C的距离CO’为半径作圆．得凸轮的理论廓线。
以O 为圆心，作圆内切于凸轮的理论廓线圆，得凸轮的基圆。
以D 为圆心，以AC 为半径作圆弧，交凸轮的理论廓线于E 点，交凸轮的圆于G 点。
用直线连接EO ’，交凸轮的实际廓线于F 点，此即为推杆在凸轮上的接触点；而∠GDE 即为摆杆的位移角；过E 点并垂直于DE 的直线与直线EF 间所夹的锐角即为此时凸轮机构的压力角。
9—9 已知凸轮角速度为1．5 rad ／s ，凸轮转角δ0~150=︒︒时，推杆等速上升16mm; δ150~180=︒︒时推杆远休，180~300δ=︒︒时推杆下降16mm;300~360δ=︒︒时推杆近休。
试选择合适的推杆推程运动规律，以实现其最大加速度值最小，并画出其运动线图。
解 推杆在推程及回程段运动规律的位移方程为：(1)推程：s=h δ／δ0 0º≤δ≤1 50º(2)回程：等加速段s=h 一2h δ2／δ`02 0º≤δ≤60º等减速段s=2h(δ’一δ)2／δ0`2 60º≤δ≤120º计算各分点的位移值如表9．3：根据表9-3可作所求图如下图：9—10设计一凸轮机构，凸轮转动一周时间为2 s。
凸轮的推程运动角为60º，回程运动角为150。
，近休止运动角为150º。
推杆的行程为15 mm。
试选择合适的推杆升程和回程的运动规律，使得其最大速度值最小，并画出运动线图。
9一11试设计一对心直动滚子推杆盘形凸轮机构，滚子半径r，=10 mm，凸轮以等角速度逆时针回转。
凸轮转角δ=0º～120º时，推杆等速上升20 mm；δ=120º～180º时，推杆远休止；δ=180º～270º时，推杆等加速等减速下降20 mm；δ=270º～：360º时，推杆近休止。
要求推程的最大压力角α。
≤30º，试选取合适的基圆半径，并绘制凸轮的廓线。
问此凸轮机构是否有缺陷，应如何补救。
9一12试设计一个对心平底直动推杆盘形凸轮机构凸轮的轮廓曲线。
设已知凸轮基圆半径rn=30 mm，推杆平底与导轨的中心线垂直，凸轮顺时针方向等速转动。
当凸轮转过120~1~r推杆以余弦加速度运动上升20。
，再转过150º时，推杆又以余弦加速度运动回到原位，凸轮转过其余90º时，推杆静止不动。
问这种凸轮机构压力角的变化规律如何?是否也存在自锁问题?若有，应如何避免?解推杆在推程及回程运动规律的位移方程为（1)推程S=h[1-cos(πδ/δ0)]/2：0º≤δ≤120º（2）回程．S=h[1+cos(πδ/δ0`)]/2 0º≤δ≤1 50º计算各分点的位移值如表9-4l：根据表9-4可作所求图如下图：这种凸轮机构的压力角为一定值，它恒等于平底与导路所夹锐角的余角．与其他因素无关。
这种凸轮机构也会是存在自锁问题，为了避免自锁．在设计时应该在结构许可的条件下，尽可能取较大的推杆导路导轨的长度。
并尽可能减小推gan 9的悬臂尺寸。
9一13 一摆动滚子推杆盘形凸轮机构(参看图9—23)，已知lOA=60 mmr0=25 mm，lAB=50 mm，rr=8 mm。
凸轮顺时针方向等速转动，要求当凸轮转过180º时，推杆以余弦加速度运动向上摆动25º；转过一周中的其余角度时，推杆以正弦加速度运动摆回到原位置。
试以作图法设计凸轮的工作廓线。
解推扦在推程及回程段运动规律的位移方程为(1)推程：s=Φ[1-cos(πδ/δ0)/2 0º≤δ≤180º(2)回程：s=Φ[1-(δ/δ`0)十sin(2πδ/δ`0)]/(2π) oº≤δ≤180º计算各分点的位移值如表9．5：根据表9。
5作图如图所示9—14试设计偏置直动滚子推杆盘形凸轮机构凸轮的理论轮廓曲线和工作廓线。
已知凸轮轴置于推杆轴线右侧，偏距e=20 mm ，基圆半径r 。
=50 mm ，滚子半径r ，=10 mm 。
凸轮以等角速度沿顺时针方向回转，在凸轮转过角占，：120。
的过程中，推杆按正弦加速度运动规律上升矗=50 mm ；凸轮继续转过炙=30。
时，推杆保持不动；其后，凸轮再回转角度如=60时，推杆又按余弦加速度运动规律下降至起始位置；凸轮转过一周的其余角度时，推杆又静止不动。
解 (1)汁算推杆的位移并对凸轮转角求导：当凸轮转角δ在o ≤δ≤2π／3过程中，推杆按正弦加速度运动规律上升h=50 rnm 。
则0012[sin()]2s h δπδδπδ=-可得001233[sin()]50[cos(3)]222s h δπδδδπδππ=-=- 0≤δ≤2π/311111233[cos()]50[cos(3)]22ds h d πδδδδδδππ=-=- 0≤δ≤2π/3当凸轮转角占在2π／3≤δ≤5π／6过程中，推杆远休。
S=50 ， 2π／3≤δ≤5π／6ds/d δ=0， 2π/3≤δ≤5π／6当凸轮转角δ在5π/6≤δ≤7π／6过程中，推杆又按余弦加速度运动规律下降至起始位置。
则`0[1cos(0]2h s πδδ=+ 可得123()505{1cos[]}{1cos[3()]}226h s πδδδπδδ--=+=+- 5π／6≤δ≤7π／61233()55sin[]3sin[3()]226ds h d πδδδππδδδδ--=-=-⋅- 5π／6≤δ≤7π／6当凸轮转角δ在7π/6≤δ≤2π过程中，推杆近休。
S=0 7π／6≤δ≤2πds/ d δ=0 7π≤δ≤2π(2)计算凸轮的理论廓线和实际廓线： i本题的计算简图如图（a)所示。
选取坐标系如图 (b)所示，由图（b)可知，凸轮理论廓线上B 点(即滚子中心)的直角坐标为 :x=(s 0+s)cos δ-esin δy=(s 0+s)sin δ+ecos δ式中：s 0=(r 02-e 2)1/2=(502-202)1/2=45.826mm由图 (b)可知凸轮实际廓线的方程即B ’点的坐标方程式为 ix`=x-r r cos θY`=y-r r sin θ因为 dy/d δ=(ds/d δ-e)sin δ+(s 0+s)cos δdx/d δ=(ds/d δ-e)cos δ-(s 0-s)sin δ所以sin cos θθ==故 x`=x-10cos θy`=y-10sin θ由上述公式可得理论轮廓曲线和工作廓线的直角坐标．计算结果如表9．6凸轮廓线如下图昕示。
