经典功率谱估计和现代功率谱估计

功率谱计算功率谱估计在现代信号处理中是一个很重要的课题，涉及的问题很多。

在这里，结合matlab，我做一个粗略介绍。

功率谱估计可以分为经典谱估计方法与现代谱估计方法。

经典谱估计中最简单的就是周期图法，又分为直接法与间接法。

直接法先取N点数据的傅里叶变换（即频谱），然后取频谱与其共轭的乘积，就得到功率谱的估计；间接法先计算N点样本数据的自相关函数，然后取自相关函数的傅里叶变换，即得到功率谱的估计.都可以编程实现，很简单。

在matlab中，周期图法可以用函数periodogram实现。

但是周期图法估计出的功率谱不够精细，分辨率比较低。

因此需要对周期图法进行修正，可以将信号序列x(n)分为n个不相重叠的小段，分别用周期图法进行谱估计，然后将这n段数据估计的结果的平均值作为整段数据功率谱估计的结果。

还可以将信号序列x(n)重叠分段，分别计算功率谱，再计算平均值作为整段数据的功率谱估计。

这2种称为分段平均周期图法，一般后者比前者效果好。

加窗平均周期图法是对分段平均周期图法的改进，即在数据分段后，对每段数据加一个非矩形窗进行预处理，然后在按分段平均周期图法估计功率谱。

相对于分段平均周期图法，加窗平均周期图法可以减小频率泄漏，增加频峰的宽度。

welch法就是利用改进的平均周期图法估计估计随机信号的功率谱，它采用信号分段重叠，加窗，FFT等技术来计算功率谱。

与周期图法比较，welch法可以改善估计谱曲线的光滑性，大大提高谱估计的分辨率。

matlab中，welch法用函数psd实现。

调用格式如下：[Pxx,F] = PSD(X,NFFT,Fs,WINDOW,NOVERLAP)X：输入样本数据NFFT：FFT点数Fs:采样率WINDOW：窗类型NOVERLAP，重叠长度现代谱估计主要针对经典谱估计分辨率低和方差性不好提出的，可以极大的提高估计的分辨率和平滑性。

可以分为参数模型谱估计和非参数模型谱估计。

参数模型谱估计有AR模型，MA模型，ARMA模型等；非参数模型谱估计有最小方差法和MUSIC法等。

功率谱估计的古典算法与现代算法的比较——选取周期图法与Burg算法为例现代信号分析中, 对于常见的具有各态历经的平稳随机信号, 不可能用清楚的数学关系式来描述, 但可以利用给定的 N 个样本数据估计一个平稳随机信号的功率谱密度叫做功率谱估计(PSD)。

功率谱估计可以分为经典功率谱估计(非参数估计)和现代功率谱估计(参数估计)。

一、古典功率谱估计古典功率谱估计是将数据工作区外的未知数据假设为零, 相当于数据加窗经典功率谱估计方法分为: 相关函数法(BT 法)、周期图法以及两种改进的周期图估计法。

1、相关法相关法是以相关函数为媒介来计算功率谱的，所以又叫间接法，它的理论基础是维纳--辛钦定理。

先对数据工作区外的未知数据赋值为零，再由序列x(n)估计出自相关函数R(n)，最后对R(n)进行傅立叶变换, 便得到 x(n)的功率谱估计。

2、周期图法周期图法是由获得的N点数据构成的有限长序列直接求fft得其频谱，取频谱幅度的平方再除以N，以此作为对x(n)真实功率谱的估计。

3、改进的周期图法改进的周期图法的主要途径是平滑和平均。

平滑是用一个适当的窗函数与算出的功率谱进行卷积，使谱线平滑，这种方法得出的谱估计是无偏的，方差也小，但分辨率下降；平均就是将截取的数据段再分成L个平均的小段，分别计算功率谱后取功率谱的平均，当L趋于无穷大的时候，L个平均的方差趋于零，可以达到一致谱估计的目的。

由于存在旁瓣，会产生两个后果：一是功率谱主瓣能量泄露到旁瓣使谱估计的方差增大，二是与旁瓣卷积后得到的功率谱完全属于干扰，严重情况下，强信号与旁瓣的卷积可能大于弱信号与主瓣的卷积，使弱信号淹没在强信号的干扰中无法检测出来。

这是古典法谱估计的主要缺点，即便是改进的周期图法也无法克服分辨率低的缺点。

我们从中选取周期图法作比较，其算法实现如下：Fs=600; %采样频率n=0:1/Fs:1;%产生含有噪声的序列xn=cos(2*pi*40*n)+cos(2*pi*90*n)+0.1*randn(size(n));n=1:length(xn);figure(1);subplot(2,1,1);plot(n,xn);window=boxcar(length(xn));%矩形窗nfft=1024;[Pxx,f]=periodogram(xn,window,nfft,Fs);subplot(2,1,2);plot(f,10*log10(Pxx));得到的图形为：二、现代谱估计参数模型法是现代谱估计中的主要内容，AR 模型参数的求解有三种方法：自相关法、Burg 递推算法和改进协方差法。

现代信号处理经典的功率谱估计《现代信号处理》姓名：李建强学号：201512172087专业：电子科学与技术作业内容：在MATLAB平台上对一个特定的平稳随机信号进行经典功率谱估计和现代功率谱估计的比较一、前言功率谱估计是信息学科中的研究热点,在过去的30多年里取得了飞速的发展。

在许多工程应用中，它能给出被分析对象的能量随频率的分布情况。

平滑周期图是一种计算简单的经典方法，它的主要特点是与任何模型参数无关，但估计出来的功率谱很难与信号的真是功率谱相匹配。

与周期图方法不同，现代谱估计主要是针对经典谱估计(周期图和自相关法)的分辨率低和方差性能不好的问题而提出的。

其使用参数化的模型，能够给出比周期图方法高得多的频率分辨率。

其内容极其丰富，涉及的学科和领域也相当广泛，按是否有参数大致可分为参数模型估计和非参数模型估计，前者有AR模型、MA模型、ARMA模型、PRONY指数模型等;后者有最小方差方法、多分量的MUSIC方法等。

二、总体概述本次实验分别使用经典的功率谱估计（如周期图法）与AR模型法对某一特定的平稳随机信号进行其功率谱估计，由图像得到信号的频率。

利用MATLAB平台，直观形象地观察并比较二者估计效果的区别，以便于加深对功率谱估计的理解和掌握。

三、具体的实现步骤1、经典法功率谱估计周期图法又称直接法，它是从随机信号x(n)中截取N长的一段，把它视为能量有限的真实功率谱的估计的一个抽样。

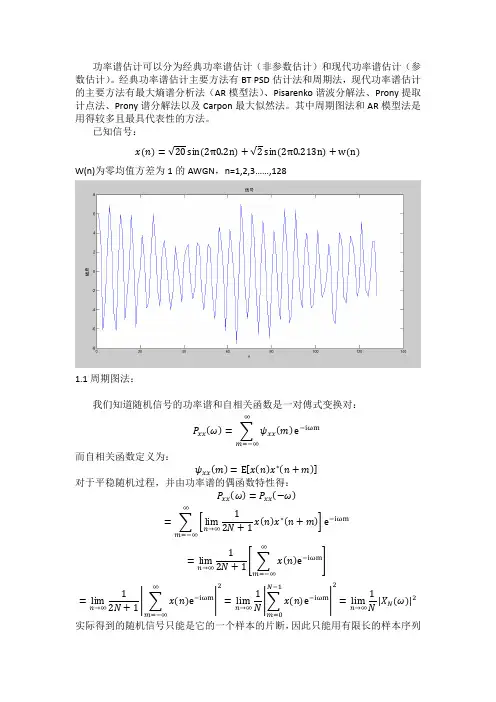
1.1、实现步骤（1）、模拟系统输出参数x(n)=A*sin(2πf1*n)+B*sin(2πf2*n)，包括序列长度N（128或512或1024，加性高斯白噪声（AGWN）功率一定，设置A，B，f1，f2，n的值。

（2）、应用周期图法（不加窗）对信号的功率谱密度进行估计，使用直接法在MATLAB平台上进行编程实现。

（3）、输出相应波形图，进行观察，记录。

1.2 MATLAB源代码实现clear all; %清除工作空间所有之前的变量close all; %关闭之前的所有的figureclc; %清除命令行之前所有的文字n=1:1:128; %设定采样点n=1-128f1=0.2; %设定f1频率的值0.2f2=0.213; %设定f2频率的值0.213A=1; %取定第一个正弦函数的振幅B=1; %取定第一个正弦函数的振幅a=0; %设定相位为0x1=A*sin(2*pi*f1*n+a)+B*sin(2*pi*f2*n+a ); %定义x1函数，不添加高斯白噪声x2=awgn(x1,3); %在x1基础上添加加性高斯白噪声，信噪比为3,定义x2函数temp=0; %定义临时值，并规定初始值为0temp=fft(x2,128); %对x2做快速傅里叶变换pw1=abs(temp).^2/128; %对temp做经典功率估计k=0:length(temp)-1;w=2*pi*k/128;figure(1); %输出x1函数图像plot(w/pi/2,pw1) %输出功率谱函数pw1图像xlabel('信号频率/Hz');ylabel('PSD/傅立叶功率谱估计');title('正弦信号x(n)添加高斯白噪声后的,周期图法功率频谱分析');grid;%------------------------------------------------------------------------- pw2=temp.*conj(temp)/128; %对temp做向量的共轭乘积k=0:length(temp)-1;w=2*pi*k/128;figure(2);plot(w/pi/2,pw2); %输出功率谱函数pw2图像xlabel('信号频率/Hz');ylabel('PSD/傅立叶功率谱估计');title('正弦信号x（n）自相关法功率谱估计');grid;1.3 matlab仿真图形（1）、用直接法，功率谱图像,采样点N=128。

功率谱估计的方法
功率谱估计是信号处理中常用的一种方法，用于分析信号在频域内的特点，通常可以分为以下几种方法：
一、经典方法
1.傅里叶变换法：将时域信号通过傅里叶变换变换到频域，然后计算功率谱密度。

2.自相关法：通过自相关函数反映信号的统计平稳性，然后通过傅里叶变换计算功率谱密度。

3.周期图法：将信号分解为若干个周期波形，然后对每个周期波形进行傅里叶变换计算周期功率谱，最后汇总得到整个信号的功率谱。

二、非经典方法
1. 时-频分析法：如短时傅里叶变换（STFT）、小波变换等，将信号分解为时域和频域两个维度的分量，从而可以分析信号在时间和频率上的变化。

2. 基于协方差矩阵的特征值分解法：通过建立协方差矩阵，在张成空
间中求解特征向量，从而达到计算信号功率谱的目的。

3. 基于频率锁定法：如MUSIC法、ESPRIT法等，是一种利用特定信号空间中的特定模式进行处理的方法。

以上方法各有特点，根据实际需求选择不同的方法可以得到相应的功率谱估计结果。

功率谱估计性能分析及Matlab 仿真1 引言随机信号在时域上是无限长的，在测量样本上也是无穷多的，因此随机信号的能量是无限的，应该用功率信号来描述。

然而，功率信号不满足傅里叶变换的狄里克雷绝对可积的条件，因此严格意义上随机信号的傅里叶变换是不存在的。

因此，要实现随机信号的频域分析，不能简单从频谱的概念出发进行研究，而是功率谱[1]。

信号的功率谱密度描述随机信号的功率在频域随频率的分布。

利用给定的N 个样本数据估计一个平稳随机信号的功率谱密度叫做谱估计。

谱估计方法分为两大类：经典谱估计和现代谱估计。

经典功率谱估计如周期图法、自相关法等，其主要缺陷是描述功率谱波动的数字特征方差性能较差，频率分辨率低。

方差性能差的原因是无法获得按功率谱密度定义中求均值和求极限的运算[2]。

分辨率低的原因是在周期图法中，假定延迟窗以外的自相关函数全为0。

这是不符合实际情况的，因而产生了较差的频率分辨率。

而现代谱估计的目标都是旨在改善谱估计的分辨率，如自相关法和Burg 法等。

2 经典功率谱估计经典功率谱估计是截取较长的数据链中的一段作为工作区，而工作区之外的数据假设为0，这样就相当将数据加一窗函数，根据截取的N 个样本数据估计出其功率谱[1]。

2.1 周期图法( Periodogram )Schuster 首先提出周期图法。

周期图法是根据各态历经的随机过程功率谱的定义进行的谱估计。

取平稳随机信号()x n 的有限个观察值(0),(1),...,(1)x x x n -，求出其傅里叶变换10()()N j j n N n X e x n e ωω---==∑然后进行谱估计21()()j N S X e Nωω-= 周期图法应用比较广泛，主要是由于它与序列的频谱有直接的对应关系，并且可以采用FFT 快速算法来计算。

但是，这种方法需要对无限长的平稳随机序列进行截断，相当于对其加矩形窗，使之成为有限长数据。

同时，这也意味着对自相关函数加三角窗，使功率谱与窗函数卷积，从而产生频谱泄露，容易使弱信号的主瓣被强信号的旁瓣所淹没，造成频谱的模糊和失真，使得谱分辨率较低[1]。

DSP课程设计对功率谱估计常用方法的探讨及应用分析进行傅里叶变换在频域中研究信号，是研究确定性信号最简单且有效的手段，但在现代信号分析中，对于常见的随机信号，不可能用清楚的数学关系式来描述，其傅里叶变换更不存在，转而可以利用给定的N个样本数据估计一个平稳随机信号的功率谱密度。

功率谱估计是数字信号处理的重要研究内容之一。

功率谱估计可以分为经典功率谱估计和现代功率谱估计。

本文介绍了各种经典功率谱估计方法，不仅从理论上对各种方法的谱估计质量进行了分析比较，而且通过Matlab进行了仿真。

在对经典谱估计进行讨论之后，还分析了现代谱估计即参数谱估计方法，通过观测数据估计参数模型再按照求参数模型输出功率的方法估计信号功率谱。

现代谱估计的内容极其丰富，设计的学科及应用的领域都相当广泛，至今每年都有大量的科研成果出来。

在本文的最后利用现代谱估计的方法讨论了功率谱方法在噪声源信号识别中的应用。

文章还给出了常见谱估计方法的比较，便于深刻理解各种方法的特点，从而在实际工作中做出合理的选择。

1.功率谱方法的发展功率谱估计是随机信号处理的重要内容，其技术渊源很长，而且在过去的40余年中获得了飞速的发展。

涉及到信号与系统、随机信号分析、概率统计、矩阵代数等一系列的基础学科，广泛应用于人民的日常生活及军事、工业、农业活动中，是一个具有强大生命力的研究领域。

本文将简要回顾一下功率谱估计的发展历程，对常用的一些方法进行总结。

功率谱的估计方法有很多，主要有经典谱估计和现代谱估计。

经典谱估计又可以分成两种：一种是BT法，也叫间接法；另一种是直接法又称周期图法。

现代谱估计的方法又大致可分为参数模型谱估计和非参数模型谱估计，前者有AR模型、MA模型、ARMA模型、PRONY模型等，后者有最小方差方法、多分量的MUSIC方法等。

1.1功率谱研究的发展过程功率谱估计是数字信号处理的主要内容之一，主要研究信号在频域中的各种特征，目的是根据有限数据在频域内提取被淹没在噪声中的有用信号。

现代谱估计实验报告1 实验目的功率谱估计在实际工程中有重要应用价值。

如在语音信号识别、雷达杂波分析、波达方向估计、地震勘探信号处理、水声信号处理、系统辨识中非线性系统识别、物理光学中透镜干涉、流体力学的内波分析、太阳黑子活动周期研究等许多领域发挥了重要作用。

本次实验的目的主要是深入理解现代谱估计的基本理论，包括ARMA 模型、ARMA 谱估计。

掌握现代谱估计的基本方法，包括SVD-TLS 算法等。

利用ARMA 功率谱估计中Cadzow 谱估计子和Kaveh 谱估计子来进行谱估计。

2 实验原理2.1 背景若离散随机过程{x(n)}服从线性差分方程)()()()(11j n e n e i n x n x q j j p i i b a -+=-+∑∑==（1）式中e （n ）是一离散白噪声，则称{x(n)}为ARMA 过程，而式（1）所示的差分方程称为ARMA 模型。

系数a 1,a 2……a p ,和b 1,b 2……b q ,分别称为自回归参数和滑动平均参数，而p 和q 分别叫做AR 阶数和MA 阶数。

式（1）所示的ARMA 过程，其功率谱密度为)()()()()(22e e P jw jw z x B B e z A z B w jw δδ=== （2）ARMA 谱估计的目的是使用N 个已知的观测数据x(0)，x(1)…..x(N-1)计算出ARMA 过程{x(n)}的功率谱密度估计。

在实际中，可以运用cadzow 谱估计子和kaveh 谱估计子来估计，cadzow 谱估计子秩序确定AR 阶数p 和估计AR 参数，而kaveh 谱估计子也只需要确定AR 阶数p 和估计AR 参数以及MA 阶数。

2.2 相关算法AR阶数p的确定用奇异值分解（SVD）,AR参数的估计用总体最小二乘法(TLS),即应用（SVD—TLS）算法来完成ARMA谱估计。

SVD—TLS算法：步骤1 计算增广矩阵B的SVD，并储存奇异值和矩阵V;步骤2 确定增广矩阵B的有效秩p；步骤3 计算矩阵S;步骤4 求S的逆矩阵S--,并计算出未知参数的总体最小二乘估计。

功率谱估计常用方法的探讨摘要:进行傅里叶变换在频域中研究信号，是研究确定性信号最简单且有效的手段，但在现代信号分析中，对于常见的随机信号，不可能用清楚的数学关系式来描述，其傅里叶变换更不存在，转而可以利用给定的N个样本数据估计一个平稳随机信号的功率谱密度。

功率谱估计是数字信号处理的重要研究内容之一。

关键词：经典谱估计；现代谱估计；BT法；周期图法；在通信系统中，往往需要研究具有目中统计特性的随机信号。

由于随机信号是一类持续时间无限长，具有无限大能量的功率信号，它不满足傅里叶变换条件，而且也不存在解析表达式，因此就不能够应用确定信号的频谱计算方法去分析随机信号的频谱。

然而，虽然随机信号的频谱不存在，但其相关函数是可以确定的。

如果随机信号是平稳的，那么其相关函数的傅里叶变换就是它的功率谱密度函数，简称功率谱。

功率谱估计是随机信号处理的重要内容，其技术渊源很长，而且在过去的40余年中获得了飞速的发展。

涉及到信号与系统、随机信号分析、概率统计、矩阵代数等一系列的基础学科，广泛应用于人民的日常生活及军事、工业、农业活动中，是一个具有强大生命力的研究领域。

功率谱的估计方法有很多，主要有经典谱估计和现代谱估计。

经典谱估计又可以分成两种：一种是BT法，也叫间接法；另一种是直接法又称周期图法。

现代谱估计的方法又大致可分为参数模型谱估计和非参数模型谱估计。

英国科学家牛顿最早给出了“谱”的概念。

后来，1822年，法国工程师傅立叶提出了著名的傅立叶谐波分析理论。

该理论至今依然是进行信号分析和信号处理的理论基础。

周期图法又称直接法。

它是从随机信号x(n)中截取N长的一段，把它视为能量有限x(n)真实功率谱Sx(ejw)的估计Sx(ejw)的抽样.周期图这一概念早在1899年就提出了，但由于点数Ｎ一般比较大，该方法的计算量过大而在当时无法使用。

只是1965年FFT出现后，此法才变成谱估计的一个常用方法。

周期图法包含了二条假设：1．认为随机序列是广义平稳且各态遍历的，可以用其一个样本x(n)中的一段xN(n)来估计该随机序列的功率谱。

中文摘要介绍了各种经典功率谱估计方法,不仅从理论上对各种方法的谱估计质量进行了分析比较,而且通过Matlab 实验仿真验证了理论分析的正确性。

着重对使用比较广泛的Welch 法进行了深入的研究,给出了窗函数选择的一般要求,通过仿真分析了不同的窗函数对Welch 法谱估计质量的影响,比较了他们的优缺点。

最后分析了采样点数较少即短数据对Welch 法谱估计质量的影响。

关键词:经典谱估计;估计质量;Welch 法;窗函数;短数据AbstractVarious classical Power Spect rum Density ( PSD) estimation methods are int roduced ,estimation quality of eachmethod is analyzed and compared in both theory and simulation using the sof tware Matlab. Then further study is made inWelch method which is used most widely. General selecting criterion of window function is presented and estimation quality ofWelch method using different window function is compared. Finally ,the impact of fewer data on estimation quality of Welchmethod is analyzed.Keywords:classical PSD estimation ;estimation quality ;Welch method ;window function ;fewer data第1章绪论 (4)1.1 引言 (4)1.2 选择背景与意义 (4)1.3 经典谱估计发展和应用 (4)第2章经典功率谱估计 (5)2.1 引言 (5)2.2 自相关函数法的估计 (10)2.3 周期图作为功率谱的估计 (13)2.4 经典功率谱估计方法的改进 (19)2.4.1 巴特利特(Bartlett)平均周期图的方法 (19)2.4.2 Welch法 (23)第3章 MATLAB仿真 (24)3.1 仿真结果 (24)3.2 仿真结果分析 (24)3.3 不同窗函数的Welch 谱估计 (25)3.4 短数据的Welch 谱估计 (25)3.5 结论 (26)第4章周期图法和Welch法的比较 (27)4.1 周期图法和Welch法 (27)4.1.1周期图法 (27)4.1.2 Welch法 (27)4.2算法流程图、MATLAB程序及谱估计的分析 (27)4.2.1 算法流程 (28)4.2.2 程序 (28)第5章总结 (30)第1章绪论1.1 引言信号的频谱分析是研究信号特性的重要手段之一,对于确定性信号,可以Fourier 变换来考察其频谱性质,而对于广义平稳随机信号,由于它一般既不是周期的,又不满足平方可积,严格来说不能进行Fourier 变换,通常是求其功率谱来进行频谱分析。