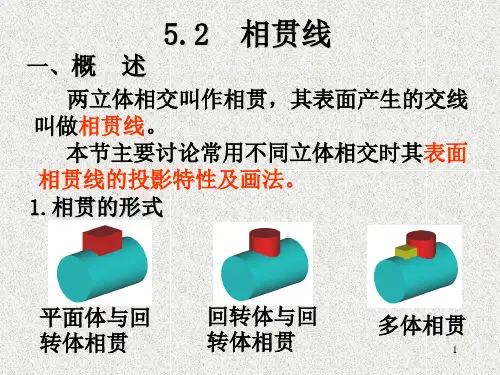
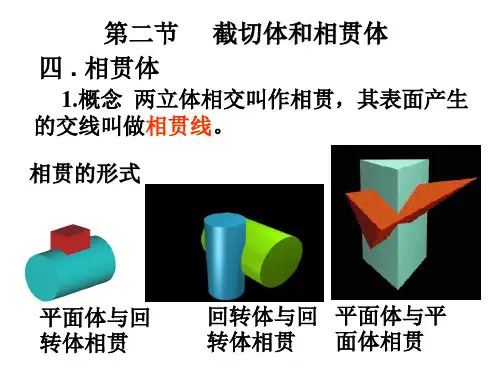
3-4相贯线的投影作图

机械制图
70作图：
（1）求特殊点。

如图4-26（b ）所示，在侧面投影圆上确定1″、2″，它们是相贯线上的最高点和最低点的侧面投影，可直接求出1′、2′，再根据投影规律求出1、2。

过圆柱轴线作水平面相交于最前、最后两条素线；与圆锥相交为一圆，它们的水平投影的交点即为相贯线上最前点Ⅲ和最后点Ⅳ的水平投影3、4，由3、4和3″、4″可求出正面投影3′、4′，这是一对重影点的投影。

（2）求一般位置点。

如图4-26（c ）所示，作水平面P 2，求得Ⅴ、Ⅵ两点的投影。

需要时还可以在适当位置再作水平辅助面求出相贯线上的点（如作水平面P 3，求出Ⅶ、Ⅷ两点的投影）。

（3）依次连接各点的同面投影，根据可见性判别原则可知：水平投影中3、7、2、8、4点在下半个圆柱面上，不可见，故为虚线，其余画实线，如图4-26（d ）所示。

4.4.4相贯线的特殊情况
相贯线常见的特殊情况有以下几种。

（1）轴线正交且平行于同一投影面的圆柱与圆柱、圆柱与圆锥、圆锥与圆锥相交，若它们能公切于一个球，则它们的相贯线是垂直于这个投影面的椭圆。

在图4-27中，圆柱与圆柱、圆柱与圆锥、圆锥与圆锥相交，轴线都分别相交，且都平行于正平面，还公切于一个球，因此，它们的相贯线都是垂直于正平面的两个椭圆。

连接它们的正面投
影的转向轮廓线的交点，即相贯线的正面投影。

图4-27公切于同一个球的圆柱、圆锥的相贯线。

学习内容教学方法任务实施（一）相贯线的性质1、相贯线的概念两个基本体相交（或称相贯），表面产生的交线称为相贯线。

本节只讨论最为常见的两个曲面立体相交的问题。

2、相贯线的性质：（1）相贯线是两个曲面立体表面的共有线，也是两个曲面立体表面的分界线。

相贯线上的点是两个曲面立体表面的共有点。

（2）两个曲面立体的相贯线一般为封闭的空间曲线，特殊情况下可能是平面曲线或直线。

求两个曲面立体相贯线的实质就是求它们表面的共有点。

作图时，依次求出特殊点和一般点，判别其可见性，然后将各点光滑连接起来，即得相贯线。

（二）相贯线的画法两个相交的曲面立体中，如果其中一个是柱面立体（常见的是圆柱面），且其轴线垂直于某投影面时，相贯线在该投影面上的投影一定积聚在柱面投影上，相贯线的其余投影可用表面取点法求出。

1、讲解例题（例3－8）如图3－21（a）所示，求正交两圆柱体的相贯线。

分析：两圆柱体的轴线正交，且分别垂直于水平面和侧面。

相贯线在水平面上的投影积聚在小圆柱水平投影的圆周上，在侧面上的投影积聚在大圆柱侧面投影的圆周上,故只需求作相贯线的正面投影。

出示模型辅助讲解。

a）立体图（b）3－21正交两圆柱的相贯线讲授法演示法任务实施边画图边讲解作图方法与步骤。

2、相贯线的近似画法相贯线的作图步骤较多，如对相贯线的准确性无特殊要求，当两圆柱垂直正交且直径有相差时，可采用圆弧代替相贯线的近似画法。

如图3－22所示，垂直正交两圆柱的相贯线可用大圆柱的D/2为半径作圆弧来代替。

图3-22 相贯线的近似画法3、两圆柱正交的类型两圆柱正交有三种情况：（1）两外圆柱面相交；（2）外圆柱面与内圆柱面相交；（3）两内圆柱面相交。

这三种情况的相交形式虽然不同，但相贯线的性质和形状一样，求法也是一样的。

如图3－23所示。

出示模型辅助讲解。

（a）两外圆柱面相交（b）外圆柱面与内圆柱面相交讲授法演示法（c）两内圆柱面相交图3－23两正交圆柱相交的三种情况（三）相贯线的特殊情况两曲面立体相交，其相贯线一般为空间曲线，但在特殊情况下也可能是平面曲线或直线。