2020年中考数学复习冲刺小卷13 投影与视图2

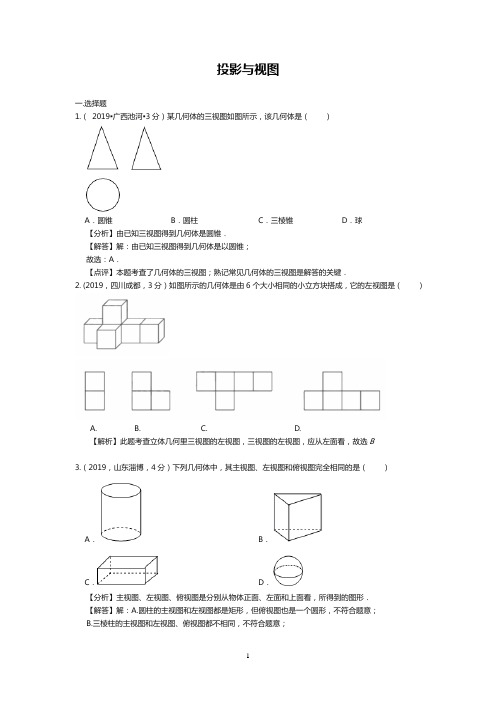
投影与视图一.选择题1.（2019▪广西池河▪3分）某几何体的三视图如图所示，该几何体是（）A．圆锥B．圆柱C．三棱锥D．球【分析】由已知三视图得到几何体是圆锥．【解答】解：由已知三视图得到几何体是以圆锥；故选：A．【点评】本题考查了几何体的三视图；熟记常见几何体的三视图是解答的关键．2. (2019，四川成都，3分）如图所示的几何体是由6个大小相同的小立方块搭成，它的左视图是（）A. B. C. D.【解析】此题考查立体几何里三视图的左视图，三视图的左视图，应从左面看，故选B3.（2019，山东淄博，4分）下列几何体中，其主视图、左视图和俯视图完全相同的是（）A．B．C．D．【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．【解答】解：A.圆柱的主视图和左视图都是矩形，但俯视图也是一个圆形，不符合题意；B.三棱柱的主视图和左视图、俯视图都不相同，不符合题意；C.长方体的主视图和左视图是相同的，都为一个长方形，但是俯视图是一个不一样的长方形，不符合题意；D.球的三视图都是大小相同的圆，符合题意．故选：D．【点评】本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．4. （2019•湖南长沙•3分）某个几何体的三视图如图所示，该几何体是（）A．B．C．D．【分析】根据几何体的三视图判断即可．【解答】解：由三视图可知：该几何体为圆锥．故选：D．【点评】考查了由三视图判断几何体的知识，解题的关键是具有较强的空间想象能力，难度不大．5. （2019•湖南邵阳•3分）下列立体图形中，俯视图与主视图不同的是（）A．正方体B．圆柱C．圆锥D．球【分析】从正面看所得到的图形是主视图，从左面看到的图形是左视图，从上面看到的图象是俯视图．【解答】解：A．俯视图与主视图都是正方形，故选项A不合题意；B．俯视图与主视图都是正方形，故选项B不合题意；C．俯视图是圆，左视图是三角形；故选项C符合题意；D．俯视图与主视图都是圆，故选项D不合题意；故选：C．【点评】此题主要考查了三视图，关键是把握好三视图所看的方向．属于基础题，中考常考题型．6. （2019•湖南湘西州•4分）下列立体图形中，主视图是圆的是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：A.主视图是三角形，故不符合题意；B.主视图是矩形，故不符合题意；C.主视图是圆，故符合题意；D.主视图是正方形，故不符合题意；故选：C．【点评】本题考查了简单几何体的三视图，熟记常见几何体的三视图是解题关键．7. （2019•湖南岳阳•3分）下列立体图形中，俯视图不是圆的是（）A．B．C．D．【分析】俯视图是从几何体的上面看物体，所得到的图形，分析每个几何体，解答出即可．【解答】解：A.圆柱的俯视图是圆；故本项不符合题意；B.圆锥的俯视图是圆；故本项不符合题意；C.立方体的俯视图是正方形；故本项符合题意；D.球的俯视图是圆；故本项不符合题意．故选：C．【点评】本题主要考查了简单几何体的俯视图，锻炼了学生的空间想象能力．8. （2019•广东•3分）如图，由4个相同正方体组合而成的几何体，它的左视图是【答案】A【解析】从左边看，得出左视图.【考点】简单组合体的三视图9. （2019•广西贵港•3分）某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A．B．C．D．【分析】先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．【解答】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B．【点评】本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．10.（2019▪黑龙江哈尔滨▪3分）七个大小相同的正方体搭成的几何体如图所示，其左视图是（）A．B．C．D．【分析】左视图有2列，从左到右分别是2，1个正方形．【解答】解：这个立体图形的左视图有2列，从左到右分别是2，1个正方形，故选：B．【点评】此题主要考查了三视图的画法，正确掌握三视图观察的角度是解题关键．11.（2019▪湖北黄石▪3分）如图，该正方体的俯视图是（）A．B．C．D．【分析】俯视图是从物体上面看所得到的图形，据此判断正方体的俯视图．【解答】解：正方体的主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形都是正方形，故选：A．【点评】本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．12. （2019•山东省聊城市•3分）如图所示的几何体的左视图是（）A．B．C．D．【考点】三视图【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．【解答】解：从左向右看，得到的几何体的左视图是．故选：B．【点评】本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．13. （2019•山东省滨州市•3分）如图，一个几何体由5个大小相同、棱长为1的小正方体搭成，下列说法正确的是（）A．主视图的面积为4 B．左视图的面积为4C．俯视图的面积为3 D．三种视图的面积都是4【考点】三视图【分析】根据该几何体的三视图可逐一判断．【解答】解：A．主视图的面积为4，此选项正确；B．左视图的面积为3，此选项错误；C．俯视图的面积为4，此选项错误；D．由以上选项知此选项错误；故选：A．【点评】本题主要考查了几何体的三种视图面积的求法及比较，关键是掌握三视图的画法．14. （2019•湖北十堰•3分）如图是一个L形状的物体，则它的俯视图是（）A．B．C．D．【分析】找到从上面看所得到的图形即可．【解答】解：从上面看可得到两个左右相邻的长方形，并且左边的长方形的宽度远小于右面长方形的宽度．故选：B．【点评】本题考查了三视图的知识，俯视图是从物体的上面看得到的视图．15. （2019•湖北天门•3分）如图所示的正六棱柱的主视图是（）A．B．C．D．【分析】主视图是从正面看所得到的图形即可，可根据正六棱柱的特点作答．【解答】解：正六棱柱的主视图如图所示：故选：B．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．16. （2019•湖北武汉•3分）如图是由5个相同的小正方体组成的几何体，该几何体的左视图是（）A．B．C．D．【分析】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从左面看易得下面一层有2个正方形，上面一层左边有1个正方形，如图所示：．故选：A．【点评】本题考查了三视图的知识，左视图是从物体的左面看得到的视图．17. （2019•湖北孝感•3分）下列立体图形中，左视图是圆的是（）A．B．C．D．【分析】左视图是从物体左面看，所得到的图形．【解答】解：A.圆锥的左视图是等腰三角形，故此选项不合题意；B.圆柱的左视图是矩形，故此选项不合题意；C.三棱柱的左视图是矩形，故此选项不合题意；D.球的左视图是圆形，故此选项符合题意；故选：D．【点评】本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．18．（2019•浙江嘉兴•3分）如图是由四个相同的小正方形组成的立体图形，它的俯视图为（）A．B．C．D．【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【解答】解：从上面看易得第一层有1个正方形，第二层有2个正方形，如图所示：故选：B．【点评】本题考查了三视图的知识，俯视图是从物体的正面看得到的视图．19．（2019•浙江宁波•4分）如图，下列关于物体的主视图画法正确的是（）A．B．C．D．【分析】根据主视图是从正面看到的图形，进而得出答案．【解答】解：物体的主视图画法正确的是：．故选：C．【点评】本题考查了三视图的知识，关键是找准主视图所看的方向．20.（2019•浙江衢州•3分）如图是由4个大小相同的立方块搭成的几何体，这个几何体的主视图是（）A B C D【答案】A【考点】简单组合体的三视图【解析】【解答】解：从物体正面观察可得，左边第一列有2个小正方体，第二列有1个小正方体.故答案为：A.【分析】主视图：从物体正面观察所得到的图形，由此观察即可得出答案.21．（2019•浙江绍兴•4分）如图的几何体由六个相同的小正方体搭成，它的主视图是（）A．B．C．D．【分析】根据从正面看得到的视图是主视图，可得答案．【解答】解：从正面看有三列，从左起第一列有两个正方形，第二列有两个正方形，第三列有一个正方形，故A符合题意，故选：A．【点评】本题考查了简单组合体的三视图，从正面看得到的视图是主视图．22.（2019•浙江金华•3分）如图物体由两个圆锥组成，其主视图中，∠A=90°，∠ABC=105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（）A. 2B.C.D.【答案】D【考点】圆锥的计算【解析】【解答】解：设BD=2r，∵∠A=90°，∴AB=AD= r，∠ABD=45°，∵上面圆锥的侧面积S= ·2πr·r=1，∴r2= ，又∵∠ABC=105°，∴∠CBD=60°，又∵CB=CD，∴△CBD是边长为2r的等边三角形，∴下面圆锥的侧面积S= ·2πr·2r=2πr2=2π×= .故答案为：D.【分析】设BD=2r，根据勾股定理得AB=AD= r，∠ABD=45°，由圆锥侧面积公式得·2πr·r=1，求得r2= ，结合已知条件得∠CBD=60°，根据等边三角形判定得△CBD是边长为2r的等边三角形，由圆锥侧面积公式得下面圆锥的侧面积即可求得答案.23. (2019安徽)（4分）一个由圆柱和长方体组成的几何体如图水平放置，它的俯视图是（）A．B．C．D．【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【解答】解：几何体的俯视图是：故选：C．【点评】本题考查了三视图的知识，俯视图是从物体的正面看得到的视图．24．（3分）(2019甘肃省陇南市)下列四个几何体中，是三棱柱的为（）A．B．C．D．【分析】分别判断各个几何体的形状，然后确定正确的选项即可．【解答】解：A.该几何体为四棱柱，不符合题意；B.该几何体为四棱锥，不符合题意；C.该几何体为三棱柱，符合题意；D.该几何体为圆柱，不符合题意．故选：C．【点评】考查了认识立体图形的知识，解题的关键是能够认识各个几何体，难度不大．25. (2019甘肃省天水市)如图所示，圆锥的主视图是（）A.B.C.D.【答案】A【解析】解：圆锥的主视图是等腰三角形，如图所示：故选：A．主视图是从正面看所得到的图形即可，可根据圆锥的特点作答．本题考查了三视图的知识，俯视图是从物体的上面看得到的视图，主视图是从物体的正面看得到的视图．10.二.填空题1. （2019•甘肃•3分）已知某几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的左视图的面积为（18+2）cm2．【分析】由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．【解答】解：该几何体是一个三棱柱，底面等边三角形边长为2cm，高为cm，三棱柱的高为3，所以，其表面积为3×2×3+2×＝18+2（cm2）．故答案为（18+2）cm2．【点评】本题考查了三视图，三视图是中考经常考查的知识内容，难度不大，但要求对三视图画法规则要熟练掌握，对常见几何体的三视图要熟悉．。

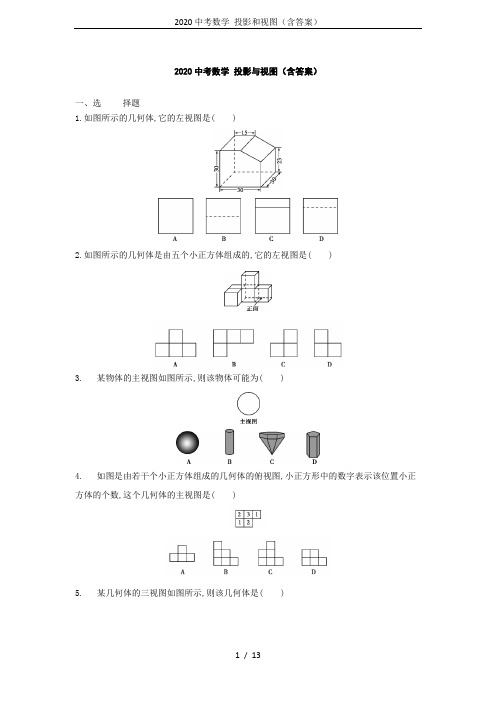
2020中考数学投影与视图（含答案）一、选择题1.如图所示的几何体,它的左视图是( )2.如图所示的几何体是由五个小正方体组成的,它的左视图是( )3.某物体的主视图如图所示,则该物体可能为( )4.如图是由若干个小正方体组成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,这个几何体的主视图是( )5. 某几何体的三视图如图所示,则该几何体是( )A.圆柱B.三棱柱C.长方体D.四棱锥6.将下列左侧的平面图形绕轴l旋转一周,可以得到的立体图形是( )7.白天在同一时刻,小明的影子比小强的影子长,那么在同一路灯下( )A.小明的影子比小强的影子长B.小明的影子比小强的影子短C.小明和小强的影子一样长D.无法判断谁的影子长8.圆桌面(桌面中间有一个直径为0.4 m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2 m,桌面离地面1 m,若灯泡离地面3 m,则地面圆环形阴影的面积是( )A.0.324π m2B.0.288π m2C.1.08π m2D.0.72π m29.如图,是一个正四面体,它的四个面都是正三角形,现沿它的三条棱AC,BC,CD剪开展成平面图形,则所得的展开图是( )二、填空题10.如图,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体的表面积为.11.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,则这个几何体的搭法共有种.12.一个侧面积为16√2π cm2的圆锥,其主视图为等腰直角三角形,则这个圆锥的高为cm.13.如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为.三、解答题14.如图,一个是由若干个完全相同的小正方体组成的几何体.(1)请画出这个几何体的左视图和俯视图;(用阴影表示)(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?15.如图,甲、乙是住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=30 m,现需了解甲楼对乙楼的采光的影响情况.(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上的高度(精确到0.1m,√3≈1.73);(2)若甲楼的影子刚好不落在乙楼的墙上,则此时太阳光与水平线的夹角为多少度?提升题一、选择题1.如图所示的几何体的左视图为( )2.一个几何体由若干个相同的正方体组成,其主视图和俯视图如图所示,则这个几何体中正方体的个数最多是( )A.3B.4C.5D.6⏜表示一条以A为圆3.如图1,有一正方形广场ABCD,图形中的线段均表示直行道路,BD心,AB为半径的圆弧形道路.如图2,在该广场的A处有一路灯,O是灯泡,夜晚小齐同学沿广场道路散步时,影子长度随行走路线的变化而变化,设他步行的路程为x (m)时,相应影子的长度为y (m),根据他步行的路线得到y与x之间关系的大致图象如图3,则他行走的路线是( )A.A→B→E→GB.A→E→D→CC.A→E→B→FD.A→B→D→C二、填空题4.如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为cm(杯壁厚度不计).三、解答题5.一位同学想利用树影测树高AB.在某一时刻测得1 m的竹竿的影长为0.7 m,但当他马上测树影时,发现影子不全落在地上,一部分落在了附近的一幢高楼上(如图).于是他只测出了留在墙上的影长CD为1.5 m,以及地面上的影长BD为4.9 m.请你帮他算一下树高到底为多少米.6.研究课题:蚂蚁怎样爬最近?研究方法:如图1,正方体的棱长为5 cm,一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处,要求该蚂蚁需要爬行的最短路程,可将该正方体右侧面展开,由勾股定理得最短路程为AC1=√AC2+CC12=√102+52=5√5cm.这里,我们将空间两点间最短路程问题转化为平面内两点间距离最短问题.研究实践:(1)如图2,正四棱柱的底面边长为5 cm,侧棱长为6 cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处,蚂蚁需要爬行的最短路程为;(2)如图3,圆锥的母线长为4 cm,圆锥的侧面展开图如图4所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.求该蚂蚁需要爬行的最短路程;(3)如图5,没有上盖的圆柱盒高为10 cm,底面圆的周长为32 cm,点A距离下底面3 cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.请求出蚂蚁需要爬行的最短路程.答案 一、选择题1.D2.D3.A4.C5.C6.D7.D8.D9.B 二、填空题 10.答案 12+15π解析 由几何体的三视图可得:该几何体是底面圆半径为2,高为3的圆柱的34, 该几何体的表面积S=2×2×3+2×270π×22360+270π×2×2360×3=12+15π.11.答案 10解析 设俯视图有9个位置,如图:1 2 3 4 5 6 7 8 9由主视图和左视图知:①第1个位置一定有4个小立方块,第6个位置一定有3个小立方块; ②一定有2个位置有2个小立方块,其余5个位置有1个小立方块;③俯视图最下面一行至少有1个位置有2个小立方块,俯视图中间列至少有1个位置有2个小立方块.则这个几何体的搭法共有10种,如下图所示:4 2 1 1 1 3 2 1 1图1 4 2 1 1 1 3 1 2 1图2 4 2 1 1 1 3 1 1 2图3 4 1 2 1 1 3 1 2 1图4 4 1 11 2 32 1 1图5 4 1 1 1 2 3 1 2 1图6 4 1 1 1 2 3 1 1 2图7 4 1 1 1 1 32 2 1图84 1 11 1 31 2 2图94 1 12 1 31 2 1图10 故答案为10.12.答案 4解析设底面半径为r cm,母线为l cm,∵主视图为等腰直角三角形,∴2r=√2l,∴S侧=πrl=√2πr2=16√2π(cm2),解得 r=4,l=4√2,∴圆锥的高为4 cm.13.答案√13解析蚂蚁的爬行路线有两种情况:(1)将正方体展开如图,连接AM.∵点M是BC的中点,BC=2,∴CM=1BC=1.2又∵CD=AD=2,∴AC=2AD=4.∴AM=√AC2+MC2=√42+12=√17.(2)将正方体展开如图,连接AM.∵点M是BC的中点,BC=2,BC=1.∴CM=12又∵AD=CD=2,∴MD=MC+CD=1+2=3,∴AM=√MD2+AD2=√32+22=√13.∵√17>√13,∴蚂蚁从A点爬行到M点的最短距离为√13.三、解答题14.答案(1)画图如下:(2)在第二层第二列第二行和第三行各加一个;第三层第二列第三行加一个,第三列第三行加1个,2+1+1=4(个).故最多可再添加4个小正方体.15.解析(1)如图,延长OB交DC于点E,作EF⊥AB于点F.在Rt△BEF中,∵EF=AC=30 m,∠FEB=30°,∴BE=2BF.设BF=x m,则BE=2x m.根据勾股定理知BE2=BF2+EF2,∴(2x)2=x2+302,解得x=10√3(负值舍去),∴x≈17.3.∴EC=AF=AB-BF=30-17.3=12.7(m).∴当太阳光与水平线的夹角为30°时,甲楼的影子在乙楼上的高度为12.7 m.(2)当甲楼的影子刚好落在点C处时,△ABC为等腰直角三角形.因此,当太阳光与水平线的夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.B组提升题组一、选择题1.D 从左边看是上长下短等宽的两个矩形,矩形的公共边是虚线,故选D.2.C 由题图易得这个几何体共有2层,结合主视图和俯视图可知,左边下层有2个正方体,左边上层最多有2个正方体;右边只有1层,且只有1个正方体.所以这个几何体中的正方体最多有5个.故选C.3.D 根据题图3可得,函数图象的中间一部分为水平方向的线段,故影子的长度不变,即沿着弧形道路步行,⏜,故中间一段图象对应的路径为BD又因为第一段和第三段图象都从左往右上升,所以第一段函数图象对应的路径为正方形的边AB或AD,第三段函数图象对应的路径为BC 或DC,故行走的路线是A→B→D→C(或A→D→B→C),故选D.二、填空题4.答案20解析如图,将圆柱侧面展开,延长AC 至A',使A'C=AC,连接A'B,则线段A'B 的长为蚂蚁到蜂蜜的最短距离.过B 作BB'⊥AD,垂足为B'.在Rt△A'B'B 中,B'B=16 cm,A'B'=14-5+3=12(cm),所以A'B=√B 'B 2+A 'B '2=√162+122=20(cm),即蚂蚁从外壁A 处到内壁B 处的最短距离为20cm.三、解答题5.解析 如图.设树高为x m,过C 作CE⊥AB 于E.则有x -1.54.9=10.7,解得x=8.5.故树高为8.5 m.6.解析 (1)2√34 cm.分两种情况:①AC 1=√(5+5)2+62=√136 cm,②AC 1=√(6+5)2+52=√146 cm, ∵√146>√136,∴最短路程为 √136=2√34 cm.(2)如图1,连接AA 1,过点O 作OP⊥AA 1,则AP=A 1P,∠AOP=∠A 1OP.由题意,OA=4 cm,∠AOA 1=120°,∴∠AOP=60°.∴AP=OA·sin∠AOP=4·sin 60°=2√3 cm.∴蚂蚁需要爬行的最短路程为AA 1=4√3 cm.(3)如图2,点B与点B'关于PQ对称,可得AC=16 cm,B'C=12 cm, ∴最短路程为AB'=2+122。

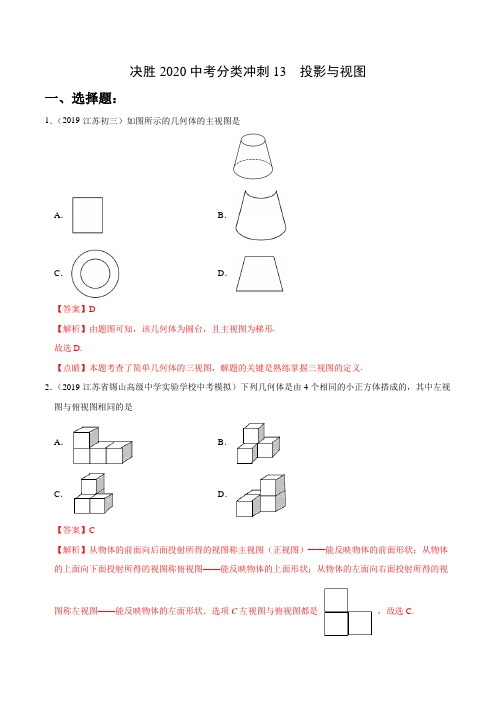
决胜2020中考分类冲刺13 投影与视图一、选择题：1．（2019·江苏初三）如图所示的几何体的主视图是A．B．C．D．【答案】D【解析】由题图可知，该几何体为圆台，且主视图为梯形.故选D.【点睛】本题考查了简单几何体的三视图，解题的关键是熟练掌握三视图的定义.2．（2019·江苏省锡山高级中学实验学校中考模拟）下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是A．B．C．D．【答案】C【解析】从物体的前面向后面投射所得的视图称主视图（正视图）——能反映物体的前面形状；从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状；从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状．选项C左视图与俯视图都是，故选C.3．（2019·江苏中考模拟）一个几何体的三视图如图所示，那么这个几何体是A．B．C．D．【答案】C【解析】由主视图和左视图可得此几何体为柱体，根据俯视图为三角形可得此几何体为三棱柱．故选C．4．（2020·吉林省第二实验学校初三期末）如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体A．主视图改变，左视图改变B．俯视图不变，左视图不变C．俯视图改变，左视图改变D．主视图改变，左视图不变【答案】D【解析】将正方体①移走前的主视图正方形的个数为1，2，1；正方体①移走后的主视图正方形的个数为1，2；发生改变．将正方体①移走前的左视图正方形的个数为2，1，1；正方体①移走后的左视图正方形的个数为2，1，1；没有发生改变．将正方体①移走前的俯视图正方形的个数为1，3，1；正方体①移走后的俯视图正方形的个数，1，3；发生改变．故选D．5．（2019·江苏中考模拟）如图是由4个大小相同的正方体组合而成的几何体，其左视图是A．B．C．D．【答案】A【解析】如图所示几何体的左视图是．故选A．【点睛】考查简单组合体的三视图；用到的知识点为：主视图，左视图，俯视图分别是从物体的正面，左面，上面看得到的图形．6．（2019·江苏中考模拟）下列几何体中，俯视图是矩形的是A．B．C．D．【答案】B【解析】选项A、D的俯视图是圆，选项B的俯视图是矩形，选项C的俯视图是三角形，故答案选B．7．（2019·江苏中考模拟）如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是A．B．C．D．【答案】C【解析】由俯视图知该几何体共2列，其中第1列前一排1个正方形、后1排2个正方形，第2列只有前排2个正方形，所以其主视图为故选C．【点睛】考查了三视图的知识，主视图是从物体的正面看得到的视图．8．（2019·江苏中考模拟）如图，几何体的左视图是A．B．C．D．【答案】A【解析】如图所示，其左视图为．故选A．【点睛】本题考查了简单组合体的三视图，从左边看得到的图形是左视图，注意看不到而且是存在的线是虚线．二、填空题：9．（2019·江苏中考模拟）一个几何体的主视图、俯视图和左视图都是大小相同的正方形，则该几何体是__________．【答案】正方体【解析】正方体的主视图、左视图、俯视图都是大小相同的正方形，故答案为正方体．【点睛】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．10．（2019·江苏初三期末）在同一时刻，直立在地上的6米高的大树的影长是4.5米．附近有一幢大楼的影长是18米，则这栋大楼的高是__________米．【答案】24【解析】设这栋大楼高为x米,得到6:4.5=x：18解得x=24,故答案为：24.【点睛】本题主要考查了相似三角形的应用，熟记同一时刻物高与影长成正比是解题的关键. 11．（2020·沭阳梦溪中学初三期末）一个物体的三视图如图所示，其中主视图和左视图是全等的等边三角形，俯视图是圆，根据图中所示数据，可求这个物体的表面积是______.【答案】3π【解析】由三视图可知：该几何体是一个圆锥，其轴截面是一个高为3的正三角形．∴正三角形的边长=3=2．∴圆锥的底面圆半径是1，母线长是2，∴底面周长为2π∴侧面积为12×2π×2=2π，∵底面积为πr2=π，∴全面积是3π．故填：3π．【点睛】本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．12．（2019·江苏中考模拟）如图，下列选项中不是正六棱柱三视图的是A．B．C．D．【答案】A【解析】根据三视图的定义可得：正六棱柱得主视图是D，左视图是C，俯视图是B，故选A. 13．（2019·江苏省盐城市射阳县实验初级中学中考模拟）一块直角三角形板ABC，∠ACB=90°，BC=12cm，AC=8cm，测得BC边的中心投影B1C1长为24cm，则A1B1长为_____cm．【答案】813【解析】∵∠ACB=90°，BC=12cm，AC=8cm，∴AB=413cm，∵△A1B1C1是△ABC的中心投影，∴△ABC∽△A1B1C1，∴A1B1：AB=B1C1：BC=2：1，即A1B1=813cm．故答案为813【点睛】本题综合考查了中心投影的特点和规律以及相似三角形性质的运用．解题的关键是利用中心投影的特点可知在这两组三角形相似，利用其相似比作为相等关系求出所需要的线段．14．（2019·江苏省锡山高级中学实验学校初三期中）如图，小明站在距离灯杆6m的点B处．若小明的身高AB=1.5m，灯杆CD=6m，则在灯C的照射下，小明的影长BE=______m．【答案】2【解析】∵AB⊥ED，CD⊥ED，∴AB∥DC，∴△ABE∽△CDE，∴AB EB CD ED=∵AB=1.5m，CD=6m，BD=6m，∴1.566EBEB=+解得：EB=2，故答案为2.【点睛】此题主要考查了相似三角形的应用，属于简单题，关键是掌握相似三角形对应边成比例是解题关键．15．（2019·江苏初三期中）如图，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动时她测得一根长为1m的竹竿的影长是0.8m，但当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，他先测得留在墙壁上的影高为1.2m，又测得地面的影长为2.4m，请你帮她算一下，树高是______．【答案】4.2m【解析】如图，设BD是BC在地面的影子，树高为x，根据竹竿的高与其影子的比值和树高与其影子的比值相同得10.8CBBD=，而CB=1.2，∴BD=0.96，∴树在地面的实际影子长是0.96+2.4=3.36，再由竹竿的高与其影子的比值和树高与其影子的比值相同得1 3.360.8x=，∴x=4.2，∴树高是4.2m.故答案为4.2m.【点睛】考查了平行投影的应用，掌握同一时刻影子长与其高度成正比是解题的关键.三、解答题：16．（2020·江苏景山中学初三期末）如图，有一路灯杆AB （底部B 不能直接到达），在灯光下，小华在点D处测得自己的影长DF =3m ，沿BD 方向到达点F 处再测得自己的影长FG =4m ．如果小华的身高为1.5m ，求路灯杆AB 的高度．【解析】∵CD ∥EF ∥AB ，∴可以得到△CDF ∽△ABF ，△ABG ∽△EFG ， ∴,CD DF FE FGAB BF AB BG==， 又∵CD =EF ， ∴DF FGBF BG=， ∵DF =3m ，FG =4m ，BF =BD +DF =BD +3，BG =BD +DF +FG =BD +7， ∴3437DB BD =++， ∴BD =9，BF =9+3=12， ∴1.5312AB =， 解得AB =6．答：路灯杆AB 的高度是6m ．【点睛】考查了相似三角形的应用和中心投影．只要是把实际问题抽象到相似三角形中，利用相似三角形的性质对应边成比例就可以求出结果．17．（2019·泰兴市洋思中学初三期中）如图，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1米，继续往前走3米到达E处时，测得影子EF的长为2米，已知王华的身高是1.5米．（1）求路灯A的高度；（2）当王华再向前走2米，到达F处时，他的影长是多少？【解析】（1）由题可知AB//MC//NE，∴，而MC=NE，∴，∵CD=1米，EF=2米，BF=BD+4，∴BD=4米，∴AB==6米，所以路灯A有6米高.（2）依题意，设影长为x，则解得米,答：王华的影子长83米．【点睛】本题难度较低，主要考查学生对相似三角形性质解决实际生活问题的能力．为中考常考题型，要求学生牢固掌握解题技巧．。

投影与视图一.选择题1．（2020·山东省济宁市·3分）如图，几何体是由3个大小完全一样的正方体组成的，它的左视图是（）A．B．C． D．【考点】简单几何体的三视图．【分析】观察几何体，找出左视图即可．【解答】解：如图，几何体是由3个大小完全一样的正方体组成的，它的左视图是，故选D2．（2020·山东省菏泽市·3分）如图所示，该几何体的俯视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据俯视图是从物体的上面看得到的视图进行解答即可．【解答】解：从上往下看，可以看到选项C所示的图形．故选：C．【点评】本题考查了三视图的知识，掌握俯视图是从物体的上面看得到的视图是解题的关键．3．（2020·山东省滨州市·3分）如图是由4个大小相同的正方体组合而成的几何体，其主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据几何体的三视图，即可解答．【解答】解：根据图形可得主视图为：故选：C．【点评】本题考查了几何体的三视图，解决本题的关键是画物体的三视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．4．（2020·山东省德州市·3分）图中三视图对应的正三棱柱是（）A．B．C．D．【考点】由三视图判断几何体．【分析】利用俯视图可淘汰C、D选项，根据主视图的侧棱为实线可淘汰B，从而判断A选项正确．【解答】解：由俯视图得到正三棱柱两个底面在竖直方向，由主视图得到有一条侧棱在正前方，于是可判定A选项正确．故选A．【点评】本题考查了由三视图判断几何体：由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．由物体的三视图想象几何体的形状是有一定难度的，可以从以下途径进行分析：根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高；从实线和虚线想象几何体看得见部分和看不见部分的轮廓线．5．（2020·山东省东营市·3分）从棱长为2a的正方体零件的一角，挖去一个棱长为a的小正方体，得到一个如图所示的零件，则这个零件的俯视图是( )DC B A 第4题图正面 【知识点】视图——判断三视图 【答案】B. 【解析】俯视图是从上面往下看到的图形，从上面往下看到的是大正方形的左下角有一个小正方形，故选择B.【点拨】自几何体的正前方向后投射，在正面投影面上得到的视图称为主视图；自几何体的左侧向右投射，在侧面投影面上得到的视图称为左视图；自几何体的上方向下投射，在水平投影面上得到的视图称为俯视图.看得见的棱用实现表示，被遮挡住的看不见的棱要用虚线表示.6. （2020·云南省昆明市·4分）下面所给几何体的俯视图是（ ）A ．B ．C ．D ．【考点】简单几何体的三视图．【分析】直接利用俯视图的观察角度从上往下观察得出答案．【解答】解：由几何体可得：圆锥的俯视图是圆，且有圆心．故选：B ．7. （2020·浙江省湖州市·3分）由六个相同的立方体搭成的几何体如图所示，则它的主视图是（ ）A．B．C．D．【考点】简单组合体的三视图．【分析】根据主视方向确定看到的平面图形即可．【解答】解：结合几何体发现：从主视方向看到上面有一个正方形，下面有3个正方形，故选A．8.（2020·福建龙岩·4分）如图所示正三棱柱的主视图是（）A．B．C．D．【考点】简单几何体的三视图．【分析】找到从正面看所得到的图形即可．【解答】解：如图所示正三棱柱的主视图是平行排列的两个矩形，故选B．9.（2020·广西桂林·3分）下列几何体的三视图相同的是（）A．圆柱B．球C．圆锥D．长方体【考点】简单几何体的三视图．【分析】找出圆柱，球，圆锥，以及长方体的三视图，即可做出判断．【解答】解：A、圆柱的三视图，如图所示，不合题意；B、球的三视图，如图所示，符合题意；C、圆锥的三视图，如图所示，不合题意；D、长方体的三视图，如图所示，不合题意；．故选B10．（2020广西南宁3分）把一个正六棱柱如图1摆放，光线由上向下照射此正六棱柱时的正投影是（）A．B．C．D．【考点】平行投影．【分析】根据平行投影特点以及图中正六棱柱的摆放位置即可求解．【解答】解：把一个正六棱柱如图摆放，光线由上向下照射此正六棱柱时的正投影是正六边形．故选A．【点评】本题考查了平行投影特点，不同位置，不同时间，影子的大小、形状可能不同，具体形状应按照物体的外形即光线情况而定．11．（2020贵州毕节3分）图中是一个少数名族手鼓的轮廓图，其主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】直接利用几何体的形状结合主视图的观察角度得出答案．【解答】解：由几何体可得：其主视图为：．故选：B．12．（2020海南3分）如图是由四个相同的小正方体组成的几何体，则它的主视图为（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是两个小正方形，第二层左边一个小正方形，故选：A．【点评】本题考查了简单组合体的三视图，从正面看得到的图形是主视图．13．（2020河南）下列几何体是由4个相同的小正方体搭成的，其中主视图和左视图相同的是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，可得答案．【解答】解：A、主视图是第一层三个小正方形，第二层中间一个小正方形，左视图是第一层一个小正方形，第二层一个小正方形，故A错误；B、主视图是第一层两个小正方形，第二层中间一个小正方形，第三层中间一个小正方形，左视图是第一层一个小正方形，第二层一个小正方形，第三层一个小正方形，故B错误；C、主视图是第一层两个小正方形，第二层左边一个小正方形，左视图是第一层两个小正方形，第二层左边一个小正方形，故C正确；D、主视图是第一层两个小正方形，第二层右边一个小正方形，左视图是第一层一个小正方形，第二层左边一个小正方形，故D错误；故选：C．【点评】本题考查了简单组合体的三视图，从正面看得到的图形是主视图，从左边看得到的图形是左视图．14. （2020·青海西宁·3分）下列几何体中，主视图和俯视图都为矩形的是（）A．B．C．D．【考点】简单几何体的三视图．【分析】分别确定四个几何体从正面和上面看所得到的视图即可．【解答】解：A、此几何体的主视图是等腰三角形，俯视图是圆，故此选项错误；B、此几何体的主视图是矩形，俯视图是矩形，故此选项正确；C、此几何体的主视图是矩形，俯视图是圆，故此选项错误；D、此几何体的主视图是梯形，俯视图是矩形，故此选项错误；故选：B．15. （2020·山东潍坊·3分）如图，几何体是由底面圆心在同一条直线上的三个圆柱构成的，其俯视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据俯视图的概念和看得到的边都应用实线表现在三视图中、看不到，又实际存在的，又没有被其他边挡住的边用虚线表现在三视图中解答即可．【解答】解：图中几何体的俯视图是C选项中的图形．故选：C．16. （2020·陕西·3分）如图，下面的几何体由三个大小相同的小立方块组成，则它的左视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据已知几何体，确定出左视图即可．【解答】解：根据题意得到几何体的左视图为，故选C．17. （2020·湖北随州·3分）如图是某工件的三视图，则此工件的表面积为（）A．15πcm2B．51πcm2C．66πcm2D．24πcm2【考点】由三视图判断几何体．【分析】根据三视图，可得几何体是圆锥，根据勾股定理，可得圆锥的母线长，根据扇形的面积公式，可得圆锥的侧面积，根据圆的面积公式，可得圆锥的底面积，可得答案．【解答】解：由三视图，得，OB=3cm，0A=4cm，由勾股定理，得AB==5cm，圆锥的侧面积×6π×5=15πcm2，圆锥的底面积π×（）2=9πcm，圆锥的表面积15π+9π=24π（cm2），故选：D．18. （2020·湖北武汉·3分）如图是由一个圆柱体和一个长方体组成的几何体，其左视图是（）【考点】简单几何体的三视图．【答案】A【解析】从左面看，上面看到的是长方形，下面看到的也是长方形，且两个长方形一样大．故选A19. （2020·吉林·2分）用5个完全相同的小正方体组合成如图所示的立体图形，它的主视图为（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层右边一个小正方形，故选：A．20. （2020·江西·3分）有两个完全相同的正方体，按下面如图方式摆放，其主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据主视图的定义即可得到结果．【解答】解：其主视图是C，故选C．21. （2020·辽宁丹东·3分）如图所示几何体的左视图为（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看第一层一个小正方形，第二层一个小正方形，第三层一个小正方形，故选：A．22.（2020·黑龙江龙东·3分）如图，由5块完全相同的小正方体所搭成的几何体的俯视图，小正方形中的数字表示在该位置小正方体的个数，其主视图是（）A．B．C．D．【考点】由三视图判断几何体；简单组合体的三视图．【分析】由已知条件可知，主视图有2列，每列小正方数形数目分别为3，1，从而确定正确的选项．【解答】解：由分析得该组合体的主视图为：故选B．23．（2020·黑龙江齐齐哈尔·3分）如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图，组成这个几何体的小正方体的个数最少是（）A．5个B．6个C．7个D．8个【考点】由三视图判断几何体．【分析】由主视图和左视图确定俯视图的形状，再判断最少的正方体的个数．【解答】解：由题中所给出的主视图知物体共2列，且都是最高两层；由左视图知共行，所以小正方体的个数最少的几何体为：第一列第一行1个小正方体，第一列第二行2个小正方体，第二列第三行2个小正方体，其余位置没有小正方体．即组成这个几何体的小正方体的个数最少为：1+2+2=5个．故选A．24．（2020·湖北黄石·3分）某几何体的主视图和左视图如图所示，则该几何体可能是（）A．长方体B．圆锥C．圆柱D．球【分析】主视图、左视图是分别从物体正面、左面看，所得到的图形，根据该几何体的主视图和左视图都是长方形，可得该几何体可能是圆柱体．【解答】解：∵如图所示几何体的主视图和左视图，∴该几何体可能是圆柱体．故选C．【点评】本题考查由三视图确定几何体的形状，主要考查学生空间想象能力，掌握常见几何体的三视图是解题的关键．25．（2020·湖北荆门·3分）由5个大小相同的小正方体拼成的几何体如图所示，则下列说法正确的是（）A．主视图的面积最小B．左视图的面积最小C．俯视图的面积最小D．三个视图的面积相等【考点】简单组合体的三视图．【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层左边一个小正方形，主视图的面积是4；从左边看第一层是两个小正方形，第二层左边一个小正方形，左视图的面积为3；从上边看第一列是两个小正方形，第二列是一个小正方形，第三列是一个小正方形，俯视图的面积是4，左视图面积最小，故B正确；故选：B．26．（2020·山东省济宁市·3分）如图，几何体是由3个大小完全一样的正方体组成的，它的左视图是（）A．B．C． D．【考点】简单几何体的三视图．【分析】观察几何体，找出左视图即可．【解答】解：如图，几何体是由3个大小完全一样的正方体组成的，它的左视图是，故选D26．（2020·山东省菏泽市·3分）如图所示，该几何体的俯视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据俯视图是从物体的上面看得到的视图进行解答即可．【解答】解：从上往下看，可以看到选项C所示的图形．故选：C．【点评】本题考查了三视图的知识，掌握俯视图是从物体的上面看得到的视图是解题的关键．27．（2020·山东省滨州市·3分）如图是由4个大小相同的正方体组合而成的几何体，其主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据几何体的三视图，即可解答．【解答】解：根据图形可得主视图为：故选：C．【点评】本题考查了几何体的三视图，解决本题的关键是画物体的三视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．28．（2020·山东省德州市·3分）图中三视图对应的正三棱柱是（）A．B．C．D．【考点】由三视图判断几何体．【分析】利用俯视图可淘汰C、D选项，根据主视图的侧棱为实线可淘汰B，从而判断A选项正确．【解答】解：由俯视图得到正三棱柱两个底面在竖直方向，由主视图得到有一条侧棱在正前方，于是可判定A 选项正确．故选A ．【点评】本题考查了由三视图判断几何体：由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．由物体的三视图想象几何体的形状是有一定难度的，可以从以下途径进行分析：根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高；从实线和虚线想象几何体看得见部分和看不见部分的轮廓线．29．（2020·山东省东营市·3分）从棱长为2a 的正方体零件的一角，挖去一个棱长为a 的小正方体，得到一个如图所示的零件，则这个零件的俯视图是( )DC B A 第4题图正面 【知识点】视图——判断三视图 【答案】 B. 【解析】俯视图是从上面往下看到的图形，从上面往下看到的是大正方形的左下角有一个小正方形，故选择B.【点拨】自几何体的正前方向后投射，在正面投影面上得到的视图称为主视图；自几何体的左侧向右投射，在侧面投影面上得到的视图称为左视图；自几何体的上方向下投射，在水平投影面上得到的视图称为俯视图.看得见的棱用实现表示，被遮挡住的看不见的棱要用虚线表示.30. （2020·云南省昆明市·4分）下面所给几何体的俯视图是（ ）A ．B ．C ．D ．【考点】简单几何体的三视图．【分析】直接利用俯视图的观察角度从上往下观察得出答案．【解答】解：由几何体可得：圆锥的俯视图是圆，且有圆心．故选：B．31. （2020·浙江省湖州市·3分）由六个相同的立方体搭成的几何体如图所示，则它的主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据主视方向确定看到的平面图形即可．【解答】解：结合几何体发现：从主视方向看到上面有一个正方形，下面有3个正方形，故选A．32.（2020·福建龙岩·4分）如图所示正三棱柱的主视图是（）A．B．C．D．【考点】简单几何体的三视图．【分析】找到从正面看所得到的图形即可．【解答】解：如图所示正三棱柱的主视图是平行排列的两个矩形，故选B．33.（2020·广西桂林·3分）下列几何体的三视图相同的是（）A．圆柱B．球C．圆锥D．长方体【考点】简单几何体的三视图．【分析】找出圆柱，球，圆锥，以及长方体的三视图，即可做出判断．【解答】解：A、圆柱的三视图，如图所示，不合题意；B、球的三视图，如图所示，符合题意；C、圆锥的三视图，如图所示，不合题意；D、长方体的三视图，如图所示，不合题意；．故选B34．（2020广西南宁3分）把一个正六棱柱如图1摆放，光线由上向下照射此正六棱柱时的正投影是（）A．B．C．D．【考点】平行投影．【分析】根据平行投影特点以及图中正六棱柱的摆放位置即可求解．【解答】解：把一个正六棱柱如图摆放，光线由上向下照射此正六棱柱时的正投影是正六边形．故选A．【点评】本题考查了平行投影特点，不同位置，不同时间，影子的大小、形状可能不同，具体形状应按照物体的外形即光线情况而定．35．（2020贵州毕节3分）图中是一个少数名族手鼓的轮廓图，其主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】直接利用几何体的形状结合主视图的观察角度得出答案．【解答】解：由几何体可得：其主视图为：．故选：B．36．（2020海南3分）如图是由四个相同的小正方体组成的几何体，则它的主视图为（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是两个小正方形，第二层左边一个小正方形，故选：A．【点评】本题考查了简单组合体的三视图，从正面看得到的图形是主视图．37．（2020河南）下列几何体是由4个相同的小正方体搭成的，其中主视图和左视图相同的是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，可得答案．【解答】解：A、主视图是第一层三个小正方形，第二层中间一个小正方形，左视图是第一层一个小正方形，第二层一个小正方形，故A错误；B、主视图是第一层两个小正方形，第二层中间一个小正方形，第三层中间一个小正方形，左视图是第一层一个小正方形，第二层一个小正方形，第三层一个小正方形，故B错误；C、主视图是第一层两个小正方形，第二层左边一个小正方形，左视图是第一层两个小正方形，第二层左边一个小正方形，故C正确；D、主视图是第一层两个小正方形，第二层右边一个小正方形，左视图是第一层一个小正方形，第二层左边一个小正方形，故D错误；故选：C．【点评】本题考查了简单组合体的三视图，从正面看得到的图形是主视图，从左边看得到的图形是左视图．二、填空题1.（2020·广西百色·3分）某几何体的三视图如图所示，则组成该几何体的小正方体的个数是5．【考点】由三视图判断几何体．【分析】根据三视图，该几何体的主视图以及俯视图可确定该几何体共有两行3列，故可得出该几何体的小正方体的个数．【解答】解：综合三视图，我们可得出，这个几何体的底层应该有4个小正方体，第二层应该有1个小正方体，因此搭成这个几何体的小正方体的个数为4+1=5个；故答案为：5．2．（2020·黑龙江齐齐哈尔·3分）一个侧面积为16πcm2的圆锥，其主视图为等腰直角三角形，则这个圆锥的高为4cm．【考点】圆锥的计算；等腰直角三角形；由三视图判断几何体．【分析】设底面半径为r，母线为l，由轴截面是等腰直角三角形，得出2r=l，代入S侧=πrl，求出r，l，从而求得圆锥的高．【解答】解：设底面半径为r，母线为l，∵主视图为等腰直角三角形，∴2r=l，2=16πcm2，∴侧面积S侧=πrl=2πr解得r=4，l=4，∴圆锥的高h=4cm，故答案为：4．3．（2020·湖北荆州·3分）如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的表面积为4πcm2．【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状，确定圆锥的母线长和底面半径，从而确定其表面积．【解答】解：由主视图和左视图为三角形判断出是锥体，由俯视图是圆形可判断出这个几何体应该是圆锥；根据三视图知：该圆锥的母线长为3cm，底面半径为1cm，故表面积=πrl+πr2=π×1×3+π×12=4πcm2．故答案为：4π．【点评】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．4.（2020·广西百色·3分）某几何体的三视图如图所示，则组成该几何体的小正方体的个数是5．【考点】由三视图判断几何体．【分析】根据三视图，该几何体的主视图以及俯视图可确定该几何体共有两行3列，故可得出该几何体的小正方体的个数．【解答】解：综合三视图，我们可得出，这个几何体的底层应该有4个小正方体，第二层应该有1个小正方体，因此搭成这个几何体的小正方体的个数为4+1=5个；故答案为：5．。

2020年中考数学考点提分专题十三投影与视图（解析版）必考点1 投影用光线照射物体，在某个平面上得到的影子叫做物体的投影，照射光线叫做投影线，投影所在平面叫做投影面．2．平行投影和中心投影由平行光线形成的投影是平行投影；由同一点(点光源)发出的光线形成的投影叫做中心投影．（1）平行投影：平行光线照射形成的投影（如太阳光线）。

当平行光线垂直投影面时叫正投影。

投影三视图都是正投影。

（2）中心投影：一点出发的光线形成的投影（如手电筒，路灯，台灯）3．正投影投影线垂直投影面产生的投影叫做正投影．要点诠释：正投影是平行投影的一种．【典例1】（2019·河北初三期末）把一个正六棱柱如图摆放，光线由上向下照射此正六棱柱时的正投影是( )A．B．C．D．【举一反三】1．把一个正五棱柱如图摆放，当投射线由正前方射到后方时，它的正投影是图中的( )A．B．C．D．2．（2019·河北初三期末）如图是胡老师画的一幅写生画，四位同学对这幅画的作画时间作了猜测. 根据胡老师给出的方向坐标，猜测比较合理的是（）A．小明：“早上8点”B．小亮：“中午12点”C．小刚：“下午5点”D．小红：“什么时间都行”3．（2019·山东初三期中）如图，小明夜晚从路灯下A处走到B处这一过程中，他在路上的影子（）A．逐渐变长B．逐渐变短C．长度不变D．先变短后变长必考点2 三视图当我们从某一角度观察一个物体时，所看到的图象叫做物体的视图．我们用三个互相垂直的平面作为投影面，其中正对我们的叫做正面，正面下方的叫做水平面，右边的叫做侧面．一个物体在三个投影面内同时进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图；在水平面内得到的由上向下观察物体的视图，叫做俯视图；在侧面内得到的由左向右观察物体的视图，叫做左视图．要点诠释：三视图就是我们从三个方向看物体所得到的3个图象．【典例2】（2019·湖北中考真题）如图是由5个完全相同的小正方形搭成的几何体，如果将小正方体A放到小正方体B的正上方，则它的（）A．主视图会发生改变B．俯视图会发生改变C．左视图会发生改变D．三种视图都会发生改变【举一反三】1．（2019·辽宁中考真题）如图所示几何体的俯视图是（）A．B．C．D．2．（2019·云南中考模拟）如图所示的工件，其俯视图是（）A．B．C．D．3．（2019·湖北中考真题）桌上摆放着一个由相同正方体组成的组合体，其俯视图如图所示，图中数字为该位置小正方体的个数，则这个组合体的左视图为（）A．B．C．D．1．（2019·陕西初三期末）下面四个图是同一天四个不同时刻树的影子，其时间由早到晚的顺序为()A．1234 B．4312 C．3421 D．42312．（2020·山东初三期末）如图，某小区内有一条笔直的小路，路的旁边有一盏路灯，晚上小红由A处走到B处，表示她在灯光照射下的影长l与行走的路程s之间关系的大致图象是（）A． B．C．D．3．（2019·山东初三期末）在某光源下，两根木棒,a b在同一平面内的影子如图所示，此时，第三根木棒c的影子表示正确的是( )A．B．C．D．4．（2019·四川初三）同一时刻，小明在阳光下的影长为2米，与他邻近的旗杆的影长为6米，小明的身高为1.6米，则旗杆的高为（）A．3.2米B．4.8米C．5.2米D．5.6米5．（2019·四川省安岳实验中学初三期末）给出下列结论正确的有（）①物体在阳光照射下，影子的方向是相同的②物体在任何光线照射下影子的方向都是相同的③物体在路灯照射下，影子的方向与路灯的位置有关④物体在光线照射下，影子的长短仅与物体的长短有关.A．1个B．2个C．3个D．4个6．（2019·陕西初三期中）如图，白炽灯正下方有一个乒乓球，当乒乓球沿竖直方向越来越远离白炽灯时，它在地面上的影子（）A．越来越大B．越来越小C．先变大后变小D．先变小后变大7．（2019·黑龙江中考真题）如图是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图，则所需的小正方体的个数最少是（）A．6B．5C．4D．38．（2019·四川中考真题）如图所示的几何体是由6个大小相同的小立方块搭成，它的俯视图是（）A．B．C．D．9．（2019·山东中考真题）以下给出的几何体中，主视图是矩形，俯视图是圆的是（）A．B．C．D．10．（2019·安徽中考真题）一个由圆柱和圆锥组成的几何体如图水平放置，它的俯视图是（）A．B．C．D．19．（2019·山东中考真题）如图是由7个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（）A．主视图不变，左视图不变B．左视图改变，俯视图改变C．主视图改变，俯视图改变D．俯视图不变，左视图改变11．（2019·山东中考真题）如图所示的几何体是由4个大小相同的小立方块搭成，它的俯视图是（）A．B．C．D．12．（2019·北京中考真题）在如图所示的几何体中，其三视图中有矩形的是______.（写出所有正确答案的序号）13．（2019·湖南中考真题）已知某几何体的三视图如图，其中主视图和左视图都是腰长为5，底边长为4的等腰三角形，则该几何体的侧面展开图的面积是____．（结果保留π）14．（2019·山东中考真题）如图，一个正方体由27 个大小相同的小立方块搭成，现从中取走若干个小立方块，得到一个新的几何体．若新几何体与原正方体的表面积相等，则最多可以取走_________个小立方块．15．（2019·湖北中考模拟）如图，由四个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体俯视图的面积是．16．（2019·山东中考模拟）如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的表面积是．17．（2019·安徽中考模拟）如图是一个几何体的三视图（图中尺寸单位：cm），根据图中数据计算，这个cm．几何体的表面积为__________218．（2012·四川中考真题）由一些大小相同的小正方形组成的一个几何体的主视图和俯视图如图所示，那么组成该几何体所需的小正方形的个数最少为_________．2020年中考数学考点提分专题十三投影与视图（解析版）必考点1 投影用光线照射物体，在某个平面上得到的影子叫做物体的投影，照射光线叫做投影线，投影所在平面叫做投影面．2．平行投影和中心投影由平行光线形成的投影是平行投影；由同一点(点光源)发出的光线形成的投影叫做中心投影．（1）平行投影：平行光线照射形成的投影（如太阳光线）。

专题13 视图重点分析中考视图与投影仍是考查重点内容，尤其视图与投影与实际生活有关系的应用问题。

在中考的难度不大，分数约占3-6分左右。

难点解读难点一：投影1．投影：在光线的照射下，空间中的物体落在平面内的影子能够反映出该物体的形状和大小，这种现象叫做投影现象．影子所在的平面称为投影面．2．平行投影、中心投影、正投影（1）中心投影：在点光下形成的物体的投影叫做中心投影，点光叫做投影中心．【注意】灯光下的影子为中心投影，影子在物体背对光的一侧．等高的物体垂直于地面放置时，在灯光下，离点光近的物体的影子短，离点光远的物体的影子长．（2）平行投影：投射线相互平行的投影称为平行投影．【注意】阳光下的影子为平行投影，在平行投影下，同一时刻两物体的影子在同一方向上，并且物高与影长成正比．（3）正投影：投射线与投影面垂直时的平行投影，叫做正投影．难点二：视图1．视图：由于可以用视线代替投影线，所以物体的正投影通常也称为物体的视图．2．三视图：1）主视图：从正面看得到的视图叫做主视图．2）左视图：从左面看得到的视图叫做左视图．3）俯视图：从上面看得到的视图叫做俯视图．【注意】在三种视图中，主视图反映物体的长和高，左视图反映了物体的宽和高，俯视图反映了物体的长和宽．3．三视图的画法1）画三视图要注意三要素：主视图与俯视图长度相等；主视图与左视图高度相等；左视图与俯视图宽度相等．简记为“主俯长对正，主左高平齐，左俯宽相等”．2）注意实线与虚线的区别：能看到的线用实线，看不到的线用虚线．难点三：几何体的展开与折叠1．常见几何体的展开图几何体立体图形表面展开图侧面展开图圆柱圆锥三棱柱2．正方体的展开图正方体有11种展开图，分为四类：第一类，中间四连方，两侧各有一个，共6种，如下图：第二类，中间三连方，两侧各有一、二个，共3种，如下图：第三类，中间二连方，两侧各有二个，只有1种，如图10；第四类，两排各有三个，也只有1种，如图11．真题演练1.如图是由5个相同的小立方块搭成的几何体，则下面四个平面图形中不是这个几何体的三视图的是（ ）A. B. C. D.【答案】D【解析】几何体三视图分别为左视图，俯视图，和主视图，根据左视图是从左面看到的图形，主视图是从正面看到的图形，俯视图是从上面的看到的图形，逐项判断即可．【详解】从正面看，从左到右小正方形的个数一次是，，，主视图如下：从左面看，从左往右小正方形的个数为，，左视图如下：从上面看，从左往右小正方形的个数为，，，俯视图如下：综上可以到的几何体的三视图故选：D．【点拨】本题考查了几何体的三视图和学生的空间想象能力，细心观察图中几何体每个正方形的位置是解题关键．2. 下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是（ ）A. B. C. D.【答案】C【解析】【详解】试题分析：从物体的前面向后面投射所得的视图称主视图（正视图）——能反映物体的前面形状；从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状；从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状．选项C左视图与俯视图都是，故选C.3.如图所示的几何体，该几何体的俯视图是（）A. B. C. D.【答案】D【解析】根据俯视图的定义即可判断．【详解】解：从上往下看得到的图形是，故选：D．【点拨】本题主要考查了三视图的知识，俯视图是从物体的上面看得到的视图．4.如图所示的几何体是由一个球体和一个长方体组成的，它的主视图是（ ）A. B.C. D.【答案】B【解析】根据主视图的意义和画法可以得出答案．【详解】解：根据主视图的意义可知，从正面看物体所得到的图形，选项B符合题意，故选：B．【点拨】本题考查了简单几何体的三视图的画法，主视图就是从正面看物体所得到的图形．5.如图是一个由正方体和一个正四棱锥组成的立体图形，它的俯视图是（）A. B. C. D.【答案】C【解析】俯视图是从上面看，注意所有的看到的棱都应表现在俯视图中．解：如图所示：它的俯视图是：．故选：C．【点拨】此题主要考查了三视图的知识，关键是树立空间观念，掌握三视图的几种看法．6.如图所示正三棱柱的主视图是（）A. B. C. D.【答案】B【解析】找到从正面看所得到的图形即可解：如图所示正三棱柱的主视图是平行排列的两个矩形，故选：B．【点拨】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．7.如图，由五个完全相同的小正方体组合搭成一个几何体，把正方体A向右平移到正方体P前面，其“三视图”中发生变化的是（ ）A. 主视图B. 左视图C. 俯视图D. 主视图和左视图【答案】C【解析】根据三视图的意义，可得答案．【详解】若把正方体A向右平移到正方体P前面，主视图与左视图均与原来的一样，没有发生变化，只有俯视图发生了变化，故选C．【点拨】本题考查了简单组合体的三视图，利用三视图的定义是解题关键．8.如图所示几何体的左视图是（ ）A．B．C．D．【答案】C【解析】根据从左面看得到的图形是左视图，可得答案．解：如图所示，几何体的左视图是：故选：C．【点拨】本题考查了简单组合体的三视图，从左面看得到的图形是左视图．9.甲和乙两个几何体都是由大小相同的小立方块搭成，它们的俯视图如图，小正方形中数字表示该位置上的小立方块个数（）A．甲和乙左视图相同，主视图相同B．甲和乙左视图不相同，主视图不相同C．甲和乙左视图相同，主视图不相同D．甲和乙左视图不相同，主视图相同【答案】D【解析】根据俯视图，即可判断左视图和主视图的形状．【详解】由甲俯视图知，其左视图为，由乙俯视图知，其左视图为，故它们的左视图不相同，但它们两个的主视图相同，都是．故选：D．【点拨】本题考查了三视图的知识，关键是根据俯视图及题意确定几何体的形状，从而可确定其左视图和主视图．10.由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示，则搭成该几何体的小正方体的个数最多为（）A．7个B．8个C．9个D．10个【答案】A【解析】根据几何体主视图，在俯视图上表上数字，即可得出搭成该几何体的小正方体最多的个数．解：根据题意得：则搭成该几何体的小正方体最多是1＋1＋1＋2＋2＝7（个）．故选：A．【点拨】此题考查了由三视图判断几何体，在俯视图上表示出正确的数字是解本题的关键．11.如图，该几何体的左视图是（）A．B．C．D．【答案】D【解析】画出从左面看到的图形即可．解：该几何体的左视图是一个长方形，并且有一条隐藏的线用虚线表示，如图所示：，故选：D．【点拨】本题考查三视图，具备空间想象能力是解题的关键，注意看不见的线要用虚线画出．12.一个几何体的三视图如图所示，则这个几何体的侧面积是（）A．B．C．D．【答案】A【解析】根据三视图可知此几何体为圆锥，那么侧面积=底面周长母线2．解：此几何体为圆锥，圆锥母线长为9 cm，直径为6cm，侧面积，故选：A．【点拨】本题考查由三视图判断几何体，圆锥的有关计算，熟知圆锥的侧面积公式是解题关键．13.一个儿何体由大小相同的小立方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小正方块的个数，能正确表示该几何体的主视图的是（）A．B．C．D．【答案】B【解析】主视图的列数与俯视图的列数相同，且每列小正方形的数目为俯视图中该列小正方数字中最大数字，从而可得出结论．【详解】由已知条件可知：主视图有3列，每列小正方形的数目分别为4，2，3，根据此可画出图形如下：故选：B．【点拨】本题考查了从不同方向观察物体和几何图像，是培养学生观察能力．。

投影与视图【考点整理】1．投影投影：物体在光线的照射下，在某个平面内形成的影子叫做______，光线叫做投射线，投影所在的平面叫做投影面．平行投影：平行的投射线所形成的投影叫做平行投影．物体的视图实际上是该物体在______光线下且光线与投影面垂直时形成的投影．中心投影：由同一点发出的投射线所形成的投影．【智慧锦囊】在阳光下，不同时刻，同一物体的影子长度不同；在同一时刻，不同物体的影子长与它们的高度成比例，即两物体影子之比_______其对应的高的比．2．物体的三视图三视图：物体在正投影面上的正投影叫做________；在水平投影面上的正投影叫做________；在左侧投影面上的正投影叫做________ ．主视图、左视图和俯视图合称三视图．三视图画法：首先确定主视图的位置，画出主视图，然后在主视图的下面画出俯视图，在主视图的右面画出左视图．主视图反映物体的_____和_____ ，俯视图反映物体的_____和_____ ，左视图反映物体的_____和_____ ．【智慧锦囊】画三视图时，主、俯视图要长对正，主、左视图要高平齐，左、俯视图要宽相等，看得见部分的轮廓线通常画成______，看不见部分的轮廓线通常画成______．3．图形的展开与折叠圆柱的表面展开图：由两个相同的圆形和一个长方形组成的．棱柱的表面展开图：按棱柱表面不同的棱剪开，可能得到不同的组合形式的平面展开图．圆锥的表面展开图：由一个圆和一个扇形组成．多面体的平面展开：通过实验操作、合理想象解决这类问题，也可先动手折一折．正方体的平面展开图：将正方体表面沿着某些棱展开成一个平面图形，需要剪开7条棱，由于剪开的方法不同，会得到11种不同形状的展开图．（1）一四一型：（2）二三一型（3）三三型⑩（4）二二二型4．正方体的常见截面形状截面一般有横截面(水平截)、纵截面(竖直截)、斜截面，得到的截面不同．【解题秘籍】1．数小正方体的个数的方法(1)主视图与俯视图的行数相同，其每列方块数是俯视图中该列中的最大数字；(2)左视图的列数与俯视图的列数相同，其每列的方块数是俯视图中该行中的最大数字．此类问题可用口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”来理解．2．三视图的正逆向思维对三视图的考查主要有两类，一是根据所给物体画三视图，二是根据三视图描述物体形状．在画三视图要注意三视图的特征和视图时看不见的线要化为虚线，此考点是中考的热点考点．【易错提醒】1．注意区分平行投影与中心投影，理解各自特点和异同．2．画圆锥的俯视图时，应注意画上圆心(表示圆锥的顶点)．3．画简单组合体的三视图，要善于观察和想象，分清图形特征与位置关系．【题型解析】1.投影【例题1】如图是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序排列正确的是（）。

投影与视图【基础知识回顾】一、投影：1、定义：一般地，用光线照射物体，在某个平面上得到得影子叫做物体的其中照射光线叫做投影所在的平面叫做2、平行投影：太阳光可以近似地看作是光线，像这样的光线所形成的投影称为平行投影3、中心投影：由同一点（点光源）发出的光线形成的投影叫做，如物体在、、等照射下所形成的投影就是中心投影【名师提醒：1、中心投影的光线平行投影的光线2、在同一时刻，不同物体在太阳下的影长与物高成3、物体投影问题有时也会出现计算解答题，解决这类问题首先要根据图形准确找出比例关系，然后求解】二、视图：1、定义：从不同的方向看一个物体，然后描绘出所看到的图形即视图。

其中，从看到的图形称为主视图，从看到的图形称为左视图，从看到的图形称为俯视图2、三种视图的位置及作用⑴画三视图时，首先确定的位置，然后在主视图的下面画出，在主视图的右边画出⑵主视图反映物体的和，左视图反映物体的和俯视图反映物体的和。

【名师提醒：1、在画几何体的视图时，看得见部分的轮廓线通常画成线，看不见部分的轮廓线通常画成线2、在画几何体的三视图时要注意主俯对正，主左平齐，左俯相等】三、立体图形的展开与折叠：1、许多立体图形是由平面图形围成的，将它们适当展开即为平面展开图，同一个立体图形按不同的方式展开，会得到不同的平面展开图2、常见几何体的展开图：⑴正方体的展开图是⑵n边形的直棱柱展开图是两个n边形和一个⑶圆柱的展开图是一个和两个⑷圆锥的展开图是一个与一个【名师提醒：有时会出现根据物体三视图中标注的数据求原几何体的表面积，体积等题目，这时要注意先根据三种视图还原几何体的形状，然后想象有关尺寸在几何体展开图中标注的是哪些部分，最后再根据公式进行计算】【重点考点例析】考点一：简单几何体的三视图例1 （2017•锦州）下列几何体中，主视图和左视图不同的是（）A．B．C．D．思路分析：分别分析四种几何体的主视图和左视图，找出主视图和左视图不同的几何体．解：A、圆柱的主视图与左视图都是长方形，不合题意，故本选项错误；B、正方体的主视图与左视图相同，都是正方形，不合题意，故本选项错误；C、正三棱柱的主视图是长方形，长方形中有一条杠，左视图是矩形，符合题意，故本选项正确；D、球的主视图和左视图相同，都是圆，且有一条水平的直径，不合题意，故本选项错误．故选：C．点评：本题考查了简单几何体的三视图，要求同学们掌握主视图是从物体的正面看到的视图，左视图是从物体的左面看得到的视图．对应训练1．（2017•黄石）如图，下列四个几何体中，它们各自的三视图（主视图、左视图、俯视图）有两个相同，而另一个不同的几何体是（）A．①②B．②③C．②④D．③④考点二：简单组合体的三视图例2 （2017•湛江）如图是由6个大小相同的正方体组成的几何体，它的左视图是（）A．B．C．D．思路分析：细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定则可．解：从物体左面看，是左边2个正方形，右边1个正方形．故选A．点评：本题考查了三视图的知识，左视图是从物体左面看所得到的图形，解答时学生易将三种视图混淆而错误的选其它选项．对应训练2．（2017•襄阳）如图所示的几何体的主视图、左视图、俯视图中有两个视图是相同的，则不同的视图是（）圆柱正方体正三棱柱球A．B．C．D．考点三：由三视图判断几何体例3（2017•扬州）某几何体的三视图如图所示，则这个几何体是（）A．三棱柱B．圆柱C．正方体D．三棱锥思路分析：如图所示，根据三视图的知识可使用排除法来解答．解：如图，俯视图为三角形，故可排除C、B．主视图以及侧视图都是矩形，可排除D．故选A．点评：本题考查了由三视图判断几何体的知识，难度一般，考生做此类题时可利用排除法解答．例4 （2017•自贡）某超市货架上摆放着某品牌红烧牛肉方便面，如图是它们的三视图，则货架上的红烧牛肉方便面至少有（）碗A．8 B．9 C．10 D．11思路分析：主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．解：易得第一层有4碗，第二层最少有3碗，第三层最少有2碗，所以至少共有9个碗．故选B．点评：考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．对应训练3．（2017•云南）图为某个几何体的三视图，则该几何体是（）A．B．C．D．4．（2017•玉林）某几何体的三视图如图所示，则组成该几何体共用了（）小方块．A．12块B．9块C．7块D．6块4．C考点四：几何体的相关计算例5（2017•贺州）如图是一个几何体的三视图，根据图中提供的数据（单位：cm）可求得这个几何体的体积为（）A．2cm3B．3cm3C．6cm3D．8cm3思路分析：根据三视图我们可以得出这个几何体是个长方体，它的体积应该是1×1×3=3cm3．解：该几何体的主视图以及左视图都是相同的矩形，俯视图也为一个矩形，可确定这个几何体是一个长方体，此长方体的长与宽都是1，高为3，所以该几何体的体积为1×1×3=3cm3．点评：本题考查了由三视图判断几何体及长方体的体积公式，本题要先判断出几何体的形状，然后根据其体积公式进行计算．对应训练5．（2017•宁夏）如图是某几何体的三视图，其侧面积（）A．6 B．4πC．6πD．12π【聚焦中考】1．（2017•烟台）下列水平放置的几何体中，俯视图不是圆的是（）A．B．C．D．2．（2017•淄博）下面关于正六棱柱的视图（主视图、左视图、俯视图）中，画法错误的是（）A．B．C．D．3．（2017•莱芜）下面四个几何体中，左视图是四边形的几何体共有（）A．1个B．2个C．3个D．4个4．（2017•滨州）如图所示的几何体是由若干个大小相同的小正方体组成的．若从正上方看这个几何体，则所看到的平面图形是（）A．B．C．D．5．（2017•潍坊）如图是常用的一种圆顶螺杆，它的俯视图正确的是（）A．B．C．D．6．（2017•青岛）如图所示的几何体的俯视图是（）A．B．C．D．7．（2017•济南）图中三视图所对应的直观图是（）A．B．C．D．8．（2017•威海）如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（）A．主视图改变，左视图改变B．俯视图不变，左视图不变C．俯视图改变，左视图改变D．主视图改变，左视图不变9．（2017•聊城）如图是由几个相同的小立方块组成的三视图，小立方块的个数是（）A．3个B．4个C．5个D．6个9．B10．（2017•临沂）如图是一个几何体的三视图，则这个几何体的侧面积是（）A．12πcm2B．8πcm2C．6πcm2D．3πcm210．C11．（2017•济宁）三棱柱的三视图如图所示，△EFG中，EF=8cm，EG=12cm，∠EGF=30°，则AB的长为cm．【备考真题过关】一、选择题1．（2017•成都）如图所示的几何体的俯视图可能是（）A．B．C．D．2．（2017•昆明）下面几何体的左视图是（）A．B．C．D．3．（2017•安徽）如图所示的几何体为圆台，其主（正）视图正确的是（）A．B．C．D．4．（2017•本溪）如图放置的圆柱体的左视图为（）A．B．C．D．5．（2017•舟山）如图，由三个小立方体搭成的几何体的俯视图是（）A．B．C．D．6．（2017•义乌）如图几何体的主视图是（）A．B．C．D．7．（2017•株洲）下列几何体中，有一个几何体的俯视图的形状与其它三个不一样，这个几何体是（）A ．B ．C ．D ．8．（2017•营口）如图，下列水平放置的几何体中，主视图是三角形的是（）A ．B ．C ． D．9．（2017•宜宾）下列水平放置的四个几何体中，主视图与其它三个不相同的是（）A ．B ．C ．D ．10．（2017•新疆）下列几何体中，主视图相同的是（ ）A ．①②B ．①③C ．①④D ．②④11．（2017•桂林）下列物体的主视图、俯视图和左视图不全是圆的是（ ）A ．橄榄球B ．兵乓球C ．篮球D ．排球12．（2017•广东）下列四个几何体中，俯视图为四边形的是（ ）A ．B ．C ．D ．13．（2017•天津）如图是由3个相同的正方体组成的一个立体图形，它的三视图是（ ）A ．B ．C ．D ．正方体 圆柱 圆锥 球14．（2017•泰州）由一个圆柱体与一个长方体组成的几何体如图所示，这个几何体的左视图是（）A．B．C．D．15．（2017•遂宁）如图所示的是三通管的立体图，则这个几何体的俯视图是（）A．B．C．D．16．（2017•南平）如图是由六个棱长为1的正方体组成的一个几何体，其主视图的面积是（）A．3 B．4 C．5 D．6 17．（2017•宿迁）如图是由六个棱长为1的正方体组成的几何体，其俯视图的面积是（）A．3 B．4 C．5 D．618．（2017•十堰）用两块完全相同的长方体摆放成如图所示的几何体，这个几何体的左视图是（）A．B．C．D．19．（2017•黔东南州）如图是有几个相同的小正方体组成的一个几何体．它的左视图是（）A．B．C．D．20．（2017•盘锦）如图下面几何体的左视图是（）A．B．C．D．21．（2017•茂名）如图，由两个相同的正方体和一个圆锥体组成一个立体图形，其俯视图是（）A．B．C．D．22．（2017•荆门）过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如图所示，它的俯视图为（）A．B．C．D．23．（2017•江西）一张坐凳的形状如图所示，以箭头所指的方向为主视方向，则它的左视图可以是（）A．B．C．D．24．（2017•大庆）图1所示的几何体，它的俯视图为图2，则这个几何体的左视图是（）A．B．C．D．25．（2017•遵义）一个几何体的三视图如图所示，则这个几何体是（）A．B．C．D．26．（2017•铁岭）如图是4块小立方块所搭成的几何体的俯视图，小正方形中的数字表示该位置小方块的个数，其主视图是（）A．B．C． D27．（2017•黑龙江）由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示，则组成这个几何体的小正方体的个数最多有（）A．4 B．5 C．6 D．728．（2017•益阳）一个物体由多个完全相同的小正方体组成，它的三视图如图所示，那么组成这个物体的小正方体的个数为（）A．2个B．3个C．5个D．10个29．（2017•孝感）如图，由8个大小相同的正方体组成的几何体的主视图和俯视图，则这个几何体的左视图是（）A．B．C．D．30．（2017•曲靖）如图是某几何体的三视图，则该几何体的侧面展开图是（）A．B．C．D．31．（2017•乐山）一个立体图形的三视图如图所示．根据图中数据求得这个立体图形的表面积为（）A．2πB．6πC．7πD．8π31．D32．（2017•杭州）如图是某几何体的三视图，则该几何体的体积是（）A．183B．543C．1083D．2163二、填空题33．（2017•南通）一个几何体的主视图、俯视图和左视图都是大小相同的圆，则这个几何体是．34．（2017•绥化）由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示，则组成这个几何体的小正方体的个数可能是．35．（2017•无锡）如图是一个几何体的三视图，若这个几何体的体积是36，则它的表面积是．。

第3章投影与视图3．1 投影知识点1 平行投影1．平行投影中的光线是(A)A．平行的B．不平行的C．聚成一点的D．向四周发散的2．下列投影是平行投影的是(A)A．太阳光下窗户的影子B．台灯下书本的影子C．在手电筒照射下纸片的影子D．路灯下行人的影子3．下列图中是太阳光下形成的影子的是(A)4．一木杆按如图所示的方式直立在地面上，请在图中画出它在阳光下的影子．(用线段AB表示)解：如图．知识点2 中心投影5．下列哪种影子不是中心投影(D)A．皮影戏中的影子B．晚上在墙上的手影C．舞厅中霓虹灯形成的影子D．林荫道上的树影6．如图，晚上小亮在路灯下散步，他从A处向着路灯灯柱方向径直走到B处，这一过程中他在该路灯灯光下的影子(A)A．逐渐变短B．逐渐变长C．先变短后变长D．先变长后变短7．画出如图中各木杆在灯光下的影子．解：如图．线段AB，A′B′是两根木杆的影子．知识点3 正投影8．如图，按照箭头所指的投影方向，图中圆柱的正投影是(B)A．圆B．矩形C．梯形D．圆柱9．(教材P99习题T4变式)画出如图物体(正三棱柱)的正投影：(1)投影线由物体前方射到后方；(2)投影线由物体左方射到右方；(3)投影线由物体上方射到下方．解：中档题10．正方形的正投影不可能是(D)A．正方形B．长方形C．线段D．梯形11．下图表示一块三角尺在光线照射下形成的投影，其中(2)是平行投影；(1)是中心投影；(3)是正投影．(1) (2) (3)12．如图分别是两棵树及其影子的情形．图甲图乙(1)哪个图反映了阳光下的情形？哪个图反映了路灯下的情形？(2)请画出图中表示小丽影长的线段；(3)阳光下小丽影子长为1.20 m，树的影子长为2.40 m，小丽身高1.88 m，求树高．解：(1)图甲反映了阳光下的情形，图乙反映了路灯下的情形．(2)如图，AB，CD是小丽影长的线段．(3)∵阳光下小丽影子长为1.20 m，树的影子长为2.40 m，小丽身高1.88 m，设树高为x m，∴1.201.88＝2.40x，解得x＝3.76.答：树的高度为3.76 m.13．如图，已知线段AB＝2 cm，投影面为P，太阳光线与地面垂直．(1)当AB垂直于投影面P时(如图1)，请画出线段AB的投影；(2)当AB平行于投影面P时(如图2)，请画出它的投影，并求出正投影的长；(3)在(2)的基础上，点A不动，线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°，请在图3中画出线段AB的正投影，并求出其正投影长．解：(1)如图，点C为所求的投影．(2)如图，线段CD为所求的投影，CD＝2 cm.(3)如图，线段CD为所求的投影，CD＝2cos30°＝ 3 cm.14．如图，校园内有一棵与地面垂直的树，数学兴趣小组两次测量它在地面上的影子，第一次是阳光与地面成60°角时，第二次是阳光与地面成30°角时，两次测量的影长相差8米，求树高AB为多少米．(结果保留根号)解：在Rt△ABD中，∵tan∠ADB＝ABBD，∴BD＝ABtan60°＝AB3.在Rt△ACB中，∵tan∠ACB＝ABBC，∴BC＝ABtan30°＝AB33＝3AB3.∵BC－BD＝8，∴3AB3－AB3＝8.∴AB＝43米．答：树高AB为43米．综合题15．如图，阳光通过窗口照到教室内，竖直窗框在地面上留下2.1 m长的影子，已知窗框的影子DE 到窗下端墙脚的距离CE＝3.9 m，窗口底边离地面的距离BC＝1.2 m，试求窗口(即AB)的高度．解：由于阳光是平行光线，即AE∥BD，∴∠AEC＝∠BDC，又∵∠BCD是公共角，∴△AEC∽△BDC.∴ACBC＝ECDC.又∵AC＝AB＋BC，DC＝EC－ED，EC＝3.9 m，ED＝2.1 m，BC＝1.2 m.∴AB＋1.21.2＝3.93.9－2.1.解得AB＝1.4.答：窗口的高度为1.4 m.。