相交线练习题

人教版七年级数学下册《5.1 相交线》同步练习题-附带答案一、选择题1．同一平面内互不重合的3条直线的交点的个数是（）A．可能是0，1，2 B．可能是0，2，3C．可能是0，1，2或3 D．可能是1，可能是32．下列图形中，∠1=∠2一定成立的是（）A．B．C．D．3．如图，要把小河里的水引到田地A处，则作AB⊥l，垂足为B，沿AB挖水沟，水沟最短．理由是（）A．两点之间，线段最短B．两点确定一条直线C．垂线段最短D．过一点作已知直线的垂线有且只有一条4．如图，将一副三角板顶点O靠在一直尺的边上，若∠AOC=50°，则∠BOD的度数（）A．30°B．40°C．50°D．60°5．如图，两只手的食指和拇指在同一平面内，在以下四种摆放方式中，它们构成的一对角可以看成内错角的是（）A．B．C．D．6．如图AD⊥BC于点D， AB=6，AC=9，AD=5 ，点P是线段BC上的一个动点，则线段AP的长度不可能是（）A．5.5 B．7 C．8 D．4.57．如图，与∠1是同旁内角的是（）A．∠2 B．∠3 C．∠4 D．∠58．如图，直线a，b被直线c所截，∠1与∠2是（）A．同位角B．内错角C．同旁内角D．对顶角二、填空题9．若∠1和∠2是对顶角，∠1＝36°，则∠2的度数是度．10．如图，若∠1+∠2=200°，则∠3=．11．如图，直线AB⊥CD于点O，EF为过点O的直线，∠1＝50°，则∠2的度数为．12．如图，给出下列结论：①∠1与∠2是同旁内角；②∠1与∠3是同位角；③∠1与∠4是内错角；④∠1与∠5是同位角；⑤∠2与∠4是对顶角．其中说法正确的是．（填序号）13．物理中有一种现象，叫折射现象，它指的是当光线从空气射入水中时，光线的传播方向会发生改变．如图，我们建立折射现象数学模型，MN表示水面，它与底面EF平行，光线AB从空气射入水里时发生了折射，变成光线BC射到水底C处，射线BD是光线AB的延长线，∠1=70°，∠2=42°，则∠DBC的度数为°．三、解答题14．如图，直线CD与EF交于点O，OC平分∠AOF，若∠AOE=40°，求∠DOE的度数．15．如图，直线AB，CD相交于点O，OM⊥AB于点O.（1）若∠BOC=4∠AOC，求∠BOD的度数.（2）若∠1=∠2，请判断ON与CD关系，并说明理由.∠COF．16．如图，已知直线EF与AB交于点M，与CD交于点O，OG平分∠DOF，若∠COM=120°，∠EMB= 12（1）求∠FOG的度数；（2）写出一个与∠FOG互为同位角的角；（3）求∠AMO的度数．参考答案1．C2．C3．C4．B5．C6．D7．D8．A9．3610．80°11．40°12．①②⑤13．2814．解：∵∠AOE=40°∴∠AOF=140°．∵OC平分∠AOF∠AOF=70°∴∠COF=12∴∠DOE=∠COF=70°15．（1）解：由邻补角的定义，得∠AOC+∠BOC＝180°∵∠BOC＝4∠AOC∴4∠AOC+∠AOC＝180°∴∠AOC＝36°由对顶角相等，得∠BOD＝∠AOC＝36°；（2）解：ON⊥CD，理由如下：∵OM⊥AB∴∠AOM＝90°∴∠1+∠AOC＝90°∵∠1＝∠2∴∠2+∠AOC＝90°即∠NOC＝90°∴ON⊥CD.16．（1）解：∵∠COM=120°∴∠DOF=120°∵OG平分∠DOF∴∠FOG=60°（2）解：与∠FOG互为同位角的角是∠BMF （3）解：∵∠COM=120°∴∠COF=60°∠COF∵∠EMB= 12∴∠EMB=30°∴∠AMO=30°。

人教版七年级下学期数学-5.1相交线练习题一、单选题1．如图，河道的同侧有、两地，现要铺设一条引水管道，从地把河水引向、两地．下列四种方案中，最节省材料的是（）A．B．C．D．2．如图，直线AB、CD相交于O，且∠AOC=2∠BOC，则∠AOD的度数为（）A．30°B．45°C．60°D．75°3．如图，直线AB，CD相交于点O，，OF平分，则的大小为（）A．40°B．50°C．65°D．70°4．如图，在中，，，垂足为点D，那么点A到直线的距离是线段（）的长．A．B．C．D．5．如图，直线AB，CD，EO相交于点O，已知OA平分∠EOC，若∠EOC：∠EOD＝2：3，则∠BOD 的度数为（）A．40°B．37°C．36°D．35°6．如图所示，与∠α构成同位角的角的个数为()A．1B．2C．3D．47．在下列语句中，正确的是（）．A．在平面上，一条直线只有一条垂线;B．过直线上一点的直线只有一条;C．过直线上一点且垂直于这条直线的直线有且只有一条;D．垂线段的长度就是点到直线的距离8．平面上三条直线两两相交最多能构成对顶角的对数是（）.A．7B．6C．5D．49．如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（）①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD ＝∠BOC.A．①②③B．①②④C．①③④D．②③④10．如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有()A．1个B．2个C．3个D．4个二、填空题11．已知直线AB与直线CD相交于点O，∠AOC：∠BOC＝2：1，射线OE⊥CD，则∠AOE的度数为．12．如图，直线AB、CD、EF相交于点O，若∠1+∠2＝150°，则∠3＝°．13．如图，直线AB、CD相交于点O，OE平分，OF平分．若，则的度数为°．14．若与是对顶角，与互余，且，则的度数为°.15．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM.若∠AOM＝35°，则∠CON的度数为.三、计算题16．如图，O为直线AB上一点，OC⊥AB，并且∠AOD＝130°．求∠COD的度数．17．如图所示，直线AB、CD、EF相交于点O，CD⊥AB，∠AOE：∠AOD=3：5，求∠BOF与∠DOF的度数.四、综合题18．如图，在所标注的角中．（1）对顶角有对，邻补角有对；（2）若，，求与的度数．19．如图，点在直线外，点在直线上，连接．选择适当的工具作图．（1）在直线上作点，使，连接；（2）在的延长线上任取一点，连接；（3）在，，中，最短的线段是，依据是．20．如图，直线、相交于点，且平分，平分.（1）求证：平分；（2）求的度数.答案解析部分1．【答案】D【解析】【解答】解：依据垂线段最短，以及两点之间，线段最短，可得最节省材料的是：故答案为：D．【分析】利用垂线段最短，以及两点之间线段最短求解即可。

初一数学相交线与平行线28道典型题（含答案和解析及考点）1、若直线AB,CD相交于O，∠AOC与∠BOD的和为200°，则∠AOD的度数为．答案：80°.解析：∵∠AOC=∠BOD，∠AOC与∠BOD的和为200°.∴∠AOC=100°.∵∠AOD与∠AOC互补.∴∠AOD=80°.考点：几何初步——相交线与平行线——对顶角、邻补角.2、已知OA⊥OB，∠AOC∶∠AOB=2∶3，则∠BOC= ．答案：30°或150°.解析：当OC在∠AOB内部时，∠BOC=30°；当OC在∠AOB外部时，∠BOC=150°.考点：几何初步——相交线与平行线——对顶角、邻补角——垂线.3、若直线a与直线b相交于点A，则直线b上到直线a距离等于2cm的点的个数是（）．A.0B.1C.2D.3答案：C.解析: 直线b的交点两侧各有一点到直线a的距离等于2cm.考点：几何初步——相交线与平行线——点到直线的距离.4、如图所示，在平面内，两条直线l1、l2相交于点O，对于平面内任意一点M，若p、q分别是点M到直线l1、l2的距离，则称（p,q）为点M的“距离坐标”．根据上述规定，“距离坐标”是（2,1）的点共有个．答案：4.解析：因为两条直线相交有四个角，因此每一个角内就有一个到直线l1、l2的距离分别是2、1，的点，即距离坐标是（2,1）的点，因而共有4个．考点：几何初步——相交线与平行线——点到直线的距离.5、若∠1和∠2是同旁内角，若∠1=50°，则∠2的度数为（ ）． A.45° B.135° C.45°或135° D. 不能确定 答案：D.解析：若∠1和∠2是同旁内角，若∠1=50°，则∠2的度数为不能确定． 考点：几何初步——相交线与平行线——三线八角.6、平面上n 条直线最少能将平面分为__________部分，最多能将平面分为__________部分． A. 最少能将平面分成n+1部分；最多分为n2+n+22.B. 最少能将平面分成n+2部分；最多分为n2+n−22.C. 最少能将平面分成n+1部分；最多分为n2+n−22. D. 最少能将平面分成n+2部分；最多分为n2−n+22.答案：A.解析：1条直线将平面分成2部分.2条直线最少将平面分成3部分，最多将平面分成4部分，其中4=1+1+2. 3条直线最少将平面分成4部分，最多将平面分成7部分，其中7=1+1+2+3. 4条直线最少将平面分成5部分，最多将平面分成11部分，其中11=1+1+2+3+4. ……n 条直线最少将平面分成n+1部分，最多将平面分成n2+n+22部分，其中n2+n+22=1+1+2+3+…+n .综上，n 条直线最少能将平面分成n+1部分,对多能将平面分成n2+n+22部分．考点：几何初步——相交线与平行线——相交线.7、如图，已知∠1=∠2，要使∠3=∠4，则需（ ）．A. ∠1=∠2B. ∠2=∠4C. ∠1=∠4D. AB ∥CD答案：D.解析：假设∠3=∠4，即∠BEF=∠CFE.由内错角相等，两直线平行，可得AB∥CD.故已知∠1=∠2，要使∠3=∠4，只要AB∥CD.考点：几何初步——相交线与平行线——平行线公理及推论.8、如图①是长方形纸带，将纸带沿EF折叠成图②，再沿BF折叠成图③．（1）若图①中的∠DEF=20°，则图②中的∠CFE度数是．（2）若图①中的∠DEF=α，则图③中的∠CFE度数是．（用含有α的式子表示）答案：（1）160°.（2）180°-3α.解析：（1）在图①中：∵AD∥BC.∴∠BFE=∠DEF=20°.∴∠CFE=160°.在图②中，根据折叠性质，∠CFE大小不变.∴∠CFE=160°.（2）在图①中，∠CFE=180°-∠BFE=180°-α.在图②中，∠CFB=∠CFE-∠BFE=180°-α.根据折叠性质，图③中∠CFB与图②中∠CFB相等.在图③中，∠CFE=∠CFB-∠BFE=180°-3α.∴图③中的∠CFE度数是180°-3α.考点：几何初步——角——角的计算与证明.相交线与平行线——平行线的性质.几何变换——图形的对称——翻折变换（折叠问题）——轴对称基础——轴对称的性质.9、已知：如图，∠D=110°，∠EFD=70°，∠1=∠2.求证：∠3=∠B.证明：∵∠D=110°，∠EFD=70°，（已知）.∴∠D+∠EFD=180°.∴_____∥ _____．（）.又∵∠1=∠2，（已知）.∴_____∥ _____．（）.∴_____∥ _____．（）.∴∠3=∠B．（）.答案：答案见解析．解析：∵∠D=110°，∠EFD=70°，（已知）.∴∠D+∠EFD=180°.∴AD∥EF．（同旁内角互补，两直线平行）.又∵∠1=∠2，（已知）.∴AD∥BC．（内错角相等，两直线平行）.∴EF∥BC．（平行于同一直线的两直线平行）.∴∠3=∠B．（两直线平行，同位角相等）.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.10、车库的电动门栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD的大小是（）．A.150°B.180°C.270°D.360°答案：C.解析：过B作CD的平行线BF，则CD∥BF∥AE.∴∠DCB+∠CBF=180°，∠ABF=90°.∴∠ABC+∠BCD=∠DCB+∠CBD+∠ABF=180°+90°=270°.考点：几何初步——角——角的计算与证明.相交线与平行线——平行线的性质.11、如图，一条公路修到湖边时，需拐弯绕湖而过；如果第一次拐角∠A是120°，第二次拐角∠B是150°，第三次拐角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C是．答案：150°.解析：如图，作BE∥AD.∴∠1=∠A=120°.∴∠2=∠ABC=∠1=150°-120°=30°.∵AD∥CF.∴BE∥CF.∴∠C+∠2=180°.∴∠C=180°-30°=150°.考点：几何初步——相交线与平行线——平行线公理及推论——平行线的性质.12、如图所示，若AB∥CD，则角α，β，γ的关系为（）．A.α+β+γ=360°B.α-β+γ=180°C.α+β+γ=180°D.α+β-γ=180°答案：D.解析：过β角的顶点为E，作EF∥AB，α+β-γ=180°.考点：几何初步——相交线与平行线平行线的判定——平行线的性质——平行有关的几何模型.13、如图AB∥CD∥EF，CG平分∠ACE，∠A=140°，∠E=110°，则∠DCG=（）.A.13°B.14°C.15°D.16°答案：C.解析：∵EF∥CD，∴∠ECD=180°-∠E=70°.同理∠ACD=40°.∴∠ACE=110°.∵CG平分∠ACE.∴∠ECG=55°.∴∠DCG=∠ECD-∠ECG=70°-55°=15°.考点：几何初步——相交线与平行线——平行线——平行线的性质——平行有关的几何模型.14、如图，AB∥EF∥CD，EG平分∠BEF，∠B+∠BED+∠D=192°，∠B-∠D=24°，求∠GEF的度数.A.15°B.20°C.25°D.30°答案：D.解析：由AB∥EF∥CD,可知∠BED=∠B+∠D.已知∠B+∠BED+∠D=192°．∴2∠B+2∠D=192°，∠B+∠D=96°.又∠B-∠D=24°，于是可得关于∠B、∠D的方程组：{∠B+∠D=96°∠B−∠D=24°.解得∠B=60°．由AB∥EF知∠BEF=∠B=60°.因为EG平分∠BEF，所以∠GEF=12∠BEF=30°.考点：几何初步——相交线与平行线——平行线——平行有关的几何模型.15、把命题“在同一平面内，垂直于同一直线的两直线互相平行”改写成“如果……，那么……”的形式：.答案：“在同一平面内，如果两条直线都垂直于同一直线，那么这两直线互相平行”.解析：略.考点：命题与证明——命题与定理.16、下列命题中，假命题是（）．A. 如果两条直线都与第三条直线平行，那么这两条直线也互相平行.B. 两条直线被第三条直线所截，同旁内角互补.C. 两直线平行，内错角相等.D. 在同一平面内，过一点有且只有一条直线与已知直线垂直.答案：B.解析：两条直线被第三条直线所截，同旁内角不一定互补，只有两直线平行时，同旁内角互补．考点：命题与证明——命题与定理.17、已知：如图，AE⊥BC,FG⊥BC，∠1=∠2，∠D=∠3+60°，∠CBD=70°.（1）求证：AB∥CD.（2）求∠C的度数．答案：（1）证明见解析．（2）∠C=25°.解析：（1）∵AE⊥BC,FG⊥BC.∴AE∥FG.∴∠2=∠A.∵∠1=∠2.∴∠1=∠A.∴AB∥CD.（2）∵AB∥CD.∴∠C=∠3.∵∠D=∠3+60°，∠CBD=70°，∠C+∠D+∠CBD=180°.∴∠C+∠C+60°+70°=180°.∴∠C=25°.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.18、已知：如图，在△ABC中，BD⊥AC于点D，E为BC上一点，过E点作EF⊥AC，垂足为F，过点D作DH∥BC交AB于点H．（1）请你补全图形．（2）求证：∠BDH=∠CEF.答案：（1）画图见解析．（2）证明见解析．解析：（1）补全图形.（2）∵BD⊥AC，EF⊥AC.∴BD∥EF.∴∠CEF=∠CBD.∵DH∥BC.∴∠BDH=∠CBD.∴∠BDH=∠CEF.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.尺规作图——过一点作已知直线的垂线——过一点作已知直线的平行线.19、已知，如图，AB∥CD，∠1=∠B，∠2=∠D．求证：BE⊥DE.答案：证明见解析．解析：过E点作EF∥AB，则∠B=∠3.又∵∠1=∠B.∴∠1=∠3.∵AB∥EF，AD∥CD.∴EF∥CD.∴∠A=∠D.又∵∠2=∠D.∴∠2=∠4.∵∠1+∠2+∠3+∠4=180°.∴∠3+∠4=90°，即∠BED=90°.∴BE⊥ED.考点：几何初步——角——角的计算与证明.相交线与平行线——平行线的判定——平行线的性质.20、如图，已知CD∥EF，∠1+∠2=∠ABC.求证：AB∥GF.答案：证明见解析．解析：延长CD、GF交于点H，∠1=∠H.故∠2+∠H=∠ABC.易得AB∥GF.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.21、如图，已知点A，E，B在同一条直线上，设∠CED=x，∠C+∠D=y.（1）若AB∥CD，试用含x的式子表示y，并写出x的取值范围．（2）若x=90°，且∠AEC与∠D互余，求证：AB∥CD.答案：（1）y=180°-x，其中x的取值范围是（0＜x＜180）.（2）证明见解析．解析：（1）∵AB∥CD.∴∠AEC=∠C，∠BED=∠D.∵∠C+∠D=y.∴∠AEC+∠BED=y.∵∠CED=x，∠AEC+∠CED+∠BED=180°.∴x+y=180°.∴y=180°-x，其中x的取值范围是（0＜x＜180）.（2）∵x=90°，即∠CED=90°.∴∠AEC+∠BED=90°.∵∠AEC与∠D互余.∴∠AEC+∠D=90°.∴∠BED=∠D.∴AB∥CD.考点：函数——函数基础知识——函数自变量的取值范围.几何初步——角——余角和补角——角的计算与证明.相交线与平行线——平行线的判定——平行线的性质.22、阅读材料：材料1：如图（a）所示，科学实验证明：平面镜反射光线的规律是：射到平面镜上的光线和反射出的光线与平面镜所夹的角相等．即∠1=∠2.材料2：如图（b）所示，已知△ABC，过点A作AD∥BC，则∠DAC=∠C，又∵AD∥BC，∴∠DAC+∠BAC+∠B=180°，∴∠BAC+∠B+∠C=180°．即三角形内角和为180°.根据上述结论，解决下列问题：（1）如图（c）所示，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b镜反射，若b反射出的光线n平行于m，且∠1=50°，则∠2= ，∠3= .（2）在（1）中，若∠1=40°，则∠3= ，若∠1=55°，则∠3= .（3）由（1）（2）请你猜想：当∠3= 时，任何射到平面镜a上的光线m经过平面镜a和b的两次反射后，入射光线m与反射光线n总是平行，请说明理由．答案：（1）1．100°.2．90°.（2）1．90°.2．90°.（3）90°.解析：（1）∵∠1=50°.∴∠4=∠1=50°.∴∠6=180°-50°-50°=80°.∵m∥n.∴∠2+∠6=180°.∴∠2=100°.∴∠5=∠7=40°.∴∠3=180°-50°-40°=90°.故答案为：100°，90°.（2）∵∠1=40°.∴∠4=∠1=40°.∴∠6=180°-40°-40°=100°.∵m∥n.∴∠2+∠6=180°.∴∠2=80°.∴∠5=∠7=50°.∴∠3=180°-50°-40°=90°.∵∠1=55°.∴∠4=∠1=55°.∴∠6=180°-55°-55°=70°.∵m∥n.∴∠2+∠6=180°.∴∠2=110°.∴∠5=∠7=35°.∴∠3=180°-55°-35°=90°.（3）当∠3=90°时，m∥n.理由是：∵∠3=90°.∴∠4+∠5=180°-90°=90°.∵∠4=∠1，∠7=∠5.∴∠1+∠7+∠4+∠5=2×90°=180°.∴∠2+∠6=180°-（∠1+∠4）+180°-（∠5+∠7）=180°.∴m∥n.故答案为：90°.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.23、如图，直线AC∥BD，连接AB，直线AC,BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA,PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）（1）如图1，当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD.，（2）如图2，当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（请画出图形并直接回答成立或不成立）（3）如图3，当动点P落在第③部分时，探究∠PAC，∠APB，∠PBD之间的关系，请画出图形并直接写出相应的结论．答案：（1）证明见解析．（2）不成立．（3）证明见解析．解析：（1）过点P作直线AC的平行线，易知∠1=∠PAC，∠2=∠PBD.又∵∠APB=∠1+∠2，∴∠APB=∠PAC+∠PBD．（2）不成立．（3）①当动点P在射线BA的右侧时（如图4）.结论是∠PBD =∠PAC+∠APB.②当动点P在射线BA上（如图5）.结论是∠PBD =∠PAC+∠APB或∠PAC =∠PBD +∠APB或∠APB=0°，∠PAC=∠PBD.③当动点P在射线BA的左侧时（如图6）.结论是∠PAC =∠PBD +∠APB.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质——平行有关的几何模型.24、如图所示，在下列条件中：①∠1=∠2；②∠BAD=∠BCD；③∠3=∠4且∠ABC=∠ADC；④∠BAD+∠ABC=180°；⑤∠ABD=∠ACD；⑥∠ABC+∠BCD=180°．能判定AB∥CD的共有（）个．A.2B.3C.4D.5答案：A.解析：由平行的判定知③⑥可以判定AB∥CD.考点：几何初步——相交线与平行线——平行线的判定.25、有下列四个命题：①如果两条直线都与第三条直线平行，那么这两条直线也互相平行.②两条直线被第三条直线所截，同旁内角互补.③在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线也互相垂直.④在同一平面内，过一点有且只有一条直线与已知直线垂直.其中所有正确的命题是（）．A. ①②B. ①④C. ②③D. ③④答案：B.解析：①④正确；②两条直线被第三条直线所截，同旁内角不一定互补，需要两条直线平行；③在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线互相平行． 考点：几何初步——相交线与平行线——平行线公理及推论——平行线的判定——平行线的性质.26、如图，DB ∥FG ∥EC ，∠ABD=60°，∠ACE=30°，AP 平分∠BAC ，求∠PAG 的度数.A.11°B.12°C.13°D.14°答案：B.解析：由DB ∥FG ∥EC.可得∠BAC=∠BAG+∠CAG=∠DBA+∠ACE=60°+36°=96°.由AP 平分∠BAC 得∠CAP=12∠BAC=12×96°=48°. 由FG ∥EC 得∠GAC=∠ACE=36°.∴∠PAG=48°-36°=12°.考点：几何初步——相交线与平行线——平行线——平行有关的几何模型.27、如图，AB ∥CD ，且∠BAP=60°-α，∠APC=45°+α，∠PCD=30°-α，则α=（ ）．A.10°B.15°C.20°D.30°答案：B.解析：得∠APC=∠BAP+∠DCP .∴45°+α=60°-α+30°-α.解得：α=15°.考点：几何初步——相交线与平行线——平行线的性质.28、已知，如图，AB∥CD，直线α交AB、CD分别于点E、F，点M在线段EF点上，P是直线CD 上的一个动点，（点P不与F重合）.（1）当点P在射线FC上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：.（2）当点P在射线FD上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：. 答案：（1）∠FMP+∠FPM=∠AEF.（2）∠FMP+∠FPM+∠AEF=180°.解析：（1）当点P在射线FC上移动时.∵AB∥CD.∴∠AEF+∠CFE=180°.又∵∠FMP+∠FPM+∠CFE=180°.∴∠FMP+∠FPM=∠AEF.（2）当点P在射线FD上移动时.∵AB∥CD.∴∠AEF=∠MFD.又∵∠FMP+∠FPM+∠CFE=180°.∴∠FMP+∠FPM+∠AEF=180°.考点：几何初步——相交线与平行线——平行线的性质.。

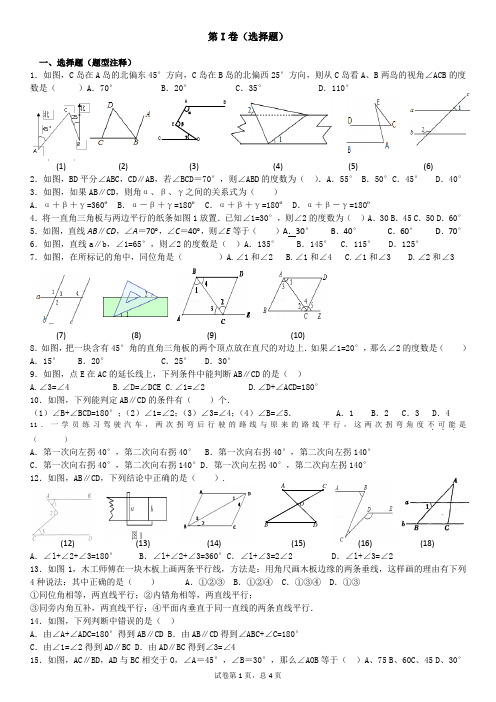
相交线与平行线练习题一、选择题1. 两条直线相交成直角，这两条直线叫做互相（）。

A. 垂直B. 平行C. 相交D. 重合2. 同一平面内，不相交的两条直线叫做（）。

A. 垂直线B. 平行线C. 相交线D. 重合线3. 直线a和直线b相交，如果a与b的交点是A，那么a和b的交点A叫做（）。

A. 交点B. 垂足C. 端点D. 焦点4. 如果直线a和直线b平行，那么a与b之间的距离（）。

A. 相等B. 不相等C. 无法确定D. 为零5. 两条直线被第三条直线所截，如果同侧的内错角相等，那么这两条直线（）。

A. 平行B. 垂直C. 相交D. 重合二、填空题6. 如果两条直线相交所构成的同位角不相等，那么这两条直线_________。

7. 两条平行线之间的距离是指这两条平行线中任意一点到另一条平行线的_________。

8. 两条直线相交，如果它们的交角是锐角，那么这两条直线_________。

9. 在同一平面内，如果两条直线都与第三条直线平行，那么这两条直线也_________。

10. 当两条直线相交，如果它们的对顶角相等，那么这两条直线_________。

三、判断题11. 如果两条直线相交成直角，那么这两条直线一定平行。

（）12. 两条直线相交，它们的交点只有一个。

（）13. 两条直线相交所成的同旁内角互补，那么这两条直线一定垂直。

（）14. 两条直线平行，同位角相等，内错角相等，同旁内角互补。

（）15. 如果两条直线被第三条直线所截，同位角不相等，那么这两条直线不平行。

（）四、简答题16. 解释什么是平行线，并给出两条直线平行的判定条件。

17. 描述什么是垂线，并说明垂线的性质。

18. 给出两条直线相交时，同位角、内错角和对顶角的定义。

19. 解释什么是相交线，并描述相交线的性质。

20. 举例说明如何判断两条直线是否平行。

五、解答题21. 在平面直角坐标系中，直线l1的方程为y=2x+3，直线l2的方程为y=-x+1。

相交线与平行线专项练习题一、选择题：1.如图，DE ∥AB ，∠CAE=31∠CAB ，∠CDE=75°，∠B=65°则∠AEB 是 ( ) A ．70° B ．65° C ．60° D ．55°1题 2题 3题 4题2.如图所示，∠1的邻补角是( )A.∠BOCB.∠BOE 和∠AOFC.∠AOFD.∠BOC 和∠AOF3.如图所示，内错角共有( )A.4对B.6对C.8对D.10对4.如图，直线a 、b 被直线c 所截，现给出下列四个条件：（1）∠1=∠5；（2）∠1=•∠7；（3）∠2+∠3=180°；（4）∠4=∠7，其中能判定a ∥b 的条件的序号是（ ）A ．（1）、（2）B ．（1）、（3）C ．（1）、（4）D ．（3）、（4）5.如图，点E 在BC 的延长线上，在下列四个条件中，不能判定AB ∥CD 的是( )A.∠1=∠2B.∠B=∠DCEC.∠3=∠4D.∠D+∠DAB=180°5题 6题7题 8题6.如图，如果AB ∥CD ，则α、β、γ之间的关系为 ( )A.α+β+γ=360°B.α-β+γ=180°C.α+β-γ=180°D.α+β+γ=180°7.如图，AB ∥CD ，那么∠A ，∠P ，∠C 的数量关系是( )A.∠A+∠P+∠C=90°B.∠A+∠P+∠C=180°C.∠A+∠P+∠C=360°D.∠P+∠C=∠A8.如图，AB ∥CD ，∠ABF=32∠ABE ，∠CDF=32∠CDE ，则∠E ∶∠F 等于（ ） A ．2：1 B ．3：1 C ．3：2 D ．4：39.如图，AB ⊥EF ，CD ⊥EF ，∠1=∠F=45°，那么与∠FCD 相等的角有（ ）B DE 1 3 A CF 2 A ．1个 B ．2个 C ．3个 D ．4个二、填空题：10.观察图中角的位置关系，∠1和∠2是______角，∠3和∠1是_____角，∠1•和∠4是_______角，∠3和∠4是_____角，∠3和∠5是______角.10题11题12题13题11.如图，已知CD ⊥AB 于D ，EF ⊥AB 于F ，∠DGC=105°，∠BCG=75°，则∠1+∠2=____度．12.如图，AB ∥CD ，∠BAE = 120º，∠DCE = 30º，则∠AEC = 度。

相交线练习题目在几何学中，相交线是指平面上的两条线段或射线相交的点。

相交线的研究在解决各种几何问题时起着重要的作用。

本篇文章将提供一些相交线的练习题目，帮助读者巩固对相交线的理解和运用。

1.求解相交线交点的坐标已知平面上两条直线的方程分别为:直线L1：y = 2x + 3直线L2：y = -x + 5求解直线L1和直线L2的交点坐标。

解答：将两条线段的方程联立起来，解得：2x + 3 = -x + 53x = 2x = 2/3将x的值代入其中一条线段方程，求得y的值：y = -x + 5y = -(2/3) + 5y = 13/3因此，直线L1和直线L2的交点坐标为(2/3, 13/3)。

2.判断直线是否相交已知平面上存在三条直线，方程分别为:直线L1：y = 2x + 1直线L2：y = -x + 3直线L3：y = 2x - 1判断直线L1、L2和L3是否相交。

解答：直线L1和直线L2的斜率分别为2和-1，斜率不相等，因此直线L1和直线L2相交。

直线L1和直线L3的斜率均为2，斜率相等，但截距不相等，因此直线L1和直线L3相交。

直线L2和直线L3的斜率均为-1，斜率相等，且截距也相等，因此直线L2和直线L3重合。

综上所述，直线L1、L2和L3相交的情况是：直线L1和L2相交，直线L1和直线L3相交，直线L2和L3重合。

3.求解相交线的夹角已知平面上两条直线的方程分别为:直线L1：y = 2x + 1直线L2：y = -x + 3求解直线L1和直线L2的夹角。

解答：直线L1的斜率为2，直线L2的斜率为-1。

两条直线的夹角公式为：tan(α) = (m2 - m1) / (1 + m1 * m2)其中，α表示直线L1和直线L2之间的夹角，m1和m2分别表示直线L1和直线L2的斜率。

将斜率代入公式，计算得到：tan(α) = (-1 - 2) / (1 + 2 * (-1))= -3 / (-1)= 3因此，直线L1和直线L2的夹角为tan^(-1)(3)，约等于71.57度。

相交线一、知识点复习知识点一：邻补角的概念两个角有一条公共边，它们的另一边互为反向延长线，具有这种关系的另个角称互为邻补角。

知识点二：对顶角的概念和性质1.对顶角的概念：如果两个角有一个公共顶点，并且它们的两边分别互为反向延长线，那么这样的两个角叫做对顶角。

2.对顶角的性质：对顶角相等。

知识点三：垂直1.垂直的概念：在两条直线AB和CD相交所成的4个角中，如果有一个角是直角，就说这两条直线互相垂直，记作“CDAB ”，读作“AB垂直于CD”，其中一条直线叫做另一条直线的垂线，它们的交点O叫做垂足。

2.垂线的画法：经过一点，画已知直线的垂线，步骤如下：①靠线：让直角三角板的一条直角边与已知直线重合；②过点：沿直线移动，使直角三角板的另一条直角边经过已知点；③画线：沿直角边画线，则这条直线就是经过这个点的已知直线的垂线。

知识点四：垂直的基本事实及性质1.基本事实：过一点有且只有一条直线垂直于已知直线。

2.性质：垂线段最短。

知识点五：点到直线的距离直线外一点到这条直线的垂线段的长度叫做点到直线的距离。

二、例题讲解1.（2017春武清区期中）平面内三条直线的交点个数可能有（）A、1个或3个B、2个或3个C、1个或2个或3个D、0个或1个或2个或3个2.（2017春河北期末）在图中，1∠是对顶角的是（）∠和23.（2017秋昌平区期末）如图，想在河堤两岸搭建一座桥，图中四种搭建方式,PA,,,最短的是。

PDPBPC4.（2017春宁河县期中）如图是小凡同学在体育课上跳远后留下的脚印，他的跳远成绩是线段的长度，这样测量的依据是。

5.（2017春召陵区期中）若点A到直线l的距离为cm7，点B到直线l的距离为3，则线段AB的长度为（）cmA.cm4 D.至少cm44 C.cm10或cm10 B.cm6.（2017春海安县校级月考）如图，P为直线l外一点，C,在l上，且lA,BPB⊥，下列说法中，正确的个数是（）①PC,三条线段中，PB最短；②线段PB的长叫做点P到直线l的距离；PBPA,③线段AB是点A到PB的距离；④线段AC的长是点A到PC的距离。

相交线练习（一）1．判断题（对的打“√”，错的打“×”）（1）没有公共边的两个角是对顶角.（）（2）有公共顶点的两个角是对顶角.（）（3）两条直线相交所成的四个角中，不相邻的两个角是对顶角.（）（4）有公共顶点且有一条公共边的两个角互为邻补角.（）（5）对顶角的补角相等.（）2．填空（1）对顶角的重要性质是 .（2）一条直线与端点在这条直线上的一条射线组成的两个角是 .（3）两个角互为邻补角，它们的平分线所成的角是度.（4）如图2—11，直线AB、CD、EF相交于点O，则∠AOC的对顶角是，∠AOD的对顶角是，∠BOC的邻补角是和，∠BOE的邻补角是和 .3．如图2—12直线AB、CD、EF相交于点O，且∠1=∠2，试说明OE是∠AOC的平分线.4．选择题（1）下列说法正确的是（）A．有公共顶点，且方向相反的两个角为对顶角B．有公共顶点，且又相等的角为对顶角C．角的两边互为反向延长线且有公共顶点的两个角为对顶角D．有公共顶点的两个角为对顶角.（2）下列说法正确的是（）A．不是对顶角就不相等 B．相等的角为对顶角C．不相等的角不是对顶角 D．上述说法都不对（3）下列各图中∠1和∠2为对顶角的是（）（4）如果两个角的平分线相交成90°的角，那么这两个角是（）A．对顶角 B．互补的两个角C．互为邻补角 D．以上答案都不对5．已知直线AB、CD相交于点O，∠AOC+∠BOD=230°，求∠BOC的度数.6．如图2—14，已知直线AB、CD、EF相交于点O，∠1：∠2：∠3=2：3：4，求∠4的度数.7．如图2—15，已知直线AB、CD相交于点O，OE平分∠BOD，且∠BOD=10°，求∠AOC的度数.【素质优化训练】1．如图2—16，点O是直线AB上的一点，OC、OD是两条射线且分别在AB的两侧，∠AOC=∠BOD（1）求∠COD的度数；（2）∠AOC与∠BOD是对顶角吗？为什么？2．如果4条不同的直线相交于一点，那么图形中有多少对对顶角呢？如果是n 条不同的直线相交于一点呢？【生活实际运用】如图A、B、C三点表示某平原的三个村庄；要建一个电视转播站，使它到三个村庄距离相等，求作电视转播的位置P.一、判断（每题1分，共10分）1.顶点相同并且相等的两个角是对顶角.( )2.相交直线构成的四个角中若有一个角是直角,就称这两条直线互相垂直.( )10756894321(1)3.直线外一点到这条直线的垂线段叫做这点到这条直线的距离.( ) 4.如图1,∠2和∠8是对顶角.( )5.如图1,∠2和∠4是同位角.( )6.如图1,∠1和∠3是同位角.( )7.如图1,∠9和∠10是同旁内角,∠1和∠7也是同旁内角.( ) 8.如图1,∠2和∠10是内错角.( ) 9.O 是直线AB 上一点,D 分别在AB 的两侧,且∠DOB=∠AOC,则C,O,D•三点在同一条直线上.( )10.如图2,其中共有4对同位角,4对内错角,4对同旁内角.( ) 二、填空（每空1分，共29分）11.如图3,直线L 截直线a,b 所得的同位角有______对,它们是_ _____;•内错有___对,它们是_____ _;同旁内角有______对,•它们 是_____ _;•对顶角_____•对,•它们是_____ _.12.如图4,∠1的同位角是________,∠1的内错角是________,∠1•的同旁内角是_______.13.如图5,直线AB,CD 相交于O,OE 平分∠AOD,FO ⊥OD 于O,∠1=40°,则∠2=•___ __,∠4=______.14.如图6,AB ⊥CD 于O,EF 为过点O 的直线,MN 平分∠AOC,若∠EON=100•°,•那么∠EOB=_____ ,∠BOM=_____ .15.如图7,AB 是一直线,OM 为∠AOC 的角平分线,ON 为∠BOC 的角平分线,则OM,ON 的位置关系是_______.16.直线外一点与直线上各点连结的线段中,以_________为最短.17.从直线外一点到这条直线的____ ____叫做这点到直线的距离.18.经过直线外或直线上一点,有且只有______直线与已知直线垂直.19.如图8,要证BO ⊥OD,请完善证明过程,并在括号内填上相应依据:∵AO ⊥CO,∴∠AOC=__________(___________).又∵∠COD=40°(已知),∴∠AOD=_______.•∵∠BOC=∠AOD=50°(已知),∴∠BOD=_______, ∴_______⊥_______(__________).20.如图9,直线AB,CD 被EF 所截,∠1=∠2,要证∠2+∠4=180°,请完善证明过D C A B NM P(2)Qla75684321b(3)564321AB NM P(4)OQ421D AB (5)OFE D C A BN M (6)OFE C ABN M (7)D C AB(8)O程,•并在括号内填上相应依据.∵直线AB 与EF 相交,∴∠1=∠3=(__________),又∵∠1+•∠4=180°(___________),∠1=∠2(已知), ∴∠2=∠3,∠2+∠4=180°(____________________) 三、选择（每题3分，共30分）. 21.下列语句正确的是( )A.相等的角为对顶角B.不相等的角一定不是对顶角C.不是对顶角的角都不相等D.有公共顶点且和为180°的两个角为邻补角22.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ) A.1 B.2 C.3或2 D.1或2或323.如图10,PO ⊥OR,OQ ⊥PR,能表示点到直线(或线段)的距离的线段有( )A.1条B.2条C.3条D.5条24.如图,OA ⊥OB,OC ⊥OD,则( )A.∠AOC=∠AODB.∠AOD=∠DOBC.∠AOC=∠BODD.以上结论都不对 25.下列说法正确的是( )A.在同一平面内,过已知直线外一点作这条直线的垂线有且只有一条B.连结直线外一点和直线上任一点,使这条线段垂直于已知直线C.作出点P 到直线的距离D.连结直线外一点和直线上任一点的线段长是点到直线的距离 26.如图12,与∠C 是同旁内角的有( ). A.2 B.3 C.4 D.5 27.下列说法正确的是( ).A.两条直线相交成四个角,如果有三个角相等,那么这两条直线垂直.B.两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直.C.两条直线相交成四个角,如果有一对对顶角互余,那么这两条直线垂直.D.两条直线相交成四个角,如果有两个角互补,那么这两条直线垂直. 28.如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是( ) A. 12(∠1+∠2) B. 12∠1 C. 12(∠1-∠2) D.12∠229.已知OA ⊥OC,∠AOB:∠AOC=2:3,则∠BOC 的度数是( )A.30°B.150°C.30°或150°D.以上答案都不对下图中共有30.右图共有几对对顶角（ ） A.18对 B.16对 C.20对 D.22 对 四、作图题（4+3=7分）(10)PQ DCAB(11)O D CAB(12)FEDA31、如图,按要求作出:(1)AE ⊥BC 于E; (2)AF ⊥CD 于F;(3)连结BD,作AG ⊥BD 于G.32、如下左图，一辆汽车在直线形的公路AB 上由A 向B 行驶，M 、N 分别是位于公路AB 两侧的村庄，（1）现在公路AB 上修建一个超市C ，使得到M 、N 两村庄距离最短，请在图中画出点C （2）设汽车行驶到点P 位置时离村庄M 最近；行驶到点Q 位置时，距离村庄N 最近，请在图中公路AB 上分别画出P 、Q 两点的位置。

相交线的练习题一、选择题1. 两条直线相交于一点，该点称为它们的：A. 交点B. 焦点C. 垂足D. 端点2. 在同一平面内，不相交的两条直线称为：A. 平行线B. 垂直线C. 相交线D. 异面直线3. 直线AB与直线CD相交于点O，若∠AOC=45°，则∠BOC的度数是：A. 45°B. 90°C. 135°D. 180°4. 在平面直角坐标系中，直线y=2x与直线y=-3x相交于：A. (0,0)B. (1,-3)C. (2,4)D. (-1,3)5. 若两条直线相交成直角，则这两条直线：A. 平行B. 垂直C. 异面D. 相交二、填空题6. 若直线l1: ax + by + c1 = 0与直线l2: dx + ey + f = 0相交，则它们的交点坐标为________。

7. 当两条直线相交，且其中一个角为直角时，这两条直线的位置关系是________。

8. 在平面直角坐标系中，若直线l1: y = x - 1与直线l2: y = -x + 2相交，则交点的横坐标为________。

9. 若两条直线相交于点P(x, y)，则点P到两直线的________相等。

10. 在平面几何中，若两条直线相交，则它们相交的角的度数之和为________。

三、简答题11. 请简述如何判断两条直线是否相交，并给出相应的几何或代数方法。

12. 在平面直角坐标系中，若已知两条直线的方程，如何求它们的交点坐标？13. 解释什么是垂直线，并给出垂直线相交时的几何特征。

14. 若两条直线相交成30°角，求这两条直线与x轴正方向的夹角。

15. 在平面几何中，若两条直线相交，它们形成的角有哪些可能的组合？四、计算题16. 已知直线l1: 2x - 3y + 6 = 0与直线l2: x + y - 5 = 0，请求它们的交点坐标。

17. 若直线l: 3x + 4y - 12 = 0与x轴相交于点A，与y轴相交于点B，求点A和点B的坐标。