17.2:空间图形与相交线和平行线
- 格式:ppt
- 大小:1.04 MB
- 文档页数:39


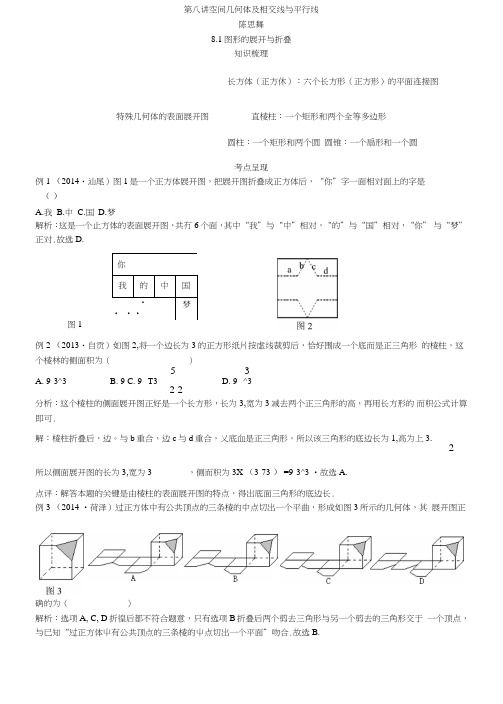
第八讲空间几何体及相交线与平行线陈思舞8.1图形的展开与折叠知识梳理长方体(正方休):六个长方形(正方形)的平面连接图特殊几何体的表面展开图直棱柱:一个矩形和两个全等多边形圆柱:一个矩形和两个圆圆锥:一个扇形和一个圆考点呈现例1 (2014・汕尾)图1是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是()A.我B.中C.国D.梦解析:这是一个止方体的表面展开图,共冇6个面,其中“我”与“中”相对,“的”与“国”相对,“你” 与“梦”正对.故选D.你我的中国• •••梦图1例2 (2013・自贡)如图2,将一个边长为3的正方形纸片按虚线裁剪后,恰好围成一个底而是正三角形的棱柱,这个棱林的侧面积为()_ 5 3A. 9-3^3B. 9C. 9--T3D. 9--^32 2分析:这个棱柱的侧面展开图正好是一个长方形,长为3,宽为3减去两个正三角形的高,再用长方形的而积公式计算即可.解:棱柱折叠后,边。
与b重合,边c与d重合,乂底血是正三角形,所以该三角形的底边长为1,高为上3.2所以侧面展开图的长为3,宽为3- ,侧而积为3X (3-73 ) =9-3^3 •故选A.点评:解答本题的关键是由棱柱的表面展开图的特点,得出底面三角形的底边长.例3 (2014 •荷泽)过正方体中有公共顶点的三条棱的中点切出一个平曲,形成如图3所示的几何体,其展开图正确的为()解析:选项A, C, D折徨后都不符合题意,只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点,与已知“过正方体屮有公共顶点的三条棱的屮点切出一个平面”吻合.故选B.点评:本题考查截一个几何体及几何体的表而展开图,解决此类问题,应考虑带有符号的而的特点及位置. 误区点拨 例(2013 •黄冈)已知一个圆林的侧面展开图为如图1所示的矩形,则其底面圆的面积为()A.TIB.4兀C.71或4兀D.2兀或4兀错解:A.剖析:圆柱的侧而展开图为矩形,圆柱侧而的高是多少? 2TI 或4兀?没有明确,因此两种可能都有, 需要分类讨论.如图2,若以471长为圆柱侧而高,则圆柱的底而圆周长为2兀,底面圆的面积为7T ;如图3,若以2兀 长为圆柱侧面高,则圆柱的底面圆周长为4兀,底面圆的面积为2加正解:C.点评:圆柱的侧面展开图是一个确定的矩形,而由确定的矩形围成圆柱,其形状就不确定了:以矩形 的长还是宽为圆柱侧面的高?又要分类!本例是选择题,选项给了暗示,只要细心观察、分析,能发现隐含的提示. 跟踪训练1.(2013 •温州)下列各图中,经过折叠能围成一个立方体的是()图形的展开与折叠考查平而图形与立体图形之间的转化,要求同学们具备一定的空间想象能力,在解题的 过程屮可以通过观察和动手操作,使问题简化.8. 2三种视图知识梳理2. (2013 •太原)如图是一个长方体包装盒,贝IJ 它的平面展开图是()卜列图形中,能通过折叠围成一个三棱柱的是( )C 第2题图D考点呈现考点1简单物体的视图例1(1) (2014 •安徽)如图1,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视 图是( )(2) (2014 •烟台)图2是一个正方体截去一角后得到的儿何体,它的主视图是( )解析:(1)俯视图是从物体上面看到的图形,选D.(2)主视图是从物体的正面看到的图形,选C.点评:木题考查了儿何体的三种视图,掌握定义是关键. 考点2 组合体的三视图例2 (1) (2014 •徐州)图3是用5个相同的立方块搭成的几何体,其主视图是()图3(2) (2014 •东营)图4是一个由多个相同小正方体堆积而成时儿何体的俯视图,图中所示数字为该位置 小正方体的个数,则这个儿何体的左视图是()视线视角盲区扌殳影回「投影r 基本概念--中心投影-平行投影- -正投影--主视图 从前向后看 -俯视图 从上向下看 -左视图 从左冋右看相关概念一视点长对正回二视图卜 高平齐1宽相等/////7 ////从正面看R解析:(1)从正而看,从左向右分3列,小正方形的个数分别是1, 1, 2,故选D;(2)从左而看,从左向右分3列,小正方形的个数分别是2, 3, 1,故选B.点评:解决此类题的关键是得出视图中每一列小止方形的个数.考点3根据视图描述简单的几何体例3 (1)图5是儿何体的三视图,该儿何体是()A.圆锥B.圆柱C.正三棱柱D.正三棱锥(2)(2014 •福州)某儿何体的三视图如图6所示,贝IJ该儿何体是圆柱D.圆锥解析:(1)选项A, B屮的几何体,三视图屮一定有一个圆,与所给的三视图不符;选项D屮的几何体的三视图是三个三角形,与所给的三视图也不符;只有选项C小的儿何体与所给的三视图相符.故选C;(2)三视图中有一个圆,排除A, B选项,而圆柱的三视图为一个圆少两个长方形,故选D.点评:本题是由三视图想彖出几何体,考查学生的空间想象能力.考点4有关三视图的计算例4 (2014 •广州)一个儿何体的三视图如图7所示,根据图示的数据计算该儿何体的全而积为________________ (结果保留n).图7第3题图4. (2014 •济宁)两个在径分别为36 cm 和16 cm 的球靠在一起放在同一水平面 上,组成如图所示的几何体,则该几何体的俯视图的圆心距是()A. 10 cmB. 24 cmC. 26 cmD. 52 cm211121221解析:由三视图知该儿何体为圆锥,其屮底面直径为6,高为4,所以母线长为V32 +42 =5. 所以底面积为35=911,侧面积为* X6 Ji X5=15 Ji ,所以该儿何体的全面积为15 Ji +9 Ji =24 n .点评:本题将几何体的三视图与全面积结合起來进行考查,既考查了同学们的观察能力,又考查了运用公 式及计算能力.误区点拨例(2013 •绥化市)由一些完全相同的小正方体组成的儿何体的主视图和俯视图如 图所示,则组成这个几何体的小正方体的个数可能是 ___________ .错解:5.图1剖析:不画图,凭空想彖,有难度,若在俯视图中尝试标注小正方体个数,如何?正解:易知这个几何体共2层,由俯视图可得最低层有3个小正方体,由主视图可得上血一层第1列 有1个或2个立方体(如图2),那么共有4或5个小正方体组成.答案为4或5.点评:本例对空间想象能力要求较高,通过画图,借助几何直观帮助分析、推理, 是解决此类问题的一个好方法.图2跟踪训练1. (2014 •赤峰)下面儿何体屮,主视图是三角形的是( )第1题图2. (2014 •海南)如图所示几何体的俯视图是()3. (2014 •鄂州)如图,几何体是由一些正方体组合而成的立体图形,则这个几何体的左视图是()匸视图俯视图主第4题图水平面笫5题图5.一个长方位:cin)12体的主视可以得出2(2014 •扬州)如图,这是图与俯视图,由图示数据(单该长方体的体积为cm\技法指导1.抓住图”概念的本质,其投影方向分別是从前向后、从左向右和从冷2.画三视图的法则是“主俯长对■正、主左高平齐、俯左宽相等”,主视图俯视图2的棱要在三视图屮表现出來,实际看到的用实线,看不到的用第7题图& 3相交线打平行线图、左视图和俯视上向下;另外需注意所有虚线.相交线与平行知识梳理考点呈现考点1有关概念例1(1)(2014 •凉山)下列图形'I', Z1与Z2是对顶角的是()(2)(2014 •海南)如图2,已知AB〃CD,与Z1是同位角的角是()A. Z2B. Z3C. Z4D. Z5(3) (2013 •六盘水)直尺与三角尺按如图3所示的方式叠放在一起,在图中所标记的角中,与Z1互余 的角有()A. 2个B. 3个C. 4个D. 5个解析:(1)根据对•顶角的概念“有公共顶点,且两边互为反向延长线”,对各选项进行分析判断,选C ;(2) 根据同位角的概念“两角在第三条直线的同旁,同在被截两条直线的上方或下方”,可知Z1与Z5 互为同位角•故选D ;(3) 根据余角的概念“两角之和为90。



空间几何的相交和平行关系空间几何是研究三维形体的相对位置和关系的学科,而其中最基本和重要的概念之一就是相交和平行关系。
在本文中,我们将探讨这两个概念的含义以及它们在空间几何中的应用。
1. 相交关系相交关系是指两个或多个图形在空间中有交集的情况。
具体来说,当两个或多个图形的部分或全部相互穿越时,我们可以说它们相交。
在空间几何中,常见的相交关系有以下几种:1) 点与直线的相交:当一条直线与一个点相交,即该点在直线上,我们可以说点与直线相交。
2) 点与平面的相交:当一个点与一个平面相交,即该点在平面上,我们可以说点与平面相交。
3) 直线与直线的相交:当两条直线在空间中有一个公共点时,我们可以说它们相交。
4) 直线与平面的相交:当一条直线与一个平面有一个公共点时,我们可以说它们相交。
5) 平面与平面的相交:当两个平面在空间中有一条直线作为它们的交集时,我们可以说它们相交。
相交关系在几何推理和几何证明中起着重要的作用。
通过分析图形的相交关系,我们可以得出很多有用的结论和性质,进而解决问题。
2. 平行关系平行关系是指两个或多个图形在空间中没有交集的情况。
具体来说,当两个或多个图形的部分或全部没有交点时,我们可以说它们平行。
在空间几何中,常见的平行关系有以下几种:1) 直线与直线的平行:当两条直线在空间中没有交点,且它们的方向相同或重合时,我们可以说它们平行。
2) 直线与平面的平行:当一条直线与一个平面没有交点,且这条直线在这个平面上的任意一条平行线上时,我们可以说它们平行。
3) 平面与平面的平行:当两个平面没有交集,且它们的法向量平行时,我们可以说它们平行。
平行关系在几何推理和几何证明中也是非常重要的。
通过研究图形的平行性质,我们可以得出很多结论和性质,从而解决各种实际问题。
总结:空间几何中的相交和平行关系是非常基础且重要的概念。
相交关系指的是两个或多个图形在空间中有交集,而平行关系指的是两个或多个图形在空间中没有交集。
空间几何中的平行线与交线在空间几何中,平行线与交线是重要的概念。
平行线指在同一个平面内永不相交的直线,而交线则是指平行线的交点或者多个直线的交点。
本文将探讨平行线与交线在空间几何中的性质和应用。
一、平行线的性质和判定在空间几何中,平行线具有以下性质:1. 平行线在同一个平面内,不会相交。
2. 平行线的斜率相等,或者说它们的方向相同。
3. 平行线之间的距离始终保持相等。
如何判定两条直线是否平行呢?在平面几何中,可以通过直线的斜率来判断两条直线是否平行。
如果两条直线的斜率相等且不相交,则可以判定它们是平行线。
然而,在空间几何中,直线没有斜率的概念,我们需要借助向量的概念来判断。
假设有两条直线L1和L2,可将它们表示为向量形式,分别记作→L1 = (x1, y1, z1) 和→L2 = (x2, y2, z2)。
如果两条直线的方向向量比例相等,即 x1/x2 = y1/y2 = z1/z2,那么我们可以判断这两条直线是平行的。
二、交线的性质和应用1. 平面内直线的交线在同一个平面内,两条直线的交线可以是一个点、一条直线或者不存在。
当两条直线的斜率不相等时,它们在平面内一定会相交于一点。
这个点即为两条直线的交点。
当两条直线的斜率相等时,它们可能相交于一点或者不存在交点。
当两条直线完全重合时,它们将有无限多个交点,也就是一条直线。
2. 空间直线的交线在空间几何中,不同平面内的直线相交所得到的交线将是一条直线。
这条直线既属于其中一个平面,也属于另一个平面。
三、平行线与交线的应用平行线与交线的应用广泛存在于实际生活和各个学科领域中,下面以几个具体的应用来说明:1. 建筑学中的应用:在建筑设计中,平行线的应用非常常见。
比如,在设计斜屋顶时,需要满足斜屋顶的梁柱之间是平行的,这样才能保证斜屋顶的稳定和美观。
此外,如果设计一个城市规划,需要考虑城市街道的平行布局,以方便交通和行走。
2. 数学和物理学中的应用:在数学和物理学中,平行线和交线有着广泛的应用。