北师大版七年级数学下册第二章相交线与平行线全套

北师大版七年级下册第二单元相交线与平行线单元——平行线的性质（全章知识梳理与考点分类讲解）【知识点一】平行线的判定方法11.方法1：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简称为：同位角相等，两直线平行.2.表达方式：因为∠1=∠2,（已知）所以a//b（同位角相等，两直线平行）特别提醒：“同位角相等，两直线平行”是通过两个同位角的大小关系（相等）推导出两直线的位置关系（平行）.它是构建起角的大小关系与直线的位置关系的桥梁.【知识点二】平行线的画法过直线外一点画已知的直线平行线的步骤一落：把三角尺的一边落在一直的直线上；二靠：紧靠三角尺的另一边放一直尺；三移：把三角尺沿着直尺移动使其经过已知点；四画：沿三角尺的一边画直线.此直线即为已知直线的平行线.特别提醒：1.经过直线上一点不可以作已知直线的平行线.2.画线段或射线的平行线是画它们所在直线的平行线.3.移动是要始终保持紧靠.【知识点三】平行线的性质及其推论1.平行线的性质：过直线外一点有且只有一条直线与这条直线平行.2.表达方式：如果a//b,b//c,那么a//b.特别提醒：平行线的性质的前提是“过直线外一点”，若点在直线上，则不可能有平行线.【考点目录】【平行线性质求角的等量关系】【考点1】同位角相等两直线平行；【考点2】内错角相等两直线平行；【考点3】同旁内角互补两直线平行；【平行线性质探究角的关系】【考点4】平行线判探究角的关系或求角度；【平行线性质性质与判定综合】【考点5】平行线判定与性质求角度；【考点6】平行线判定与性质证明;【平行线间的距离】【考点7】平行线间的距离（应用）.【平行线性质求角的等量关系】【考点1】同位角相等两直线平行【答案】相等；理由见分析【分析】根据平行投影可得∠B＝∠E，再根据垂直可得∠C＝∠F＝90°，然后利用“角边角”证明△ABC 和△DEF全等，根据全等三角形对应边相等即可得证．解：两根旗杆的高度相等．理由如下：∵太阳光线AB与DE是平行，∴∠B＝∠E，∵两根旗杆都垂直于地面放置，∴∠C＝∠F＝90°，∵两根旗杆在太阳光下的影子一样长，∴BC ＝EF ，∵在△ABC 和△DEF 中B E BC EF C F ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝∴△ABC ≌△DEF （ASA ），∴AC ＝DF ，即两根旗杆的高度相等．【点拨】本题考查了全等三角形的应用，根据题意找出三角形全等的条件，然后证明两三角形全等是解题的关键．【变式1】（2023·黑龙江齐齐哈尔·统考中考真题）如图，把一块三角板的30︒角顶点A 放在直尺的一边BC 上，若1:23:7∠∠=，则2∠=（）A ．126︒B ．118︒C ．105︒D ．94︒【答案】C 【分析】根据平行线的性质和平角的定义即可得到结论．解：如图，由题意知：DE BC ∥，∴31∠=∠，∵1:23:7∠∠=，∴3:23:7∠∠=，∴3327∠=∠，∵2330180∠+∠+︒=︒，∴322301807∠+∠+︒=︒，∴2105∠=︒．故选：C ．【点拨】本题考查的是平行线的性质和平角的定义．熟练掌握两直线平行，同位角相等是解题的关键．【变式2】（2022·甘肃嘉峪关·校考一模）如图两平行线a、b被直线l所截，且∠1=60°，则∠2的度数为.【答案】60°/60度【分析】由a∥b，根据两直线平行，同位角相等，即可求得∠3=∠1=60°，又由对顶角相等，即可求得答案．解：∵a∥b，∴∠3=∠1=60°，∴∠2=∠3=60°．故答案为：60°．【点拨】此题考查了平行线的性质．此题比较简单，注意掌握数形结合思想的应用．【考点2】内错角相等两直线平行【例2】（2014下·贵州铜仁·七年级统考期末）已知：如图，点D、E分别在AB、BC上，DE AC∥，165∠=︒，265∠=︒，请说明：F CBF ∠=∠．（不必注明依据）【答案】证明见分析【分析】根据平行线的性质得出165C ∠=∠=︒，得出2C ∠=∠，根据平行线的判定得出AF BC ∥，再根据平行线的性质即可得证．解：∵DE AC ∥，165∠=︒，265∠=︒，∴165C ∠=∠=︒，∴2C ∠=∠，∴AF BC ∥，∴F CBF ∠=∠．【点拨】本题考查平行线的判定和性质，能灵活运用平行线的性质和判定定理进行推理是解题的关键．【变式1】（2023·吉林白城·校联考三模）已知，如图，AB ∥CD ，∠A=70°，∠B=40°，则∠ACD=（）A ．55°B ．70°C ．40°D ．110°【答案】B解：AB CD ∥.A ACD ∴∠=∠70.A ∠=︒ 70.ACD ∠=︒故选B.【点拨】两直线平行，内错角相等.【变式2】（2023·辽宁阜新·统考中考真题）如图，直线a b ，直线l 与直线a 相交于点P ，直线l 与直线b 相交于点Q ，PM l ⊥于点P ，若155∠=︒，则2∠=.︒【答案】35【分析】本题主要考查平行线性质以及垂线的性质．根据平行线性质得3155∠=∠=︒，利用垂线性质即可求得2∠．解：直线a b ，3155∴∠=∠=︒，又PM l ⊥ 于点P ，90MPQ ∴∠=︒，2903905535∴∠=︒-∠=︒-︒=︒．故答案为：35．【考点3】同旁内角互补两直线平行【例3】（2023下·山东烟台·六年级统考期末）如图，ABD ∠和BDC ∠的角平分线交于点E ，BE 交CD 于点F ，1290∠+∠=︒．（1）试说明：//AB CD ．（2）若228∠=︒，求3∠的度数．【答案】（1）见分析；（2）62︒【分析】（1）根据角平分线的定义，结合1290∠+∠=︒，可得180ABD BDC ∠+∠︒＝，进而即可得到结论；（2）由228∠=︒，得162∠=︒，进而得62ABF ∠=︒，结合//AB CD ，即可得到答案．解：（1）∵ABD ∠和BDC ∠的角平分线交于点E ，∴21ABD ∠∠＝，22BDC ∠∠＝，又∵1290∠+∠=︒，∴2(12)180ABD BDC ∠+∠∠+∠=︒＝，∴//AB CD ；（2）∵228∠=︒，1290∠+∠=︒，∴162∠=︒，又∵BF 平分ABD ∠，∴162ABF ∠=∠=︒，又∵//AB CD ，∴362ABF ∠=∠=︒．【点拨】本题主要考查角平分线的定义，平行线的判定和性质定理，掌握“同旁内角互补，两直线平行”，“两直线平行，内错角相等”，是解题的关键．【变式1】（2012下·广东茂名·七年级统考期中）两条平行线被第三条直线所截，一对同旁内角的比为4：5，则这两个角中较小的角的度数为（）A ．20︒B ．80︒C ．100︒D ．120︒【答案】B【分析】根据比例设两个角为4x 、5x ，再根据两直线平行，同旁内角互补列式求解即可．解：设两个角分别为4x 、5x ，∵这两个角是两平行线被截所得到的同旁内角，∴45180x x +=︒，解得20x =︒，480x =︒，5100x =︒，所以较小的角的度数等于80︒．故选：B ．【点拨】本题考查了平行线的性质，主要利用了两直线平行，同旁内角互补的性质，熟记性质是解题的关键．【变式2】（2023下·辽宁大连·七年级统考期末）如图，AB ∥CD ，射线AE 交CD 于点F ，若∠1＝116°，则∠2的度数等于．【答案】64°【分析】根据两直线平行，同旁内角互补可求出∠AFD 的度数，然后根据对顶角相等求出∠2的度数．解：∵AB ∥CD ，∴∠1+∠AFD =180°．∵∠1=116°，∴∠AFD =64°．∵∠2和∠AFD 是对顶角，∴∠2=∠AFD =64°．故答案为64°．【点拨】本题考查了平行线的性质，解题的关键是掌握两直线平行，同旁内角互补．【平行线性质探究角的关系】【考点4】平行线判探究角的关系或求角度【例4】（2017下·北京东城·七年级统考期中）已知：直线AB CD ，点M 、N 分别在直线AB 、直线CD 上，点E 为平面内一点，（1）如图1，请写出AME ∠，E ∠，ENC ∠之间的数量关系，并给出证明；（2）如图2，利用（1）的结论解决问题，若30AME ∠=︒，EF 平分MEN ∠，NP 平分ENC ∠，EQ NP ∥，求FEQ ∠的度数；（3）如图3，点G 为CD 上一点，AMN m EMN ∠=∠，GEK m GEM ∠=∠，EH MN 交AB 于点H ，GEK ∠，BMN ∠，GEH ∠之间的数量关系（用含m 的式子表示）是．【答案】（1）MEN AME ENC ∠=∠+∠，证明见分析；（2）15︒；（3）180GEK BMN m GEH ∠+∠-∠=︒．【分析】（1）过点E 作EE AB ' ，根据平行线的性质进行证明即可；（2）利用EF 平分MEN ∠，NP 平分ENC ∠，可得11,22NEF MEN ENP ENC ∠=∠∠=∠，再根据MEN AME ENC ∠=∠+∠，进行等量代换进行计算即可；（3）由已知条件可得11,22NEF MEN ENP ENC ∠=∠∠=∠，1EMN HEM AMN m∠=∠=∠，再根据平行线的性质进行各角的等量转换即可．解：（1）MEN AME ∠=∠+∠，证明如下：如图1所示，过点E 作EE AB ' ，∵AB CD ，∴AB CD EE 'P P ，∴1,2AME ENC ∠=∠∠=∠，∵12MEN ∠=∠+∠，∴MEN AME ENC ∠=∠+∠．（2）∵EF 平分MEN ∠，NP 平分ENC ∠，∴11,22NEF MEN ENP ENC ∠=∠∠=∠．∵EQ NP ∥，30AME ∠=︒，∴12QEN ENP ENC ∠=∠=∠．∵MEN AME ENC ∠=∠+∠，∴30MEN ENC AME ∠-∠=∠=︒，∴111130152222FEQ FEN QEN MEN ENC AME ∠=∠-∠=∠-∠=∠=⨯︒=︒．（3）180GEK BMN m GEH ∠+∠-∠=︒．证明如下：∵AMN m EMN ∠=∠，GEK m GEM ∠=∠，∴1EMN AMN m ∠=∠，1GEM GEK m∠=∠．∵EH MN ，∴1EMN HEM AMN m∠=∠=∠，∵11GEH GEM HEM GEK AMN m m ∠=∠-∠=∠-∠，∴m GEH GEK AMN ∠=∠-∠，∵180AMN BMN ∠=︒-∠，∴()180m GEH GEK BMN ∠=∠-︒-∠，180GEK BMN m GEH ∠+∠-∠=︒．故答案为：180GEK BMN m GEH ∠+∠-∠=︒．【点拨】本题考查了平行线的判定和性质，角的平分线，熟练掌握平行线的判定和性质是解题的关键．【变式1】（2022下·贵州黔南·七年级统考期中）如图，在五边形ABCDE 中，AE BC ∥，则C D E ∠+∠+∠=（）A ．540︒B ．360︒C ．270︒D ．180︒【答案】B 【分析】首先过点D 作DF AE ∥，交AB 于点F ，由AE BC ∥，可证得AE DF BC ∥∥，然后由两直线平行，同旁内角互补可知180E EDF Ð+Ð=°，180CDF C Ð+Ð=°，继而证得结论．解：过点D 作DF AE ∥，交AB 于点F ，AE BC ∥，AE DF BC ∴∥∥，180E EDF ∴∠+∠=︒，180CDF C Ð+Ð=°，360C CDE E \Ð+Ð+Ð=°．故选：B ．【点拨】此题考查了平行线的性质，注意掌握辅助线的作法，注意数形结合思想的应用．【变式2】（2023下·广东江门·七年级统考期末）如图，AB ∥CD ，∠ABF =23∠ABE ，∠CDF =23∠CDE ，则∠E ：∠F 等于【答案】3：2解：如图，过点E、F分别作EG∥AB、FH∥AB，又因AB∥CD，根据平行线的传递性可得AB∥EG∥FH∥CD，∵AB∥FH，∴∠ABF=∠BFH，∵FH∥CD，∴∠CDF=∠DFH，∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF；同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE；∵∠ABF=23∠ABE，∠CDF=23∠CDE，∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=23（∠ABE+∠CDE）=23∠BED，∴∠BED：∠BFD=3：2．故答案为：3：2．【点拨】本题主要考查了平行线的性质，解决这类题目要常作的辅助线（平行线），充分运用平行线的性质探求角之间的关系是解题的关键．【平行线性质性质与判定综合】【考点5】平行线判定与性质求角度【例5】（2023上·广东潮州·八年级校考阶段练习）如图，A B、两处是灯塔，船只在C处，B处在A 处的南偏西45°方向，C处在A处的南偏东15°方向，C处在B处的北偏东80°方向，求船只与两灯塔的视角ACB的度数．【答案】85°【分析】根据方向角的定义，可得∠BAE=45°，∠CAE=15°，∠DBC=80°，然后根据平行线的性质与三角形内角和定理即可求解．解：如图，根据方向角的定义，可得∠BAE=45°，∠CAE=15°，∠DBC=80°．∵∠BAE=45°，∠EAC=15°，∴∠BAC=∠BAE+∠EAC=45°+15°=60°．∵AE ，DB 是正南正北方向，∴BD ∥AE ，∵∠DBA=∠BAE=45°，又∵∠DBC=80°，∴∠ABC=80°-45°=35°，∴∠ACB=180°-∠ABC-∠BAC=180°-60°-35°=85°．题的关键．【变式1】（2023下·甘肃白银·八年级统考期末）如图所示，已知AB EF ∥，那么BAC ACE CEF ∠+∠+∠=（）A ．180°B ．270°C ．360°D ．540°【答案】C 【分析】先根据平行线的性质得出180180BAC ACD DCE CEF ∠+∠=︒∠+∠=︒，，进而可得出结论．解：过点C 作CD EF ∥，∥Q AB EF ，AB CD EF \∥∥，∴180180BAC ACD DCE CEF ∠+∠=︒∠+∠=︒①，②，由①②+得，360BAC ACD DCE CEF ∠+∠+∠+∠=︒，即360BAC ACE CEF Ð+Ð+Ð=°．故选：C ．【点拨】本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．【变式2】（四川省成都市金牛区2020-2021学年七年级下学期期末数学试题）一副直角三角板如图放在直线m 、n 之间，且//m n ，则图中1∠=度．【答案】15【分析】如图，过点A 作AC ∥m ，则有////AC m n ，然后可得,45BAC CAD CAD ADE ∠=∠∠=∠=︒，进而问题可求解．解：如图所示，过点A 作AC ∥m ，∵//m n ，∴////AC m n ，∴1,45BAC CAD ADE ∠=∠∠=∠=︒，∵60BAC CAD ∠+∠=︒，∴115BAD CAD ∠=∠-∠=︒；故答案为15．【点拨】本题主要考查平行线的性质与判定，熟练掌握平行线的性质与判定是解题的关键．【考点6】平行线判定与性质证明【例6】（2023下·七年级课时练习）如图，BD 平分ABC ∠，ED BC ∥，130∠=︒，4120∠=︒．（1）求2∠，3∠的度数；（2）证明：DF AB ．【答案】（1）230∠=︒，360∠=︒；（2）见详解【分析】（1）根据BD 平分ABC ∠，112ABD ABC ∠=∠=∠，即有130ABD ∠=∠=︒，60ABC ∠=︒，再结合ED BC ∥，即可求解；（2）由60ABC ∠=︒，4120∠=︒可得ABC ∠4=180+∠︒，则DF AB ，问题得解．解：（1）∵BD 平分ABC ∠，130∠=︒，∴112ABD ABC ∠=∠=∠，∴130ABD ∠=∠=︒，60ABC ∠=︒，∵ED BC ∥，∴2130∠=∠=︒，360ABC ∠=∠=︒，即：230∠=︒，360∠=︒；（2）∵60ABC ∠=︒，4120∠=︒，∴ABC ∠4=180+∠︒，∴DF AB ．【点拨】本题主要考查了角平分线的定义，平行线的判定与性质等知识，掌握两直线平行同位角相等；两直线平行同位角相等；两直线平行，同旁内角互补是解答本题的关键．【变式1】（2020上·河南洛阳·七年级统考期末）如图，若12∠=∠，DE BC ∥，则下列结论：①FG DC ；②AED ACB ∠=∠；③CD 平分ACB ∠；④190B ∠+∠=︒；⑤BFG BDC ∠=∠．其中，正确结论的个数为（）A ．2个B ．3个C ．4个D ．5个【答案】B 【分析】由平行线的性质得出内错角相等、同位角相等，得出②正确；再由已知条件证出2DCB =∠∠，得出FG DC ，①正确；由平行线的性质得出⑤正确；即可得出结果．解：DE BC ∥，1DCB ∴∠=∠，AED ACB ∠=∠，故②正确；12∠=∠ ，2DCB ∴∠=∠，FG DC ∴∥，故①正确；BFG BDC ∴∠=∠，故⑤正确；而CD 不一定平分ACB ∠，1B ∠+∠不一定等于90︒，故③，④错误；故选：B ．【点拨】本题考查了平行线的判定与性质；熟练掌握平行线的判定与性质，并能进行推理论证是解决问题的关键．【变式2】（2021下·江苏盐城·七年级统考期中）如图a b ，c 与a 相交，d 与b 相交，下列说法：①若12∠=∠，则3=4∠∠；②若14180∠+∠=︒，则c d ∥；③4231∠-∠=∠-∠；④1234360∠+∠+∠+∠=︒正确的有（填序号）【答案】①②③【分析】根据平行线的性质和判定逐一进行判断即可．解：如图，①若∠1=∠2，则b ∥e ，则∠3=∠4，故原说法正确；②若∠1+∠4=180°，则c ∥d ；故原说法正确；③由a ∥b 得到∠1=∠6，∠5+∠4=180°，由∠2+∠3+∠5+180°-∠6=360°得，∠2+∠3+180°-∠4+180°-∠1=360°，则∠4-∠2=∠3-∠1，故原说法正确；④由③得，只有∠1+∠4=∠2+∠3=180°时，∠1+∠2+∠3+∠4=360°．故原说法错误．正确的有①②③，故答案为：①②③．【点拨】本题考查了平行线的判定与性质，熟练掌握平行线的性质与判定是解题的关键．【平行线间的距离】【考点7】平行线间的距离（应用）【例7】（2022下·贵州遵义·七年级校考阶段练习）如图，直线a b ∥，AB 与a ，b 分别交于点A ，B ，且AC AB ⊥，AC 交直线b 于点C ．（1）若160∠= ，求2∠的度数；（2）若6,8AC AB ==，10BC =，求直线a 与b 的距离．【答案】（1）30︒；（2）245【分析】（1）由直线a b ∥，根据平行线的性质得出3160∠=∠=︒，再由AC AB ⊥，根据垂直的定义即可得到结果；（2）过A 作AD BC ⊥于D ，根据1122ABC S AB AC BC AD =⨯⨯=⨯⨯ ，即可求解．解：（1）∵a b∥∴3160∠=∠=︒又∵AC AB⊥∴290330∠=︒-∠=︒（2）如图，过A 作AD BC ⊥于D ，则AD 的长即为直线a 与b 的距离∵6,8AC AB ==，10BC =，ABC 是直角三角形∵1122ABC S AB AC BC AD =⨯⨯=⨯⨯ ∴8624105AB AC AD BC ⨯⨯===∴直线a 与b 的距离245【点拨】本题考查了平行线的性质及三角形的面积，解题的关键是掌握：从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离．【变式1】（2021下·安徽合肥·八年级统考期末）如图，123////l l l ，且相邻两条直线间的距离都是2，A ，B ，C 分别为1l ，2l ，3l 上的动点，连接AB 、AC 、BC ，AC 与2l 交于点D ，90ABC ∠=︒，则BD 的最小值为（）A．2B．3C．4D．5【答案】A【分析】求BD的最小值可以转化为求点B到直线AC的距离，当BD⊥AC时，BD有最小值，根据题意求解即可．解：由题意可知当BD⊥AC时，BD有最小值，此时，AD=CD，∠ABC=90°，∴BD=AD=BD=12AC=2，∴BD的最小值为2．故选：A．【点拨】本题考查平行线的性质，需结合图形，根据平行线的性质推出相关角的关系从而进行求解．【变式2】（2019下·上海金山·七年级统考期中）已知直线a∥b∥c，a与b的距离是5cm，b与c的距离是3cm，则a与c的距离是．【答案】8cm或2cm【分析】直线c的位置不确定，可分情况讨论．（1）直线c在直线b的上方，直线a和直线c之间的距离为5cm+3cm=8cm；（2）直线c在直线a、b的之间，直线a和直线c之间的距离为5cm-3cm=2cm．解：（1）直线c在直线b1：直线a和直线c之间的距离为5cm+3cm=8cm；（2）直线c在直线a、b的之间，如图2：直线a和直线c之间的距离为5cm-3cm=2cm；所以a与c的距离是8cm或2cm，故答案为8cm或2cm．【点拨】此题考查两线间的距离，本题需注意直线c的位置不确定，需分情况讨论．。

课 题第二章 相交线与平行线1、两条直线的位置关系（第1课时）教 学 目 标1．知识与技能：在具体情境中了解相交线、平行线、补角、余角、对顶角的定义，知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等，并能解决一些实际问题。

2．过程与方法：经历操作、观察、猜想、交流、推理等获取信息的过程，进一步发展空间观念、推理能力和有条理表达的能力。

3．情感与态度：激发学生学习数学的兴趣，认识到现实生活中蕴含着大量的数量和图形的有关问题，这些问题可以抽象成数学问题，用数学方法予以解决。

教学重、难点1. 2.教 学 过 程 教 学 内 容可根据学生实际增减内容 第一环节 走进生活 引入课题 活动内容一：两条直线的位置关系1． 巩固练习：教师展示下列图片，学生快速回答：2.1—1 2.1—2 结论：1.一般地，在同一平面内，两条直线的位置关系有两种： 和 . 2.定义分别为： 。

问题1：在2.1—1中，直线m 和n 的关系是 ；a 和b 是 ；a 和n 是 。

问题2：在2,1—2你能提出哪些问题？第二环节 动手实践 探究新知动手实践一m nab请先画一画：两条直线直线和，交于点O,再回答下列问题..问题1：观察2.1—4：∠1和∠2的位置有什么关系？大小有何关系？为什么？小组合作交流，尝试用自己的语言描述对顶角的定义。

问题2:剪子可以看成图2.1—4，那么剪子在剪东西的过程中，∠1和∠2还保持相等吗？∠3和∠4呢？你有何结论？ 问题3：下列各图中，∠1和∠2是对顶角的是（ ）问题4：如图2.1—6所示，有一个破损的扇形零件，利用图中的量角器可以量出这个扇形零件的圆心角的度数吗？你能说出所量角是多少度吗？为什么？动手实践二补角定义：一般地，如果两个角的和是1800，那么称这两个角互为补角（ ） 余角定义：如果两个角的和是900，那么称这两个角互为余角（ ） 动手实践三打台球时，选择适当的方向，用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2，将图2.1—7抽象成图2.1—8，与交于点O ，∠∠900，∠1=∠2小组合作交流，解决下列问题：在图2.1—8中 问题1：哪些角互为补角？哪些角互为余角？1 2 1 2 1 212A B CD 注意：互余与互补是指两个角之间的数量关系，与它们的位置无关。

1北师大版七年级下数学第二章《相交线与平行线》教案 《2.1两条直线的位置关系》教案一：教学目标1、掌握两条直线平行与垂直的条件；2、会运用条件判断两直线是否平行或垂直；3、能运用条件确定两平行或垂直直线的方程系数.二：教学重点、难点两条直线平行与垂直的条件， 两条直线平行与垂直的条件的应用.三：教学设计（一）情景引入A ：两条直线位置关系当中平行为简单；现在我们来研究平面内两条直线平行的关系. ①先入为主的思想；在研究直线问题时首先考虑特殊情况：α=90°时，画图.这个情况很简单：当α=90°时只要x 1≠x 2，则两条直线平行.②一般情况：α≠90°时，则k 存在，∴y 1=kx +b 1 y 2=kx +b 2已知直线l 1，l 2的斜截式方程为：l 1：y =k 1x +b 1 l 2：y =k 2x +b 2，若l 1//l 2，则有α1=α2且b 1≠b 2，∴tan α=tan α [α1∈[0，180°），α2∈[0，180°）]∴k 1=k 2反之，是否成立？若k 1=k 2且b 1≠b 2则有tan α=tan α，∵0≤α1，α2＜π，∴α1=α2且b 1≠b 2，∴l 1//l 2结论一：①特殊情况：若两条直线l 1，l 2斜率都不存在也不重合，则两直线l 1，l 2平行； ②有斜率的两条直线l 1//l 2 <=> k 1=k 2且b 1≠b 2∴判断不重合的两条直线平行的程序：两条直线方程——两条直线斜率都不存在且不重合→平行.两条直线方程——化为斜截式方程→求两条直线斜率.若k 1=k 2且b 1≠b 2→平行若k 1≠k 2→相交或者若A 1B 2≠B 1A 2且B 1C 2≠B 2C 1或A 1B 2=A 2B 1且A 1C 2≠A 2C 1 则两条直线平行.例1：已知两条直线l 1:4x +2y -7=0，l 2:2x -y -5=0求证l 1∥l 212122∵l 1的斜率为，l 2的斜率为 ∴k 1=k 2∴l 1∥l 2 例2：求过点A （1，-4）且与直线2x +3y +5=0平行的直线的方程？解：已知直线的斜率为-，因为所求直线与已知直线平行，因此它的斜率也是-. 根据点斜式，得到所求直线的方程是：y +4=-（x -1）即2x +3y +10=0 例3：如果直线ax +2y +2=0与3x -y -2=0平行，那么系数a =（）A .3B .-6C .-D . 例4：求与直线3x +4y +1=0平行，且在两坐标轴上截距之和为的直线l 的方程？ 法一：设直线方程为3x +4y +m =0，交x 轴于点（-，0）交y 轴于点（0，-），由题意可得（-）+（-）=即m =-4， ∴所求直线l 的方程为3x +4y -4=0， 法二：设直线方程为+=1， ∴a +b =，-=-，可得a =，b =1， ∴所求直线l 的方程为3x +4y -4=0B ：平时我们已经理解了；接下来我们来研究两直线相互垂直的关系.①同样的先考虑特殊情况：若已知一条直线的倾斜角为90°，x =x 1，则求其另一条与它垂直的直线方程.②一般情况：若已知两条直线l 1:y =k 1x +b 1，l 2:y =k 2 x +b 2，相互垂直则k 1与k 2有何关系？ α+（π-β）= ∴α-β=- ∴β=α+ 21213232322332373m 4m 3m 4m 37a x b y 37a b 43342π2π2π3tan β=tan （α+）=-cot α ∴tan α·tan β=tan α·（-cot α）=-1∴最后我们得证:若两条直线垂直则k 1k 2=-1.③α=90°时=>β=0°（特殊情况）k 1=0，k 2不存在.或者k 1不存在，k 2=0.例4:已知直线l 1：ax -y +2a =0与l 2：（2a -1）x +ay +a =0互相垂直，求a 的值一、①当α=90°即a =0时，l 2：x =0 ∴l 1：y =0 ∴l 1⊥l 2②当α≠90°则k 1·k 2=a ·（-）=-1 ∴a =1 二、A 1A 2+B 1B 2=0 =>a （2a -1）-a =0 2a ²-2a =0 =>a =1或a =0例5：求与3x +4y +1=0平行，且在两坐标轴上截距之和为7/3的直线l 的方程.（一）设直线方程为3x +4y +m =0，交x 轴于点（-，0）交y 轴于点（0，-） ∴（-）+（-）= ∴m =-4∴所求直线l 的方程为3x +4y -4=0（二）设直线方程为+=1 =>a +b =；-=-=>a =，b =1 ∴l ：3x +4y -4=0例6：已知三角形两条高线为x +y =0和2x -3y +1=0且一个顶点C （1，2），求三角形AC ，BC 边所在直线的方程.∵AC ，BC 与两条高线垂直∴AC ，BC 的斜率为1和- ∴边AC ，BC 所在直线的方程为y -2=1（x -1），y -2=-（x -1） 即x -y +1=0，3x +2y -7=0《2.2探索直线平行的条件》教案一、导学目标1.使学生能够熟练识别同位角；2πaa )12(-3m 4m 3m 4m 37a xb y 37a b 433423232.使学生会用同位角相等判定二条直线平行.二、重点难点1.重点（1）识别同位角.（2）用同位角相等判定二条直线平行.2.难点用同位角相等判定二条直线平行.三、导学过程一、自主学习：操作---观察---探索如图：3根木条（或硬纸条）相交成∠1、∠2，固定木条b、c，转动木条a.问：1.在木条a的转动过程中，木条a、b的位置关系发生了什么变化？∠2与∠1的大小关系发生了什么变化？2.改变图中∠1的大小，按照上面的方式再试一试，当∠2与∠1的大小满足什么关系时，木条a与木条b平行？二、合作探究：活动一：利用平移三角尺的方法画平行线，探索直线平行的条件.当∠1与∠2相等，直线a、b就；当∠1与∠2不相等时，直线a、b平行吗？活动二：通过观察、比较，认识“同位角”，探索直线平行的条件.直线a、b被第三条直线c所截而成的8个角中，像∠1与∠2这样的一对角称为.请问图中还有没有其他的同位角？4归纳：相等，两直线.活动三：例题讲解.例：如图，∠1=∠C，∠2=∠C，请找出图中互相平行的直线，并说明理由.三、拓展提高：1.∠1与∠C、∠2与∠B、∠ 3与∠ C分别是哪两条直线被哪一条直线截成的同位角？2.如图，直线a、b被直线c所截，∠1=35°，∠2=145°，问：直线a与b平行吗？四、达标检测：1.如图，∠1与∠B是直线和被直线所截构成的同位角；∠2与∠A直线和被直线所截构成的同位角.2.如图，∠1、∠2、∠3中，和是同位角.3.如图，如果∠B=∠1，根据，那么可得DE//BC；如果∠B=∠2，根据同位角相等，两直线平行，那么可得// .4.如图，已知直线AB、CD被直线EF所截，如果∠BMN＝∠DNF，∠1＝∠2，那么MQ∥NP，为什么？AB CD EF13256《2.3平行线的性质》教案教学目标：理解平行线的性质的推导，掌握平行线的性质.教学重点：平行线的性质以及应用.教学难点：平行线的性质公理与判定公理的区别.教学过程：一、梳理旧知，引出新课平行线的判定：判定方法1、同位角相等，两直线平行.判定方法2、内错角相等，两直线平行.判定方法3、同旁内角互补，两直线平行.问题：反过来也成立吗？过去我们学过：如果两个数的和为0，这两个数互为相反数.反过来，如果两个数互为相反数，那么这两个数的和为0.这两个句子都是正确的.现在换一个例子：如果两个角是对顶角，那么这两个角相等.它是对的.反过来，如果两个角相等，这两个角是对顶角.对吗？再看下面的例子：“如果一个整数个位上的数字是5，那么它一定能够被5整除.”对吗？这句话反过来怎么说？对不对？【结论】如果一个句子是正确的，反过来说（因果对调），就未必正确.二、动手操作，归纳性质上一节课，我们学过：同位角相等，两直线平行.反过来怎么说？它还是对的吗？（板书）性质1、两直线平行，同位角相等.P Q M N21F ED C B A7如果把平行线性质1：“两直线平行，同位角相等”看作是基本事实（公理），我们可以利用这个公理证明平行线性质2：“两直线平行，内错角相等”.【例】如图，已知：直线a 、b 被直线c 所截，且a ∥b ，求证：∠1=∠2.证明：∵a ∥b ，∴∠1=∠3（__________________）.∵∠3=∠2（对顶角相等），∴∠1=∠2（等量代换）.（板书）性质2、两直线平行，内错角相等【变式】下面我们来证明平行线的性质3：两直线平行，同旁内角互补.请模仿范例写出证明.如图，已知：直线a 、b 被直线c 所截，且a ∥b ，求证：∠1+∠2=180º.证明：（略）（板书）性质：两直线平行，同旁内角互补三、巩固新知，深化理解例1、如图，平行线AB ，CD 被直线AE 所截.（1）从∠1=110º．可以知道∠2是多少度吗？为什么？（2）从∠1=110º可以知道∠3是多少度吗？为什么？（3）从∠1=110º可以知道∠4是多少度吗？为什么？例2、如图，已知AB ∥CD ，AE ∥CF ，∠A = 39°，∠C 是多少度？为什么？ab1 2 3 c ab 1 23c ED CB A12348方法一解：∵AB ∥CD ， ∴ ∠C=∠1．∵ AE ∥CF ，∴ ∠A=∠1．∴ ∠C=∠A ．∵∠A = 39º，∴∠C = 39º．方法二解：∵AB ∥CD ，∴ ∠C=∠2.∵ AE ∥CF ，∴ ∠A=∠2.∴ ∠C=∠A .∵∠A = 39º，∴∠C = 39º．练习1：如图，已知直线a 、b 被直线c 所截，在括号内为下面各小题的推理填上适当的根据： （1）∵a ∥b ，∴∠1=∠3（___________________）；（2）∵∠1=∠3，∴a ∥b （_________________）.（3）∵a ∥b ，∴∠1=∠2（__________________）；（4）∴a ∥b ，∴∠1+∠4=180º（_____________________________________）（5）∵∠1=∠2，∴a ∥b （___________________）；（6）∵∠1+∠4=180º，∴a ∥b （_______________）.练习2：教材第51页 随堂练习四、盘点收获，布置作业1、（1）平行线的性质是什么？（2）你能用自己的语言叙述研究平行线性质的过程吗？（3）性质2和性质3是通过简单推理得到的，在推理论证中需要注意哪些问题？2、作业G FED C B Aa b12 3 c 49《2.4用尺规作角》教案教学目的：1、经历尺规作角的过程，进一步培养学生的动手操作能力，增强学生的数学应用和研究意识.2、能按作图语言来完成作图动作，能用尺规作一个角等于已知角.教学重点：能按作图语言来完成作图动作，能用尺规作一个角等于已知角.教学难点：作图步骤和作图语言的叙述，及作角的综合应用.教学过程：一、问题的提出如图，要在长方形木板上截一个平行四边形，使它的一组对边在长方形木板的边缘上，另一组对边中的一条边为AB .（1）请过点C 画出与AB 平行的另一条边.（2）如果你只有一个圆规和一把没有刻度的直尺，你能解决这个问题吗？二 、新课内容一：（请按作图步骤和要求操作，别忘了留下作图痕迹）（一） 用尺规作一个角等于已知角.（1）已知：∠AOB求作：∠A′O′B′，使∠A′O′B′=∠AOB（2）已知：∠10求作：∠AOB ，使∠AOB=∠（二）用尺规作一个角等于已知角的倍数：（3）已知：∠1求作：∠MON ，使∠MON=2∠1∠COD ，使∠COD=3∠1（三）用尺规作一个角等于已知角的和：（4） 已知：∠1、∠2、∠3求作：①∠AOB ，使∠AOB=∠1+∠2②∠POQ ，使∠POQ=∠1+∠2+∠3③∠MON ，使∠MON=2∠1+∠2（四）用尺规作一个角等于已知角的差：已知：∠、∠、∠求作：①∠AOB ，使∠AOB=∠－∠②∠POQ ，使∠POQ=∠－∠－∠③求作一个角，使它等于2∠－∠（五） 综合练习：（通过以下练习，意味着你掌握了作角的真本领，多动一下脑筋，你一定会完成得很出色的）1、已知：线段AB 、 ∠、∠αα1αβγαβγαβαβγβγαβ13211求作：分别过点A 、点B 作∠CAB=∠、∠CBA=∠2、如图，点P 为∠ABC 的边AB 上的一点，过点P 作直线EF//BC .3、已知：直线L 和L 外一点P ，求作：一条直线，使它经过点P ，并与已知直线L 平行.4、已知：△ABC ，求作：直线MN ，使MN 经过点A ，且MN//BC .5、如图，以点B 为顶点，射线BA 为一边，在∠ABC 外再作一个角，使其等于∠ABC .（六）小结（七）作业αβLA αβ。

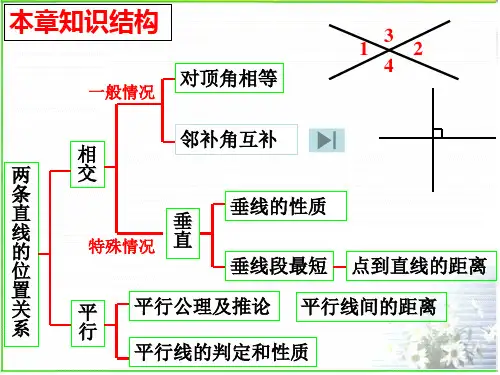
北师大版七年级数学下
第二章平行线和相交线
内容二：
议一议：
（1）用剪刀剪东西的时候，哪对角同时变大或变小？
（2）如果将剪刀简单的表示为右图，那么∠1和∠2有什么位置关系？它们的大小有什么关系？能试着说明理由吗？
1
2
2
由此引出对顶角的概念和“对顶角相等”的结论。

学生观察课件
的演示过程，获得直观的体会，在观察中总结出对顶角的特征，并
用自己的语言表达出来。

思考：如图所示，有一个破损的扇形零件，利用图中的量角器可以量出这个扇形零件的圆心角的度数，你能说出所量角的度数
是多少度吗？你的根据是什么？
小结：（1）余角、补角的概念。

（2）同角或等角的余角相等，同角或等角的补角相等。

（3）对顶角的概念和“对顶角相等”。

作业：课本P52 习题2.1：1、2、3。

板书
设计
2.1余角与补角
一、导入2、对顶角及其性质四、小结
二、探究新知三、巩固练习五、作业
1、余角、补角的概念1、
2、
课后
反思
北师大版七年级数学下
第二章平行线和相交线
北师大版七年级数学下
第二章平行线和相交线。

《相交线与平行线》全章复习与巩固（基础）知识讲解【学习目标】1．熟练掌握对顶角，余角，补角，邻补角及垂线的概念及性质，了解点到直线的距离与两平行线间的距离的概念；2. 区别平行线的判定与性质，并能灵活运用；3. 了解尺规作图的概念，熟练掌握用尺规作角或线段的方法.【知识网络】【要点梳理】要点一、两条直线的位置关系1.同一平面内两条直线的位置关系：相交与平行要点诠释：（1）只有一个公共点的两条直线叫做相交直线，这个公共点叫做交点.（2）在同一平面内不相交的两条直线叫做平行线.平行用符号“∥”表示.2.对顶角、补角、余角（1）定义：①由两条直线相交构成的四个角中，有公共顶点且两边互为反向延长线的两个角叫做对顶角.②如果两个角的和是180°，那么这两个角互为补角，简称互补，其中一个角叫做另一个角的补角．类似地，如果两个角的和是90°，那么这两个角互为余角．简称互余，其中一个角叫做另一个角的余角．（2）性质：同角或等角的余角相等．同角或等角的补角相等．对顶角相等．3.垂线（1）垂线的定义：两条直线相交所成的四个角中，有一个角是直角时，就称这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫垂足．垂直用符号“⊥”表示，如下图．（2）垂线的性质：①在同一平面内，过一点有且只有一条直线与已知直线垂直．②垂线段最短．（3）点到直线的距离：从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．要点二、平行线的判定与性质1．平行线的判定判定方法1：同位角相等，两直线平行．判定方法2：内错角相等，两直线平行．判定方法3：同旁内角互补，两直线平行．要点诠释：根据平行线的定义和平行公理的推论，平行线的判定方法还有：（1）平行线的定义：在同一平面内，如果两条直线没有交点（不相交），那么两直线平行. （2）如果两条直线都平行于第三条直线，那么这两条直线平行（平行线的传递性）. （3）在同一平面内，垂直于同一直线的两条直线平行.（4）平行公理：经过直线外一点，有且只有一条直线与这条直线平行.2．平行线的性质性质1：两直线平行，同位角相等；性质2：两直线平行，内错角相等；性质3：两直线平行，同旁内角互补.要点诠释：根据平行线的定义和平行公理的推论，平行线的性质还有：（1）若两条直线平行，则这两条直线在同一平面内，且没有公共点．（2）如果一条直线与两条平行线中的一条直线垂直，那么它必与另一条直线垂直．3．两条平行线间的距离如图，直线AB∥CD，EF⊥AB于E，EF⊥CD于F，则称线段EF的长度为两平行线AB与CD间的距离.要点诠释：（1）两条平行线之间的距离处处相等.（2）初中阶级学习了三种距离,分别是两点间的距离、点到直线距离、平行线间的距离.这三种距离的共同点在于都是线段的长度,它们的区别是两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是一条直线上的一点到与之平行的另一直线的距离.（3）如何理解“垂线段”与“距离”的关系：垂线段是一个图形，距离是线段的长度，是一个量，它们之间不能等同.要点三、用尺规作线段和角1.用尺规作线段（1）用尺规作一条线段等于已知线段.（2）用尺规作一条线段等于已知线段的倍数.（3）用尺规作一条线段等于已知线段的和.（4）用尺规作一条线段等于已知线段的差.2.用尺规作角（1）用尺规作一个角等于已知角.（2）用尺规作一个角等于已知角的倍数.（3）用尺规作一个角等于已知角的和.（4）用尺规作一个角等于已知角的差.【典型例题】类型一、两条直线的位置关系1.如图，直线AB、CD、EF相交于点O，那么互为对顶角（平角除外）的角共有对，它们分别是，共有对邻补角.【思路点拨】根据邻补角定义和对顶角定义，每一个顶点处有四个角，可以组成四对邻补角和两对对顶角，而本题图形中，三个顶点重叠在一起，所以再乘以3即可．【答案】6,∠AOC与∠BOD，∠AOF与∠BOE，∠COF与∠DOE, ∠BOC与∠AOD，∠BOF与∠AOE, ∠DOF与∠COE ,12．【解析】找对顶角或邻补角，先从某一个角开始，顺时针或逆时针旋转，这样做，既不漏也不重.【总结升华】两条直线相交得到的四个角中，共有2对对顶角，4对邻补角.举一反三：【变式】如图所示，已知∠AOD=∠BOC，请在图中找出∠BOC的补角,邻补角及对顶角.【答案】解：因为∠BOC＋∠AOC=180º（平角定义）,所以∠AOC是∠BOC的补角.因为∠AOD＋∠BOD=180º（平角定义）,∠AOD=∠BOC（已知）,所以∠BOC＋∠BOD=180º.所以∠BOD是∠BOC的补角．所以∠BOC的补角有两个：∠BOD和∠AOC.而∠BOC的邻补角只有一个∠AOC，且∠BOC没有对顶角.2.已知：如图，直线a、b、c两两相交，且a⊥b，∠1＝2∠3，，求∠4的度数.【答案与解析】解：∵a⊥b,∴∠2＝∠1＝90°.又∵∠1＝2∠3，∴90°＝2∠3，∴∠3＝45°,又∠3与∠4互为邻补角，所以∠3+∠4＝180°即45°+∠4＝180°.所以∠4＝135°.【总结升华】涉及到角的运算时，充分利用已知条件和隐含条件（平角、余角、补角、对顶角等）是解题的关键．类型二、平行线的性质与判定3.如图，EF∥AD，∠1=∠2，∠BAC=70°，将求∠AGD的过程填写完整：因为EF∥AD，所以∠2= （）又因为∠1=∠2，所以∠1=∠3所以AB∥（）所以∠BA C＋ =180°（）因为∠BAC=70°，所以∠AGD= .【答案】∠3，两直线平行，同位角相等；DG，内错角相等，两直线平行；∠AGD，两直线平行，同旁内角互补；110°.【解析】首先由已知EF∥AD根据两直线平行同位角相等可得∠2=∠3，再由∠1=∠2，利用等量代换可得∠1=∠3，根据内错角相等，两直线平行可得AB∥DG，再根据两直线平行同旁内角互补可得∠BAC+∠AGD=180°，进而得到答案．【总结升华】本题主要考查的是平行线的判定与性质，平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．此外注意证明题规范的书写格式.举一反三：【变式】如图，已知∠ADE＝∠B，∠1＝∠2，那么CD∥FG吗？并说明理由.【答案】解：平行，理由如下：因为∠ADE=∠B，所以DE∥BC（同位角相等，两直线平行），所以∠1=∠BCD（两直线平行，内错角相等）.又因为∠1=∠2（已知），所以∠BCD=∠2.所以CD∥FG（同位角相等，两直线平行）.4.（2015春•杭州期末）如图，已知BC∥GE，AF∥DE，∠1=50°．（1）求∠AFG的度数；（2）若AQ平分∠FAC，交BC于点Q，且∠Q=15°，求∠ACB的度数．【答案与解析】解：（1）∵BC∥EG，∴∠E=∠1=50°．∵AF∥DE，∴∠AFG=∠E=50°；（2）作AM∥BC，∵BC∥EG，∴AM∥EG，∴∠AFM=∠AFG=50°．∵AM∥BC，∴∠QAM=∠Q=15°，∴∠FA Q=∠AFM+∠FAQ=65°．∵AQ平分∠FAC，∴∠QAC=∠FA Q=65°，∴∠M AC=∠QAC+∠QAM=80°．∵AM∥BC，∴∠ACB=∠MAC=80°．【总结升华】本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．类型三、用尺规作线段和角5. 在如图中，补充作图：（1）在AD的右侧作∠DCP=∠DAB（尺规作图，不写作法，保留作图痕迹）；（2）CP与AB会平行吗？为什么？【思路点拨】（1）根据作一个角等于已知角的方法即可作出；（2）根据平行线的判定方法即可判断．【答案与解析】解：（1）作图如下：（2）会平行．用同位角相等，两直线平行．【总结升华】本题考查了基本作图：作一个角等于已知角，以及平行线的判定定理，正确掌握基本作图是关键．举一反三：【变式】（2014秋•娄底期中）尺规作图的画图工具是（）A．刻度尺、量角器 B．三角板、量角器C．直尺、量角器 D．没有刻度的直尺和圆规【答案】D提示：尺规作图的画图工具是没有刻度的直尺和圆规．类型四、实际应用6.如图，107国道a上有一个出口M，想在附近公路b旁建一个加油站，欲使通道最短，应沿怎样的线路施工？【答案与解析】解：如图，过点M作MN⊥b，垂足为N，欲使通道最短，应沿线路MN施工.【总结升华】灵活运用垂线段最短的性质是解答此类问题的关键.《相交线与平行线》全章复习与巩固（基础）巩固练习【巩固练习】一、选择题1．下列图中,∠1和∠2是对顶角的有()个.A．1个B．2个C．3个D．4个2．如图所示是同位角关系的是()．A．∠3和∠4 B．∠1和∠4 C．∠2和∠4 D．不存在3．下列说法正确的是()．A．相等的角是对顶角.B．两条直线被第三条直线所截，内错角相等.C．如果两条直线都和第三条直线平行，那么这两条直线也互相平行.D．若两个角的和为180°，则这两个角互为余角.4．（2015•宜昌）如图，AB∥CD，FE⊥DB，垂足为E，∠1=50°，则∠2的度数是（）A．60°B．50° C．40° D．30°5．用尺规作图，已知三边作三角形，用到的基本作图是（）．A．作一个角等于已知角B．作已知直线的垂线C．作一条线段等于已知线段D．作角的平分线6．一个人从A点出发向北偏东60°方向走到B点，再从B点出发向南偏西15°方向走到C点，那么∠ABC等于()．A．75°B．105°C．45°D．135°7．下列说法中，正确的是()．A．过点P画线段AB的垂线.B．P是直线AB外一点，Q是直线AB上一点，连接PQ，使PQ⊥AB.C．过一点有且只有一条直线垂直于已知直线.D．过一点有且只有一条直线平行于已知直线.8．如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )．A. 50°B. 60°C.70°D.80°二、填空题9. 如图所示，AB∥CD，EF分别交AB、CD于G、H两点，若∠1＝50°，则∠EGB＝________．10．如图所示，已知BC∥DE，则∠ACB＋∠AOE＝．11．每天小明上学时，需要先由家向东走150米到公共汽车站点，然后再乘车向西900米到学校，每天小明由家到学校移动的方向是________，移动的距离是________．12. (广东湛江)如图所示，请写出能判断CE∥AB的一个条件，这个条件是：①：________ ②：________ ③：________13．如图，已知AB∥CD，CE，AE分别平分∠ACD，∠CAB，则∠1+∠2=________.14．如图所示，直线AB与直线CD相交于点O，EO⊥AB，∠EOD＝25°，则∠BOD= ，∠AOC＝，∠BOC＝．15. 如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°．甲、乙两地间同时开工，若干天后，公路准确接通，则乙地所修公路的走向是南偏西．Array 16．（2015秋•丰台区期末）阅读下面材料：在数学课上，老师提出如下问题：小聪、小明、小敏三位同学在黑板上分别画出了设计方案：根据以上信息，你认为同学的方案最节省材料，理由是．三、解答题17．如图所示，直线AB、CD、EF相交于点O，若∠1+∠2＝90°，∠3＝40°，求∠1的度数，并说明理由．18．（2015春•监利县期末）如图，已知∠ABC=180°﹣∠A，BD⊥CD于D，EF⊥CD于F．（1）求证：AD∥BC；（2）若∠1=36°，求∠2的度数．19. 如图所示，已知∠1＝50°，∠2＝130°，∠4＝50°，∠6＝130°，试说明a∥b，b∥c，d∥e，a∥c．20．如图所示，点P是∠ABC内一点．(1)画图：①过点P画BC的垂线，垂足为D；②过点P画BC的平行线交AB于点E，过点P画AB的平行线交BC于点F．(2)∠EPF等于∠B吗? 为什么?【答案与解析】一、选择题1. 【答案】A；【解析】只有第三个图中的∠1与∠2是对顶角.2. 【答案】B；【解析】同位角的特征：在截线同旁，在两条被截直线同一方向上．3. 【答案】C；【解析】一个角的平分线分得两个角相等，但不是对顶角，A错误；内错角相等的前提必须是两条直线平行，B错误；若两个角的和为180°，这两个角互为补角，D错误；C是平行公理的推论，正确．4. 【答案】C；【解析】∵FE⊥DB，∴∠DEF=90°．∵∠1=50°，∴∠D=90°﹣50°=40°．∵AB∥CD，∴∠2=∠D=40°．故选C．5. 【答案】C；【解析】根据三边做三角形用到的基本作图是：作一条线段等于已知线段．故选C．6. 【答案】C；【解析】根据直线平行，内错角相等，从A点北偏东60°方向等于从B点南偏西60°，再从B点向南偏西15°方向到C点，∠ABC应等于这两个角的差，故C正确．7.【答案】C；【解析】应是过一点画线段所在直线的垂线，不能是画线段的垂线，故A错误；P是直线AB外一点，Q是直线AB上一点，如果P点不在过Q点与AB垂直的直线上，或Q 点不在过P点与AB垂直的直线上，连接PQ，不可能有PQ⊥AB，故B错误；过一点画直线的平行线，这点不能在直线上，否则是同一条直线，故D错误；只有C是垂线的性质，故C正确．8.【答案】A；【解析】平行线的判定与性质综合应用．二、填空题9.【答案】50°；【解析】因为AB∥CD，所以∠1＝∠AGF，因为∠AGF与∠EGB是对顶角，所以∠EGB ＝∠AGF，故∠EGB＝50°．10.【答案】180°；【解析】由BC∥DE可知∠ACB＝∠EOC，又因为∠AOE+∠EOC＝180°，故可得解．11.【答案】向西，750米；【解析】移动的方向是起点到终点的方向，移动的距离是起点到终点的线段的长度. 12．【答案】∠DCE＝∠A，∠ECB＝∠B，∠A+∠ACE＝180°；【解析】根据平行线的判定，CE∥AB成立的条件可以是∠DCE＝∠A或∠ECB＝∠B 或∠A+∠ACE＝180°．13.【答案】90°；【解析】∠BAC+∠ACD＝180°，11BAC+ ACD22∠∠＝90°，即∠1+∠2＝90°.14.【答案】115°，115°，65°；【解析】邻补角或对顶角的性质进行求解.15.【答案】48°；【解析】内错角相等，两直线平行.16.【答案】小聪；两点之间线段最短；点到直线垂线段最短；【解析】小明与小聪的方案比较：在小明的方案中∵AD+BD＞AB，∴小聪的方案比小明的节省材料；小聪与小敏的方案比较：小聪方案中AC＜小敏的方案中AC∴小聪同学的方案最节省材料，理由：两点之间线段最短；点到直线垂线段最短．三、解答题17.【解析】解：因为∠2＝∠3(对顶角相等)，∠3＝40°(已知)，所以∠2＝40°(等量代换)．又因为∠1+∠2＝90°(已知)，所以∠1＝90°-∠2＝50°．18.【解析】（1）证明：∵∠ABC=180°﹣∠A，∴∠ABC+∠A=180°，∴AD∥BC；（2）解：∵AD∥BC，∠1=36°，∴∠3=∠1=36°，∵BD⊥CD，EF⊥CD，∴BD∥EF，∴∠2=∠3=36°．19.【解析】解：因为∠1＝50°，∠2＝130°(已知)，所以∠1+∠2＝180°．所以a∥b(同旁内角互补，两直线平行)．所以∠3＝∠1＝50°(两直线平行，同位角相等)．又因为∠4＝50°(已知)，所以∠3＝∠4(等量代换)．所以d∥e(同位角相等，两直线平行)．因为∠5+∠6＝180°(平角定义)，∠6＝130°(已知)，所以∠5＝50°(等式的性质)．所以∠4＝∠5(等量代换)．所以b∥c(内错角相等，两直线平行)．因为a∥b，b∥c(已知)，所以a∥c(平行于同一直线的两直线平行)．20.【解析】解：如图所示，(1)①直线PD即为所求；②直线PE、PF即为所求．(2)∠EPF＝∠B，理由：因为PE∥BC(已知)，所以∠AEP＝∠B(两直线平行，同位角相等)．又因为PF∥AB(已知)，所以∠EPF＝∠AEP(两直线平行，内错角相等)，∠EPF ＝∠B(等量代换)．。